Guidelines for the Investigation of Mediating Variables in Business Research

Abstract

Business theories often specify the mediating mechanisms by which a predictor variable affects an outcome variable. In the last 30 years, investigations of mediating processes have become more widespread with corresponding developments in statistical methods to conduct these tests. The purpose of this article is to provide guidelines for mediation studies by focusing on decisions made prior to the research study that affect the clarity of conclusions from a mediation study, the statistical models for mediation analysis, and methods to improve interpretation of mediation results after the research study. Throughout this article, the importance of a program of experimental and observational research for investigating mediating mechanisms is emphasized.

This piece is the sixth in the Method Corner series featured by this Journal. This series focuses on some of the methodological issues encountered by business psychologists. Past pieces described aggregation of multidimensional constructs (Johnson et al. 2011), methods to identify the importance of regression models (Tonidandel and LeBreton 2011), polynomial regression (Shanock et al. 2010), and method bias (Conway and Lance 2010). The detection of mediators is also a methodological issue important to business psychology. Many theories in business research postulate a mediator (M) that transmits the effect of a predictor variable (X) to an outcome variable (Y) in a causal sequence such that X causes M and M causes Y. In more general terms, a mediating variable explains the process by which one variable causes another. Theories across many disciplines focus on mediating processes and many research questions lend themselves to these models. In intervention research, theory and prior empirical research determine which mediating variables are included as part of study design. If an intervention substantially changes a mediating variable that is causally related to an outcome, then a change in the mediator will produce a change in the outcome. For example, if organizational skills create more efficiency among employees, an employee program teaching organizational skills should increase organizational skills, resulting in greater employee efficiency.

Mediation theory is also applicable to studies that do not include an intervention. An observational variable can serve as a predictor or antecedent variable in a mediation model. For example, it has been suggested that the effects of psychological climate perceptions on performance are mediated by employee work attitudes (Parker et al. 2003), where psychological climate does not represent an intervention but is an observed variable measured for each employee. Psychological climate is an observed variable and is not randomized, thus limiting conclusions regarding the causal nature of the mediating process. The lack of randomization makes it difficult to rule out alternative explanations of the relationship. Examples of alternative explanations include changes in employee work attitudes causing changes in psychological climate or that there is another variable causing changes in both psychological climate and employee work attitudes.

Since the classic articles on mediation by Alwin and Hauser (1975), Judd and Kenny (1981), James and Brett (1984), and Baron and Kenny (1986), thousands of articles have applied mediation analysis in many fields, including psychology (e.g., Fritz and MacKinnon 2007; Mackinnon et al. 2002), medicine (Begg and Leung 2000), business (Chiaburu and Byrne 2009; Hung et al. 2009), and many other fields (see MacKinnon 2008). The popularity of mediation analysis is growing because the method focuses on what is often the central scientific hypothesis: the process by which one variable affects another.

Mediators and Moderators and Confounders and Covariates

Before delving into the details of mediation analysis, we begin with definitions of several key terms that come into play when considering how three variables can be related. These potential relationships are important to understanding when mediation analysis is the appropriate choice for answering specific research questions. When considering the relationship of an independent variable (X) and a dependent variable (Y), an additional third variable (Z) may fill one of several roles. Each role for the third variable describes both a different theoretical model of the relationship between X, Y, and Z, as well as a different approach to the statistical analysis.

A third variable that is both unrelated to the predictor X and has little to no effect on the relationship between X and Y is called a covariate; a covariate is not often of primary theoretical interest but is used to account for additional variation in the outcome Y. A third variable, Z, can be related to both X and Y in such a way that the inclusion of Z changes the relationship between X and Y. Such a variable is called a confounder, because it confounds or conceals the simple relation between X and Y (see Greenland and Morgenstern 2001 for information on confounders). A variable that is a moderator affects the direction and strength of the relationship between two variables such that the relationship between X and Y is different for varying levels of Z. A moderator is typically expressed as an interaction between the independent variable and the moderator, such that the effect of the independent variable on the dependent variable is conditional on the level of the moderator. A moderator may be a factor in an experimental manipulation with random assignment to varying levels (e.g., time between treatments) or a moderator may be a non-manipulated variable (e.g., age or gender). The understanding of a moderator effect is often a critical component to the generalizability of research findings to other populations, locations, and domains.

The focus of this article is on the third variable as a mediator variable. A simple mediation model is shown in Fig. 1. A mediation relationship is one in which the independent variable causes the mediator which then causes the dependent variable (Mackinnon 2008). Although variations of the definition of mediation exist in the literature (e.g., Holmbeck 1997 identifies terminological inconsistencies), we will assume a mediator to be a variable that transmits the effect of an independent variable to a dependent variable. Although the terms “mediator” and “mediated effect” will be used throughout this manuscript, other terms are used to describe these variables and effects in different areas of research. For example, the “mediated effect” is often referred to as the “indirect effect” because it represents the effect of the independent variable effect on the dependent variable effect via the mediator variable (i.e., indirectly rather than directly). The “mediator” is sometimes called the “intervening variable” because it is intermediate between the independent and the dependent variables.

Fig. 1.

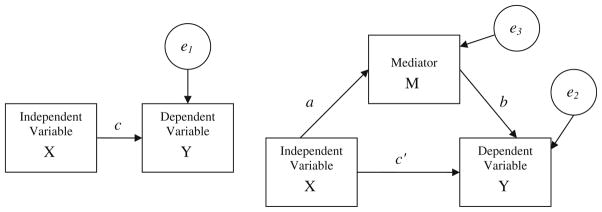
Illustration of the mediation model using path diagrams

Though the primary focus of this article is mediation analysis, we feel obligated to spend some time comparing mediation and moderation effects. Both mediation effects and moderation effects are examined in psychological research with some frequency and involve a third variable. This often results in difficulties for researchers who are inexperienced in the nuances of these two types of effects; some may be confused about whether they should be performing a mediation analysis or not, while others may perform a mediation when their research question actually involves moderation (or vice versa). We would like to emphasize that determining whether to investigate a mediator effect versus a moderator effect depends entirely on the research question of interest. In general, moderators provide information on the circumstance under which effects are present, whereas mediators address the mechanisms by which an effect occurs. Mediation effects are exemplified by the question “How did it work?” because mediation examines the means by which the intervention affects outcomes. Moderation effects are exemplified by the question “Who did it work for?” because moderation examines which subgroups (e.g., boys vs. girls) show effects of the intervention on outcomes (James and Brett 1984; Fairchild and MacKinnon 2008; MacKinnon 2011).

Mediation in Business Psychology

Theories across many substantive disciplines focus on mediating processes as explanations for how and why an antecedent variable is related to an outcome variable; business psychology is no exception. A casual review of the Journal of Business and Psychology found that between 2007 and 2010, over 30 articles purported to be addressing theoretical questions involving mediation or using mediation analysis. Of these, more than 20 articles cited classic mediation sources such as Baron and Kenny (1986) and Sobel (1982).

Basic Mediation Model

A simple mediation model with one independent variable, X, one mediator, M, and one outcome variable, Y, provides information to investigate mediation by estimating three regression equations. The relationships between X, M, and Y are shown as path diagrams in Fig. 1. Consider the study by Leach et al. (2009), in which the relationship between meeting design characteristics (design) and perceived meeting effectiveness (perception) was mediated by attendees’ involvement during the meeting (involvement). In this example, design is the independent variable X, perception is the outcome variable Y, and involvement is the mediator M.

Equation (1) represents the relationship between the independent variable X and the dependent variable Y:

$$Y=i_1+cX+e_1.$$ (1)

In terms of the example, this equation represents the relationship between design and perception, where the coefficient c represents the effect of design on perception, i is the intercept, and e₁ is the residual variance (i.e., the part of perception that is not explained by design). Equation 2 represents the relationship between the independent variable X and the mediator M:

$$M=i_2+aX+e_2.$$ (2)

In the example, this equation represents the relationship between design and involvement. Equation 3 represents the somewhat more complex relationship between X, M, and Y:

$$Y=i_3+c^{\prime }X+bM+e_3.$$ (3)

This equation shows how perception can be predicted by both design and involvement. Since there are two predictors here, both c′ and b are partial regression coefficients; each regression coefficient is the effect of that predictor on the outcome, controlling for the effect of the other predictor. Using the example, the b coefficient is the effect of involvement on perception, controlling for design, and the c′ coefficient is the effect of design on perception, controlling for involvement. There are several important assumptions of this single mediator model, including temporal precedence of the X → M →Y relationship and the assumption that no variables are omitted from the relationship; these assumptions, some of which are testable and some of which are not testable, are discussed later. As an aside, although we are presenting the mediation model in terms of three regression equations, regression is a special case of a structural equation model (SEM) and the methods described can often be done in either the regression or the structural equation model framework. However, structural equation modeling allows for more comprehensive modeling of measurement error, change over time, and multivariate dependent variables that are impossible or cumbersome with multiple regression analysis.

Decisions Prior to Mediation Analysis

Despite the extensive use of complex statistical modeling in the behavioral sciences, the quality of a research project is largely determined by the design decisions that are made before any analysis is done and even before the study is conducted. The conceptualization of a mediation analysis requires forethought about the relationships between the variables of interest and the theoretical meaning behind those relationships. Several other issues are important for researchers to consider prior to conducting a mediation analysis. Some of these decisions are common to all studies, but we will focus on the decisions that are of particular importance when planning a mediation analysis. In any study, a researcher must address the issues of manipulation versus observation, omitted variables that may be influencing results, reliability and validity of measures, and sample size to adequately detect effects. In addition, the theoretical task of choosing which variables will serve as mediators is critical. Table 1 summarizes some of the issues for consideration prior, during, and after mediation analysis.

Table 1.

Summary of issues before, during, and after mediation analysis

Decisions made prior to mediation analysis

What is the best way to randomize participants?

Determine realistic randomization schema—realistically this often means only randomizing X

Ideally use “double randomization” and randomize participants to levels of both X and M

Determine if the use of blockage or enhancement designs is appropriate

When double randomization is not possible, use theory and prior research to address that Ignorability Assumptions regarding omitted variables are not violated

Which mediators should be included in the study?

Rely on action and conceptual theory to choose mediators

Are the measures reliable and valid?

Choose measures that have high levels of reliability if a mediated effect is hypothesized since unreliability can considerably reduce the power to detect the mediated effect

Ideally, minimize unreliability by using multiple indicators of the latent variable of interest (assuming the researcher has access to an adequately sized sample for such a model)

Insure that the measures reflect the hypothesized construct

What should our sample size be?

Mediation studies are often underpowered so conduct appropriate power analyses to determine that you will have enough power to detect a mediated effect

Consider timing or longitudinal effects for X to M and M to Y and other variables

Specify when X will affect M and when M will affect Y. Based on these ideas select times to measure these variables in a longitudinal study

Decisions made during mediation analysis

What statistical test should we conduct?

Determine the mediation model based on the research question of interest

Test mediators individually and all together. Include relevant moderators

Identify covariates to include in the models

Use the distribution of the product (PRODCLIN) or Bootstrapping methods to estimate the 95% confidence interval

Correct for measurement error if necessary

Decisions made following mediation analysis

What steps can we take in the next study to further understand the causal process by which our mediators cause change?

What are the limitations of the mediation study and what information would improve identification of a mediation process?

Discuss the veracity of the action theory and conceptual theory of the study

Randomization

Random assignment of subjects to experimental conditions is the gold standard for making causal inference about the relationship between two variables. In the case where X represents randomly assigned condition, the coefficients a and c represent causal effects under certain reasonable assumptions. The coefficients b and c′ represent adjusted relations. Even though there is random assignment to experimental groups, the b and c′ coefficients do not have a clear interpretation as causal effects because participants select their own value of the mediating variable. This ambiguity of self-selection to value of the mediator is a primary focus of modern causal inference approaches to mediation to be described later. Random assignment to the levels of X is common in many mediation studies but a second random assignment to the value of M (called “double randomization”) is rare and often difficult for ethical or logistical reasons. In double randomization studies, one randomized study evaluates the X to M relation and a second randomized study evaluates the M to Y relation adjusting for X (MacKinnon 2008; MacKinnon and Pirlott 2011; Stone-Romero and Rosopa 2011; Spencer et al. 2005).

A second type of design to obtain some level of randomization of the mediating variable is called a blockage design. In this design, a manipulation is used to block or prevent the mediation process thereby demonstrating that the mediator was crucial (MacKinnon 2008; Robins and Greenland 1992). If the blocking manipulation removes the mediation relation, this provides support for a mediational process. As an example of blockage design, return to the example in which the relationship between meeting design characteristics (design) and perceived meeting effectiveness (perception) was mediated by attendees’ involvement during the meeting (involvement). Using a blockage design, participants in the study may be assigned to a blocking treatment condition where deep involvement in the meeting was prevented (e.g., by a mildly distracting task or by not allowing communication with others at the meeting) in addition to the manipulation of the meeting design characteristics. If involvement is a mediator of the design-to-perception relationship, mediation effects should be related to the amount of involvement across groups and participants in the blockage treatment condition should not show as large of a mediated effect as participants in the control condition because the mediating process was blocked. A closely related type of design is the enhancement design which seeks to enhance (rather than eliminate as in the blockage design) the mediated effect in the treatment group. In the meeting perception example, participants in the study may be assigned to an enhancement treatment condition which creates even deeper involvement in the meeting (e.g., by telling them that a promotion will be offered to the person who learns the most from the meeting). If involvement is a mediator of the design to perception relationship, mediation effects should again be related to the amount of involvement across groups and participants in the enhancement treatment condition should show larger mediated effects than the participants in other examples (see other examples in MacKinnon 2008; Maxwell et al. 1986; Klesges et al. 1986).

Several options exist to strengthen causal arguments when randomization of X and/or M is not possible, including the selection of covariates before the study that may explain the X to M and the M to Y relations. Similarly, these covariates may be used in a propensity score model to address omitted variable explanations of mediated effects (Coffman 2011; Jo et al. 2011). Instrumental variables may be used to estimate causal effects when randomization (particularly of X) is not feasible (MacKinnon 2008, Chap. 13; Lockhart et al. 2010). In addition to statistical adjustments, experimental design methods such as the blockage and enhancement designs can strengthen causal interpretation by focusing on testing the consistency and specificity of mediation relations across different contexts, subgroups, and measures of the mediating and outcome variables (MacKinnon and Pirlott 2011).

Omitted Variables

The term “ignorability” refers to the assumption that the relationship between two variables is unaffected by other variables (such as covariates, confounders, or moderators). Mediation analysis contains two major relationships that may be influenced by other variables: the X →M relationship and the M →Y relationship. Mediation therefore assumes a two part sequential ignorability assumption. There are many issues that arise in the causal interpretation of the single mediator model which stem from the two part sequential ignorability assumption (Imai et al. 2010; Lynch et al. 2008; ten Have et al. 2007). The ignorability assumption for the X →M relationship can largely be addressed by randomizing the levels of X; the ignorability assumption for the M →Y relationship is more difficult to justify and represents a challenging aspect of mediation analysis. Ignorability for the M to Y relation assumes randomization of participants at each level of X. In most research, this randomization is not possible and participants usually self-select their value of M. The extent to which sequential ignorability is a valid assumption may differ depending on the type of mediating variable. For example, if the mediators are selected because theory and prior empirical research suggest that they are causally related to the outcome variable, it may be reasonable to conclude that the b effect is known. Thus, it is only required that the levels of M be changed. In this case, the manipulation that changes the X to M relation will have the same expected change in the M to Y relation. Replication experiments can also further clarify the actual mediator from a host of other potential omitted variables. In this respect, replication studies with different manipulations are critical for identifying mediating variables.

Reliability

As in all research, the reliability and validity of proposed measures are best assessed prior to conducting the study. The reliability of a measurement is the extent to which a measure consistently reproduces values of the underlying true score. Valid measures measure the construct they are designed to measure. A program of research is typically needed to develop reliable and valid measures. Measurement is critical to mediation analysis and the search for mediating variables can be considered a measurement problem where science is advanced by more accurate measures of the mediating process (MacKinnon 2008).

Studies on measurement error highlight the need for reliable measures when detecting a mediator. Hoyle and Kenny (1999) demonstrated that as the reliability of M decreases (i.e., as the reliability coefficient departs from one), the observed effect of M on the Y and b is underestimated and the observed effect of X on the Y and c′ is overestimated. This results in an underestimation of the mediated effect and a decrease in the statistical power to detect the mediated effect. Due to the potential impact unreliability has on masking mediational effects, reliable mediating measures are crucial. One way to increase reliability is to obtain multiple indicators of the variable of interest and create a latent construct representing the variable of interest. The use of a latent variable model allows the estimation of associations between latent variables which are free of measurement error. However, using a latent variable model requires sufficiently large sample sizes and this is not always plausible. Modeling approaches which incorporate the effects of multiple methods such as multiple reporters or item types may yield more reliable relations than those ignoring method effects (Geiser and Lockhart, under review) and may provide promising tools for investigating mediation effects with more reliable measures.

Sample Size

Selection of sample size for adequate statistical power is an important part of designing any study. Although a large a sample size is ideal, sample size is often limited for reasons outside the control of a researcher, such as a small available population (e.g., local individuals of a specific age) or financial issues (e.g., excessive time or cost of measurements). However, even with an extremely large sample size, it will be important to obtain some measure of effect size to judge the importance or size of an effect. Mediation studies have traditionally been underpowered because the sample size requirements are much larger than those of simpler models, such as simple linear regression. Fritz and MacKinnon (2007) used simulations to determine sample sizes to obtain 0.80 power for small, medium, and large effect sizes in the single mediator model. A sample size of approximately 74 is required to detect a mediation effect when the path for the X to M relation and the M to Y relation is medium. A more complex mediation model would require a larger sample. The careful use of covariates can decrease the required sample size and repeated measures and longitudinal data can also improve the ability to detect effects. Required sample size and statistical power for more complicated mediation models has been outlined by Thoemmes et al. (2010) using a Monte Carlo approach in a covariance structure analysis program.

Choosing Mediators

The theoretical interpretation of the links in a mediation model can be thought of in terms of the theory for the process underlying the manipulations. These two processes are called the action theory and the conceptual theory (Chen 1990; MacKinnon 2008). As shown in Fig. 2, action theory corresponds to how the manipulation will affect the mediators (the relationship between X and M) and conceptual theory focuses on how the mediators are related to the outcome of interest (the relationship between M and Y). Consider an intervention designed to increase knowledge of the benefits of exercise and nutrition designed to increase employee well-being, which is measured as the number of sick days the employee uses. The action theory is that the program will increase the employees’ knowledge of exercise and nutrition. Conceptual theory says that knowledge of the benefits of exercise and nutrition will increase employee well-being, reducing the number of sick days. The use of action and conceptual theory can be used to demonstrate how a manipulation leads to changes in the dependent variable (Ashby 1956; Lipsey 1993; MacKinnon 2008).

Fig. 2.

Action and conceptual theory

The informed choice of possible mediators often emerges from action and conceptual theory. Typically, conceptual theory is based on prior research that provides information about the relationship between a potential mediator and the outcome of interest. However, action theory can also inform the selection of mediators, based on what variables are able to be changed by experimental manipulation or intervention. For example, an experimental manipulation can change an individual’s beliefs about a product, but it typically cannot change aspects of an individual’s personality (Table 1).

Table 2 summarizes six methods suggested by Mackinnon (2008) to choose mediators. Depending on the information available and the current state of a particular research area, any one of the six approaches may be a viable approach to choosing mediators. When the area of study is well-researched and a great deal of prior research is available on which to build, mediators can be chosen by performing a literature review to determine empirical relations between potential mediating variables and the outcome variable of interest, by targeting mediators based on an established theoretical framework in the area of substantive research, or based on prior mediation research. In particular, the “theory-driven” approach has received considerable support in the literature (Chen 1990; Lipsey 1993; Sidani and Sechrest 1999). When the area of research is new and little prior research is available to guide the selection of mediator variables, different approaches to selecting mediators must be employed. Mediators may be identified by studying correlates of the outcome measure to identify mediators based on the conceptual theory of the outcome, using qualitative methods such as focus groups, or on the basis of common sense or intuition about what seems to be the best target of a program. Although these are less scientifically driven methods, they may be a good approach in newly developing fields.

Table 2.

Methods of choosing /mediators

When there is substantial prior research on the topic	When little prior research is available on the topic
Literature review to determine conceptual theory and action theory links	Look for correlates of the outcome measure to determine conceptual theory links
Based on a psychological theory of the process	Focus groups and other qualitative methods
Prior mediation analysis	Common sense or intuition

Testing Multiple Mediators

Many studies include more than one mediator of an X–Y relationship. For example, Chen and Chiu (2008) examined several mediators of the relationship between supervisor support of employees and employee organizational citizenship behavior. They found that job satisfaction, person-organization fit, and job tension mediated the relationship between supervisor support and citizenship behavior. When there are multiple mediators, a simple approach is to evaluate one mediator at a time. Using the Chen and Chiu study as an example, one may initially examine the supervisor support → job satisfaction → citizenship behavior relationship. Looking at a single mediator at a time is a useful approach because specific theoretical hypotheses often focus on single mediators rather than groups of mediators. It is also wise to examine any potential moderator or interaction effects (discussed in more detail shortly) at the single-mediator stage. If the study involves many mediators, it will be necessary to implement some control for experiment-wise error due to multiple tests; the alpha or Type I error rate increases rapidly with multiple tests.

A model including all measured mediators should be estimated in addition to single mediator models. This is accomplished by expanding Eq. 3 to include all mediating variables. For example, in the case of three mediating variables, Eq. 3 can be reexpressed as:

$$Y=i_4+c^{\prime }X+b_1{M}_1+b_2{M}_2+b_2{M}_3+e_4.$$ (4)

Evaluating a model that includes all measured mediators is important because it is possible that the effect of a mediator may change in the presence of other mediators. Recall that the b and c′ coefficients in these models are partial regression coefficients controlling for all other predictors, so the exclusion of some mediators could potentially change these values in the complete model. Including all measured mediators also produces a model which more closely matches reality, where all potential mediators are present. An additional benefit of multiple mediator models is the identification of mediation pathways that lead to beneficial relations on the outcome measures and mediating pathways that are actually counterproductive. These inconsistent mediation models, defined as mediation models where at least one mediated effect has a different sign than the direct effect, are more clearly identified in multiple mediator models (MacKinnon et al. 2000).

Moderator Effects in Mediation Models

As previously described, moderation is an effect involving a third variable that changes the direction or magnitude of the relationship between two other variables. For example, the relationship between stress and health is moderated by social contacts; individuals with many friends show little relationship between stress and health while individuals with few friends have a strong positive relationship between stress and health (Cohen and Wills 1985).

Moderator relationships can occur with mediation relationships. The combination of moderation and mediation can take on several forms. We briefly discuss these situations involving both mediation and moderation because they occur frequently within psychological research and can be confusing to understand. Moderation of a mediated effect occurs when a moderator variable (Z) affects the direction or strength of any or all the mediation regression coefficients. There are a number of ways to incorporate moderator effects into a mediation model. If the moderator is binary, such as gender, moderator effects can be evaluated by conducting analyses by group. Individual regression coefficients or estimates of the mediated effect can be compared across groups using t tests (see MacKinnon 2008, p. 292). This method is straightforward and makes interpretation simpler, but it can only be used for binary moderators. More complex approaches are needed for continuous moderators and moderators with several categories.

In order to include continuous moderators in a mediation model, the moderators are incorporated into Eqs. 1–3 as interaction terms. For example, if a continuous variable, Z, is hypothesized to moderate the effect of X on M, Eq. 2 becomes:

$$M=i_5+aX+fZ+\mathit{gXZ}+e_5,$$ (5)

where coefficient f represents the main or conditional effect of the moderator Z on the mediator M and coefficient g represents the interaction or moderator effect of X and Z. Tein et al. (2004) present a framework for testing moderation of all four mediation paths. This framework also allows for the inclusion of baseline covariates. For example, in evaluating a program to improve management and supervisor skills, a researcher may wish to control for pre-program level of skill by including this variable as a covariate.

Timing and Longitudinal Effects

The mediation model is a longitudinal model in that X precedes M and M precedes Y. However, in practice, tests of mediation may be conducted using cross-sectional data. There are a number of problems and limitations with using cross-sectional data to investigate longitudinal mediational processes, as outlined by several researchers (Cheong et al. 2003; Cole and Maxwell 2003; MacKinnon 2008; Maxwell and Cole 2007). Conceptually, a problem arises because mediation is inherently a process that unfolds over time and cross-sectional data do not measure this unfolding over time. Statistically, several studies have shown that estimates of the cross-sectional-mediated effect are severely biased when compared to the estimates of the longitudinal mediated effect (Maxwell and Cole 2007). The bias may be either positive or negative, further complicating the use of cross-sectional data.

The best-designed studies employ repeated measures because power to detect mediated effects is greatly enhanced. In addition, longitudinal studies allow for the measure of change in response to a manipulation (Cohen 1988; Singer and Willet 2003). The methodological literature has emphasized the importance of temporal precedence in the investigation of mediation (Gollob and Reichardt 1991; Judd and Kenny 1981; Kraemer et al. 2002; MacKinnon 1994) and has described methods for assessing longitudinal mediation (Cheong et al. 2003; Cole and Maxwell 2003; MacKinnon 2008; Maxwell and Cole 2007). The evaluation of longitudinal mediation models is an important step in advancing mediation methods. Although there are several choices of longitudinal models described in the literature such as autoregressive models and latent change score models, latent growth curve models are a common choice for longitudinal mediation models (Cheong 2002; Cheong et al. 2003). More detailed information on longitudinal mediation models can be found in Mitchell and James (2001) and MacKinnon (2008).

Although longitudinal mediation modeling is the preferred method for evaluation of the mediation process, there are situations where only cross-sectional data are available. For example, secondary mediation analysis of data from a previously collected study may require the use of cross-sectional data. In this case, estimates of the cross-sectional mediated effect may not reflect the longitudinal mediated effect and researchers must provide evidence for temporal relations from theory or empirical research.

Decisions During Mediation Analysis

Recall the path model in Fig. 1, which shows the directional relations between X, M, and Y for the single-mediator model. For the mediation framework that is most commonly used in psychology (Baron and Kenny 1986; MacKinnon 2008), three regression equations are used to describe the relations in this model. These regression equations describe the effect of X on Y (Eq. 1), the effect of X on M (Eq. 2), and the effect of X on Y, controlling for M (Eq. 3). The c coefficient is the total effect of X on Y. The c′ coefficient is the direct effect of X on Y, controlling for M. The a coefficient corresponds to the “action theory” for the model, whereas the b coefficient corresponds to the “conceptual theory” for the model (Fig. 2).

Baron and Kenny (1986) proposed a causal steps approach to testing whether statistical mediation is present in such a model. The causal steps approach describes a series of tests of regression coefficients that, together, can show mediation is occurring. The first step in this approach is to test whether changes in X produce changes in Y, i.e., whether there is an effect to be mediated. This is determined by the significance of the c regression coefficient in Eq. 1. If there is no relation between X and Y, the causal steps approach stops. If there is a relation between X and Y, the next step is to determine if there is a relation between X and M by testing the a regression coefficient in Eq. 2. Given that the independent variable significantly affects the mediator, the next step is to test whether M is related to Y, after controlling for the effect of X on Y. This is shown by testing the significance of the b regression coefficient in Eq. 3. Finally, it must be shown that the effect of X upon Y, after controlling for M, is not significantly different than zero. The test of the c′ coefficient in Eq. 3 should not be significant.

The requirements of the causal steps approach that c ≠ 0 and that c′ = 0 results in reduced statistical power to detect a mediated effect. The requirement that c ≠ 0 is problematic because statistical tests are not absolute; there is always the potential for a Type I or Type II error in this decision. Additionally, if subgroups of participants (e.g., men vs. women) have opposing effects, ignoring these subgroups could result in a non-significant c value. The causal steps mediation approach also requires that c′ = 0, meaning all effects from X to Y must be transmitted through M; this type of mediation model is called a complete mediation model. The complete mediation model is the most defensible mediation conclusion from a research study, but it suffers from low statistical power when the causal steps approach is used. The complete mediation model is discussed in more detail shortly.

Modern methods of mediation analysis use regression (as well as structural equation modeling, an expansion of the regression framework) to quantify the mediated effect as a single number for which confidence intervals and significance tests can be calculated. The theory of mediation states that there is a causal relation in a mediation model, such that X causes M and M causes Y. Therefore, the mediated effect of X to Y via M can be quantified as the product of the regression coefficient relating X to M and the regression coefficient relating M to Y, or ab (using Eq. 2 and above). The test of ab can be more powerful than the test of c because it is a more precise explanation of how X affects Y; the requirement that c be significant is not necessary for mediation to exist. Although modern methods pose that the test of c may not be as important in determining the mediating effect, the test of c is clearly important in its own right. A lack of statistically significant c is important in assessing manipulation and conceptual theory for future studies.

When both M and Y are observed and continuous (so that linear regression or structural equation modeling is used to estimate Eqs. 1–3) and there are no missing data, it can be shown that the difference between the total effect of X on Y and (c), and the direct effect of X on Y and (c′) is numerically equivalent to ab. As previously noted, this result holds only for linear models such as linear regression, but not for non-linear models such as logistic regression (Pearl, in press). The c–c′ estimate of the mediated effect reflects that any difference between the total relation between X and Y (the c coefficient) and the direct effect of X on Y while controlling for M (the c′ coefficient) must be due to the indirect or mediated effect. Some researchers have suggested that only c–c′ should be used for making causal inferences. The reasoning behind this stance is that, typically, only X is randomly assigned, whereas M is observed or self-selected by the participant. Therefore, the c–c′ estimate of the mediated effect involves using only regression coefficients that are based upon random assignment to experimental conditions. The point of contention is often irrelevant because the two quantities ab and only c–c′ are identical in linear regression and structural equation modeling of continuous measures. For logistic regression or other nonlinear statistical methods, the two estimators of the mediated effect may not be equal and may have different meanings (Imai et al. 2010; Pearl 2011).

Complete Versus Partial Mediation

Some researchers (e.g., James and Brett 1984) suggest a slightly different approach to quantifying the mediated effect than has been presented here. James and Brett suggest that the model described by Eqs. 1–3 implicitly assumes partial mediation, i.e., the mediated path via M accounts for only some of the effect of X on Y. In other words, this approach implies a non-zero direct path or c′ coefficient. James et al. (2006) suggest an alternative approach that begins from an assumption of complete mediation (sometimes also called “full mediation”), where the c′ path is assumed to be zero and all effects of X on Y are transmitted through the mediator M. In the complete mediation framework, two regression coefficients are estimated. First, the effect of X on M is estimated using the a coefficient in Eq. 2 above. Second, the effect of M on Y is estimated using the expression

$$Y=i_6+b^{\prime }M+e_6,$$ (6)

where b′ is a new regression coefficient representing the relation of M and Y, completely ignoring X. The mediated effect is calculated as ab′ and reflects the use of this new coefficient.

The complete mediation approach has several attractive features. First, fixing the value of the c′ path to zero means that, from a structural equation modeling perspective, the complete mediation model is identified and has degrees of freedom, allowing for goodness-of-fit tests. Goodness-of-fit tests allow a researcher to test how closely the model matches the observed data, in addition to testing whether individual paths and the mediated effect are significantly different from zero. Second, the complete mediation model is a more parsimonious explanation of the causal relation from X to M to Y. From a philosophy of science perspective, a simpler or more parsimonious model is preferred. However, complete mediation is uncommon in many areas of psychology so it is likely that there is a direct effect of X on Y, and testing for complete mediation as a first step may not be informative for psychological research; this is a weakness shared by the causal steps approach to mediation described in Judd and Kenny (1981), which requires that the null hypothesis that the c′ path is equal to zero is not rejected.

Tests of Mediation and Confidence Limit Estimation

There are many statistical tests to evaluate the mediated effect. Some tests of the mediated effect involve dividing the estimate of the mediated effect by an estimate of its standard error (Wald 1943) and this ratio is then compared to an appropriate statistical distribution, such as the normal distribution. Other tests of the mediated effect are non-parametric, resampling tests such as bootstrapping which use the observed data to determine the distribution and standard error of the mediation estimate. MacKinnon et al. (2002) provide an evaluation of fourteen different methods of evaluating the mediated effect, including methods of calculating the standard errors for ab and c–c′.

One of the most common tests of the ab mediated effect is based on the multivariate delta standard error (Sobel 1982). The ratio of the mediated effect to its standard error is compared to a standard normal (z) distribution to test significance. This method has reduced power because the product of two normally distributed regression coefficients is not normally distributed and instead follows the distribution of the product. The distribution of the product is variable in shape depending on the magnitude of the coefficients and is often asymmetric and highly kurtotic (Aroian 1947; Craig 1936).

As described in MacKinnon et al. (2002), tests of the mediated effect that are based on the distribution of the product have more accurate Type I error rates and have more power than many other tests. Critical values for the distribution of the product produce more accurate confidence intervals for the mediated effect. PRODCLIN (distribution of the PRODuct Confidence Limits for INdirect effects) automates the selection of critical values for the distribution of the product (MacKinnon et al. 2007). The user inputs values of a, b, their respective standard errors, and the desired Type I error rate (e.g., α = .05); the program returns the upper and lower asymmetric confidence limits for the mediated effect. A new version of this program (RMEdiation; Tofighi and MacKinnon 2011) now provides several additional capabilities including plots of the distribution of the product and several options for confidence limits. Mackinnon et al. (2004) found that tests of significance based on the distribution of the product outperformed other single-sample methods in terms of Type I error rates, power, and accuracy of confidence limits.

Bootstrapping is a resampling technique that is often used to evaluate a test statistic (such as the mediated effect) when the true distribution of the statistic is either unknown or difficult to obtain. The bootstrapping method involves taking many (e.g., 1000) repeated “samples” from the observed sample, calculating the statistic of interest, and producing a distribution based on these values of the statistic. Confidence intervals are obtained empirically, i.e., by observing the value in the bootstrapped distribution beyond which a certain proportion of the test statistics lie. For example, for a two-tailed test with an alpha value of .05, order the 1000 bootstrap statistics from lowest to highest, and choose the value of the (1000 × 0.025) = 25th observation as the lower critical bound of the confidence interval and the value of the (1000 × 0.975) = 975th observation as the upper bound of the confidence interval. Bootstrap methods for determining the significance of the mediated effect generally perform well in terms of power and Type 1 error (see MacKinnon et al. 2004). Routines to perform bootstrap analyses are included in many common statistical software programs, including AMOS, Mplus, and EQS and programs for conducting bootstrap analyses in SAS and SPSS are also available (Lockwood and MacKinnon 1998; Preacher and Hayes 2004). Another advantage of bootstrap methods is that they can be easily expanded as the complexity of the model increases; for example, bootstrapping can easily be applied to a multiple mediator model in which X →M₁ →M₂ →Y, where the mediated effect is calculated as the product of three regression coefficients.

In summary, an ideal method includes an estimate of the mediated effect along with a confidence interval for the indirect effect. Confidence intervals may be made with a bootstrap method or the distribution of the product. The effect size for the paths in the mediation model such as the standardized coefficients or partial correlation measure should be reported. Note that it is important to report statistical tests of the relation of X to Y (i.e., the c coefficient from Eq. 1 in the single mediator model), but this relation is not necessary for mediation to exist. In fact, a test of mediation may be more important when there is not a statistically significant relation of X to Y because the path from X to M represents a test of action theory and the path from M to Y represents a test of conceptual theory. When reporting mediation analyses, it is important to provide detailed information regarding the models tested along with the coefficients from these models (e.g. a, b, c′, and ab) and the confidence intervals (Mackinnon 2008).

Decisions Following Mediation Analysis

Several assumptions were made for the regression equations described earlier that can be addressed in the design phase of the study or by appropriate statistical analysis. However, several assumptions are untestable and cannot be completely addressed using design or statistical approaches. These assumptions are related to confounders of the mediated effect, higher order relations between X and M, the causal ordering of X, M, and Y, and measurement error. Many aspects of these assumptions can be addressed by sensitivity analysis, a method of assessing how much the results of an analysis may change due to violation of assumptions. Typically, sensitivity analysis involves systematically changing values of specific parameter values in the model (for example, the a path from X to M) to determine how much the parameter must change in order to change the substantive interpretation (i.e., significance) or change the estimates by a specific, pre-determined amount (e.g., to change the estimate of the mediated effect by 25%). Sensitivity analysis is one of the most challenging aspects of mediation analysis, but there has been considerable development in these methods in recent years.

Confounders

For the ab estimator of the mediated effect and ordinary least squares regression, the errors in Eqs. 2 and 3 are assumed to be independent. The uncorrelated errors assumption may be violated if there are confounding variables that are omitted from the analysis. Confounders can have a substantial effect on the analysis of the mediated effect. Figure 3 shows how confounders can potentially influence multiple paths in a mediation model. Ideally, measures of the potential confounding variables are included in the statistical model, but if they are not, the confounders may result in biased estimates. As with any study, even when some potential confounders are included in the analysis, there is no guarantee that all possible confounders were included.

Fig. 3.

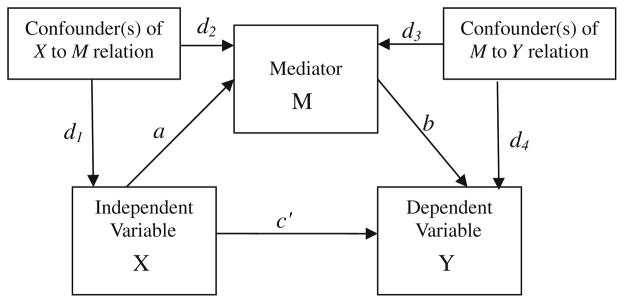
Confounders of mediation relations. The true model requires d₁, d₂, d₃, and d₄, otherwise the coefficients are confounded

Sensitivity analysis is one way to assess the influence of omitted variables on the observed mediation relations. Since randomization of X theoretically eliminates confounders in the X →M relationship, the goal of sensitivity analysis in mediation for experimental studies is typically to assess how large a confounder effect on the M →Y relation (i.e., sequential ignorability) must be in order to invalidate the conclusions of the analysis (Frank 2000; Li et al. 2007; Lin et al. 1998; Rosenbaum 2002). The correlation between the errors in Eqs. 2 and 3 reflects the contribution of omitted variables to the observed relation of M to Y, or the degree to which the assumption of sequential ignorability is violated. Thus, by systematically increasing the correlation between the errors in Eqs. 2 and 3, one can evaluate how much the b and c′ coefficients change due to violation of this assumption (Imai et al. 2010).

Promising approaches to improving causal inference by addressing the bias introduced by omitted variables have been proposed (Frangakis and Rubin 2002; Holland 1988; Jo 2008; Murphy et al. 2001; Pearl 2009, in press; Robins and Greenland 1992; Robins et al. 1992; Rubin 2004; Shipley 2000; Sobel 1998, 2008; Winship and Morgan 1999) but most have not been extensively evaluated in simulation studies and applied settings. Vander Weele (2008, 2010) has formalized several useful methods to probe bias in mediation relations when one or both assumptions of Sequential Ignorability have been violated. Imai et al. (2010) describe another method and include a computer program to assess the sensitivity of the results to potential confounders. These methods allow the researcher to draw a conclusion about the direction of the bias by suggesting relations of unmeasured confounders on relations in the mediation model.

X–M Interaction

The standard single mediator model assumes that Eqs. 2 and 3 represent causal relations that are linear, additive, and recursive (Holland 1988; James and Brett 1984; James et al. 2006; McDonald 1997). An additivity assumption implies that there is no interaction between X and M (Collins et al. 1998; Judd and Kenny 1981), i.e., the effect of X on Y does not depend on the value of M and the effect of M on Y does not depend on the value of X. The additivity assumption can be directly tested by including the interaction of X and M; if the interaction term is significant, the assumption of additivity is violated. In this context, the mediated effect differs across levels of X and further analyses can explore the size and significance of the mediated effect at different values of X.

Causal Ordering

Since mediation is a causal model, it is important to clearly define the causal chain from X to M to Y. The mediation model makes the assumption that the correct causal order has been specified, such that X causes M and M causes Y. When X is randomly assigned, it is clear that X occurs before M and Y. However, the ordering of M and Y is less clear and theory and prior empirical research can help make the causal ordering more concrete.

Hill (1965) outlined nine considerations for clarifying the ordering of causal relations. These points were initially developed to investigate smoking as a cause of cancer but have applications to establishing causal ordering in mediation models. These are substantive considerations rather than statistical tests, so they require a substantive researcher to carefully evaluate the variables involved. The nine criteria are (1) strength, (2) consistency, (3) specificity, (4) temporality, (5) biological gradient, (6) plausibility, (7) coherence, (8) experiment, and (9) analogy. According to Hill, causality is implied by (1) a stronger relation rather than a weaker relation, (2) consistent findings by multiple people in multiple samples, (3) specific findings (e.g., about a specific disease rather than general unhealthiness), (4) the “cause” occurring prior to the “effect” in time, (5) a larger effect seen with larger exposure to the “cause,” (6) a plausible and sensible mechanism by which the causal relationship occurs, (7) agreement between laboratory and observational studies, (8) experimental evidence of the causal relationship, and (9) similar “causes” resulting in similar “effects.” These criteria can be applied to M and Y (or to X, M, and Y, if X is not randomized) to provide evidence that the presented causal ordering is the correct ordering.

Measurement Error

Mediation analysis assumes that the measures are both reliable and valid (Baron and Kenny 1986; Holland 1988; James and Brett 1984; MacKinnon 2008; McDonald 1997). As previously discussed, Hoyle and Kenny (1999) showed that unreliability of the mediator leads to underestimation of the b path and overestimation of c′ which results in underestimation of the mediated effect and lower power to detect the mediated effect.

After the study is completed, a correction for unreliability in measured variable models can be applied to obtain estimates of coefficients if reliability is assumed to be a certain value (see MacKinnon 2008, p. 189). This new model results in the estimation of coefficients that have been adjusted for more or less reliable measures. Limitations of this method are that the reliability estimate used may not always be accurate and the correction approach may not adequately address measures that are actually composed of more than one factor. In addition, if there are multiple factors for some measures, the relationship of these factors may have important relationships with other variables in the model that will be ignored (Bagozzi and Heatherton 1994).

Planning for the Next Study

Every study can be thought of as a single piece of an overall body of research; each study builds upon previous studies, resulting in an accumulation of knowledge. Studies involving statistical mediation are no different. In this article, we have discussed a number of potential limitations to the interpretation of mediation analysis, particularly causal inference limitations. For example, we discussed potential confounders of the mediated effect, including experimental design methods that can help rule out the presence of potential confounders and newly developed sensitivity analysis methods that can determine the amount of bias caused by omitted confounders. The consideration of limitations of interpretability and generalizability of results may be especially important for mediation studies because of the number of omitted variables that may affect observed results. As an illustration, consider a study involving a non-randomly assigned X variable. There are several limitations of the interpretation of the mediated effects in this study. The relationship between X and M may be biased for several reasons; the true causal ordering of X and M is potentially unclear and there may be confounders that bias the estimate of the relationship between X and M. A follow-up study can address both of these limitations by incorporating a randomly assigned manipulation of the X variable. Random assignment of the X variable ensures the causal ordering of X and M because X is randomly assigned before M is measured; random assignment also ensures that there are no confounders of the relationship between X and M. If the follow-up study produced results that match the initial study, the researcher can be confident that causal inference based on the X →M relationship is sound. If the follow-up study produces conclusions that differ from the initial study, further research is needed; for example, confounders of the M →Y relationship may be affecting the results. In either situation, multiple studies are typically required to produce a clear picture of the true relationships.

Conclusion

Statistical mediation analysis is a powerful tool for testing the process by which an effect occurs in both experimental and observational studies. In this article, we discussed how design decisions made prior to conducting a study and statistical choices made during analysis influence the conclusions that can be drawn from a study that involves statistical mediation. We also discussed the limitations of interpretation of a mediation process for even well-designed and analyzed studies. The major point is that the investigation of mediation processes requires careful planning and is part of a cumulative program of research using evidence from a variety of sources including clinical observation, qualitative studies, and replication (MacKinnon 2008). Mediation analysis is popular because it directly addresses important theoretical questions about processes by which effects occur. This importance of mediating variables for scientific understanding was identified many years ago (Lazarsfeld 1955; Woodworth 1928) and there is now a body of statistical techniques to test and evaluate mediation theory. Business research is an ideal area for the application of these techniques to evaluate whether a variable is truly intermediate in a causal sequence.