Explicit Polarization: A Quantum Mechanical Framework for Developing Next Generation Force Fields

Conspectus

Molecular mechanical force fields have been successfully used to model condensed-phase and biological systems for a half century. By means of careful parametrization, such classical force fields can be used to provide useful interpretations of experimental findings and predictions of certain properties. Yet, there is a need to further improve computational accuracy for the quantitative prediction of biomolecular interactions and to model properties that depend on the wave functions and not just the energy terms. A new strategy called explicit polarization (X-Pol) has been developed to construct the potential energy surface and wave functions for macromolecular and liquid-phase simulations on the basis of quantum mechanics rather than only using quantum mechanical results to fit analytic force fields. In this spirit, this approach is called a quantum mechanical force field (QMFF).

X-Pol is a general fragment method for electronic structure calculations based on the partition of a condensed-phase or macromolecular system into subsystems (“fragments”) to achieve computational efficiency. Here, intrafragment energy and the mutual electronic polarization of interfragment interactions are treated explicitly using quantum mechanics. X-Pol can be used as a general, multilevel electronic structure model for macromolecular systems, and it can also serve as a new-generation force field. As a quantum chemical model, a variational many-body (VMB) expansion approach is used to systematically improve interfragment interactions, including exchange repulsion, charge delocalization, dispersion, and other correlation energies. As a quantum mechanical force field, these energy terms are approximated by empirical functions in the spirit of conventional molecular mechanics. This Account first reviews the formulation of X-Pol, in the full variationally correct version, in the faster embedded version, and with systematic many-body improvements. We discuss illustrative examples involving water clusters (which show the power of two-body corrections), ethylmethylimidazolium acetate ionic liquids (which reveal that the amount of charge transfer between anion and cation is much smaller than what has been assumed in some classical simulations), and a solvated protein in aqueous solution (which shows that the average charge distribution of carbonyl groups along the polypeptide chain depends strongly on their position in the sequence, whereas they are fixed in most classical force fields). The development of QMFFs also offers an opportunity to extend the accuracy of biochemical simulations to areas where classical force fields are often insufficient, especially in the areas of spectroscopy, reactivity, and enzyme catalysis.

1. Introduction

Molecular mechanical (MM) force fields are widely used in computer simulations of macromolecular systems, including proteins and nucleic acids in aqueous solution.^1,2 Although these models are computationally efficient for applications to large systems, there are also a number of well-known limitations that are not easily resolved in the MM context.^3,4 There is a great need to further improve the accuracy to achieve quantitative prediction of biomolecular interactions such as ligand binding, electron and energy transfer, and enzymatic reactions. It is timely to ask what type of potential energy functions will be used in the future for biomolecular simulations. One possibility is to continue improving the current MM approach, including classical polarization terms and charge transfer in the force fields. The second is to develop a new theoretical framework with the capability of including quantum mechanical effects explicitly to model intermolecular interactions.⁵⁻⁹

Quantum mechanics, in principle, can provide both reactive and nonreactive potential energy surfaces, including electrostatics, electron correlation, polarization, and charge transfer. Yet, it is limited by the computational cost, which increases rapidly with the size of the system. To overcome this limitation, a variety of fragment-based electronic structure methods,¹⁰ many of which are illustrated in this Special Issue, have been developed to increase the computational speed for large molecular systems. For example, Gordon and co-workers developed the effective fragment potential method,¹¹ York and co-workers employed a version of the divide-and-conquer strategy for linear-scaling quantum-mechanical (QM) representation of a macromolecular system as a force field,^8,9,12 and Herbert and co-workers discussed the issue of error propagation in many-body expansion theory.¹³ A key issue is the requirement for a suitable level of electronic structure theory for monomers.^13,14 For brevity, we shall not make an extensive list of fragment methods, but the introduction of a recent paper may be consulted for ∼70 relevant references.³¹ This Account presents one especially promising fragment method, namely, the explicit-polarization method (X-Pol),^5,6,14−17 for the construction of a next-generation force field on the basis of quantum mechanics.¹⁸

The X-Pol model is a fragment-based QM method,^5,6,17 in which the entire system is divided into molecular subunits, which can consist of one or more molecules, ions, ligands, cofactors, or amino acid residues. The key assumption in the X-Pol method is that the wave function of the entire system is approximated as a Hartree product of the antisymmetric wave functions of individual fragments.⁵ Then, the optimization of the total wave function can be reduced to the optimization of each fragment embedded in and polarized by the rest of the system; this reduces the computational cost to nearly linear scaling with respect to the number of fragments.¹⁹ Clearly, variational optimization of the mutual dependence of the fragmental wave functions is critical to the success of this method.^16,17 As a force field, the energy of each fragment is determined by the electronic structure method used, whereas intermolecular interactions are modeled through electrostatic embedding.¹⁵ The short-range exchange-repulsion interactions, charge transfer, and long-range dispersion interactions and correlation energy between different fragments can be modeled empirically as in MM.^5,6,15,20 Alternatively, these energy contributions can be modeled by density-dependent functionals, by Hartree–Fock (HF) exchange, or by making use of many-body expansion corrections.^10,14,38

In the following, we describe the theoretical approach of X-Pol and illustrate computational results that demonstrate the feasibility and accuracy of macromolecular simulations employing the X-Pol quantum mechanics force field (QMFF).

2. Theoretical Background

In X-Pol, a system is partitioned into molecular fragments,^5,6,15 which may be called monomers. For solutions with small solute molecules, a fragment can be a single solute or solvent molecule.^15,18,21 For a polypeptide chain, the peptide unit as defined by the IUPAC nomenclature (rather than the conventional residue)²² is assigned to be the smallest fragment that contains the atoms −C_α^IR^ICO–NHC_αH– in the conventional residues I and I + 1, where each C_α atom is shared by two adjacent peptide units (Figure 1).^6,23 Several peptide units can be combined into the same fragment, if desired, which can be useful for modeling systems containing disulfide bonds. The connection approach is an extension of the generalized hybrid orbital (GHO) method,²⁴ originally developed for combined QM/MM applications.²⁵ Unlike schemes that involve capping by a hydrogen atom,²⁶ the GHO method does not alter the number of degrees of freedom or the electrostatic interactions between neighboring fragments. Thus, the hybrid orbital approach provides a seamless transition from one fragment to the next across chemical bonds, and a buffering scheme was used to accelerate the convergence.²⁷

Figure 1.

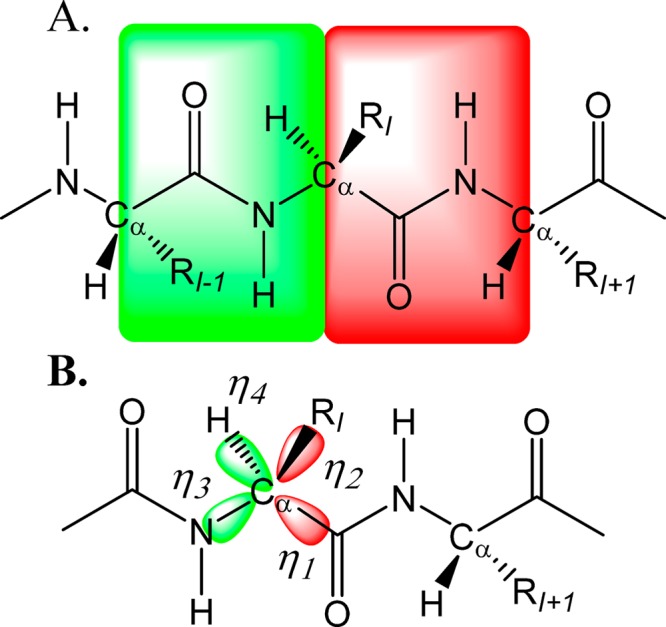
Schematic depiction of the division of a polypeptide chain into peptide units (A). Two fragments are highlighted in green and red, respectively, corresponding to residues I – 1 and I. The C_α boundary atom connecting these two peptide units is shown in panel B, and its four hybrid orbitals are equally partitioned into the two neighboring fragments.

The X-Pol model is derived from a conventional electronic structure method by a hierarchy of three approximations.^5,6,17 First, the wave function of the entire system is approximated as a Hartree product of the antisymmetric wave functions of the individual fragments,

1

where N is the number of fragments. The effective Hamiltonian of the system is given by

2

where the first term sums over the Hamiltonians of all isolated fragments {Ĥ_A^o}, and the double summation accounts for pairwise interactions among all the fragments; Ĥ_A[V_E^B] represents electrostatic interactions between fragments A and B with V_E being the potential due to B, and the final term, ΔE_AB^XCD, specifies exchange-repulsion (X), charge delocalization (C), and dispersion and other interfragment correlation (D) energy contributions.

A general approach for representing the external potential, V_E^B, due to the charge density of fragment B is to use a multicenter multipole expansion,^5,6,17,28 of which the simplest form is to limit the expansion to the monopole terms, so the result only depends on the partial atomic charges.¹⁵ The use of partial atomic charges to approximate V_E is particularly convenient for constructing the effective Hamiltonian of eq 2, and this is the strategy that has been adopted in the X-Pol method.^{5,6,15−18,21} This strategy has also been used in other studies.^9,13,29−32

The total energy of the system in the X-Pol method is given by

3

There are two ways of constructing the Fock matrix for optimizing the fragmental wave functions, and they distinguish the variational X-Pol method from other fragment-based methods.

2.1. Variational X-Pol

With the use of partial atomic charges to approximate V_E^B, the Fock operator for a fragment, A, is derived variationally to yield^16,17,27

4

where F_μν^A,o is the Fock matrix element for the Hamiltonian of isolated fragment A, q_b is the point charge on atom b of fragment B, I_b^B is the matrix of the one-electron integrals of the embedding potential due to fragment B, and the last term represents the response of the charge density of fragment B due to variational optimization of the wave function of fragment A (X_a is the derivative of the energy with respect to the atomic charge on a, and Λ_a^A is the charge derivative with respect to the density, see ref (33)).

2.2. Embedded X-Pol

If each fragment is considered to be embedded in the static field of the rest of the system, one can construct a Fock operator for fragment A heuristically,^5,11,15,34 akin to a combined QM/MM approach;²⁵ this yields

5

In this charge-embedding approach, the mutual polarization among all fragments in the system is achieved by iteratively updating the partial atomic charges. However, eq 5 is not variational, and it does not include the response of the charge density to the changes of other charges. To emphasize this difference and to emphasize that the full X-Pol algorithm is a variational method, in the rest of this Account, the method in section 2.1 will be called variational X-Pol, and the subsequent many-body expansion corrections (to be introduced below) will be called VMB2 and VMB3. The embedding approach (section 2.2) is simply called embedded X-Pol, and the many-body corrections to it will be called EMB2 and EMB3. When we just say X-Pol, MB2, or MB3, it applies to either.

The variational X-Pol method has the advantage over embedded X-Pol of allowing the computation of analytic gradients for efficient geometry optimization and dynamics simulations.^16,17,27 Furthermore, the total energy obtained from the variational procedure is necessarily lower than that from the charge-embedding scheme. Consequently, it is expected that the use of the variational X-Pol energy as the monomer energy reference state in many-body energy expansion should lead to smaller corrections than other alternatives.¹⁴ Although it is possible to obtain analytic gradients for the nonvariational, charge-embedding approaches,³⁵ it generally involves solution of coupled-perturbed self-consistent field equations. Sometimes the response terms in fragment-based methods have been neglected.³⁶

2.3. Many-Body Improvements

The errors in the procedures presented so far are sometimes unacceptably large. In such cases, we can consider those procedures to constitute the one-body term in a many-body expansion and systematically improve the results by including higher-order terms in the expansion.

Two alternatives can be followed, which correspond to the use of X-Pol as a multilevel quantum chemical method,^14,36,37 as exemplified by the examples to be presented in section 3.1, or as a quantum mechanical force field that introduces empirical energy terms,^5,6,18 as in section 3.2. The Hartree product wave function in eq 1 implies that interfragment charge delocalization and exchange-repulsion interactions arising from the Pauli exclusion principle are neglected.^38,39 However, these interactions as well as interfragment dispersion interactions make critical contributions to intermolecular interactions. Together, they are included in a term called ΔE_XCD, and they must be properly accounted for.³⁸⁻⁴⁰ A brute force approach is to employ variational many-body expansion (VMB) theory to make two-body, three-body, and higher order corrections,^10,14 but nonvariational approaches are also possible.^11,30,34 When two- and three-body terms are included, we have, respectively, the corresponding VMB2 and VMB3 corrections,

6

7

In eqs 6 and 7, E_IJ and E_IJK are, respectively, the X-Pol energies when two and three monomers are grouped into a single superfragment. Thus, the difference in parentheses in eq 6 gives the two-body correction energy, ΔE_IJ, accounting for exchange and charge delocalization effects at the Hartree–Fock level plus dispersion-correlation contributions when correlated methods are used. Typically, the dimer and trimer fragments are significantly smaller than the full system, making the computation costs for a single oligomer negligible compared with the cost for a single calculation of the entire system. However, the number of trimer and higher-order terms increases rapidly with the number of fragments, rendering these terms impractical. Thus, in using this approach, it is critical to define a reference state for the monomer energy such that terms of order higher than 2 are negligible.^14,37

When the X-Pol method is used as a theoretical framework to develop force fields for condensed-phase and macromolecular systems, a simpler, empirical approach can be adopted, such as Lennard-Jones or Buckingham potentials (as used in molecular mechanics)^{2,3,8,15,17,20} or perturbation theory⁴¹ to estimate the dimer ΔE_AB^XCD terms.

3. Illustrative Examples

3.1. Multilevel X-Pol as a Quantum Chemical Model for Macromolecules

The X-Pol method can be used with different electronic structure representations for different fragments. This provides a general, multilevel QM/QM treatment for large systems, where the region of most interest could be modeled by a high-level electronic structure theory, embedded in an environment modeled by a lower-level representation.³³ To illustrate this possibility, a number of formulations of different electronic structure models have been used to describe the bimolecular complexes between CH₃CO₂H and H₂O and between a Zundel ion H₅O₂⁺ and four water molecules.³³ In multilevel X-Pol calculations with different QM models, the interaction between different fragments is coupled by the electrostatic potential, V_E^B, in eq 2. Two different charge models, namely, Mulliken population analysis (MPA) and electrostatic potential (ESP) charge-fitting, have been used to construct the charge-embedding Fock matrix (eq 5), whereas only the MPA charges were used in the variational X-Pol (eq 4) model.

The variational and embedded X-Pol interaction energies between H₅O₂⁺ and (H₂O)₄ are listed in Table 1, and they tend to overestimate the binding interactions since interfragment exchange-repulsion interactions are neglected. With the inclusion of the ΔE_XCD energy, derived from an energy decomposition analysis⁴⁰ using CCSD/MG3S and HF/MG3S results, the computed binding energies are significantly improved. The variational CCSD/MG3S:M06/MG3S combination yielded reasonable agreement (−68.0 kcal/mol) with the binding energy obtained from a higher-level CCSD(T)/MG3S calculation (−69.7 kcal/mol). The errors from the other combinations in the table range from 2.3 to 8.9 kcal/mol. This demonstrates that it is important to develop a systematic procedure to improve the accuracy of X-Pol (both variational and embedding models) beyond the monomer approximation.

Table 1. Computed Electrostatic Interaction Energies, ΔE_elec (kcal/mol), between H₅O₂⁺ (A) and (H₂O)₄ (B) Using Multilevel X-Pol with the Charge-Embedded and Variational Interaction Hamiltonians^a.

		charge-embedding		variational
A	B	ESP	MPA	MPA	ΔEXCD	ΔEb
M06	M06	–89.1	–87.5	–91.0	15.9	–75.1
M06	B3LYP	–87.7	–85.2	–88.1	15.9	–72.2
M06	HF	–92.0	–91.7	–94.5	15.9	–78.6
MP2	HF	–92.9	–92.7	–94.4	15.9	–78.5
CCSD	M06	–89.5	–88.0	–83.9	15.9	–68.0

^aThe 6-31G(d) basis set was used in all calculations with M06/MG3S optimized monomer and dimer geometries, and ΔE_XCD was estimated using HF and CCSD/MG3S energies.

The errors due to the Hartree-product approximation for the molecular wave function in X-Pol can be systematically corrected using variational^10,14 and embedding^5,34,42−45 many-body expansions (VMBn and EMBn). Table 2 displays the total interaction energies of four local-minimum-energy structures for the water hexamer, determined up to the third order VMB correction, as calculated by the Hartree–Fock (HF) and recently introduced polarized molecular orbital (PMO) methods.¹⁸ Although there are significant errors at the monomer level due to neglecting the ΔE_XCD contributions, the binding energies are significantly improved with the dimer correction (VMB2),¹⁴ and the computed results at the VMB3 level are in quantitative agreement with those from the corresponding full QM calculations.

Table 2. Computed Interaction Energies for Water Hexamer Structures from Unfragmented Quantum Mechanical Calculations, The Variational Many-Body Expansion (VMB), and Embedded Many-Body Expansion (EMB) Models at the HF/6-311G(d,p) and Polarized Molecular Orbital (PMO) Levels.

	book		cage		cyclic		prism
	HF	PMO	HF	PMO	HF	PMO	HF	PMO
Full QM	–45.1	–44.9	–45.9	–47.6	–44.3	–41.8	–47.1	–46.9
VX-Pol	–53.9	–26.8	–49.9	–25.0	–58.0	–28.7	–49.1	–24.3
VMB2	–42.5	–43.6	–44.9	–45.7	–39.8	–40.0	–46.2	–45.9
VMB3	–44.4	–44.8	–44.9	–46.5	–43.6	–41.6	–46.0	–46.8
EX-Pol	–39.2	–22.5	–37.2	–21.2	–41.2	–24.1	–36.8	–20.7
EMB2	–40.3	–39.0	–43.2	–41.1	–37.5	–35.3	–44.7	–41.3
EMB3	–44.4	–44.2	–44.9	–46.1	–43.3	–40.9	–45.9	–46.3

The VMB results are in systematically better agreement with the binding energies from full QM calculations than are the results of the corresponding charge-embedding approach. The difference is particularly striking at the two-body correction level, with average errors of 2.2 and 1.5 kcal/mol from VMB2@HF and VMB2@PMO, as compared with 4.2 and 6.1 kcal/mol for EMB2@HF and EMB2@PMO, respectively. This emphasizes the critical role of defining a good monomer energy in MB expansion theory, and the variational X-Pol energy leads to better convergence in correction terms. Including three-body energies, the errors are of chemical accuracy.

Although results for the small water clusters are encouraging, we found that significant errors exist for larger water clusters (Table 3). We examined a system containing 65 molecules, taken from a configuration in liquid simulations by keeping water molecules within 7.5 Å of a selected monomer center. We used HF, MP2, B3LYP and B3LYP-D, and PMO electronic structure methods to describe the monomers and dimers, all with the 6-31G(d) basis set (except PMO, which has a method-specific basis set). The absolute binding energies are not converged in these calculations; one may note in passing that the performance of the semiempirical PMO model¹⁸ for water is exceptionally good, but the main purpose here is to test the performance of many-body expansion theory. Among the four ab initio and density functional models, the average unsigned error using the variational model at the VMB2 level is about 60 kcal/mol, or about 1 kcal/mol per monomer. We see that the error is small employing the EMB2 approach with EX-Pol background charges; in particular, it is about 11 kcal/mol for the complex or 0.17 kcal/mol per monomer. For comparison, a fragment molecular orbital calculation (in particular by the FMO2 procedure, which is very similar to the MB2 approach) for a 64-water cluster yielded an error of 0.003 au (1.9 kcal/mol) per monomer by employing MP2.⁴⁶ The origin of relatively large errors in VMB is due to charge penetration effects in X-Pol optimization. While this is not significant with a minimal basis such as that employed in semiempirical methods, it can become unphysically large when extended basis sets are used.⁴⁷ In some cases, an explicit exchange repulsion potential may be needed to prevent these effects.

Table 3. Computed Interaction Energies for a (H₂O)₆₅ Water Cluster Using Variational and Embedding X-Pol and Two-Body Corrections^a.

	Full QM	VX-Pol	VMB2	EX-Pol	EMB2
HF	–645.5	–1008.7	–691.2	–942.4	–638.8
MP2	–975.6	–915.3	–917.3	–877.3	b
B3LYP	–887.1	–861.5	–953.7	–797.6	–874.4
B3LYP-D	–1042.7	–861.5	–1109.4	–797.6	–1030.1
PMO	–735.5	–432.6	–720.9 (−734.7)c	–344.8	–602.6 (−722.3)c

^aThe 6-31G(d) basis set was used in ab initio and DFT calculations.

^bNot calculated.

^cEntries in parentheses are by VMB3 and EMB3.

Charge penetration effects are much smaller in many-body corrections using the PMO semiempirical method, as illustrated for a range of water clusters with and without periodic boundary conditions. In this case, both VMB3 and EMB3 binding energies are nearly in quantitative agreement with the unfragmented QM results (see Supporting Information); however, embedded MB3 is much more efficient than VMB3 in energy calculations since the SCF is carried out on trimer fragments with fixed background charges.

Figure 2 displays the interaction energy due to charge delocalization with respect to charge transferred for the cluster of 65 water molecules at the two-body VMB2 level with HF/6-31G(d). The figure shows a good correlation between charge transfer energy and the net amount of charge migration between two monomers; such correlations are critical to the success of MM force fields, in which charge transfer are not explicitly included. Similar correlations have been observed in cation−π complexes from energy decomposition analysis, and they can be rationalized based on perturbation theory.⁴⁸

Figure 2.

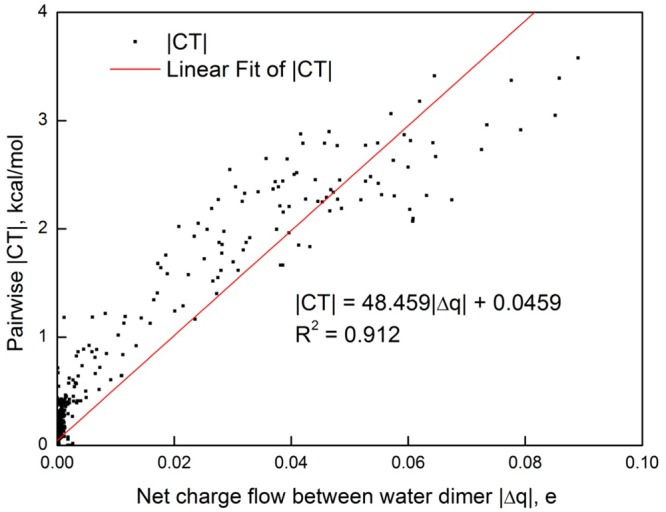
Computed dimeric charge transfer energy versus the amount of charge transferred from a donor water molecule into an acceptor water molecule for a water cluster system consisting of 65 water molecules.

3.2. X-Pol as a Quantum Mechanical Force Field

Although ab initio molecular orbital theory and density functional theory can be used to improve the accuracy of X-Pol results, it is still impractical to use these methods to perform molecular dynamics simulations on large systems for an extended period of time. With increased computing power, this will become feasible in the future; however, at present, it is desirable to use semiempirical methods such as neglect of diatomic differential overlap (NDDO)⁴⁹ methods or the more recent self-consistent-charge density functional tight-binding (SCC-DFTB)⁵⁰ method to model condensed-phase systems and biomacromolecules.

The construction of a QMFF based on the variational X-Pol formalism has two components. First, a computationally efficient quantum chemical model is needed to describe the electronic structure of individual molecular fragments. Here we use the PMO method,⁵¹ which is based on the MNDO formalism with the addition of a set of p-orbitals on each hydrogen atom. It was found that the computed molecular polarizabilities for a range of compounds containing hydrogen, carbon, oxygen, and fluorine are significantly improved in this method.^21,51,53 In addition to the enhancement in computed molecular polarizability, a damped dispersion function is included as a post-SCF contribution to the electronic energy.⁵⁴ Second, a practical and parametrizable procedure is desired to model interfragment electrostatic and exchange-dispersion interactions. For the electrostatic component, a dipole-preserving and polarization consistent (DPPC) method has been used to derive partial atomic charges that can exactly reproduce the instantaneous molecular dipole moment from the polarized electron density of each fragment.⁵⁵ Since the DPPC charges are optimized by a Lagrange multiplier technique, there are no new empirical parameters. For the ΔE_XCD term, pairwise Lennard-Jones potentials were adopted with monatomic parameters; such potentials contain two parameters for each atomic number.^15,17,20 Employing this strategy, X-Pol quantum chemical models for water¹⁸ and for hydrogen fluoride²¹ have been developed for fluid simulations.

3.2.1. Water

The water model is called XP3P, and the system-specific parametrization of the PMO method that is used as part of this model is called PMOw. The results from simulations of liquid water¹⁸ are displayed in Table 4 for 25 °C and 1 atm, along with results from the TIP3P pairwise potential and from two polarizable force fields, namely, AMOEBA and SWM4-NDP. The data in Table 4 were obtained from an assemblage of over 900 million configurations in Monte Carlo simulation and 500 ps of molecular dynamics simulation for a cubic system containing 267 water molecules;¹⁸ the latter took about 24 h (1 fs integration step) on an eight-core workstation, while about 7 million configurations can be executed in Monte Carlo sampling. The average density and heat of vaporization of the XP3P water are within 1% of the experimental values. Quantities involving intermolecular fluctuations such as isothermal compressibility, coefficient of thermal expansion, and dielectric constant are more difficult to converge, but overall, the agreement with experiment is good,¹⁸ and the performance of the XP3P model is as good as any other empirical force field in dynamics simulations.

Table 4. Computed Liquid Properties of the XP3P Model for Water along with Those from Experiments, and the TIP3P, AMOEBA, and SWM4-NDP Models^a.

	XP3P	TIP3P	AMOEBA	SWM4-NDP	expt
ΔHv, kcal/mol	10.42 ± 0.01	10.41	10.48	10.51	10.51
density, g/cm3	0.996 ± 0.001	1.002	1.000	1.000	0.997
Cp, cal mol–1 K–1	21.8 ± 1.0	20.0	20.9		18.0
106κ, atm–1	25 ± 2	60			46
105α, K–1	37 ± 3	75			26
μgas, D	1.88	2.31	1.77	1.85	1.85
μliq, D	2.524 ± 0.002	2.31	2.78	2.33	2.3–2.6
105D, cm2/s	2.7	5.1	2.02	2.3	2.3
ε	97 ± 8	92	82	79 ± 3	78
τD, (ps)	8.8			11 ± 2	8.3
τNMR, (ps)	2.6			1.87 ± 0.03	2.1

^aΔH_v, heat of vaporization; C_p, heat capacity; κ, isothermal compressibility; α, coefficient of thermal expansion; μ, dipole moment; D, diffusion constant; ε, dielectric constant; τ_D, Debye relaxation time; and τ_NMR, NMR rotational relaxation time.

Adapted with permission from ref (18). Copyright 2013 AIP Publishing LLC

Monte Carlo simulations of liquid water were performed at temperatures ranging from −40 to 100 °C, and Figure 3 shows the distribution of the instantaneous molecular dipole moments. We can infer from the broadness of the observed distribution that water molecules in the liquid experience a wide spectrum of instantaneous electrostatic fields from the rest of the system. Figure 3 indicates that the maximum value in the dipole probability density distribution is the same at different temperatures, despite the large change in the dipole fluctuations, suggesting that there is polarization saturation in liquid water. The average molecular dipole moment of water in the liquid at 25 °C was determined to be 2.524 ± 0.002 D, which represents an increase of 35% relative to the gas-phase value (1.88 D) from the PMOw Hamiltonian. There is no experimental data for direct comparison, but Sprik concluded that an average dipole moment of 2.5–2.6 D in liquid water would most likely yield the correct dielectric constant.⁵⁶

Figure 3.

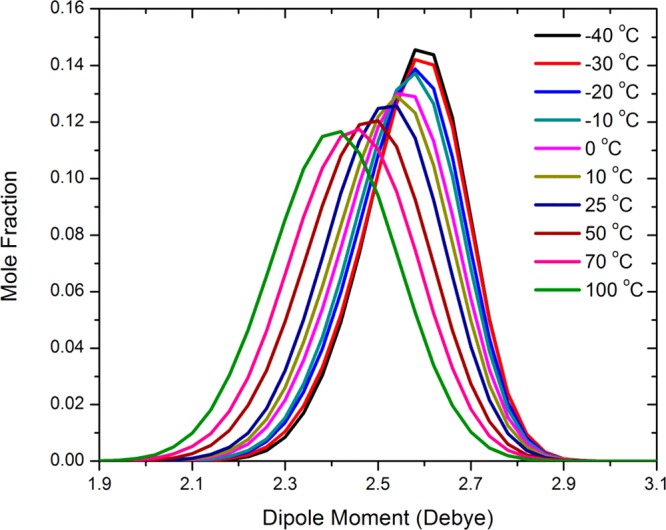
Distribution of the molecular dipole moment of water in the liquid at temperatures ranging from −40 to 100 °C. Adapted with permission from ref (18). Copyright 2013 AIP Publishing LLC.

All other thermodynamic and dynamic properties determined using the XP3P model in Table 4 agree reasonably well with experiments and are of similar accuracy to results by other empirical models.¹⁸ Figure 4 shows the structure of liquid water characterized by radial distribution functions, g_xy(r). In comparison with the neutron scattering data,⁵⁷ the computational results are in excellent agreement with experiments. In particular, a well-resolved minimum was obtained following the first peak in the O–O distribution, which with the XP3P potential is at 2.78 ± 0.05 Å with a peak height of 3.0. The corresponding experimental values are 2.73 Å and 2.8 from neutron diffraction.⁵⁷

Figure 4.

Computed (blue) and experimental (red) radial distribution functions for the O–O pair in liquid water at 25 °C. Adapted with permission from ref (18). Copyright 2013 AIP Publishing LLC.

3.2.2. Ionic Liquid

The X-Pol method was used in molecular dynamics simulations for a system consisting of 125 pairs of 1-ethyl-3-methylimidazolium (EMIM) cations and acetate anions in a periodic box using the AM1 model⁵⁸ to represent each ion as a molecular fragment. Conventional molecular dynamics simulations of ionic liquids often employ charge-scaled force fields to approximate charge transfer effects between anions and cations, and scaling factors ranging from 0.7 to 0.9 have been used.⁵⁹⁻⁶¹ With the VMB2 scheme, it was found that there is a relatively small amount of charge transfer between acetate and EMIM, with an average departure of only 0.03 from unit ionic charges. In contrast, the average charge transfer over five minimum energy configurations in the gas phase was 0.10, similar to other studies.⁵⁹ Thus, it appears that condensed phase polarization effects significantly reduce the amount of charge transfer between cations and anions in ionic liquids; this casts doubt on modeling them with charge-scaling factors significantly deviating from unity.

3.2.3. Protein Simulations

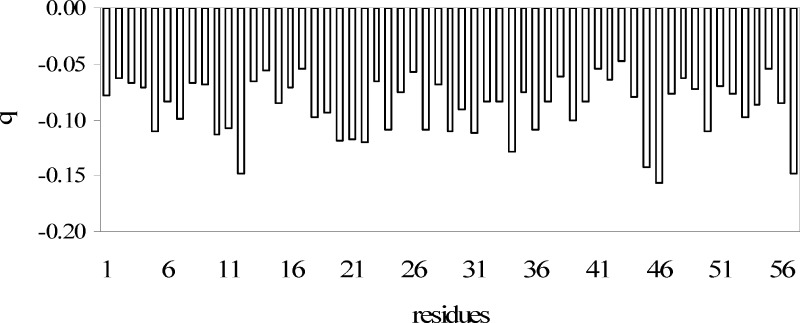
The small protein bovine pancreatic trypsin inhibitor (BPTI) was simulated in water with periodic boundary conditions using the AM1 electronic structure method.²³ The simulation involved 14 281 atoms and 29 026 basis functions, for which 3.2 ps (1 fs time-step) could be performed per day on a single processor (1.66 GHz) computer. Figure 5 depicts the average partial atomic charge of the carbonyl group for each amino acid of the polypeptide chain. There is significant fluctuation of the charge distribution in the backbone carbonyl group depending on its sequence location because of its different electrostatic environment as a result of specific hydrogen-bonding interactions with the solvent and polarization by nearby residues. (Since standard semiempirical methods are known to underestimate intermolecular polarization effects, the findings from this study likely represent a lower limit of the polarization effects.) This study illustrates the importance of electronic polarization effects in macromolecular simulations. For comparison, the standard CHARMM22 force field makes use of neutral group convention where the total net atomic charge of the peptide carbonyl group is zero, and the partial atomic charges in the group are the same in all conformational substates.

Figure 5.

Average partial charges (in atomic units) on the backbone carbonyl (C=O) groups of BPTI, arranged in order of sequence number. Adapted with permission from ref (23). Copyright 2009 American Chemical Society.

4. Concluding Remarks

In this Account, we presented a new strategy to construct potential energy surfaces for macromolecular and liquid-phase systems on the basis of quantum mechanics. Electronic structure theory is directly used to model intermolecular interactions, rather than using quantum mechanical calculations to fit analytical potentials. Potential energy surfaces produced by this approach are called quantum mechanical force fields (QMFFs).

Our strategy, called X-Pol, is based on the partition of condensed-phase and macromolecular systems into fragments to achieve computational efficiency. The intrafragment polarization and the mutual polarization between different fragments are treated explicitly using self-consistent quantum mechanical calculations. The present theory can be used as a single-level method in which all fragments are treated in the same way or more generally as a multilevel electronic structure model in which different fragments are represented by different quantum chemical methods. The X-Pol wave function can be optimized either using a variational Fock operator or through a charge-embedding iterative approach. In both cases, interfragment electrostatic interactions are directly included, whereas the remaining effects, called ΔE_XCD, consisting of exchange-repulsion, charge delocalization, and missing dispersion and correlation energies, can be systematically incorporated using a many-body expansion or by approximating ΔE_XCD with empirical functions.

So far, we have shown the feasibility of X-Pol for molecular dynamics simulations of a solvated protein in aqueous solution and the accuracy of the X-Pol QMFF for condensed-phase simulations, including liquid water and hydrogen fluoride. The method can also model physical properties that cannot be directly obtained using classical force fields. The project of developing broadly applicable parameters for using X-Pol as a QMFF is still in its infancy, but the method has great promise.

Biographies

Jiali Gao studied at Beijing University, followed by graduate education at Purdue and postdoctoral research at Harvard. He was on the faculty of the State University of New York at Buffalo, and he is currently a Professor of Chemistry with partial appointments at the University of Minnesota and Jilin University.

Donald G. Truhlar earned a B.A. from St. Mary’s College of Minnesota and a Ph.D. from Caltech. He is Regents Professor of Chemistry, Chemical Physics, Nanoparticle Science and Engineering, and Scientific Computation at the University of Minnesota, where he has served on the faculty since 1969.

Yingjie Wang earned a B.S. in chemistry (2009) from Nanjing University. He is currently a fifth-year graduate student of Chemical Physics at University of Minnesota.

Michael J. M. Mazack received a B.S. in mathematics with a physics minor from Western Washington University in 2007. He obtained an M.S. in mathematics from the same institution in 2009, studying numerical linear algebra under Professor Tjalling Ypma. He completed a Ph.D. in scientific computation at the University of Minnesota in 2014 under Professor Jiali Gao, researching the explicit polarization theory and developing coarse-grained models for proteins.

Patrick Löffler earned a B.S. in biology (2009) from the University of Erlangen-Nuremberg and a M.S. in bioinformatics (2012) from the University of Hamburg. After having spent time as a Visiting Researcher at the University of Minnesota, he is currently a Ph.D. student at the University of Regensburg.

Makenzie Provorse received a B.S. in Chemistry from Kansas State University in 2009 and a M.S. and Ph.D. in Chemistry from the University of Minnesota under the guidance of Prof. Jiali Gao in 2010 and 2014, respectively. She is currently a postdoctoral associate with Assistant Prof. Christine Isborne at the University of California at Merced.

Pavel L. Rehak earned a B.S. from SUNY Stony Brook in 2010, double majoring in Chemistry and Mathematics. He is currently a graduate student under the supervision of Dr. Jiali Gao.

Supporting Information Available

A table containing the PMO energies from variational and charge-embedding X-Pol and many-body expansion theory up to three-body terms for water clusters and periodic systems is provided, along with the Cartesian coordinates for a cluster of 65 water molecules. This material is available free of charge via the Internet at http://pubs.acs.org.

We thank the National Institutes of Health (Grants GM46376 and GM091445) for partial support of this research.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States