Accounting for Photophysical Processes and Specific Signal Intensity Changes in Fluorescence-Detected Sedimentation Velocity

Abstract

Fluorescence detected sedimentation velocity (FDS-SV) has emerged as a powerful technique for the study of high-affinity protein interactions, with hydrodynamic resolution exceeding that of diffusion-based techniques, and with sufficient sensitivity for binding studies at low picomolar concentrations. For the detailed quantitative analysis of the observed sedimentation boundaries, it is necessary to adjust the conventional sedimentation models to the FDS data structure. A key consideration is the change in the macromolecular fluorescence intensity during the course of the experiment, caused by slow drifts of the excitation laser power, and/or by photophysical processes. In the present work, we demonstrate that FDS-SV data have inherently a reference for the time-dependent macromolecular signal intensity, resting on a geometric link between radial boundary migration and plateau signal. We show how this new time-domain can be exploited to study molecules exhibiting photobleaching and photoactivation. This expands the application of FDS-SV to proteins tagged with photoswitchable fluorescent proteins, organic dyes, or nanoparticles, such as those recently introduced for subdiffraction microscopy and enables FDS-SV studies of their interactions and size distributions. At the same time, we find that conventional fluorophores undergo minimal photobleaching under standard illumination in the FDS. These findings support the application of a high laser power density for the detection, which we demonstrate can further increase the signal quality.

Sedimentation velocity (SV) analytical ultracentrifugation (AUC) is a classical technique of physical biochemistry that allows observing the strongly size-dependent migration and diffusion of macromolecules in the gravitational field of an ultracentrifuge.¹ In recent decades, the introduction of modern computational analysis, among them direct boundary modeling with numerical solutions of the partial differential equation of centrifugal transport,²⁻⁴ the Lamm equation (eq 5), and their use as a kernel in the differential sedimentation coefficient distribution c(s)⁶ and its multispectral extension c_k(s),⁷⁻⁹ in combination with progress in the theory of sedimentation of interacting systems^4,10−13 have significantly expanded the sensitivity, resolution, and scope of applications of SV. The latter span a wide range of topics, including protein and other macromolecular interactions,¹⁴ multiprotein complexes,^15,16 hydrodynamic modeling,^17,18 the quantitation of trace oligomers in the pharmaceutical industry,¹⁹ and the characterization of nanoparticles.²⁰ Furthermore, SV is highly complementary to other biophysical techniques for studying multisite protein interactions in solution, due to the potential of simultaneously resolving size and population of different coexisting states and can be quantitatively combined with data from isothermal titration calorimetry, surface plasmon resonance, and/or fluorescence polarization.^21,22

Fluorescence optical detection for AUC has been developed by several groups,²³⁻²⁶ and a design by Laue and co-workers^27,28 resembling a moveable confocal microscope was recently developed into a commercially available accessory for AUC by AVIV Biomedical, Inc. FDS-SV has the potential for a further transformation of SV, chiefly due to its many orders of magnitude greater sensitivity, which brings it into the same concentration range as fluorescence correlation spectroscopy²⁹ and below. This was exploited in many applications to study the size distribution, conformation, and interactions of proteins and assemblies.³⁰⁻⁴³ Initially, the majority of applications were aimed at more qualitative questions of protein oligomeric states in dilute solutions or in crowded environments,^27,28 partly due to concerns of signal nonlinearity and photobleaching leading to limited accuracy.^27,28,30 However, the analysis has undergone rapid development, and we and others have demonstrated the potential for highly quantitative analyses and for determination of binding constants in high-affinity protein interactions.^37,43−48 In particular, taking advantage of the statistical properties of c(s) analysis, and using Raman scattering of water as a meniscus marker, we have demonstrated low picomolar detection limits, allowing the determination of the binding energy of very high-affinity systems with K_D as low as 20 pM.⁴⁷ Further, we and others have shown that signal linearity is usually not a concern at nM concentrations and below.^45,46 In fact, the intrinsic data quality is superb, leading to fits with models for macromolecular sedimentation and diffusion that rival that of the best conventional detection system, but only after characteristic data structure of this detection system is accounted for.⁴⁶ Besides factors governed by beam geometry and out-of-plane movement of the focal point, a slowly time-dependent drift in the signal intensity was recognized as a crucial component of the boundary model.⁴⁶

In the present work, we explore the time-dependent signal intensity changes in closer detail, using as models fluorescent protein variants and FITC-labeled protein. We show that the evolution of signal boundary profiles in SV offers an internal reference of intrinsic signal intensity and its changes with time. We demonstrate that an additional time-domain for signal intensity changes of fluorophores can be folded into the boundary analysis, such that it retains a reliable measurement of the macromolecular sedimentation parameters. As a result, it is possible to study a wider range of fluorophores, especially now including photoswitchable fluorescent proteins and organic dyes which may decrease or increase their fluorescence upon excitation and are frequently used in super-resolution fluorescence microscopy. At the same time, we find that photobleaching of standard fluorophores such as EGFP (enhanced green fluorescent protein) and FITC is negligible under illumination conditions in FDS-SV. Finally, we demonstrate the improved signal/noise ratio with a higher powered laser than previously in use.

Methods

Fluorescent Proteins

The cDNA for Dronpa⁴⁹ was purchased from Amalgaam (Nagoya, Japan), amplified using the N-terminal primer 5″-GACGGATCCATGAGTGTGATTAAAC-3″ containing a BamHI site and the C-terminal primer 5″-GACGAATTCTTACTTGGCCTGCC-3″ containing an EcoRI site, and cloned into pRSETA (Invitrogen). Plasmid (pQE31) containing the cDNA for histidine tagged Padron⁵⁰ was a gift from Stefan Jakobs. All proteins including enhanced green fluorescent protein (EGFP) were prepared as described previously.⁴⁶ Bovine serum albumin (BSA, #A7030, Sigma, St. Louis) was fluorescently labeled with FITC using standard amine coupling chemistry (#53027, Thermo Fisher Scientific, Rockford, IL). Unless mentioned otherwise, proteins were used at a concentration of 100 nM dissolved in phosphate buffered saline (PBS), pH 7.4.

Fluorescence Detected Sedimentation Velocity Analytical Ultracentrifugation

FDS-SV experiments were carried out in an Optima XL-A analytical ultracentrifuge (Beckman Coulter, Indianapolis, IN) with a fluorescence detection system FDS (Aviv Biomedical Inc., Lakewood, NJ). The FDS instrument used was equipped with an operating software-adjustable 50 mW diode laser at 488 nm, which is a feature of all currently built FDS instruments. This adjustable laser has replaced the fixed power 10 mW solid-state laser (an integrated package of an infrared laser diode frequency doubled to 488 nm) that was used in older instruments but discontinued in 2013 by the laser manufacturer.

Emission is collected between 505 and 565 nm with a standard bandpass filter. Briefly, 400 μL samples of protein dissolved in phosphate buffered saline (PBS) to final concentrations between 50 and 500 nM were loaded in cell assemblies with standard 12 mm double sector centerpieces, inserted in a eight-hole rotor, and placed in the chamber of the ultracentrifuge which was evacuated to high vacuum (zero or a few micron pressure). The laser power was adjusted to the target level and warmed up for at least 10 min. For adjustment of the detection settings, the rotor was accelerated to a rotor speed of 3000 rpm. At a focal depth of 4 mm, photomultiplier voltage and gain were set as to allow for data acquisition with a signal/noise ratio on the order of 100:1, at the same time not exceeding ∼3000 counts/s. Angular data acquisition windows were adjusted for each cell conservatively to eliminate signal contributions from the autofluorescence of the charcoal-filled Epon centerpiece. As described previously,⁴⁸ after optics adjustments at 3000 rpm, it is necessary to stop the run, to allow for a well-defined start of the sedimentation process.⁵¹ When working with photoswitchable molecules and at high laser power, a potential concern is that the stationary illumination during this phase may potentially cause local photophysical effects creating a blip or dip in intensity. To create uniform conditions, it may be necessary to resuspend the solution after the initial optics adjustment; otherwise the first few scans will have to be discarded until diffusion has diminished this local feature. Gently rotating the cell assemblies will also resuspend material that may have settled at the low centrifugal field. Temperature was equilibrated at 20 °C for between 1 and 3 h at rest, prior to rotor acceleration from 0 to 50 000 rpm. Fluorescence scans were acquired at the highest possible rate for 10 h. Data were processed with the automatic sorting function for FDS data in SEDFIT and analyzed in the same software taking into account the structure of fluorescence scan data,⁴⁶ with the extensions described below. In the calculations, the standard solvent density and viscosity was used, with a protein partial specific volume of 0.73 mL/g. All plots were created with GUSSI (kindly provided by Dr. Chad Brautigam).

Data Analysis

The experimental sedimentation data a(r,t) were modeled with an extension of the c(s) distribution,⁶ where we have replaced the kernel from being a simple normalized Lamm equation solution χ₁(r,t) that describes the spatiotemporal evolution of the concentration distribution of ideally sedimenting species at unit concentration,^2,52 by the signal χ̃₁(r,t) that would be measured with the fluorescence optical system for the same ensemble of particles. To this end, the signals were expressed as a radial convolution

1

(with the normalization factor for convolution N^–1 = ∫_r–3σ^r+3σ e^{–(r–r)2/σ2} dr′) to account simultaneously for the limited optical resolution with half-width σ,⁴⁶ the factor B(r_b, δ, r) with

2

to describe the shadow from obstruction of the excitation and/or emission cone by the sample holder at the end of the solution column at radius r_b, obscuring part of the circular beam with diameter δ,⁴⁶ as well as the factor

3

for describing the linearly changing signal magnification with radius. The latter is normalized relative to the meniscus position r_m, with the constant coefficient α_r ≡ dM/dr, and caused by the unavoidable misalignment of the plane of rotation with the line of optical focus through the sample.⁴⁶

Most important in the present context is the temporal modulation T(t). In our previous work, we expressed this as a linearly increasing function (1 + α_tt) with the constant coefficient α_t to account for a temporal laser drift.⁴⁶ For the present context, we have extended this by a single-exponential process

4

with a rate constant k toward a new steady-state amplitude A that can be completely (A = 0) or partially (0 < A < 1) photobleached or photoactivated (A > 1; with A = 1 describing a temporally constant signal).

It is instructive to consider the source of information on these slowly time-dependent processes: In concentration units, the solution χ(r,t) of the Lamm equation

5

due to the mass balance in sector-shaped geometry, obeys the square dilution law

6

that firmly links the ratio of plateau concentrations (c_plateau) and loading concentration (c₀) at any time to the radial position of the boundary midpoint (r_mid). However, under the influence of a temporal modulation of signal intensity the plateau signals will deviate from eq 6. In fact, in a simplistic analysis assuming a hypothetical diffusion free sedimentation process, one could even determine the temporal modulation directly from the plateau signals as

7

However, this is not attempted due to the diffusion broadening of the boundaries and ubiquitous sample imperfections (especially polydispersity) making it very difficult to accurately define a single boundary midpoint. On the other hand, in the form of eq 4, an explicit model for the temporal modulation of signal can be incorporated into the sedimentation model such as to take advantage of the same source of information intrinsic to SV data.

Proceeding from here as in the standard c(s) method, the data are modeled as a superposition of such signals χ̃₁(r,t) from species with sedimentation coefficients s and a diffusion coefficient D(s), superimposed by a radial-dependent but temporally constant TI baseline term b(r)^53,54

8

where D(s) is calculated with the standard hydrodynamic scaling law for compact particles and scaled by a signal-average frictional-ratio f/f₀, which is adjusted in nonlinear regression of the experimental data.⁵⁵ After an initial fit determining the beam diameter δ and an estimate of the meniscus position r_m, the left fitting limit was adjusted to a radius of approximately r_m + δ, so as not to include reflection and refraction effects from the meniscus in the data set to be analyzed.

Results

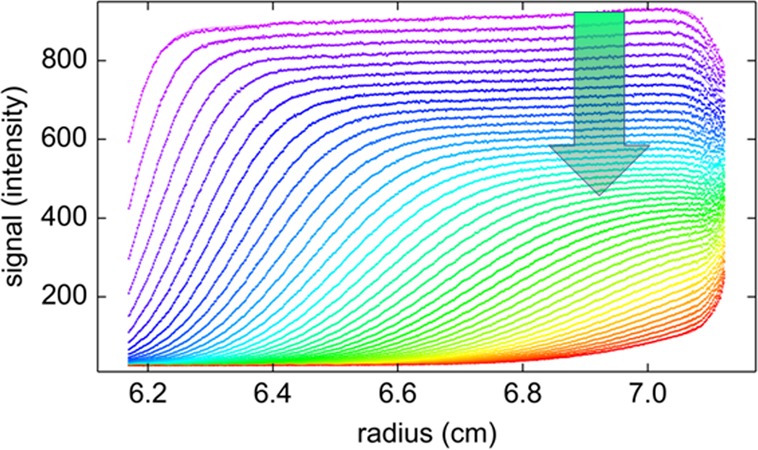
As a test for the theoretical model of sedimentation including photophysical processes, we acquired FDS-SV data of Dronpa, a monomeric mutant of a fluorescent coral protein developed as a reversibly photoswitchable molecule,⁴⁹ currently widely used in cell biological applications and super-resolution microscopy.^56,57 In order to create a comprehensive data set with varying degrees of photobleaching or photoswitching to an off state, as a test whether macromolecular sedimentation properties could be modeled in all cases, the laser power of the 488 nm excitation beam was varied in consecutive experiments, using settings of 50.2 mW, 8.4 mW, and 2.1 mW. Lower laser power was partially compensated for by using higher photomultiplier voltages and gain settings to keep the signal/noise ratio high. Data were acquired for a duration of ∼6 h, after which the concentration boundary has traversed the solution column at a rotor speed of 50 000 rpm (Figure 1). In deviation from conventionally detected SV, they all possess the expected characteristic structure of FDS data previously reported,⁴⁶ including a radial-dependent increase in the signal magnification from scanning out of plane of rotation (not to be confused with sloping plateaus due to aggregate formation, which is confined to early scans only), and a drop in signal intensity close to the end of the solution column from the shadow of the sample holder (dashed red line and red arrow in Figure 1A). In addition, a very strong depletion of the plateau signal with time can be discerned. In Figure 1, it is highlighted by the gray vertical arrows, which measure the relative decrease of the plateau for equivalent scans where the boundary has moved approximately 4 mm into the solution column. This feature is most obvious in the data at 50.2 mW, and less at 8 mW. For reference, the depletion of the plateau signal at 2 mW corresponds to solely the geometrically imposed square dilution law; in fact, only a statistically insignificant increase in the rmsd of fit from 5.944 to 5.956 is obtained when not allowing for any time-dependent drift (T(t) = 1.0 at all times), indicating the absence of detectable photobleaching. Conversely, any excess vertical spread of boundary plateau signals visually indicates the temporal modulation of signal T(t) (eq 7).

Figure 1.

Sedimentation velocity data of 100 nM Dronpa at 50 000 rpm, with 488 nm excitation at laser power settings of 50.2 mW (A), 8.4 mW (B), and 2.1 mW (C), and emission detected through a standard 505–565 nm bandpass with photomultiplier and gain settings adjusted to keep the signal in an appropriate range. Shown in the upper panels are data points (symbols) and best-fit model (lines) following eq 8 with exponential decay T(t) as in eq 4, with α_t = 0; residuals are shown in the lower panels. The color temperature indicates the progression of time, violet for early times and red for late times. Characteristic features of FDS data are a radial gradient of signal intensity, α_r, indicated by the dashed red line, and a shadow of the end of the solution column, indicated by the red arrow in panel A. The laser power-dependent temporal modulation of signal T(t) is indicated in all plots as gray vertical arrows, which, for visual reference, highlight the plateau depletion within the first 2.5 h of the sedimentation process. For the 2.1 mW data, the plateau depletion corresponds to solely the geometrically imposed radial dilution.

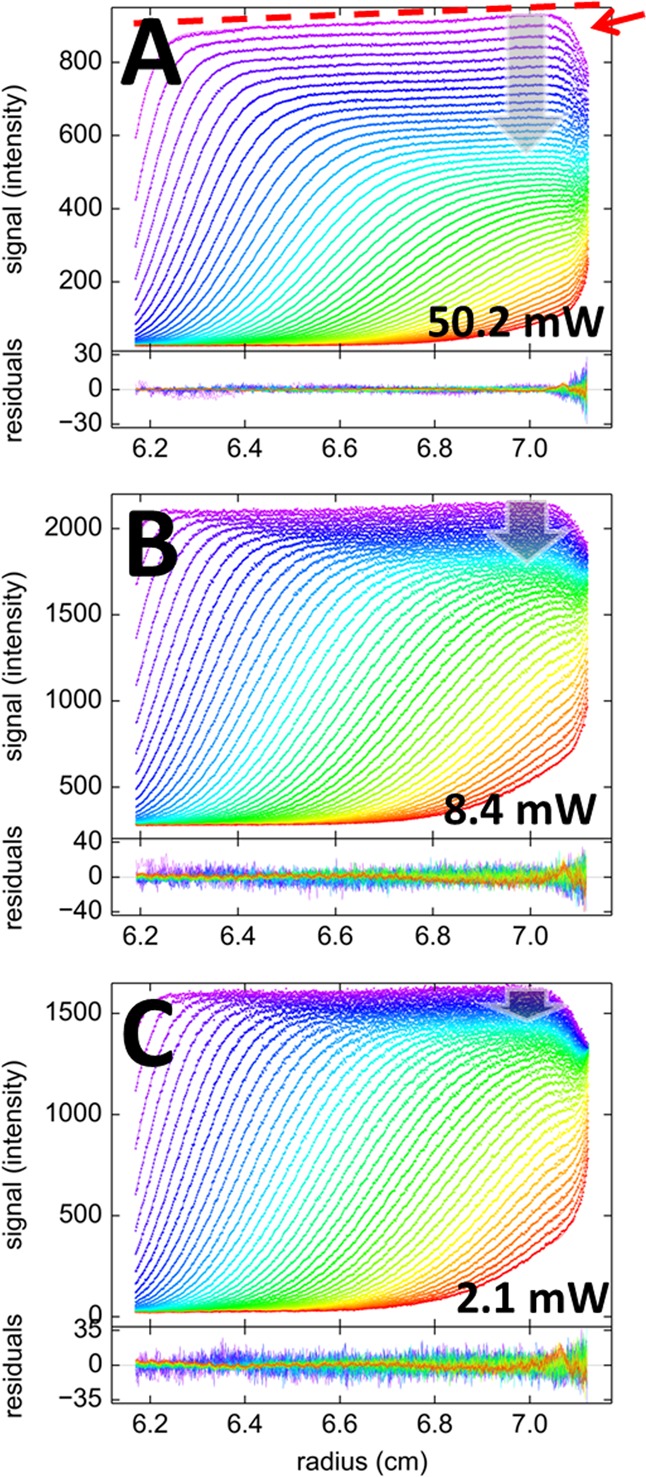
All SV data at all power settings for Dronpa in Figure 1 can be modeled with an excellent quality of fit, taking into account the slow temporal signal modulation as a single exponential process (eq 4). The best-fit parameter estimates are summarized in Table 1. Not surprisingly, the final signal/rmsd ratio increases with decreasing laser power, at the highest setting reaching a value of 480, which rivals that of the best conventional detection systems. The best-fit rate constant of photobleaching increases roughly proportional with laser power. As shown in Figure 2, the sedimentation coefficient distributions c(s) derived from these fits are essentially indistinguishable at different laser power settings, all showing a single species with consistent S-values and with consistent best-fit frictional ratios implying apparent molecular weights of ∼31.9 kDa, which is within uncertainty of buoyancy consistent with the theoretical molecular weight of 29.6 kDa for the Dronpa construct used (Table 1). This shows that despite the very substantial photobleaching at the higher laser power, the sedimentation properties of Dronpa have been correctly obtained with the sedimentation model of eq 8.

Table 1. Sedimentation and Photophysical Parameters of Different Fluorescent Proteins as a Function of Laser Power^a.

molecule	rotor speed	power (mW)	signal/rmsd ratio	rate (1/h)	spatial drift (%/cm)	s (S)	f/f0c
Dronpa	50 000	50.2	480	0.257 (0.250–0.265)	7.1 (6.3–7.9)	2.75	1.31
	50 000	8.4	320	0.030d (0.028–0.032)d	3.4 (2.6–4.0)d	2.74	1.31
	50 000	2.1	260	0 (<0.004)d	2.5	2.77	1.30
	3000	50.2		0.219
Padron	50 000	50.2	114	1.46 (1.37–1.53)	0.7 (−1.1–2.8)	2.64	1.25
	50 000	8.4	90	0.29 (0.16–0.45)	10.6 (−13–43)	2.58	1.25
	50 000	2.1	14.4	0.038	9.9	2.68	1.34
	3000	50.2		1.43
EGFP pH 7.4, PBS	50 000	50.2	222	0.86% (0.4–1.1)	9.4 (7–14)	2.72	1.40
	50 000	8.4	84	0.21% (−0.1–1.1)	11.4 (6–18)	2.71	1.45
	50 000	2.1	64	0.74%	6.8	2.75	1.38
EGFPe pH 5.7, ce6	50 000	50.2	289	0.52%b (0.3–0.8)	11.9 (9–15)	2.72	1.37

^aAll samples at the same laser power and rotor speed were measured side-by-side in the same run. All protein concentrations are 100 nM. Error intervals calculated by F-statistics on a 68% confidence interval.

^b%/hour linear drift.

^cUncorrected for solvent buoyancy, viscosity, and protein partial-specific volume.

^dWith A constrained to zero (limit of complete photobleaching) to avoid correlation with the rate.

^eIn the presence of 100 μM chlorin e₆, phosphate buffered saline at pH 5.7.

Figure 2.

Sedimentation coefficient distributions c(s) corresponding to the fits of the FDS-SV data of Dronpa in Figure 1.

We carried out a control experiment to independently measure the time dependence of the fluorescence signal. At a rotor speed of 3000 rpm sedimentation of Dronpa is virtually absent, such that scans with the FDS are radially uniform and report solely the time-course of fluorescence, after subtraction of a baseline fluorescence determined from a final high-speed sedimentation phase depleting the macromolecules. The resulting decrease of average fluorescence signal across the solution column for Dronpa at 50.2 mW illumination (Supporting Information Figure S1) was well described over the 6 h period by a single exponential with a rate constant of 6.08 × 10^–5 s^–1. This value compares reasonably well with the best-fit bleaching rate constants from modeling the SV data of 7.1 (6.9–7.5, 68% CI) × 10^–5 s^–1 at 50.2 mW. Slight differences in the rate constant may arise from different hydrodynamic friction⁵⁸ or pressure in the two experiments, or from different scan times. However, the determination of the sedimentation properties is unaffected by these considerations.

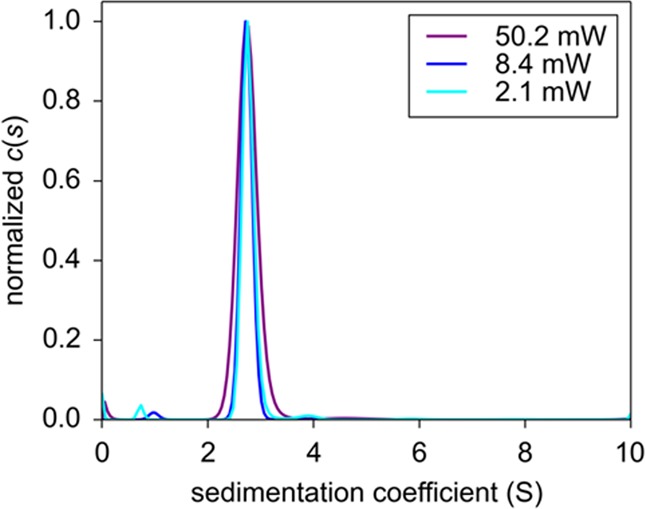
The opposite temporal behavior is exhibited by Padron,⁵⁰ as it is switched on with 488 nm excitation, resulting in signal increases in fluorescence to ∼160% its initial value at 50.2 mW of illumination in the FDS (Figure 3). The time-constant is 3.9× 10^–4 s^–1 at 50.2 mW, which causes the signal increment to attain a steady-state halfway through the sedimentation process. In the second half of the sedimentation experiment, the dominant effect is the decrease of plateau signals with time in a way that is coupled to boundary movement and radial dilution as predicted by the square dilution law. This time behavior is also very well described with a superposition of temporally modulated Lamm equation solutions, eq 8. In experiments at intermediate laser power (data not shown), the photophysical rate constant is lower and the bleaching/activation steady-state is not reached during the run; therefore a correlation exists between the temporal signal modulation rate constant and the extrapolated final amplitude. Like Dronpa, at the lowest laser power, Padron did not exhibit significant photophysical processes, and a model with constant signal increment can describe the data well (data not shown). The resulting c(s) distributions at the different laser power settings are shown in Figure 3B. They all virtually superimpose, with main peaks of consistent signal-weighted average sedimentation coefficients and diffusional boundary spreads implying consistent apparent molecular weights (Table 1). The control experiment under high laser power illumination and nonsedimenting conditions provides a best-fit rate constant in excellent agreement with the SV analysis (Table 1) but at later times also reveals a slow time-dependent drift of −0.7%/h (Supporting Information Figure S1).

Figure 3.

Sedimentation of 100 nM Padron at 50 000 rpm. (A) FDS-SV data acquired at a laser power of 50.2 mW (symbols) and best-fit distributions (lines) with the c(s) model eq 8 with temporal signal modulation eq 4 with A = 1.58 and k = 1.46/hour. Residuals are shown in the lower plot. (B) Best-fit c(s) distributions obtained at different laser excitation power settings.

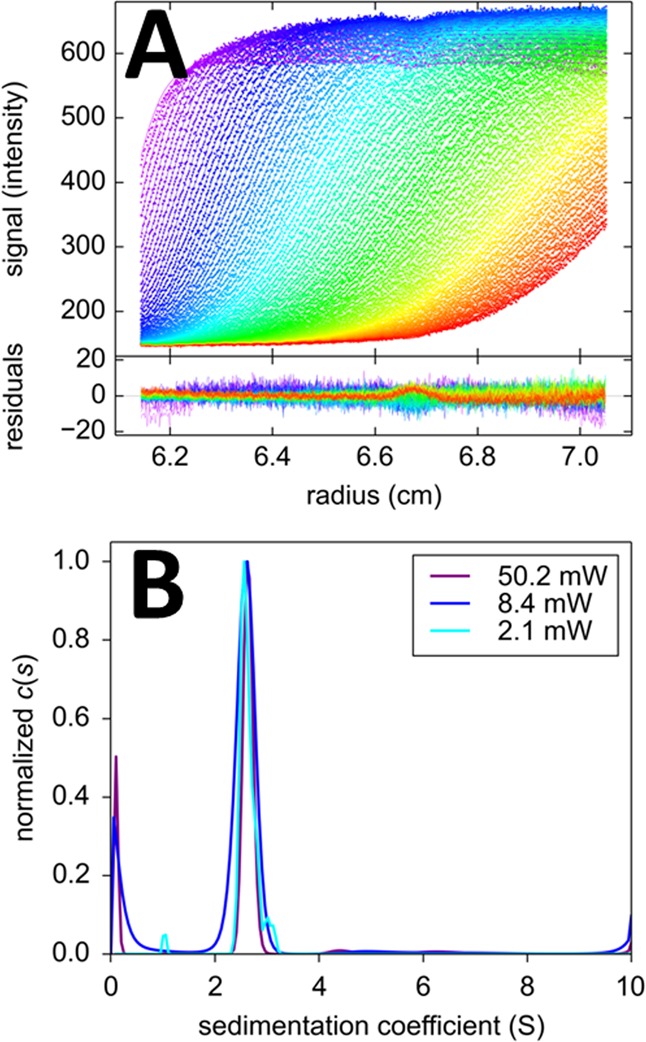
The quantum yield for photoswitching to the off state of Dronpa is 3.2 × 10^–4,⁴⁹ ∼40–100-fold higher than EGFP photobleaching.^59,60 Having determined the experimental switching rate constant of 0.257/h in FDS-SV at 50.2 mW for Dronpa, at the same illumination we would expect the experimental bleaching rate for EGFP in FDS-SV to be 40–100-fold smaller, i.e., < 0.006/h; it is therefore highly unlikely that any significant photobleaching would be observable with EGFP by FDS-SV even at the highest power settings, as this value would be within the error of detection, and additionally be obscured by the observed laser drift.⁴⁶ Even more so, at a laser power of 12 mW, corresponding to the default setting in the FDS systems, on the basis of the ratios of the quantum yield and the apparent photon flux in the geometry in the FDS, for EGFP a bleaching rate of ∼0.1%/h would be expected, i.e. a drop in signal of only ∼ −0.6% during the entire time-course of sedimentation. We tested this in FDS-SV experiments with EGFP (Figure 4). Based on the expectation, the temporal change in the signal increment was described as a linear drift with the constant coefficient α_t. With this model, excellent fits were achieved for EGFP at any power setting, with best-fit drift parameters describing a positive increase in signal at a rate of approximately +0.9%/h (Table 1).

Figure 4.

Sedimentation of 100 nM EGFP in PBS at 50 000 rpm. (A) FDS-SV data acquired at a laser power of 50.2 mW (symbols) and best-fit distributions (lines) with the c(s) model eq 8 with temporal signal modulation eq 4 consisting of a linear drift factor only, with best-fit α_t of +0.86%/h. Residuals are shown in the lower plot. (B) Best-fit c(s) distributions obtained at different laser excitation power settings.

Since the FDS-SV data of the EGFP samples were acquired side-by-side in the same centrifuge run as the Padron and Dronpa samples, it is possible to use this estimate of the laser intensity drift as an independently measured constraint for the linear drift parameter α_t in the samples exhibiting the photophysical signal modulation. For the 50.2 mW and 8.4 mW Dronpa SV data discussed above, introduction of this linear drift (constrained to the value estimated from the EGFP data) in addition to the exponential photobleaching leads to slightly different photobleaching or photoswitching rate constants (Table 1) at a statistically indistinguishable quality of fit. For the 50 mW Padron data, a statistically slightly better fit was achieved, with an additional constraint of the spatial signal magnification drift α_r in the Padron data to be fixed to the value estimated from the EGFP data.

In order to examine the photostability of EGFP under the illumination of the FDS in different solution conditions, we carried out experiments at a lower pH of 5.7 and in the presence of the photosensitizer chlorin e₆.⁶¹ We could not detect a significant difference in either the sedimentation behavior or the temporal stability of the signal to EGFP in PBS at pH 7.4 (Table 1). Similarly, as a further test for photostability of common dyes in FDS-SV, we studied FITC-labeled BSA. The photobleaching quantum yield of fluorescein is approximately 4–10-fold higher than that of EGFP^59,60,62 but still an order of magnitude below the photoswitching off rate of Dronpa. Photobleaching of fluorescein can be observed when the focal point is stationary (which is observed in the process of optical alignment in detector maintenance; data not shown). By contrast, during normal scanning operation of the FDS, there was no indication of bleaching, even at the highest power setting of 50 mW. The difference can be attributed to the 2.5° sector angle of the solution column in centrifugation resulting in a duty cycle of <1%, and the radial movement of the focal point during the scan. The best fit was achieved with a small linear drift for an increase in signal with time (data not shown), at a magnitude statistically indistinguishable from that seen in the EGFP samples. Only when 10% H₂O₂ was added to the FITC-BSA solution, photobleaching was achieved in the FDS at a rate constant of 0.148/h at 50 mW, in addition to a significant drop in overall signal intensity (data not shown).

Discussion

In the present work, we have demonstrated that SV data inherently offer information on a time-domain of slowly changing signal intensities over the time-course of hours during the sedimentation experiment. This allows fluorescence-detected SV with molecules that exhibit significant photophysical changes, including irreversible photobleaching or reversible photoswitching, such as photoswitchable dyes, proteins, and nanoparticles. Similarly, it should be possible to study molecules undergoing irreversible photoactivation or photoconversion. In particular, in recent years, reversibly photoswitchable fluorescent proteins (FPs) have come to play an important role in emerging techniques such as super-resolution microscopy, optical control of protein activity, and optical data storage, and many cell biology studies of protein localization and function rely on the expression of fusion proteins with reversibly photoswitchable FPs.^57,63−65 Thus, a technique for carrying out hydrodynamic studies of protein oligomeric states and protein interactions exploiting FDS-SV should be very useful, both for the characterization of the self-association of such FPs and the size-distribution of nanoparticles themselves, as well as for studies of self- and heterogeneous interactions of proteins expressed in fusion with photoswitchable FPs (using the same constructs as in cell biological studies), either in dilute solution or crowded environments such as cell lysates. Hydrodynamic experiments by FDS-SV on protein interactions have proven extremely useful in many studies of protein quaternary structure and function,³⁰⁻⁴³ and the present work expands this technique to increasingly commonly used fluorophores.

While many photophysical processes may involve multiple states, and in theory require multiexponentials description,⁶⁶ within the limited time range available for observation in the SV experiment these were not resolved in the present work. A single exponential decay described the experimental data of the photoswitchable molecules under study extremely well, leading to a quality of fit on par with the best conventionally detected data sets. It seems possible, however, to incorporate more complicated time-dependencies into the model in future work.

A second practical finding from the present study is that standard fluorophores commonly used in conjunction with the 488 nm excitation in FDS-SV, such EGFP and fluorescein and its derivatives, would seem unlikely to undergo significant photobleaching under the scanning illumination conditions of the FDS, unless applying extreme solvent conditions. This emerges from considering photobleaching quantum yields in comparison with the observed rates of signal decrease in FDS-SV and was corroborated in experiments with FITC-labeled protein and EGFP in different solvents. This can be attributed to the relatively low time-average power density any solution region is exposed to during the scan of the focal point through the solution column. The time-dependent signal intensity drifts that were previously described^27,45,46 can now be attributed to slow drifts in the laser intensity. However, these drifts do not seem problematic, as constant drifts can be accounted for in the data analysis as well,⁴⁶ now in addition to the exponential photophysical processes. Since the incident laser power is common to all samples, drifts may be separately measured using EGFP in one of the 14 sample cells, again making use of the information from the time-dependence of the plateau signals as an internal reference. This may additionally be useful as an independent reference for solvent viscosity when working in complex solvents. Jointly, the apparent absence of significant photobleaching of GFP and fluorescein, as well as the potential to account for photophysical processes in the data analysis should they occur, suggest that there will be little penalty of increasing the laser power. We would expect this to lead to lower detection limits, on the basis of the increase in the signal/noise ratio observed here.

Supporting Information Available

Time-dependent fluorescence intensity in the sample of Dronpa, Padron, and EGFP across the solution column under FDS illumination with 50.2 mW under nonsedimenting conditions. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States