Abstract

Nitrate (NO3–) is a widespread contaminant of groundwater and surface water across the United States that has deleterious effects to human and ecological health. This study develops a model for predicting point-level groundwater NO3 at a state scale for monitoring wells and private wells of North Carolina. A land use regression (LUR) model selection procedure is developed for determining nonlinear model explanatory variables when they are known to be correlated. Bayesian Maximum Entropy (BME) is used to integrate the LUR model to create a LUR-BME model of spatial/temporal varying groundwater NO3– concentrations. LUR-BME results in a leave-one-out cross-validation r2 of 0.74 and 0.33 for monitoring and private wells, effectively predicting within spatial covariance ranges. Results show significant differences in the spatial distribution of groundwater NO3 contamination in monitoring versus private wells; high NO3– concentrations in the southeastern plains of North Carolina; and wastewater treatment residuals and swine confined animal feeding operations as local sources of NO3 in monitoring wells. Results are of interest to agencies that regulate drinking water sources or monitor health outcomes from ingestion of drinking water. Lastly, LUR-BME model estimates can be integrated into surface water models for more accurate management of nonpoint sources of nitrogen.
Introduction
Nitrate (NO3–) is a widespread contaminant of groundwater and surface water across the United States that has deleterious effects to human and ecological health.1,2 The maximum contaminant level of 10 mg/L established by the U.S. Environmental Protection Agency was based on the prevention of methemoglobinemia in infants;3 moreover, there is concern of many cancer types4−6 and from lower concentration exposures.7 Excessive NO3 inputs into the environment can result in adverse changes to ecosystems such as eutrophication and harmful algal blooms.8−10
Protection of drinking water sources is mandated by the Safe Drinking Water Act; however, private well drinking water is unregulated in contrast to regulated public water systems.11 In North Carolina where more than 1/4 of the population relies on private wells for drinking water,12 quantifying potential exposures is important to protect public health. Monitoring programs such as the U.S. Geological Survey’s (USGS) National Water Quality Assessment (NAWQA) Program13 and the NC Division of Water Resources (NC DWR) ambient monitoring program14 are effective because they use consistent sampling and analytical methods, yet this water quality monitoring data is spatially and temporally sparse.
Land use regression15−21(LUR) is a proven method that complements monitoring programs and provides effective means for water quality exposure assessments. Previous studies have related land use characteristics to NO3– contamination in surface waters22−25 and groundwater. Additionally, regression-based methods have been implemented for estimating loading to surface waters.21,23,24 In North Carolina, groundwater discharge to streams (baseflow) accounts for roughly two-thirds of annual streamflow in the Coastal Plains region of North Carolina26 and may be contributing excess nutrient loads in streams;27 however, current surface water models do not directly account for this large source of NO3 from baseflow.
For linear regression models, traditional statistical methods to select predictor variables include forward, backward, and stepwise selection. These methods can lead to erroneous models with high multicollinearity when the candidate variables are related. However, for LUR model studies, model selection methods have been modified to accommodate the potential high multicollinearity from selection variables that differ only by a hyperparameter.16,19 Additionally, lasso28 and elastic net29 regression are potential methods for selecting linear LUR models, but to the authors’ knowledge has not been employed for LUR model selection. For nonlinear regression, methods for model selection based on a large candidate variable space include stepwise logistic regression30,31 and regression tree analysis which approximates nonlinear relationships;32,33 still for continuous variable outcomes with nonlinear models, less rigorous methods for model selection have been developed. The number of candidate variables is generally consolidated to a tractable number through expert knowledge or single variable regression, and then various combinations of models are tested until one finds the best model in terms of a validation statistic like R2 or Akaike Information Criterion (AIC).15,21,24
The advanced geostatistical method of Bayesian Maximum Entropy (BME) has also been shown to successfully estimate groundwater quality contaminants.19,34 An advantage of BME is its ability to quantify spatial and temporal variability which is then used in the estimation process at unmonitored locations. BME, like all geostatistical methods, is data driven and can only provide reliable estimates within the vicinity of measured values. However, BME utilizes Bayesian epistemic knowledge blending to combine multiple sources of data, which has been successfully demonstrated with incorporation of deterministic mean trend functions into BME for groundwater.19
Local spatial and temporal variability have lead previous studies to reduce NO3– variability with a combination of spatial smoothing and temporal averaging.15,35,36 For instance, Nolan and Hitt spatially smoothed NO3 by taking watershed averages over their study time period, based on watersheds with an average size of approximately 2000 square-kilometers. They not only helped elucidate trends and potential explanatory variables, but they were able to explain a large percentage in the variability of spatially smoothed NO3– with a r2 of 0.80 for shallow aquifer NO3 and 0.77 for deep aquifer NO3–. However, this advantage of reducing groundwater NO3 variance is also a limitation because factors affecting spatially smoothed and temporally averaged NO3– might not affect point-level NO3, and vice versa. Furthermore, since groundwater NO3– contains significant local variability, the need to provide local estimates of its variability naturally follows. Models developed for predicting spatially smoothed and temporally averaged NO3 will likely not be successful in predicting observed, point-level NO3–.
The objectives of this study are to (1) develop a novel nonlinear regression model for spatial point-level and time-averaged groundwater NO3– concentrations in monitoring and private wells of North Carolina, (2) produce the first space/time estimates of groundwater NO3 concentrations across a large study domain by integrating LUR models into the BME framework, and (3) compare space/time NO3– concentration models to the current standard of spatially averaged NO3 concentration models. Two nonlinear models, whose form is adopted from Nolan and Hitt15 with components that represent NO3– sources, attenuation, and transport, are created and selected with a new model selection framework for nonlinear regression models with correlated explanatory variables. We then integrate the LUR models into the BME framework to model space/time point-level NO3. Results are of interest to agencies that regulate drinking water sources or that monitor health outcomes from ingestion of drinking water. Additionally, the results can provide guidance on factors affecting the point-level variability of groundwater NO3– and new resources for more accurate management of NO3 loads.
Materials and Methods
Nitrate Data
NO3– data across North Carolina are obtained from three data sources (Supporting Information (SI) Figure S1), which are detailed as follows:
North Carolina Division of Water Resources (NC-DWR) collects data near select permitted, dedicated wastewater treatment residual (WTR) application fields via monitoring wells. The second source is U.S. Geological Survey (USGS) data obtained through the National Water Information System (NWIS). Well depth information is not linked directly to each monitoring well although a subset of well depth information is available. Based on the subset with depth information, they have a mean depth of 33 feet with a standard deviation of 32 feet. Together, the NCDWR and USGS data represent shallow aquifer monitoring wells (n = 12 322), which hereafter will be referred to as “monitoring well data.”
The last data set of groundwater NO3– comes from private well data collected by the North Carolina Department of Health and Human Services (NC-DHHS). Groundwater NO3 was obtained and address geocoded using the same process outlined in Messier et al.19 Well depth information is not linked to water quality measurements, but a separate database on private well construction contains well depths. The mean depth is 95 feet with a standard deviation of 109 ft. This data will hereafter be referred to as “private well data” and this data is assumed to represent a deeper aquifer model of groundwater NO3– (n = 22 067).
The median NO3– concentrations for the NC-DWR, USGS, and private well data are 1.30, 0.10, and 0.62 mg/L respectively. The means are 4.61, 6.14, and 1.66 mg/L respectively. The percent observed above the detection limit is 79.7, 61.4, and 30.6 respectively. Additional basic statistics for the data set are available in the SI (Table S1).
Spatial and Temporal Observation Scales
In this work we develop models for NO3– at three observation scales. The finer scale corresponds to the space/time point-level NO3 data, that is, NO3– data as it is sampled. An intermediate observation scale corresponds to the time-averaged data, whereby NO3 at each well is averaged. The time-averaged data provides point-level spatial resolution, but no time variability. Finally, the coarser resolution observation scale corresponds to the spatially smoothed/time-averaged data, which was obtained by spatially smoothing the time-averaged data using a 25 km exponential kernel function. We choose 25 km as it is approximately the average size of watersheds in many NAWQA groundwater studies.15,37 While previous works over large study domains have developed models for spatially smoothed/time average NO3– data, very few models, if any, have been developed for point-level NO3 data over large study domains. Our work therefore fills that knowledge gap.
Maximum Likelihood Estimation of Nitrate Distributions
Our notation for variables denotes a single random variable Z in capital letter, its realization, z, in lower case; and vectors and matrices in bold faces, for example, Z = [Z1,...,Zn]T and Z = [z1,...,zn]T.
Due to the high percentage of nondetect (left-censored) data in both the monitoring well and private well databases, a maximum likelihood estimation (MLE) is used for the estimation of monitoring well and private well distribution parameters,38 which is assumed to follow a log-normal distribution. MLE can directly account for the nondetect values by modifying the likelihood equation, with the censored observations given by the cumulative distribution function (CDF) evaluated at the detection limit. The MLE equation then becomes38
| 1 |
where fμ,σ(zi) denotes the normal probability distribution function (PDF) of log-transformed (natural log) point-level NO3–, zi, with mean and standard deviation parameters μ and σ, and Fμ,σ(ti) denotes the CDF of the distribution taken at the log of the detection limit ti. The estimated distributions are used to quantify the extent of contamination in monitoring and private wells and to handle nondetect data. For the regression analysis, the log-NO3 concentration of a measurement below detection limit ti is assigned a value equal to the mean of the normal distribution N(μ,σ) truncated above log(ti), whereas the geostatistical analysis can handle the full truncated normal distribution.19
Spatial Explanatory Variables
Spatial explanatory variables representing possible groundwater NO3– sources, attenuation, and transport factors were constructed prior to model development. Potential variables are summarized below with details available in the SI (Table S2).
All of the explanatory variables have an inherent spatial distance parameter such as circular buffer radius or exponential decay range, which hereinafter is referred to as the hyperparameter. Each variable is calculated with multiple hyperparameter values since optimal distance is unknown a priori. In the final model selection process, a maximum of one hyperparameter value is allowed to be selected from each variable to avoid multicollinearity and effectively optimize the hyperparameter. The following variables adopted from Nolan and Hitt15 are NO3– sources calculated as kg-NO3/yr/ha within a circular buffer: Sources include farm fertilizer, nonfarm fertilizer, manure, and NO3– atmospheric deposition. Each National Landcover Database (NLCD) category is calculated as a percent within a circular buffer. On-site wastewater treatment plant variables, septic density and average nitrate loading, are created following the methods of Pradhan et al.39 The following point sources are calculated as the sum of exponentially decaying contribution:19 Wastewater treatment residual field application sites (WTR), swine confined animal feeding operations (CAFOs), poultry CAFOs, cattle farms, and wastewater treatment plants (WWTP). Mean slope in degrees and topographic wetness index40 (TWI) are calculated within circular buffers. Water withdrawals in cubic meters per second are calculated using USGS water use estimates.12 Lastly, population density is calculated within circular buffers from U.S. Census block data assuming an even distribution of population per census block.
Nonlinear Regression Model Selection
In order to develop a LUR model for NO3– we adopt a similar nonlinear multivariable model implemented by groundwater vulnerability assessment(GWAVA)15 which is also similar to the surface water counterpart spatially referenced regression on watershed Attributes (SPARROW).21,23,24 We partition explanatory variables into source, attenuation, and transport terms. Following Nolan and Hitt,15 the nonlinear multivariable model is constructed as follows:
| 2 |
where zi is the log-transform of NO3– concentration at point i, β0 is the intercept, Yi(λk) is the k-th source predictor variable at point i with hyperparameter value λk, βk is its source regression coefficient, Yi(l)(λl) is the l-th attenuation predictor variable at point i with hyperparameter value λl, γlis its attenuation regression coefficient, Yi(λm) is the m-th transport predictor variable with hyperparameter value λm, δm is its transport regression coefficient, and εi is an error term. The model contains an additive, linear submodel for sources, and multiplicative exponential terms for the attenuation and transport variables that act directly on the source terms.15 For example Yi(k)(λk) may be equal to a land cover variable or a point source variable. The attenuation variables,Yi, physically represent areas that are associated with removing NO3– from groundwater such as wetlands and histosol soil. The transport variables, Yi(λm)., may be equal to any variable that effects the movement of NO3– in the groundwater such as the soil permeability and average slope. The attenuation variable coefficients, γl, are constrained to be negative allowing them to only decrease NO3 concentrations, while the transport variable coefficients, δm, are unconstrained allowing variables to increase or decrease NO3– concentrations.
We developed a nonlinear model regression model selection technique that accommodates variables that differ only by a hyperparameter and can be adapted for various nonlinear model forms. Our model selection procedure is essentially a nonlinear extension of adistance decay regression selection strategy (ADDRESS),16 since to the authors’ knowledge there is not a regression selection strategy for nonlinear LUR. We implement constrained forward nonlinear regression with hyperparameter optimization (CFN-RHO) whose simple algorithm is as follows (SI Figure S2):
-
(1)
Initialization: Linear regression on all candidate variables to obtain the initial values for the nonlinear model fitting.
-
(2)
Candidate Variables: In the first iteration, the candidate variables consist of the source variables only. In the second iteration, candidate variables consist of attenuation and transport variables only. This is done so as to obtain an initial model with at least one source and one attenuation or transport variable. In every iteration afterward the candidate variables can be any variable.
-
(3)
Nonlinear Regression: Nonlinear regression is performed by adding each candidate variable to the current model one at a time. Note that candidate variables are added according to their predetermined place in the nonlinear model (i.e., Source variables are in a linear submodel; Attenuation and transport in the exponential submodel.).
-
(4)
Variable Selection: The variable that results in the highest R-Squared (lowest AIC is also an option) while constrained to maintaining all variables in the model statistically significant (p-value <0.05), is selected and added to the model. R-Squared ties beyond the thousandth decimal place are settled by the lowest p-value.
-
(5)
Hyperparameter Optimization: The rest of the candidate variables that differ from the selected variable by only a hyperparameter are removed from the candidate variable pool, effectively optimizing the hyperparameter value.
-
(6)
Selection Criteria: The new model must increase R-squared over user-defined selection criteria such as a one percent increase. If the model passes the selection criteria, then the iterative process continues to step 2. If it does not, then the algorithm ends with the final model being the i-th minus one model since the last variable did not pass the selection criteria.
BME Estimation Framework for Space/Time Mapping Analysis
To improve estimation accuracy, we integrate the time-averaged LUR results into the bayesian maximum entropy (BME) method of modern spatiotemporal geostatistics.41,42 BME is a space/time geostatistical estimation framework grounded in epistemic principles that reduces to the space/time simple, ordinary, and universal Kriging methods as its linear limiting case when considering a limited, Gaussian, knowledge base, while also allowing the flexibility to process a wide variety of additional knowledge bases (physical laws, empirical relationships, non-Gaussian distributions, hard and soft data, etc.). We only provide the fundamental BME equations for mapping NO3–; the reader is referred to other works for more detailed derivations of BME equations41,43 and LUR integration into BME.19
Let Z(p)be the space/time random field (S/TRF) describing the distribution of groundwater log-NO3– across space and time, where p = (s,t), s is the space coordinate and t is time. The knowledge available is organized in the general knowledge base (G-KB) about the space/time trend and variability (e.g., mean, covariance) of NO3 across the study domain, and the site-specific knowledge base (S-KB) corresponding to the hard and soft data zd available at a set of specific space/time points pd.
First, we define the transformation of log-NO3– data zd at locations pd as
| 3 |
where oZ(ph) may be any deterministic offset that can be mathematically calculated at any space/time coordinate p. We then define X(p) as a homogeneous/stationary S/TRF representing the variability and uncertainty with the transformed data xd, that is, such that xd is a realization of X(p). Finally we let Z(p) = X(p) + oz(p) be the S/TRF representing groundwater log-NO3–. In this study, we consider two choices for oz(p): (1) a constant value determined by the MLE mean resulting in a purely BME model, and (2) the LUR estimate Lz(ph) from CFN-RHO resulting in a LUR-BME model.
The G-KB for the S/TRF X(p) describes its local space/time trends and dependencies. In this work, the general knowledge consists of the space/time mean trend function mx(p) = E[X(p)], and the covariance function CX(p,p′)=E[[X(p) – mx(p)][X(p′) – mx(p′)]] of the S/TRF X(p). The S-KB consists of hard data and soft data; with hard data, xh = zh – Lz(ph), for data points where zh is observed over the detection limit and soft data, Xs, is at locations ps where NO3– is observed below the detecti limit. Following Messier et al.,19 the BME soft data for log-NO3 is modeled as a Gaussian distribution truncated above the log of the detection limit.
The overall knowledge bases considered consist of G = {mx(p), CX(p,p′)}, and S = {fs(·), Xh}. In this case the BME set of equations reduces to
| 4 |
where fK(xk) is the BME posterior PDF for the offset-removed log NO3–(xk) at some unmonitored estimation point pk, fG(xh, xs, xk) is the (maximum entropy) multivariate Gaussian PDF for (xh, xs, xk) with mean and variance-covariance given by G-KB, fS(xs) is the truncated Gaussian PDF of Xs, and A–1is a normalization constant. After the BME analysis is conducted, oZ(p) is added back to obtain log-NO3 concentrations.
Validation Statistics
The robustness of CFN-RHO is tested with a 10-fold cross-validation procedure. In 10-fold cross-validation data is randomly partitioned into 10 equal size subsamples. A single subsample is retained as the validation data for testing the model, and the remaining nine subsamples are used as training data. Each of the 10 subsamples is used exactly once as the validation data. Similar variable selections (which may differ only by hyperparameter) for subsamples demonstrate model selection robustness.
Models are compared with a leave one-out cross-validation (LOOCV) mean squared error (MSE) and R-squared. Spatially smoothed/time-averaged NO3– and time-averaged NO3 models are also tested on how well they predict at the smaller observation scales. In LOOCV, each log-NO3– value Zj is removed one at a time, and re-estimated using the given model based only on the remaining data. Let Z*(k)be the re- estimate for method k, then MSE(k) = (1/n)∑j = 1(Zj*(k) −Zj)2 and the cross-validation R-Squared is R2(Z,Z*(k)).
Results
Nitrate Concentrations
The MLE of the statewide monitoring concentrations resulted in a geometric mean and standard deviation of the log-normal distribution of 0.62 and 14 mg/L, respectively (SI Figure S3). MLE for private wells resulted in a geometric mean and standard deviation of 0.45 and 5.1 mg/L (SI Figure S3).
Spatially Smoothed/Time-Averaged Nitrate
The 25 km spatially smoothed/time-averaged NO3– LUR model cross-validation results (Table 1) in a r2 of 0.69 and 0.68 for monitoring and private wells, respectively, which is of similar magnitude to current literature.15 However, as expected, the LUR model calibrated for spatially smoothed/time-averaged NO3 underperforms and does progressively worse (top row, moving left to right in Table 1) as it predicts time-averaged NO3– and point-level NO3 with lower r2 and higher RMSE. The variables selected for this model via CFN-RHO are available in the SI (Table S3).
Table 1. Leave-One-out Cross-Validation Statistics Comparing for Four Estimation Methods That Predict Spatial/Temporally Averaged NO3– Concentrations, Temporal Averaged NO3 Concentrations, And Point-Level Observed NO3– Concentrationsa.
| predicted
value |
|||||||
|---|---|---|---|---|---|---|---|
| spatially smoothed/time-averaged NO3– |
time-averaged NO3– |
point-level NO3– |
|||||
| method | MW (n = 951) | PW (n = 18,664) | MW (n = 951) | PW (n = 18,664) | MW (n = 12,300) | PW (n = 22,062) | |
| spatially smoothed/time-averaged LUR | r2 | 0.69 | 0.68 | 0.27 | 0.08 | 0.15 | 0.08 |
| RMSE | 0.895 | 0.293 | 2.23 | 1.19 | 2.40 | 1.27 | |
| time-averaged LUR | r2 | 0.37 | 0.09 | 0.23 | 0.09 | ||
| RMSE | 2.08 | 1.19 | 2.28 | 1.27 | |||
| space/time BME | r2 | 0.70 | 0.25 | ||||
| RMSE | 1.39 | 1.23 | |||||
| space/time LUR-BME | r2 | 0.74 | 0.33 | ||||
| RMSE | 1.27 | 1.08 | |||||
Note that methods were used to predict at scales more refined or equal to its calibration scale. MW = Monitoring Well model. PW= Private Well model. n = number of observations at that scale. Time averaging results in fewer observations. RMSE = root mean squared error. Units of NO3– concentration = mg/L.
10-fold cross-validation of spatially smoothed/time-averaged NO3– LUR models was done to demonstrate the stability of CFN-RHO (SI Tables S4, S5). All variables were selected 7 and 10 out of 10 iterations for the monitoring and private well models, respectively.
Time-Averaged Nitrate
The LUR variables selected through CFN-RHO for time-averaged NO3– observed at monitoring wells and private wells are shown in Table 2. The LUR calibrated to predict time-averaged NO3 obtains a r2 of 0.37 and 0.09 for monitoring wells and private wells, respectively (Table 1, second row). Moreover, the LUR model predicts point-level NO3– with a r2 of 0.23 and 0.09 for monitoring and private well, respectively. LUR maps are available in SI Figure S4.
Table 2. Nonlinear Regression Model Variables Selected via CFN-RHO and Parameter Estimates for Time-Averaged NO3– Monitoring (Left) and Private Well (Right) Modelsa.
| monitoring well |
private well |
|||||
|---|---|---|---|---|---|---|
| variable | variable range | coefficient estimate | standard error | variable range | coefficient estimate | standard error |
| Constant | n/a | –3.71 | 0.191 | n/a | –1.570 | 0.0382 |
| Source Variables | ||||||
| manurea | 250 m | 0.0759 | 0.0317 | – | – | – |
| wastewater treatment residuals (WTR)b | 5 km | 0.245 | 0.0274 | – | – | – |
| farm fertilizera | 250 m | 0.132 | 0.0193 | 250 m | 0.0432 | 0.0025 |
| swine CAFO’sc | 2 km | 0.117 | 0.0218 | – | – | – |
| swine lagoonsb | – | – | – | 6 km | 0.1079 | 0.0146 |
| developed lowd | 250 m | 0.112 | 0.0214 | – | – | – |
| developed (all combined)d | – | – | – | 100 m | 0.0112 | 7.08e-4 |
| atmospheric depositiona | 250 m | 0.477 | 0.129 | 25 km | 2.94e-11 | 2.53e-10 |
| Attenuation and Transport Variables | ||||||
| forest (all combined)d | 2 km | –0.0064 | 0.00281 | – | – | – |
| deciduous forestd | – | – | – | 4 km | –0.0151 | 0.00127 |
| herbaceous wetlandsd | 5 km | –0.531 | 0.079 | – | – | – |
| histosold | 25 km | –0.0427 | 0.0111 | 25 km | –0.106 | 0.0126 |
| hydrologic soil group dd | – | – | – | 500 m | –0.012 | 0.0010 |
| slopee | 25 km | –0.074 | 0.0261 | – | – | – |
All variables are significant with p-value < 0.025. Variables units: a, kg-NO3–/yr/ha; b, dimensionless; c- 100 pigs; d, percent; e, degrees; (−) not a variable in the model.
10-fold cross-validation of time-averaged NO3– LUR models was conducted (SI Table S6, S7). All variables selected from the monitoring well model are selected in at least six iterations of the 10-fold cross-validation runs. The majority of variables in the private well model were also stable; however swine lagoons and deciduous forest were only selected 2 and 0 out of 10 times. In both models, when a variable is not selected in the 10-fold cross validation it is likely due to other variables that capture similar source, attenuation, or transport processes (i.e., Forest instead of Deciduous, Swine CAFO’s instead of Swine Lagoons).
Point-Level Nitrate
We modeled the space/time covariance of the LUR offset removed log-NO3– S/TRF, X(p), using a two-component, space/time nonseparable, exponential covariance model following Messier et al:19
| 5 |
where c1 = 0.67 (log – mg/L)2, ar1 = 93m, aτ1 = 15 days, c2 = 3.6 (log-mg/L)2, ar2 = 1750m, aτ2 = 15840 days for monitoring wells (SI Figure S5) and a one-component, space/time exponential covariance model for private well where c1 = 0.76 (log – mg/L)2, ar1 = 1181m,aτ1 = 8640 days (SI Figure S6).
The LUR-BME model, which integrates the time-averaged LUR as the offset best predicts space/time point-level NO3– concentrations with a r2 of 0.74 and 0.33 (Table 1) for monitoring and private wells, respectively. However, the LUR-BME predictions have a large variance at locations farther than the covariance model spatial range. Figure 1 maps the point-level NO3 concentrations estimated by LUR-BME for 1 day during the study period for both monitoring and private well models. These are the first results to show that there is a 4-fold improvement in predicting point-level NO3– when the LUR-BME method is used in comparison to previous studies that use models for spatially smoothed/time-averaged NO3, and five percent improvement in r2when integrating a LUR model into the BME framework, over purely BME. A link to a movie of LUR-BME maps is available in the SI.
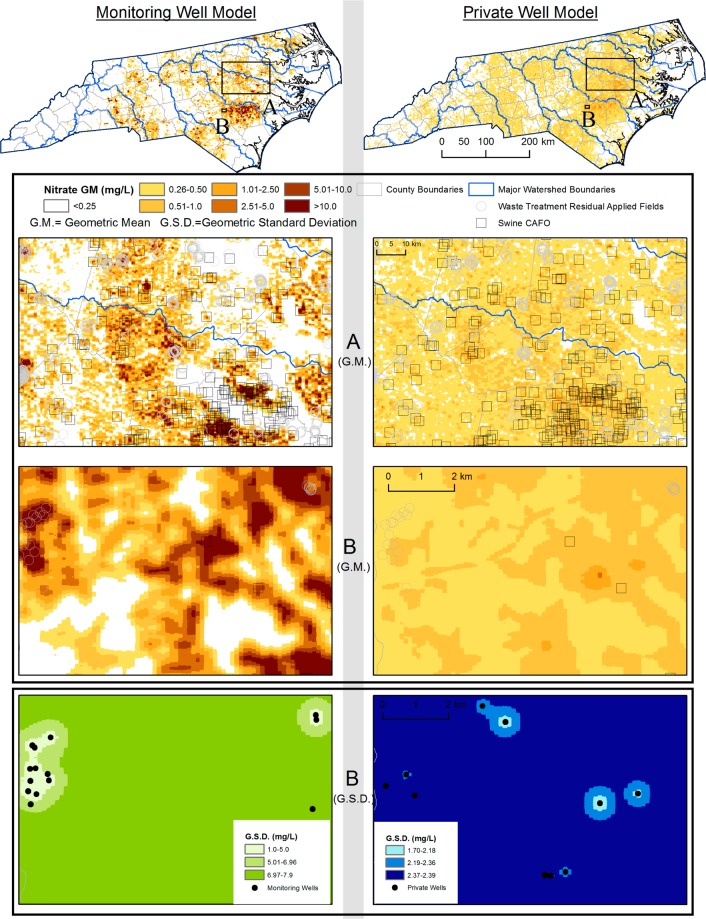
Figure 1.
Comparison of LUR-BME results between the monitoring well (left of gray bar) model and private well (right of gray bar) model NO3– concentrations. The extent rectangles shows zoomed in portions of the state and are identical areas for both models. Extent (B) shows geometric mean predictions and then geometric standard deviation.
Discussion
Groundwater Nitrate Maps
This study presents a LUR model for point-level NO3– in North Carolina that elucidates processes affecting its local variability, and then utilizes the strengths of BME to create the first LUR-BME model of groundwater nitrate’s spatial/temporal distribution including prediction uncertainty. The first major finding is the LUR-BME model for monitoring wells, assumed to represent surficial aquifers, (Figure 1, SI Movie S1) shows groundwater NO3 that is highly variable with many areas predicted above the current standard of 10 mg/L.
Contrarily, the private well results (Figure 1) depict widespread, low-level NO3– concentrations, which is consistent with the current physical understanding in which sources tend to pollute the surficial aquifer, but then transport over time to the deeper drinking-water supply aquifers where concentrations are lower. This finding is significant because of the studies demonstrating potential significant health effects at concentrations as low as 2.5 mg/L.4−7 Additionally, concentrations of NO3 could impact ecological function since there are potential large reserves in deeper aquifers that can discharge to surface waters.27 The standard deviation maps (Figure 1) demonstrate the importance of NC-DWR and USGS monitoring wells and private well testing because areas within the spatial covariance range are well characterized, whereas those outside are less reliable.
The second major finding is the LUR-BME maps (Figure 1) show that groundwater NO3– in monitoring wells is elevated in the southeastern plains of North Carolina (SI Figure S7) due to the larger amount of NO3 sources and the lack of subsurface attenuation factors (SI Movie S2) that are present in the coastal plain region. This corroborates the findings of Nolan and Hitt,15 which also show spatially smoothed/time-averaged NO3– to be the highest in the southeastern plains of North Carolina. This expands that finding with point-level results showing significant point-level variability within regional trends. Additional concerns arise since groundwater flow of the southeastern plains contributes significantly to surface water flow.27 Our LUR-BME model can be used with surface water models to quantify the effect of groundwater NO3 contributing to surface water contamination.
The use of the methods in this study provide estimates at a finer resolution and down to smaller NO3– values than Nolan and Hitt,15 resulting in new findings. Nolan and Hitt15 generally show greater concentrations than the LUR-BME model potentially due to their model using significantly less training data and averaging NO3 over watersheds. Our LUR-BME models benefit from the large amount of monitoring (n = 12 322) and private well (n = 22 067) data, whereas they used 2306 and 2490 across the U.S. for their shallow and drinking water models, respectively.
LUR-BME benefits from the exactitude property of BME, thus our model results are in 100% agreement at monitoring locations. Contrarily, when our observed data is compared with Nolan and Hitt15 by grouping results according to the bins of Figure 1, Nolan and Hitt15 overpredicts 48% and 59% of the time for monitoring and private wells, respectively (SI Figure S8,S9). As a result of the finer resolution of our maps and their improved ability to predict low level NO3–, our results lead to a significant new finding about the extent of areas with low level contamination. Our results show private well concentrations are greater than 0.25 mg/L while monitoring well concentrations are less than 0.25 mg/L in 30.6% of North Carolina’s area, compared to 2.6% for Nolan and Hitt15 (SI Table S8,S9). Likewise, our results show monitoring and private wells are both above or below 0.25 mg/L at the same location in 68% of North Carolina, compared to 91% for Nolan and Hitt.15 Hence whereas Nolan and Hitt15 results suggest the geographical extent of the low level contamination of drinking water aquifer is limited to that of the shallow aquifer, which is consistent with downward transport of NO3 contamination, our LUR-BME models shows that in fact the geographical extent of the contamination of the drinking water extends over a much larger area than that of the shallow aquifer. This major new finding provides new evidence indicating that in addition to downward transport, there is also a significant outward transport of groundwater NO3– in the drinking water aquifer to areas outside the range of sources. This is especially significant because it indicates that the deeper aquifers are acting as a reservoir that is not only deeper, but also wider than the reservoir formed by the shallow aquifers.
LUR Variable Interpretations
Variables selected through CFN-RHO show processes influencing monitoring well and private well NO3– concentrations. Interpretations of regression sources parameters are based on the nonlinear model formulation: Since NO3 was log-transformed and the nonlinear model has multiplicative interaction, the percent increase of the geometric mean of NO3– is the exponential of the source coefficient multiplied by the result of the attenuation and transport terms held to their mean value. For instance, in the monitoring well model, the percent increase in the geometric mean of NO3 in mg/L for every 1 kg/yr/ha of farm fertilizer is exp(0.132 × 0.456) = 1.06 = 5% where 0.456 is the exponential of the mean attenuation and transport variables multiplied by their coefficients. For the private well model, the percent increase in the geometric mean of NO3– for every 1 kg/yr/ha of farm fertilizer is exp(0.0432 × 0.4636) = 1.02 = 2%. Every other source coefficient interpretation for time-averaged NO3 is provided in the SI.
Comparing variables selected between the spatially smoothed/time-averaged NO3– LUR and the time-averaged NO3 LUR help elucidate effects the spatial scale has on groundwater NO3– concentrations. The variable hyperparameters selected by CFN-RHO help elucidate potential scales at which the variables affect groundwater NO3 concentrations. For example, the short buffer range of developed low likely captures the small size of single-family housing yards and their associated fertilizer applications. The monitoring well model WTR has an exponential decay range of 5 km. A possible explanation of this medium range is due to the volatization of NO3– into the air, which can then be transported over longer distances than subsurface transport mechanisms alone. Long buffer ranges for attenuation and transport variables such as percent histosol soil and mean slope represent variables with larger, regional scale effects.
The third major finding is that both wastewater treatment residuals (WTR) and swine CAFOs were selected as local sources of groundwater NO3– contamination, which to our knowledge have not yet been previously identified as sources in multivariable models that included regional sources. To help aide state-wide policy decisions concerning regional versus local sources, Figure 2 shows the elasticity of LUR predicted sources in monitoring wells, or the percent change in the geometric mean of groundwater NO3 within an area in response to the percent decrease in a LUR model source given all other sources remain at current levels. Farm fertilizer and atmospheric deposition result in the greatest decrease in groundwater NO3– state-wide (Figure 2A). Reducing WTR (Figure 2B) and swine CAFOs (Figure 2C) within 1 km of the source leads to significant reductions in groundwater NO3 in the local area surrounding the sources, demonstrating the importance of sources on local area NO3– variability.
Figure 2.
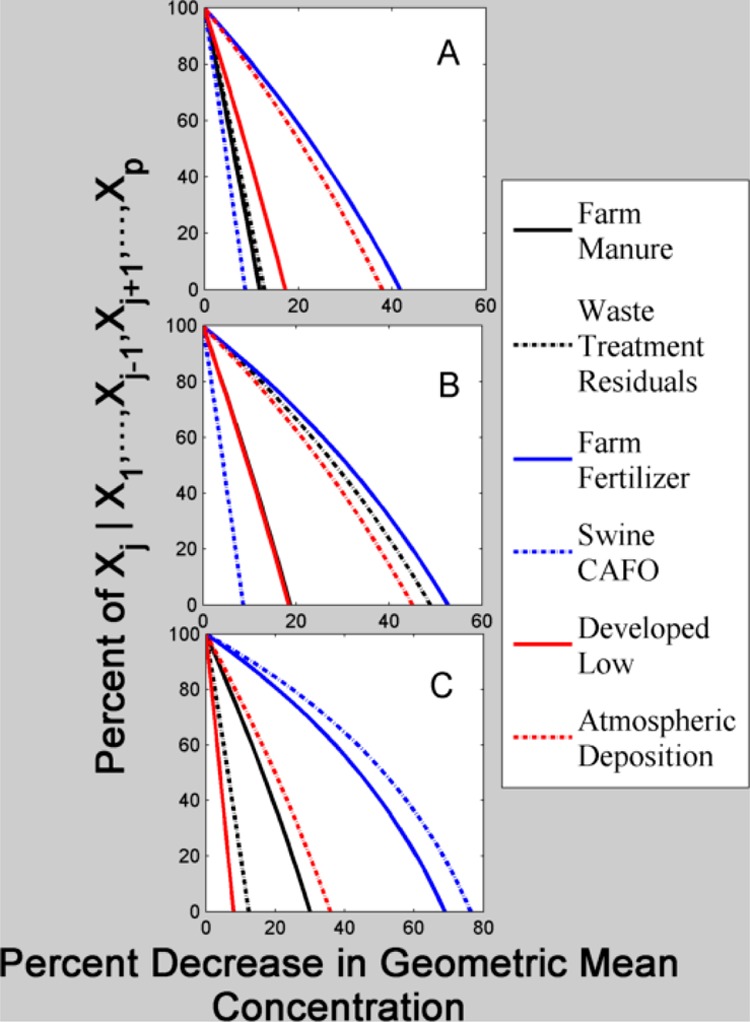
Elasticity curves for monitoring well sources. Y-axis is the percent decrease in a source and the X-axis is the percent decrease in geometric mean, for (A) state-wide, (B) within 1 km of wastewater treatment residuals, and (C) within 1 km of swine CAFO’s.
Recommendations and Limitations
This work represents the first step in the development of modeling observed NO3– over large domains without averaging. In previous studies, spatial averaging is utilized because it provides results at the domain (state, regional, or national) desired for policy making decisions and sheds light on processes influencing groundwater NO3. We demonstrated that a LUR at the point-level in space is currently limited in terms of model predictive capability but when integrated into the BME framework, the improved model can estimate within the spatial covariance range similar to LUR models for spatially smoothed/time-averaged groundwater NO3– concentrations. Potential explanatory variables that can explain the remaining variability in the point-level LUR will need primary data collection. For instance, we found WTR to be a significant variable even though we just used location of fields. If records of timing and amounts of WTR applications were improved, then the temporal variability in monitoring wells near WTR application fields could be improved.44 Similarly, a parcel-level query of farm fertilizer application practices could distinguish farms that use NO3 fertilizers efficiently versus farms that apply excessively or with poor timing. For private wells, the short spatial autocorrelation range may be due to differences in effectiveness of on-site wastewater treatment systems or residential fertilizer use. Additionally, we note that candidate variables not selected via CFN-RHO does not necessarily indicate they have no effect on groundwater NO3– concentrations in surficial or confined drinking-water aquifers of North Carolina. Many factors both statistically and physically can affect the selection such as correlation between candidate variables and local hydrogeology conditions being overwhelmed by larger scale trends. This study lacked well depth for the majority of monitoring and private wells. The monitoring and private well models clearly demonstrate a difference in concentrations based on depth, so well depth could quantify this more explicitly as opposed to categorically as done by this study. Furthermore, pumping rate information was not available for the private well data set thus the effect of local pumping could not be quantified. The USGS water use report12 has information on domestic-use water withdrawals; however, it is at the county-scale, based on county populations, and cannot be down-scaled like the agricultural water withdrawals variable, thus it was not included as a candidate variable. Additionally, the detection limit of 1 mg/L for the private well data is high and lowering that detection limit would improve the ability of the model to delineate areas with low level contamination that may act as reservoir to surface water NO3 recharge. The high detection limit is also potentially responsible for the lower r2in the private well LUR model for time-averaged nitrate because it results in a low dependent variable variance. Predictions of the private well LUR model for time-averaged nitrate are likely biased toward the detection limit; however, the LUR-BME model for private well models likely avoids this bias due to the exactitude property along with the good spatial coverage of private well data across North Carolina. Moreover, greater uncertainty in attenuation processes in deeper aquifers is likely contributing to the lower r2.
In conclusion, a LUR model with a novel model selection procedure can elucidate important predictors of point-level groundwater NO3– in North Carolina monitoring and private wells. The methods are translatable to other study areas in the United States. LUR-BME models can be used to predict spatial/temporal varying groundwater NO3 and provide uncertainty assessments. Further research should integrate groundwater NO3– results into surface water models to determine the extent of groundwater’s contribution to surface water contamination. Lastly, results will be useful in identifying localities of elevated NO3 for increased monitoring.
Acknowledgments
This research was supported in part by funds from the NIH T32ES007018, NIOSH 2T42OH008673, and North Carolina Water Resources Research Institute (WRRI) project number 11-05-W.
Supporting Information Available
Additional information as noted in text. This material available free of charge via the Internet at http://pubs.acs.org/.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- US Environmental Protection Agency. Basic Information About Nitrate in Drinking Water http://water.epa.gov/drink/contaminants/basicinformation/nitrate.cfm (accessed November 1, 2012).
- Doering O. C. I.; Galloway J. N.; Theis T. L.; Aneja V.; Boyer E.; Cassman K. G.; Cowling E. B.; Dickerson R. R.; Herz W.; Hey D. L.; et al. Reactive Nitrogen in the United States: An Analysis of Inputs, Flows, Consequences, and Management Options, EPA-SAB-11-013; Washington DC, 2011. [Google Scholar]
- Spalding R. F.; Exner M. E. Occurrence of Nitrate in Groundwater—A Review. J. Environ. Qual. 1993, 22, 392–402. [Google Scholar]
- Ward M. H.; Mark S. D.; Cantor K. P.; Weisenburger D. D.; Correa-Villasenor A.; Zahm S. H. Drinking water nitrate and the risk of non-Hodgkin’s lymphoma. Epidemiology 1996, 7, 465–471. [PubMed] [Google Scholar]
- Ward M. H.; DeKok T. M.; Levallois P.; Brender J.; Gulis G.; Nolan B. T.; VanDerslice J. Workgroup report: Drinking-water nitrate and health—Recent Findings and research needs. Environ. Health Perspect. 2005, 113, 1607–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Roos A. J.; Ward M. H.; Lynch C. F.; Cantor K. P. Nitrate in public water supplies and the risk of colon and rectum cancers. Epidemiology 2003, 14, 640–649. [DOI] [PubMed] [Google Scholar]
- Weyer P. J.; Cerhan J. R.; Kross B. C.; Hallberg G. R.; Kantamneni J.; Breuer G.; Jones M. P.; Zheng W.; Lynch C. F. Municipal drinking water nitrate level and cancer risk in older women: The Iowa Women’s Health Study. Epidemiology 2001, 12, 327–338. [DOI] [PubMed] [Google Scholar]
- Paerl H. W. Coastal eutrophication and harmful algal blooms: Importance of atmospheric deposition and groundwater as “ new ” nitrogen and other nutrient sources. Limnol. Oceanogr. 1997, 42, 1154–1165. [Google Scholar]
- Zhou M.; Shen Z.; Yu R. Responses of a coastal phytoplankton community to increased nutrient input from the Changjiang (Yangtze) River. Cont. Shelf Res. 2008, 28, 1483–1489. [Google Scholar]
- Smith V. H.; Tilman G. D.; Nekola J. C. Eutrophication: Impacts of excess nutrient inputs on freshwater, marine, and terrestrial ecosystems. Environ. Pollut. 1999, 100, 179–196. [DOI] [PubMed] [Google Scholar]
- USEPA. http://water.epa.gov/lawsregs/rulesregs/sdwa/index.cfm.
- Kenny J. F.; Barber N. L.; Hutson S. S.; Linsey K. S.; Lovelace J. K.; Maupin M. A.. Estimated use of water in the United States in 2005. In USGS Circ. 1344, 2005.
- Fuhrer G. J.; Gilliom R. J.; Hamilton P. A.; Morace J. L.; Nowell L. H.; Rinella J. F.; Stoner J. D.; Wentz D. A.. The quality of our nation’s waters: Nutrients and pesticides. In USGS Circ. 1225, 1999.
- Daniel C. C.; Dahlen P. R.. Preliminary hydrogeologic assessment and study plan for a regional ground-water resource investigation of the blue ridge and piedmont provinces of North Carolina. IN USGS Investigations Report 02-4105 2002.
- Nolan B. T.; Hitt K. J. Vulnerability of shallow groundwater and drinking-water wells to nitrate in the United States. Environ. Sci. Technol. 2006, 40, 7834–7840. [DOI] [PubMed] [Google Scholar]
- Su J. G.; Jerrett M.; Beckerman B. A distance-decay variable selection strategy for land use regression modeling of ambient air pollution exposures. Sci. Total Environ. 2009, 407, 3890–3898. [DOI] [PubMed] [Google Scholar]
- Nuckols J. R.; Beane Freeman L. E.; Lubin J. H.; Airola M. S.; Baris D.; Ayotte J. D.; Taylor A.; Paulu C.; Karagas M. R.; Colt J.; et al. Estimating water supply arsenic levels in the New England Bladder cancer study. Environ. Health Perspect. 2011, 1002345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim D.; Miranda M. L.; Tootoo J.; Bradley P.; Gelfand A. E. Spatial modeling for groundwater arsenic levels in North Carolina. Environ. Sci. Technol. 2011, 45, 4824–4831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Messier K. P.; Akita Y.; Serre M. L. Integrating address geocoding, land use regression, and spatiotemporal geostatistical estimation for groundwater tetrachloroethylene. Environ. Sci. Technol. 2012, 46, 2772–2780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodríguez-Lado L.; Sun G.; Berg M.; Zhang Q.; Xue H.; Zheng Q.; Johnson C. A. Groundwater arsenic contamination throughout China. Science 2013, 341, 866–868. [DOI] [PubMed] [Google Scholar]
- Hoos A. B.; Mcmahon G. Spatial analysis of instream nitrogen loads and factors controlling nitrogen delivery to streams in the southeastern United States using spatially referenced regression on watershed attributes (SPARROW) and regional classification frameworks. Hydrol. Process. 2009, 23, 2275–2294. [Google Scholar]
- Howarth R. W.; Billen G.; Swaney D.; Townsend a.; Jaworski N.; Lajtha K.; Downing J. a.; Elmgren R.; Caraco N.; Jordan T.; et al. Regional nitrogen budgets and riverine N & P fluxes for the drainages to the North Atlantic Ocean: Natural and human influences. Biogeochemistry 1996, 35, 75–139. [Google Scholar]
- Smith R. A.; Schwarz G. E.; Alexander R. B. Regional interpretation of water-quality monitoring data. Water Resour. Res. 1997, 33, 2781–2798. [Google Scholar]
- Qian S. S. Nonlinear regression modeling of nutrient loads in streams: A Bayesian approach. Water Resour. Res. 2005, 41, 1–10. [Google Scholar]
- Cressie N.; Majure J. J. Spatio-temporal statistical modeling of livestock waste in streams. J. Agric. Biol. Environ. Stat. 1997, 2, 24–47. [Google Scholar]
- Giese G. I.; Eimers J. L.; Coble R. W.. Simulation of ground-water flow in the coastal plain system of North Carolina. In US Geol. Surv. Prof. Pap. 1404-M, 1993, p 142.
- Tesoriero A. J.; Duff J. H.; Saad D. A.; Spahr N. E.; Wolock D. M. Vulnerability of Streams to Legacy Nitrate Sources. Environ. Sci. Technol. 2013, 47, 3623–3629. [DOI] [PubMed] [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar]
- Zou H.; Hastie T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B 2005, 67, 301–320. [Google Scholar]
- Peduzzi P. N.; Hardy R. J.; Holford T. R. A stepwise variable selection procedure for nonlinear regression models. Biometrics 1980, 36, 511–516. [PubMed] [Google Scholar]
- Hosmer D. W.; Lemeshow S.. Applied Logistic Regression; John Wiley and Sons, 2000. [Google Scholar]
- Huang C.; Townshend J. R. G. A stepwise regression tree for nonlinear approximation: Applications to estimating subpixel land cover. Int. J. Remote Sens. 2003, 24, 75–90. [Google Scholar]
- Harden S. L.; Cuffney T. F.; Terziotti S.; Kolb K. R.. Relation of Watershed Setting and Stream Nutrient Yields at Selected Sites in Central and Eastern North Carolina, 1997–2008. In USGS. Investigative Report 2013-5007, 2013
- Sanders A. P.; Messier K. P.; Shehee M.; Rudo K.; Serre M. L.; Fry R. C. Arsenic in North Carolina: Public health implications. Environ. Int. 2011, 38, 10–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLay C. D.; Dragten R.; Sparling G.; Selvarajah N. Predicting groundwater nitrate concentrations in a region of mixed agricultural land use: A comparison of three approaches. Environ. Pollut. 2001, 115, 191–204. [DOI] [PubMed] [Google Scholar]
- Gurdak J. J.; Qi S. L. Vulnerability of recently recharged groundwater in principle aquifers of the United States to nitrate contamination. Environ. Sci. Technol. 2012, 46, 6004–6012. [DOI] [PubMed] [Google Scholar]
- Moran M. J.; Zogorski J. S.; Squillace P. J. Chlorinated solvents in groundwater of the United States. Environ. Sci. Technol. 2007, 41, 74–81. [DOI] [PubMed] [Google Scholar]
- Helsel D. R. More than obvious: Better methods for interpreting nondetect data. Environ. Sci. Technol. 2005, 39, 419A–423A. [DOI] [PubMed] [Google Scholar]
- Pradhan S. S.; Hoover M. T.; Austin R. E.; Devine H. A.. Potential Nitrogen Contributions from On-site Wastewater Treatment Systems to North Carolina’s River Basins and Sub-Basins; Raleigh, NC, 2007. [Google Scholar]
- Beven K. J.; Kirkby M. J. A physically based, variable contributing area model of basin hydrology. Hydrol. Sci. 1979, 24, 43–69. [Google Scholar]
- Christakos G. A Bayesian/maximum-entropy view to the spatial estimation problem. Math. Geol. 1990, 22, 763–777. [Google Scholar]
- Serre M. L.; Christakos G. Modern geostatistics: Computational BME analysis in the light of uncertain physical knowledge—The Equus Beds study. Stoch. Environ. Res. Risk Assess. 1999, 13, 1–26. [Google Scholar]
- Christakos G.; Bogaert P.; Serre M. L.. Temporal GIS: Advanced Function for Field-Based Applications; Springer: New York, NY, 2002. [Google Scholar]
- Keil A.; Wing S.; Lowman A. Suitability of public records for evaludating health effects of treated sewage sludge in North Carolina. N. C. Med. J. 2011, 72, 98–104. [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.