Using Quantum Mechanical Approaches to Study Biological Systems

Conspectus

Quantum mechanics (QM) has revolutionized our understanding of the structure and reactivity of small molecular systems. Given the tremendous impact of QM in this research area, it is attractive to believe that this could also be brought into the biological realm where systems of a few thousand atoms and beyond are routine. Applying QM methods to biological problems brings an improved representation to these systems by the direct inclusion of inherently QM effects such as polarization and charge transfer. Because of the improved representation, novel insights can be gleaned from the application of QM tools to biomacromolecules in aqueous solution.

To achieve this goal, the computational bottlenecks of QM methods had to be addressed. In semiempirical theory, matrix diagonalization is rate limiting, while in density functional theory or Hartree–Fock theory electron repulsion integral computation is rate-limiting. In this Account, we primarily focus on semiempirical models where the divide and conquer (D&C) approach linearizes the matrix diagonalization step with respect to the system size. Through the D&C approach, a number of applications to biological problems became tractable. Herein, we provide examples of QM studies on biological systems that focus on protein solvation as viewed by QM, QM enabled structure-based drug design, and NMR and X-ray biological structure refinement using QM derived restraints.

Through the examples chosen, we show the power of QM to provide novel insights into biological systems, while also impacting practical applications such as structure refinement. While these methods can be more expensive than classical approaches, they make up for this deficiency by the more realistic modeling of the electronic nature of biological systems and in their ability to be broadly applied. Of the tools and applications discussed in this Account, X-ray structure refinement using QM models is now generally available to the community in the refinement package Phenix.

While the power of this approach is manifest, challenges still remain. In particular, QM models are generally applied to static structures, so ways in which to include sampling is an ongoing challenge. Car–Parrinello or Born–Oppenheimer molecular dynamics approaches address the short time scale sampling issue, but how to effectively use QM to study phenomenon covering longer time scales will be the focus of future research. Finally, how to accurately and efficiently include electron correlation effects to facilitate the modeling of, for example, dispersive interactions, is also a major hurdle that a broad range of groups are addressing

The use of QM models in biology is in its infancy, leading to the expectation that the most significant use of these tools to address biological problems will be seen in the coming years. It is hoped that while this Account summarizes where we have been, it will also help set the stage for future research directions at the interface of quantum mechanics and biology.

Introduction

Quantum mechanics (QM) has revolutionized our understanding of the structure and reactivity of small molecular systems. For example, QM based methods provide structural information in excellent agreement with experiment, match experimental barrier heights for chemical reactions, and provide chemically accurate interaction energies for hydrogen-bonded or dispersive systems.^1,2 Given the tremendous impact QM has had for systems of <100 atoms, it is attractive to believe that this impact could also be brought into the biological realm where systems of a few thousand atoms and beyond are standard. To achieve this goal, the bottlenecks of QM methods have to be addressed. Depending on the method employed, various steps in a QM calculation can be rate determining. In semiempirical methods, matrix diagonalization is rate limiting, while in density functional theory (DFT) or Hartree–Fock (HF) theory electron repulsion integral computation is rate-limiting.³ These theories neglect the correlation energy, which is important to account for to obtain highly accurate results including barrier heights and interaction energies (especially dispersion dominated ones). In this case, the correlation treatment of choice is rate-limiting be it Møller–Plesset (MP) theory or coupled-cluster (CC) methods.³

State-of-the-art linear-scaling algorithms, which linearize the computational cost with the system size, have attracted much attention.⁴⁻⁶ Significant effort has been devoted to the development of linear-scaling methods to compute the total energy of large molecular systems at the HF or DFT level.⁷⁻¹⁴ One of the challenges is to speed up the calculation of long-range Coulomb interactions when assembling the Fock matrix elements. Fast multipole based approaches have successfully reduced the scaling in system size to linear^{11,12,15−17} and made HF and DFT calculations affordable for larger systems when small to moderate sized basis sets are utilized. There are also fragment-based methods for QM calculation of protein systems including the divide and conquer (D&C) method of Yang,⁸ Yang and Lee,⁹ Dixon and Merz,^18,19 Gogonea et al.,²⁰ Shaw and St-Amant,²¹ and Nakai and co-workers,²²⁻²⁵ the adjustable density matrix assembler (ADMA) approach method of Exner and Mezey,^13,26−28 the fragment molecular orbital (FMO) method of Kitaura and co-workers,²⁹⁻³¹ the X-pol model of Gao and Xie,³² and the molecular fractionation with conjugate caps (MFCC) approach developed by Zhang and co-workers.^33,34 Most applications of these methods to protein systems have been largely limited to semiempirical, HF, and DFT calculations. Among these approaches, FMO has been applied to higher level ab initio calculations such as second-order Møller–Plesset perturbation theory (MP2)³⁵ and coupled cluster theory (CC).³⁶ Nakai and co-workers have described D&C-MP2^22,25,37 and D&C-CCSD³⁸ approaches and applied them to linear or near-linear systems.

QM excels at the static modeling of a molecular system. However, in chemistry and biology, fluctuations are important to describe a broad range of effects. Thus, the ensemble picture of a molecular system is more appropriate, and while molecular dynamics (MD) methods are beginning to address dynamical issues using classical potentials, how to address this “sampling” issue when using more expensive QM based approaches will need to be addressed.

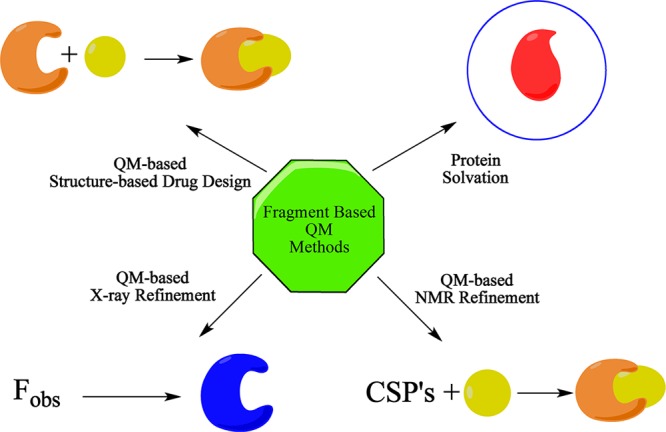
Herein we briefly review work carried out in my laboratory over the past decade in exploiting fully QM methods in the study of biological systems (see Scheme 1). In particular, we will discuss the use of D&C techniques to address the matrix diagonalization step in semiempirical methods and in HF and DT approaches. After summarizing the technical aspects of how to compute the QM energy of many thousands of atoms, we will review several fully QM application studies carried out for the first time in my laboratory on biological systems. Finally, I will discuss the future outlook of using QM to solve biological problems and the ongoing challenges of using a fully QM model on large systems.

Scheme 1. Application of QM Methods to Biological Problems.

Divide-and-Conquer Approach for Hartree–Fock Based Calculations

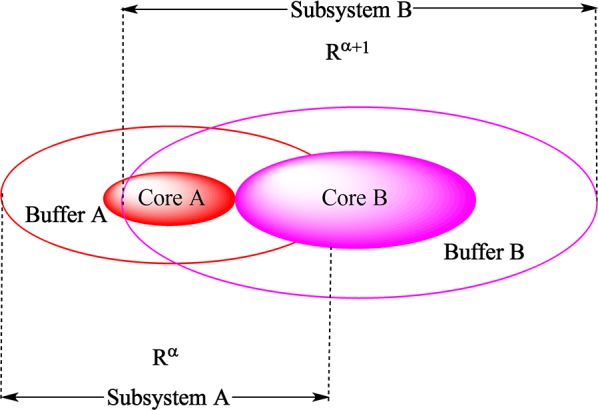
In biological systems, the D&C approach⁸ takes advantage of chemical locality. Details of the implementations of this approach at the semiempirical,^9,18,19 HF and post-HF^21−25,39 levels of theory are given in the literature, so below we only give a brief overview. In this approximation, it is assumed that the atoms that are far away from the region of interest only weakly influence local regions of a protein. Hence, the entire system is divided into fragments called core regions (Core^α) with an associated buffer region (Buffer^α) assigned to each core region to account for the local environmental effects. The combination of every core region and its buffer region constitutes a subsystem (R^α) (see Scheme 2). Local MOs of each subsystem are solved by the Roothaan–Hall equation

1

where F^α and S^α are local Fock overlap matrices, respectively.

2

Scheme 2. D&C Subsetting (Fragmentation) Scheme.

After the local MO coefficient matrices C^α are obtained, the total density matrix system is given by

3

where D_μν^α is the partition matrix,

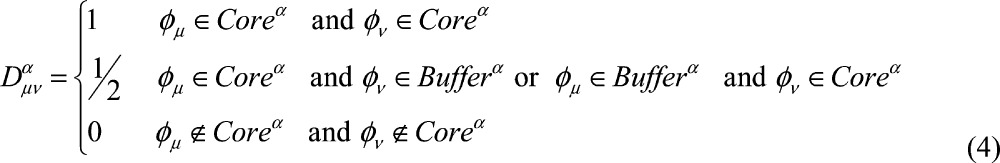4

and p_μν^α is the local density matrix defined by

5

where n_i^α is a smooth approximation to the Heaviside step function:

6

ε_F is determined through the normalization of the total number of electrons in the entire system.

7

After the density matrix is converged, the total HF energy is given as

8

where H_μν^α is the local one-electron core Hamiltonian matrix defined similarly to the local Fock matrix (see eq 2).

For HF calculations, the construction of the Coulomb matrix and exchange matrix along with the diagonalization of the Fock matrix are the three most time-consuming steps, while the diagonalization of the Hamiltonian matrix scales as O(N³). In the D&C scheme, the diagonalization calculation is performed for each subsystem, linearizing the diagonalization step as a function of the number of subsystems. However, it is important to realize that the D&C algorithm does not help to reduce the scale of computation of the Coulomb matrix and exchange matrix. Other approaches¹⁸ provide ways to linearize these steps. However, for semiempirical methods where matrix diagonalization is rate-limiting, the D&C approach greatly enhances the capabilities of these methods.^9,18,19

Applications of Fragment QM to Biological Problems

We have used our fragment QM methods (largely at the semiempirical level) to study biological problems with a focus on protein structure and solvation,⁴⁰⁻⁴⁴ structure-based drug design^45,46 and biological structure refinement by NMR and X-ray spectroscopy.⁴⁷⁻⁶⁴ Below we will briefly highlight work done in our laboratory using these methods to address specific biological problems.

A New View of the Protein–Water Interface

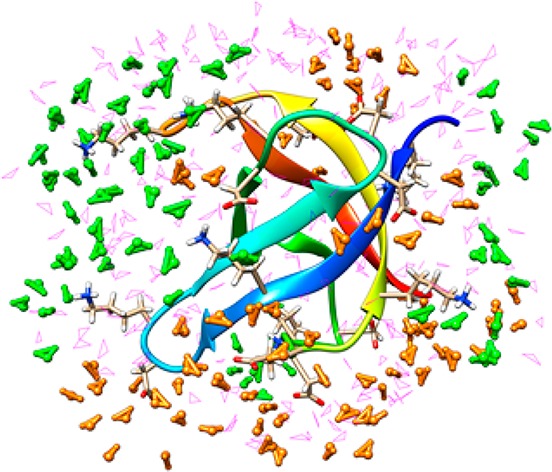
The interface between a biological molecule and water affects its stability and function.⁶⁵ The classical picture of this interface does not allow for the commingling of the electron density (the so-called charge transfer (CT) effect) between the protein and the surrounding aqueous environment. We examined the QM nature of a small protein (E. coli cold-shock protein A; CspA) in aqueous solution through the use of semiempirical D&C calculations over 100 snapshots. The surprising result was the observation that two units of charge were transferred from the protein surface to that of the water molecules. Thus, water molecules, at the protein interface, are perturbed not only by the rugged protein interface but also electronically. Via integration over the entire protein surface, the net results of numerous small net transfer of charge yield the observed value of 2 units of charge. Not surprisingly, the main participants in this charge transfer effect are charged amino acids at the protein–water interface (see Figure 1). The magnitude of the CT transfer effect on the energetics of hydrogen bond interactions has been debated,^44,66−68 but we reported⁴⁴ a value of ∼30% for a series of dimers using a Kitaura-Morokuma analysis⁶⁹ (this latter paper also reports a similar CT effect for the water dimer), a value later supported by more sophisticated calculations.⁶⁷ We carried out extensive validation studies of the nature of CT⁴⁴ because our pioneering studies employed semiempirical models. Through these studies, we concluded that in terms of the magnitude of the CT effect the semiempirical models employed were reliable. Subsequent work using ab initio FMO⁷⁰ and ab initio MD calculations⁷¹ reconfirmed our initial predictions.

Figure 1.

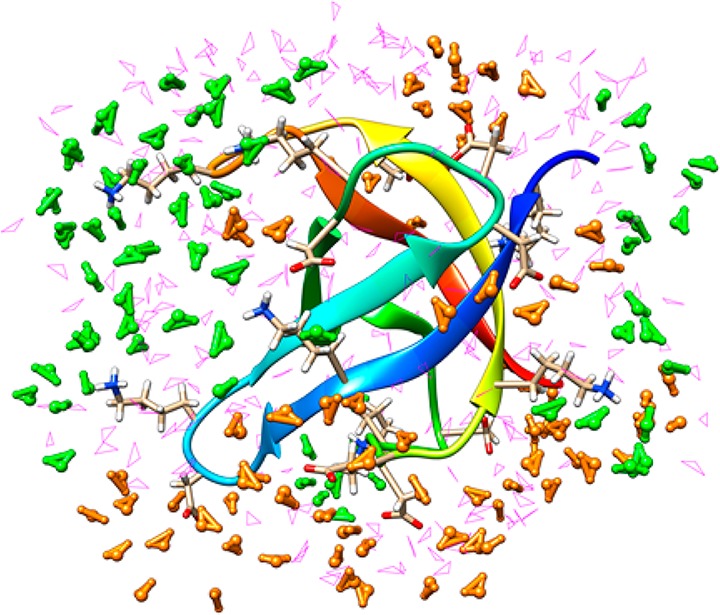
E. coli cold-shock protein A (CspA) surrounded by a water layer. The green water molecules are near Lys residues and experience a slight loss of electron density (∼0.06e in aggregate), while the orange water molecules are near Glu/Asp residues gain electron density (∼0.2e in aggregate). The magenta water molecules are not within 5 Å of the charged residues.

In related work, charge transfer in receptor ligand interactions in the context of SBDD has been examined by my laboratory.⁴⁵ In a study of 165 noncovalent protein–ligand complexes, we found that 11% of the complexes had more than 0.1e of charge transferred from the protein to ligand. Not surprisingly, in 49 metalloenzyme complexes, on average, there is 0.6e transferred between the protein and the ligand. The direction of the CT effect depended on the nature of the protein–ligand complex. For example, in matrix metalloproteases (MMP), charge was transferred from the protein to the ligand, while for human carbonic anhydrase (HCA) and carboxypeptidases (CPA) charge was transferred n the opposite direction.

The view that the interface between a protein, water, or a ligand is electronically altered via polarization and CT effects is now generally accepted. Indeed, the observation of CT at the protein–water interface highlights the need to include this effect in modern force field methods, and work is being pursued along these lines.^72,73 However, without the aid of QM based methods, this effect would not have been discovered and its importance might have gone unappreciated for some time.

QM in Structure-Based Drug Design (SBDD)

The docking and subsequent scoring of small molecules bound to receptors has been a mainstay of modern SBDD tools.^74,75 However, the reliability of these approaches has been debated.⁷⁵⁻⁷⁷ Most tools in this class utilize approximate potentials to study the interaction between the protein and its ligand. We reasoned that the use of more advanced QM based methods might improve the outcome.^45,46

We reported the first application of linear-scaling methods to SBDD where we calculated the binding affinity of ligands bound to the HCA and CPA with reasonable accuracy.⁴⁶ The free energy of binding in solution was calculated using the following set of equations:

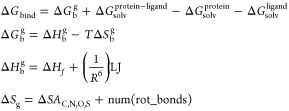9

where the free energy of binding in solution was calculated as the sum of the gas-phase interaction energy (ΔG_b^g) and a solvation correction (ΔG_solv terms). The gas-phase interaction energy consisted of enthalpic (semiempirical computed ΔH_f’s) and entropic components. The electrostatic part of the enthalpic component was calculated using the DivCon program, employing semiempirical Hamiltonians.⁴⁶ A dispersion correction was lso utilized (the (1/R⁶)LJ term). The solvation correction was calculated as a difference of the solvation free energies of the protein–ligand complex (PL), the protein (P), and the ligand (L). The solvation free energy was calculated using a Poisson–Boltzmann (PB) based self-consistent reaction field (PB/SCRF) method.⁷⁸ A major advantage of PB is the internal dielectric of the protein need not be preset as in classical treatments.⁷⁸ Finally, an empirical entropy term depending on the change in solvent accessible area (ΔSA) and a ligand rotatable bond count.

In further studies, we carried out a larger scale validation of this QM based scoring function for predicting binding affinity. We calculated interaction energies for a diverse range of protein–ligand complexes comprising of 165 noncovalent complexes and 49 metalloenzyme complexes.⁴⁵ For the 165 noncovalent complexes, the interaction energies, without any fitting, agreed with experimental binding affinity within 2.5 kcal/mol. When different parts of the scoring function were fit to experimental free energy of binding using regression methods, the agreement was within 2.0 kcal/mol. For metalloenzymes, the agreement with experiments without fitting was within 1.7 kcal/mol, and with fitting was within 1.4 kcal/mol. Overall, the correlation with experiment was satisfactory with R² values of 0.69⁴⁶ and 0.55,⁴⁵ respectively. However, while the method performed reasonably it was not a “quantum” improvement over traditional methods

Much further work has been done to explore the use of QM and QM/MM approaches to predict protein–ligand binding affinities^79,80 with the general conclusion that,while QM does help, it is not a panacea, at least in the current incarnation. Beyond simply having a better level of theory, many issues remain to be resolved to produce robust computed binding affinities including the inclusion of explicit water molecules⁸¹ and incorporation of receptor flexibility. These effects plague both simpler and more sophisticated model Hamiltonians and is the subject of much on ongoing research.⁸²

QM Based Structure Refinement

QM NMR Refinement of Protein/Ligand Complexes

NMR spectroscopy has proven itself to be a powerful and versatile tool for the study of protein–ligand interactions. The three-dimensional structures of protein–ligand complexes are determined by combining interproton distance restraints derived from nuclear Overhauser effect (NOE) with other restraints from J coupling constants, hydrogen bonds, and/or residual dipolar couplings. Since Fesik and co-workers introduced SAR (structure–activity relationship) by NMR,⁸³ many NMR-based screening methods have been developed to identify potential drug molecules in pharmaceutical research.⁸⁴⁻⁸⁸ All these techniques take advantage of the fact that, upon ligand binding, significant perturbations can be observed in NMR parameters of either the receptor or the ligand. These perturbations can be utilized qualitatively to detect complex formation or quantitatively to measure the binding affinity.

Among these NMR parameters, chemical shifts are exquisitely sensitive on the chemical environments of compounds. Therefore, theoretical calculation of chemical shift perturbations (CSP) upon ligand binding provides insights into protein–ligand interactions at the molecular level.

There are two categories of computational approaches to calculate NMR chemical shifts: classical/empirical models and QM. The classical/empirical models⁸⁹⁻⁹⁵ are parametrized to experimental data or DFT results. These approaches are fast so that they can be easily applied to proteins, but are less general being largely focused on protein chemical shifts. In this case, the generality of a QM based approach offers a significant advantage.

We developed a fast and accurate approach⁹⁶ to calculate NMR chemical shifts using the D&C method at the semiempirical level of theory. Along with this approach, we have reported the automatic fragmentation QM/MM (AF-QM/MM) method that computes chemical shifts for large systems using ab initio methods.⁵⁴ This approach was first applied to the FKBP-GPI complex (see Figures 2 and 3).⁴⁸ By comparing calculated proton chemical shifts of the ligand to experimental data, it was possible to determine the best binding site pose. To further validate this approach, we generated several hundred poses of GPI using different docking programs and then scored them by calculating CSPs and then comparing them to experiment.⁹⁷ We have found that the deviation of the computed CSPs from experiment better differentiate decoy poses from native poses than scoring functions used in docking studies. This demonstrates that CSP based approaches can provide an accurate way in which to predict protein/ligand complex structure using in silico NMR approaches.

Figure 2.

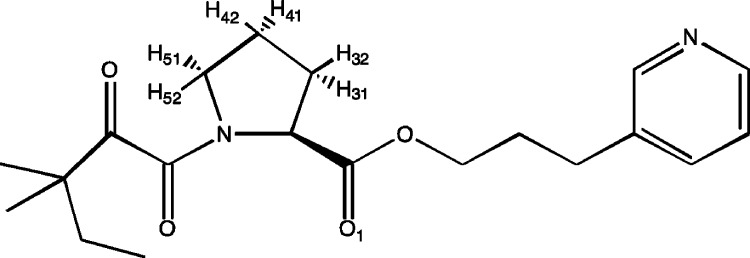
Structure of GPI.

Figure 3.

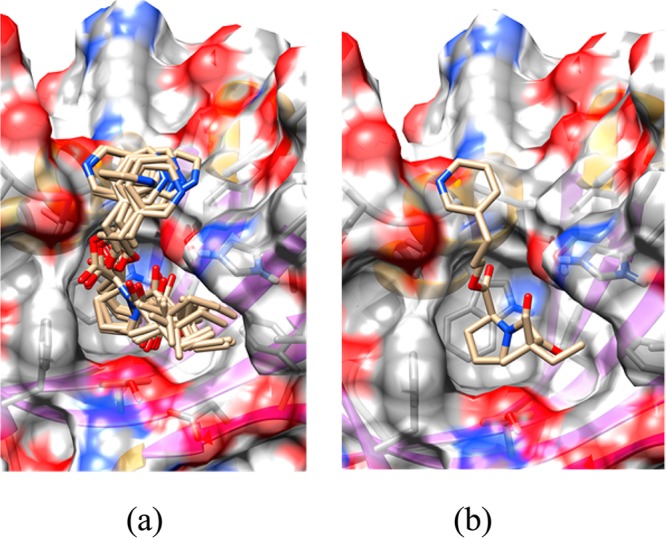
By comparing CSP RMSDs the preferred pose for the FKBP-GPI complex can be determined. Left hand panel (a) shows 10 possible poses, while after analysis by CSP RMSDs between experimental and computed chemical shifts, one pose gives the best agreement between theory and experiment.

QM X-ray Refinement

We have also explored the use of QM based methods in X-ray refinement. We utilized D&C QM calculations to refine an entire protein,⁹⁸ and we have carried out several studies looking at the QM/MM refinement of small molecules.⁵⁹⁻⁶² One of the strengths of QM is the ability of these methods to provide high quality structural models of both the protein and the small molecule. Modern X-ray refinement of protein structures typically uses a pseudoenergy formalism where a chemical model (E_Chem) is combined with the X-ray signal (E_X-ray) for which the gradients are obtained and the energy minimized.⁹⁹ In this formulation, the quality of the results depends on both the chemical model term and the quality of the experimental data. For proteins, highly parametrized expressions are available for the E_Chem term, but the quality of this term for small molecules is variable. However, QM models can treat both the protein and ligand equally well with no parametrization.

As an example of how a QM (in this case a QM/MM refinement) can improve structure quality, I briefly describe our work on benzamidine ligands bound to a number of receptors.⁵⁵ In the case of benzamidines, the amidine group (see Figure 4) prefers to be out of the plane of the benzene ring by ∼ ±40°; however, many of the reported protein X-ray structures model this group as planar. Using QM/MM X-ray refinement approaches, we demonstrated that this moiety was indeed nonplanar and that the models employed in the earlier refinements did not accurately represent this functional group. Figure 5 shows an example of this for PDBID 1Y3X, where we show the result before and after QM/MM X-ray refinement. Moreover, the standard R, R_free, and real-space R standard structure quality metrics all improved in the QM/MM X-ray refined structures.⁵⁵

Figure 4.

Benzamidine with the amidine group indicated.

Figure 5.

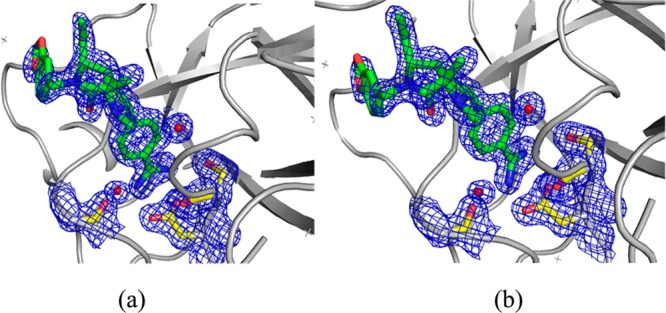
Left-hand panel (a) shows the benzamidine derivative refined using standard approaches, while the right-hand panel (b) shows the results from QM/MM X-ray refinement. Note the out of plane twist of the amidine group.

The Future of QM in Biology

QM has already had a major impact on the study of biological systems primarily through its use to build sophisticated classical force field representations of biological macromolecules. Via QM/MM methods,¹⁰⁰ enzymatic catalysis can be routinely studied and this development was awarded the Nobel Prize in Chemistry in 2013. However, it is important to keep in mind that the computational study of biological systems at the molecular-level faces two daunting challenges: We must both accurately^101−106 calculate the energies and forces involved, but we must also sample all relevant states of a system. QM largely addresses the former, but how to extensively sample biological systems at the QM level of theory remains a challenging issue. Beyond the creation of faster and more accurate QM models, strategies to address the sampling issue will also have to be devised. This will likely be addressed via a combination of classical and QM models⁸² and remains an active area of research.

Biography

Kenneth M. Merz, Jr. is the Joseph Zichis Chair in Chemistry and Director of the Institute for Cyber Enabled Research (iCER) at Michigan State University. His research interest lies in the development of theoretical and computational tools and their application to biological problems including structure and ligand based drug design, mechanistic enzymology, and methodological verification and validation. He has received a number of honors including election as an ACS Fellow, the 2010 ACS Award for Computers in Chemical and Pharmaceutical Research, election as a fellow of the American Association for the Advancement of Science, and a John Simon Guggenheim Fellowship.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States