Abstract
How do we apply learning from one situation to a similar, but not identical, situation? The principles governing the extent to which animals and humans generalize what they have learned about certain stimuli to novel compounds containing those stimuli vary depending on a number of factors. Perhaps the best studied among these factors is the type of stimuli used to generate compounds. One prominent hypothesis is that different generalization principles apply depending on whether the stimuli in a compound are similar or dissimilar to each other. However, the results of many experiments cannot be explained by this hypothesis. Here we propose a rational Bayesian theory of compound generalization that uses the notion of consequential regions, first developed in the context of rational theories of multidimensional generalization, to explain the effects of stimulus factors on compound generalization. The model explains a large number of results from the compound generalization literature, including the influence of stimulus modality and spatial contiguity on the summation effect, the lack of influence of stimulus factors on summation with a recovered inhibitor, the effect of spatial position of stimuli on the blocking effect, the asymmetrical generalization decrement in overshadowing and external inhibition, and the conditions leading to a reliable external inhibition effect. By integrating rational theories of compound and dimensional generalization, our model provides the first comprehensive computational account of the effects of stimulus factors on compound generalization, including spatial and temporal contiguity between components, which have posed longstanding problems for rational theories of associative and causal learning.
Imagine choosing the destination of your next vacation. You love large cities, but also enjoy beaches. Would you predict even more pleasure from going to a large city near a beach? In contrast, suppose that you want to invest in the stock market, and you read in two different financial newspapers that a certain stock is predicted to rise 10-15% over the next year. In the past, the predictions from each newspaper have been accurate and you trust both of them. Would you predict a higher profit given the two sources of information, as compared to one source? And would this change if you knew that the two newspapers base their predictions on different market variables?
When confronted with combinations of stimuli that are predictive of an outcome, why do we summate predictions for outcomes in some cases (e.g., predictions for enjoyment from the city and from the beach), but average predictions in other cases (e.g., the stock market)? What factors affect how we combine the effects of multiple stimuli, and how does the similarity between different stimuli (two financial newspapers that use the same vs. different variables for their analyses) affect our tendency to summate predictions?
These questions are important not only to vacation planners and stock market investors, as they represent instantiations of a general problem in daily life: although our environment is complex and multidimensional, we naturally try to isolate what elements in a certain situation were predictive of consequences such as pleasure or pain. We then have to combine these learned predictions anew each time we are faced with a different combination of the elements. In essence, this is a problem of generalization: how do we apply learning from one situation to another that is not identical?
For psychologists studying learning, this question is fundamental: we may understand how animals and humans learn to associate simple stimuli such as lights and tones with rewards, but without understanding the principles that determine generalization across compound stimuli in associative and causal learning tasks, we will not be able to explain anything but the simplest laboratory experiment. Not surprisingly, this problem of compound generalization has been the focus of one of the most active areas of research in the psychology of learning for the past 20 years.
Two types of explanations, mechanistic and rational, have been proposed for compound generalization phenomena. Mechanistic explanations explicitly propose representations and processes that would underlie the way in which an agent learns and behaves. Rational explanations (also called normative or computational; Anderson, 1990; Marr, 1982) formalize the task and goals of the agent, and derive the optimal rules of behavior under such circumstances. Although sometimes viewed as mutually exclusive, these two types of explanations can provide complementary accounts of behavior (Marr. 1982).
Most recent research on compound generalization has been motivated by a controversy between two types of mechanistic theory: configural and elemental models. These models agree in that they represent knowledge about the environment in the form of associations (e.g., an association between beaches and enjoyment and between large cities and enjoyment), but they disagree on how the stimuli are represented when they are presented in a compound (e.g., the large-city-on-the-water compound), and thus on how the compound can be associated with a predicted outcome.
Elemental theories, such as the Rescorla-Wagner model (Rescorla & Wagner, 1972), propose that associations with an outcome are acquired and expressed separately by each of the elements in a compound. In the Rescorla-Wagner model, the associative strength of a compound is equal to the algebraic sum of the associative strength of its components. For example, the model would predict that since beaches and cities were each independently associated with enjoyable vacations in the past, compounding the two should be expected to double the pleasure; that is, the model predicts a “summation” effect.
In contrast, configural theories, such as Pearce's (1987; 1994; 2002) model, propose that associations with an outcome are acquired and expressed by entire stimulus configurations. In Pearce's model, generalization from one configuration to another depends on the components shared by the configurations. In particular, generalization strength is computed according to the proportion of elements from the trained configuration that are present in the new configuration multiplied by the proportion that these shared elements comprise of in the new configuration. According to this theory, if cities and beaches are each independently associated with enjoyment, then a vacation in a city by the beach should be expected to yield 50% of the enjoyment expected from a big city (as 100% of the components of the trained ‘big city’ stimulus are present in the compound, but they comprise only 50% of the compound), plus 50% of the enjoyment expected when vacationing at a beach; that is, the model predicts an “averaging” effect instead of summation.
The most important difference between elemental and configural theories is not so much the type of representation that they propose (both theories require some form of configural and elemental representation to work), but the principles of generalization that they implement. Configural theories predict less generalization across compounds sharing a given number of elements than do elemental theories.
What generalization principles do animals and humans use in compound generalization tasks? As suggested by the examples above, the answer is that it depends. Both humans and animals seem to use different generalization principles depending on a number of factors, including the type of stimuli used to form compounds and the structure of tasks which they have previously experienced (reviewed in Melchers, Shanks, & Lachnit, 2008; Wagner, 2003, 2007).
Among all the factors known to affect compound generalization, one has attracted the most attention in the field: the type of stimuli used to create compounds. For example, animal associative learning studies have found that a summation effect is easily observed with components that belong to different sensory modalities, but not with those belonging to the same modality (Kehoe, A. J. Horne, P. S. Horne, & Macrae, 1994). Similar effects have been observed using other generalization tests and discrimination designs (Wagner, 2003, 2007), and it is now generally accepted that many contradictory results in the literature can be explained as a function of the type of stimuli used in each study.
More generally, many authors (Harris, 2006; Kehoe et al., 1994; Myers, Vogel, Shin, & Wagner, 2001; Wagner, 2003, 2007) hypothesize that elemental processing, like that proposed by the Rescorla-Wagner model, should occur more easily with stimuli that are very dissimilar, such as stimuli coming from different modalities. On the other hand, configural processing, like that proposed by Pearce's configural theory, should occur with similar stimuli, such as those coming from the same modality. A number of flexible models, which can act as configural or elemental theories depending on changes in their free parameters (Harris, 2006; Kinder & Lachnit, 2003; McLaren & Mackintosh, 2002; Wagner, 2003, 2007), can implement this similarity hypothesis by changing parameter values as a function of stimulus similarity.
The similarity hypothesis makes intuitive sense, because a group of similar stimuli would be more easily processed as parts of a configuration which predicts one shared outcome (two newspapers predicting a single outcome of stock market value), whereas a group of disparate stimuli (beach, city) would be more easily processed as independent entities that each predict its own outcome.
Although there is evidence in line with the similarity hypothesis (reviewed by Melchers et al., 2008; Wagner, 2003, 2007), there are also examples of compound generalization effects that are not modulated by type of stimuli (e.g., Pearce & Wilson, 1991) and compound generalization effects that show more “configural” processing with more dissimilar stimuli (e.g., Gonzalez, Quinn, & Fanselow, 2003). Also, other stimulus factors besides similarity affect elemental/configural processing in similar ways. For example, both spatial and temporal contiguity seem to foster configural encoding of stimuli, while spatial and temporal separation fosters elemental encoding (Glautier, 2002; Livesey & Boakes, 2004; Martin & Levey, 1991; Rescorla & Coldwell, 1995).
Thus, similarity between elements is not truly a unifying principle that explains the effect of stimulus factors in compound generalization. One approach to discovering a unifying principle is to formalize a model of the computational task that a learner is faced with in compound generalization situations. Such a theory would generate predictions about how a rational agent should act. Knowledge about why some specific circumstances foster the use of a particular strategy might enlighten the search for mechanisms to explain how this happens.
The motivation for the present work is to develop such rational theory of compound generalization. In the following sections, we first briefly review the literature on rational theories of compound generalization and on rational theories of dimensional generalization. We then propose a new model that combines concepts from both types of theory, and can explain compound generalization phenomena through rational principles of dimensional generalization. We show that this proposed model can explain both data for which mechanistic explanations already exist (e.g., the similarity hypothesis) and data that cannot be explained by current mechanistic models. Importantly, as a rational model, our model suggests a new conceptualization of the principles underlying compound generalization in causal learning.
Rational theories of compound generalization
Two types of rational models have been proposed that are applicable to compound generalization in causal and associative learning tasks. A large class of models, most of them proposed in the field of human causal and contingency learning (e.g., Cheng, 1997; Dayan, Kakade, & Montague, 2000; Griffiths & Tenenbaum, 2005, 2007; Kakade & Dayan, 2002; Lu, Yuille, Liljeholm, Cheng, & Holyoak, 2008; Novick & Cheng, 2004), assume that observable stimuli can directly cause an outcome. According to these models, the task of the learner is to infer the strength of the causal relations between stimuli and outcomes, which determine the probability distribution of the outcome conditional on the presence or absence of the stimuli. Work using these models has focused largely on the problem of how people learn estimates of causal strength, but has ignored the issue of compound generalization. As a result, we know little about the ability of these models to explain most generalization phenomena.
In contrast, generative models are a class of models that define a causal structure that is presumed to generate the observable events in the world. These models propose that all observable events, that is, both the stimuli and the outcomes are generated by latent (unobserved) causes. Intuitively, the distinction between observable events (stimuli and outcomes) and latent causes is similar to the distinction between the symptoms of a disease and the virus causing the disease. Imagine that you wake up one morning with a sore throat. Later in the day, you also start coughing and get a fever. Instead of inferring that your sore throat caused your coughing and fever, you immediately realize that there is an unobserved cause for all these symptoms: you caught a cold. In this example, you have learned about a latent cause (the cold virus) by making inferences from observable events (your symptoms).
Thus, the task of the learner according to the generative modeling perspective is to infer the latent causes responsible for generating observable variables. One model in this tradition, due to Courville and colleagues (Courville, 2006; Courville, Daw, & Touretzky, 2002) is able to explain a number of compound generalization phenomena in Pavlovian conditioning (Pavlov, 1927).
Figure 1a shows a schematic representation of the latent cause model of Courville and colleagues. Each circle represents a different variable, either a latent cause (represented by the letter Z), an observable stimulus (represented by letters A-D), or an observable outcome (represented by the letter R for reward). Arrows represents causal links between latent causes and observable events. There is a weight associated with each of these links, and the probability that a stimulus or outcome is observed when the latent cause is active is a function of those weights. For simplicity, assume that all links in Figure 1a are positive and strong, so that if a latent cause is present, it generates a linked observable variable with very high probability. In this particular example, whenever the latent cause Z1 is active it generates two stimuli, A and B, but no outcome due to the absence of a link from Z1 to R. Whenever latent cause Z2 is active, it generates two stimuli, C and D, and also an outcome.
Figure 1.
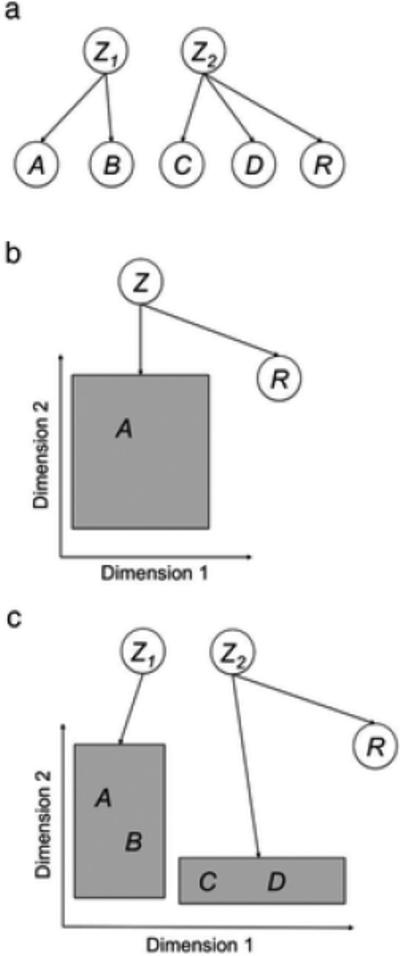
Schematic representations of the most important rational models discussed here. In each model, latent causes (Z) are assumed to generate observable stimuli (A-D) and outcomes (R). This generative process is represented by arrows. In the latent causes model of Courville and colleagues (panel a; Courville, Daw & Touretzky, 2002), one or more latent causes can produce one or more stimuli. In the rational theory of dimensional generalization (panel b), a single latent cause produces a single stimulus with values in a number of stimulus dimensions. In our model (panel c), one or more latent cause can produce one or more stimuli with values in a number of stimulus dimensions.
In order to predict the observable events (and specifically, the outcomes), the learner must infer both which latent causes are active in each trial, and the links between each latent cause and observable stimuli, from the (observable) training data alone. When a new stimulus compound is presented during a generalization test, the previously inferred knowledge allows the animal to estimate the probability of an outcome given the observed stimulus compound. This is done by inferring what latent causes are more likely to be active, given the observed stimulus configuration, and what is the probability of an outcome given these latent causes.
This latent cause model is able to explain a number of basic phenomena of compound generalization (Courville et al., 2002). Consider a summation effect, in which A and B are separately paired with an outcome, and presentation of AB leads to a larger response than presentation of A or B. The model can explain some forms of summation by assuming learning of the following structure: one latent cause, Z1, produces A with high likelihood and the outcome with medium likelihood, and a second latent cause, Z2, produces B with high likelihood and the outcome with medium likelihood. When the learner is presented with AB, she infers that both Z1 and Z2 must be active and thus the likelihood of the outcome being produced is higher than when only one of them is active.
This model, however, cannot explain why different stimuli can lead to different predictions (summation versus averaging) in this same experimental design. Furthermore, because in Courville et al.'s (2002) model the outcome is a binary variable, the only thing that can be estimated during compound generalization is probability of the outcome's occurrence. As such, the model cannot explain summation for two 100% reliable stimuli, that is, the observation that sometimes animals respond more to a compound of two stimuli that each reliably predict an outcome than to each stimulus alone (e.g., Kehoe, A. J. Horne, P. S. Horne, & Macrae, 1994; Collins & Shanks, 2006; Rescorla, 1997; Rescorla & Coldwell, 1995; Soto, Vogel, Castillo & Wagner, 2009; Whitlow & Wagner, 1972). As Courville et al. (2002) admit, it seems likely that the summation effect is concerned with the estimation of expected outcome magnitude and not just its probability.
More recently, Gershman, Blei and Niv (2010) used a generative model to explain results from extinction procedures. In extinction, a stimulus that was previously paired with an outcome is repeatedly presented without the outcome, until the learner eventually stops responding as if the stimulus predicts the outcome. Interestingly, this ‘extinction learning’ is fragile, with various manipulations showing that the prediction of the outcome is but dormant, and can be revived. To explain this, Gershman et al. (2010) suggested that the learner attributes training trials and extinction trials to separate latent causes. Thus manipulations that promote inference of the existence of the latent cause that was active at training, will lead to renewed outcome predictions.
An important advance introduced by this model was the inclusion of an infinite-capacity distribution from which latent causes are sampled on each trial. Such a distribution allows the learner to add new latent causes as needed, meaning that the number of possible latent causes need not be determined in advance. However, the distribution over latent causes in this model allows for only one latent cause to be active on each trial, and thus cannot account for compound generalization effects, as Courville et al.'s model does.
How could the class of rational theories be extended to account for the effect of stimulus factors on compound generalization? One way, which we explore here, is by integrating Courville et al.'s latent causes theory of compound generalization with the rational theory of dimensional generalization (Navarro, 2006; Navarro, Lee, Dry, & Schultz, 2008; Shepard, 1987; Tenenbaum & Griffiths, 2001a, 2001b) which we detail in the next section.
The rational theory of dimensional generalization
Dimensional generalization refers to the finding that if a stimulus controlling a response is changed in an orderly fashion along an arbitrarily chosen physical dimension (e.g., color, size), then the probability of the response decreases in an orderly monotonic fashion as the difference between the training stimulus and the testing stimulus increases (Guttman & Kalish, 1956).
Despite the robustness of this finding, the exact shape of the function relating response probability and changes in the relevant physical dimension tends to vary, depending on the choice of sensory continuum, species, training conditions, and even the particular dimensional value that originally controls the response (Shepard, 1965, 1987). Roger Shepard (1965) provided a solution to this problem based on the idea that there is a non-arbitrary transformation of the dimensional scale that makes generalization gradients that were obtained for the same physical dimension (each time using a different value as the rewarded stimulus) assume the same shape.
If such a transformation is found, then the re-scaled dimensional values represent the distance between stimuli, not measured on a physical scale, but in “psychological space.” Work with such a scaling procedure, and later work with multidimensional scaling, has shown that stimulus generalization follows an exponential-decay function of psychological distance for a variety of stimulus dimensions, training conditions, and species (Shepard, 1987).
To explain the shape of the generalization function, Shepard (1987) proposed that when an animal encounters a stimulus S1 followed by some significant consequence, S1 is represented as a point in a psychological space. The animal assumes that any such stimulus is a member of a natural class associated with the consequence. This class occupies a region in the animal's psychological space, called a consequential region. The only information that the animal has about this consequential region is that it overlaps with S1 in psychological space. If the animal encounters a new stimulus, S2, the inferential problem that it faces is to determine the probability that S2 belongs to the same natural kind as S1—the same consequential region—thus leading to the same consequence.
Assuming that the consequential region is connected and centrally symmetric, it is possible to compute the probability that a consequential region overlapping S1 would also overlap S2, given a particular size of the consequential region. Because this size is unknown, Shepard proposed putting a prior over this parameter and integrating over all possible sizes to obtain the probability that S2 falls in the consequential region, given that S1 does. Importantly, Shepard showed that, regardless of the choice of the prior over size, this probability falls approximately exponentially with distance between S1 and S2 in psychological space.
In Shepard's theory, observed stimuli and consequential regions are sampled independently. Tenenbaum and Griffiths (2001a) replaced this with the assumption that observed stimuli are directly sampled from all possible values of the consequential region, incorporating consequential regions into the generative model that produces observable data in a task. Under this assumption, consequential regions act as latent causes that produce observed stimuli. This is schematically represented in Figure 1b, where latent cause Z is linked not to discrete stimuli, as in Figure 1a, but to a whole region in stimulus space. The latent cause is also linked to some significant consequence, represented by the variable R. In this model, the learner knows that stimulus A belongs to a consequential region linked to R, but it doesn't know the size or location of the region. The inferential task is to determine the probability that a new stimulus was also caused by Z, depending on its position in stimulus space.
An important consequence of sampling stimuli from the consequential regions is that the likelihood of any particular stimulus is higher for smaller, more precise consequential regions, what Tenenbaum and Griffiths named the size principle. As a result, as more stimuli with similar values in a dimension are observed to lead to a particular consequence, the learner will tend to infer smaller sizes for the consequential region, and generalization to values outside the observed range will decrease. Tenenbaum & Griffiths (2001a, 2001b) review evidence from the literature on concept and word learning in human adults and children that agrees with this prediction (see also Navarro, Dry, & Lee, 2012; Navarro & Perfors, 2010; Xu & Tenenbaum, 2007).
Some evidence suggests that the extent to which people use the size principle during generalization is variable and might depend on factors such as the specific task to which they are exposed and their previous knowledge about the task (Navarro, Dry, & Lee, 2012; Navarro, Lee, Dry, & Schultz, 2008; Tenenbaum & Griffiths, 2001b; Xu & Tenenbaum, 2007). However, it is likely that the assumption that stimuli are sampled directly from consequential regions is a good approximation to the processes generating observations in a number of environmental settings, which has led to the proposal that the size principle could be considered a “cognitive universal” (Tenenbaum & Griffiths, 2001a), holding across a number of cognitive tasks and domains.
More recently, Navarro (2006) has extended the rational theory of dimensional generalization to explain some stimulus categorization phenomena. In Navarro's model, each category is composed of a number of subtypes, each associated with a particular consequential region. This structure is proposed to implement the fact that complex natural categories are likely composed of objects with disparate sensory features, thus consisting of more than one consequential region. Navarro has shown how this rational model can explain typicality and selective attention effects in categorization.
In the following section, we present a latent cause model of compound generalization that incorporates central ideas from the rational theory of dimensional generalization developed by Shepard and others. We will see that the concept of consequential regions addresses the shortcomings of earlier latent cause models, enabling it to explain the effect of stimulus factors on compound generalization.
The Model
Generative Model
We assume that the task of the animal during an associative learning situation, and the task of humans in a causal learning or contingency learning experiment, is to infer the latent causes that have produced observable stimuli and an outcome.
More specifically, we assume a generative model of the observed stimuli in which each latent cause is linked to a consequential region (see Figure 1c), from which stimuli are sampled. Each latent cause also generates an outcome with a specific magnitude (which could be zero) and valence (positive or negative). Thus, in our model stimulus values are generated as in the rational theory of dimensional generalization (Figure 1b). However, several latent causes can be active in any given trial and each of them can generate any number of observable stimuli, as in the latent causes theory of Courville and colleagues (Figure 1a).
If the learner could infer the latent causes that produce each particular configuration of stimuli and outcome value, this knowledge would allow solving two more specific inferential tasks. First, given the observation of a number of stimuli, it would be possible to predict future outcome values. Second, given that inferences about outcomes are based on the presence or absence of latent causes and not the observable stimuli produced by those causes, any learning about a specific latent cause would automatically generalize to other stimuli produced by the same cause.
Figure 2 shows a schematic representation of the generative process implemented in our model. The information that the learner observes on each trial t is: (1) a number of stimuli (indexed by i) observed at the beginning of trial t, each described by a vector xti = {xti1, ..., xtiJ} of J continuous variables or stimulus dimensions, and (2) a scalar rt representing the magnitude of the outcome occurring at the end of trial t. The generative process that produces these data is as follows. On each trial, the process starts (Step 1 in Figure 2) by sampling active latent causes from a distribution (the Indian Buffet Process, explained in detail below). In Figure 2, latent causes are represented through nodes labeled z1, z2,..., zk, and shaded nodes represent latent causes active during a trial (in the example, latent causes z1 and z3 are active during trial t). Each of the active latent causes can generate a number of observable stimuli, with the number sampled from a geometric distribution (Step 2 in Figure 2). In the example shown in Figure 2, in trial t latent cause z1 generates one stimulus (n1t = 1) and latent cause z3 generates two stimuli (n3t=2). Each of the stimuli has a value on each of a number of dimensions; such dimensional values are sampled from a consequential region ck associated with the latent cause (Step 3 in Figure 2). The consequential regions, represented by shaded rectangles in Step 3 of Figure 2, determine all possible values that a stimulus can have along dimensions 1, 2, ..., J. In this example, the number of dimensions is two, the stimulus produced by latent cause z1 has values {3,4} in these dimensions, whereas the two stimuli produced by latent cause z3 have values {8,7} and {11,6}. Finally, all latent causes together produce an outcome with magnitude rt (Step 4 in Figure 2). Each latent cause is associated with a single weight parameter wk. The total outcome magnitude observed is sampled from a normal distribution with mean equal to the sum of the weights of all active latent causes. In the example shown in Figure 2, the final sampled value of outcome magnitude is 1. Our model thus differs from most previous rational models of associative and causal learning, in that it assumes that the outcome can vary in magnitude from trial to trial, instead of simply being present or absent. The following sections describe in more detail each of the steps in this generative process.
Figure 2.
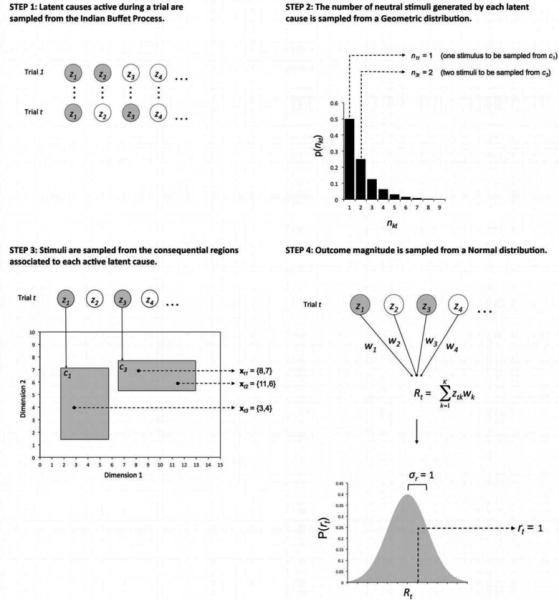
A schematic representation of the generative process assumed by the model. In trial t of a compound generalization experiment, each active (shaded) latent cause zk for k=1, 2,...K (Step 1) generates a number nkt of observed stimuli (Step 2). The values of each of these stimuli on several dimensions are sampled from a consequential region ck associated with the latent cause (Step 3). The active latent causes also produce an outcome with magnitude rt, which is sampled from a normal distribution around the sum of weights associated with all active latent causes (Step 4).
Latent Causes
Latent causes in this model (see Step 1 in Figure 2) are defined as binary variables with zkt=1 if the kth cause is active on trial t, and zkt=0 if the cause is not active. One can think of all the latent causes in the experiment as a matrix Z with K columns representing latent causes and T rows representing experimental trials. The choice of distribution on Z should implement the assumption that several latent causes can be present during a single trial and independently produce the observed stimuli. This is the assumption that allowed Courville et al. (2005) to explain basic phenomena of compound generalization, such as summation. On the other hand, the number of causes that could possibly be present (K) is not known in advance, as in the model presented by Gershman et al. (2010). Following earlier work on models with simultaneously active latent causes of a priori unknown number (e.g., Austerweil & Griffiths, 2011; Navarro & Griffiths, 2008), we use the Indian Buffet Process (IBP; see Griffiths & Ghahramani, 2011) as an infinite-capacity distribution on Z:
| (1) |
The IBP generates sparse matrices of zeros and ones with an infinite number of latent causes (columns) and a limited number of experimental trials (rows). Although there are an infinite number of columns in a matrix produced by the IBP, the matrix becomes sparse as K→∞, with most columns completely filled with zeroes (that is, most latent causes are never active and thus can be ignored). For a more complete description of the IBP, see Appendix A. For a tutorial introduction to Bayesian nonparametric models, including the IBP, see Gershman & Blei (2012).
The IBP has a single free parameter, α, that governs the number of different latent causes that will be active in an experiment with a given length. The value of α was fixed to 5 in all the simulations reported here.
Generation of Stimuli
The observation of a compound of stimuli in trial t is represented by N vectors xti, each describing a single discrete stimulus in a continuous multidimensional stimulus space. Following previous work (Navarro, 2006; Navarro & Perfors, 2009; Shepard, 1987; Tenenbaum & Griffiths, 2001a), we assume that each latent cause zk is associated with a consequential region ck in the stimulus space, which determines the range of possible observations xi that can be produced by that latent cause. Each region ck is assumed to be an axis-aligned hyperrectangle parameterized by two vectors of variables θk={mk,sk}. The position parameter vector mk determines the center of the region in the stimulus space in each of the dimensions, whereas the size parameter vector sk determines the extent of the region on each dimension of the space. Step 3 in Figure 2 shows a schematic representation of a set of latent causes and their associated consequential regions in a two-dimensional space.
Unlike other models involving consequential regions, in which a single stimulus is sampled in each trial, our model requires a way to implement the assumption—from Courville et al.'s latent cause theory—that a single latent cause can generate any number of observable stimuli within a single trial (see Figure 1a). This assumption was implemented by setting a distribution on the number of observable stimuli sampled from each active consequential region.
The generative process by which stimuli are produced on each trial is the following. First, for each active latent cause, it is determined whether or not the cause generates stimuli during this trial, through draws from a Bernoulli distribution. The Bernoulli distribution parameter λ was fixed to .99 in all our simulations to permit a small, non-zero probability that an active latent cause does not generate any observable stimuli on a particular trial. This simplifies inference in the model, as discussed below and in Appendix B. Second, for each latent cause that generates stimuli, a number of observations, nkt, is sampled from a geometric distribution with parameter π (fixed to .9 in all our simulations, giving high prior probability for each latent cause to produce only a small number of stimuli). That is, the probability of sampling nkt stimuli from region ck on trial t is given by:
| (2) |
The geometric distribution has the desirable property of allowing any number of stimuli to be sampled, while favoring a small number. This biases the model to infer a larger number of active latent causes as the number of observed stimuli grows, rather than infer that a small number of latent causes each generate many different stimuli.
In the final step of the generative process, nkt stimuli (values of x) are sampled from the consequential region k. The distribution of observations xti on the consequential region ck is uniform along each jth dimension:
| (3) |
Given that the consequential regions are shaped as hyperrectangles with size sj in dimension j, then the probability density of sampling any particular stimulus xti from region ck is equal to:
| (4) |
for all xti that fall within the consequential region, and 0 otherwise, where skj is the length of region ck on dimension j.
For inference purposes, we will need to evaluate how likely a set of specific stimuli are, given a specific configuration of active latent causes and their consequential regions. If we knew exactly what active consequential regions have generated each stimulus, we could use equations 2 and 4 (and the probability λ of each latent cause generating observations) to compute the likelihood of the stimuli presented during trial t:
| (5) |
However, it is not always possible to know which consequential regions have generated each stimulus on trial t. For example, if a particular stimulus lands within the area in which two consequential regions overlap, the likelihood will usually differ depending on whether the stimulus was generated by one consequential region or the other. In cases such as this, we have a number Y of possible assignments y of stimuli to consequential regions. Given that Y is a small number in all the situations that will be of interest here, it is possible to compute the likelihood of xt: by marginalizing over all possible assignments:
| (6) |
If we assume that all assignments have equal prior probability, then we have:
| (7) |
where nkt|y is the value of nkt for assignment y. Finally, assuming that xt: is sampled independently for different trials, the likelihood term for the whole set of observations X is the product of the likelihood of the observations in each individual trial:
| (8) |
Prior on the size and location of consequential regions
Following Navarro (2006), we assume the existence of a consequence distribution over the possible locations and sizes of regions, which is shared by all latent causes. The location parameter mkj for ck along each dimension j is drawn from a Gaussian distribution with zero mean and variance :
| (9) |
where is given a large value relative to the scale of the stimulus space, resulting in a diffuse prior over locations ( in all simulations presented here). Regarding skj, it is assumed that the possible sizes of consequential regions have both a lower bound a and an upper bound b (here, a and b were fixed to 0 and 5, respectively), and all sizes within those bounds are equally likely:
| (10) |
Two important things must be noted about the consequence distribution. First, the values of the parameters μm, , a, and b can vary for different dimensions j, to represent the different scale of each stimulus dimension. For our simulations, a simpler distribution that scaled all dimensions similarly sufficed.
Second, the way in which the size of the consequential region is generated for each dimension in the space will have important consequences for the predictions derived from the model. Because of the uniform distribution for x within a region, small regions have a higher likelihood to have produced a particular data point than large regions (see Equation 4). As noted before, this “size principle” will be important in explaining compound generalization phenomena. Here we assume that the sizes for each dimension j of a consequential region are generated independently from each other, leading to hyperrectangular consequential regions. Note that since the area of the region is the product of the length of its sides, a small value on any one dimension is sufficient to reduce the overall area and thus to increase the likelihood of stimuli that are sampled from this region.
Because consequential regions in our model are axis-aligned, generalization is stronger along the axes of the stimulus space (Austerweil & Griffiths, 2010; Shepard, 1987). Empirically, such a pattern of generalization is observed for stimuli with dimensions that are psychologically distinct (e.g., shape and orientation), known as separable dimensions (Garner, 1974). This suggests that separable dimensions should each be represented as a separate axis (and dimension) in our stimulus space.
On the other hand, dimensions that are not psychologically distinct (e.g., brightness and saturation), known as integral dimensions (Garner, 1974), are not privileged with respect to generalization. In this case, there is no reason to align consequential regions with these stimulus dimensions, and one way in which consequential regions theory has dealt with integrality is by allowing for inference of consequential regions that are aligned in any direction in space (Austerweil & Griffiths, 2010; Shepard, 1987)1. Assuming such non-aligned consequential regions, and since our model preferentially infers smaller consequential regions, we can approximate all integral dimensions using a single axis in space, because for two stimuli differing on any number of integral dimensions the smallest consequential region will be a line connecting the stimuli. As we will discuss later in the context of an experiment involving three stimuli, for more than two stimuli this approximation does not necessarily hold, however, even in that case integral dimensions are different from separable dimensions.
In sum, only when two dimensions are assumed to be separable we will consider them as distinct dimensions in stimulus space. When two stimuli vary on a number of integral dimensions, each of them separable from dimension j, we will represent the set of integral dimensions as a single dimension in stimulus space, with consequential regions aligned to this axis, as defined above.
Both theoretical and practical arguments support our suggestion to treat multidimensional stimuli with integral dimensions as varying along a single dimension. Most important among these are issues relating to the concepts of correspondence and dimensional interaction. Correspondence (Dunn, 1983) refers to the assumption— widespread in research and theory involving multidimensional stimuli (e.g., Ashby & Townsend, 1986; Dunn, 1983; Hyman & Well, 1967; Ronacher & Bautz, 1985; Soto & Wasserman, 2010)—that stimulus dimensions manipulated or identified by a researcher correspond to perceptual dimensions. In general, there is no reason that the dimensions chosen by a researcher would necessarily correspond to atomic units of processing in perceptual systems. For example, in some applications color hue is treated as a single stimulus dimension, although a higher-dimensional space could be used (e.g., the RGB color model). Conversely, in other cases hue is combined with other color and shape properties into extremely abstract dimensions (e.g., “identity” and “emotional expression” of faces; see recent examples in: Fitousi & Wenger, 2013; Soto & Wasserman, 2011). Representing hue as a single dimension is thus not fundamentally different from, say, representing the integral dimensions of hue and saturation as a single dimension, as we will do here. The arbitrariness of the dimensions selected to represent a set of stimuli is a problem that plagues the study of multidimensional generalization and is in no way aggravated by the assumptions of our model. That is, although our choice to represent several perceptually real (integral) dimensions as a single dimension may be a violation of correspondence, this assumption is violated in most work with multidimensional stimuli.
The popularity of the correspondence assumption, despite it being wrong for most applications, is perhaps due to the fact that it allows one to focus on the more interesting problem of dimensional interaction. That is, regardless of whether or not two perceptual dimensions represent indivisible atoms of perceptual processing, the question is how do those two dimensions or their components interact with each other (Ashby & Townsend, 1986). Following this tradition, our model implies different interaction rules for separable and integral dimensions: as demonstrated below, stimuli differing on separable dimensions (that is, dimensions that lie on distinct axes of stimulus space in our generative model) tend to give rise to inference of separate consequential regions, whereas stimuli differing on integral dimensions are more likely to be attributed to a common consequential region.
Finally, we note that there is a theoretical precedent to our implementation of integrality, as one interpretation of integrality is that dimensions that interact in this way are, in effect, combined into a single new stimulus dimension (Felfoldy & Garner, 1971; Garner, 1970). Thus, our representation of integral dimensions can be seen as an implementation of this “integration of dimensions” interpretation, in addition to being an approximation to other interpretations of integrality from consequential regions theory, as previously discussed. However, there are many other ways in which dimensions can be integral (see Ashby & Maddox, 1994; Maddox, 1992; Pomerantz & Sager, 1975), as integrality is not a single form of dimensional interaction, but rather a blanket category used to refer to dimensions that are not separable. While there is no doubt that a more complete treatment of this issue is worth pursuing in the future, our results will show that our simple implementation of integrality is sufficient to account for the empirical results of most interest to our study of compound generalization.
Generation of outcome magnitudes
All latent causes present during trial t produce an outcome with magnitude rt according to the following distribution:
| (11) |
where
| (12) |
The outcome observed in a trial is generated from a normal distribution with mean Rt and variance (in our simulations, the variance was fixed to ). Each latent cause influences the mean of the outcome distribution through its weight wk and we assume that the influences of different latent causes are additive, such that the mean of the outcome distribution is equal to the sum of the weights of all active causes.
The values of wk are also sampled from a normal distribution:
| (13) |
with the parameters fixed at μw = 0 and in our simulations. Step 4 of Figure 2 shows schematically how the latent causes z generate rt in the model.
Inference Algorithm
Inferences in our model are aimed at determining the expected value of the outcome on test trial t, or rt, given the current observation of the compound of stimuli xt:, and the data observed on previous trials. That is, inference is focused on finding E(rt | X, r1:t-1, θ), where θ is a vector of all the variables describing the prior, which are fixed and assumed as known in our model θ = {α = 5, π = 0.9, λ = 0.99, a = 0, b = 5, μm = 0, σm = 101/2, μw = 0, σw = 11/2, σr = 0.011/2}, X is a matrix of observed stimuli (both those observed so far and the current observation), and r1:t-1 is a vector of previously observed outcome values. In order to calculate the distribution p(rt | X, r1:t-1, θ) and from it the expected value of rt, a number of hidden variables of the model that are not specified and thus not known, need to be integrated out (or averaged over). Specifically:
| (14) |
Since this integral is not tractable, we approximate it using a set of L samples {, Z1:L, w1:L, m1:L, s1:L} drawn from the posterior distribution using a Markov Chain Monte Carlo (MCMC) procedure. Our MCMC algorithm involves a combination of Gibbs and Metropolis-Hastings sampling (Gilks, Gilks, Richardson, & Spiegelhalter, 1996). The general strategy is to use a Gibbs sampler to cycle repeatedly through each variable, sampling them from its posterior distribution conditional on the previously sampled values of all the other variables. In the cases in which the conditional posterior is itself intractable, we use Metropolis-Hastings to approximate sampling from the posterior. A more complete description of the inference algorithm can be found in Appendix B.
For the simulations presented here, the MCMC sampler was run for at least 3,000 iterations so as to converge on the correct posterior distribution (“burn in”). Then, the algorithm was run for another 2,000 iterations, from which every 20th iteration was taken as a sample, for a total of 100 samples. This sampling interval was used because successive samples produced by the MCMC sampler are not independent from each other. The approximated expected value of rt is then the average of the 100 samples:
| (15) |
Note that a small number of samples is sufficient to accurately compute the expected outcome value, as the standard error of this estimator decreases as the square root of the number of samples (Mackay, 2003).
Finally, we assume that behavioral measures in Pavlovian conditioning experiments (e.g., rate or strength of response to a stimulus), and in human contingency and causal learning experiments (e.g., causal ratings), are monotonically related to the outcome expectation computed according to Equation 15. However, the exact mapping between outcome expectation and response measures in different paradigms is unknown and not necessarily linear. Therefore, the simulations presented next have the aim of documenting the ability of our model to reproduce only the qualitative patterns of results observed in the experimental data.
Simulation of empirical results
In this section, we evaluate the predictions of our model against empirical data from several experiments in compound generalization. To evaluate the model's performance, it will be useful to compare its predictions against those from previous models of associative and causal learning. No previous rational model can handle the effects of stimulus factors on compound generalization, but there are several flexible mechanistic models that have been developed with this goal in mind (Harris, 2006; Kinder & Lachnit, 2003; McLaren & Mackintosh, 2002; Wagner, 2003, 2007). We will compare the predictions of our model to those of two of these flexible models: the replaced elements model (REM; Wagner, 2003, 2007) and an extension of Pearce's configural model (ECM; Kinder & Lachnit, 2003). These two models represent recent extensions to traditional elemental (REM) and configural (ECM) models of associative learning, and show enough flexibility to predict opposite patterns of results for compound generalization experiments depending on the value of free parameters in the model.
Simulations with REM and ECM were carried out using the simulation software ALTSim (Thorwart et al., 2009; which can be downloaded from http://www.staff.unimarburg.de/~lachnit/ALTSim/). All parameters were set to their default values, except for the free parameters controlling the proportion of replaced elements in REM, represented here by ρ (r in the original articles), and the amount of generalization across configurations in ECM, represented by δ (d in the original article). Due to space limitations, the interested reader should consult the original articles by Wagner (2003), Kinder and Lachnit (2003), and Thorwart et al. (2009) for a more detailed description of the models and their implementation.
Two features of these models are important for a correct interpretation of the results of our simulations. First, REM and ECM are mechanistic models of associative learning, so they provide a different kind of explanation of behavioral phenomena than the rational model presented here. However, the two types of explanation can constrain each other, so that a successful rational explanation gives clues to what is required from a successful mechanistic explanation, and vice-versa. Thus we provide predictions from mechanistic models only as a benchmark to compare our model to. We do not present a systematic comparison of the different models with the aim of showing that one is categorically better than others, neither in terms of simulating all the relevant data from the literature, nor in terms of evaluating what model offers the best quantitative fit to the data.
Second, both REM and ECM include a free parameter that affects the amount of associative strength that is generalized from one stimulus configuration to another. This allows both models to flexibly reproduce any possible result from several experimental designs in the literature. However, the models can be constrained by fixing their free parameters to the same value for all experiments using similar stimuli. For example, Wagner (2007) has pointed out that results from experiments using stimuli from different modalities are reproduced by REM with ρ = 0.2, whereas results from experiments using stimuli from the same modality are reproduced by using ρ ≥ 0.5. Accordingly, here we present simulations of REM with ρ equal to 0.2, 0.5 and 0.8.
Similarly, the ECM acts as Pearce's configural model when its free parameter δ is equal to 2. Lower values lead to behavior that is more similar to elemental models of associative learning and higher values lead to more configural processing. Here, we present simulations of ECM with δ equal to 1, 2 and 3.
In sum, both REM and ECM can implement the similarity hypothesis, if we assume that larger values of their free parameters correspond to stimuli that are more similar (e.g., within the same modality), whereas lower values correspond to stimuli which are more dissimilar (e.g., from different modalities). What our model adds is a principled explanation for why parameters of a specific mechanistic implementation may differ between conditions. In addition, as will be seen below, despite their flexibility, the REM and ECM cannot account for the full range of phenomena that our model explains.
Associative and rational models offer different and complementary explanations of behavior, and thus we do not conduct a quantitative comparison of the models, but rather concentrate on qualitative comparisons. Additional considerations discourage an evaluation of quantitative fits of the models to data: In general, quantitative predictions are outside the scope of most associative models, including REM and ECM. These models make predictions about an unobservable theoretical quantity, usually termed “associative strength.” Although this quantity is assumed to be monotonically related to overt behavior, the shape of this relation is left unspecified. This should not be seen as a criticism of REM and ECM – our model makes the same assumption regarding the relation between expected outcome value and measures of behavior. However, as a result of this assumption, it is difficult to adjudicate between the three models based on quantitative fits to behavioral data. Moreover, even if we added some simple assumptions to the models (e.g., a linear relation between associative strength/expected outcome and a response measure) and obtained measures of model fit to data, it would be unclear whether a better quantitative fit is due to a model's ability to capture a psychological process versus simply being more flexible than its competitors. To perform quantitative model selection taking into account model complexity, it would be necessary to make further modifications to associative models to make them not only quantitative, but also statistically defined (Pitt et al., 2008). Such modifications could potentially change the predictions of the original associative models (see Lee, 2008). As a result, we believe that the qualitative comparison proposed here is the most informative comparison of the models as defined.
Simple summation with stimuli from the same or different modalities
A summation experiment involves training with two stimuli separately paired with an outcome until both acquire a strong response (presumably due to prediction of the outcome), followed by a test in which each stimulus is presented separately, as well as in compound, and the strength of responding is measured. The critical comparison is the degree of responding to the compound as compared to that for the separate stimuli. Elemental models of associative learning predict that the response to the compound should be larger than the response to each of its components due to summation of the predictions for each element, whereas configural models predict that the response to the compound should be equal or lower than the average of the response to each component due to generalization decrement for a never-seen compound that is not wholly similar to any of the previous conditioning trials.
Early literature reviews by Weiss (1972) and Kehoe and Gormezano (1980) concluded that summation tests in Pavlovian conditioning can lead to any of these results. Thus, empirical evidence regarding this test does not allow us to reach any conclusion about whether stimulus processing is elemental or configural. More recent investigations have led to the same pattern of results, with some finding response summation (e.g., Kehoe et al., 1994; Rescorla, 1997), others something closer to response averaging (e.g., Rescorla & Coldwell, 1995), and still others a response to the compound that is lower than the average response to the components (e.g., Aydin & Pearce, 1995, 1997).
One important difference among summation studies leading to different results is that many of those supporting a configural hypothesis (i.e., no summation) have used stimuli from the same sensory modality, whereas those supporting an elemental hypothesis (i.e., summation of predictions) have used stimuli from different sensory modalities. Kehoe et al. (1994; see also Rescorla & Coldwell, 1995) directly tested the consequences of training with stimuli from the same or different modalities for the summation effect in rabbit nictitating membrane conditioning. Their results, reproduced in the left panel of Figure 3, show that the response to a compound of tone and light is larger than the response to each individual stimulus, whereas the response to a compound of a tone and a noise is closer to the average of the response to each individual stimulus.
Figure 3.
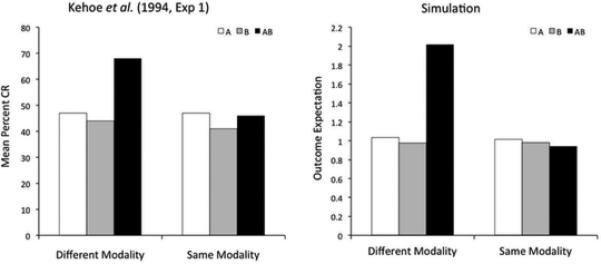
Experimental data (left) and simulated results (right) of an experiment by Kehoe et al. (1994) on the modulation of the summation effect by stimulus modality. A significant summation effect was found with stimuli from the different modalities, but not with stimuli from the same modality.
To simulate this experiment using our model, each stimulus was represented by a vector of two variables, one encoding sound and the other encoding visual stimulation. Representing the tone and noise stimuli as each varying along a single perceptual dimension is appropriate for two reasons. First, it is commonly assumed that the primary perceptual dimensions of a sound are pitch, loudness and timbre (e.g., Melara & Marks, 1993). Kehoe et al. matched the loudness of the tone and noise, and the latter does not have a characteristic pitch. Therefore, the two sounds varied mostly in timbre. Second, there is some evidence that these three sound dimensions are not separable (e.g., Grau & Nelson, 1988; Melara & Marks, 1993). On the other hand, different modalities are the quintessential example of stimulus dimensions that are separable (Garner, 1974). Although there is evidence suggesting violations of separability between dimensions, such violations seem to stem from decisional rather than perceptual processes (for a review, see Marks, 2004). Thus we represent stimuli from different modalities as varying along two separable dimensions. This means that, in our framework, multimodality can be seen as a special case of dimensional separability. We assumed that all stimuli are represented in a common stimulus space and have a value on each dimension. Finally, only dimensions relevant for the experimental task were included in this simulation and all those that follow.
To simulate the “different modality” condition, the tone was represented as the vector (sound=1, visual=0), whereas a light was represented as the vector (sound=0, visual=1). To simulate the “same modality” condition, the tone was represented as the vector (sound= 21/2, visual=0) and the noise was represented as the vector (sound=0, visual=0). These values were chosen to match the distance between stimuli in the two simulations, so as to establish that inference of a common latent cause in our model is determined due to the alignment of stimuli along a dimension rather than their distance. Note that here a value of zero is arbitrary and does not represent the absence of a feature (i.e., there was visual stimulation coming from the speaker and the noise had a particular timbre).
The right panel of Figure 3 shows the results of our simulations. The model correctly predicts the observed pattern of results, and Figure 4 presents a schematic explanation of the reason behind this success. When the two stimuli are from different modalities (left panel of Figure 4), their spatial separation is too large for them to have been generated by a single large consequential region. Instead, the model infers the presence of two different small regions, each producing a single stimulus and an outcome of magnitude one. When the two stimuli are presented together during the compound test, the model infers that both latent causes are active, and so the outcome magnitudes produced by each cause are added together (according to Equation 12) and a summation effect occurs.
Figure 4.
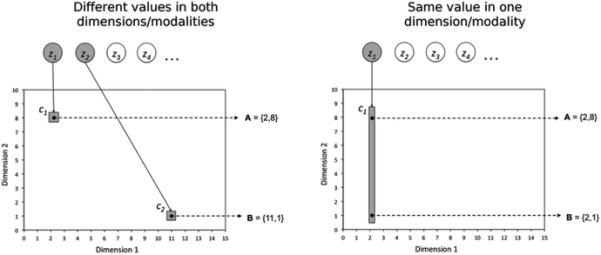
Schematic explanation of why the model predicts a summation effect with stimuli from different modalities/dimensions (left panel) and the lack of a summation effect with stimuli from the same modality/dimension (right panel). Active latent causes and their consequential regions are shaded.
On the other hand, when the two stimuli are from the same modality (right panel of Figure 4), the model infers that a single consequential region, very small along the irrelevant dimension (Dimension 1 in Figure 4) and elongated along the relevant dimension (Dimension 2 in Figure 4), has produced both observations. This is true even for stimuli that are very dissimilar along the relevant dimension, because the size of the consequential region along the irrelevant dimension can be arbitrarily small, leading to a small area for the region and a high likelihood for stimuli contained in that area (see Equation 4). Because the two stimuli are inferred to be generated by one latent cause, the expected value of the outcome for trials with each single stimulus and their compound is the same (one unit of outcome, as typically generated by this latent cause) and no summation is observed.
In sum, the likelihood function for stimuli (Equation 4) embeds in it the principle that stimuli that have similar values on a particular dimension are likely to have been produced by the same latent cause. This is an instantiation of the size principle proposed by the rational theory of dimensional generalization of Tenenbaum and Griffiths (2001a), which was discussed in the introduction section. The size principle explains why stimuli varying on a single dimension do not produce summation effects, and it will prove useful in explaining several other contradictory results observed in the literature on compound generalization.
It is important to underscore that what our model predicts is an effect of separability and integrality of stimulus dimensions on the summation effect. The effect of stimulus modality is considered a special case of the separability/integrality distinction, with different modalities being one case of separable dimensions. However, regardless of whether cues vary within a modality or across modalities, the model predicts a summation effect if cues vary across separable dimensions and no summation effect if cues vary across integral dimensions. This also means that, according to our model, stimuli used in previous studies finding no summation effect (notably, experiments using visual stimuli and autoshaping with pigeons) must have varied either along integral dimensions or along a single dimension, as in Kehoe et al. (1994).
According to previous mechanistic theories (Harris, 2006; McLaren & Mackintosh, 2002; Wagner, 2003, 2007), similarity between two stimuli is what modulates the extent to which they are processed configurally, that is, as a whole rather than as a sum of their parts. Figure 5 shows the predictions of the REM (top) and ECM (bottom) models for a summation experiment. Assuming that more similar stimuli produce more configural processing (larger values of ρ and δ), both models can correctly reproduce the experimental results of Kehoe and colleagues (Figure 3).
Figure 5.
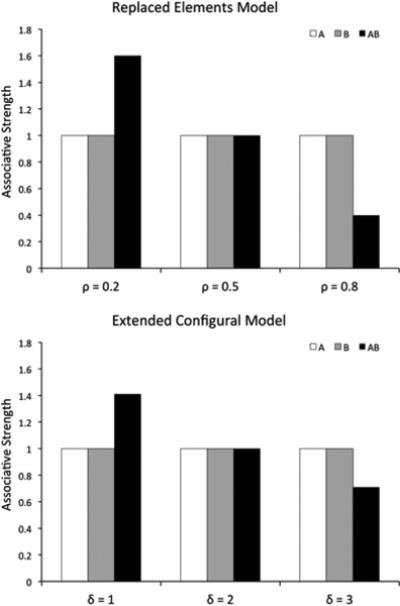
Results of simulations of a summation experiment using REM (top) and ECM (bottom). Each simulation was run using three different values of the free parameters ρ and δ. Both models can predict any pattern of results from a summation experiment, with responding to the compound higher, equal or lower than to each stimulus alone.
However, explanations based on the concept of stimulus similarity have difficulty explaining the results of a related experiment by Rescorla and Coldwell (1995, Experiment 6), who found that although simultaneous presentations of two visual stimuli in compound does not produce a summation effect, the sequential presentation of the same stimuli does lead to such effect. The problem for approaches based on the concept of similarity is that it is difficult to think of stimuli that are close in time as more “similar” to each other than the same stimuli when they are separated in time. Our model incorporates the idea that similarity is an important factor in compound generalization, because distance along several dimensions can be interpreted as inversely proportional to the similarity between two stimuli. However, the model also expands beyond the limitations of the similarity hypothesis, because for other dimensions distance is better interpreted as inversely proportional to the contiguity between two stimuli. This is the case for the relative temporal and spatial position of stimuli during an experimental trial. Temporal contiguity–and spatial contiguity, as we will see later–can both be cast as differences on the dimensions of time and space, so that stimuli that are closer together in these dimensions have a higher likelihood of having been produced by the same latent cause.
The only additional assumption required to apply our model to such dimensions is that the origin of each dimension is set in each trial by a landmark event. The position of stimuli in space and time is encoded relative to such landmarks. For example, “trial time” would be encoded relative to an event that signals the beginning of a trial, such as the beginning or end of an inter-trial interval (as demarcated by the outcome in a previous trial, or the first stimulus in the current trial, respectively). This is a reasonable assumption as our model is a trial level model, in which we assume that latent causes become active at the beginning of a trial and only stimuli happening after that point (and before the beginning of the next trial) can be generated by the active latent causes. Similarly, “task space” would be encoded relative to the position of a landmark stimulus, such as the corner of a monitor or the experimental chamber. Importantly, one of the cues could itself serve the function of a landmark to set up ‘trial time’ and ‘task space’ (e.g., the first cue presented or the most salient cue in a compound). These assumptions are common to most other theories dealing with contiguity, which usually parse an experiment coarsely into individual trials, simulating events within a single trial.
To summarize, a focus on generalization as an inference task gives a unified and principled explanation of the effects of stimulus modality and temporal separation over the summation effect.
Differential summation with stimuli from the same and different modalities
A variant of the summation design involves training with three stimuli, A, B, and C, followed by an outcome, and testing with the compound ABC. In this experiment there are two training conditions: in the single condition, all stimuli are independently paired with the outcome (A+, B+, C+), whereas in the compound condition, all combinations of two stimuli are paired with the outcome (AB+, AC+, BC+). If one of these conditions leads to a higher level of responding during the summation test with ABC, then a “differential summation” effect is said to be found (Wagner, 2003). Traditional elemental models (Rescorla & Wagner, 1972) predict more summation in the single condition, whereas traditional configural models (e.g., Pearce, 1987) predict more summation in the compound condition.
The left panel of Figure 6 shows the results of a differential summation experiment carried out by Myers and colleagues (Myers, Vogel, Shin, & Wagner, 2001, Exp. 2) using a tone, a light and a vibrotactile stimulus as conditioned stimuli. The experiment confirmed the predictions of elemental theory, finding higher summation in the single condition than in the compound condition. The middle panel of Figure 6 shows the results of a differential summation experiment carried out by Ploog (2008), using only visual stimuli that differed in color and size. In this case, there was no evidence of summation for either condition (responding to ABC was not higher than to the training stimuli) and the small difference between conditions observed in the figure is not statistically significant.
Figure 6.
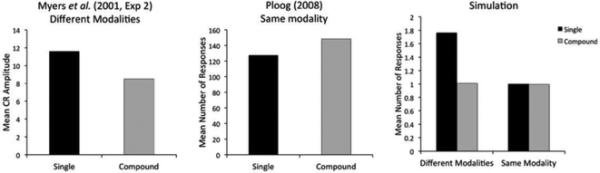
Experimental data from differential summation experiments using stimuli from different modalities (left) and from the same modality (middle panels), and simulated results (right). Bar height represents responding to the compound ABC in the different conditions. The difference between conditions found by Myers et al. (2001; left) was statistically significant, whereas Ploog (2008, middle) did not find a statistically significant difference between the conditions. The simulation (right) reproduces this pattern of results.
To simulate the experiment of Myers et al. (2001), which used stimuli from different modalities, we represented the tone as the vector (sound=1, visual=0, somatosensory=0), the light as (sound=0, visual=1, somatosensory=0) and the vibrotactile stimulus as (sound=0, visual=0, somatosensory=1). To simulate the experiment of Ploog (2008), which used stimuli from the same modality, we represented the first visual stimulus as (sound=0, visual=0, somatosensory=0), the second as (sound=0, visual=21/2, somatosensory=0) and the third as (sound=0, visual=2×21/2, somatosensory=0). That is, our simulation assumes that the dimensions of size and color are integral for pigeons, at least in the stimuli used in this experiment. To the best of our knowledge, there is currently no empirical evidence that contradicts this assumption. In both cases, our choice of values on each dimension makes the present simulation comparable to the simulation of a simple summation effect presented in the previous section.
The results from our simulation are presented in the last panel of Figure 6. It can be seen that the model predicts the results obtained by Myers et al. (2001) using stimuli from different modalities and the results obtained by Ploog (2008) using stimuli from the same modality. The explanation is the same as for our simulation of the simple summation effect: stimuli that vary along multiple separable dimensions lead to the inference of a separate latent cause for each stimulus, whereas stimuli that vary along a single dimension lead to the inference of a single latent cause for all stimuli (see Figure 4).
Using visual stimuli and the same experimental paradigm as Ploog (2008), Pearce and colleagues (Pearce, Aydin, and Redhead, 1997, Exp. 1) found higher summation in the compound condition than in the single condition. As is clear from our simulation, the latent causes model cannot predict this result using the current parameter values and stimulus encoding. However, the differential summation effect found by Pearce and colleagues was statistically significant only in 5 out of 15 testing trials, and no correction for multiple comparisons was applied in this analysis. Thus, both the experiments of Ploog (2008) and those of Pearce et al. (1997) seem to suggest that it is difficult to obtain a reliable differential summation effect using stimuli from the same modality.
Flexible mechanistic models, such as REM and ECM, can predict all the observed patterns of results in differential summation experiments. This can be seen in Figure 7, which shows the results from simulating these models. However, both models run into the same problem as our latent causes model when attempting to explain the contradictory results of Ploog (2008) and Pearce et al. (1997). These studies used similar visual stimuli, the same species and the same experimental paradigm, so there is little reason to justify different values of ρ and δ to explain their different results. Only further empirical research will shed light on whether specific experimental conditions can produce a robust differential summation effect using visual stimuli.
Figure 7.
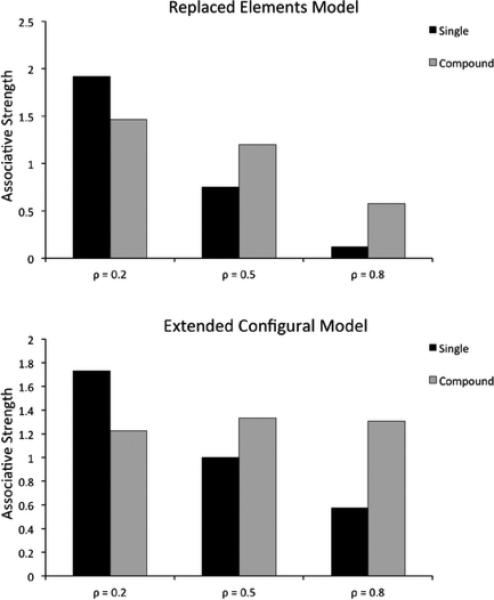
Results of simulations of a differential summation experiment using REM (top) and ECM (bottom). Bar height represents responding to the compound ABC in the different conditions. Each simulation was run using three different values of the free parameters ρ and δ. Both models can predict any pattern of results from a differential summation experiment, with responding to ABC in the single condition being lower, equal or higher than responding to ABC in the compound condition.
As these are the only experiments involving more than two stimuli varying along integral dimensions discussed in this paper, a short discussion of the validity of our assumptions in the case of three stimuli is in line. In our simulation of the study by Ploog (2008) we have represented all visual stimuli as varying along a single dimension, as exemplified in Figure 8a. As discussed previously, variation along a single dimension is a good approximation for cases in which two stimuli vary along integral dimensions, because if consequential regions can orient in any direction of integral space (Shepard, 1987), the size principle will result in the regions orienting in the direction of a line connecting the two stimuli, which is equivalent to representing the stimuli as points along one axis in stimulus space.
Figure 8.
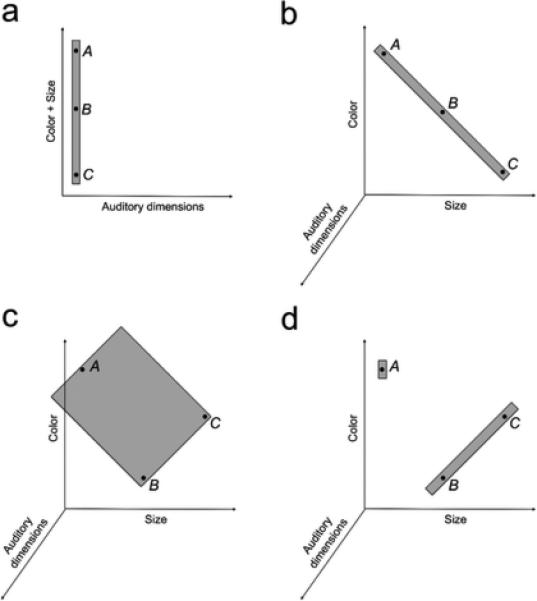
Schematic explanation of how the latent causes model explains the effect of stimulus modality on differential summation. In our implementation, the integral dimensions of size and color are collapsed in a single dimension (a). A separable auditory dimension is also depicted, for didactic purposes. The application of the size principle would be similar if each of the two dimensions was represented separately and the three stimuli were aligned, as regions can be oriented in any direction in integral space (b). However, the size principle applies even without stimulus alignment as long as the consequential regions are small along the auditory dimension (in the figure, the size on this dimension is so small that the regions are essentially planes), as they can then include more than one cue with relatively high likelihood (c). Moreover, because in integral space consequential regions do not have to be aligned to axes, the size principle can be applied again to generate two consequential regions, essentially a line and a point in space, rather than three (d). Thus integral dimensions imply less summation than separable dimensions, even for more than two non-aligned stimuli.
What happens when three (or more) stimuli differ on two integral dimensions? In this case, if the stimuli are aligned in integral space (that is, if they can be connected by a straight line, as in Figure 8b), our choice to represent the stimuli as points along a single axis is still reasonable as in the integral subspace consequential regions need not be aligned to axes. If the stimuli are not aligned the approximation of consequential regions that are not axis-aligned by representing all integral dimensions as one axis no longer holds. However, even in this case, we argue that application of the size principle would still lead to more “configural” representations when stimuli vary on two integral dimensions, as in Ploog (2008), as compared to three separable dimensions as in Myers et al. (2001), for two reasons. First, even if we represent size and color as two separate axes in stimulus space, large regions encompassing two or three stimuli are more likely in the two-dimensional space of color and size (as shown in Figure 8c) than in the three-dimensional auditory-visual-tactile space needed to represent Myers et al.'s (2001) multimodal stimuli, because a hyperrectangle in a two dimensional plane has a much smaller volume than one in a three dimensional space. In general, low-dimensional consequential regions are considerably more likely than high-dimensional ones. This is demonstrated in Figure 8b-d by using the auditory dimension, on which consequential regions are essentially planes regardless of the configuration of stimuli in the dimensions of color and size. Second, because within the two-dimensional integral space consequential regions do not have to be aligned to axes (as no specific direction of axes is privileged), in integral space hypotheses involving thin elongated regions that include pairs of cues as in Figure 8d are possible. Due to the size principle, such hypotheses will have high posterior probability, thus implying a summation effect that is smaller than when each cue is produced by its own latent cause, as would be the only high probability solution for three separable dimensions. If color and size were separable dimensions rotation of consequential regions would not be possible, so unless two stimuli shared values on either of the dimensions, this configuration of consequential regions would not be possible.
In sum, regardless of whether we choose to represent the integral dimensions of size and color as one or two axes in space, that is, whether Ploog's (2008) cues are aligned in the integral space or not, the theory predicts that cues varying along two integral dimensions should lead to less elemental summation than cues that differ on three clearly separable dimensions. Our simulations capture this effect of modality on differential summation qualitatively by collapsing integral dimensions into a single axis in stimulus space, as in Figure 8a, but the results would not change qualitatively if we assumed a two dimensional space with consequential regions that are not necessarily axis-aligned, as in Figure 8d.
Summation with a recovered inhibitor
Perhaps the best-known design for the study of inhibitory learning involves a feature-negative discrimination, in which presentations of a stimulus followed by an outcome (denoted A+) are intermixed with presentations of the same stimulus in compound with a second stimulus and not followed by the outcome (AB-). After this training, B acquires the ability to inhibit responding to an excitatory stimulus (Rescorla, 1969).
Elemental and configural theories make different predictions about what would happen if the inhibitory stimulus, B, were paired with the outcome after the feature-negative discrimination is learned. The Rescorla-Wagner model predicts that pairing B with the outcome would make this stimulus gradually lose its inhibitory properties and acquire excitation; thus, after training with B+, responding to AB should be higher than responding to A, because the excitatory properties of both stimuli should summate. On the other hand, Pearce's configural model predicts that there will be less responding to AB than to A during test, because the compound as a whole would keep some of its inhibitory properties despite the B+ training, and B would only produce some excitation to AB through generalization.
Pearce and Wilson (1991) performed a series of experiments with variations of this basic design that supported configural theory: even after extensive training with B+ following a feature-negative discrimination, subjects showed responding to AB that was equal or lower than their response to A. Importantly, responding to AB was not higher than responding to A regardless of whether the stimuli were from the same or different modalities, as shown in the left panel of Figure 92. Thus, these results provide evidence against the similarity hypothesis.
Figure 9.
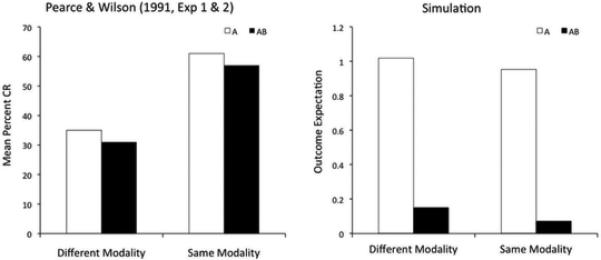
Experimental data (left) and simulated results (right) of experiments conducted by Pearce and Wilson (1991) on summation with a recovered inhibitor. Both the experimental data and the simulation show higher responding to A than to AB regardless of whether the stimuli were from different modalities or the same modality.
Shanks, Charles, Darby and Azmi (1998) have shown that essentially the same pattern of results is found in human causal learning experiments using foods as stimuli and allergic reaction as the outcome. Although the stimuli in these experiments did not come from different modalities (they were all food names presented visually on a computer screen), other studies have shown that they produce a robust summation effect when they are separately paired with the outcome and presented in compound (Collins & Shanks, 2006; Soto et al. 2009). In sum, there is good evidence that stimuli that usually produce a summation effect in compound generalization experiments do not produce the same effect if the compound has been explicitly paired with no outcome early in the experiment.
As is shown in Figure 9, our latent-cause model can explain this paradoxical pattern of results. The results of a simulation of the Pearce and Wilson (1991) design are presented in the right panel of Figure 9. Importantly, this simulation used the same stimulus representations used in our simulations on simple summation. The experimentally observed difference in mean percent responding between A and AB (left panel of Figure 9) is not as large as the difference in outcome expectation predicted by the model (right panel of Figure 9). However, the model correctly reproduces the qualitative pattern of results: lower responding to AB than to A regardless of whether the stimuli come from the same or different modalities.
As in a simple summation experiment, the early A+ trials and the late B+ trials can be explained either by two different latent causes each producing a single stimulus and an outcome of magnitude 1.0, or by a single latent cause producing both stimuli and an outcome of magnitude 1.0. The first solution is favored with stimuli from different modalities, whereas the second solution is favored with stimuli from the same modality. However, both solutions make the data observed during the early AB- trials very unlikely. In both solutions, if the same latent cause(s) that produced A and B separately is (are) active during the AB- trials, this would explain the observation of both A and B, but it would also mean that the outcome should be generated from a normal distribution with a very high mean (about 2.0 in the first solution, and about 1.0 in the second solution). The likelihood of observing an outcome of magnitude equal to 0.0 generated from such distribution is so small, that the inference algorithm must consider alternative hypotheses about the causal structure underlying the observed data. An example of such an alternative hypothesis would be a structure in which independent latent causes generate A or B together with an outcome magnitude of 1.0 (these latent causes account for single cue trials and are inactive during compound trials), and a different latent cause, accounting for compound trials, generates both A and B together with an outcome of magnitude of 0.0 (that is, no outcome).
Figure 10 shows the predictions of REM and ECM for this design. Both models are capable of reproducing the experimental results with large values for their free parameters (ρ ≥ 0.5 in REM and δ ≥ 2 in ECM). However, the parameter value of ρ = 0.2, proposed by Wagner to explain compound generalization with stimuli from different modalities, cannot explain the observed higher responding to A than AB with stimuli from different modalities (see Figure 9). It is possible to find values of the parameters ρ and δ that reproduce the qualitative pattern of results in Figure 9, while also showing a summation effect. However, the stimulus similarity hypothesis predicts that stimulus modality should modulate the magnitude of the difference in responding between A and AB in this experiment, and the experimental results show no indication of such modulation.
Figure 10.
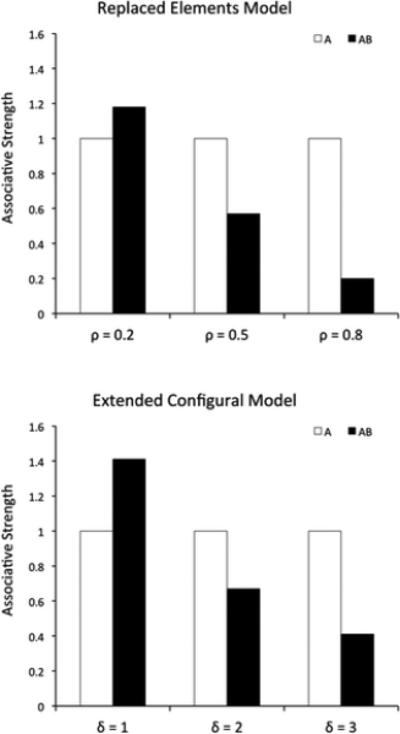
Results of simulations of an experiment on summation with a recovered inhibitor using REM (top) and ECM (bottom). Each simulation was run using three different values of the free parameters ρ and δ. Both models predict a modulation of the difference in responding to A and AB depending on stimulus similarity.
Effect of the spatial position of stimuli on the blocking effect
A well known feature of Pavlovian conditioning and other forms of associative learning is that “stimulus competition” effects arise when several stimuli are presented in compound and paired with an outcome (e.g., Kamin, 1969; Rescorla, 1968; Wagner, Logan, Haberlandt, & Price, 1968). The typical result of stimulus competition experiments is that those stimuli in a compound that are best predictors of the outcome interfere with the acquisition of a response by other stimuli.
The best known stimulus competition effect is blocking. In the first phase of a blocking experiment, a stimulus A is repeatedly paired with an outcome; in the second phase, a compound AB of the blocking stimulus A and a target stimulus B is paired with the same outcome. In the typical control condition, a compound CD is paired with the outcome during the second phase, with neither C or D being previously trained. The main finding is that presentations of A followed by the outcome during the first phase reduce the amount of responding that B acquires during compound training (Kamin, 1969). Responding to the target stimulus B is lower than responding to either C or D, despite the fact that responding to the latter stimuli is already quite low due to an overshadowing effect–that is, lower responding to a stimulus when it is trained in a compound, compared to when it is trained by itself. The blocking effect shows that the predictive value of a stimulus depends not only on its own history of pairings with the outcome, but also on how well other simultaneously present stimuli predict the outcome.
Because the blocking effect is considered such a fundamental associative learning phenomenon, most contemporary theories of associative learning have been designed to predict it. However, there are also many reports of failures to observe blocking empirically (e.g., Lovibond, Siddle, & Bond, 1988; Martin & Levey, 1991; Williams, Sagness, & McPhee, 1994). More importantly, some studies have been able to identify factors that determine whether or not blocking will occur. These include properties of the stimuli presented in the compound, as detailed below.
In a human eyelid conditioning study using lights of different colors as conditioned stimuli, Martin and Levey (1991) found that spatial separation of the blocking (A) and target (B) stimuli enhanced the blocking effect. As shown in the left panel of Figure 11, no blocking occurred in a group for which the two stimuli were presented adjacent to each other (Group 1 of Experiment 1), whereas a robust blocking effect occurred when the two stimuli were spatially separated (Experiment 4). Although this modulation of the blocking effect also depended on the order in which test stimuli were presented, it is clear from this study that spatial separation of the target and blocking stimuli enhances the blocking effect.
Figure 11.
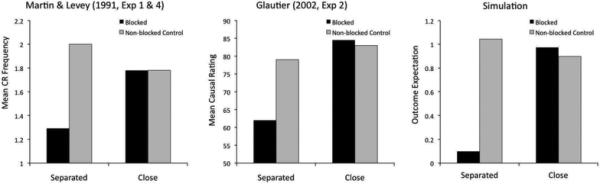
Simulated results (right) and experimental data from studies on Pavlovian conditioning (left; Martin & Levey, 1991) and human contingency judgments (middle; Glautier, 2002) on the effect of spatial contiguity between stimuli over the blocking effect. Both experiments found a reliable blocking effect with spatially separated stimuli, but not with spatially close stimuli. The simulation reproduced these results.
The same result has been found in human contingency learning experiments. The middle panel of Figure 11 shows the results of an experiment carried out by Glautier (2002, Experiment 2; see also Livesey & Boakes, 2004) using a “casino game” task in which participants were presented with cards with different shapes and colors printed on them and asked to predict whether or not the card would produce a cash payout. As can be seen in Figure 11, here as well a blocking effect was found with spatially separated stimuli (presented on different cards), but no blocking effect was found with spatially contiguous stimuli (presented on the same card).
To simulate these results, we assumed that stimuli varied on two dimensions: spatial position and color. Although the separability of these dimensions has not been established empirically, some researchers have deemed these two dimensions ‘highly separable’ (Fific, Nosofsky, & Townsend, 2008, p. 361). The stimuli in Glautier (2002) varied both in shape and color, but there is some evidence of integrality for those dimensions (see Cohen, 1997), and thus we modeled them as a single dimension. In our simulation, the value on the color dimension was either one (for A) or zero (for B). Close stimuli were represented through position values of 0 and 0.2, whereas distant stimuli were represented with position values of 0 and 3.
The results of the simulation are shown in the right panel of Figure 11. As can be seen, our model correctly predicts a blocking effect with spatially separated stimuli, and the absence of such effect with spatially contiguous stimuli. The model predicts this result for the same reason that it predicts modulation of the summation effect by stimulus modality. Adjacent stimuli lead the model to infer a single cause for A, B and the outcome, thus B cannot be blocked by A since they represent different stimuli produced by the exact same cause. On the other hand, spatially separated stimuli lead to the inference of a different cause for A and B. Because the cause that generates A must have generated an outcome during the first experimental phase and should be present during the second phase, the model infers that the cause that generates B must not be generating any additional outcome in the second phase (otherwise, the magnitude of the outcome during AB+ trials would be larger than that observed during A+ trials). As a result, at test there is no responding to B in the second case, and intact responding to B (equivalent to the responding to A) in the first case.
The results of simulations with REM and ECM are shown in Figure 12. Both models predict a blocking effect across a large range of values of their free parameters; that is, responding to the blocked stimulus is low across all simulations. Changes in the free parameters ρ and δ only modulate the response to the non-blocked control, representing the level of generalization from a compound to one of its components (i.e., the size of the overshadowing effect). This is at odds with the experimental results that show the opposite effect: a release from the blocking effect with stimuli closer in space, with responding to the control stimulus staying at relatively high values. The prediction of a blocking effect is robust across values of ρ and δ because it stems from the adoption of an error-driven learning rule for updating associations between stimuli and outcomes in both models. That is, blocking is a learning effect in these models. The free parameters in REM and ECM affect only generalization across stimulus compounds, not associative learning and thus the models cannot predict the observed release from blocking.
Figure 12.
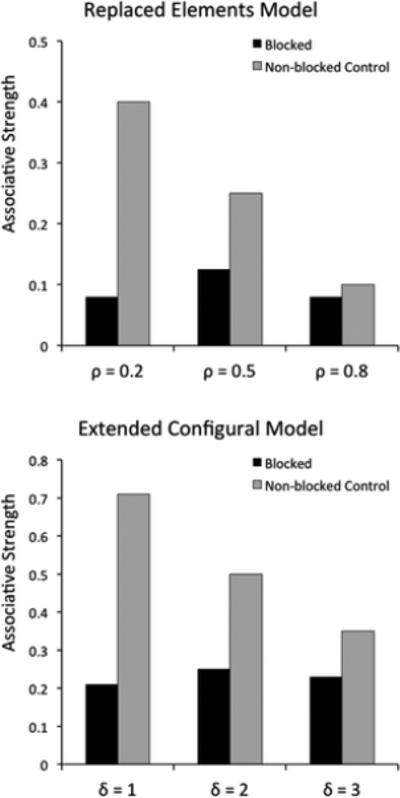
Results of simulations of a blocking experiment using REM (top) and ECM (bottom). Each simulation was run using three different values of the free parameters ρ and δ. Blocking is a robust prediction of these models across variations in free parameters. Only responding to the control stimuli is modulated by such variations.
The distance between stimuli is not the only spatial variable that can affect the blocking effect. In a human predictive learning study, Dibbets, Maen and Bossen (2000) showed that the blocking effect is abolished if the position of stimuli is varied from trial to trial. They used a stock market task in which participants were presented with a list of stock names ordered in a column and information about whether the stock had been traded or not. The participants’ task was to predict whether the value of the entire stock market would change or remain equal. In two different experiments, Dibbets et al. trained people in a blocking design using this task. The main difference between the two experiments was whether the position of the stocks in the list was fixed across trials (Experiment 2) or it was variable (Experiment 3). Mean ratings for the most important stimuli in the design are shown in the left panel of Figure 13. Whereas a fixed position of the stocks led to a blocking effect, randomization of stimulus position abolished blocking.
Figure 13.
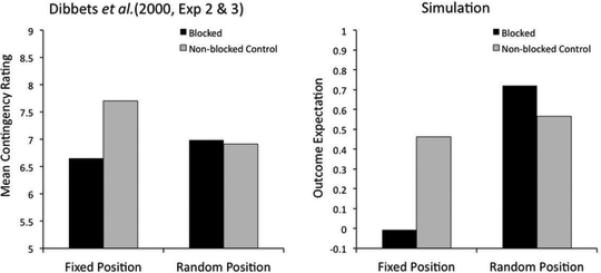
Experimental data (left) and simulated results (right) of a human predictive learning experiment by Dibbets, Maen and Bossen (2000), which studied the blocking effect with stimuli whose spatial position either remained fixed or varied across training trials. The experiment found a reliable blocking effect with spatially fixed stimuli, but not with randomly positioned stimuli. The simulation reproduced these results.
In our simulation of this study, stock identity was coded along a single stimulus dimension and spatial position along a different, orthogonal dimension. Thus, it was assumed that the two dimensions were separable and that different stocks varied only along integral dimensions. Both the position and identity of the objects were represented through the values 1, 2, 3, and 4. The difference between the fixed and random position conditions was that only in the former each stimulus was assigned to a specific position throughout the experiment. The simulated results are presented in the left panel of Figure 13. The model reproduces the results of Dibbets et al., namely, a blocking effect with fixed stimulus position and no effect with randomized stimulus position. However, note that in Dibbets et al.'s experiment the effect of randomizing stimulus position is both an increase in responding to the blocked stimulus and a reduction in responding to the nonblocked control. Our model can only reproduce the first part of the effect.
The reason for the model's behavior is that when the compound AB is presented with the components in a fixed spatial position, the model infers that two different latent causes have generated A and B, producing blocking. With randomized positions, however, both stimuli are varied across an overlapping area of the spatial dimension, leading the model to infer a single cause for them, linked to a large consequential region. As a result, in this case no blocking effect is observed.
The above reasoning leads to a yet untested prediction: If the positions are randomly varied such that they do not overlap (e.g., one stimulus in each visual hemifield), then different causes should still be inferred for each stimulus, leading to a blocking effect.
REM and ECM, like most other models of associative learning, do not offer a way to straightforwardly encode spatial position in their stimulus representation. Thus, the models do not make any predictions for the Dibbets et al. (2000) experiment without further assumptions. In associative learning theory, a standard way to deal with aspects of a stimulus that are experimentally varied is by representing discrete stimuli through many “elements” that can be common across stimuli or unique to a particular stimulus (e.g., Atkinson & Estes, 1963; Blough, 1975; Mackintosh, 1995; Rescorla, 1976; Soto & Wasserman, 2010). For example, we can present the model with the compound AP1 for trials in which stimulus A is presented in position one, the compound AP2 for trials in which A is presented in position two, the compound BP1 for trials in which B is presented in position one, and so on. This way, the common element P1 represents a common location for A and B. Encoding stimuli this way allows to simulate the Dibbets et al. (2000) experiments using REM and ECM.
The results of those simulations are shown in Figure 14. Neither REM or ECM seem able to reproduce the pattern of results observed by Dibbets et al. (2000), when the experiment is modeled using this “common elements” assumption. As in the previous simulation, the models predict a blocking effect in both conditions for most values of the free parameters. In those cases in which the blocking effect is considerably reduced for the random-position condition (REM with ρ ≥ 0.5; ECM with δ = 3), the same happens for the fixed-position condition.
Figure 14.
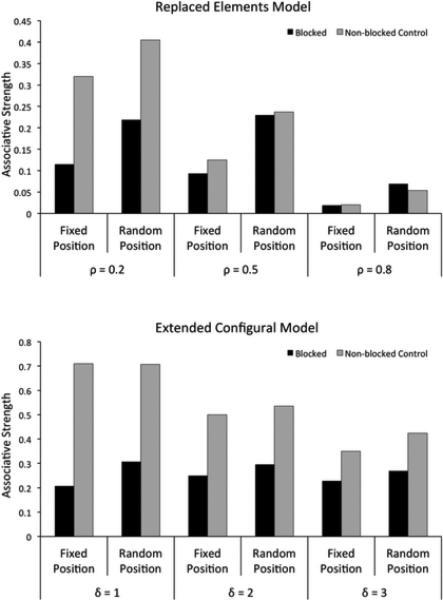
Results of simulations of the effect of randomizing spatial position of stimuli on the blocking effect using REM (top) and ECM (bottom). The original models do not make any predictions for this experiment and additional assumptions were made to obtain these results (see main text). Each simulation was run using three different values of the free parameters ρ and δ. Blocking is a robust prediction of these models and it is not affected by variations in the spatial position of stimuli.
Notably, the notion of consequential regions in stimulus space generalizes easily to the dimensions of space and time, explaining the effects of variations in these dimensions as just another manifestation of the inferential problem posed by stimulus generalization. The same is not true for the notion of stimulus similarity used by some mechanistic models of compound generalization. Spatial and temporal distances are not usually considered stimulus properties that can be used for the computation of similarity—stimuli are not inherently more similar when they are closer in time or space. (but see Brown, Neath, & Chater, 2007 for a model in which temporal distance determines the confusability of memory traces). It is only when we consider the inferential task faced by an animal in compound generalization that distance in space and time can be treated just as distance in any other stimulus dimension.
Asymmetrical generalization decrement after adding or subtracting stimuli from compounds
Another type of compound generalization test involves pairing a stimulus or a compound of stimuli with an outcome until a strong response is acquired, and then either adding or subtracting stimuli from the training compound during a generalization test. Pavlov (1927) was the first to report that the addition of a novel stimulus to a trained stimulus produces a decrement in responding, an effect that he termed “external inhibition.” He also reported that the subtraction of a stimulus from a training compound produces a similar decrement (i.e., an overshadowing effect; see also Kamin, 1969).
Many studies of these two effects have been reported since then. Importantly, most studies that have compared the magnitude of the generalization decrement in overshadowing and external inhibition have found that the two effects are asymmetrical: the decrement found by adding a stimulus to a training compound is lower than the decrement found by subtracting a stimulus from a training compound (Brandon, Vogel, & Wagner, 2000; Glautier, 2004; González, Quinn, & Fanselow, 2003; Thorwart & Lachnit, 2010; Wheeler, Amundson, & Miller, 2006).
The left panel of Figure 15 presents results from a study by Gonzalez et al. (2003) reporting this asymmetry. In this study, rats were first trained with either one (A+) or two stimuli (AB+) signaling the presentation of a shock and then tested with the configurations A, AB and ABC. As can be seen in Figure 15, for rats trained with A+ the addition of one or two new stimuli produced a small generalization decrement, which in both cases was not statistically significant. The same was true for rats trained with AB+ and tested with ABC. On the other hand, training with AB+ and testing with A led to a larger and statistically significant decrement in responding. Indeed, the magnitude of the generalization decrement after a stimulus was subtracted from the training compound was larger than the magnitude of the generalization decrement after a stimulus was added to both a single training stimulus (A+) and to a training compound of two stimuli (AB+).
Figure 15.
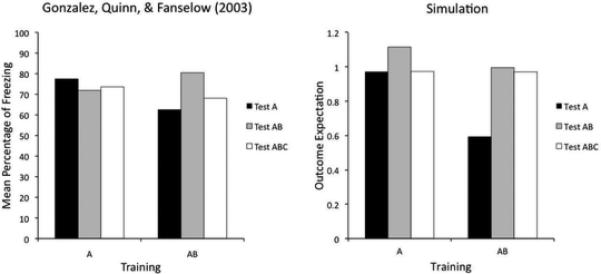
Experimental data (left) and simulated results (right) of an experiment by Gonzalez, Quinn and Fanselow (2003) on asymmetrical generalization decrements after the addition and subtraction of stimuli from a training compound. Note that responding to the training stimulus is represented by the black bar in the “Training A” condition, but by the grey bar in the “Training AB” condition. The only statistically significant reduction in responding in the experimental data is for stimulus A after training with AB. Responding to all other test stimuli is not statistically different from responding to the training stimuli. The simulation qualitatively reproduces this pattern of results.
All stimuli in this experiment were from different modalities, so as in previous simulations using such stimuli, to model this experiment we used a three-element vector. The presence of a particular stimulus was represented by 1 and its absence by 0. As shown in the right panel of Figure 15, our simulation reproduced the experimental results: no generalization decrement in any of the testing conditions, except for the overshadowing test (AB+ then test with A). The asymmetrical generalization decrement is correctly reproduced by the model. Because all the stimuli in this experiment were from different modalities, causal structures in which a different latent cause produces each of the training stimuli were favored during inference. Specifically, AB followed by an outcome led to inference of two latent causes, which together produce an outcome of magnitude 1.0. The presentation of a single stimulus during the overshadowing test thus leads to the inference that a single latent cause is active during this trial, and so the learner predicts an outcome with magnitude lower than 1.0, leading to an overshadowing effect.
Conversely, an external inhibition effect is not predicted because in this case the presentation of a completely new stimulus leads to the inference of an additional new latent cause being active. Because there is no evidence about the exact magnitude of outcome produced by this new latent cause, the model defaults to its best guess in absence of information: the prior. The prior on wk has a mean of 0.0, which means that, on average, new latent causes do not produce any change in the expected magnitude of outcome.
Thus, our model does not predict the external inhibition effect found by other studies (Pavlov, 1927; Brandon, Vogel, & Wagner, 2001; Thorwart & Lachnit, 2010; Wheeler, Admunson, & Miller, 2006, Experiment 2) using the parameter values that we have used in all other simulations. This, however, might be a strength of the model, as at least three recent studies reported finding an overshadowing effect but no external inhibition effect, using the exact same stimuli to test both effects (Glautier, 2004; Gonzalez, Quinn, & Fanselow, 2003; Wheeler, Admunson, & Miller, 2006, Experiment 1). Furthermore, although Brandon et al. (2001) indicate that in their results “there was a decrement due to the adding of stimuli” (p. 71), and some of the observed decrements were indeed quite large (e.g., in the test with ABC after training with A+, see Figure 16), they did not report statistical tests to support the reliability of these results. Thus, the only result that is robust across experiments is the asymmetric generalization after the addition and subtraction of stimuli from a training compound, which our model reproduces.
Figure 16.
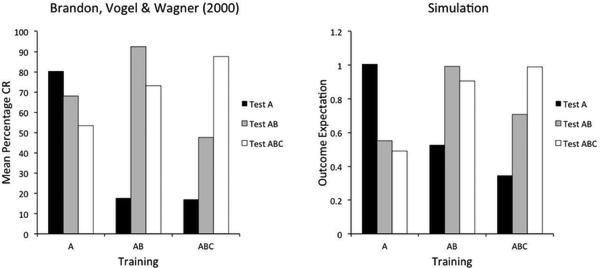
Results of an experiment (left panel) conducted by Brandon et al. (2000) on asymmetrical generalization decrements after the addition and subtraction of stimuli from a training compound. The right panel shows the results of a simulation with the model, using a prior distribution over outcome magnitude with μw = -0.3.
Furthermore, the use of within-modality or between-modality stimuli does not seem to be the only factor determining whether or not external inhibition occurs, since Kehoe et al. (1994) did not find any evidence of external inhibition under either condition, using the same stimuli that produced a robust modulation of the summation effect as discussed earlier.
Our model does, however, provide an explanation of why external inhibition might happen under some particular circumstances, while not being a phenomenon with the generality of other compound generalization effects. Recall that when a new stimulus is presented during an external inhibition test, the model infers a new latent cause that generates both the new stimulus and normally distributed outcome with mean 0.0, a value that comes from the prior on wk. Thus, the model predicts an external inhibition effect only if the prior distribution over outcome magnitude is assumed to have a mean in the opposite direction than the outcome used in the experiment. Assuming such a prior seems adequate when past history has suggested that new latent causes are likely to result in an outcome of such value, instead of no outcome at all. The left panel of Figure 16 shows the results of an experiment conducted by Brandon et al. (2000), which found both overshadowing and external inhibition effects. In this experiment, different groups of rabbits were trained in an eyelid conditioning preparation with either one (A), two (AB) or three (ABC) stimuli of different modalities, followed by an aversive outcome. Testing was conducted with all three compounds in all groups. As shown in Figure 16, the response decrement due to overshadowing was larger than the response decrement due to external inhibition. The right panel of Figure 16 shows the results of a simulation with our model, using a prior over outcome magnitude with μw = -0.3. As expected, with this assumption the model reproduced all the important aspects of the experimental results.
Figure 17 shows the results of simulations of Brandon et al.'s (2000) experiments using REM and ECM. The first thing to notice is that the ECM cannot reproduce the asymmetric generalization after the addition and subtraction of stimuli from a training compound, regardless of what value is given to the parameter δ. For example, responding to test AB after training with A (external inhibition) is the same as responding to test A after training with AB (overshadowing), for all values of δ. Wagner's REM reproduces this asymmetry with any values for ρ, and provides a quite good fit to the experimental data with ρ = 0.2.
Figure 17.
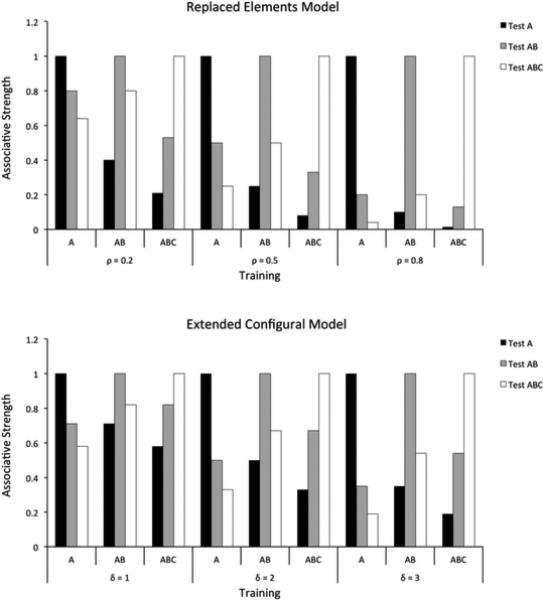
Results of simulations of an experiment testing generalization decrements after the addition and subtraction of stimuli from a training compound using REM (top) and ECM (bottom). Each simulation was run using three different values of the free parameters ρ and δ. Only REM can reproduce an asymmetrical generalization decrement. ECM predicts the same decrement in responding after adding or subtracting stimuli from a compound.
The success of our latent causes model in explaining Brandon et al.'s (2000) data might seem to be the result of a rather arbitrary choice for a prior over wt. However, two independent pieces of evidence are in line with the interpretation of these results offered by the present model.
First, as discussed by Wheeler et al. (2006), external inhibition is more likely to arise in experiments using stimuli that are “clearly separable” (pp. 1222), which would explain why these authors could find an external inhibition effect using different foods as stimuli in a human causal learning paradigm, while others (Glautier, 2004) were unable to find an external inhibition effect using different parts of the same object as component stimuli. Indeed in our model, inferring a new latent cause for novel test stimuli is necessary for the external inhibition effect to occur, and a new latent cause is inferred only if the novel test stimuli are sufficiently separated from the training stimuli in stimulus space. Thus, even using a prior over outcome magnitude different than zero, the model predicts external inhibition only for distantly separated stimuli.
The fact that using clearly separable stimuli increases the likelihood of observing an external inhibition effects is also important because Wagner's REM model and the ECM both predict the opposite pattern of results. As seen in Figure 17, REM predicts that lower values of ρ, which have been linked to more dissimilar stimuli, decrease the magnitude of the external inhibition effect. The same is true for lower values of δ in the ECM. These models interpret both the external inhibition and overshadowing effects as arising from equivalent mechanisms of compound generalization. Our model, on the other hand, does not explain external inhibition as the result of a generalization decrement, but as the result of inhibition from a novel stimulus which is itself associated with a predicted outcome. Thus, stimulus similarity affects external inhibition differently from other compound generalization phenomena in the latent causes model, with separable stimuli increasing the likelihood of observing this effect. Other mechanistic models of compound generalization (Harris, 2006; McLaren & Mackintosh, 2002) offer explanations that are more in line with the latent causes model.
Moreover, the data indicate that simply using dissimilar stimuli is not sufficient to obtain a reliable external inhibition effect, because Gonzalez et al. (2003) found no indication of an external inhibition effect with stimuli from different modalities, although their methods yielded a reliable overshadowing effect (see also Kehoe et al., 1994, for a report of an increase in responding using stimuli from different modalities). In agreement with this empirical finding, dissimilarity is not sufficient in our model as well, but rather a negative prior over wk is required in order to produce an external inhibition effect. Such a prior might be an idiosyncratic feature of some, but not all, experimental preparations used to study associative learning.
Second, according to our interpretation, external inhibition can only happen when a stimulus previously paired with an outcome is presented in compound with a completely novel stimulus. If the external inhibitor is not novel, but has been paired with either no outcome or an outcome of some magnitude, then the model would infer a value for wk based on that experience, instead of defaulting to the prior. This prediction of the model has been confirmed by Reiss and Wagner (1972), who found that nonreinforced pre-exposure to a stimulus decreases its ability to produce external inhibition. Importantly, the results plotted in Figure 16 and those of Reiss and Wagner (1972) were obtained using the same species, paradigm and methods. Thus, as a whole, these results provide convergent evidence supporting our use of different priors to explain the conditions under which external inhibition should be seen.
Pavlov (1927) himself interpreted the external inhibition effect as the result of interruption of responding by a competing orienting response elicited by the novel test stimulus. In this view, the decrement in responding results from a response controlled by the novel stimulus, rather than as a result of incomplete generalization of the response controlled by the original stimulus to the new compound. This is similar to the interpretation we offer here, although Pavlov's explanation is mechanistic in nature.
Discussion
We have presented a rational (Bayesian) model of compound generalization in associative learning that provides a principled explanation of several previously puzzling effects of stimulus manipulations on compound generalization. Our generative model extends both the latent cause theories of compound conditioning (Courville, 2006; Courville, Daw, & Touretzky, 2002; Gershman, Blei, & Niv, 2010) and other rational models of associative and causal learning (e.g, Cheng, 1997; Griffiths & Tenenbaum, 2005, 2007; Lu, Yuille, Liljeholm, Cheng, & Holyoak, 2008; Novick & Cheng, 2004) by including new assumptions about how observable stimuli with specific values in physical dimensions are generated from latent causes. To achieve this, we used the notion of consequential regions, first developed in the context of rational theories of multidimensional generalization (Navarro, 2006; Navarro et al., 2008; Shepard, 1987; Tenenbaum & Griffiths, 2001a, 2001b), which provides a unified framework to understand both dimensional and compound generalization phenomena using the same theoretical principles.
Similar to some previous rational theories of dimensional generalization (e.g., Navarro, 2006; Tenenbaum & Griffiths, 2001a, 2001b), our model uses a generative process for observed stimuli that is based on the assumption that stimuli are directly sampled from consequential regions. This assumption would lead humans and animals to use the “size principle” during inferences about consequential regions: for a given set of stimuli, small regions containing those stimuli are more likely to be inferred than large regions. Our simulations show that several results in the literature on compound generalization can be explained as resulting from this size principle. These results have been found in both Pavlovian conditioning and causal learning studies, using diverse species as experimental subjects. Thus, our simulations support the claim that the size principle is a cognitive universal, which should hold not only for humans, but also for non-human animals and across different tasks (Tenenbaum & Griffiths, 2001b).
Table 1 shows a summary of the results of our simulations. For each empirical result that we have discussed, the table indicates whether the latent causes model can reproduce the result and, if so, what assumptions are required for its success. In most cases the assumptions we made are about the interaction between different stimulus dimensions, specifically, whether they are separable or integral. We have discussed many cases in which our assumptions are supported by previous research. However, this is not true of all cases listed in Table 1. For example, the lack of summation observed in experiments using autoshaping with pigeons can only be explained assuming that the visual stimuli used in these studies are integral. To the best of our knowledge, there is currently no empirical evidence to evaluate the validity of this assumption. Indeed, rather than an assumption, this can be construed as a prediction of our model: if the model is correct in its explanation of the lack of summation, then the visual stimuli in the experiment must have integral dimensions. Fortunately, good tests of dimensional separability/integrality involve relatively simple experiments (for a review, see Ashby & Soto, in press), thus our predictions are easily testable. More generally, we recommend that future research in compound generalization should be integrated with research in multidimensional generalization and scaling, with the latter providing constrains on the correct representation of stimuli for the former. In particular, studies should be carried out to determine how similar are stimuli in compound generalization studies and the number and type of dimensions on which they differ. We believe that such integration would be not only useful for a better evaluation of our model's predictions, but would provide a better picture of the relation between compound and dimensional generalization and of the factors driving the results of compound generalization studies.
Table 1.
Summary of the results of our simulations. Each cell provides information about whether a model can reproduce a specific empirical result and, if it can, the assumptions that are required for its success.
| Empirical Result | Latent Causes Model | REM | ECM |
|---|---|---|---|
| Effect of modality on simple summation (Kehoe et al., 1994). | YES Noise and tone varied in timbre; no other assumptions are necessary. |
YES Assuming higher replacement for unimodal than multimodal stimuli. |
YES Assuming more configurality for unimodal than multimodal stimuli. |
| Effect of temporal separation on simple summation (Rescorla & Coldwell, 1995). | YES Assuming that temporal separation is separable from visual dimensions. |
NO Unless the model is developed further. |
NO Unless the model is developed further. |
| Effect of modality on differential summation (Myers et al., 2001; Ploog, 2008). | YES Assuming that color and size are integral for pigeons. |
YES Assuming that more similar stimuli produce higher replacement. |
YES Assuming that more similar stimuli produce more configural processing. |
| Summation with a recovered inhibitor not affected by modality (Pearce & Wilson, 1991). | YES No other assumptions are necessary |
NO Unless it is assumed that modality does not affect replacement, which contradicts first entry above. |
NO Unless it is assumed that modality does not affect configurality, which contradicts first entry above. |
| Effect of the spatial position of stimuli on the blocking effect (Glautier, 2002; Martin & Levey, 1991). | YES Assuming that spatial position and color are separable dimensions. Glautier's results also require assuming that color and shape are integral dimensions. |
NO | NO |
| Prevention of a blocking effect by random variation in position of cues (Dibbets et al., 2000). | YES Assuming that stock identity can be encoded as a single dimension, separable from spatial position. |
NO | NO |
| Asymmetrical generalization decrement after addition and subtraction of cues to/from compound (e.g., Brandon et al., 2000). | YES Assuming sufficiently dissimilar stimuli. |
YES Assuming replacement value larger than zero. |
NO |
| External inhibition effect (e.g., Brandon et al., 2000) | YES Assuming a prior on the outcome with mean lower than zero. |
YES Assuming replacement value larger than zero. |
YES Assuming suffficient configurality. |
Table 1 also includes information about the results of simulations using REM and ECM. Although the table suggests that our model can explain a greater number of the results, because the latent causes model provides a different explanation of behavior than mechanistic models, we believe that simply counting the number of successes of the different models is rather uninformative. More productive is to understand how our model suggests that mechanistic theories could be developed in the future to provide better accounts of behavior. First, our results suggest that mechanistic theories must go beyond the similarity hypothesis and incorporate spatial and temporal contiguity as factors affecting stimulus configurality. Second, results and simulations of summation with a recovered inhibitor suggest that some compound generalization effects are immune to the influence of stimulus modality. Thus, the similarity hypothesis should be relaxed to allow for such exceptions. Third, the effect of spatial position on blocking suggests that the blocking effect may not be as robust as mechanistic models predict. Under some predictable circumstances, no blocking effect occurs. Our successful simulation of this phenomenon suggests ways in which mechanistic models could be modified to predict such effects. One possibility is to allow A, B and AB to be treated as essentially the same cue (i.e., with no generalization decrement among them) under some special circumstances. Apart from these suggestions, perhaps the most important challenge faced by mechanistic models is to provide a unified theory for stimulus generalization, able to explain both compound generalization and dimensional generalization within the same framework, as we have done here with the rational theory of stimulus generalization.
Our model expands upon earlier latent cause theories by making a distinction between the processes that generate stimuli and those that produce outcomes. In our model, the outcome is assumed to be a continuous scalar variable with a mean that equals the sum of outcome magnitudes produced by all active latent causes in a trial (see Equation 12). This feature makes the generative process for outcome magnitude in our model similar to that proposed by the Kalman filter model of Pavlovian conditioning (Dayan, Kakade, & Montague, 2000; Kakade & Dayan, 2002). However, in our model the outcome is produced by latent causes, whereas in the Kalman filter the outcome is directly caused by observable stimuli and the only latent variables are the weights connecting stimuli to outcomes. The generative process we assume for the outcome allows our model to explain the summation effect (e.g., Kehoe et al., 1994; Collins & Shanks, 2006; Rescorla & Coldwell, 1995; Soto et al., 2009; Whitlow & Wagner, 1972), which cannot be explained by latent cause models in which the outcome is assumed to be a binary, non-additive variable (Courville, 2006; Courville, Daw, & Touretzky, 2002).
In addition to these improvements, the present model inherits from previous latent cause theories the ability to explain a number of important phenomena in associative learning that were not our focus here (see Courville, 2006). Our simulations above demonstrate the ability of the model to explain stimulus competition effects such as blocking and overshadowing. As other Bayesian models of associative learning, the model is also capable of explaining so-called retrospective revaluation effects, such as unovershadowing and backward blocking (e.g., Chapman, 1991; Chapman & Robbins, 1990; Denniston, Miller, & Matute, 1996; Miller & Matute, 1996; Shanks, 1985; Urcelay, Perelmuter, & Miller, 2008; Wasserman & Berglan, 1998). Retrospective revaluation refers to a group of experimental observations indicating that humans and animals are able to update their knowledge about some events even in the absence of those events. For instance, in a backward blocking experiment (e.g., Chapman, 1991; Miller & Matute, 1996; Shanks, 1985) participants are first presented with a number of trials involving a compound of two stimuli followed by an outcome (AB+). Learning during this phase generalizes to both A and B (with possible overshadowing), as can be seen by their ability to individually produce a response indicative of their association with the outcome. In a second phase, participants are presented with A alone followed by the outcome. Test trials show that this A+ training reduces the ability of B to produce a response, even though B was not seen or trained in these latter trials.
Most mechanistic models of associative learning have difficulty explaining retrospective revaluation effects, because they assume that experience only modifies the predictive properties of stimuli that are physically present in a trial. Although extensions to traditional associative learning models have been proposed to deal with retrospective revaluation phenomena (e.g., Aitken & Dickinson, 2005; Dickinson & Burke, 1996; Van Hamme & Wasserman, 1994), the same models cannot explain the results of compound generalization experiments.
In contrast, rational Bayesian models of human causal learning (e.g., Griffiths & Tenenbaum, 2005, 2007; Lu et al., 2008) and Pavlovian conditioning (Courville, 2006; Courville, Daw, & Touretzky, 2002; Dayan, Kakade, & Montague, 2000; Kakade & Dayan, 2002) can readily explain backward blocking and other retrospective revaluation phenomena. A feature of Bayesian inference is that if an observation can be explained equally well by either of two hypotheses, new observations that favor one of the hypotheses will decrease the posterior probability of the other hypothesis. In the case of backward blocking, the observation of AB followed by an outcome is consistent with the hypotheses that stimulus A, stimulus B or both (or their latent causes) produced the outcome. The later observation of A paired with the outcome gives evidence for the hypothesis that this stimulus (or its latent cause) produces the outcome, “explaining away” the hypothesis that B might have produced the outcome (Dayan & Kakade, 2001).
Thus, the present work represents a step forward toward providing a more unified theory of associative learning. Although our model says nothing about the mechanisms that give rise to phenomena such as retrospective revaluation and compound generalization, it could guide and constrain the development of new mechanistic explanations for such effects. One possibility would be to build models that combine the machinery of Bayesian inference with heuristics to explain behaviors that are interpreted to be deviations from rationality. An example is the “locally Bayesian” learning algorithm recently developed by Kruschke (2006), which assumes that the cognitive system is divided into several processing modules or layers, each one performing Bayesian inference and optimizing its output to other modules as a function of its input from previous modules in the processing sequence. This algorithm can explain not only backward blocking, but also trial-order effects that are more difficult to explain by globally rational models. A second possibility would be to interpret generic algorithms used to approximate exact Bayesian inference (MCMC, particle filters, etc.) as possible mechanistic models of how our rational model might be achieved in the brain (Daw, Courville & Dayan, 2008; Sanborn, Griffiths, & Navarro, 2010). A third, related possibility would be to build mechanistic models of associative learning that can approximate the behavior of a specific rational model, without being restricted to use the generic algorithms for approximate inference developed in the machine learning and statistics literature (e.g., Danks, Griffiths, & Tenenbaum, 2003).
Another way in which our model improves over previous rational models of associative learning is by explaining the effects of temporal and spatial contiguity between stimuli as cases of the more general inferential problem posed by stimulus generalization: determining the regions in stimulus space corresponding to particular latent causes. This opens up the possibility of explaining temporal phenomena of associative learning within the framework of a rational Bayesian theory. Most previous rational models of associative and causal learning (e.g, Cheng, 1997; Courville, Daw, & Touretzky, 2002; Griffiths & Tenenbaum, 2005, 2007; Lu, Yuille, Liljeholm, Cheng, & Holyoak, 2008; Novick & Cheng, 2004) are silent about how temporal factors within each experimental trial (e.g., temporal separation between a stimulus and an outcome) can alter what is learned about the events observed in those trials (see Courville, 2006, for a notable exception). This is a significant shortcoming of rational theories of associative learning because there is much evidence indicating that temporal contiguity between events within in a trial strongly affects learning in both Pavlovian conditioning (e.g., Davis, Schlesinger, & Sorenson, 1989; Smith, Coleman & Gormezano, 1969) and human causal learning (e.g., Reed, 1992; Shanks, Pearson, & Dickinson, 1989; Schlottmann & Shanks, 1992). Our model can explain the effects of contiguity between two stimuli on inference of a common or different latent causes, and as such, is directly applicable to the effects of temporal factors in phenomena such as sensory preconditioning and second-order conditioning (e.g., Lavin, 1976; Rescorla, 1980).
There are several ways in which future work can improve upon the present model. Our model was focused exclusively on the task of compound generalization; that is, transfer of learning from a trained stimulus compound to a new stimulus compound, based on their shared components. Stimulus factors may also have an effect on compound discrimination; that is, the process of learning to discriminate different compounds that share some components. Experiments have shown that the relative difficulty of different compound discrimination tasks might depend on stimulus factors. As in the case of compound generalization, experiments using stimuli from different modalities seem to favor elemental theory (e.g., Bahçekapili, 1997), whereas experiments using stimuli from the same modality tend to favor configural theory (e.g., Pearce & Redhead, 1993).
Our model was designed to account for generalization behavior after all learning is complete. It uses a batch inference algorithm, in which all the data gathered across the experiment are used to make inferences. Therefore, compound discrimination phenomena, which are studied by examining learning curves, are currently outside its scope. One possibility, however, would be to use the same or a similar generative model, together with an on-line inference algorithm, such as sequential Monte Carlo methods (for reviews, see Arulampalam, Maskell, Gordon, & Clapp, 2002; Cappé, Godsill, & Moulines, 2007), to produce trial-by-trial predictions. An on-line inference algorithm would also provide a tool to explore whether the model can explain the effect of stimulus factors on configural processing in latent inhibition (Honey & Hall, 1988, 1989; Reed, 1995), in which pre-exposure to a stimulus without an outcome leads to a reduction in learning rate during subsequent pairings of the stimulus and an outcome.
Compound discrimination is influenced by several variables besides stimulus factors (reviewed in Melchers et al., 2008). For example, previous experience with compound discrimination tasks seems to have an effect on the strategy that rats (Alvarado & Rudy, 1992) and humans (Mehta & Williams, 2002; Melchers, Lachnit, & Shanks, 2004; Melchers, Lachnit, Üngör, & Shanks, 2005; Williams & Braker, 1999; Williams, Sagness & McPhee, 1994) use to solve new compound discrimination tasks. One way to model such “learning to learn” effects is through hierarchical Bayesian modeling (Gelman, Carlin, Stern, & Rubin, 2004). For example, several parameters in our model influence the likelihood that different latent causes are inferred for different stimuli in a compound. One of these parameters is α (see Equation 1), which controls the probability of sampling a novel latent cause in a new trial of the experiment. Putting a prior on the value of this parameter and inferring it from data rather that setting it arbitrarily, would allow previous experience in discrimination tasks to influence inference in novel tasks.
Our model assumes a particular causal structure in which latent causes produce both stimuli and outcomes. As indicated in the introduction, a whole different class of models assume a different causal structure in which stimuli directly produce outcomes. This latter causal structure might be a better description of many learning tasks (or the assumptions made by the learner) than the latent causes structure. This could be the case for some causal learning experiments, in which participants are directly instructed to learn causal relations between stimuli and outcomes. For example, humans learning causal relations between foods and allergy show a summation effect (Collins & Shanks, 2006; Soto et al., 2009). Our model can explain this result only if it is assumed that different foods vary along separable dimensions, but some models (e.g., the Kalman filter) that assume a stimulus-generates-outcome structure can explain summation in this experiment without resorting to assumptions about separability. More empirical and theoretical work will be necessary to determine which kind of theory provides a better explanation for the data as a whole. Currently, however, only the latent causes theory presented here is able to explain the effect of stimulus factors on compound generalization.
An important assumption of our model is that the correct way to represent integral dimensions in consequential regions theory is through regions which can be oriented in any direction of space. This assumption is crucial for the success of our model in explaining compound generalization phenomena. However, a different view of integrality within consequential regions theory, favored by Shepard (1987, 1991), is that the sizes of consequential regions along integral dimensions are correlated (e.g., regions are squares or circles). Both hypotheses are capable to reproduce the shape of generalization gradients for integral dimensions, but only the hypothesis that consequential regions can orient in any direction of space can explain compound generalization, at least in the framework of our model. An important goal for future research is to directly test these two hypotheses about integrality.
Finally, our model deals only with cases in which learning is generalized to new stimuli and compounds on the basis of their similarity or shared components. There is evidence that human causal learning can also be generalized on the basis of rules (e.g., Shanks & Darby, 1998). Hierarchical Bayesian modeling is capable of handling such examples of rule-based generalization (e.g., Kemp, Goodman & Tenenbaum, 2007) and it could be used in the future to provide a unified account of dimensional, compound and rule-based forms of generalization.
In sum, both rational and mechanistic theories of generalization have treated generalization across compounds and generalization across dimensions as separate phenomena. However, recent work in associative and causal learning questions these assumptions, by showing that changes in stimulus dimensions can have an important effect on generalization across stimulus compounds. Although much more work can be done to improve the rational theory of generalization, the present work represents an advance as it expands the scope of latent cause theories of compound generalization and bridges between these theories and the rational theory of dimensional generalization.
Acknowledgments
Fabian Soto was supported by a fellowship for the Advanced Course in Computational Neuroscience Internship Program and by a Sage Center Junior Research Fellowship. Samuel Gershman was supported by a graduate research fellowship from the National Science Foundation. Yael Niv was supported by NIMH grant R01MH098861 and by an Alfred P. Sloan Fellowship. The content is solely the responsibility of the authors and does not represent the official views of the National Institutes of Health.
Appendix A: The Indian Buffet Process
Recall that Z in our model is a matrix of zeros and ones, with columns representing different latent causes and rows representing different experimental trials. To define a distribution on Z, the main goal is that several latent causes can be simultaneously active on a particular trial to jointly produce the observed data. Also, because we do not know the total number of latent causes in advance, we need a distribution capable of generating Z with an unbounded number of columns. A simple stochastic process that can generate Z with such characteristics is the Indian Buffet Process (IBP; Griffiths & Ghahramani, 2011).
The IBP was originally explained by its authors through a culinary metaphor: N customers enter a restaurant with a buffet of infinitely many dishes arranged in a line. The first customer starts at the beginning of the buffet and samples a Poisson(α) number of dishes. The tth customer moves along all the dishes already sampled by previous customers, sampling dish k with probability qk/t, where qk is the number of previous customers that have already sampled the dish. After considering all the previously sampled dishes, the customer samples from a Poisson(α/t) number of new dishes.
It can be shown (see Griffiths & Ghahramani, 2011) that if we attend only to those columns for which qk>0 (taking into account those matrices that can be made equivalent after a re-ordering of their columns) then the probability of obtaining a matrix Z from this process equals:
| (A1) |
where K+ is the number of columns with qk > 0, Kh is the number of columns whose entries correspond to the binary number h (e.g., 1000..., 0100..., 1100...), and HN is the nth harmonic number, .
This distribution has the following important properties: (1) the effective number of latent causes K+ follows a Poisson(αHN) distribution, (2) the number of latent causes sampled on a trial follows a Poisson(α) distribution, (3) Z remains sparse as K→∞, and (4) the distribution is “exchangeable”, that is, the probability of a matrix Z is unaffected by the order of trials.
Appendix B: Inference Algorithm
The general strategy of this inference algorithm is to use a Gibbs sampler to cycle repeatedly through each variable, sampling them from their posterior distribution conditional to the sampled values for all the other variables. Whenever the conditional posterior is intractable, we use Metropolis-Hastings to approximate sampling from the conditional posterior.
Sampling z
Given that ztk is a discrete variable with only two possible values, it is possible to compute the conditional posterior probabilities by enumeration. From our generative model and Bayes rule we have that:
| (B1) |
Here, Z-tk represents all entries in the matrix Z except for ztk. The first likelihood term in the right side of this equation is given by Equation 7, while the second likelihood term is given by the Gaussian distribution defined in Equations 11 and 12. Values for the final term, p(ztk = v | Z-tk), can be computed thanks to the exchangeability of the IBP. We start by assuming that the tth customer is the last to enter the restaurant. This customer should sample each dish that has already been sampled with p = q-tk/T, where q-tk is the number of ones in column z:k for all cells except ztk, T is the total number of clients, and then the customer should sample Poisson(α/T) new dishes. This means that we can start at the leftmost position on each row of Z, and then sample each individual zt for that row taking into account that there are two possibilities for ztk. If q-tk > 0, then p(ztk = 1 | Z-tk) = q-tk/T. If q-tk = 0, then ztk can be considered as being sampled for the first time, together with all other columns with no entries.
After the Gibbs sampler cycles through all the values of row t for which q-tk > 0, we are left with the task of sampling new dishes from the IBP. Because K = ∞, we cannot enumerate all possibilities in this case. However, we can take advantage of the fact that the IBP produces sparse matrices and assume a limited maximum number of new dishes, denoted by K+ (set to 9 in the simulations presented here). This way, we have a finite number of hypotheses about the Knew number of new dishes, going from 0 to K+, and the conditional posterior can be computed by enumeration using the following equation:
| (B2) |
Again, the first two likelihood terms are given by Equations 7 and 11, respectively, whereas the last term is computed from the Poisson probability density function:
| (B3) |
Sampling w
The generative model for r in this model is an example of a linear Gaussian model, with a Gaussian prior over w which is conjugate for the Gaussian likelihood over r. Thus, the posterior can be derived analytically and has the form of a multivariate Gaussian:
| (B4) |
where
| (B5) |
and
| (B6) |
Sampling m
Due to non-conjugacy, the conditional posterior for m is not available in closed form, and we approximate sampling from it through a Metropolis sampler using a Gaussian proposal distribution with . At each step of the process, we sample a candidate from . Then is accepted with probability:
| (B7) |
which is achieved by sampling a random number u from Uniform(0,1) and accepting if , and setting otherwise.
Sampling s
Again, we must resort to a Metropolis-Hastings approach to approximate sampling from the conditional posterior over s. In this case, we wanted the sampler to explore the whole range of possible values of s at each step, because we expected that in some occasions a region elongated along one axis would be very likely to have generated some data patterns. Allowing the sampler to “jump” from small to large sizes of consequential regions seems like a desirable feature. Thus, to sample s we used an independence Metropolis-Hastings sampler (Gilks et al., 1995) with the prior distribution p(sk) as the proposal distribution. Here, we sample a candidate from the prior and we accept it with probability:
| (B8) |
which, again, is achieved by sampling u from Uniform(0,1) and setting if , and otherwise.
Notice that the acceptance probability depends only on the likelihood ratio because in the independence sampler candidates are generated independently from the current state of the sampler. Thus, the acceptance probability for a candidate value z’ is defined as
| (B9) |
where . Given that in this sampler the proposal is the prior, w(z) = likelihood(z).
Footnotes
Although Shepard (1987; 1991) was the first to propose this hypothesis about the origins of integrality, he advocated the view that integral dimensions are those for which the extent of the consequential regions is correlated (e.g., squared regions, in which all sides have the same size); using all possible orientations of consequential regions to make inferences about integral dimensions would have only the minor role of better approximating generalization gradients typical of integrality (see Shepard, 1991, p. 68).
The results presented in Figure 9 come from two experiments that used different testing conditions. In experiment 1, both A and AB were not reinforced throughout the test, whereas in experiment 2, A was always reinforced and AB not reinforced. Only the data from the first test session of experiment 2—before any considerable re-learning of the A+, AB- discrimination had occurred—are shown in Figure 8, in order to show more comparable results for the two conditions.
References
- Alvarado MC, Rudy JW. Some properties of configural learning: An investigation of the transverse-patterning problem. Journal of Experimental Psychology: Animal Behavior Processes. 1992;18:145–153. doi: 10.1037//0097-7403.18.2.145. [DOI] [PubMed] [Google Scholar]
- Anderson JR. The adaptive character of thought. Lawrence Erlbaum Associates; Hillsdale, NJ: 1990. [Google Scholar]
- Aitken MRF, Dickinson A. Simulations of a modified SOP model applied to retrospective revaluation of human causal learning. Learning & Behavior. 2005;33(2):147–159. doi: 10.3758/bf03196059. [DOI] [PubMed] [Google Scholar]
- Arulampalam MS, Maskell S, Gordon N, Clapp T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Transactions on Signal Processing. 2002;50(2):174–188. [Google Scholar]
- Ashby FG, Maddox WT. A response time theory of separability and integrality in speeded classification. Journal of Mathematical Psychology. 1994;38(4):423–466. [Google Scholar]
- Ashby FG, Soto FA. Multidimensional signal detection theory. In: Busemeyer JR, Townsend JT, Wang ZJ, Eidels A, editors. Oxford handbook of computational and mathematical psychology. Oxford University Press; in press. [Google Scholar]
- Ashby FG, Townsend JT. Varieties of perceptual independence. Psychological review. 1986;93(2):154. [PubMed] [Google Scholar]
- Atkinson RR, Estes WK. Stimulus sampling theory. In: Luce RD, Bush RB, editors. Handbook of Mathematical Psychology. Wiley; New York: 1963. pp. 212–268. [Google Scholar]
- Austerweil JL, Griffiths TL. Learning hypothesis spaces and dimensions through concept learning.. Proceedings of the 32nd Annual Conference of the Cognitive Science Society; 2010.pp. 73–78. [Google Scholar]
- Austerweil JL, Griffiths TL. A rational model of the effects of distributional information on feature learning. Cognitive Psychology. 2011;63(4):173–209. doi: 10.1016/j.cogpsych.2011.08.002. [DOI] [PubMed] [Google Scholar]
- Aydin A, Pearce JM. Summation in Autoshaping with short- and long-duration Stimuli. The Quarterly Journal of Experimental Psychology. 1995;48B(3):215–234. [Google Scholar]
- Aydin A, Pearce JM. Some determinants of response summation. Animal Learning & Behavior. 1997;25(1):108–121. [Google Scholar]
- Bahçekapili HG. Unpublished Doctoral Dissertation. Yale University; 1997. An evaluation of Rescorla and Wagner's elementistic model versus Pearce's configural model in discrimination learning. [Google Scholar]
- Blough DS. Steady state data and a quantitative model of operant generalization and discrimination. Journal of Experimental Psychology: Animal Behavior Processes. 1975;104(1):3–21. [Google Scholar]
- Brandon SE, Vogel EH, Wagner AR. A componential view of configural cues in generalization and discrimination in Pavlovian conditioning. Behavioral Brain Research. 2000;110(1-2):67–72. doi: 10.1016/s0166-4328(99)00185-0. [DOI] [PubMed] [Google Scholar]
- Brown GDA, Neath I, Chater N. A temporal ratio model of memory. Psychological Review. 2007;114(3):539–576. doi: 10.1037/0033-295X.114.3.539. [DOI] [PubMed] [Google Scholar]
- Cappé O, Godsill SJ, Moulines E. An overview of existing methods and recent advances in sequential Monte Carlo. Proceedings of the IEEE. 2007;95(5):899–924. [Google Scholar]
- Chapman GB. Trial order affects cue interaction in contingency judgment. Journal of Experimental Psychology: Learning Memory and Cognition. 1991;17(5):837–854. doi: 10.1037//0278-7393.17.5.837. [DOI] [PubMed] [Google Scholar]
- Chapman GB, Robbins SJ. Cue interaction in human contingency judgment. Memory & Cognition. 1990;18(5):537–545. doi: 10.3758/bf03198486. [DOI] [PubMed] [Google Scholar]
- Cheng PW. From covariation to causation: A causal power theory. Psychological Review. 1997;104(2):367–405. [Google Scholar]
- Cohen DJ. Visual detection and perceptual independence: Assessing color and form. Perception & psychophysics. 1997;59(4):623–635. doi: 10.3758/bf03211870. [DOI] [PubMed] [Google Scholar]
- Collins DJ, Shanks DR. Summation in causal learning: Elemental processing or configural generalization? The Quarterly Journal of Experimental Psychology. 2006;59(9):1524–1534. doi: 10.1080/17470210600639389. [DOI] [PubMed] [Google Scholar]
- Courville AC. Unpublished doctoral dissertation. Carnegie Mellon University; 2006. A latent cause theory of classical conditioning. [Google Scholar]
- Courville AC, Daw ND, Touretzky DS. Similarity and discrimination in classical conditioning: A latent variable account. In: Saul LK, Weiss Y, Bottou L, editors. Advances in neural information processing systems. MIT Press; Cambridge, MA: 2002. pp. 313–320. [Google Scholar]
- Danks D, Griffiths TL, Tenenbaum JB. Dynamical Causal Learning.. In: Becker S, Thrun S, Obermayer K, editors. Advances in Neural Information Processing Systems 15: Proceedings of the 2002 Conference; Cambridge, MA. MIT Press; 2003. pp. 67–74. [Google Scholar]
- Davis M, Schlesinger LS, Sorenson CA. Temporal specificity of fear conditioning: effects of different conditioned stimulus-unconditioned stimulus intervals on the fear-potentiated startle effect. Journal of Experimental Psychology: Animal Behavior Processes. 1989;15:295–310. [PubMed] [Google Scholar]
- Daw ND, Courville AC, Dayan P. Semi-rational models of conditioning: the case of trial order. In: Chater N, Oaksford M, editors. The Probabilistic Mind: Prospects for Bayesian Cognitive Science. Oxford University Press; Oxford: 2008. pp. 431–452. [Google Scholar]
- Dayan P, Kakade S, Montague PR. Learning and selective attention. Nature Neuroscience. 2000;3:1218–1223. doi: 10.1038/81504. [DOI] [PubMed] [Google Scholar]
- Denniston JC, Miller RR, Matute H. Biological significance as a determinant of cue competition. Psychological Science. 1996;7(6):325–331. [Google Scholar]
- Dickinson A, Burke J. Within-compound associations mediate the retrospective revaluation of causality judgements. Quarterly Journal of Experimental Psychology. 1996;49B(1):60–80. doi: 10.1080/713932614. [DOI] [PubMed] [Google Scholar]
- Dibbets P, Maes JHR, Vossen JMH. Interaction between positional but not between non-positional cues in human predictive learning. Behavioural Processes. 2000;50(2-3):65–78. doi: 10.1016/s0376-6357(00)00092-9. [DOI] [PubMed] [Google Scholar]
- Dunn JC. Spatial metrics of integral and separable dimensions. Journal of Experimental Psychology: Human Perception and Performance. 1983;9(2):242. doi: 10.1037//0096-1523.9.2.242. [DOI] [PubMed] [Google Scholar]
- Felfoldy GL, Garner WR. The effects on speeded classification of implicit and explicit instructions regarding redundant dimensions. Perception & Psychophysics. 1971;9(3):289–292. [Google Scholar]
- Fific M, Nosofsky RM, Townsend JT. Information-processing architectures in multidimensional classification: A validation test of the systems factorial technology. Journal of Experimental Psychology: Human Perception and Performance. 2008;34(2):356. doi: 10.1037/0096-1523.34.2.356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garner WR. The stimulus in information processing. American Psychologist. 1970;25(4):350. [Google Scholar]
- Garner WR. Attention: The processing of multiple sources of information. In: Carterette EC, Friedman MP, editors. Handbook of perception: Vol. 2. Psychophysical measurement and judgment. Academic Press; New York: 1974. pp. 29–39. [Google Scholar]
- Gelman A, Carlin JB, Stern HS, Rubin DB. Bayesian Data Analysis. Chapman and Hall; Boca Raton, FL: 2004. [Google Scholar]
- Gershman SJ, Blei DM. A tutorial on Bayesian nonparametric models. Journal of Mathematical Psychology. 2012;56(1):1–12. [Google Scholar]
- Gershman SJ, Blei DM, Niv Y. Context, learning, and extinction. Psychological Review. 2010;117(1):197–209. doi: 10.1037/a0017808. [DOI] [PubMed] [Google Scholar]
- Ghahramani Z, Griffiths TL, Sollich P. Bayesian nonparametric latent feature models. Bayesian Statistics. 2007;8:1–25. [Google Scholar]
- Ghirlanda S, Enquist M. A century of generalization. Animal Behaviour. 2003;66:15–36. [Google Scholar]
- Gilks WR, Gilks WR, Richardson S, Spiegelhalter DJ. Markov chain Monte Carlo in practice. Chapman & Hall; London: 1996. [Google Scholar]
- Glautier S. Spatial separation of target and competitor cues enhances blocking of human causality judgements. The Quarterly Journal of Experimental Psychology. 2002;55B(2):121–135. doi: 10.1080/02724990143000207. [DOI] [PubMed] [Google Scholar]
- Glautier S. Asymmetry of generalization decrement in causal learning. The Quarterly Journal of Experimental Psychology. 2004;57B(4):315. doi: 10.1080/02724990344000169. [DOI] [PubMed] [Google Scholar]
- González F, Quinn JJ, Fanselow MS. Differential effects of adding and removing components of a context on the generalization of conditional freezing. Journal of Experimental Psychology: Animal Behavior Processes. 2003;29(1):78–83. [PubMed] [Google Scholar]
- Grau JW, Nelson DK. The distinction between integral and separable dimensions: Evidence for the integrality of pitch and loudness. Journal of Experimental Psychology: General. 1988;117(4):347. doi: 10.1037//0096-3445.117.4.347. [DOI] [PubMed] [Google Scholar]
- Griffiths TL, Ghahramani Z. The Indian Buffet Process: An Introduction and Review. Journal of Machine Learning Research. 2011;12:1185–1224. [Google Scholar]
- Griffiths TL, Tenenbaum JB. Structure and strength in causal induction. Cognitive Psychology. 2005;51(4):334–384. doi: 10.1016/j.cogpsych.2005.05.004. [DOI] [PubMed] [Google Scholar]
- Griffiths TL, Tenenbaum JB. From mere coincidences to meaningful discoveries. Cognition. 2007;103(2):180–226. doi: 10.1016/j.cognition.2006.03.004. [DOI] [PubMed] [Google Scholar]
- Guttman N, Kalish HI. Discriminability and stimulus generalization. Journal of Experimental Psychology. 1956;51(1):79–88. doi: 10.1037/h0046219. [DOI] [PubMed] [Google Scholar]
- Harris JA. Elemental representations of stimuli in associative learning. Psychological Review. 2006;113(3):584–605. doi: 10.1037/0033-295X.113.3.584. [DOI] [PubMed] [Google Scholar]
- Honey RC, Hall G. Overshadowing and blocking procedures in latent inhibition. The Quarterly Journal of Experimental Psychology. 1988;40B(2):163. [PubMed] [Google Scholar]
- Honey RC, Hall G. Attenuation of latent inhibition after compound pre-exposure: Associative and perceptual explanations. The Quarterly Journal of Experimental Psychology. 1989;41B(4):355. [PubMed] [Google Scholar]
- Hyman R, Well A. Judgments of similarity and spatial models. Perception & Psychophysics. 1967;2(6):233–248. [Google Scholar]
- Kakade S, Dayan P. Acquisition and extinction in autoshaping. Psychological Review. 2002;109(3):533–544. doi: 10.1037/0033-295x.109.3.533. [DOI] [PubMed] [Google Scholar]
- Kamin LJ. Selective association and conditioning. In: Mackintosh NJ, Honig WK, editors. Fundamental Issues in Associative Learning. Dalhousie University Press; Halifax: 1969. pp. 42–64. [Google Scholar]
- Kehoe EJ, Gormezano I. Configuration and combination laws in conditioning with compound stimuli. Psychological Bulletin. 1980;87(2):351. [PubMed] [Google Scholar]
- Kehoe EJ, Horne AJ, Horne PS, Macrae M. Summation and configuration between and within sensory modalities in classical conditioning of the rabbit. Animal Learning and Behavior. 1994;22(1):19–26. [Google Scholar]
- Kemp C, Goodman ND, Tenenbaum JB. Learning causal schemata. Proceedings of the 29th Annual Cognitive Science Society. 2007:389–394. [Google Scholar]
- Kinder A, Lachnit H. Similarity and discrimination in human Pavlovian conditioning. Psychophysiology. 2003;40(2):226–234. doi: 10.1111/1469-8986.00024. [DOI] [PubMed] [Google Scholar]
- Kruschke JK. Locally Bayesian learning with applications to retrospective revaluation and highlighting. Psychological Review. 2006;113(4):677–699. doi: 10.1037/0033-295X.113.4.677. [DOI] [PubMed] [Google Scholar]
- Lavin MJ. The establishment of flavor-flavor associations using a sensory preconditioning procedure. Learning and Motivation. 1976;7:173–183. [Google Scholar]
- Lee MD. Three case studies in the Bayesian analysis of cognitive models. Psychonomic Bulletin & Review. 2008;15(1):1–15. doi: 10.3758/pbr.15.1.1. [DOI] [PubMed] [Google Scholar]
- Livesey EJ, Boakes RA. Outcome additivity, elemental processing and blocking in human causality judgements. The Quarterly Journal of Experimental Psychology. 2004;57B(4):361. doi: 10.1080/02724990444000005. [DOI] [PubMed] [Google Scholar]
- Lovibond PF, Siddle DA, Bond N. Insensitivity to stimulus validity in human Pavlovian conditioning. The Quarterly Journal of Experimental Psychology. 1988;40B(4):377–410. [PubMed] [Google Scholar]
- Lu H, Yuille AL, Liljeholm M, Cheng PW, Holyoak KJ. Bayesian generic priors for causal learning. Psychological Review. 2008;115(4):955–984. doi: 10.1037/a0013256. [DOI] [PubMed] [Google Scholar]
- Mackay DJC. Information theory, inference and learning algorithms. Cambridge University Press; Cambridge, UK: 2003. [Google Scholar]
- Mackintosh NJ. Categorization by people and pigeons. Quarterly Journal of Experimental Psychology. 1995;48A(3):193–214. [Google Scholar]
- Maddox WT. Perceptual and decisional separability. In: Ashby FG, editor. Multidimensional models of perception and cognition. Erlbaum; Hillsdale, NJ: 1992. pp. 147–180. [Google Scholar]
- Marks LE. Cross-modal interactions in speeded classification. In: Calvert GA, Spence C, Stein BE, editors. Handbook of multisensory processes. MIT Press; Cambridge, MA: 2004. pp. 85–105. [Google Scholar]
- Martin I, Levey AB. Blocking observed in human eyelid conditioning. The Quarterly Journal of Experimental Psychology. 1991;43B(3):233. [PubMed] [Google Scholar]
- Marr D. Vision, a computational investigation into the human representation and processing of visual information. W. H. Freeman; San Francisco: 1982. [Google Scholar]
- McLaren IPL, Mackintosh NJ. Associative learning and elemental representation: II. Generalization and discrimination. Animal Learning & Behavior. 2002;30(3):177–200. doi: 10.3758/bf03192828. [DOI] [PubMed] [Google Scholar]
- Mehta R, Williams DA. Elemental and configural processing of novel cues in deterministic and probabilistic tasks. Learning and Motivation. 2002;33:456–484. [Google Scholar]
- Melara RD, Marks LE. Interaction among auditory dimensions: Timbre, pitch, and loudness. Perception & Psychophysics. 1990;48(2):169–178. doi: 10.3758/bf03207084. [DOI] [PubMed] [Google Scholar]
- Melchers KG, Lachnit H, Shanks DR. Past experience influences the processing of stimulus compounds in human Pavlovian conditioning. Learning and Motivation. 2004;35:167–188. [Google Scholar]
- Melchers KG, Lachnit H, Üngör M, Shanks DR. Prior experience can influence whether the whole is different from the sum of its parts. Learning and Motivation. 2005;36:20–41. [Google Scholar]
- Melchers KG, Shanks DR, Lachnit H. Stimulus coding in human associative learning: Flexible representations of parts and wholes. Behavioural Processes. 2008;77(3):413–427. doi: 10.1016/j.beproc.2007.09.013. [DOI] [PubMed] [Google Scholar]
- Miller RR, Matute H. Biological significance in forward and backward blocking: Resolution of a discrepancy between animal conditioning and human causal judgment. Journal of Experimental Psychology: General. 1996;125(4):370–386. doi: 10.1037//0096-3445.125.4.370. [DOI] [PubMed] [Google Scholar]
- Myers KM, Vogel EH, Shin J, Wagner AR. A comparison of the Rescorla-Wagner and Pearce models in a negative patterning and a summation problem. Animal Learning and Behavior. 2001;29(1):36–45. [Google Scholar]
- Navarro DJ. From natural kinds to complex categories.. Proceedings of the 28th Annual Conference of the Cognitive Science Society.2006. pp. 621–626. [Google Scholar]
- Navarro DJ, Dry MJ, Lee MD. Sampling assumptions in inductive generalization. Cognitive Science. 2012;36:187–223. doi: 10.1111/j.1551-6709.2011.01212.x. [DOI] [PubMed] [Google Scholar]
- Navarro DJ, Griffiths TL. Latent features in similarity judgments: A nonparametric Bayesian approach. Neural Computation. 2008;20(11):2597–2628. doi: 10.1162/neco.2008.04-07-504. [DOI] [PubMed] [Google Scholar]
- Navarro DJ, Lee MD, Dry MJ, Schultz B. Extending and testing the Bayesian theory of generalization.. Proceedings of the 30th Annual Conference of the Cognitive Science Society; Austin, TX. Cognitive Science Society; 2008. pp. 1746–1751. [Google Scholar]
- Navarro DJ, Perfors AF. Similarity, feature discovery, and the size principle. Acta Psychologica. 2010;133(3):256–268. doi: 10.1016/j.actpsy.2009.10.008. [DOI] [PubMed] [Google Scholar]
- Novick LR, Cheng PW. Assessing interactive causal influence. Psychological Review. 2004;111(2):455–485. doi: 10.1037/0033-295X.111.2.455. [DOI] [PubMed] [Google Scholar]
- Pavlov IP. Conditioned Reflexes: An Investigation of the Physiological Activity of the Cerebral Cortex. Oxford University Press; London: 1927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearce JM, Wilson PN. Failure of excitatory conditioning to extinguish the influence of a conditioned inhibitor. Journal of Experimental Psychology: Animal Behavior Processes. 1991;17(4):519–529. [Google Scholar]
- Pearce JM. A model for stimulus generalization in Pavlovian conditioning. Psychological Review. 1987;94(1):61–73. [PubMed] [Google Scholar]
- Pearce JM. Similarity and discrimination: A selective review and a connectionist model. Psychological Review. 1994;101:587–607. doi: 10.1037/0033-295x.101.4.587. [DOI] [PubMed] [Google Scholar]
- Pearce JM. Evaluation and development of a connectionist theory of configural learning. Animal Learning & Behavior. 2002;30:73–95. doi: 10.3758/bf03192911. [DOI] [PubMed] [Google Scholar]
- Pearce JM, Aydin A, Redhead ES. Configural analysis of summation in autoshaping. Journal of Experimental Psychology: Animal Behavior Processes. 1997;23(1):84. [Google Scholar]
- Pearce JM, Redhead ES. The influence of an irrelevant stimulus on two discriminations. Journal of Experimental Psychology: Animal Behavior Processes. 1993;19:180–190. [Google Scholar]
- Pitt MA, Myung JI, Montenegro M, Pooley J. Measuring model flexibility with parameter space partitioning: An introduction and application example. Cognitive Science. 2008;32(8):1285–1303. doi: 10.1080/03640210802477534. [DOI] [PubMed] [Google Scholar]
- Ploog BO. Summation and subtraction using a modified autoshaping procedure in pigeons. Behavioural processes. 2008;78(2):259–268. doi: 10.1016/j.beproc.2008.02.015. [DOI] [PubMed] [Google Scholar]
- Pomerantz JR, Sager LC. Asymmetric integrality with dimensions of visual pattern. Perception & Psychophysics. 1975;18(6):460–466. [Google Scholar]
- Reed P. Effect of a signalled delay between an action and outcome on human judgement of causality. Quarterly Journal of Experimental Psychology. 1992;44B:81–100. [Google Scholar]
- Reed P. Enhanced latent inhibition following compound pre-exposure. The Quarterly Journal of Experimental Psychology. 1995;48B(1):32. [PubMed] [Google Scholar]
- Rescorla RA. Probability of shock in the presence and absence of CS in fear conditioning. Journal of Comparative and Physiological Psychology. 1968;66(1):1–5. doi: 10.1037/h0025984. [DOI] [PubMed] [Google Scholar]
- Rescorla RA. Pavlovian conditioned inhibition. Psychological Bulletin. 1969;72(2):77–94. [Google Scholar]
- Rescorla RA. Stimulus generalization: Some predictions from a model of Pavlovian conditioning. Journal of Experimental Psychology: Animal Behavior Processes. 1976;2(1):88–96. doi: 10.1037//0097-7403.2.1.88. [DOI] [PubMed] [Google Scholar]
- Rescorla RA. Simultaneous and successive associations in sensory preconditioning. Journal of Experimental Psychology: Animal Behavior Processes. 1980;6(3):207–216. doi: 10.1037//0097-7403.6.3.207. [DOI] [PubMed] [Google Scholar]
- Rescorla RA. Summation: Assessment of a configural theory. Animal Learning & Behavior. 1997;25(2):200–209. [Google Scholar]
- Rescorla RA, Coldwell SE. Summation in autoshaping. Animal Learning & Behavior. 1995;23(3):314–326. [Google Scholar]
- Rescorla RA, Wagner AR. A theory of Pavlovian conditioning: Variations in the effectiveness of reinforcement and nonreinforcement. In: Black AH, Prokasy WF, editors. Classical conditioning II: Current theory and research. Appleton-Century-Crofts; New York: 1972. pp. 64–99. [Google Scholar]
- Ronacher B, Bautz W. Human pattern recognition: Individually different strategies in analyzing complex stimuli. Biological cybernetics. 1985;51(4):249–261. doi: 10.1007/BF00337150. [DOI] [PubMed] [Google Scholar]
- Sanborn AN, Griffiths TL, Navarro DJ. Rational approximations to rational models: Alternative algorithms for category learning. Psychological Review. 2010;117(4):1144–1167. doi: 10.1037/a0020511. [DOI] [PubMed] [Google Scholar]
- Shanks DR. Forward and backward blocking in human contingency judgement. The Quarterly Journal of Experimental Psychology. 1985;37B(1):1–21. [Google Scholar]
- Shanks DR, Charles D, Darby RJ, Azmi A. Configural processes in human associative learning. Journal of Experimental Psychology: Learning Memory and Cognition. 1998;24(6):1353–1378. doi: 10.1037//0097-7403.24.2.136. [DOI] [PubMed] [Google Scholar]
- Shanks DR, Darby RJ. Feature-and rule-based generalization in human associative learning. Journal of Experimental Psychology: Animal Behavior Processes. 1998;24(4):405. doi: 10.1037//0097-7403.24.2.136. [DOI] [PubMed] [Google Scholar]
- Shanks DR, Pearson SM, Dickinson A. Temporal contiguity and the judgement of causality by human subjects. Quarterly Journal of Experimental Psychology. 1989;41B:139–159. [Google Scholar]
- Shepard RN. Approximation to uniform gradients of generalization by monotone transformations of scale. In: Mostofsky DI, editor. Stimulus Generalization. Stanford University Press; Palo Alto, CA: 1965. pp. 94–110. [Google Scholar]
- Shepard RN. Toward a universal law of generalization for psychological science. Science. 1987;237(4820):1317–1323. doi: 10.1126/science.3629243. [DOI] [PubMed] [Google Scholar]
- Smith MC, Coleman SR, Gormezano I. Classical conditioning of the rabbit's nictitating membrane response at backward, simultaneous, and forward CS-US intervals. Journal of Comparative and Physiological Psychology. 1969;69(2):226–231. doi: 10.1037/h0028212. [DOI] [PubMed] [Google Scholar]
- Soto FA, Vogel EH, Castillo RD, Wagner AR. Generality of the summation effect in human causal learning. Quarterly Journal of Experimental Psychology. 2009;62(5):877–889. doi: 10.1080/17470210802373688. [DOI] [PubMed] [Google Scholar]
- Soto FA, Wasserman EA. Integrality/separability of stimulus dimensions and multidimensional generalization in pigeons. Journal of Experimental Psychology: Animal Behavior Processes. 2010;36(2):194. doi: 10.1037/a0016560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenenbaum JB, Griffiths TL. Generalization, similarity and Bayesian inference. Behavioral and Brain Sciences. 2001a;24(4):629–640. doi: 10.1017/s0140525x01000061. [DOI] [PubMed] [Google Scholar]
- Tenenbaum JB, Griffiths TL. Some specifics about generalization. Behavioral and Brain Sciences. 2001b;24(4):772–778. doi: 10.1017/s0140525x01000061. [DOI] [PubMed] [Google Scholar]
- Thorwart A, Lachnit H. Generalization decrements: Further support for flexibility in stimulus processing. Learning & behavior. 2010;38(4):367–373. doi: 10.3758/LB.38.4.367. [DOI] [PubMed] [Google Scholar]
- Urcelay GP, Perelmuter O, Miller RR. Pavlovian backward conditioned inhibition in humans: Summation and retardation tests. Behavioural Processes. 2008;77(3):299–305. doi: 10.1016/j.beproc.2007.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Hamme LJ, Wasserman EA. Cue competition in causality judgments: The role of nonpresentation of compound stimulus elements. Learning and Motivation. 1994;25(2):127–151. [Google Scholar]
- Wagner AR. Context-sensitive elemental theory. Quarterly Journal of Experimental Psychology. 2003;56B(1):7–29. doi: 10.1080/02724990244000133. [DOI] [PubMed] [Google Scholar]
- Wagner AR. Evolution of an elemental theory of Pavlovian conditioning. Learning & Behavior. 2007;36(3):253–265. doi: 10.3758/lb.36.3.253. [DOI] [PubMed] [Google Scholar]
- Wagner AR, Logan FA, Haberlandt K, Price T. Stimulus selection in animal discrimination learning. Journal of Experimental Psychology. 1968;76(2):171–80. doi: 10.1037/h0025414. [DOI] [PubMed] [Google Scholar]
- Wagner AR, Rescorla RA. Inhibition in Pavlovian conditioning: Applications of a theory. In: Boakes RA, Haliday MS, editors. Inhibition and learning. Academic Press; New York: 1972. pp. 301–336. [Google Scholar]
- Wasserman EA, Berglan LR. Backward blocking and recovery from overshadowing in human causal judgement: The role of within-compound associations. Quarterly Journal of Experimental Psychology. 1998;51B(2):121–138. doi: 10.1080/713932675. [DOI] [PubMed] [Google Scholar]
- Weiss SJ. Stimulus compounding in free-operant and classical conditioning: A review and analysis. Psychological Bulletin. 1972;78(3):189–208. doi: 10.1037/h0032956. [DOI] [PubMed] [Google Scholar]
- Wheeler DS, Amundson JC, Miller RR. Generalization decrement in human contingency learning. The Quarterly Journal of Experimental Psychology. 2006;59(7):1212. doi: 10.1080/17470210600576342. [DOI] [PubMed] [Google Scholar]
- Whitlow JW, Wagner AR. Negative patterning in classical conditioning-summation of response tendencies to isolable and configural components. Psychonomic Science. 1972;27:299–301. [Google Scholar]
- Williams DA, Braker DS. Influence of past experience on the coding of compound stimuli. Journal of Experimental Psychology: Animal Behavior Processes. 1999;25:461–474. [Google Scholar]
- Williams DA, Sagness KE, McPhee JE. Configural and elemental strategies in predictive learning. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1994;20(3):694–709. [Google Scholar]
- Xu F, Tenenbaum JB. Sensitivity to sampling in Bayesian word learning. Developmental Science. 2007;10(3):288–297. doi: 10.1111/j.1467-7687.2007.00590.x. [DOI] [PubMed] [Google Scholar]


