Validation of an axially distributed model for quantification of myocardial blood flow using ¹³N-ammonia PET

Abstract

Background

Estimation of myocardial blood flow (MBF) with cardiac PET is often performed with conventional compartmental models. In this study, we developed and evaluated a physiologically and anatomically realistic axially distributed model. Unlike compartmental models, this axially distributed approach models both the temporal and the spatial gradients in uptake and retention along the capillary.

Methods

We validated PET-derived flow estimates with microsphere studies in 19 (9 rest, 10 stress) studies in five dogs. The radiotracer, ¹³N-ammonia, was injected intravenously while microspheres were administered into the left atrium. A regional reduction in hyperemic flow was forced by an external occluder in five of the stress studies. The flow estimates from the axially distributed model were compared with estimates from conventional compartmental models.

Results

The mean difference between microspheres and the axially distributed blood flow estimates in each of the 17 segments was 0.03 mL/g/minute (95% CI [−0.05, 0.11]). The blood flow estimates were highly correlated with each regional microsphere value for the axially distributed model (y = 0.98x + 0.06 mL/g/minute; r = 0.74; P <.001), for the two-compartment (y = 0.64x + 0.34; r = 0.74; P<.001), and for three-compartment model (y = 0.69x + 0.54; r = 0.74; P<.001). The variance of the error of the estimates is higher with the axially distributed model than the compartmental models (1.7 +/− 0.2 time higher, mean +/− 1 SD).

Conclusion

The proposed axially distributed model provided accurate regional estimates of MBF. The axially distributed model estimated blood flow with more accuracy, but less precision, than the evaluated compartmental models.

INTRODUCTION

PET imaging with ¹³N -ammonia is an accepted technique for measuring qualitative and quantitative myocardial blood flow (MBF). ¹³N-Ammonia has favorable properties as a qualitative method because of its high-extraction fraction, rapid trapping of ammonia metabolites, and relatively long half-life (10 minute) leading to high count statistics in static images. Dynamic imaging of ¹³N-ammonia can lead to quantitative estimates of MBF through application of kinetic models. Numerous methods have been proposed and extensively evaluated.^1–4

Of the quantitative analysis methods, compartmental models are the most common approach to estimate regional flows from dynamic cardiac PET images. A major assumption in compartmental models is that each region is a stirred tank, with no internal spatial variation in concentration.⁵ In reality, as capillary lengths of about a millimeter are 200 times their diameter, there are longitudinal gradients in concentrations during transients and during steady state, when there is uptake. Axially distributed models can account for these gradations in concentration, and, therefore, exchange potential, along the capillary-tissue unit.⁶

In clinical PET applications, there have been mixed results for⁷ and against distributed models. To the best of our knowledge, there has been no study proposing a distributed model for MBF estimation with clinical PET. In the past, distributed models have been considered too computationally complex and practitioners have opted for more simple compartmental models. We propose a distributed model based on several motivations. First, they are more realistic, anatomically and physiologically, than compartmental models and can give realistic estimates of capillary and cell permeabilities, avoiding the biases inevitable with compartmental analysis. Second, computation speed has exponentially improved supporting the application of more computationally complex solvers/optimizers. Finally, PET instrumentation has improved in terms of count rate capabilities and sensitivity. These improved systems support better temporal resolution than available during the development and validation of the initial compartmental MBF models. Higher temporal resolution and higher fidelity signals at each time frame may provide sufficient information for optimizing more complex distributed models.

This study proposes an axially distributed model for MBF estimation with ¹³N-ammonia, accounting for intracapillary gradients and entry and prolonged trapping in cardiac cells. We present this model and compare the results obtained with the two- and the three-compartment models. We test the validity of the estimates of regional flows against those from the deposition of microspheres in dogs.

METHODS

Axially Distributed Model

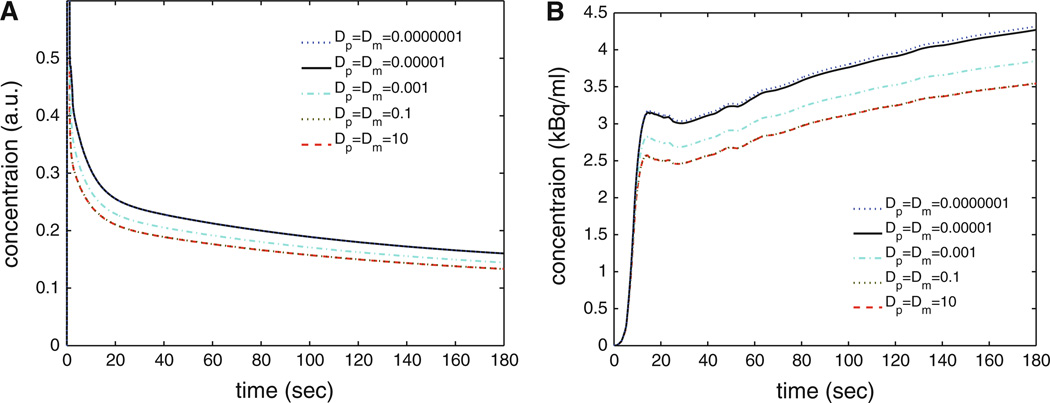
Conventional compartmental models assume spatially uniform concentrations of tracers, as a function of time, within a region of interest (ROI) of myocardium, even though it is recognized that such uniformity is a physical impossibility. Axially distributed models account for the spatial gradients, but are otherwise conceptually similar to the compartmental models with respect to membrane permeation and intracellular reaction. The shapes of model responses to sharp pulse inputs in the two cases are different, and give different estimates for tracer permeation kinetics, but relatively similar estimates of regional flows. With temporally dispersed inputs and noisy data the distinctiveness of the shapes diminishes. Figure 1 compares the shape of models with varying degrees of axial dispersion, demonstrating that realistic dispersion results in a different response than the common assumption of fully stirred regions. In this study, we model the myocardial tissue as a two-region capillary-tissue unit and incorporate the reactions among the ¹³N species of NH₃, glutamine, and glutamate in each region. The proposed model is a simplification of more general models describing the blood-tissue exchange processes.⁶

Figure 1.

Examples of model solutions for a pulse input (A) and realistic stress input function (B) demonstrating influence of axial diffusion coefficients on shape of solutions. The compartmental model assumes fully stirred regions, identical to D_p = D_m = 10 mm²/s. In this study, we use D_p = D_m = 1E−5 mm²/s presented in the solid black line. All other model parameters are fixed (F_p= 2.5 mL/g/minute, G_N = 3.2 mL/g/minute, spill = 0.1).

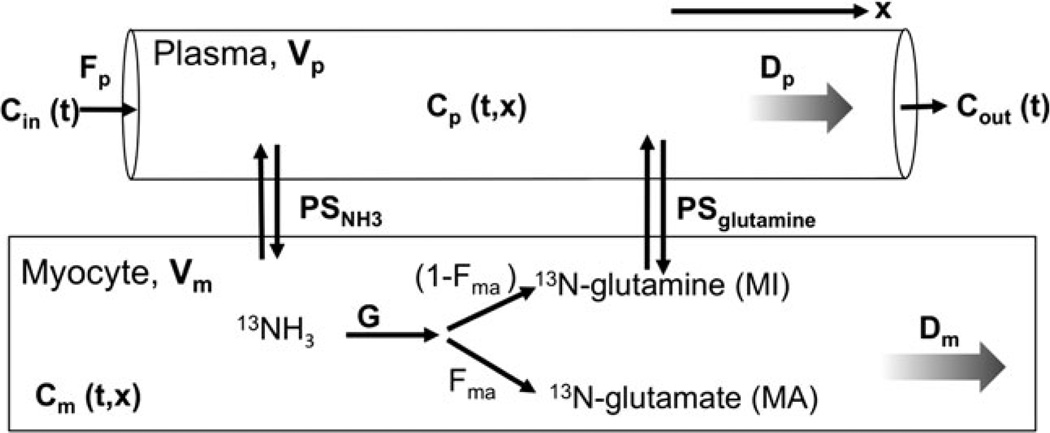
The NH₃ distributed model is described in detail in “Appendix.” The major components are represented graphically in Figure 2 and the model parameters are listed in Table 1.

Figure 2.

Graphical representation of the major components of the axially distributed model. The plasma and myocyte regions contain spatially varying concentrations of N13 species with variation defined by dispersion coefficients D_p and D_m, respectively. Each region has a volume of distribution (V).

Table 1.

List of parameters from NH₃ distributed model

	Values	Units	Definition
Model inputs
Fp	*	mL/g/minute	Flow of 13N containing plasma
PSn; PSmi	0.2+ 1.9 .Fp† 0.04 + 0.1 Fp†	mL/g/minute	Permeability surface area product for NH3 and glutamine, respectively
G	*	mL/g/minute	Regional consumption of NH3 into glutamine and glutamate
DcavDpDm	lE–5§	mm2/s	Diffusion coefficient in blood, plasma, and myocyte, respectively
Vcav, Vp, Vm	*, 0.06§, 0.56§	mL/g	Volumes, Vcav between input cavity and blood tissue unit, Vp capillary plasma, and in myocytes, Vm, respectively
L	0.8§	mm	Regional capillary length
Fma	0.4†	-	Fraction of consumed NH3 sequestered as glutamate
spill	*	mL/g	Spillover from LV cavity to myocardium
Cin (t)		mmoI/mL	Input function time-activity curve
Model dependent variables
t	[0, 180]	Seconds	Time from start of input function
X	[0,L]	mm	Distance along capillary length
z	[0, Lz	mm	Distance from input function ROI to myocardium
Model outputs
CNcav(t,z); CNp(t,x); CN,m(t,x)		mmoI/mL	Concentration of NH3 in cavity, plasma, and myocyte, respectively
CMI,P(tx); CMIm(tx)		mmoI/mL	Concentration of glutamine in plasma and myocyte, respectively
CMA,m(tx)		mmoI/mL	Concentration of glutamate in myocyte
Qtot(t)		mmoI/mL	Total residue signal of 13N in myocyte (fit to myocardial TAC)

^*Value is estimated.

^†Value/relationship derived from training data sets.

^§Value/relationship from.^25–27

Conventional Compartmental Models

The proposed axially distributed model was compared with conventional compartmental models. Compartment models assume no spatial gradients in distributions; in other words, each compartment is a fully stirred tank.

Schelbert et al ^2,3,9 proposed and tested a two-compartment model for estimating blood flow (F_p) from NH₃. This model assumes that ¹³N is in a freely diffusible state (C_F) (intra- and extravascular) or a metabolically trapped state (C_T) and can be expressed as

$$\frac{\mathrm{d}{C}_{\mathrm{F}}}{\mathrm{d}t}=-\frac{(F_{\mathrm{p}}+K_1)}{V}{C}_{\mathrm{F}}+k_2{C}_{\mathrm{T}}+F_{\mathrm{p}}{C}_{\text{in,delayed}},\frac{\mathrm{d}{C}_{\mathrm{T}}}{\mathrm{d}t}=\frac{K_1}{V}*C_{\mathrm{F}}-k_2{C}_{\mathrm{T}},$$

where V = 0.96 mL/g is the volume of the freely diffusible compartment and the rate K₁ is a function of the blood flow as determined from dog studies² according to

$$K_1=(F_{\mathrm{p}}/0.607)e^{(1.25/F_{\mathrm{p}})}-F_{\mathrm{p}}.$$

The total ¹³N concentration, Q_2C, based on the geometrical model of the ROI representation¹⁰ and defined as

$$Q_{2c}=(1-\text{spill})(C_{\mathrm{T}}+C_{\mathrm{F}})/V+\text{spill}·C_{\text{in,delayed}}$$

is fitted to the measured myocardial time-activity curve (TAC). In this model, F_p and spill were estimated and will be denoted as two-compartment in all the results.

Hutchins et al^4,11 proposed and validated a multi-compartment model for NH₃. This model assumes an extravascular and trapped compartment governed by

$$\frac{\mathrm{d}{C}_1}{\mathrm{d}t}=-(k_2+k_3)C_1+K_1{C}_{\text{in,delayed}},\frac{\mathrm{d}{C}_2}{\mathrm{d}t}=k_3{C}_1.$$

Under the assumption that extraction of NH₃ across the capillary wall is high, K₁ equals F_p. Similar to the two-compartment above, the total ¹³N concentration is

$$Q_{3c}=(1-\text{spill})(C_1+C_2)/V+\text{spill}·C_{\text{in,delayed}}.$$

In this model, K₁, k₂, k₃, and spill are estimated and will be denoted as three-compartment in all the results.

In order to provide a fair comparison with the distributed approach which includes a model of delayed arrival of tracer, the arrival of the input function at the myocardium is delayed by a time such that C_{in, delayed} (t) = C_in(t − t_delay). For all segments, the value of t_delay is estimated for both the two- and the three-compartment models.

Model Implementation

All models were implemented in the JSim modeling environment.¹² To ensure an impartial comparison, estimated parameters in each model were varied to minimize the root mean square error between the model solution and the measured data with the same optimization algorithm (SEN-SOP¹³). All optimizations were run to convergence defined as having <0.1% change in estimated parameters. All methods were evaluated with identical TACs, temporal range (0–180 seconds), temporal step sizes (0.2 seconds) for model solutions, and weighting functions based on the count statistics of each frame.

Model Validation

The flow estimates from the models were evaluated in 19 (9 rest and 10 stress) studies in five dogs. In this University of Washington IACUC approved study, adult dogs (19.4–21.7 kg) were anesthetized with IV diazepam (0.5 mg/kg) and ketamine (7.5 mg/kg), intubated and maintained on O₂ and isoflurane. Five French sheaths were placed in both femoral arteries for pressure monitoring and blood withdrawal during microsphere injections. A left thoracotomy was performed with a 2-mm polyvinyl catheter placed in the left atrial appendage for microsphere injections and a snare placed around the left anterior descending (LAD) coronary artery at the origin of a diagonal vessel. This served as a locater for subsequent anatomic sectioning and for coronary occlusion during stress. The animal was positioned in the PET tomograph (SHR-7700, Hamamatsu Photonics¹⁴) such that the left ventricle was in the center of the field of view. Heart rate and blood pressure were monitored continuously.

For the rest study, ~ 16 mCi of ¹³N-NH₃ was injected intravenously and dynamic PET images acquired for 3 minutes. After four half-lives of ¹³N decay (40 minutes), 0.2-mg regadenoson (Astellas Pharma, Derrfield, IL), an adenosine A2a agonist, was injected over 10 seconds, followed by a 10-mL saline bolus. One minute after starting the regadenoson infusion, ~16 mCi of ¹³N-NH₃ was injected and dynamic PET images were acquired. In four of the five animals, a second baseline imaging study was performed. In all the animals, a second stress was performed immediately after full snare occlusion of the LAD. Simultaneous to all PET image acquisitions, 15 µm fluorescent microspheres were injected and duplicate arterial samples withdrawn over 2 minutes. Four distinct color fluorescent microspheres were used to assess each flow state. After image acquisition was complete, the animal was killed by IV injection of a lethal dose of KC1. The heart was excised, rinsed free of blood, and the LV cavity filled by expandable polyurethane foam. The heart was then cut into equal thickness short-axis slices, excluding the apex where there was no cavity and any slice that included mitral annulus. Each slice was then cut into eight equal sectors, weighed and processed for identification of fluorescent microspheres through tissue digestion as described previously.¹⁵ The slices and sectors were oriented to correspond to the PET processing described below.

PET image acquisition

Starting with ¹³N-NH₃ injection, dynamic PET images were acquired (15 × 2 second frames, then 9×5 second, then 10 × 10 second) in 2D mode. Images were reconstructed into 0.6 × 0.6 × 3.6 mm voxels using filtered backprojection and sent to a locally developed image processing program where the transaxial images were reoriented into short-axis, vertical and horizontal long axis slices. This software permits placement of a spherical ROI within the center of the left atrium (LA) and automatically segments the left ventricle myocardium into 17 segments conforming to ASNC/ACC requirements.¹⁶ The segments were automatically centered on the center of the myocardium in the short axis images and were all 4 mm thick. TACs were generated for the LA cavity and each of the 17 segments and decay and background subtracted to the time of injection. These TACs were analyzed using the models described above. The left atrial ROI TAC was chosen to be the fundamental input used in the optimization because this ROI lies far enough away from the LV myocardium that spillover of counts from the myocardium into the LA ROI was negligible during the tail of the curve. This spillover would have potentially been a problem given the small cavity in these animals.

Noise Analysis

The errors in estimated parameters have several sources including errors in model assumptions, errors from biases in PET data, and noise in the PET data. Dynamic PET data are inherently noisy due to limited photon statistics. It is well appreciated that this noise contributes to errors,¹⁷ although it is often difficult to assess the largest source of error in estimated parameters. In this analysis, we sought to evaluate errors in flow estimation due to noise and limited temporal resolution.

We simulated noise-free TACs using the proposed axially distributed model for a nine states (F_p= [0.8, 1.6, 2.4] mL/g/ minute × G = [0.8, 1.6, 2.4] mL/g/minute) and with other component descriptors and parameters remaining unchanged. For each of these nine artificial data curves, we added noise to mimic [1/4, 1/2, 1, 2, 4] times standard counts rates, with the standard count level equal to the average count rate present in the measured animal studies. The noise was modeled as zero-mean Gaussian distributed with variance proportional to the count rate and we generated 20 independent and identically distributed noise realizations for each scenario. We simulated four different temporal sampling schemes, representing dynamic PET acquisition techniques defined as: “1 sec” scheme: [30 × 1 seconds, 30 × 2 seconds, 9 × 10 seconds]; “2 sec” scheme: [15 × 2 seconds, 12 × 5 seconds, 9 × 10 seconds]; “5 sec” scheme: [6 × 5 seconds, 6 × 10 seconds, 6 × 15 seconds]; “10 sec” scheme: [3 × 10 seconds, 3 × 20 seconds, 3 × 30 seconds]. For all these schemes, we shifted the start acquisition by zero, quarter, and half of the initial temporal window to simulate capturing different phase samplings of the TACs. We evaluated the axially distributed model estimates of flow for each simulated TAC. This exploration will provide the probability density function defining the variance and bias in estimates attributable to noise and temporal averaging.

In an identical simulation framework (same noise and temporal sampling variations), we simulated TACs using the three-compartment model for a nine states (F_p= [0.8, 1.6, 2.4] mL/g/minute × K₂ = [0.2, 0.4, 0.8]1/second). We evaluated the three-compartment model estimates of flow for these simulated TACs.

This analysis is based solely on the premise that the underlying model is perfect, and only assesses the sensitivity to noise and temporal sampling distortion. This ignores issues of model validity, and also fails to address other issues such as the effects of spillover, choice of site of input function, and error in other parameters not freed in the optimization.

RESULTS

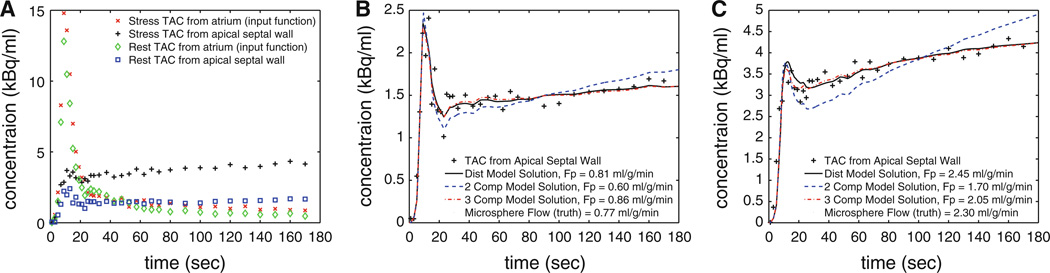
TACs for the input function and for each of the 17 segments in the LV myocardium were extracted. The MBF was estimated for each segment and compared with the corresponding microsphere estimate of flow. Examples of TACs are presented in Figure 3 for an apical septal wall segment at rest and stress state. The early contribution of spillover of right ventricular activity is apparent in these TACs. The model solutions for each of the three models are plotted. This example is representative of the trend that the distributed model and three-compartment model provide better flow estimates and fitted solutions than the two-compartment model.

Figure 3.

Examples of TACs for measured data for rest and stress study (A), with zoomed views of one of 17 segments of the myocardium for rest (B) and stress (C) states. The model solutions for the two-compartment, three-compartment, and distributed model are presented with the optimal flow estimate.

Tables 2 and 3 summarize the flow estimates for the 9 rest studies and 10 stress studies for each of the models. The microsphere flow estimates along with the model estimates are listed showing generally good agreement for each study. The root mean square error between the TAC generated from the model solutions and the measured TAC (RMSE fit) is listed to compare the goodness of fit of the model and the data. On average across all segments for rest and stress studies, the distributed model provided model solutions with a RMSE 34% lower than the three-compartment model and 52% lower than the two-compartment model. Based on a two-sided t test, the error of the fit with the distributed model was significantly lower than both of the compartmental models (P < .0001).

Table 2.

Rest flow estimates and RMSE of model solutions compared with measured TACs (mean ± standard deviation presented)

Subject/ study		Microsphere flow (mL/g/ minute)	Distributed		Two-compartment		Three-compartment
			Flow (mL/g/ minute)	RMSE flt (kBq/mL)	Flow (mL/g/ minute)	RMSE flt (kBq/mL)	Flow (mL/g/ minute)	RMSE flt (kBq/mL)
1	R1	0.71 ± 0.08	0.75 ±0.12	0.12 ±0.07	0.69 ±0.12	0.21 ± 0.08	0.93 ±0.13	0.20 ± 0.08
1	R2	1.69 ±0.15	1.76 ±0.31	0.11 ±0.04	1.82 ±0.28	0.23 ± 0.09	2.11 ±0.27	0.18 ±0.10
2	R1	0.56 ±0.10	0.64 ± 0.08	0.24 ±0.10	0.51 ± 0.05	0.40 ±0.14	0.72 ±0.10	0.37 ± 0.14
3	R1	0.67 ± 0.08	0.66 ± 0.08	0.11 ±0.04	0.55 ± 0.05	0.17 ± 0.05	0.75 ± 0.09	0.16 ±0.06
3	R2	1.79 ±0.18	0.96 ±0.15	0.16 ±0.03	0.69 ± 0.08	0.29 ± 0.04	0.96 ±0.11	0.25 ± 0.05
4	R1	1.67 ± 0.14	1.17 ±0.29	0.09 ± 0.06	1.31 ±0.41	0.13 ± 0.06	1.54 ± 0.49	0.13 ±0.06
4	R2	1.60 ±0.18	1.53 ±0.17	0.05 ± 0.02	1.28 ±0.17	0.09 ± 0.03	1.60 ±0.16	0.06 ± 0.03
5	R1	1.04 ± 0.20	1.01 ±0.12	0.05 ± 0.01	0.83 ±0.10	0.09 ± 0.02	1.06 ±0.10	0.07 ± 0.02
5	R2	3.44 ± 0.64	4.05 ± 0.31	0.06 ± 0.02	2.31 ± 0.24	0.18 ± 0.03	2.98 ± 0.24	0.10 ±0.03
Combined		1.37 ±0.89	1.27 ± 1.02	0.12 ±0.09	0.97 ± 0.59	0.22 ±0.12	1.25 ± 0.73	0.19 ±0.12

Table 3.

Stress flow estimates and RMSE of model solutions compared with measured TACs (mean ± standard deviation presented)

Subject/ study		Microsphere flow (mL/g/ minute)	Distributed		Two-compartment		Three-compartment
			Flow (mL/g/ minute)	RMSE flt (kBq/mL)	Flow (mL/g/ minute)	RMSE flt (kBq/mL)	Flow (mL/g/ minute)	RMSE flt (kBq/mL)
1	S1	1.93 ±0.23	3.16 ±0.80	0.15 ±0.09	1.72 ± 0.27	0.41 ±0.13	2.52 ± 0.30	0.28 ±0.18
1	S2	1.18 ± 0.54	1.09 ±0.55	0.17 ± 0.14	1.16 ±0.59	0.29 ±0.18	1.47 ± 0.53	0.26 ±0.17
2	S1	2.23 ±0.19	2.61 ± 0.22	0.19 ±0.05	2.36 ± 0.21	0.45 ± 0.05	2.39 ±0.14	0.24 ± 0.07
2	S2	2.46 ± 0.27	3.16 ±0.41	0.17 ± 0.04	2.09 ± 0.25	0.52 ± 0.07	2.43 ± 0.22	0.22 ± 0.06
3	S1	2.44 ± 0.20	2.20 ± 0.27	0.21 ±0.10	1.69 ±0.15	0.43 ±0.10	1.97 ±0.18	0.31 ±0.13
3	S2	2.26 ± 0.25	2.17 ±0.31	0.20 ± 0.08	2.12 ±0.19	0.42 ±0.17	2.29 ± 0.22	0.31 ±0.18
4	S1	2.18 ±0.20	1.54 ± 0.20	0.06 ± 0.04	1.46 ±0.18	0.13 ± 0.06	1.66 ± 0.24	0.11 ±0.07
4	S2	2.37 ± 0.40	1.74 ±0.32	0.10 ±0.06	1.76 ±0.35	0.19 ± 0.09	1.90 ±0.31	0.17 ±0.10
5	S1	1.99 ±0.43	1.83 ±0.28	0.07 ± 0.04	2.06 ± 0.69	0.14 ± 0.07	2.11 ±0.58	0.12 ±0.07
5	S2	1.85 ±0.83	2.65 ± 1.23	0.04 ± 0.01	1.66 ±0.61	0.11 ± 0.02	2.20 ± 0.68	0.06 ± 0.02
Combined		2.19 ±0.43	2.34 ± 0.78	0.13 ±0.09	1.88 ±0.29	0.31 ± 0.17	2.16 ±0.28	0.20 ± 0.09

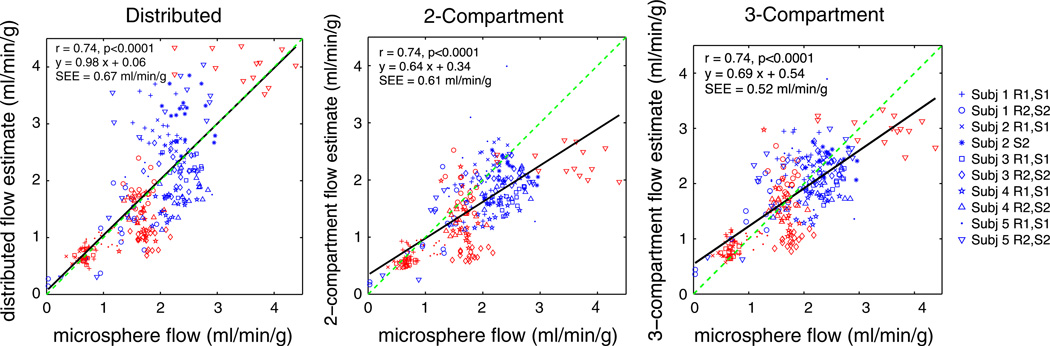
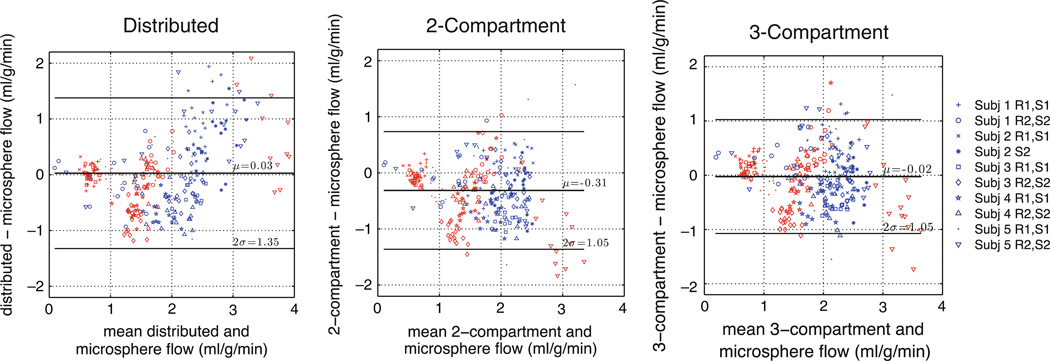
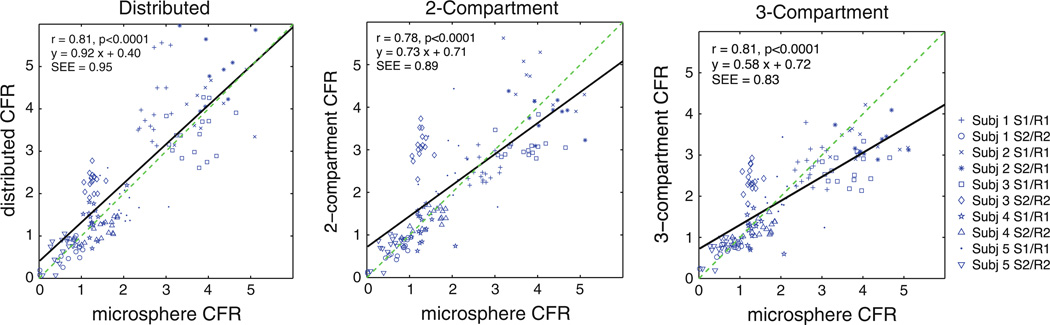
Figures 4 and 5 present comparisons of model flow estimates and microsphere values. In these plots, estimates from each of the 10 different rest/stress imaging studies performed in five dogs are plotted with a different marker. In Figure 4, estimates from all the three models had significant correlation (r = 0.74, P < .001) with the microsphere estimates, which serve as the reference standard. The distributed model provided estimates with a slope of 0.98 [95% confidence interval: 0.88, 1.08]. The slopes of the estimates from two- and three-compartment models are significantly lower than the distributed model and are significantly lower than 1 (P < .0001). Figure 5 presents Bland-Altman plots to evaluate the difference between the estimates and the microspheres. The distributed model provided flow estimates with a mean error of 0.03 ± 0.04 mL/g/minute with respect to microspheres. A paired t test of the error of the estimates suggests that there is sufficient evidence of a real difference in error between the distributed and two-compartment estimates (P < .0001) and insufficient evidence of a statistically significant difference between the distributed and three-compartment model (P = .09). The variance of the errors from the distributed model is 1.7 [1.3, 2.1] times higher than the the compartmental models (95% confidence intervals presented in brackets).

Figure 4.

Blood flow estimates from ammonia studies versus microspheres, “truth,” for three different modeling approaches. Each marker represents one of 17 segments in myocardium. Red markers from rest study and blue from stress study.

Figure 5.

Bland-Altman plots of blood flow estimates from PET and microspheres for three different modeling approaches. Each marker for one of 17 segments of myocardium. Red markers from rest study and blue from stress study.

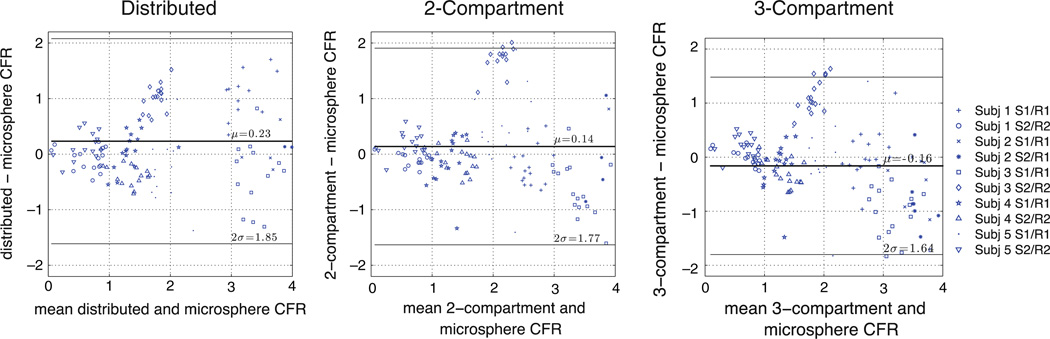
Figure 6 plots the coronary flow reserve (CFR, stress estimate divided by rest estimate) for each of the 10 rest/stress studies. Again, all models provide flow estimates with significant correlation with those from microspheres (r > 0.78, P < .001). The compartmental estimates had slopes significantly lower than 1 (P < .0001), while there is not sufficient evidence to suggest that the distributed estimates were different from 1. Figure 7 contains the Bland-Altman plots for CFR.

Figure 6.

CFR estimates from ammonia studies versus microsphere estimates, “truth,” for three different modeling approaches. Each marker represents one of 17 segments in myocardium.

Figure 7.

Bland-Altman plots of CFR estimates from PET and microsphere values for three different modeling approaches. Each marker represents one of 17 segments in myocardium.

The performance of the models compared to microspheres is summarized in Table 4. This table lists the relative dispersion (standard deviation/mean) of the flow estimates in normal regions. Normal regions are defined as all segments in the rest studies and all segments from the non-occluded stress studies. There is not sufficient evidence to suggest that there is a real difference in the dispersion of the estimates from the distributed model versus the microsphere data or the other model approaches.

Table 4.

Summary of MBF and CFR estimation performance

	Microsphere	Distributed	Two- compartment	Three- compartment
Relative dispersion in normal regions	13%	14%	16%	13%
RMSE model solution (kBq/mL)		0.125 ± .005	0.26 ± .01*	0.19 ± .008*
Blood flow estimation
Mean of error# (mL/g/minute)		0.03 ± 0.04	−0.31 ±0.03*	−0.03 ± 0.03
Standard deviation of error (mL/g/minute)		0.67	0.52*	0.53*
Slope of regression		0.98 [0.88, 1.08]	0.64 [0.57, 0.71]*	0.69 [0.62, 0.76]*
Correlation coefficient		0.74	0.74	0.74
Blood flow SEE (mL/g/minute)		0.67	0.61	0.52
CFR estimation
Mean of error*		0.23 ± 0.08	0.14 ± 0.07*	0.16 ±0.07
Standard deviation of error		0.92	0.88	0.82
Slope of regression		0.92 [0.81, 1.03]	0.73 [0.63, 0.82]*	0.58 10.52, 0.65]*
Correlation coefficient		0.81	0.78	0.81
CFR SEE		0.95	0.89	0.83

^*Significant difference between distributed metric and compartment metric.

^#Mean ± standard error of mean presented.

Table 4 summarizes population statistics from this analysis. The mean and standard deviation of the error in flow estimates are defined as the mean and s.d. of residuals between estimated flow and microsphere flow. The standard error of the estimates (SEE) is the s.d. about the regression line for estimated flow versus microsphere flow.

Noise Analysis

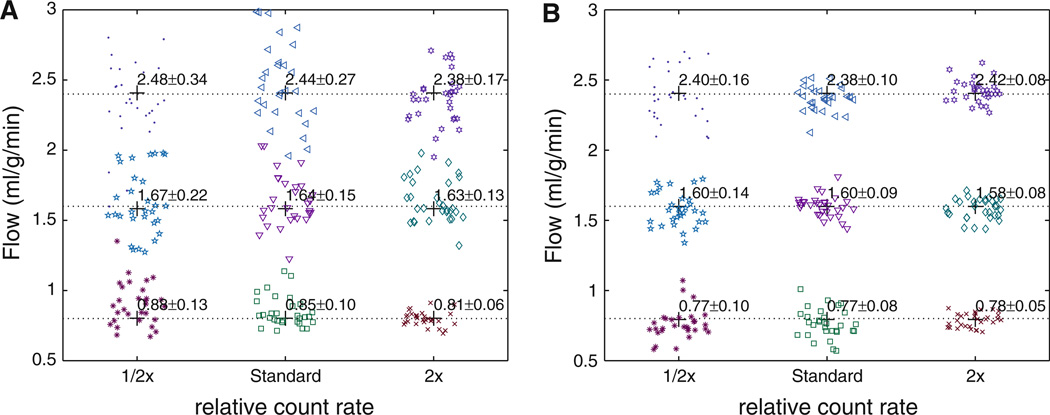
Representative flow estimates from a portion of the simulated results are presented in Figure 8 for the “2 sec” temporal sampling scheme. The noise and temporally averaged sampling resulted in substantial variance in the flow estimates but only minor bias. We did not test flow estimation by fitting one model to the test sets created from the other. Each model is tested only against itself, with the noise levels being the same. The noise has more effect on the model solutions with the higher frequency content, namely, the distributed model as it has higher sharper peaks than the lumped compartmental model. Noise caused less variance in the compartment model flow estimates (average variance = 0.09) than in the axially distributed flow estimates (variance = 0.15) under identical conditions.

Figure 8.

Summary of portion of simulated noise analysis results demonstrating flow estimates derived from distributed model (A) and three-compartment model (B). Presents parameter estimation errors for solely the error introduced by noise levels and limited temporal resolution (assumes model is perfect in the mean). Model solutions were evaluated for three flow states (flow = 0.8, 1.6, 2.4 mL/g/minute) for several count rates. Noise causes greater variance in distributed model estimates than in the compartmental model estimates (markers plotted with horizontal jitter for visualization).

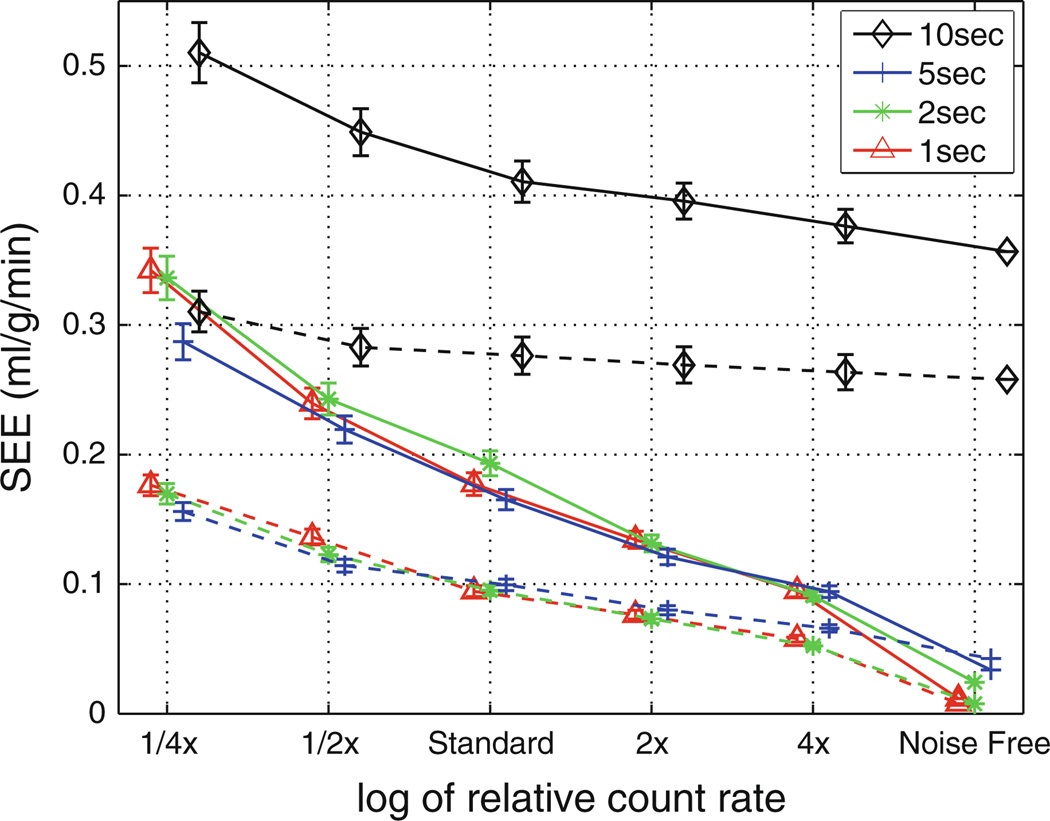
Figure 9 summarizes the results for over 20,000 TACs (representing multiple flow states, noise realizations, and sampling schemes) reporting the standard error of the estimates introduced by noise and temporal averaging. For a fixed count rate and using the same model, there is no significant difference in errors for the 1, 2, 5 seconds sampling schemes. The axially distributed flow estimates had errors approximately two times larger than the compartment model.

Figure 9.

Standard error of the flow estimates derived from simulated noise analysis versus relative count rates for both the axially distributed model (solid lines) and three-compartment model (dashed lines). Temporal sampling schemes based on initial 1, 2, 5, and 10 second sampling are presented demonstrating that overall count rate has a larger impact on error than sampling choices (when sampling is 5 seconds or shorter) (markers are presented slightly horizontally displaced from each other for visualization).

DISCUSSION

The proposed axially distributed model provided accurate estimates of MBF. The estimates had a mean error of 0.03 ± 0.04 mL/g/minute compared with the microsphere values. There were a few subjects where the distributed model incorrectly estimated flow; for example, for both stress studies for subject 2, the estimated flow values were higher than the microsphere values. In these studies, the model provided a solution with a good fit to the data (RMSE < 0.19 kBq/mL). The error in estimated flow is likely due to the use of a fairly simple global partial volume correction technique; in this study, we assumed a global correction factor. Specifically, we assumed that all myocardial TACs were 0.75 lower than the input function TAC due solely to partial volume effects (this is based on average dimension difference of the atrial cavity and myocardial thickness). On average, this factor led to unbiased estimates, but it fails in some instances.

The comparison of methods revealed that all the three methods provided flow estimates that were strongly correlated with the microsphere data (r > 0.74). The standard error of the blood flow estimates with the distributed model was slightly greater than the other two methods (0.67 vs 0.52 mL/g/minute), suggesting that the distributed model performs worse in mean square error. On the other hand, the regression line for individual flow estimates with the distributed model had a slope closer to 1 (m = 0.98) than the two-compartment (m = 0.64) and the three-compartment model (m = 0.69) demonstrating more accuracy. Likewise, the distributed model provided CFR estimates that were more accurate with respect to the regression versus microsphere-based estimates. These results suggest that the distributed model is less likely to underestimate flow at high flow states than the conventional compartmental models.

Finally, the distributed model provided estimates with similar dispersion around the myocardium in normal regions (dispersion = 14%) as the two-compartment (16%) and three-compartment methods (13%). The observed dispersion is similar to other myocardial flow evaluations of similarly sized myocardial segments (2.0 ± 0.7 g). Previous studies evaluating myocardial flow heterogeneity between 2 g samples of myocardium from three species estimate an inherent flow dispersion of approximately 13%.¹⁸ This inherent dispersion, in addition to dispersion from measurement error, leads to the observed dispersion presented in Table 4.

The simulated noise analysis reveals that the error introduced solely by noise and temporal sampling is roughly two times greater when using the axially distributed model compared to the three-compartment model. This suggests that the contribution of PET noise to the axially distributed model to microsphere standard error (0.68 mL/g/minute) is greater than to the three-compartment model standard error (0.52 mL/g/minute) as presented in Table 4. Several factors, including (1) PET image noise, (2) PET image bias, and (3) model flaws, contribute to the error in flow estimates. Considering the microsphere axially distributed SEE is only ~ 30% greater the three-compartment, it is reasonable to infer that its model flaws are less than the three-compartment method. That said, with the count rates used in this animal validation study the negative impact of noise exceeds the value of the more correct axially distributed model, in terms of standard error.

A motivation for this study was to use a more physiologically realistic model with the potential for more accurate estimates of flow. The results demonstrate that this model led to flow estimates that are on average slightly more accurate than the three-compartment model, but with increased variance. This model offers a general methodology for estimating blood-tissue exchanges for multiple species. Therefore, it may be advantageous for scenarios with significantly less noise or for other tracers with more complicated kinetics, such as the F perfusion tracers.

LIMITATIONS

This study did not apply several additional enhancements that could further improve the accuracy of estimates. We did not apply metabolite correction to account for primarily urea and glutamine contamination in the input function. We anticipate this to be a small effect considering we only estimate based on the first 3 minute post-injection and during this time frame >70% of the ¹³N in the blood pool remains as ammonia in dogs and an even greater percentage remains in humans. Studies correcting for metabolites using only the first 2–3 minutes of dynamic data have shown minor changes in estimates.²¹

Furthermore, we assume a global recovery coefficient of 0.75 to account for resolution loss. This oversimplification could be improved by applying a regional correction for resolution loss based on estimates of myocardial thickness and variable resolution in reoriented images.^22,23 In addition, we did not incorporate other improved processing methods such as a regional spillover term to account for potential spillover from the right ventricle.

Previous Comparison Studies

Previous efforts have compared models for estimating blood flow with NH3. Choi et al¹² compared numerous estimation techniques including compartmental models, graphical analysis, and simple uptake measures. They concluded that “method 2” is the preferred method for analysis, motivating our implementation of their method 2 as our two-compartment model. In addition, our three-compartment is similar to “method 3” from Choi. Our implementation of method 3 differed from Choi in that we only estimate based on the initial 3 minutes as opposed to 10 minutes in Choi. As admitted by the authors, the longer TAC may lead to inaccuracies in estimates due to subject motion, contamination of the input function by 13 N metabolites, and changes in MBF during the acquisition. With this potential bias in Choi’s analysis of the three-compartment model, in general our results confirm that the 2- and three-compartment models are well correlated with microsphere data and both are viable methods for blood flow estimation.

In a similar study, Khorsand et al²⁴ demonstrated the use of the two- and three-compartment models in human studies. They showed that the methods provide estimates that are well correlated with each other, but that the actual estimates differ significantly depending on the method. In their study, they used different regions of interest for each approach and applied different interpretations of the spillover correction factor. In brief, they used thin (4 mm width) centered myocardial ROIs for the two-compartment model and thick (>10 mm) ROIs with some cavity signal for the three-compartment model. This difference leaves open the question of whether differences in estimates are due to the number of compartments and free-parameters, or more to the differences in spillover interpretation.

In our study, we attempted to keep processing issues identical for each method to ensure a more fair comparison of strictly the model of the blood-tissue kinetics. Unlike the Choi paper, we choose to use identical TACs for all methods. Unlike the Khorsand paper, we used the same ROIs for all methods and implemented the geometric correction factor interpretation of the spillover term for the compartmental models. Our study shows that the three-compartment model provides better model solutions (lower RMSE fit), lower mean error of flow estimates, and lower standard error of its estimates than the two-compartment model.

CONCLUSION

We proposed and evaluated a two-region axially distributed model for quantitative estimation of blood flow. The proposed method provided accurate estimates of flow that were strongly correlated with microsphere values. The comparison of this method with the established approaches of the two-compartment and three-compartment model reveals that it provides model solutions with lower RMSE with the measured TACs. The proposed model provided flow estimates with slightly better accuracy and worse precision than the 2- and three-compartment models. Noise analysis demonstrates that image noise has a more detrimental impact on flow estimates from the distributed model than the three-compartmental model. The flexibility of the proposed model may be advantageous for perfusion tracers with more complicated kinetics or significantly less noise.

APPENDIX.

Axially Distributed Model

The input function TAC was taken from a region of interest in the left atrium. In order to account for the delay from this site and the coronary arterial inflow to the individual ROI, the tracer traversed a dispersive convective tube of length L_z given by

$$\frac{V_{\text{cav}}\partial C_{\text{N,cav}}}{\partial t}=-F_p{L}_z\frac{\partial C_{\text{N,cav}}}{\partial z}+V_{\text{cav}}{D}_{\text{cav}}\frac{{\partial }^2{C}_{\text{N,cav}}}{\partial z^2}.$$

This relationship allows for a finite time for passage from the input function ROI (the first term on the right) and realistic dispersion of the signal (the second term) and is optimized for each blood flow estimate by estimating F_p and V_cav. The initial condition for the concentration in the unit is zero. The boundary condition at the outflow is simple reflection so there is no diffusion into the outflow, only convection, ∂C_N,cav/∂z = 0, and C_out = C_N,cav(z = L). At the inflow, the boundary condition is such that the diffusion upstream and the convection downstream are matched: F_pL · (C_in − C_N,cav)/V_lv + D_cav · ∂C_N,cav/∂z = 0, where C_in, is the input function.

The major components for the two-region unit are represented graphically in Figure 2. The regional concentrations of ¹³N-NH₃ and ¹³N-glutamine in the plasma are each defined in terms of mol/mL and are functions of capillary axial position, x, and of time, t. For example, the partial differential equation for the concentration of NH₃ in the plasma, C_N,p, is

$$\frac{V_{\mathrm{p}}\partial C_{\text{N,p}}}{\partial t}=-F_{p}L\frac{\partial C_{\text{N,p}}}{\partial x}+{\text{PS}}_{\mathrm{N}}(C_{\text{N,m}}-C_{\text{N,P}})+V_{\mathrm{p}}{D}_{\mathrm{p}}\frac{{\partial }^2{C}_{\text{N,p}}}{\partial x^2}$$ (2)

and for NH₃ in the myocyte, C_N,m, is

$$\frac{V_{\mathrm{m}}\partial C_{\text{N,m}}}{\partial t}={\text{PS}}_{\mathrm{N}}(C_{\text{N,p}}-C_{\text{N,m}})-G{C}_{\text{N,m}}+V_{\mathrm{m}}{D}_{\mathrm{m}}\frac{{\partial }^2{C}_{\text{N,m}}}{\partial x^2}$$

The boundary conditions in the capillary are analogous to those in the delay line above, and in the tissue are reflecting boundaries at x = 0 and x = L. The concentration of glutamine in the plasma and myocyte follows similar governing equations as (1) and (2) and for trapped glutamate in the myocyte as (2). The plasma region has the known initial boundary condition of the input function, C_N,cav(z = L) and the output boundary condition of C_out. The total ¹³N-ammonia in a region of interest at any given time, t, is measured in mol/g as

$$Q_{\text{tot}}=V_{\mathrm{p}}\underset{0}{\overset{L}{\int }}(C_{\text{N,p}}+C_{\text{MI,p}})\mathrm{d}x+V_{\mathrm{m}}\underset{0}{\overset{L}{\int }}(C_{\text{N,m}}+C_{\text{MI,m}}+C_{\text{MA,m}})\mathrm{d}x+\text{spill}\times C_{\text{N,lvout}},$$

where spill (mL/g) is the fraction of the delayed input function that has spilled over into the myocardial ROI. This model is available for download and independent testing at http://www.physiome.org/jsim/.