Flowing Gas in Mass Spectrometer: Method for Characterization and Impact on Ion Processing

Abstract

Mass spectrometers are complex instrumentation systems with ions transferred though different pressure regions and mass analyzed at high vacuum. In this work, we have investigated the impacts of the gas flows that exit almost universally in all pressure regions and developed a method incorporating the dynamic gas field with the electric (E) field in the simulation of ion trajectories. The capability of the electro-hydrodynamic simulation (EHS) method was demonstrated for characterizing the ion optical systems in atmospheric pressure interfaces. With experimental validation, the trapping of the externally-injected ions in a linear ion trap at low pressure has also been studied. Further development of the EHS method and the knowledge acquired in this research are expected to be useful in the design of hybrid instruments and study of ion energetics.

Introduction

Mass spectrometers (MS) are complex instrumentation systems, largely due to the need to perform the mass analysis in vacuum and the restrict conditions required for obtaining good resolution and accuracy. The mass analysis is highly dependent on the ion trajectories and the role of electromagnetic field has been well understood. The theoretical modeling and numeric simulation of the effects associated with the electromagnetic field is also very mutual and frequently used in assistance to the instrument design and optimization.^1–7 The role of the gas field, however, is much more complicated. The collisions between the ions and background gas molecules put an adverse effect to the performance of mass analyzers such as sectors, ⁸ time-of-flight (TOF),⁹ ion cyclotron resonance (ICR)¹⁰ and orbitrap;¹¹ the cooling effect by collisions, however, is effectively used for ion trap to achieve high resolution and high mass accuracy.¹² Static gas field is typically assumed, with a molecular flow model, in the studies for ion trap, which provides relatively accurate results if an even distributions of gas density are maintained with no bulk gas flow at pressures of several millitorrs or lower. In practical implementation, a damping factor was used in the theoretical modeling ^13–15 and the Monte Carlo method were used for the simulations, as in SIMION,^16–19 ITSIM,^20–23 and other home written programs.^{24, 25}

In real cases of mass spectrometers, dynamic gas fields exist across almost all pressure ranges. For example, in an atmosphere pressure interface (API) typically used for introducing ions from atmospheric pressure ^26–28 or ambient ionization sources,^29–31 there is a significant pressure drop from 760 torr to several millitorrs. The gas dynamic features of the ion optics have a huge impact on the ion transfer efficiency.^{32, 33} The development of the simulations for the transition pressure regions is of an increasing interest.^{34, 35} The impact by the dynamic gas fields at lower pressure ranges (< 1 mtorr), however, is much less recognized and poorly characterized or understood. This is mainly due to the difficulty in experimental characterization and the lack of effective modeling or simulation methods incorporating the effects by both the electric and the dynamic gas fields. The dynamic gas fields are expected in the instrument whenever the ions need to be transferred between two regions at different pressures. This is often seen in the hybrid instruments such as LTQ Velos,³⁶ LTQ-Orbitrap (Thermo Scientific, San Jose, CA),^{37, 38} QTrap,³⁹ and QStar (AB Sciex, Concord, Canada),^{40, 41} etc. The recent development of the Fusion (Thermo Scientific)⁴² represents a trend of performing highly multiplex ion processing using a single instrument. The ions are transferred through different paths with multiple mass analyzers at various pressures. The transfer efficiency is critical for the overall sensitivity. The understanding of the impacts by the dynamic gas fields at lower pressures (< 1 mtorr) on both ion transfer and mass analysis is very important for the instrument development.

In a previous study,³⁴ we have shown that the dynamic gas fields could be simulated using the direct simulation Monte Carlo (DSMC) method.⁴³ It was demonstrated by characterizing the gas flows through the transition pressure range (e.g. from 1 torr to 1 mtorr) as well as the gas expansion starting at 10⁻⁵ torr with the discontinuous atmospheric pressure interface.^{44, 45} In the current study, we have developed a method to incorporate both the electric (E-) and dynamic gas (hydrodynamic, H) fields for the numeric simulation of the ion trajectory. Here we describe this E-H simulation method and demonstrate it for characterizing the ion transfers through a simple Einzel lens with only DC field as well as through more complicated ion optics involving rf ion guide in a transition pressure region of an API. Moreover, we report a study on the transfer of ions into a linear ion trap with the consideration of a dynamic gas field with the E-H simulations validated by experimental characterization. This type of studies otherwise could not be done with other methods using static flow models.

Theory and Method

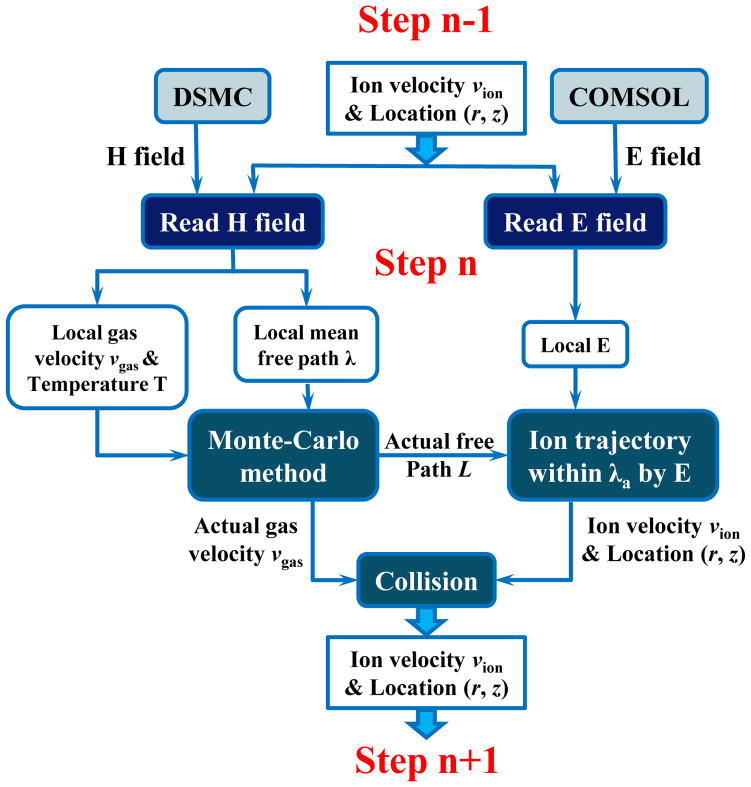
The general procedure to perform the EHS is described with the flowchart in Figure 1. For each step of the trajectory simulation, a collision-free ion motion under electric field was simulated followed by a modification of the ion velocity due to a collision. The local electric field of each step was extracted from the field solved using COMSOL (ver. 4.3a, COMSOL AB, Stockholm, Sweden) and the collision-free distance was calculated based on the collision probability extracted from the hydrodynamic field, which was solved using DSMC (DS2V program, developed by Dr. Bird, Dept. of Aerospace Engineering, University of Sydney, Australia). A simulation program was written using Fortran 90 (IBM, Armonk, NY) to perform EHS simulation of ion trajectories. A conventional hard-sphere ion-neutral collision model⁴³ was used for the subsequent collision that modify the ion velocity at the end of a collision-free motion.

Figure 1.

Illustration of combining the dynamic gas (H) field and the electric (E) for ion trajectory simulation.

For extraction of the local electric field strength, the E field solved by COMSOL was divided equally (typically, 0.1 mm) for sampling. The dynamic gas field simulated by DSMC was also equally divided for extracting the parameters including pressure, temperature, number density, velocity, and the mean free path. The initial conditions of the ions were set based on the properties of the local gas flow, which was also extracted from the simulated H field. The number of simulated ions in each grid cell was proportional to the local number density of the gas. The velocity distribution of these ions is a function of gas temperature and velocity, known as Maxwell distribution:⁴³

$$f(v_i)=\sqrt{\frac{m}{2\pi k_{b}T}}exp\left[\frac{-m{(v_i-v_{i0})}^2}{2k_{b}T}\right](i=x,yorz)$$ (1)

where ν_i and ν_i0 are the velocity of the ion and the bulk velocity of the gas field in the x, y or z direction, respectively. T is gas temperature, m is the mass of the ion, k_b is Boltzmann constant.

From the gas hydrodynamic simulation, the actual collision-free path, L, can be derived from the mean free path of the ion, λ_ion (see Eq. S13 in Supporting Information):

$$L=-{\lambda }_{\text{ion}}ln({\alpha }_1)$$ (2)

where α₁ is a random number uniformly distributed from 0 to 1. Within a distance of L, the ion can be assumed to have a collision-free motion guided only by the electric field.^{12, 46, 47} Subsequently, an ion-neutral collision occurs, and the actual velocity of the gas molecule at the collision is sampled using the Eq. 1. The velocity vector of the ion modified by the collision can then be used for the collision-free motion under electric field in the next step of the simulation.^{16–25, 43} These steps were repeated to produce an ion trajectory within a specified time. See the Supporting Information for more details about the EHS method.

Results and Discussions

The principle for the EHS method, in theory, should be applicable for simulations of ion trajectories at all pressure ranges; however, the computational burden of EHS is nearly proportional to the number of ion-neutral collisions, which makes it difficult to use at high pressures. In the study reported here, we applied the EHS method for the transitional pressure range (1 mtorr to 1 torr), such as the first and second differential pressure range in a typically atmospheric pressure interface. We also used it with low pressures that are suitable for mass analyzers (several millitorrs or lower) and demonstrated a difference from the methods using static molecular flow models.

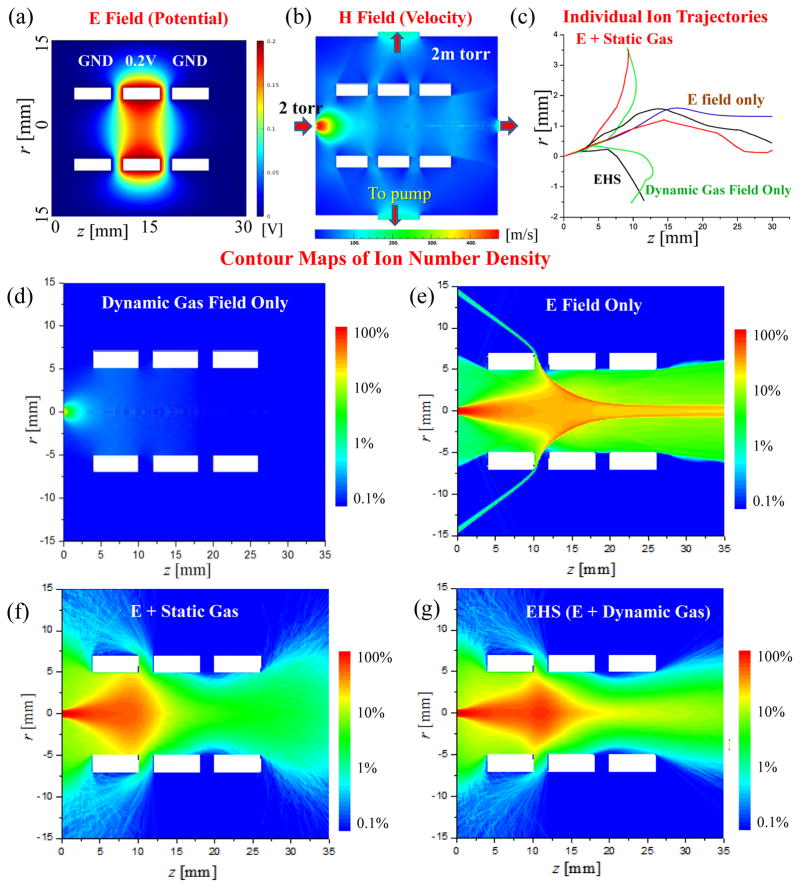
For a simple demonstration and illustration purpose, a simulation was performed using the EHS method for the ion transfer through a dynamic gas field with DC potentials implemented by an Einzel lens system. As shown in Figure 2a, the Einzel lens was located right after a pinhole between two differential pumping stages at 2 torr and 2 mtorr, respectively. The radius of the pinhole inlet was 0.5 mm. The radius and the thickness of each of the three ring electrodes were 5mm and 6 mm, respectively, with a gap of 2 mm between each two. When ions were transferred through the pinhole, their trajectories were under influence of both the DC electric field (Figure 2a) by the Einzel lens and the gas flow expansion (Figure 2b). The DC voltage applied on the center lens was chosen as 0.2 V to make the electric effect comparable with the possible impact by the gas expansion. The kinetic energy E_k of an ion m/z 200 injecting through the pinhole, was estimated based on the surrounding gas molecules and was in the vicinity of 0.2eV by

Figure 2.

Contour maps of (a) electric potential and (b) gas flow speed for a 2 mtorr region with an Eizel lens. (c) Individual ion trajectories simulated with (i) only dynamic gas field, (ii) only electric field, (iii) electric field with static gas field and (iv) electric field with dynamic gas field. Contour maps of ion distribution with ion injection for 0.1 ms at a flux of 10¹³/s, simulates with (d) only dynamic gas field, (e) only electric field, (f) electric field with static gas field and (g) electric field with dynamic gas field.

$$E_k=\frac{1}{2}{mv}^2$$ (3)

where ν was the maximum flow speed, which was about 480 m/s based on the DSMC simulation (Figure 2b).

For the EHS, the physical space was divided into 0.1 mm×0.1mm grid cells, for which the electric field strength was extracted from the simulated E field and the gas pressure, temperature, number density, mean free path and velocity were extracted from the simulated H field. Figure 2c shows the individual trajectories simulated for one ion m/z 200 under different combinations of the E and gas fields. The ion was placed at the center of the pinhole, entering the Einzel lenses with an initial axial velocity v_z= 400 m/s and an initial radial velocity v_r=30 m/s. The total simulation time was 0.1 ms with a time step at 10⁻⁸ s for the Runge-Kutta method,^46–48 which was much shorter than the mean free time (Figure 2S and 3S in Supporting Information). The combinations of the fields included (i) dynamic gas field only, (ii) E field only, (iii) E field with static gas field, or (iv) E field with hydrodynamic gas field. Multiple simulations were performed to generate individual ion trajectories for each of the cases. As expected, reproducible trajectories could only be observed with the “electric field only”, while some randomness was presented once the collision with gas molecules was considered in the simulation, regardless by static or dynamic gas field. This was due to the uncertainty in the collisions in real scenario which was modeled using the Monte Carlo methods to describe the possibility.

While the simulations of individual ion trajectory do not reveal the difference associated with the static and the dynamic gas fields, meaningful conclusions could be made based on the statistical results with simulation of trajectories for a large number of ions. Thereby simulations with 10⁹ ions were performed again for each of the cases, with these ions continuously entering the pinhole at a flux of 10¹³/s for 0.1 ms. The initial conditions of these ions were randomly selected based on the local gas flow field property as described in Theory and Method. The locations of all of 10⁹ ions at 0.1 ms were counted to calculate the densities in each grid cell that are shown with the contour maps in Figure 2d–g. If the ions had reached any electrodes or the boundary of the area, they were not counted for the intensity. These contour maps are snapshots of the distributions of ions at particular moments in dynamic systems.

As expected, the majority of the ions could not reach the other end of the Einzel lens if there was only a gas flow with an expansion but no electric field for the focusing (Figure 2d). It was also not a surprise to observe that the majority of the ions could be well transferred through the Einzel lens with a very weak electric field if there were no collisions with gas molecules (Figure 2e). When the collisions with a static background gas at 2 mTorr was considered and treated with Monte-Carlo method, in addition to the electric field effect, only very few ions could pass the Einzel lens (Figure 2f) under the DC field set. However, when the gas flow due to the expansion was considered with the H field used in the EHS, many more ions could pass through the Einzel lens (Figure 2g). In a real MS system, the gas expansion through a pinhole between 2 torr and 2 mtorr could result in a maximum flow speed over 400 m/s (Figure 2b). The bulk flow movement actually helps with the ion transfer in the case described here, which would not be characterized if a static gas flow model was used in the simulation.

Ion Transfer through Transitional Pressure Ranges

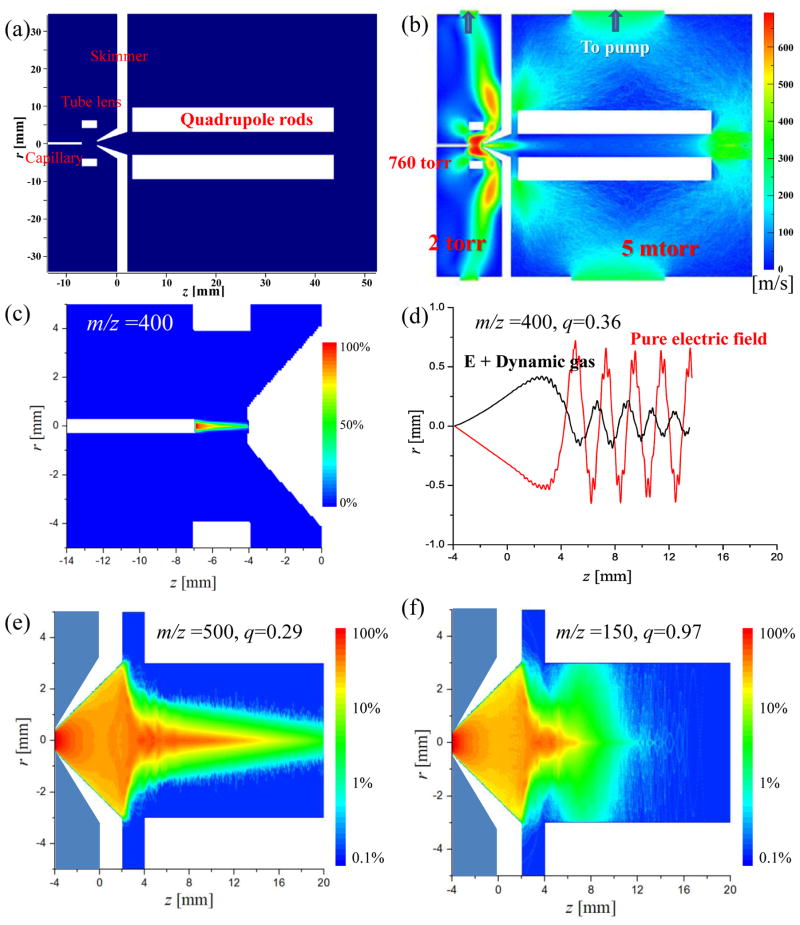
The EHS method has also been performed for an atmospheric pressure interface, which usually has differential pumping stages and with a skimmer separating the regions at several torrs and millitorrs in one of the popular implements shown in Figure 3a. The ions were introduced from 760 Torr to 2 Torr via a capillary and passed through a tube lens region and a skimmer into an rf-only quadrupole ion guide at 5 mTorr. The capillary i.d. was 0.6 mm, the height of the skimmer was 6.0 mm and the i.d. was 0.8 mm for the skimmer entrance hole and 6.0 mm for the outlet. The capillary and tube lens were applied with DC voltages of 25V and 35V, respectively, for the purpose of focusing the ions against the gas expansion. A dipolar rf of 300V_0-p with 1 MHz was applied on the quadrupole ion guide, which has a radius r₀ = 3 mm. The contour map for electric potential is shown in Figure 4S in Supporting Information. At capillary exit, the flow was choked at the local sound speed;⁴⁹ hence the initial gas pressure and speed were set as 380 torr and 317 m/s, respectively.³⁴ The contour map of the flow speed in the gas hydrodynamic field is shown in Figure 3b.

Figure 3.

(a) Schematic of an atmospheric pressure with a heated capillary, a tube lens, a skimmer and an rf ion guide for transferring ions from 760 torr to 2 torr and then to 2 mtorr. (b) Contour map of flow speed simulated for the dynamic gas field. (c) Contour map of ion distribution (ion flux 10¹⁶/s for 0.01 ms) simulated for the capillary-to-skimmer region. (d) Individual ion trajectories simulated with only electric field or electric field with dynamic gas flow. Contour maps of ion distribution (ion flux: 10¹³/s for 0.1 ms) in the rf-only quadrupole ion guide for (e) ions of m/z 500, q=0.29 and (f) ions of m/z 150, q=0.97.

The EHS method was used to simulate the ion trajectories from the capillary exit to the quadruple ion guide. The simulation results for the capillary-to-skimmer area are shown in Figure 3c. The grid size and the method for selecting the initial conditions of the ions were the same as described above. A total number of 10⁹ ions at m/z 400 with were injected at a flux rate of 10¹⁶/s from the capillary exit. The simulation time was 10⁻⁵ s with each time step 10⁻¹¹ s used in Runge-Kutta method. Due to the gas expansion (Figure 3b), ion transfer efficiency from the capillary exit to the skimmer aperture was only about 2.5% with the tube lens grounded.^{33, 50} This transfer efficiency were increased to about 50% with a focusing by the tube lens at 35V (Figure 3c).^{33, 35}

After the electric focusing of tube lens, ions were transferred from the skimmer to the rf-only quadrupole ion guide (Figure 3d–f). Simulation time of 0.1 ms and a time step of 10⁻⁸ s were used for the Runge-Kutta method. Figure 3d shows two simulated trajectories, one with and one without the consideration of the gas expansion, respectively, for a single ion of m/z 400 passing through the center of the skimmer hole with its initial velocity set by randomly samplings of the local gas dynamic field. The rf amplitude was set as 300 V, corresponding to a q = 0.36 stable (<0.907) for m/z 400. With only the electric field, the ion was shown to absorb the energy from the rf field and oscillate in the ion guide with a constant amplitude in the radial direction. With the dynamic gas flow, the oscillation motion was observed to be quickly damped due to the collisions with the surrounding gas molecules and the ion was cooled down to the center axis of the quadrupole ion guide.

In a real case, the radial velocity of an ion entering through skimmer could be significantly larger due to the gas expansion, which could cause a problem for trapping it in the x-y plane of the ion guide even with the damping by the collisions. The rf field enforced by the quadrupole ion guide also has major impact on the the complicated situation can now be comprehensively characterized using the EHS method. As an example, the simulation with ion m/z 500 and 150 (10⁹ of each) was then performed with an ion flux of 10¹³/s for a duration of 0.1 ms. The initial velocities of these ions were set by randomly sampling the local gas dynamic field at the entrance of the skimmer, covering the broad distribution of the velocities in the radial direction. Figure 3e and f show the contour maps of ion number density after 0.1 ms for ion m/z 500 and 150, respectively, at an rf voltage of 300 V. The q values for these two ions could be calculated using the Mathieu equation:¹²

$$q=\frac{4{\mathit{zeV}}_{rf}}{{mr}_0^2{\mathrm{\Omega }}^2}$$ (4)

where z is the charge number, e is the electron charge, m is the ion mass, V_rf is the amplitude of the dipolar rf applied to the quadrupole with a secular frequency Ω, and r₀ is nominal radius of the quadrupole. The q value was calculated as 0.29 for m/z 500 but 0.97 for m/z 150. Since the stability boundary is at q = 0.908,¹² the ions m/z 500 should be able to pass through the ion guide while ions m/z 150 should not. Based on the simulation, about 81% of ions m/z 500 could be transferred from the skimmer entrance to the end of the rf ion guide. As shown in Figure 3e, the axial speed of the ions decreased due to the collisions while the they were transferred along the ion guide, which resulted in much lower densities observed after z = 16 mm on the density contour map. For the ions of m/z 150, the ion density decreased much quickly after they entered the ion guide. This was due to a fast amplitude increase of the oscillating motion in radial direction by the excitation of the rf filed (Figure 3f).

Trapping Ions in Linear Ion Traps at Low Pressures

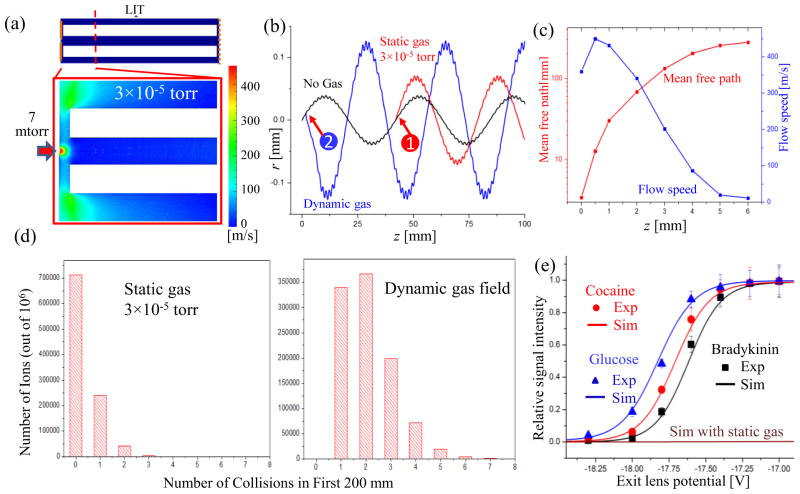
As discussed above, gas expansions exist at low pressures as well. In the previous studies of ion trapping and mass analysis using an quadrupole ion trap with an inside pressure several millitorrs ⁵¹ or lower,³⁹ the ion-neutral collisions were typically treated with the static molecular flow model. In this study using the EHS method with the dynamic gas field involved, we were able to characterize the effect due to the uneven distribution for background gas molecules on the ion transfer, trapping and mass analysis in a linear ion trap (LIT).² Figure 4a shows a case where ions are transferred from a region at 7 mtorr into a LIT at 3×10⁻⁵ torr with N₂ as the background gas (Figure 4a). The typical dimensions for the Q3 LIT in a commercial QTrap4000 mass spectrometer (AB SCIEX, Toronto, Canada)³⁹ were used for simulations, with a simplification of combining the stubby and the long rods⁵² into a single section. The quadrupole had a radius r₀ of 4.17 mm and a length of 200 mm. The entrance lens was 2 mm distant from the rf rods and had an aperture with a radius of 0.85 mm. The gap was 3 mm between the rf rods and the exit mesh lens, which was treated as a plate electrode for electric field solving but absent for gas field solving. The quadruple rods were floated at −23 V DC and a dipolar rf of 162 V at 1 MHz was applied for trapping (corresponding to a low mass cutoff, LMCO, of m/z 100). A DC voltage of −20 V was applied on the entrance lens.

Figure 4.

(a) Contour map of the flow speed simulated for the entrance region of the linear ion trap. (b) Trajectories of a single ion simulated with (i) only electric field, (ii) electric field with static gas field, collision at location “1” and (iii) electric field with dynamic gas field, collision at location “2”. (c) The mean free path and flow speed along the LIT center axis calculated based on the simulation as a function of the distance from the LIT entrance. (d) Number of ions vs. their collisions with gas molecules when they pass through the LIT, calculated based on static gas model (left) and the simulated dynamic gas field (right). (e) Relative abundances of the ions [Glucose + H]⁺, [Cocaine + H]⁺ and [Bradykinin + 3H]³⁺ passing through the exit lens, measured (Exp) or simulated (Sim) at different DC potentials applied on the exit lens.

Figure 4b shows three trajectories of an ion m/z 400, each simulated with a different consideration for the gas flow, viz. i) without background gas, ii) with static background gas at 3×10⁻⁵ torr, or iii) with dynamic gas flow from 7 mtorr to 3×10⁻⁵ torr. The ion entered the LIT with an initial velocity of 1200 m/s (3eV) in the z direction and 30 m/s in radial direction. The trajectory simulated without background gas represents the predicted path steered only by the electric field. With the existence of the gas molecules, the ion motion deviated from this path after the first collision with the gas molecule, as shown with the event 1 and 2 of the collisions in Figure 4b for the static gas and dynamic gas field, respectively. The ion-neutral collisions, with randomness for each individual event, play an important role for trapping the ions. A static DC potential well along the axial direction is topically used in LITs for trapping the ions in the z direction.² According to the conservation of energy, an ion entering the LIT would not be trapped in the z direction unless its kinetic energy is reduced, typically through collisions with the background gas molecules.¹⁹ As shown in Figure 4b, the kinetic energy of the ion in z direction was decreased after the collisions, which was necessary for the trapping of the ion in the z direction.

Although two random cases shown in Figure 4b indicated that collisions could occur with both static gas and dynamic flow, there is a significant difference in the probability of collision when considering a large number of ions for transferring and trapping in this LIT. The mean free path is longer than 200 mm at 3×10⁻⁵ torr, which means a very small probability of collision during the first path through the entire linear ion trap. In a real case, as long as the LIT is connected to a region at higher pressure (typically for collision induced dissociation), the local gas density in the area close the entrance to LIT is always higher and the mean free path can be significantly smaller. As shown in Fig 4c, the mean free path in a dynamic gas field could be calculated as a function of the z distance inside the LIT based on the gas dynamic field solved for the LIT. The mean free path could be as short as 0.5 mm at the entrance to the LIT, corresponding to a relatively high probability of collision.

In simulations for comparison between the static and dynamic flow model, a total number of 10⁶ ions m/z 400 with initial kinetic energy 3 eV were transferred into the LIT rf field and the number of collisions during the first 200 mm in z direction was counted for each ions and summarized as shown in Figure 4d. When static gas field was assumed, more than 70% of the ions did not experience any collisions; however, with the gas expansion modeled and used for the simulation, 100% of the ions had at least one collision and more than 65% of them had multiple collisions. This would explain why the linear ion traps located at low pressures in the QTrap 4000, LTQ Velos and Fusion could still have relatively high efficiency in trapping. As shown in Figure 4c, the majority of the collisions occurred in the first 6 mm, within the gas expansion. It is noteworthy that the radial velocity of the ions could also be significantly increased due to the collisions in a gas expansion (Fig 4b).

Simulations were further carried out with experimental verification using a QTrap 4000 for characterizing the kinetic energies of the ions after passing through the Q3 LIT. In the simulation, the ions with 3 eV kinetic energy at the entrance lens (at −20V) entered the Q3 LIT floated at −23V, and the exit lens voltage was varied while counting the number of ions reaching the exit lens. The assumption of 3 eV for the initial kinetic energy of the ions was made based on the experimental measurement, which will be further described later in this manuscript. In the experiment, the ions were first trapped and cooled in the Q2 floated at −17 V and the voltage on the Q3 entrance lens was then dropped from −12 V to −20V to allow the ions to enter the Q3 LIT. Same voltages of DC float (−23V) and rf were applied on the stubby and the main rods of Q3, to make it consistent with the single-section configuration used in the simulation (Figure 4a). The voltage on the Q3 exit lens was varied while the intensity of the ions passing through the exit lens was monitored by the ion detector. The simulations and experimental characterization were performed for three different ions, [Glucose + H]⁺ (m/z 181), [Cocaine + H]⁺ (m/z 304), and [Bradykinin + 3H]³⁺ (m/z 354), with the results shown in Figure 4e. A low mass cutoff of m/z 100 was used. The curves shown in Figure 4e profile the energy distributions of the ions when they reached the exit lens, which are dependent on the initial kinetic energies of the ions and the energy loss due to the collisions with the gas molecules.

In the experiments, the target ions were selected by Q1 filter, trapped and cooled in Q2, and then injected into the Q3 LIT by lowering the entrance lens voltage. The Q2 has a LINAC configuration,⁵³ which is known to push the ions toward the Q3, so the ions were assumed to be all trapped close to the Q3 entrance lens; thereby a relatively narrow kinetic energy distribution was assumed for them when entering the Q3 LIT. The experimental results (Figure 4e) showed that no ions could pass through the exit lens when its voltage was at −17, which was 3 V higher than the entrance lens; and a maximal transfer was achieved at −19 V, which was 1 V higher than the entrance lens. The difference in the ion kinetic energy for the ions reaching the Q3 exit lens was due to the number of collisions with the gas molecules during the journey between the entrance and the exit lens. The initial kinetic energy of the ions was therefore identified as 3 eV, which was retained for some of the ions that did not experience any collisions. A maximal loss of 1eV occurred to ions having a maximum number (7, according to the simulation, Figure 4d) of collisions.

The same initial kinetic energy of 3eV was also used in the simulations. The expansion flow was modeled and used in the EHS simulations of the ion trajectories while varying the DC potential on the Q3 exit lens. The simulated results for [Glucose + H]⁺ (m/z 181), [Cocaine + H]⁺ (m/z 304), and [Bradykinin + 3H]³⁺ (m/z 354) could then be plotted in Figure 4e. A relatively good agreement with the experimental results was observed. A curve was also simulated for transferring these ions in a static gas field at 3×10⁻⁵ torr (Figure 4e), which indicate that the majority of the ions would retain their initial kinetic energy.

The kinetic energy distractions after the collisions in Q3 LIT can be derived as shown in Figure 6S in Supporting Information, with the one for the bradykinin m/z 354 centered at a higher kinetic energy than the cocaine m/z 304 and glucose m/z 181. The higher molecular mass of the bradykinin ions resulted in a lower energy loss after each collision, but the number of collisions was not significantly different for ions within the mass range. This type of characterizations can now be performed with a relatively specific details using the EHS method incorporating the dynamic gas fields into the simulations of the ion trajectories, which otherwise would not be possible with the assumption of the static gas background.

Conclusion

The gas flows and expansions exist in mass spectrometers in different regions at a broad range of pressure. In addition to the dynamic gas fields recognized for the atmospheric pressure interfaces, the gas expansion at high vacuum can have a very significant impact on the ion transfer and mass analysis, which ultimately affect the sensitivity and the specificity of the chemical analysis. Including the dynamic gas field with the electric field in the direct simulation of the ion trajectories is a major step forward for performance characterization and optimization of the ion optics and mass analyzers. The local temperature and collision condition also become available in the simulation, which can be further developed for studying the change of the internal energy and dissociation of the charged particles when they are intake to and transferred in the mass spectrometers. This could be particular interesting for studying the desolvation process of the charged droplets. Important future developments would include the application of this method for simulations with a full pressure range up to atmospheric pressure and with consideration of space charge effects. Both of these efforts would call for good solutions⁵⁴ to overcome the computation burden associated with the large number of particles used in the simulation.