Effects of system net charge and electrostatic truncation on all-atom constant pH molecular dynamics

Abstract

Constant pH molecular dynamics offers a means to rigorously study the effects of solution pH on dynamical processes. Here we address two critical questions arising from the most recent developments of the all-atom continuous constant pH molecular dynamics (CpHMD) method: 1) What is the effect of spatial electrostatic truncation on the sampling of protonation states? 2) Is the enforcement of electrical neutrality necessary for constant pH simulations? We first examined how the generalized reaction field and force shifting schemes modify the electrostatic forces on the titration coordinates. Free energy simulations of model compounds were then carried out to delineate the errors in the deprotonation free energy and salt-bridge stability due to electrostatic truncation and system net charge. Finally, CpHMD titration of a mini-protein HP36 was used to understand the manifestation of the two types of errors in the calculated pK _a values. The major finding is that enforcing charge neutrality under all pH conditions and at all time via co-titrating ions significantly improves the accuracy of protonation-state sampling. We suggest that such finding is also relevant for simulations with particle-mesh Ewald, considering the known artifacts due to charge-compensating background plasma.

INTRODUCTION

The past decade has witnessed significant progress in the development of the so-called constant pH techniques to properly account for solution pH conditions in molecular dynamics (MD) simulations^1,2. In the λ-dynamics³ based continuous constant pH MD (CpHMD), an additional set of coordinates {λ_i}, representing the titration progress of the ionizable groups are simultaneously propagated with the atomic positions^4,5. The λ_i is sampled between 0 and 1, where the values approaching 0 represent the protonated state while the values approaching 1 represent the deprotonated state. The coupling between conformational dynamics and sampling of protonation states is realized through the linear interpolation of the van der Waals interaction as well as the partial atomic charges on the ionizable group between the unprotonated and protonated forms,

$$q_{i\alpha }\left({\lambda }_i\right)={\lambda }_i{q}_{i\alpha }^{\mathrm{U}}+(1+{\lambda }_i)q_{i\alpha }^{\mathrm{P}},$$ (1)

where indices i and α refer to the titration and atomic coordinates, respectively. It follows that the Coulombic force on the titration coordinate becomes

$$F_{\lambda }^0=\frac{\partial U^{\mathrm{elec}}({\lambda }_i,r)}{\partial {\lambda }_i}=k(q_{i\alpha }^{\mathrm{U}}-q_{i\alpha }^{\mathrm{P}})\frac{q_{\beta }}{r},$$ (2)

where r is the distance between atoms α and β, and k ≈ 332Å · kcal · mol⁻¹ · atomic charge⁻². Atom β is a titratable or nontitratable atom.

While the CpHMD method based on the Generalized Born (GB) implicit-solvent model for propagating conformational and protonation degrees of freedom^4,5,6 has been successfully applied to the quantitative prediction of protein pK _a values^7,8 and mechanistic studies of pH-dependent conformational dynamics and folding of proteins^9,10, its accuracy is limited by the GB model, which gives slightly distorted local conformational environment at solute-solvent interface^7,11 and inaccurate solvation free energies for deeply buried sites⁷. Furthermore, dynamics of surfactant systems in GB solvent deviates significantly from that in explicit solvent¹².

To alleviate the problems related to the GB model, we developed a hybrid-solvent scheme, which combines the more accurate conformational sampling in explicit solvent with the more efficient calculation of solvation free energies by the GB model for propagating the titration coordinates¹¹. The hybrid-solvent CpHMD offers higher accuracy in pK _a prediction for proteins^11,13 and enables the modeling of proton titration¹⁴ and pH-dependent self-assembly and phase transition of surfactants^15,16, which is not possible with the GB-based CpHMD. However, beyond the bulk salt effect, which is implicitly taken into account by an approximate Debye-Hückel screening term, the effect of explicit ions cannot be accounted for¹⁴. Moreover, due to the fact that the solvation forces are calculated using explicit water molecules for conformational dynamics while they are derived from the GB energies for updating titration coordinates, a potential artifact is that solvent molecules around titratable sites may not have enough time to adapt to the change in the protonation state.

To remove the dependence on the GB model, three groups have attempted to extend the CpHMD framework to fully explicit-solvent simulations^{17,18,19,20,21,22}. There are two major differences in these developments. The first difference lies in the treatment of long-range electrostatics for both spatial and titration coordinates. In the development of Brooks and coworkers, the atom-based force-shifting (FSh) scheme was used^20,21, while in our development, the generalized reaction field (GRF) scheme was used^19,22. Finally, in the development of Grubmüller and coworkers, the particle mesh Ewald (PME) method was used for conformational dynamics; however, it was not mentioned whether PME was used to derive forces on the λ coordinates¹⁷. In fact, it is not straightforward to calculate the λ derivative of the charge density interpolated on a grid. Thus, in this work we will focus on the comparison between the FSh and GRF schemes. We note that the artifacts in conformational dynamics due to simple electrostatic truncation^23,24,25 are well understood, and those related to the use of long-range treatment schemes such as GRF^26,27,28 and FSh²⁹ have also been intensively studied in the literature. However, studies of the latter effects on protonation state sampling have, to our best knowledge, never been carried out.

The second major difference is a charge-leveling technique developed by us to enforce charge neutrality for the simulation system, which the other two developments did not consider^17,18,20,21. In constant pH MD, the net charge of the system varies at different pH and fluctuates with time, as titratable groups are allowed to protonate and deprotonate in response to the change in conformational environment and pH condition. In the charge-leveling technique, each titratable group is assigned a so-called co-ion, randomly placed in the simulation box at the beginning, and cotitrates such that the net charge of the pair is constant. Thus, electrical neutrality can be achieved at all time and under all pH conditions. We note that a conceptually similar strategy based on λ-dependent charge on the counter-ion was employed in the past by Chipot and coworker to ensure charge neutrality in free energy simulations³⁰. In a previous work we demonstrated that maintaining electrical neutrality is critical for the accurate description of the interactions between ionizable and charged sites and hence the accuracy of the calculated pK _a's in fully explicit-solvent CpHMD simulations with the GRF scheme¹⁹. Here we will address the question as to whether the enforcement of electrical neutrality is also necessary for all-atom CpHMD simulations with other electrostatic truncation schemes such as FSh. We note that electric neutrality is not necessary for pHMD techniques that use implicit-solvent models to sample protonation states (see test data and discussion in our previous work¹¹). We will show that the system net charge affects the protonation-state equilibria. Therefore, maintaining charge neutrality is also relevant for other pHMD techniques including those based on discrete protonation states. Finally, we would like to emphasize that the current work focuses on the net charge effects on protonation-state sampling, while the related problems for conformational dynamics were addressed in the past by several groups including Levy³¹, Hummer³² and Brooks³³ and most recently by Hub, Groenhof and coworkers³⁴.

The paper is organized as follows. First, we will contrast the GRF and FSh schemes in terms of reduction of the Coulombic forces on the spatial and λ coordinates. Next, the instantaneous and average forces on the λ coordinates due to the two truncation schemes will be examined using thermodynamic integration. The resulting potential of mean force will be tested in the CpHMD titration. We will then conduct free energy simulations to establish the effects of electrostatic truncation and system net charge on the charging free energy of positive and negative ions in water and the stability of a salt-bridge. Finally, the effects of electrostatic truncation and system net charge will be studied using the CpHMD titration of a mini-protein HP36 with both GRF and FSh schemes as well as three net-charge setting (without ions; with three chlorides and with charge-leveling co-ions).

METHODS AND PROTOCOL

All-atom continuous constant pH molecular dynamics.

Here we briefly describe the all-atom CpHMD method, while the details can be found in a recent publication¹⁹. The CpHMD methods make use of the λ-dynamics technique³ to determine the protonation states of ionizable sites onthe-fly^4,5,11. In the all-atom CpHMD, the protonation titration of acidic and basic sites is coupled to the ionization/neutralization of the corresponding co-ions.

$$\begin{array}{cc}\hfill \mathrm{A}\tilde{\mathrm{H}}+{\tilde{\mathrm{I}}}^{-}& \rightleftharpoons {\mathrm{A}}^{-}+{\tilde{\mathrm{I}}}^0;\hfill \\ \hfill \mathrm{B}\tilde{\mathrm{H}}+{\tilde{\mathrm{I}}}^0& \rightleftharpoons {\mathrm{B}}^0+{\tilde{\mathrm{I}}}^{+}\hfill \end{array}$$ (3)

Here A and B denote acidic and basic sites, respectively,Ĥ is the dummy hydrogen atom, and _Î represents the coupling co-ion. Thus, for a pair of titratable site and corresponding co-ion, the total charge remains constant, i.e., −1 for an acidic site and +1 for a basic site.

Structure preparation

The model compounds are single amino acids acetylated at the N-terminus (ACE) and N-methylamidated at C-terminus (CT3). The starting structure of HP36 is based on the NMR model (PDB ID: 1VII). Hydrogens were added using the HBUILD facility in CHARMM³⁵. The N-terminus of HP36 was left free while the C-terminus was N-methylamidated (CT3). A truncated octahedral water box was used to solvate the model compounds or protein. Water molecules within 2.6Å of any heavy atom of the solute were deleted. The minimal distance between the solute and the edges of the water box was 10 Å. To relax the hydrogen positions, energy minimization was performed using the method of steepest descent followed by the adopted basis Newton-Raphson method.

Molecular dynamics protocol

All simulations were performed using an in-house version of the CHARMM program (version c36b2)³⁵ which contains the implementation of the all-atom CpHMD¹⁹ and pH replica-exchange method¹¹. The solvated model compounds and protein were represented by the CHARMM22/CMAP force field with the modified TIP3P water model^36,37. The SHAKE algorithm³⁸ was applied to all bonds involving hydrogen atom to allow a 2-fs time step. The van der Waals energies and forces were smoothly turned off over the range of 10–12Å via a switching function³⁹. For treatment of long-range electrostatic interactions, two schemes were used: generalized reaction field (GRF) and force-shifting (FSh). Unless otherwise specified, the cutoff distance was set to 12 Å. All simulations were performed with periodic-boundary conditions at ambient temperature (300 K) and pressure (1 atm) by using the Hoover thermostat⁴⁰ and Langevin piston pressure-coupling algorithm⁴¹. Following the energy minimization, the simulation system of HP36 underwent heating and equilibration prior to the titration simulation. In the heating step, the temperature was raised from 0 to 300 K in 120 ps with the heavy atoms harmonically restrained with a force constant of 5 kcal/mol/A². In the equilibration step, the force was gradually reduced to 0 within 60 ps followed by a 20-ps unrestrained dynamics run. The titration coordinates were propagated using Langevin dynamics with a collision frequency of 5 ps^{− 1}. The mass of the fictitious λ particles was set to 10 atomic mass units. The energy barrier along λ was set to 2 kcal/mol.

pH replica-exchange protocol and calculation of pK_a values

In all titration simulations, the pH replica-exchange protocol¹¹ was applied with the exchange frequency of 100 MD steps. In the simulations of model compounds, the pH range was set to 8.4–12.4 for Lys, 2–6 for Asp, and 2.4–6.4 for Glu with an interval of one pH unit. In the simulation of Lys with a chloride ion, higher pH conditions were used: 11.4–15.4 with GRF and 10.4–14.4 with FShift. In the simulation of HP36, the pH range was set to 1–6.5 with an interval of 0.5 pH unit. The simulation length for model compounds was 5 ns per replica without co-ion or 10 ns per replica with co-ion, as the pK _a converged more slowly for the latter systems. For HP36, the simulation length was 10 ns per replica.

Following the previous work^5,6, the protonated and deprotonated states are defined as λ < 0:1 and λ > 0:9, respectively. The intermediate λ values were discarded as unphysical states. The pK _a value and Hill coefficient were then obtained by fitting the unprotonated fractions at different pH to the modified Henderson-Hasselbalch equation (Hill equation).

Free energy simulations

To determine the potential of mean force (PMF) along the λ-coordinate for model Lys, Asp and Glu, thermodynamic integration, $\Delta G=\int {\langle dU∕d\theta \rangle }_{\theta }d\theta$ was applied. The average force, 〈dU/dθ 〉, was obtained from 1-ns CPT simulation⁵ at λ values of 0.2, 0.4, 0.6, 0.7854, 1.0, 1.2, and 1.4 for single-site titration (Lys) or a combination of θ_λ (titration) and θ_x (tautomerization) for double-site titration (Asp and Glu). The reference pK _a's for Lys, Asp, and Glu were set to 10.4, 4.0, and 4.4, respectively.

Umbrella sampling was used to obtain the PMF for the salt-bridge interaction between charged Lys and Asp, which were represented by methylammonium and acetate, respectively. The distance between the ammonium nitrogen and the carboxylate carbon atoms was used as the reaction coordinate. The two molecules were first separated at a reaction-coordinate distance of 12Å and solvated by about 1000 water molecules in a rectangular box with periodic boundary conditions. Sodium and chloride ions were added to reach an ionic strength of 150 mM. For the simulation with a net charge of +1, one additional sodium ion was added, while for the simulation with a net charge of -1, one additional chloride was added. Biased sampling along the reaction coordinate was carried out with a harmonic restraint potential (force constant of 10 kcal/mol/Ų₎ applied to the distance between the ammonium nitrogen and carboxylate oxygen atoms. GRF was used for calculating long-range electrostatics. 46 windows were used to cover the range of 3–12Å with an interval of 0.2 Å. For each window, a 200-ps equilibration run was performed at constant pressure (1 atm) and temperature (300 K), followed by a 2-ns production run at constant temperature and volume with Langevin thermostat, where the collision frequency was set to 5 ps^{− 1}. The potential of mean force was calculated using the weighted histogram analysis method (WHAM)⁴² as implemented by Grossfield⁴³. A Jacobian correction was applied to raw PMF as suggested by Khavrutskii et al.⁴⁴.

The free energy perturbation (FEP) method as implemented in the PERT module of CHARMM was used to calculate the solvation energy of an acetate. The method utilizes a staged simulation scheme with three coupling parameters: λ, ξ, and s⁴⁵. For the electrostatic contribution, the coupling parameter λ was set to the values between 0 and 1 with an interval of 0.1. The Lennard-Jones potential was split into repulsive and dispersive contributions according to the Weeks-Chandler-Anderson scheme⁴⁶. For the dispersive part, the coupling parameter ξ was set to the values between 0 and 1 with an interval of 0.1, while the electrostatic interaction was off (λ = 0). For the repulsive part, the coupling parameter s was set to the values between 0 and 1 with an interval of 0.1, while both the electrostatic and dispersive interactions were turned off (λ = 0 and ξ = 0). For each value of λ or ξ, a simulation of 100-ps equilibration and 1-ns production was carried out at constant temperature (300 K) and pressure (1 atm). For each value of s, a simulation of 100-ps equilibration and 1-ns production was carried out for both the initial and final states. The energy sampled from the simulations were post-processed using WHAM^42,47. The same protocol was applied for calculating the free energy in vacuo. The final solvation energy is the difference between the free energies calculated in solvent and in vacuo.

RESULTS AND DISCUSSION

Comparison between the GRF and FSh schemes

In the atom-based force-shifting (FSh) scheme³⁹, the Coulombic potential is modified at all distances and gradually reduced to zero at the cutoff distance R_c via a multiplicative function,

$$U^{\mathrm{elec}}(r,{\lambda }_i)=k\frac{q_{i\alpha }{q}_{j\beta }}{r}{\left(1-\frac{r}{R_{\mathrm{c}}}\right)}^2,r\le R_{\mathrm{c}}.$$ (4)

while the magnitude of the force along the spatial coordinate is shifted by a constant up to the cutoff distance where it vanishes,

$$F_r=F_r^0+k\frac{q_{i\alpha }{q}_{j\beta }}{R_{\mathrm{c}}^2}=F_r^0\left(1-\frac{r^2}{R_{\mathrm{c}}^2}\right).$$ (5)

Here superscript 0 refers to the original Coulombic force. By contrast, the electrostatic force on the titration coordinate is gradually reduced to zero in the same manner as the electrostatic potential,

$$F_{\lambda }=F_{\lambda }^0{\left(1-\frac{r}{R_{\mathrm{c}}}\right)}^2.$$ (6)

The generalized reaction field (GRF) scheme accounts for the long-range electrostatic effects using the Poisson-Boltzmann reaction field forces generated by the dielectric continuum outside of a cutoff sphere^48,19,

$$U^{\mathrm{elec}}(r,{\lambda }_i)=k{q}_{i\alpha }{q}_{\beta }\left(\frac{1}{r}+0.5\frac{C_{\mathrm{RF}}{r}^2}{R_{\mathrm{c}}^2}-\frac{1+0.5C_{\mathrm{RF}}}{R_{\mathrm{c}}}\right),r\le R_{\mathrm{c}}.$$ (7)

where C_RF is a parameter that depends on the dielectric constants used to describe inside (∊₁) and outside (∊₂) of the cutoff sphere and the Debye screening length. At zero ionic strength, ∊₁ = 1 and ∊₂ = 80, C_RF = 0:987. In the GRF scheme, the electrostatic force on the spatial coordinate is given as

$$F_r=F_r^0+C_{\mathrm{RF}}k\frac{q_{i\alpha }{q}_{j\beta }r}{R_{\mathrm{c}}^3}=F_r^0\left(1-C_{\mathrm{RF}}\frac{r^3}{R_{\mathrm{c}}^3}\right),$$ (8)

while the force on the titration coordinate can be written as,

$$F_{\lambda }=F_{\lambda }^0\left(1+0.5C_{\mathrm{RF}}\frac{r^3}{R_{\mathrm{c}}^3}-(1+0.5C_{\mathrm{RF}})\frac{r}{R_{\mathrm{c}}}\right).$$ (9)

Comparing Eq. 5 and 8, one can see that the reduction of the electrostatic force within the cutoff sphere by GRF is smaller than that by the FSh scheme.

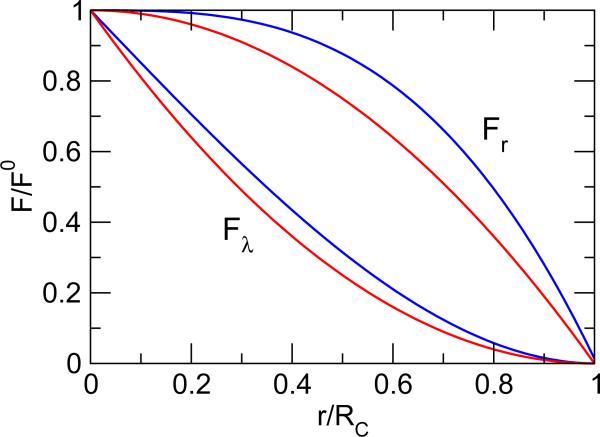
To further compare the difference in the forces calculated by the two truncation schemes, we plot the ratio between the calculated and Coulombic force as a function of the interatomic distance relative to the cutoff (Figure 1). For both spatial coordinates (real space) and titration coordinates (λ space), GRF gives larger F=F ⁰ at any r=R_c, indicating a more gradual reduction in force, which is not surprising, since the force beyond the cutoff is partially accounted for through the Poisson-Boltzmann reaction field. Most noticeably, the force reduction in the λ space is much greater than the real space, as can be seen from the concave shape of the curves. For example, at a distance of 5.5 Å, which corresponds to the distance of the second minimum in the PMF for the Asp-Lys interaction (Fig. 3), F_λ obtained with GRF and FSh is reduced to about 40% and 30%, respectively. By contrast, F_r is reduced to 91% for GRF and 79% for FSh. Thus, we speculate that potential artifacts related to the spatial long-range electrostatic approximation may be more severe in protonation-state sampling as compared to conformational sampling.

Figure 1.

Ratio between the electrostatic force on the spatial and titration coordinates calculated using the GRF (blue, Eq. 8) or FSh (red, Eq. 5) scheme and that using the Coulombic potential as a function of the interatomic distance relative to the cutoff. In the GRF calculation, C_RF = 0:987.

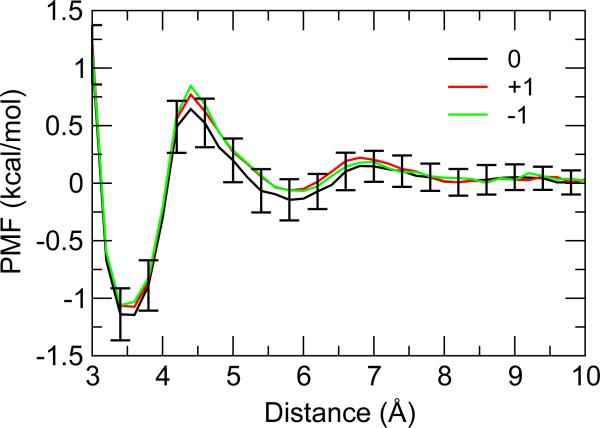
Figure 3.

Potential of mean force for the interaction between methylammonium and acetate. The legend gives the system net charge as well as the ionic strength. The distance is measured between the nitrogen of N-butyl-ammonium and the carboxylate carbon of acetate. Errors were estimated using the boot strap method⁴³.

Effect of electrostatic treatment on the free energy of deprotonation of lysine

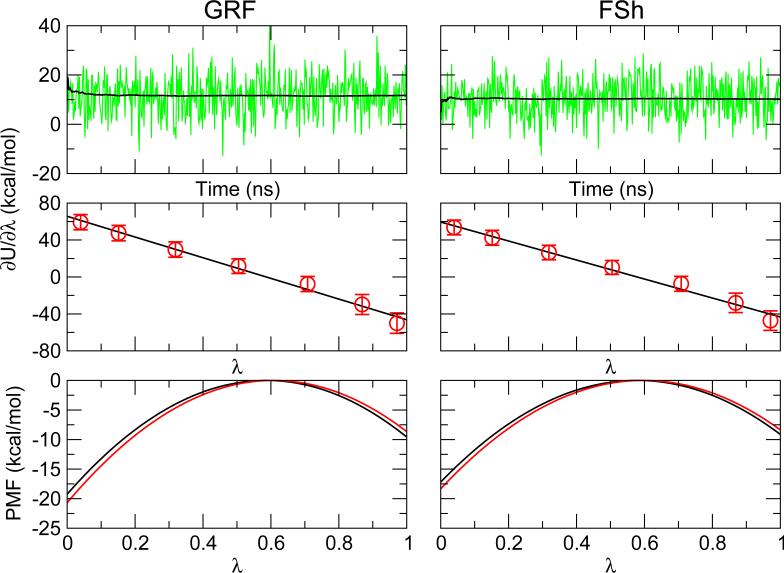
To understand how electrostatic approximation impacts the free energy of titration, we first examine the calculated force in λ space using a model Lys. With both schemes, the cumulative average of the force obtained with thermodynamic integration converges within 1 ns (Figure 2 left). Fitting of the mean force to the linear function of λ , 〈∂U/∂ 〉 = 2A(λ − B), is excellent (Figure 2 middle), which can be explained by the linear response theory⁴⁹, and is agreement with our previous work^19,22. Small deviation from linearity is observed where λ is close to 1, resulting in a small difference between the calculated pK _a and the reference value, which can be corrected by modifying the fitting parameters in the PMF function (see disscusion in our previous work¹¹).

Figure 2.

Forces on the titration coordinate for Lys obtained with the GRF and FSh schemes. Top: instantaneous force (green) at λ = 0:5 as a function of simulation time. Cumulative averages are shown in black. Middle: average force with standard deviation at different λ values. Black line is the linear fit. Bottom: Potential of mean force along λ. Black and red curves refer to the simulations without and with a chloride ion, respectively.

We compare the values of A, B and ΔG obtained from the GRF and FSh simulations in the absence of any ion (net charge of +1). ΔG represents the deprotonation free energy and can be obtained by ΔG( = 0 → 1) = A(1 − 2B). While the difference in B is small, the magnitude of A is 4.6 kcal/mol greater with GRF, which results in a larger ΔG by 1.6 kcal/mol as compared to FSh. Assuming that GRF is more accurate than FSh, this difference suggests that electrostic truncation (by FSh or GRF) leads to an underestimation of ΔG. To test this conjecture, an additional GRF simulation was performed with the cutoff distance extended to 14Å (from 12 Å). The resulting ΔG is increased by 0.82 kcal/mol. Thus, the underestimation of ΔG is supported.

Effect of system net charge on the deprotonation free energy of lysine

Now a chloride ion is added to the simulation to understand the effect of system net charge on the deprotonation free energy of Lys. At λ = 0, Lys is in the fully charged state. The system net charge decreases from +1 to 0 upon the addition of a chloride. On the contrary, at λ = 1, Lys is in the neutral state. The system net charge decreases from 0 to -1 upon adding a chloride. We inspect the effect of the net charge on the potential of mean force (PMF) (Figure 2, bottom). With both GRF and FSh, the PMF at the end points, i.e., λ of 0 or 1, becomes more negative when the net charge is zero, which indicates that removal of the system net charge leads to stabilization of the system. Considering these changes, one can deduce that the deprotonation free energy is greater in the presence of chloride. Table 1 shows that ΔG increases by 2.3 kcal/mol and 1.9 kcal/mol upon the addition of a chloride to the GRF and FSh simulations, respectively. These results are expected, as chloride stabilizes the positive charge on lysine. To ensure convergence of ion sampling and to test the effect of salt, the GRF and FSh simulations were repeated with additional 150 mM salt (2 sodium and 2 chloride ions). The resulting PMF functions remain almost identical. The maximal change in the resulting ΔG is 0.1 kcal/mol (data not shown). Thus, low concentrations of salt does not affect the deprotonation free energy of lysine.

Table 1.

Effect of electrostatic treatment and system net charge on the deprotonation free energy of lysine

	A		B		ΔG
Ion	no	Cl–	no	Cl–	no	Cl–
GRF (12 Å)	−56.0	−56.1	0.586	0.607	9.7	12.0
GRF (14 Å)	−58.1	n/a	0.590	n/a	10.5	n/a
FSh (12 Å)	−51.4	−51.4	0.578	0.597	8.1	10.0

A and B are the fitting parameters in the PMF function A(λ – B)², while ΔG is the resulting deprotonation free energy. Cutoff distance is given in parenthesis.

Effect of electrostatic treatment on the solvation free energy of acetate

Now we turn to a negatively charged solute, acetate (surrogate of Asp), and examine the system net charge on the calculated solvation free energy using the free energy perturbation method. Following Roux and coworker⁴⁵, the calculated solvation energy is broken down into contributions from the van der Waals repulsion, dispersion and charging energies. The latter dominates the total solvation free energy and is the only term that can be affected by the electrostatic treatment scheme or the system net charge.

We first compare the GRF and FSh results in the absence of ion. The calculated charging and total solvation free energy of acetate with GRF is -59.7 kcal/mol, which is 8.6 kcal/mol more negative than that with FSh (Table 2). This difference amounts to about 14% and is similar to the difference in the protonation (or charging) free energy of Lys (16% or 1.6 kcal/mol). To estimate the effect of finite cutoff, simulations were repeated by extending the cutoff distance from 12 to 15 Å. The charging as well as the total solvation energies are increased in magnitude by about 6 and 8 kcal/mol, or 10% and 14%, for the GRF and FSh simulations, respectively (Table 2). Noting that the experimental solvation free energy is -80.65 kcal/mol⁵⁰, these data indicate that electrostatic truncation results in underestimation of the charging free energy for acetate, and the error with FSh is greater than GRF, in agreement with the data for lysine.

Table 2.

Effect of electrostatic treatment and system net charge on the solvation free energy of acetate

	GRF			FSh
Ion	no	Na+	Cl–	no
Repulsion	10.3 (10.4)	10.3	10.3	10.2 (10.3)
Dispersion	−8.2 (−8.4)	−8.2	−8.2	−8.2 (−8.4)
Charging	−61.8 (−68.1)	−64.7	−58.7	−53.2 (−60.9)
Total	−59.7 (−66.2)	−62.6	−56.6	−51.1 (−59.0)

The cutoff was 12 Å except for the data listed in parenthesis which were obtained with a cutoff of 15 Å.

Effect of system net charge on the solvation free energy of acetate

To examine the effect of net charge, we performed two additional GRF simulations, one with a sodium ion and one with a chloride ion. Inclusion of a sodium, which compensates for the negative charge on acetate, increases the magnitude of the charging and the solvation energy by 2.9 kcal/mol, due to electro-static stabilization (Table 2). On the contrary, inclusion of a chloride, which increases the system net charge, results in a decrease of the magnitude of the charging and solvation energy by about 3.1 kcal/mol, due to electrostatic repulsion (Table 2). Thus, in agreement with the results of lysine, these data show that with a net charge in the system the magnitude of charging free energy of acetate is understimated.

To ensure sampling convergence of ion distributions, we repeated the above simulations by adding 150 mM salt (2 sodium and 2 chloride ions). Consistent with the lysine data, changes in the charging and solvation free energies are negligible (smaller than 0.1 kcal/mol), suggesting that low ionic strength does not affect the calculated free energies, consistent with the work by Donnini et al⁵¹.

Effect of system net charge on the salt-bridge interaction

Another possible effect of system net charge on proton titration is through modulation of ion-pair interactions. To explore this effect, we conducted umbrella sampling simulations to determine the PMF for the salt-bridge interaction between model Lys (methylammonium) and model Asp (acetate), as frequently observed in protein structures. The two molecules were placed 12Å apart and moved towards each other in a specific orientation along a reaction coordinate, which is defined as the distance between the nitrogen atom of Lys and the carboxyl carbon of Asp. Three simulation settings were used: a) net charge 0; b) net charge +1 (with one sodium added); and b) net charge -1 (with one chloride added). As displayed in Figure 3, all the resulting PMFs contain a deep contact minimum at about 3.5Å and a shallow minimum at the solvent-separated distance of 5.7 Å, consistent with a previous study by Lazaridis and coworker⁵². The depth of the contact minimum, which represents the free energy of formation or stability of the Lys Asp salt bridge, is about 1.2 kcal/mol for the neutral system and about 1.1 kcal/mol for the charged systems. The small difference (0.1 kcal/mol) is negligible as it is within the estimated statistical error of the PMF calculation. To ensure convergence of the ion distribution, the above simulations were repeated with additional salt ions (3 Na⁺ and 3 Cl) which resulted in an ionic strength of 150 mM. The depth of the contact minimum becomes 1.1 kcal/mol for the neutral system and 1.2 kcal/mol for the charged systems (data not shown). The small changes (±0.1 kcal/mol) relative to the simulations without additional salt ions are again within the error bars. Thus, these data suggest that adding a small net charge to the simulation system does not impact the stability or conformational distribution of salt-bridge interactions.

System net charge in the CpHMD simulation varies as a function of pH and simulation time

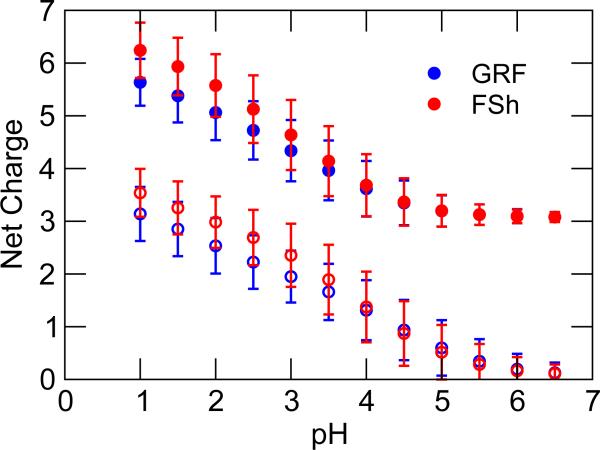
Without the charge-leveling co-ions, the net charge in a CpHMD simulation varies as a function of pH and simulation time. Consider a miniprotein HP36, which has four acidic residues (Asp/Glu), seven basic residues (Lys/Arg and the free N-terminus). The net charge (in the absence of ions) is expected to vary between +3 at high pH conditions when acidic groups are fully deprotonated (charge -1) and the basic groups are fully protonated (charge +1), and 7 at low pH conditions when acidic groups are fully protonated. Indeed, the net charge for HP36 varies in range of 3–5.5 in the GRF simulation and 3–6.1 in the FSh simulation (Figure 4). The small difference is due to the slightly different deprotonated fractions at each pH in the two simulations. To illustrate a typical setting in MD simulations, three chlorides were added to the system, which serve as counterions to offset the net charge of +3 at pH 7 (assuming model pK _a values for all groups). As shown in Figure 4, the overall net charge is reduced but still varies between 0 and 4. The latter reflects the uncompensated charge at low pH conditions.

Figure 4.

System net charge at various pH conditions in the CpHMD simulation of HP36 with the GRF and FSh schemes. Filled circles: without ions. Empty circles: with three chlorides. Error bar indicates the fluctuation of the net charge during the 10-ns simulation.

Without co-ions, the net charge in a CpHMD simulation also fluctuates with time as titratable groups alternate between charged and neutral forms. The magnitude of the fluctuation depends on the number of titratable group and the pH condition (larger if multiple groups titrate). In the simulation of HP36, the fluctuation is larger than one unit at pH below 4, when several acidic groups titrate, and almost vanishes at pH above 5, when all acidic groups are fully deprotonated (see error bars in Figure 4).

CpHMD simulation of a mini protein with different system net charge, salt concentration, and electrostatic truncation scheme

We investigate the effect of system net charge on the CpHMD simulation of HP36 with five settings: a) without ions; b) with 3 chloride ions (to neutralize the system at pH 7); c) with additional salt ions (21 sodium and 21 chloride added to b) to match the experimental ionic strength of 160 mM; d) with 4 co-ions added to b) to maintain the charge neutrality at all time and pH; and e) with salt ions (21 sodium and 21 chloride) added to d) to maintain charge neutrality and match experimental ionic strength. Each setting was combined with either the GRF or FSh scheme, resulting in a total of 10 simulations. The calculated pK _a values and Hill coefficients are listed in Table 3. Note that the experimental pK _a's for Asp44, Glu45, and Asp46 are shifted lower than the model values (4.0 for Asp and 4.4 for Glu), reflecting the fact that the charged forms of these sidechains are stabilized in the protein.

Table 3.

Effect of system net charge and electrostatic treatment on the pK_a calculation of HP36

	Expt	GRF					FSh
Setting		a	b	c	d	e	a	b	c	d	e
Qnet	0	3–7	0–4	0–4	0	0	3–7	0–4	0–4	0	0
Salt	yes	no	no	yes	no	yes	no	no	yes	no	yes
pK a
Asp44	3.10	≤0	0.8	1.2	2.2	2.4	0.3	0.8	1.2	2.7	1.7
Glu45	3.95	1.9	2.9	3.0	4.4	4.4	2.3	3.3	3.1	4.2	4.2
Asp46	3.45	1.7	2.4	2.7	3.7	4.0	2.4	3.0	3.0	4.0	3.8
Glu72	4.37	2.7	3.7	3.7	4.8	5.0	3.1	3.9	4.0	4.9	4.8
AAE n		≥2.1	1.3	1.1	0.5	0.6	1.7	1.0	0.9	0.4	0.6
Asp44	1.30	0.6	1.0	0.9	1.1	1.0	0.8	1.0	1.0	1.1	1.1
Glu45	0.90	0.8	0.7	0.8	0.9	0.9	0.7	0.8	0.8	0.9	0.9
Asp46	1.05	0.8	0.9	0.9	0.9	1.0	0.7	0.8	0.8	1.0	0.8
Glu72	1.00	0.8	0.8	0.9	0.9	1.0	0.8	0.8	0.8	1.0	1.1

Q^net (net charge) of 3–7, 0–4, and 0 refer to the simulations without ions (setting a), with 3 chlorides (settings b and c), and with 4 co-ions in addition to 3 chlorides (settings d and e), respectively. Experimental pK_a's were obtained with an ionic strength of 160 mM⁵⁵. In the row of Salt, “yes” denotes the addition of 160 mM salt ions (21 sodium and 21 chloride ions). AAE denotes the average absolute error.

For the GRF and FSh simulations under Setting a, the calculated pK _a values for all groups are underestimated. The average absolute errors are 2.1 and 1.7, respectively. The largest error occurs for Asp44, which has the lowest experimental pK _a due to the salt-bridge interaction with Arg55. The predicted pK _a's in the two simulations are at least 2.8 units lower than experiment. The overestimation of the pK _a downshifts (as compared to the model values of 4.0 for Asp and 4.4 for Glu) is the result of overstabilization of the negative aspartates and glutamates by the net positive charge, which exceeds 3 units at all pH (Figure 4). Interestingly, the calculated Hill coefficients are all smaller than one, even for Glu72 which does not interact with other acidic residues, further suggesting that the protonation-state sampling in the charge-uncompensated CpHMD simulation is inaccurate.

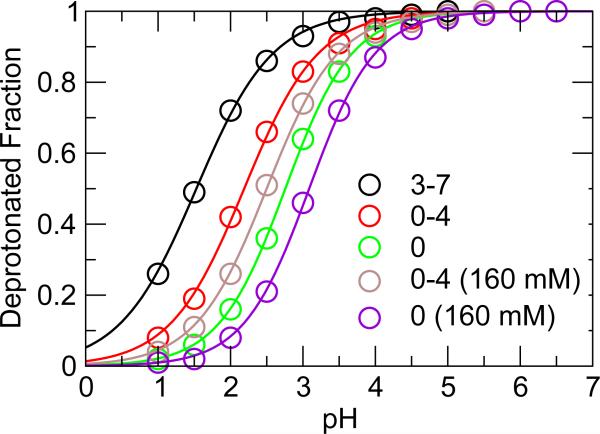
The addition of three chloride ions to the simulation system (Setting b) lifted the pK _a's for all groups, bringing the average absolute error down to 1.3 and 1.0 for GRF and FSh simulations, respectively. The improvement can be explained by the smaller net positive charge as compared to Setting a. Take, for example, the titration of Asp46 in the GRF simulations. At pH 2, the system net charge decreases from 5 in the simulation under Setting a to 2.5 under Setting b (Figure 4). Consequently, the deprotonated fraction of Asp46 is lowered from 0.72 to 0.42, respectively. The decrease in the net positive charge shifts the titration equilibrium towards the protonated side at all pH, shifting the titration curve to higher pH (compare red and black curves in Figure 5). Thus, the pK _a value is increased by 0.7 units to 2.4 (Table 3).

Figure 5.

Simulated titration data of Asp46 in HP36. Black: no ions; red: three chlorides; green: three chlorides and four co-ions; brown: three chlorides and additional 160 mM salt; violet: three chlorides, four co-ions, and 160 mM salt. Solid lines are fits to the Hill equation. The legends indicate the system net charge with the value in the parenthesis referring to the ionic strength.

We examine the simulations under Setting d, where the system net charge is zero at all pH and at any simulation time. Again, all pK _a values are lifted higher, resulting in a further reduction of the average absolute errors to 0.5 and 0.4 for the GRF and FSh simulations, respectively. Compared to Setting b, the pK _a of Asp46 is further increased to 3.7 in the GRF simulation (Table 3), which is due to the shift of titration equilibrium due to removal of the positive charge at low pH conditions (compare green and red curves in Figure 5). The most drastic improvement is however for Asp44, bringing the pK _a value up to 2.2 and 2.7, representing an improvement of 1.4 and 1.9 units for the GRF and FSh simulations, respectively, as compared to the corresponding simulations with three chlorides only. Nevertheless, the pK _a of Asp44 remains underestimated by 0.9 and 0.4 units in the GRF and FSh simulations, respectively. We suggest that it is a consequence of limited sampling, i.e., infrequent barrier crossing between the charged and neutral states, which leads to an overpopulation of the thermodynamically more stable state. This argument is supported by the increase in pK _a in a test simulation using a two-dimensional protocol that combines temperature and pH replica-exchange (Shen group, unpublished data). In addition to the improvement of the calculated pK _a's, the Hill coefficients are also brought closer to experiment (close to one), which is another indication of the more accurate representation of the protonation-state equilibria. Note that, unlike the other three acidic, the calculated Hill coefficient for Asp44 (from both GRF and FSh simulations) is slightly higher than one, which is consistent with experiment although magnitude is somewhat underestimated.

An important question is whether the observed effect of co-ions can be mainly attributed to dielectric screening by mobile salt ions. We examine the calculated pK _a's with 160 mM salt ions added to the system that is neutralized at pH 7 (net charge 0–4, Setting c) as well as the system that is neutralized at all pH (net charge 0, Setting e). We note that the number of added salt ions (21 sodium and 21 chloride ions) is sufficiently large such that statistical sampling of ion motions can be assured. Under Setting c, the most depressed pK _a of Asp44 shows the most evident change with an increase of 0.4 units in both GRF and FSh simulations, which is expected because of the dielectric screening of the salt-bridge interaction with Arg55 by the salt ions. However, the changes of the rest of the pK _a's are smaller and not in the same direction comparing the GRF and FSh data. As a result, the average absolute errors are reduced only by 0.2 and 0.1 units to 1.1 and 0.9 for GRF and FSh simulations, respectively. Clearly, they are much larger than the errors from the charge-neutralized simulations, which are 0.5 and 0.4 with the GRF and FSh schemes, respectively. Note, the pK _a of Asp44 remains underestimated by 1.9 units in both simulations. Under Setting e, the extra salt ions do not improve the pK _a's relative to the corresponding simulations without salt ions (Setting d). In fact, the average absolute errors are increased by 0.1 unit for both GRF and FSh simulations. In contrast, a significant improvement is seen for most pK _a's when comparing data from Setting e to the corresponding ones without charge-leveling (Setting c). The avg abs errors are reduced by 0.5 and 0.3 units with the GRF and FSh schemes, respectively. Together, these data indicate that while the effect of co-ions includes dielectric screening, the bulk of it is due to the removal of the net positive charge, which significantly shifts the protonation equilibria of acidic residues towards the neutral states.

We compare the calculated pK _a's with the GRF and FSh schemes. Interestingly, in the absence of any ion (Setting a, charge 3–7), the avg abs error with FSh is 0.4 units smaller than with GRF. In the presence of three chlorides (Setting b and c, net charge 3–7), the avg abs errors with FSh are respectively smaller by 0.3 and 0.2 compared to GRF. In the charge-neutralized simulations (Setting d and e, charge 0), however, FSh and GRF give equal performance. These data suggest that FSh is less sensitive to the system net charge, which is consistent with the data obtained by Brooks and coworker^20,21.

Since pK _a shift is proportional to the difference in the deprotonation free energy between the protein environment and solution: ΔG^deprot(HA^protein) - ΔG^deprot(HA^sol), one may wonder if the errors due to electrostatic truncation cancel out. Using a thermodynamic cycle, it can be shown that ΔΔG^deprot is equal to ΔΔG^transf (from solution to protein) between the neutral and charged tates: ΔΔG^deprot = ΔG^transf(A⁻ ) - ΔG^transf(HA). For a buried titratable group, the latter can be considered as the difference in desolvation. Clearly, the truncation error in the desolvation free energy for the charged species is greater than that for the neutral counterpart. This is because the interaction between a charged solute and polar solvent (charge-dipole interaction) is longer ranged than the interaction between the neutral solute and polar solvent (dipole-dipole interaction). Another argument is that the desolvation energy of a charged species is at least an order of magnitude greater than the neutral counterpart. Thus, the truncation error for the model does not cancel that for the protein.

Why inclusion of co-ions improves the calculated pK_a's

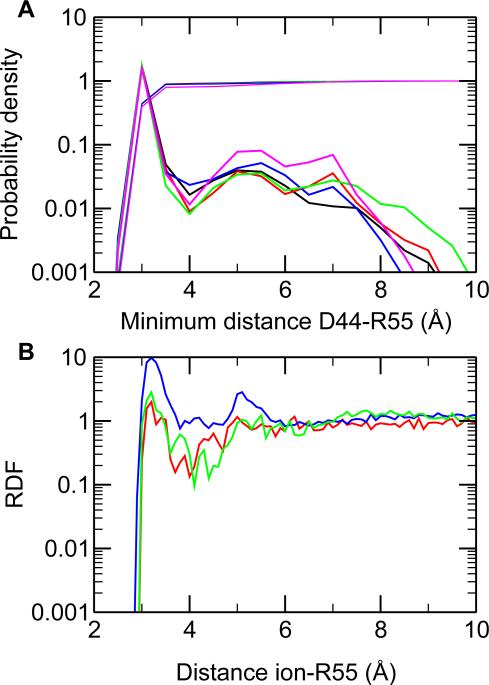
Analysis of the pK _a data for HP36 establishes that the inclusion of charge-leveling co-ions reduces the average absolute error by about 0.5 units, and the bulk of the effect is not through dielectric screening. Now we ask if the improvement is due to the change in conformational sampling, for example, breakage of salt-bridge interaction, or through specific ion-solute interaction. To address these questions, we consider Asp44, for which the calculated pK _a is lifted by by more than 1 unit comparing the GRF simulations without co-ions (setting b and c) and those with co-ions (settings d and e). The probability distributions of the minimum distance between Asp44 and the salt-bridge partner Arg55 under all five simulation settings were calculated (Figure 6A). The position and amplitude of the major peak in the distribution, which represents the salt-bridge interaction, are virtually identical under all settings. The probability for the Asp44... Arg55 distance to be within 4Å is also the same (see integration curves in Figure 6A). Thus, the net charge does not affect conformational dynamics or stability of the salt bridge, consistent with the finding based on the model salt bridge Asp... Lys (Figure 3).

Figure 6.

Effect of co-ions on the salt-bridge interaction in HP36. A. Probability distribution of the minimum distance between Asp44 and Arg55 in simulations with GRF at pH 6. Asp44 is fully charged. The colors black, red, blue, green, magenta represent the simulations with setting a, b, c, d and e, respectively. To help visualize the differences in probability or probability density, logarithmic scale is used.

B. Radial distribution function (RDF) for the distance between co-ions (setting d) or regular chlorides (setting b and c) and Arg55. The same color scheme is used as in A.

To address the question as to whether the increased pK _a of Asp44 in the presence of coions is due to direct screening of salt bridge via specific ion-solute binding, we examine two pH conditions. At (high) pH conditions when acidic sidechains are charged, the co-ions are neutral and have no effect. At (low) pH conditions when Asp44 is neutral, the co-ions are charged and behave like regular chloride ions which can accumulate around the positively charged Arg55 (salt-bridge partner of Asp44 at high pH). We compare the RDF of the co-ions around Arg55 in setting d (4 co-ions) with the RDF of the regular chlorides in setting b (3 chlorides) and c (24 chlorides in total). As seen from Figure 6B, the co-ion RDF (setting d) is similar to that of the regular chlorides (setting b). The peak intensity of both RDF's is lower than that of the one in setting c. Thus, the 1-unit pK _a increase in going from setting c to setting d is not caused by specific binding of co-ions. The co-ions “operate” rather through a mechanism of long-range charge compensation.

Concluding Remarks

In this work, we examined two critical questions arising from the recent developments of the all-atom continuous constant pH molecular dynamics (CpHMD) method^{17,18,19,20,21,22}: 1) What is the effect of spatial electrostatic truncation on the sampling of protonation states (λ space)? 2) Is the enforcement of electrical neutrality necessary for all-atom CpHMD simulations? We focus on two electrostatic truncation schemes currently implemented in the CpHMD programs, the generalized reaction field (GRF) and force-shifting (FSh).

We showed that the electrostatic force on λ coordinates is reduced significantly more rapidly with distance than the force on spatial coordinates. This suggests that potential artifacts due to electrostatic approximation may be more severe in protonation-state sampling as compared to conformational sampling. Free energy calculations for the deprotonation of lysine and solvation of acetate revealed that electrostatic truncation via GRF and FSh leads to the underestimation of the favorable charging and solvation free energies of a charged solute in water. Since the interaction between a charged solute and polar solvent (charge-dipole interaction) is attractive and longer ranged than that for the neutral counterpart (dipole-dipole interaction), the truncation error is greater for the charged as opposed to the neutral state, leading to a bias towards the latter. Using thermodynamic cycle, one can show that the difference in the titration free energy between the model and protein is the same as the difference in the transfer free energy (from solution to protein) between the charged and neutral forms. Thus, the truncation error for the model does not cancel that for the protein, leading to errors in the calculated pK _a's of the protein.

The effect of system net charge was first examined at the level of model compounds. As expected, compensation of the net charge leads to stabilization of the charged solute. On the other hand, a small net charge has a negligible effect on the stability of the ion-pair. In agreement with these results, in the CpHMD titration of HP36, which carries a net positive charge at all pH conditions in the absence of any ion, the pK _a values of Asp and Glu are severely underestimated due to the overstabilization by the net charge. The errors in the pK _a's are partially alleviated by adding three chlorides, which compensates for the net charge at pH above 4. However, due to the net charge at lower pH conditions the pK _a's remain underestimated. Inclusion of co-ions to ensure charge neutrality at all pH conditions further reduces the errors, bringing the calculated pK _a's in both GFR and FSh simulations to within 0.5 units from experiment. We also addressed the question as to whether the effect of co-ions can be mainly attributed to dielectric screening, by repeating all simulations with an additional 160 mM salt. The resulting data indicate that while co-ions do provide dielectric screening, the bulk of the effect is due to removal of the net positive charge, which significantly shifts the protonation equilibria of the acidic residues towards the neutral states.

The presented data demonstrate that maintaining system charge neutrality significantly improves the accuracy of protonation-state sampling in constant pH molecular dynamics. Although current study was carried out using two electrostatic truncation schemes, we believe that charge neutrality is also important for pHMD simulations where PME is used for driving λ dynamics. In pHMD simulations the system net charge varies with pH and fluctuates with simulation time. A very large net charge can occur at low or high pH conditions and when many groups have similar pK _a's. In this case, artifacts due to the charge-compensating background plasma may be particularly severe^33,34. Thus, maintaining charge neutrality via a charge-leveling technique such as the titratable co-ions presents an attractive and physically sound option. We would like to note our charge-leveling technique is still under development. Most recently, a titratable water model has been developed to avoid potential artifacts due to co-ion aggregation and to improve physical realism²². Another topic of future direction is a more accurate treatment of long-range electrostatic forces in the λ space. The implementation of λ force with the PME method is appealing. Finally, we note that although the present study suggests that system net charge leads to a systematic error in all-atom pHMD simulations, limited sampling accounts for a large extent of the deviation between calculated and experimental pK _a values as shown in the previous work by us and others^13,22,21. Thus, there is a need for continued development and application of enhanced sampling techniques for constant pH simulations^6,53,54,11