From single fiber to macro-level mechanics: A structural finite-element model for elastomeric fibrous biomaterials

Abstract

In the present work, we demonstrate that the mesoscopic in-plane mechanical behavior of membrane elastomeric scaffolds can be simulated by replication of actual quantified fibrous geometries. Elastomeric electrospun polyurethane (ES-PEUU) scaffolds, with and without particulate inclusions, were utilized. Simulations were developed from experimentally-derived fiber network geometries, based on a range of scaffold isotropic and anisotropic behaviors. These were chosen to evaluate the effects on macro-mechanics based on measurable geometric parameters such as fiber intersections, connectivity, orientation, and diameter. Simulations were conducted with only the fiber material model parameters adjusted to match the macro-level mechanical test data. Fiber model validation was performed at the microscopic level by individual fiber mechanical tests using AFM. Results demonstrated very good agreement to the experimental data, and revealed the formation of extended preferential fiber orientations spanning the entire model space. We speculate that these emergent structures may be responsible for the tissue-like macroscale behaviors observed in electrospun scaffolds. To conclude, the modeling approach has implications for (1) gaining insight on the intricate relationship between fabrication variables, structure, and mechanics to manufacture more functional devices/materials, (2) elucidating the effects of cell or particulate inclusions on global construct mechanics, and (3) fabricating better performing tissue surrogates that could recapitulate native tissue mechanics.

1-INTRODUCTION

Fibrous biomaterials are ubiquitous and have important function in numerous biomedical applications which motivates the development of more advanced modeling strategies for these materials. Research efforts on this front engage a very broad spectrum of both basic and applied approaches: non-woven and woven 3D meshes [1], cell compacted collagen gels [2-4], electrospun polyurethane scaffolds [5-6], collagen-agarose gels and fibers networks [7],[8] engineered heart valves [9], decellularized tissue [10], arterial walls tissue [11], skeletal muscle tissue [12], actin networks [13-14]. Historically, the term “tissue engineering” was attributed in 1988 to Y.C. Fung [15]. The term underscored the importance of “the application of principles and methods of engineering and life sciences toward a fundamental understanding of structure-function relationships in normal and pathologic mammalian tissues and the development of biological substitutes to restore, maintain, or improve tissue function.” Thus, it is imperative that fundamental structure-function relations of the fibrous biomaterials be established to guide the reproduction of native tissue equivalent behaviors if they are to emulate the native tissue counterparts successfully [16].

From these considerations, the connection of the structure and function of fibrous biomaterials have been conducted in a variety of studies. For example, multi layered fibrous materials have been designed to replicate the annulus fibrous [5], native cartilage [1], and cardiac tissue anisotropy [17]. As related to cell-matrix biology, substrate stiffness is known to play a key role in directing stem cell lineage specification [18], and as well as responding to the stiffness and deformation of their substrate [19-20]. It was also noted [21] that the macroscopic strain of the extracellular matrix (ECM) during engineered cardiovascular tissue growth induced modifications in gene expression and protein synthesis similar to those produced by modulating local deformations [22]. Matrix structure and mechanics were determined to be relevant factors in the etiology and pathological remodeling of cancer development [23] as well as in atherogenesis [24].

In structural deterministic approaches, the constituent microstructure is typically modeled by reproducing the material geometry at the fiber level using idealized fiber networks that are stochastically generated. The mechanics can be solved at its original micro meso scales [25-27], or can be coupled to the macroscopic scale through a multi-scale technique such as volume averaging or homogenization[4, 6]. These models have shown predictive capacity potential at multiple length scales.

At the macroscopic scale (≥1 mm), a large number of models [2-4, 6-9, 11-12, 27-31] have been implemented to predict the uniaxial mechanical response and relate it to the biomaterial microscopic architecture (e.g. overall fiber orientation). Such structural deterministic models have had fundamental implications for (1) gaining insight on the intricate relationship between fabrication variables, structure, and mechanics to manufacture more functional devices/materials [32-33], (2) elucidating the effects of cell or particulate inclusions on global construct mechanics [34], and (3) fabricating better performing tissue surrogates [1, 5, 17] that could recapitulate native tissue mechanics both in terms of in-plane behavior (e.g. non-linearity, anisotropy and elastic moduli [35]) and of out-of-plane behavior (e.g. bending stiffness [36]). At smaller scales (mesoscopic scale with a characteristic length of ~100 μm), various model predictions [2-4, 9, 12, 25, 28] can estimate fibers network kinematics and mechanics [37] and elucidate the effects of macroscopic deformations and micro architecture on cells/inclusions. For example, the global-local strain transfer at focal adhesion complexes [19]. Going smaller (microscopic scale ~1 μm), structural deterministic models [14, 38-39] are used to describe single fiber mechanics [40], or determine intrinsic material mechanical properties (e.g. elastic and shear moduli, Poisson ratio) [33, 40].

Yet, current structural deterministic models utilize idealized fiber geometries and generally lack experimental validation at the various length scales [42]. The lack of fiber-level geometric realism can be a limiting factor in model fidelity and utility. For example, current models can assist material fabrication by indentifying which fiber network geometries can reproduce specific macro level mechanics [5, 17]. However, specific changes in structure cannot be utilized to predict nor to elicit a desired level of local strain on embedded inclusions at the mesoscopic scale [19, 37]. There is thus a need to extend present approaches in modeling fibrous scaffolds starting from the level of the fiber and proceeding up to macro-level stress-strain responses.

The purpose of the present work is to explore the potential benefits of incorporation of actual measured fiber geometry into a structural finite element model for elastomeric fibrous scaffolds. We utilized both isotropic and anisotropic electrospun polyurethane (ES-PEUU) scaffolds, both with and without particulate inclusions, to explore a wide range of architectures. We also utilized electrospun polyethylene terephthalate (Dacron), a relatively stiff material, for further model validation. Fiber material model parameters were obtained by fitting the model to corresponding biaxial mechanical data, and further validated at the microscopic level by individual fiber mechanical tests using AFM techniques.

2 - METHODS

2.1 - Fabrication

Due to its widely documented capacity of generating elastomeric and fibrous materials with controlled architectures [5-6, 9-10, 32-34, 36-37, 41-42], electrospinning was selected as the fabrication platform to validate and test the model. Five different materials were synthesized and fabricated as described previously [34, 43-44]: isotropic and anisotropic poly(ester-urethane)urea (PEUU), vascular smooth muscle cell integrated (VSMC) PEUU, polystyrene microsphere integrated PEUU and isotropic Dacron. Isotropic and anisotropic PEUU scaffolds were adopted to assess the capacity of the model to capture mechanical anisotropy by simply representing network with different level of fiber alignment. Similarly, the VSMCs and particles integrated scaffolds were selected to assess the capacity of the model in predicting the impact of inclusions (e.g. higher number of fiber intersections [34, 36]) on the material mechanics. Finally, the Dacron was selected as an example of non-elastomeric material having higher values of elastic modulus thus stiffer response at macro, meso and single fiber level.

Materials were synthesized and fabricated by electrospinning (Fig.1) following protocols described in details in [34, 43-44]. In brief, 12%(w/v) solution of PEUU or Dacron in 1,1,1,3,3,3-hexafluoroisopropanol (Oakwood Products, Inc.) was delivered with a flow rate of 1.5 ml/h through a stainless steel tube (inner diameter: 1.2 mm) charged to 12 kV. The collecting target was an aluminum mandrel of 114 mm diameter for the isotropic PEUU, Dacron and the anisotropic PEUU. Polymer injector – target gap distance was 17 cm, the mandrel voltage was -4 kV. Tangential velocity was 1.5 and 4.5 m/s for the isotropic and anisotropic samples respectively [33, 45], rastering speed was 0.3 cm/s. For the VSMCs and polystyrene integrated material a steel mandrel of 6 mm diameter was utilized to reduce the inclusions collecting region [44], polymer voltage was reduced to 10 kV, inclusions solution voltage (cell media for the VSMCs and PBS for the particles) was 8 kV, flow rate 15 ml/h. The target inclusions injector gap was 4.5 cm, rastering velocity 3 cm/s, mandrel tangential velocity ~ 8 cm/s. Cells and polystyrene microspheres (10 micrometer diameter, Invitrogen) had a concentrations of 10 and 7 million/ml respectively [19, 34]. VSMCs were selected for their recognized value in cardiovascular applications and for the benefit of comparing materials characteristic with our existing data base [19, 32, 34, 44]. VSMCs were isolated from Lewis rat aortas and expanded on tissue culture polystyrene culture flasks using Dulbecco's modified Eagle medium (DMEM) (Lonza) supplemented with 10% fetal bovine serum and 1% penicillin-streptomycin. Following fabrication, VSMCs constructs were incubated in cell culture medium overnight at 37°C [19, 44].

Figure 1. SEM images of polystyrene spheres and VSMCS integrated PEUU scaffolds.

a, b spheres integrated PEUU cross section showing the inclusions homogenously distributed over the material thickness. c, d VSMCs integrated PEUU, details showing cells integrated on the material surface. e,f isotropic and anisotropic PEUU scaffolds.

2.2 - Scaffold imaging and fiber architecture characterization

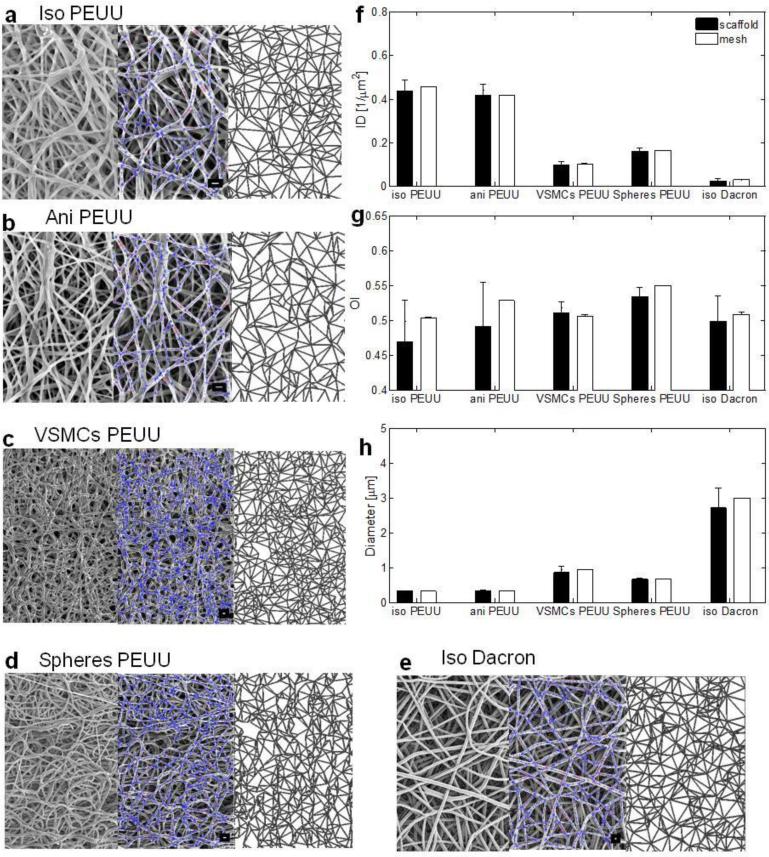
For surface analysis, materials were dried for 24 hrs, then sections were gold sputter coated and imaged with SEM (JEOL JSM6330F)[45]. Fiber micro-architectural features were detected and quantified from images (n≥5 per sample) using a method previously described [10]. VSMCs and microspheres integrated samples were washed with PBS to remove inclusions for quantitative analysis (Fig 2 a-e) or left intact for qualitative observation (Fig. 1). The following fiber geometric data were acquired from the detected network [34, 36] (Fig. 2 a-e, Fig. 3, Supplementary Fig. 1-5):

1. The fiber intersection density (ID).

2. The connectivity distribution [46], defined as the percentage of fiber intersections vs. number of fibers crossing a fiber intersection.,

3. The fiber diameter (D).

4. The fiber orientation distribution function (ODF).

Since the fiber ODF was found to be symmetrical, we utilized an orientation index (OI), defined as the average over all fiber segments of cos²( ), where represents the angle between a fiber segment and the direction of alignment. This metric for fiber alignment has been utilized for scaffolds structure quantification [10, 34, 36], with OI equal to 0.5 for isotropic networks and 1 for parallel set of fibers. This form of OI was adopted to compare the new findings of this study with the structural and image analysis previously conducted in [47].

Figure 2. Real and simulated materials topologies characterization and comparison.

a-e, from left to right qualitative comparison: original material SEM micrograph (left), image analysis with overlaid detected fiber network (center), corresponding simulated topology (right). a PEUU isotropic, b PEUU anisotropic, c VSMCs integrated PEUU, d polystyrene integrated PEUU, e isotropic Dacron (additional details on supplementary figures 8-12), scale bar = 1 μm. Quantitative comparison of micro architectural features characterizing the real and simulated fiber networks: f intersection density (ID) defined as the number of fiber overlaps/μm², g orientation index (OI) metric for fiber alignment (0.5 for purely isotropic network, 1 for a set of parallel fibers), h fiber diameter (D) defined as the mean of the fiber network diameter distribution (μm).Additional materials have been characterized and included in this classification (supplementary figure 7, data were presented as mean ± st.d.) n≥5 images/material were utilized for the image analysis and n≥5 meshes/material were generated and quantified.

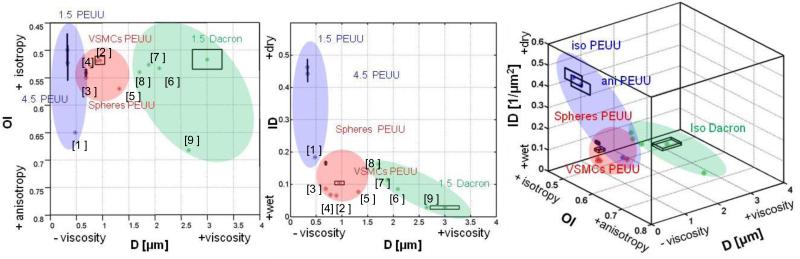
Figure 3. Material topology design space.

3D representation of the material design space (ID-OI-D), the three variables can me independently controlled in electrospinning. Design variables choice enabled material “clusters” identification characterizing different fabrication modality : dry fabrication (blue region), wet fabrication/micro integration (red region), high viscosity (green region) in addition to the five materials modeled and discussed in this work several others: ( 0.3 cm/s ,1.5 cm/s, 30 cm/s raster wet PEUU [34], PBS wet PECUU, 75/25, 50/50, 25/75 PEUU/PCL [36], 4.5 m/s Dacron, 9.0 m/s dry PEUU [10]) were included in the 3D space to prove the capacity of this classification to efficiently group categories of materials on the basis of their main architectural features. Data are presented as mean, standard deviation (n≥5 images/material) are provided for isotropic and anisotropic PEUU, VSMCs and spheres integrated PEUU and isotropic Dacron.

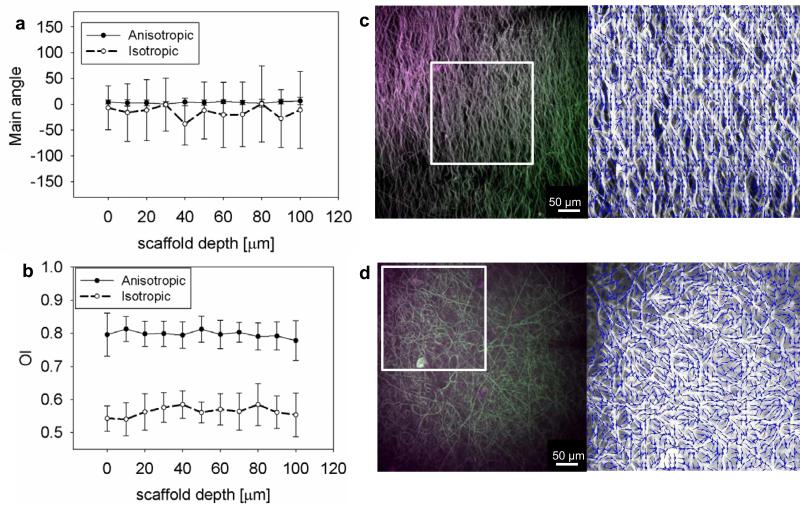
Multi photon imaging was also utilized to detect transmural variations in structure [48] otherwise not accessible troughout SEM. For each sample (8 mm × 8 mm × ~250 μm) 50 μg of Red CMTPX (Molecular Probes®) was diluted in 5 μL of dimethyl sulfoxide, next the solution was diluted further in 50 μL of distilled water and added to the sample on a rocker for 12 hrs. This key step enhanced the material emission signal allowing for image analysis to be performed layer by layer (n≥5 samples, image depth of 100 μm from the surface with step 10 μm) without stack creation (Fig. 4 and Supplementary Fig. 6-7). An Olympus FV 1000 multi-photon microscope (Center Valley, PA) was used with excitation wavelength of 805 nm, laser power 6-8%, sampling speed of 40 μs/pixel. Emission signal was acquired at 400±50 nm and 525±50 nm. Fiber angle distribution was quantified utilizing the algorithm developed in[49-50] and the OI definition previously described. OI and main direction of alignment were quantified over the material thickness (Fig. 4) to assess the validity of the 2D assumption adopted in this work.

Figure 4. Volumetric image analysis by multi photon microscopy revealed the 2D nature of the problem.

Multi photon imaging of isotropic (c) and very anisotropic (9.0 m/s) (d) dry PEUU, the materials were scanned along the thickness every 10 μm, n≥6 different samples were utilized. a, b Main angle of orientation and OI were quantified, showing constant values for both the main angle theta and the OI across the material depth. This result proved that the materials modeled in this work can be modeled as 2D structures. As expected, OI values were higher for the anisotropic than the isotropic PEUU. Conversely, the theta st.d. were higher in the isotropic samples than in the very anisotropic samples.

2.3 - Mechanical evaluation

In order to characterize in plane mechanics biaxial tests were conducted. Samples (n=5) were cut into 10 mm × 10 mm sections. Slices of polypropylene suture (Ethicon) were used to form four small markers of ~ 1 mm in diameter in the central region. Tests were performed in a physiological saline solution at room temperature adopting a Lagrangian membrane tension (T) controlled protocol as previously described [35-36, 45]. Equi-biaxial tension was imposed up to a maximum of 90 N/m to facilitate comparison with previous studies [35-36, 45]. Data post processing was completed using a preconditioned free-float reference, and was converted to stresses using measured specimen dimensions.

2.4 - AFM measurements of single fiber stress-strain behavior

PEUU or Dacron fibers were electrospun over a TGZ3 calibration grating (NT-MDT, Moscow, Russia ) and imaged by AFM (Dimension V, Veeco, Santa Barbara, CA) in tapping mode with a k=61N/m ACL cantilever (AppNano, Mountain View, Ca) to assess the dimensions of the suspended fibers. To precisely evaluate the applied load, the cantilever spring constant was measured using the vibration resonance method incorporated in the AFM proprietary software. Force-distance curves were performed on each imaged fiber as described in [40], in a regimen of small deflections. Curves were then converted to force-displacement and the curves at the middle point of the channels were averaged for comparison with the FEM simulations.

2.5 - Experimentally derived fiber network geometry generation

The network generator algorithm was based on three main steps aimed to create an simulated material geometry utilizing key measured architectural features. While the image analysis technique developed in [10] utilizes real fibers network detected on SEM images as inputs and produces orientation index, fibers angle distribution, intersection density, diameter, connectivity as outputs (Fig. 2 and Supplementary Fig. 1-5 left) the mesh generator introduced in the current section focuses on the opposite process. The algorithm utilizes orientation index, fiber angle distribution, intersection density and fiber diameter as input variables to generate artificial fibers network as outputs (Fig. 2 and Supplementary Fig. 1-5 right). The algorithm was implemented in Matlab (The Math-Works, Natick, MA) as follows.

• Step 1: Duplicate material intersection density (ID). It has been shown by image analysis that fiber intersections are homogeneously distributed over the biomaterial surface area [10, 34, 36]. Therefore, in this step a random distribution of points with the same biomaterial ID was generated to reproduce the original 2D spatial distribution of fiber intersections over a desired area.

• Step 2: Duplicate the fiber ODF. A Delaunay network algorithm [10, 25, 46] was applied to the cloud of fibers intersections generated in step 1. The resulting generated network was divided into sub regions aligned perpendicular and parallel to the preferred fiber alignment direction, respectively. In each subset, fiber intersections positions were modified by translating the fiber coordinates perpendicular or parallel to the preferred fiber alignment direction [8]. These translational displacements induced fiber alignment towards a desired direction and were adjusted until the desired degree of fiber ODF was obtained.

• Step 3: Duplicate material connectivity [26, 46]. The connectivity distribution (original Delaunay networks have higher number of connections when compared with the real material networks[10]) was controlled by simply eliminating a random fraction of fibers from the starting simulated networks. Isolated local networks of fibers and fibers with one connection only were eliminated to avoid singularities [28].

2.6 - Finite element (FE) simulations

FE simulations were performed in Abaqus 6.9 (Dassault Systèmes, Waltham, MA). Boundary conditions were imposed to reproduce the equi-stress conditions used in [45]. Due to the symmetry of the system, one quarter (500 μm × 500 μm) of the sample only was modeled, similarly to [26]. Constrains on the edges were: left (u_x=0), bottom (u_y=0), top (u_y=L_y × L_y), right (u_x=L_x × L_x). Large deformations [45], Newton-Raphson method [7-8] were activated on the FEA solver. An incompressible Yeoh strain energy function was used:

$$\psi =\sum _{\mathrm{i}=1}^3{\mathrm{C}}_{\mathrm{i}0}{({\mathrm{I}}_{\mathrm{C}}-3)}^{\mathrm{i}}$$ (1)

where Ψ is the strain energy, C_i0 are material parameters, I_C is the first strain invariant of the right Cauchy Green Stretch tensor C=F^TF, where F is the deformation gradient tensor. Generally, C₃₀ is two order of magnitude smaller than C₁₀ and C₂₀ thus was assumed negligible [51] this was further verified in fitting the experimental data showing no loss of accuracy. The forces acting along the vertical and horizontal directions of the model (aligned with the circumferential and longitudinal directions of the electrospun mandrel, respectively) were obtained by the sum of the nodal contributions at the top and right edges of the model multiplied by a scaling factor obtained by the ratio between the real sample and the model cross sections. The model thickness was estimated by the image analysis technique developed previously [10]. 2-D stress/displacement truss elements T2D2 and T2D2H were tested, since bending and stretching are considered the main deformation modalities [38 39] for the studied materials beam elements were considered as a more suitable alternative . The full set of 2D, non pipe, beam elements available in Abaqus 6.9 has been tested including B21, B21H, B22, B22H, B23, B23H. Due to the L/D ratio [26, 30-31] of the fibers Timoshenko (shear flexible) beams elements B21, B21H, B22, B22H were preferred to the Euler-Bernoulli (slenders) beams B23 and B23H. Finally, the 3-node quadratic beam B22 was selected, this choice was supported by the non liner deformations measured by the AFM test on a single fiber previously described. Fiber intersections [30] were modeled as rotating joints with negligible rotational stiffness, as done in [37]. Similarly, fiber friction was assumed to be negligible [46]. The number of beam elements was dictated by the real material intersections density, for an area of 250000 μm², 377932, 316640, 110957, 77271, 20746 B22 elements were utilized for the isotropic PEUU, anisotropic PEUU, micro particles integrated, VSMCs integrated and dacron scaffold respectively. Since the elements number was strictly imposed by the real material geometry mesh independency of solution was not tested. In contrast, model size effects were studied by identifying the proper Representative Element Volume (RVE) size. Changes in the initial elastic modulus vs. mesh size were quantified as suggested in [26, 46]. Solution stability depends on the model size [26, 52-53], details on the model size estimation are provided in the next section. A constant fiber diameter value was utilized for the whole fiber population [6, 25, 27]. The initial configuration was assumed to be stress free [26]. Fibers were modeled as straight at the stress-free configuration. The initial tortuosity and uncrimping effects were modeled throughout the non-linearity of the strain energy function [9]. In addition it has been shown that filament undulations only have a minor effect, merely postponing the transition from bending to stretching [29].

To match the biaxial data, the resulting Lagrangian stress P vs. stretch curves were first calculated based on C₁₀ and C₂₀ values from linearized estimates for elastomeric materials (E=5-20 MPa [43]) and then were systematically varied (using steps of 0.25 MPa) until r² ≥ 0.9 for the totality of the scaffolds utilizing the same raw material. Initial elastic modulus E₀ was derived from the C₁₀ Yeoh [51] strain equation coefficient (Eq. 1) and G=2C₁₀, E=2G(1+2)X. Stress vs. strain [45] curves, nodal displacements maps, as well as force deformation curves for single fibers [40] were obtained directly by Abaqus CAE. E_f single fiber Green strain for each fiber within the network and NAR vs. strain [19, 54-55] were derived from simulation of strip biaxial stress state.

In order to estimated NAR values the resulting deformed network configurations were imported and further processed in Matlab, where the polygons space complimentary to the space occupied by the fiber network were detected [42]. Each void was approximated by an ellipsoid, major axis were then calculated for the complete set of ellipsoids representing the total scaffold void space. Finally, NAR was defined as the major axis ratio, values were averaged throughout the entire voids population. NAR variation was estimated from each of the inter fibers polygons change of shape. NAR variation – strain curve was obtained analyzing the NAR variation in subsequent strain configurations using the method presented in [19]. The prediction was compared with its corresponding experimental data from [19]. Single fiber force-displacements curves measured by AFM were used to verify the accuracy (micro scale R² in table 1) of FE single fiber model prediction. The latter was created utilizing the same conditions described above for the fibers network models including element type (B22), constitutive equation (eq. 1) and constants selection (C₁₀, C₂₀, C₃₀) . To summarize same model formulation was utilized to predict biaxial response (macro scale), NAR vs. stretch curves and E_f histograms (meso scale) and, single fiber force displacement response (micro scale).

Table 1.

Biaxial response, and AFM R² values for experimental data and model prediction.

MACRO Scale	Isotropic PEUU	Anisotropic PEUU	VSMCs PEUU	Micro-Spheres PEUU	Isotropic Dacron
R2	0.9973	0.9964	0.9848	0.9101	0.9793

MICRO Scale	PEUU				Dacron
R2	0.9968				0.9940

2.7 - RVE size determination

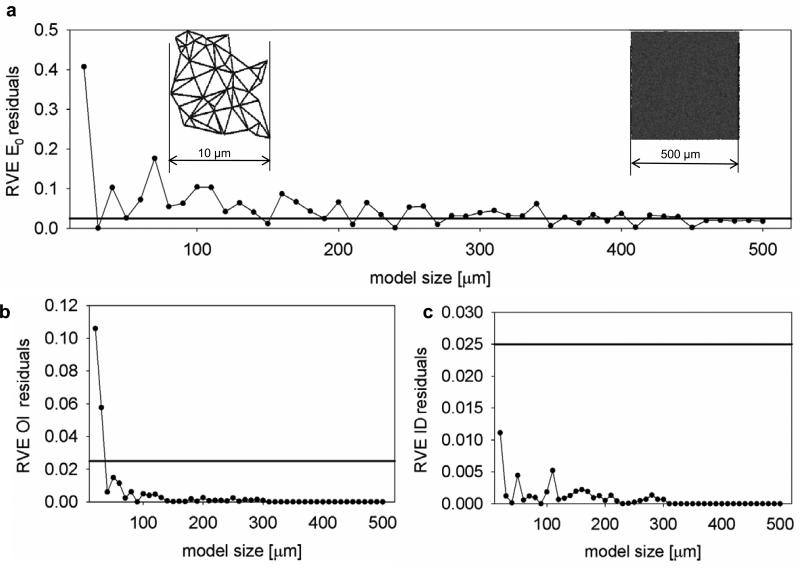
Appropriate RVE sizes were calculated for the macroscopic, mesoscopic and microscopic scales, respectively. For the macroscale, FE simulations under equi-biaxial stress conditions were performed on isotropic PEUU RVE models of increasing sizes, ranging over 10-500 μm in steps of 10 μm, representing one quarter of the total model size. Using the predicted strains, an averaged RVE effective modulus E_RVE for the current size was then computed [26, 52, 56]. The effective modulus is a well accepted variable of interest to estimate RVE relevant for the macro scale mechanics [52-53, 57]. Different phenomena with different characteristic lengths require different model/RVE sizes [58]. As a consequence, while effective modulus E_RVE was utilized to identity appropriate model size to predict the biaxial mechanics (macro scale), meso scale architectural features such as OI and ID were utilized to capture appropriate model/RVE size to predict NAR vs. strain response (meso scale).

The variables of interest residuals were determined using:

$${\mathrm{RVE}}_{\text{residuals}}=\frac{\mathrm{abs}[\mathrm{y}(\mathrm{n}+1)-\mathrm{y}\left(\mathrm{n}\right)]}{\mathrm{y}\left(\mathrm{n}\right)}$$ (Eq. 2)

where y(n) represented one of the studied variables (E_RVE, OI, ID), and n a sequence of square shaped mesh models with side lengths within the 10-500 μm size range. An acceptable RVE size was obtained when the residuals were smaller than the threshold of 2.5% [52, 56-57].

3 - RESULTS

3.1 Fiber networks

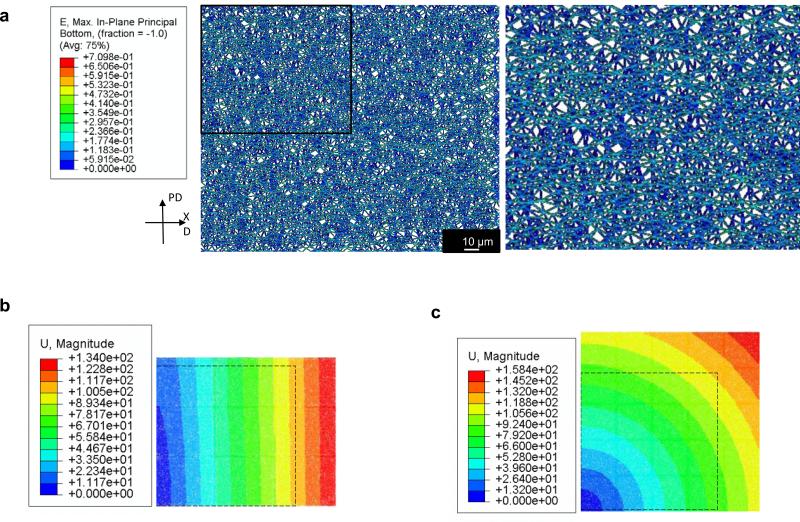
Results of the image analysis fully characterized scaffold micro geometry (Fig 2 a-e, Supplementary Fig. 1-5). Transmural analysis demonstrated that both OI and preferred fiber direction remained constant over the material thickness (Fig. 4), supporting the 2D assumption adopted in this model. The mesh duplication algorithm ability to develop geometrically real material fiber networks (Fig.2 a-e, Supplementary Fig. 1-5) was corroborated by the quantitative analysis presented in (Fig.1 F-H). ID, OI, D and connectivity (data presented as mean ± std), were individually controlled by the mesh generator algorithm and quantified for the first time [2-4, 6-9, 11-12, 25-31, 46]. Optimal RVE sizes for the macroscopic, mesoscopic, and microscopic scales were found to be 880 μm, 80 μm, and 40 μm, respectively (Fig. 6). Using the symmetry of the loading conditions, only one quarter of the material was modeled. As a consequence, final mesh edge dimensions of 1000 μm (reduced to 500 μm Fig. 6 a) and 228 μm (reduced to 114 μm Fig. 6 b) were utilized to predict biaxial response and the cellular deformations, respectively.

Figure 6. Representative volume element (RVE) estimation.

a, nodes (fibers intersections) and elements for generation of isotropic PEUU models of increasing size (from 10 to 500 μm). b OI, ID, D versus model size showing the stabilization of the architectural features as the model size increases. Residuals vs. model size for the macroscopic mechanical response (c), OI (d), ID (e). The mechanical response, OI, ID and D were stable at 880 μm > 140 μm > 60 μm >0.64 μm respectively. The totality of the simulations discussed in this work were performed on meshes of 500 μm representing by symmetry a quarter of a sample of 1 mm. This size was large enough to minimize size effects as highlighted by (RVE macro scale > 10 fiber diameter) [26], (RVE macro 1 mm RVE meso 50 μm )[37], (RVE macro 1 mm) [52];

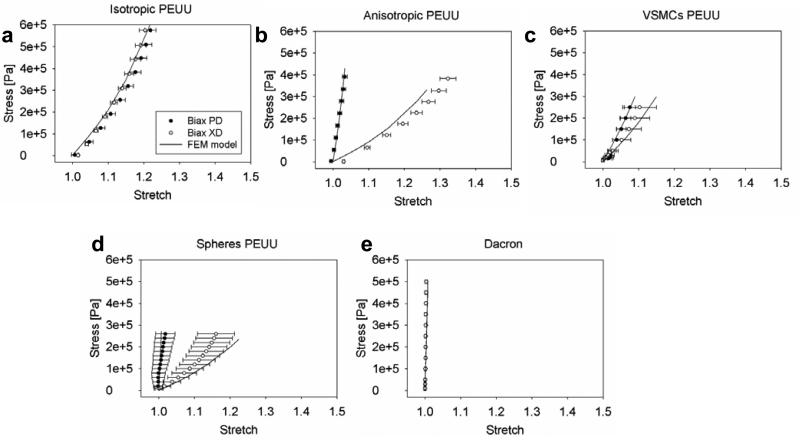
3.2 - Macro scale level validation and prediction

FE model mechanical response predictions for isotropic PEUU, anisotropic PEUU, VSMCs PEUU, microspheres PEUU, and isotropic Dacron (Fig.5) were in good agreement (Table 1) with the experimental data. In addition, displacements maps representing a quarter (500 μm × 500 μm) of the sample area 1 mm × 1mm (Figs. 9 b-c) showed consistency between the displacement field and the biaxial response prediction. In addition to corroborating the biaxial prediction, displacement maps provided additional detail on the fibers kinematics proofing the uniformity of the displacement field over the entire RVE. As expected, anisotropic materials (Fig. 5b, d, Fig.9 b) showed higher displacement values along the most compliant directions, whereas isotropic materials (Figs. 5 a,c,e and Fig 9c) exhibited higher displacement values at the top right corner of the meshes in a typical isotropic displacement field.

Figure 5. Macro scale level validation and prediction.

Biaxial response prediction vs. experimental data and deformation maps: u distribution on a quarter of the sample 500 μm × 500 μm. a, e the network topology alone was capable of recapitulating the mechanics of five different materials, data were presented as mean ± st.d. Dashed lines in the deformation maps represent the network models starting configuration, warm colors (unit on the legends, μm) indicate the highly displaced elements of the mesh. Bulk responses consistently highlight mechanical isotropy for isotropic PEUU, VSMCs integrated PEUU and isotropic Dacron a, c, e. Similarly, anisotropic PEUU and spheres integrated PEUU showed anisotropic characteristics.

Figure 9. Preferential loading pathways formation.

a In plane maximum green strain mapping on anisotropic PEUU under equistress biaxial conditions enabled to visualize the formation of preferential loading pathways spanning the whole length of the sample and oriented along the material most compliant direction. b, c consistently with the bulk response in figure 5 the displacement patterns highlight differences in mechanics between the anisotropic and isotropic PEUU.

3.3 - Meso scale level validation and prediction

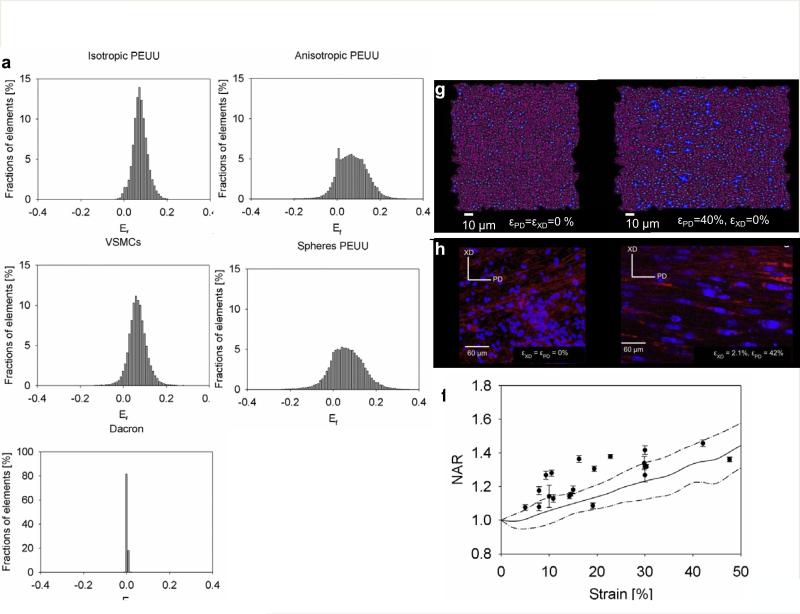
Single fiber Green's strain, E_f under full loading was derived for each fiber within the simulated scaffold. This information was presented as histogram reporting the percentage of fibers within the fibers network characterized by E_f vs. E_f . In order to attain comparable measurements of deformation from the simulations, the E_f histograms were derived at an equi-stress of 200 kPa. Finally, E_f histograms were determined for each scaffold type (Fig. 7 a-e). The mean E_f and the full network macroscopic stretch (model instantaneous side length divided by the model initial side length ) at 200 kPa for each fiber network were compared in (Table 2). Model prediction for NAR vs. strain were provided in (Fig.7 f-h) showed good agreement with the experimental data [19] (Fig.7 f) and a good capacity to qualitatively (Fig.7 g-h) represent inter-fiber void deformations. The latter was used as a metric to represent cell nuclei deformations.

Figure 7. Meso scale level validation and prediction.

a, e fiber E₁₁ histograms for isotropic PEUU, anisotropic PEUU, VSMCs PEUU, microspheres PEUU, isotropic Dacron. In order to make comparable measurements, histograms were obtained at equi-stress of 200kPa. The width of the histograms increased with the level of anisotropy showing a higher fraction of fibers under compression (a, c isotropic materials vs. b, d anisotropic materials). As expected, higher stiffness reported for the Dacron induced tighter distribution of E_f. The ID had an impact on the peak in the E_f distribution, peak value increased with increasing ID, i.e., the denser the fiber network, the higher the E_f on a single fiber (a-d, Tab.1). Model prediction for NAR vs. strain are provided in (f-h), and compared quantitatively (f) and qualitatively (g-h) with the experimental data[19], inter fibers voids are represented in dark purple at ε_PD=ε_XD= 0% (starting configuration g-h left) and ε_PD= 40%, ε_XD= 0% (final stretched configuration g-h right) whereas the fibers are represented in magenta, figure h was readapted from[19].

Table 2.

Bridging scale lengths. The macroscopic biaxial data (Fig. 5 a-e) enabled the estimation of the initial elastic and shear moduli at the macro scale and the prediction of NAR vs. strain characteristic (Fig. 7 f-h) and single fiber deformations (Fig. 8 a-d) at the meso and micro scales respectively. Similarly, the AFM data enabled to determine the initial elastic and shear moduli at the micro scale and the prediction of NAR vs. strain characteristic and biaxial response at the meso and macro scale respectively. E_f mean from the fiber networks and E_f histograms (Fig. 7 a-e) can be compared to the global stretch prediction at macro scale length. Single fiber geometry characterization from AFM, (Fig. 8 c-d) data presented as mean ± st.d.

MACRO Scale	Isotropic PEUU	Anisotropic PEUU	VSMCs PEUU	Micro-Spheres PEUU	Isotropic Dacron
E0[MPa]	7.5	7.5	7.5	7.5	180
G0[MPa]	2.5	2.5	2.5	2.5	60
λPD at 200 kPa	1.095	1.017	1.063	1.005	1.003
λXD at 200 kPa	1.094	1.184	1.108	1.201	1.003

MESO Scale	Isotropic PEUU	Anisotropic PEUU	VSMCs PEUU	Micro-Spheres PEUU	Isotropic Dacron
Mean E11 at 200kPa	0.075±0.033	0.070±0.067	0.066±0.043	0.063±0.078	0.0025±0.0023

MICRO Scale	PEUU	Dacron
E0[MPa]	7.5	180
G0[MPa]	2.5	60
D [nm]	490±280	740±70
L [nm]	2300±500	1950±120

3.3 - Micro scale level validation and prediction

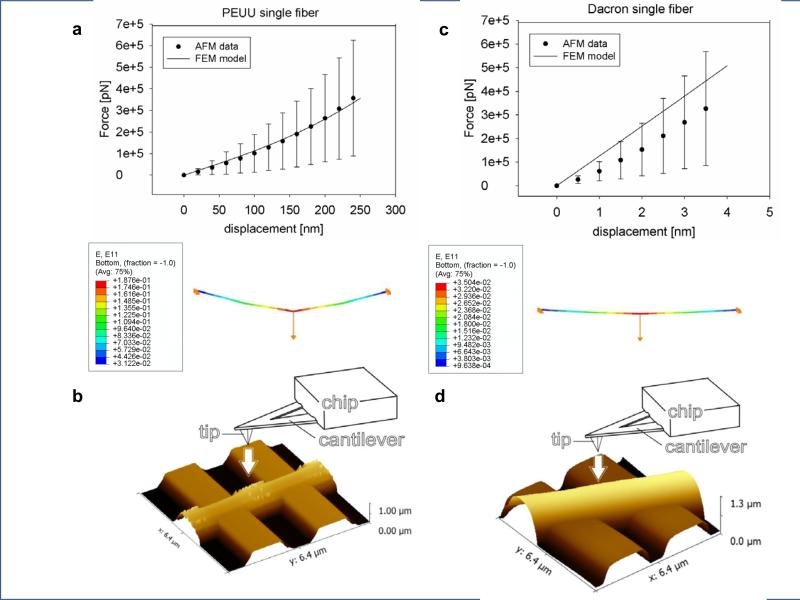
Single fiber model predictions obtained by FEM agreed well (Table 1) with the AFM single fiber force-displacement data for both PEUU and Dacron (Figs. 8 a,c). Consistently with experimental observations (Fig.8 b, d), E₁₁ single fiber prediction (Fig.8 a, c) showed higher fiber deformation values at the point of fiber-AFM cantilever contact. The fiber length and diameter used to define fiber geometry in the FEM model were measured by AFM microscopy (Fig.8 b, d), (Table 2).

Figure 8. Micro scale level validation and prediction.

a, c single fiber model prediction and AFM single fiber force-displacement data for both PEUU fibers (n=5) and Dacron fibers (n=5) (Fig.4 A, C). E₁₁ prediction for PEUU and Dacron single fiber (Fig.4 A, C) (data were presented as mean ± st.d.) Note the different scale in the two X axes.

4 - Discussion

4.1 - Geometrical considerations

A modeling strategy to guide fibrous material design towards the simulation of native tissue mechanics by connecting structure with macro-level mechanical behavior was presented. The mesoscopic level prediction showed the potential to provide a better understanding of the local mechanical environment surrounding particulate inclusions as well as cellular mechanical and metabolic response to local micro-structural deformations in engineered and native tissues. The adoption of a structural deterministic approach was further justified by the experimentally observed [37] and numerically investigated [7, 12] non affine and heterogeneous deformations. Similar to the real fiber topologies [10, 34], the simulated networks reported a realistic coordination [46] with a minimum value of 2, a variable maximum and a maximum of 3 in the connectivity histogram (variable coordination with peak at 3).

The importance of quantitative comparison of real and simulated meshes architectures has been emphasized previously [46, 58]. Discrepancies between the real material and the simulated fibers networks topologies are generally partially quantified [46, 58]. Fibers intersection density, diameter, orientation and connectivity values have never been fully reproduced and quantified by a network mesh generator algorithm [10]. In addition, the limited size of the unit cells affects the capability of these models to elucidate the complex multi scale nature of fibrous material and native tissues [26, 46, 52, 56]. For example heterogeneous deformation at micro level and web-like structures formation under strain reported by Stella et al. [37] is not reproduced. This class of models generally lacks of experimental validation at meso and micro level. For instance, NAR-strain curves, equivalent descriptors of material-cells interactions [19, 54] or AFM single fiber responses [33, 40] have never been reported. This limitation and the high computational demand of multiscale solutions [9, 28, 46] ultimately lead to a relatively modest capacity of bridging the scales [46, 58] .

The adoption of the mesh design space (Fig. 2 - 3) highlighted the flexibility of the network generation algorithm in any type of material in the OI-ID-D space. This is particularly valuable as it enables to assess novel materials prior to their actual fabrication with respect to their multiscale behavior. The selection of OI, ID and D as design variables was dictated by their well reported influence on cell proliferation [42] (effects OI and D on fibroblasts) [1, 17, 33], migration, lineage specification, morphology (effects of OI, ID, D on chondrocytes, neonatal rat heart cells, mesenchymal stem cells), and inclusion micromechanics [34, 41] (effects of ID and OI on fibers and micro inclusions). Each variable can be independently controlled during the fabrication process. For example in electrospinning, for a given difference in voltage, and gap distance, OI, ID and D can be independently controlled by mandrel velocity [45] (OI:0.5-0.7), mandrel rastering velocity [34, 36] (ID: 0.02-0.06 intersections/μm²), and polymer/solvent concentration [32] (D: 0.1-10 μm).

Furthermore, our choice of design variables enabled the identification of material “clusters” characterizing the main electrospinning modalities: wet fabrication/micro integration [44] and dry fabrication, as well as distinguishing between high/low viscosity polymers (Fig. 2 - 3). In addition to the five materials described earlier, several others ( 0.3 cm/s ,1.5 cm/s, 30 cm/s rastered wet processed PEUU [34], wet processed poly(ester carbonate urethane) urea (PECUU), anisotropic Dacron, highly anisotropic PEUU [10], as well as mixed fiber populations of PEUU and polycaprolactone in volume fractions of 75/25, 50/50, and 25/75 [36]) have been included in the 3D design space to further prove the capacity of this classification to efficiently group categories of materials on the basis of their fiber network architectural features. Predicting the isolated or combined effects of OI, ID and D on the scaffold mechanics at macro, meso and single fiber levels has significant implications for other fabrication and polymer processing technologies such as melt electrospinning [59], spinneret-based tunable engineered parameters (STEP) [60], or excimer laser ablation [17] which are able to provide better definition and higher degree of control over the scaffold architecture than dry or wet electrospinning.

4.2 - RVE size

RVE sizes were consistent with other studies [26, 52, 56]. This suggested that for a given physical system the studied variables were characterized by different RVE sizes, which were in turn dictated by the characteristic lengths of the observed phenomenon. Thus as expected [26, 52, 56], the bulk response was stable at the macro scale (880 μm ) whereas the topology related OI, ID and D at the meso (80 μm - 40 μm), (Fig. 6) respectively. All simulations (Fig. 5) were performed on meshes of 500 μm × 500 μm size, representing by symmetry one quarter of a 1 mm sample. This length was determined to be large enough to minimize size effects, consistent with findings reported on previous studies (RVE macro scale ≥ 10 fiber diameter) [26], (RVE macro=1 mm, RVE meso=50 μm ) [37], (RVE macro=1 mm) [52]. This result was also corroborated by the small values for the st.d reported in (Fig. 2 f, g, h) for the generated geometries (n=5 meshes/material).

4.3 - Mechanics

The simulated network geometries alone were capable of recapitulating the mechanical behavior of each of the five different scaffolds using the same material model and model parameters. The results in Fig.5 A-E validated the model and, more importantly, provided an example of its predictive capacity. The impact of any combination of the described architectural features together with the material properties (Eq. 2) can be estimated on a generic mesh model. For example, the effect of changes in mechanics due to OI were evidenced by comparing isotropic vs. anisotropic PEUU (Fig.4 a-b) or VSMCs vs. spheres integrated PEUU, which exhibited comparable ID and D but different OI [34, 36](Fig.2 f-h).

As expected, a higher degree of fiber alignment corresponded to higher mechanical anisotropy [45]. Similarly, effects of ID were evidenced by comparing anisotropic PEUU and spheres integrated PEUU, which had comparable OI and D but different ID [34, 36]. As expected, Dacron mechanical response (Fig.2 E) was significantly stiffer than the other materials with E =180 MPa, G =60 MPa vs. E =7.5 MPa, G =2.5 MPa for PEUU (Table 1). PEUU predicted E was in good agreement with studies in the literature that estimated values between 34 MPa [43] and 2.5 MPa [44].

The high degree of detail on the micro architecture provided by the experimentally derived mesh generation simplified the form of the strain energy equation and, more importantly, greatly reduced the number of constants necessary to identify material properties. Geometrical information were already embedded into the mesh voiding the need for a statistical formulation to represent the fiber angle distribution. For the same given chemistry four different materials have been modeled with two strain energy function constants [51], C₁₀ and C₂₀ (Eq. 1, methods section), whereas in previous structural statistical approaches [45] 16 parameters were necessary(e.g. the modified Cauchy distribution [45] requires 2 parameters to describe fiber distribution, this information is than coupled with 2 more constants utilized in the constitutive equation giving 4 constants/material for a total of 16 to model isotropic, anisotropic , VSMCs and micro particles integrated PEUU).

In addition, these findings confirmed that, given specific intrinsic properties, the topology is fully dictating the material mechanics (e.g. isotropic and anisotropic scaffolds are characterized by the same elastic modulus but different OI)[34, 36, 41]. Few structural deterministic models described in literature [3, 9] utilized biaxial equi-stretch data. In contrast, equi-stress biaxial data, which are widely accepted as the ideal metric for assessing engineered constructs mechanics in the physiological range [19, 33, 35], have never been utilized for structural deterministic model validation/prediction.

Due to the complex nature of fibrillar, 3D matrix adhesions, focal adhesions and focal complexes [20, 55] a definitive parameter for mechanotransduction at the meso level still remains to be determined. Two likely mechanisms of strain transfer between the cells and the substrate might involve fiber stretch and/or inter fiber voids deformations. This speculation was the impetus for the study of two different parameters at the mesoscopic level: E_f and NAR. Consistently with the findings of Sander et al. [3], the width of the histograms increased with the level of anisotropy, showing a higher fraction of fibers undergoing compression (isotropic materials Fig.7 a, c vs. anisotropic materials Fig.7 b, d). As expected, the higher stiffness reported for the Dacron induced a narrower distribution of E_f values (Fig.7 E). Interestingly, the peak value of the E_f distribution increased with increasing ID (Fig.7 A-D, Tab.2). This result was analogous to a previous report by Lake et al. [8] in which mean fiber stretch increased with agarose concentration within the modeled collagen-agarose co-gels. The macroscopic stretches of the 1 mm samples (Table 2 MACRO) were correlated to the fiber network mean E₁₁ (Table 2) showing comparable results (anisotropic PEUU at equi-stress of 200 kPa λ_y = 1.01, λ_x = 1.17 and E_f = 0.07) with the works of Lake et al.[8] and Sander et al. [3] where a collagen gel of about E = 6.8 MPa was exposed to biaxial equi-stretch of 1.21 producing a mean fiber stretch of 1.11±0.09 (E_f= 0.11).

In plane maximum fiber Green's strain under equi-stress biaxial conditions enabled visualization the formation of preferential loading pathways spanning the entire length of the sample and oriented along the most compliant direction of the material (Fig. 9). This effect, experimentally observed previously in fibrous materials [37] and described in native tissues [32-33], was not fully captured before by modeling approaches utilizing the volume averaging/unit cell approach [46]. The single fiber predictions (Fig.8) were produced utilizing the same material constants (C₁₀ , C₂₀) [51] used at the macro and meso scales (Tab. 2) and derived by the biaxial data. Similarly, AFM data could be utilized to estimate C₁₀ and C₂₀ at the micro scale and predict the mechanical behavior at the macro and meso scales. This bidirectional validation/prediction loop proved the capacity of this methodology to bridge the different length scales.

4.4 - Limitations

In the present work, experimentally derived fiber networks were produced and the discrepancies between the real and simulated fiber networks quantified. In spite of these advances this work requested several simplifying assumptions: the model network was 2D only, fibers were modeled as straight with no tortuosity and with constant diameter, cells/inclusion contribution was ignored. We also note that the parameters used to quantify the 2D fiber geometry, while comprehensive and shown to be produce the desired results, have not yet been shown to be a necessary and complete set. Moreover, they are dependent on the ability to be derived from experimental imaging data, which can be prone to errors. Continued work in this area will be necessary to further the present results. We note finally that fiber intersections were modeled as rotating (i.e. pin) joints. All available experimental data, coupled with the close results obtained in the present study suggest that rotational joint stiffness is a most small and can be neglected.

4.5 - Conclusions

The developed approach has implications for (1) gaining insight on the intricate relationship between fabrication variables, structure, and mechanics to manufacture more functional devices/materials [32-33], (2) elucidating the effects of cell or particulate inclusions on global construct mechanics [34], and (3) fabricating better performing tissue surrogates [1, 5, 17] that could recapitulate native tissue mechanics both in terms of in-plane behavior (e.g. non linearity, anisotropy and elastic moduli [35]) and of out-of-plane behavior (e.g. bending stiffness [36]). The presented methodology was able to duplicate the fibrous geometry and to predict the effects on mechanics of critical material micro architecture parameters (fibers intersections, fiber connectivity, fiber orientation, fiber diameter) at different length scales (macro-meso-micro). To conclude, results demonstrated the capacity of approaches that connect fibrous materials structure and function thus providing a critical tool to assist material design and to elucidate target native tissue mechanics.