Accurate scoring of non-uniform sampling schemes for quantitative NMR

Abstract

Non-uniform sampling (NUS) in NMR spectroscopy is a recognized and powerful tool to minimize acquisition time. Recent advances in reconstruction methodologies are paving the way for the use of NUS in quantitative applications, where accurate measurement of peak intensities is crucial. The presence or absence of NUS artifacts in reconstructed spectra ultimately determines the success of NUS in quantitative NMR. The quality of reconstructed spectra from NUS acquired data is dependent upon the quality of the sampling scheme. Here we demonstrate that the best performing sampling schemes make up a very small percentage of the total randomly generated schemes. A scoring method is found to accurately predict the quantitative similarity between reconstructed NUS spectra and those of fully sampled spectra. We present an easy-to-use protocol to batch generate and rank optimal Poisson-gap NUS schedules for use with 2D NMR with minimized noise and accurate signal reproduction, without the need for the creation of synthetic spectra.

1. Introduction

Non-uniform sampling (NUS) affords significant time-savings in acquisition of NMR data by sampling only a percentage of the indirect time domain, extending the range of NMR to highly multidimensional experiments as well as to protein systems with poor signal-to-noise [1–3]. Recent advances in reconstruction and sampling methods for NUS have focused on increasing sensitivity and resolution over reduced or similar measurement times [1,4]. The utilization of the time savings and sensitivity gains of NUS in quantitative NMR experiments, such as CPMG relaxation dispersion, T₁, T₂, and T₁ρ relaxation, and heteronuclear NOE experiments, are only now starting to be explored [5]. Artifacts from the reconstruction and the sampling scheme can be tolerated for multidimensional qualitative experiments, but are detrimental in quantitative NMR experiments that rely entirely on measured peak intensities. Many NUS reconstruction methods have been developed [6–11], with a few, such as compressed sensing, SIFT (Spectroscopy by Integration of Frequency and Time domain information), and CLEAN promising the greatest accuracy of intensity reproduction over a high dynamic range [12–17].

The NUS scheme is a crucial determinant of the reconstructed spectral quality. Sensitivity can be increased by adding a forward weight to the data collection so that a higher percentage of the early (strongest) portion of the exponential decaying time-domain signal is collected [2,18,19]. On the other hand, randomization of the sampling scheme helps prevent systematic violation of the Nyquist sampling theorem and is an important factor in minimizing spectral artifacts [18,20–22]. Many sampling methodologies balance the requirement for randomization and the desire for forward weighted collection [1,2,21–23]. Still, it has been found that the quality of a sampling scheme depends heavily on the random seed used to create the scheme [1,24]. Some methods, such as sine-weighted Poisson-gap sampling [1,24], have demonstrated a weaker dependence on the random seed compared to other random NUS methods, such as complete random, hybrid uniform/non-uniform, and exponentially weighted random sampling. Still, an increase in dependence on the random seed in reconstruction quality with Poisson gap schemes has been suggested when a higher percentage of points or lower number of reconstructed increments are used, since the points available for selection become limited [1]. Other sampling methods make use of a deterministic schedule, eliminating the need for a random seed altogether [25]. However, these deterministic schedules require knowledge of the spectra prior to NUS data collection and therefore are not suited for all situations. It has also been suggested that random sampling schemes are more robust and only slightly less sensitive than knowledge based sampling [26].

2. Performance of Poisson-gap sampling schemes

We chose to use the sinusoidal weighted Poisson-gap sampling method to generate schemes for quantitative NMR [24]. In order to evaluate the performance of sinusoidal weighted Poisson gap sampling, with increments routinely used in quantitative 2D NMR, we tested a variety of conditions varying in sampling completeness (%NUS) and total number of increments. For a given Poisson-gap sampling condition (%NUS and total increments) 2,000 to 10,000 schemes, from code derived from reference 24, were generated (see details in SI). Various synthetic 2D ¹⁵N HSQC and ¹³C HSQC spectra were created with linewidths and number of resonances approximating an 18kDa protein. Discrete Fourier transform (DFT) of non-reconstructed data and non-convex iterative re-weighted least squares compressed sensing reconstruction [12,27] were used with the NUS synthetic data to create 2D spectra with the programs MDDNMR and NMRPipe [8,12,28]. Following reconstruction, identical processing was performed on all data. Minimal apodization, by a cosine window function, was utilized in the reconstructed dimension. The quality of each reconstructed spectrum was measured by taking the total RMS difference between the full linearly sampled synthetic spectrum containing no noise and the NUS reconstructed spectrum. The RMS calculation was performed with the NMRPipe software package [28]. The resulting RMS can be considered a measure of the total sampling artifacts and accuracy of peak reconstruction because it is sensitive to peak position, peak shape, and peak intensity in the reconstructed spectrum.

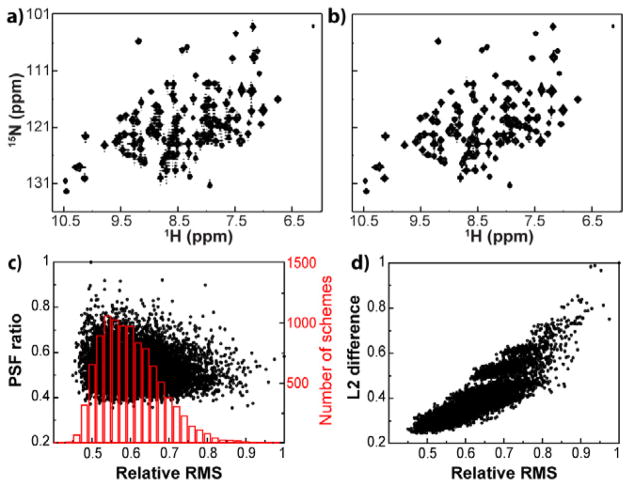
Using 60% NUS with a typical number of increments in the indirect dimension (e.g. 128 complex pairs) we found that a strong dependence of RMS on random seed in Poisson-gap sampling emerges (Figure 1). Examples of the worst and best RMS reconstructed spectra are shown in Figures 1a–b, respectively. The severity of the sampling artifacts is also demonstrated by the difference spectra between the reconstructed and uniformly sampled spectra for the best and worst RMS schemes (SI). A very small percentage of schemes give a greater than 2-fold improvement in reconstruction compared to the worst scheme. For example, we found that only 0.05% (40/10,000) of the schemes lead to low artifact intensity in the best 5% of measured RMS (Figure 1c -histogram). This necessitates the generation and evaluation of a very large number of schemes (≫200) in order to obtain at least one optimal scheme. It is worth noting that the histogram for the Poisson-gap generated schemes in Figure 1c is skewed towards ‘good’ RMS, in agreement with reference 24, which found that as opposed to other random-seed based schemes the Poisson-gap method produces a large percentage of schemes that have very little variation in performance. The loss of some of this performance for data sets with fewer total reconstructed complex pairs (< 1024) as discussed in reference 1 is also apparent here.

Figure 1.

Comparison of NUS schedules and currently used scoring methods. The (a) worst and (b) best reconstruction based on RMS for identically processed synthetic data containing no noise. (c) The PSF ratio (max side-lobe:zero frequency peak) of the sampling scheme does not accurately predict artifacts in reconstructed spectra (black circles). The number of NUS schedules that result in a given reconstruction RMS is shown in red. (d) The l₂ norm, or the non-normalized root mean squared difference between a linearly sampled synthetic spectrum and the NUS spectrum, is able to predict artifacts in other spectra sampled with the same NUS schemes (black circles).

3. Current NUS scoring functions

We next examined the best way to select an optimal sampling schedule, without batch reconstruction. Various methods to score NUS schemes prior to data collection have been given [1,29,30]. These make use of the point-spread-function (PSF) of the sampling scheme in some way. The PSF is the frequency domain response of the sampling schedule. Therefore the PSF is an indicator of the quality of an NUS schedule. A comparison of current NUS scoring functions was performed using the aforementioned synthetic ¹⁵N-HSQC-like dataset. A commonly cited scoring function, the PSF ratio [2, 29], is expected to predict with the lowest ratio the scheme that yields the lowest artifacts. However, this was not observed in our simulations. In 10,000 sampling schemes the PSF ratio was unable to predict the amplitude of reconstruction artifacts (RMS) yielding a correlation coefficient of ρ = 0.09 (Figure 1c). Another popular scoring method makes use of the difference or l₂ norm between NUS and fully sampled signal [1]. To obtain an l₂ norm, fully sampled and NUS synthetic 2D spectra containing 4 to 20 randomly positioned cross peaks were compared, similarly to the RMS calculation. Not surprisingly, the l₂ norm method was able to predict the propensity of a sampling scheme to produce artifacts in a 2D experiment (ρ = 0.87) (Figure 1d). However, the l₂ norm requires reconstruction of a synthetic spectrum for each sampling scheme, which is time-consuming and not a straightforward task. Thus there is a need for a robust, fast, and easy to use scoring method.

4. A quantitative NUS scoring method

In order to empirically score Poisson-gap sampling schemes we first considered the two conflicting characteristics that must be balanced to obtain a spectrum with high sensitivity and minimal artifacts. These two elements are 1) forward weighted collection to increase sensitivity and 2) random selection of points to reduce spectral artifacts. A score was developed to determine how well a sampling scheme follows the desired weight of Poisson-gap sampling. This was based on the probability mass function (PMF) of a sinusoidal weighted Poisson gap distribution:

$${\beta }_{\mathit{PMF}}=({\lambda }^k/k!)e^{-\lambda }$$

which gives the probability of a gap, k, between increments (e.g. between two consecutive points, k=1) and where λ depends on a sinusoidal weight of the increment position defined in reference 24 as:

$$\lambda =\alpha sin\theta$$

where α is the weighting factor and θ varies from 0 to π/2 as more increments are selected. A score to account for randomness was also designed. This takes the summation of a two point moving average of the point-spread function:

$${\beta }_{\mathit{PSF}}=\sum _i[\mathit{PSF}(i)+\mathit{PSF}(i+1)]/2$$

where PSF(i) is the real point spread function of the sampling schedule at frequency i. The zero-frequency peak is omitted in the summation so that only PSF artifacts contribute to the score. We found that by de-weighting the first and last points of the PSF, or the frequencies closest and farthest from the reconstructed peak, the β_score became a more accurate predictor of the quality of the sampling scheme. An empirically derived combination of the 2 scores was found to give the best results:

$${\beta }_{\mathit{score}}={\beta }_{\mathit{PMF}}{w}_{\mathit{PMF}}+{\beta }_{\mathit{PSF}}{w}_{\mathit{PSF}}$$

where β_score is the score for the NUS scheme and w_PSF and w_PMF are empirically derived weights. w_PSF = 2/3 and w_PMF = 2^−64/td, where td is the total number of complex pairs in the final reconstructed spectrum. Thus, as a higher number of complex pairs are collected the β_PMF score becomes a better predictor of sampling scheme quality. The value of 64 was chosen because, in our experience, this is near the lower limit of complex pairs normally acquired. It is worth reemphasizing that the weights given to each score are completely empirical, but the overall score as shown below performs very well across a wide range of sampling conditions.

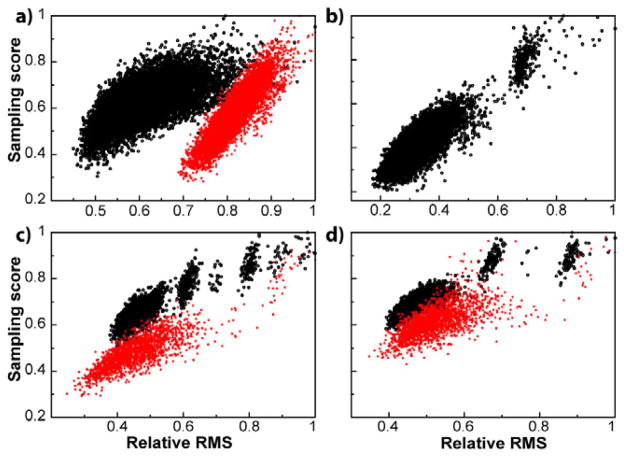
In 10,000 sampling schemes under the same conditions as above we found a very good correlation between our NUS score and the RMS of reconstructed spectra (with a correlation coefficient of ρ = 0.66) (Figure 2a). The top 10 schemes predicted by the scoring function are in the top 20% of the sampling schedules. In addition, within the top 10 there are schemes that lie within the best 0.03% of all 10,000 sampling schedules, with respect to RMS. To test whether there is a scoring bias towards a specific spectrum, a synthetic ¹³C HSQC spectrum was also reconstructed from 10,000 NUS datasets and found to have a similar correlation (ρ = 0.77) to the original results (Figure 2b).

Figure 2.

Empirically derived NUS scoring function obtained with synthetic data. (a) The same synthetic data and schemes used in Figure 1 were analyzed with the NUS scoring function. A correlation coefficient, ρ, of 0.66 was found between RMS and the NUS score when spectra were reconstructed using compressed sensing (black). The correlation coefficient of DFT spectra was found to be ρ = 0.88 (red). (b) Synthetic spectra with linewidths similar to a ¹³C methyl HSQC were used to test the generality of the scoring function. A correlation coefficient, ρ, of 0.77 was found with compressed sensing reconstruction. (c) Sampling scores for 30%(60%) NUS of 256 linear increments in black(red). The correlation coefficient for scores and RMS for 30%(60%) NUS was found to be ρ = 0.75(0.87). (d) Sampling scores for 30%(60%) of 512 linear increments in black(red) have a correlation coefficient of ρ = 0.71(0.62).

Since compressed sensing reconstruction used in the examples above may have introduced bias into our empirical NUS scoring method, we compared the score to spectra processed with DFT (Figure 2a). As opposed to compressed sensing, where missing points are reconstructed, in DFT points that have not been collected are set to 0. This exaggerates sampling artifacts and reflects the convolution of the PSF and uniformly sampled spectra. Since the sampling score here has contributions from the PSF it is not surprising that there is a good correlation between the RMS and NUS score of the DFT spectra. This suggests that the scoring function may be generally applicable to other statistical reconstruction methods, such as those in reference 11.

Next, the NUS scoring method was tested for any dependence on the parameters used to generate the sampling schedules. Schemes at 30% and 60% NUS at both 256 and 512 total linear increments were examined and found to give good correlations (ranging from ρ = 0.62 to ρ = 0.87) between score and RMS (Figure 2c,d). These results suggest that our NUS scoring method is mostly independent of NUS parameters.

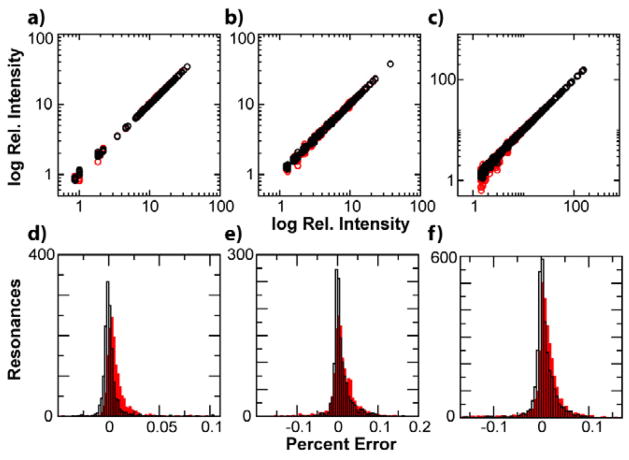
We also reconstructed real NMR data to further investigate the generality of our scoring method. The ¹H-¹⁵N TROSY spectrum of a 43kDa protein (the MAP kinase p38γ) was reconstructed using 2,000 sampling schemes at 60% NUS. Again a good correlation between score and RMS was found (ρ = 0.80, SI). Finally, application of scoring methods to quantitative NMR requires identification of schemes that give accurate reconstructed peak intensities over a high dynamic range. Our scoring method should also predict the accuracy of peak reconstruction since the RMS measurement partially reflects this attribute. Indeed, we found this to be the case. Peak intensities were measured [31] for the ten best and worst scored schemes at 60% NUS for the 18kDa globular protein dihydrofolate reductase (DHFR), the 43kDa kinase p38γ, and the globular 17kDa protein apomyoglobin. The accuracy of the intensity reconstructions for the ten best and ten worst scoring sampling schemes for these proteins are shown in Figures 3a–c. The best schemes accurately reproduce the intensities of the uniformly sampled spectra for all 3 proteins, with higher fidelity than the worst schemes. Resonances closer to the noise (e.g. <4x the noise) show greater susceptibility to be poorly reconstructed by the worst schemes. The 10 best schemes have a greater number of resonances that are reconstructed with close to 0% error and a narrower distribution of errors than the 10 worst schemes (Figure 3d–f)

Figure 3.

Intensities derived from reconstructed NUS data at 60% sampling. Correlation between cross peak intensities resulting from reconstruction of NUS data versus intensities in uniformly sampled spectrum for the 10 best(worst) sampling schemes in black(red) for ¹H-¹⁵N HSQC/TROSY spectra of (a) DHFR, (b) apoMb, and (c) p38γ. The percent error in intensity reconstruction for the 10 best(worst) scored schemes for resonance cross-peaks in black(red) of (d) DHFR, (e) apoMb, and (f) p38γ.

5. Conclusions

We have developed software that generates a large number of schemes based on user input for the desired percent NUS and weight. The software scores the schemes and presents the user with the top 10 scores. The highest scoring schemes will likely perform in the top 20% of all schemes generated in terms of minimal sampling artifacts and optimal peak reconstruction. The method does not require any synthetic reconstruction to obtain scores, however the top-10 scores, which represent generally optimal schemes, may be tested using the RMS method described above with fully sampled spectra of the protein of interest to find the scheme within the top-10 scores that is best suited for each particular case. Although we have presented the scoring function in the context of the Poisson-gap sampling the same basic concepts are likely applicable for choosing optimal schemes from other random-seed generated sampling methods, for example with relaxation-matched exponential sampling. The software, written in C++ and python, has been tested on hardware running Linux and Mac OS X and is available online for download (http://www.scripps.edu/wright).

Appendix A. Supplementary material

Supplementary figures and details of the methods used to generate sampling schemes and to reconstruct the spectra are given in the supporting information.