Stochastic Geometric Network Models for Groups of Functional and Structural Connectomes

Abstract

Structural and functional connectomes are emerging as important instruments in the study of normal brain function and in the development of new biomarkers for a variety of brain disorders. In contrast to single-network studies that presently dominate the (non-connectome) network literature, connectome analyses typically examine groups of empirical networks and then compare these against standard (stochastic) network models. Current practice in connectome studies is to employ stochastic network models derived from social science and engineering contexts as the basis for the comparison. However, these are not necessarily best suited for the analysis of connectomes, which often contain groups of very closely related networks, such as occurs with a set of controls or a set of patients with a specific disorder. This paper studies important extensions of standard stochastic models that make them better adapted for analysis of connectomes, and develops new statistical fitting methodologies that account for inter-subject variations. The extensions explicitly incorporate geometric information about a network based on distances and inter/intra hemispherical asymmetries (to supplement ordinary degree-distribution information), and utilize a stochastic choice of networks' density levels (for fixed threshold networks) to better capture the variance in average connectivity among subjects. The new statistical tools introduced here allow one to compare groups of networks by matching both their average characteristics and the variations among them. A notable finding is that connectomes have high “smallworldness” beyond that arising from geometric and degree considerations alone.

Introduction

The study of the empirical brain networks has taken great strides in recent years, allowing analysis of the brain “system” with its complex interconnections. The construction of the brain networks, or connectomes, from clinical MR data is becoming commonly available and is providing both deep insights into the functioning of the human brain and also into the differences between normal and abnormal (diseased or injured) brains. (Bullmore and Sporns 2009, Sporns 2011).

The foundations of these approaches have been largely based on techniques developed in the social sciences and engineering, in particular for networks of people or computer networks (Albert et. al. 1999, Watts 2004, Jackson 2010), as well as applications in biological and biochemical networks (Jeong et. al. 2001). In these settings one typically has only a single, very large network (or several related but fundamentally different networks) to analyze, which has led to the development of very powerful approaches in those settings (Newman 2003).

However, current study of groups of brain networks requires different tools. Here, one often has groups of closely related networks wherein although the exact edges may differ from subject to subject, nonetheless the number and basic attributes of nodes remain comparable between subjects. This comparability of nodes between different networks allows for a variety of new types of analyses and models, including the construction of detailed geometric properties of the network.

This consideration also allows one to view a group of networks from a distributional sense – for example, one can ask what is the distribution of networks for a population of subjects of a certain type, such as controls or those with a specific disorder or injury. In many instances, understanding the entire distribution is in fact crucial, as simple averages may sometimes conceal critical information (as noted but not formalized in Simpson et. al. 2012). For instance, a recent paper analyzing structural connectomes in subjects with agenesis of the corpus callosum (AgCC) revealed that a key difference between the AgCC subjects and the controls was that the AgCC patients exhibited higher inter-subject variability in their networks (Owen et. al. 2012).

In order to understand these distributions of networks, an underlying stochastic network model is commonly assumed in brain network studies. The choice of underlying model figures implicitly in the design of network measures. For example, computations of modularity and the clustering of nodes in a connectome typically employ a definition of “modularity” that is inherently based on the assumption of an underlying Degree-Distributed stochastic network, since it “weights” edges based on the degree of the nodes that it connects (e.g. if two nodes are both of high degree then an edge between them is not as “informative” as an edge between two low-degree nodes, which is in some sense less likely to arise by chance (Girvan and Newman 2002)). The choice of underlying model also figures prominently in computing the significance of a network measure. For example, the “smallworldness” of a network is often compared to the smallworldness of a matched random network (Sporns and Zwi 2004). The choice of such a comparison network can prove to be crucial. For example, for resting state fMRI networks, the smallworldness of the two most popular random network models -- the Erdos-Renyi model and the Degree Distributed random model -- typically differ by a factor of 2 on empirical brain networks (Newman 2009). Alternatives include choosing the average or median consensus network or a single representative one (Simpson et. al. 2011). As well discussed in Simpson et. al. (2012) there are many more examples exposing the importance of the underlying model network, ranging from their use as null networks as discussed above, to modularity analyses (Joyce et al., 2010; Meunier et al., 2009a,b; Valencia et al., 2009), to representing an individual's network based on several experimental runs (Zuo et al., 2011), to visualization tools (Song et al., 2009; Zuo et al., 2011), to their ability to assess a group of networks (Achard et al., 2006), to identifying hub/node types (Joyce et al., 2010), to constructing representative networks for brain dynamics studies (Jirsa et al., 2010). Additional examples for modularity include Expert et. al. (2012), Bassett et. al. (2013) and Henderson and Robinson (2013).

The goal of modeling a group of networks, as in this paper, does affect our choices for analysis. The goal is to have a stochastic model that generates networks that “fits the entire group of networks” and is constructed to match basic network properties, such as degree distribution or geometry. This is in stark contrast to random network models that try to fit network measures, such as implemented by Vertes et. al. (2013) or Simpson et. al. (2011) which consider classes of random networks and then fit them to the empirical measures – while these can provide deep insights into the structure of the empirical networks, they do not provide simple intuitive models for comparison.

To see this point more clearly, consider the work by Vertes et. al. (2013) which considers similar stochastic network models to those in this paper. While there are important differences in the models such as the use of preferential attachment terms in their models and inter/intra-hemispheric terms in ours, the differences in implementation are more significant. They choose important parameters in their models (such as those for the distance and preferential attachment terms) by maximizing an energy function that tries to match the mean of the subjects' global network measures (efficiency, clustering and modularity) to those of the stochastic networks. (Note that their models use the variability in network measures to scale the energy function but do not match the variability of these measures, as we do below.) This generates a network that fits the means of the data closely, but because of the complex nonlinear interactions between the parameters and the network measures can lead to networks with different parameters than would have been attained by directly fitting to the baseline network information. For example, the distribution of edge lengths in their models often differ significantly from the empirical distribution as seen clearly in their figures.

To see why this arises, consider a simple stochastic network model in which the probability of an edge between two nodes is given by a function of the distance between those two nodes. Clearly one could find a distance function that differs significantly from the true one that yields the same specified clustering coefficient. Similarly, one could likely fit the random networks to exactly match the small-worldness of the empirical networks, but then one cannot discuss the excess small-worldness (as we do later in this paper). In addition, standard random network modeling, such as that typically used for degree distributions (wherein each empirical network is individually matched to one or several random networks with the exact same degree distribution) differs significantly from our approach as this is in some sense over-fitting and only generates networks that have the exact degree distribution of one of the empirical networks (Newman 2009), while one would expect that a new subject would not exactly match the degree distribution of one of the existing networks. (One could see this statistically using standard cross-validation techniques, such as the well know leave-one-out cross-validation.)

Another key difference between connectomes and most traditional network models is that nodes in connectomes have a physical location. This is extremely important as connections between different areas of the brain definitively depend upon relative location, particularly the distance between various regions (Scannel 1999, Kaiser and Hilgetag 2004a,b, Sporns et al. 2004). As we will show, the use of such geometric information appears to be important in the development of good generative models, as was suggested by Expert et al. (2011), applied in Vertes et. al. (2013) and motivated by the analysis in Alexander-Bloch (2013). Figure 1 (which will be explained more fully later), previews the various stochastic network models (both traditional ones and newer ones incorporating geometric information) that will be considered and compared in this paper.

Figure 1.

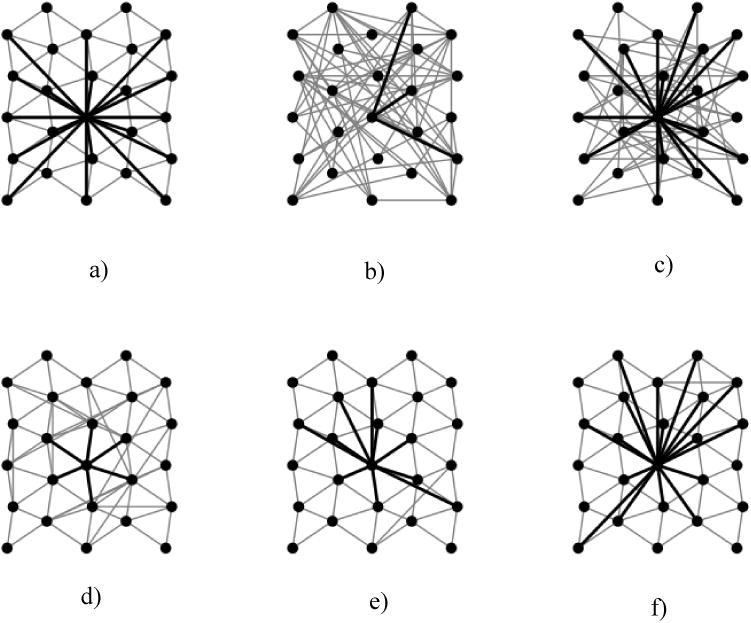
Stochastic Network Models. (a) Illustrative example of a network with local geometric structure and a skewed degree distribution. Here, all nodes have local edges, while the middle node's edges (shown darker) include some nonlocal ones. (b) A Matched Erdos Renyi model (ER) (matched to the network shown in (a)). Note that the ER model loses all geometric and topological structure, which leading to a lower clustering coefficient (CLUST). (c) Matched Degree Distributed model (DD) (again, matched to (a)) captures high degree nodes (e.g., compare the middle nodes in (c) with (a)), but loses geometrical structure, leading to low CLUST. (d) Geometric model (GEO) captures geometrical structure but loses high degree nodes; it preserves high CLUST but increases average path length (APL). (e) Matched Geometric Degree Distributed model (GDD) matches both geometric structure and high degree nodes but has too few edges. (f) Normalized Geometric Degree Distributed model (NGDD) provides an excellent match to the original network (a).

An additional important aspect in the study of connectomes is the choice of threshold type and value, as both fMRI and dMRI generate continuous valued matrices that are then thresholded to create a binary matrix representing the network, where the network density is determined by the threshold value which can be chosen for fixed density (every network has exactly the same density) or variable density (every network uses the same threshold). While we do not directly analyze the optimal choice of threshold type and value (if there indeed is one; see van Wijk et al. 2010), we do consider the effects of such a threshold on the distribution of generated networks. Note that, as discussed in van Wijk et. al. (2010), while fixed threshold networks may be superior in certain settings to fixed density networks, they are also more difficult to analyze due to the effects of the density variations on network measures; however we believe that the use of appropriate null networks can mitigate these difficulties. We also note that recent work has also considered using weights directly in the network analysis and not thresholding the data (e.g.,Rubinov et al. 2011 and Liu et al. 2013). Alternatively, one can treat “multiple thresholds simultaneously” (Ginestet et al. 20110; Bassett et al. 2012).

One important but unrecognized consequence of applying a fixed threshold to all the empirical networks in the group is that it leads to wide variations in their densities, which, as we show later, well exceed those appearing in standard stochastic network models. Accordingly, we will demonstrate that in order to effectively capture the variability found in real connectome studies, one needs to allow density to vary in the underlying stochastic network models. (See Figure 2)

Figure 2.

Effects of variable density random networks. This figure shows heatmaps for connection matrices for randomly generated Erdos-Renyi networks. The top row (a) contains three Erdos-Renyi networks with fixed density (p=0.5 -- chosen for visual clarity), while the ones in the bottom row (b) vary in density from p=0.3 to p=0.7, which is comparable to the 95% confidence interval for densities in the functional connectomes. Note in particular that the variance in density in the fixed density networks (top row) due to random variation is significantly smaller: the 95% confidence interval is about [0.45,0.55].

In this paper, we take a principled empirical approach towards these issues. We compare a variety of stochastic network models on both functional and structural brain networks to understand which of the standard network metrics are well captured and which are not and how to design models that better capture these properties of connectome data. In addition, we extend some traditional statistical methods so as to quantify and illuminate the variation in these groups of networks. Towards this end, we develop a novel, natural distributional measure that encompasses the observed variation of networks, and implement an exact nonparametric test, Cross-match (Rosenbaum 2005), which allows one to evaluate the closeness of two groups of networks.

To reiterate, our analysis demonstrates the effectiveness of combining geometric information with degree-distribution information when constructing generative models of empirical brain networks. Moreover, we introduce novel statistical tools that provide a way of comparing network by matching not only their averages but also their variations. We discuss several interesting properties (and differences) between functional and structural brain networks revealed by our analysis.

Closely Related Work

Recent work by Alexander-Bloch et. al. (2013) incorporates geometric distance information in brain network analyses and thus provides an underpinning for our approach. Others have taken complementary approaches: As discussed in (Simpson et.al. 2011), these include various empirical approaches such as taking either the mean of the network (which will correspond to a “matched ER model” in our language) or taking a simple representative network (which discards a large amount of important statistical information). Another approach (Simpson 2011,2012) considers the class of p* network models, in which one constructs a distribution of networks that correspond to the group of empirical networks on specified network measures, such as degree or clustering coefficient. This allows one to construct an (admittedly ad-hoc) distribution over networks which, though it has many useful applications (Achard et al., 2006; Joyce et al., 2010; Jirsa et al., 2010; Meunier et al., 2009a,b; Song et al., 2009; Valencia et al., 2009; Zuo et al., 2011), nonetheless provides less intuition and understanding of the network structure than our geometric and degree based models.

There has been much work on the basic geometric properties of brain connections. One key insight into the physical structure of the connections arises from the metabolic costs of long range functional and structural connections in the brain (Attwell and Laughlin SB 2001, Niven and Laughlin 2008) and related work which has shown that the geometric structure of these connections balances out cost minimization with robustness and computational ability (Kaiser M, Hilgetag 2006, Chen et. al. 2006, Bassett et. al. 2008 and 2010, Bullmore and Sporns 2012). This can be seen in other animals ranging from humans to C. Elegans (Bassett 2008, Itzhack and Louzoun 2010, Bullmore and Sporns 2012). It can also be seen in development, as human children appear to have more local connections than adults (Fair et. al. 2009) and task dependence, as increased cognitive effort appeared to increase long distance functional connections (Kitzbichler et. al. 2011).

In addition, these properties are often disrupted by brain disorders, such as schizophrenia (Bassett et. al. 2010) and Alzheimer's disease (Liu et. al. 2013), with an increase in long-range connections in the former and a loss of them in the latter among other changes.

These geometric insights can also be used to create sophisticated, but abstract models that capture key properties of brain networks (Henderson and Robinson 2013) or deep insights into the underlying structure of these networks (Vertes et. al. 2012).

Methods

Subjects

We recruited 40 right-handed healthy controls (mean age 28.1+-8.8 years; 27 males and 13 females). Written informed consent was obtained from all participants and/or their legal guardians under a study protocol approved by the institutional review board at UCSF medical center.

Image Acquisition

MR imaging was performed on a 3T EXCITE MR scanner (GE Healthcare, Waukesha, WI, USA) using an 8-channel head phased-array radio-frequency head coil. High-resolution structural MR imaging of the brain was performed with an axial 3D inversion recovery fast spoiled gradient-recalled-echo T1-weighted sequence (TE =1.5 ms, TR = 6.3 ms, TI=400 ms, flip angle of 15°) with a 230 mm FOV, and one hundred fifty-six 1.0 mm contiguous partitions at a 256×256 matrix. Structural MR images of all subjects were interpreted by an attending neuroradiologist certified by the American Board of Radiology.

Whole-brain diffusion was performed with a multislice 2D single-shot spin-echo echo-planar sequence with 55 diffusion-encoding directions, the array spatial sensitivity encoding technique for parallel imaging with a reduction factor of 2, a diffusion-weighting strength of b = 1000 s/mm²; TR/TE=14,000/63 ms; NEX=1; interleaved 1.8-mm axial sections with no gap; in-plane resolution of 1.8 × 1.8 mm with a 128×128 matrix; and a field of view of 230 mm. An additional image set was acquired with minimal diffusion weighting (b =10 s/mm²). The total acquisition time for diffusion imaging was 13 minutes.

A 7 minute BOLD fMRI multislice gradient echo echoplanar acquisition used a FOV 22×22 cm, 64×64 matrix, 4 mm interleaved slices with no gaps, and repetition time (TR) of 2 sec and echo time (TE) of 28 msec. After 10 dummy volumes to reach equilibrium longitudinal magnetization, 200 volumes were collected with the subject's eyes closed to minimize exogenous visual activation and with instructions to remain awake.

Connectome Construction

Structural Connectome

The data were preprocessed using tools from FSL (Jenkinson et. al. 2012) including eddy and motion correction, brain extraction, and calculation of fractional anisotropy (FA) maps. The T1-weighted MR images were automatically segmented using FreeSurfer 5.1.0 (Fischl et al., 2004) resulting in 68 cortical regions, 34 per hemisphere, and 14 subcortical regions, 7 per hemisphere. These 82 regions represent the nodes of the network and were used as the seeds for the probabilistic fiber tractography performed with probtrack×2 (Behrens et al, 2007). The tractography results from each of the 82 seeds were masked by each of the other 81 regions, referred to as targets, and then the number of streamlines was summed across voxels obtaining a connection strength between each seed and target pair. This measure of connection strength was then divided by the total number of voxels in the seed and target regions to account for differences in volume between the various cortical and subcortical regions (Owen et. al. 2012, Li et. al. 2012). Since tractography cannot determine directionality due to the antipodal symmetry of diffusion imaging, the normalized connection strength between each seed and target pair in both directions was summed and the connection strength of a seed with itself was set to zero. The resulting connection matrix is a symmetric matrix and yields an undirected connectome for each control. A more detailed description of the pipeline can be found in Owen et al. (2012,2013).

Functional Connectome

All pre-processing for the fMRI data was performed with FSL tools. Motion correction was applied by registering each fMRI volume with the median volume with six degrees of freedom. Brain extraction was performed and the fMRI image of each subject was first registered to the same subject's T1-weighted image, then the T1-weighted image was registered to the MNI152 2mm standard template. The transformation in the latter step was then applied to the registered fMRI image in the first step to obtain the fMRI images registered to the MNI152 atlas space. Spatial smoothing was applied by spatially convolving each fMRI volume with a 5×5×5mm Gaussian kernel. Band-pass filtering was applied to each voxel time series with the pass band between 0.01 to 0.125Hz. T1-weighted image of each subject was segmented to obtain the masks for white matter and cerebrospinal fluid (CSF). The masks of the two regions were inverse-registered to the fMRI data to extract the mean time series in those three regions in fMRI. A linear regression was applied to the fMRI time series at each voxel to regress out a constant baseline, a linear trend, the six motion parameters from motion correction, and the two mean time series from white matter and CSF. The residual time series were then masked by the 116 regions in the Automatic Anatomic Labeling (AAL) atlas (Tzourio-Mazoyer et. al. 2002) and the mean time course was calculated for each region. The Pearson's correlation coefficient was calculated between each pair of regions and the correlation was taken as the strength of functional connectivity. As in the structural connectomes, the resulting networks are undirected and the correlation of a region with itself was set to zero.

Two types of networks were constructed. For the “fixed threshold” networks a common threshold was set for each type of network, one for all functional networks and a different one for all structural networks, while for the “fixed density” networks individualized thresholds (i.e., one for each individual network) was chosen. These thresholds are then used to binarize the networks, retaining edges for any correlation/weight above that threshold. For convenience, we will discuss networks where the thresholds chosen so that the average degree is 9 for the FNs and 8 for the SNs, which correspond to average density ratios of (9/89) = 0.101 and (8/81)= 0.099 respectively. Our qualitative results are unchanged under the standard density ratios that appear in the literature, 0.05-0.3, which give rise to well connected but reasonably sparse networks, and to simplify the presentation we focus on the given density ratio. (Note that for ratios outside this range many of the standard network measures are not particularly informative.) In addition, we will discuss functional networks without the cerebellar regions as is common; however, including the cerebellar regions did not significantly change any of the results.

Network Measures

We consider a variety of common network measures. Some are global, with a single value for each network, while others are node based, with a potentially different value for each node in each network. For node-based metrics we report the mean (over nodes in a specific network) and two important measures of variation: the standard deviation (sd) and the quintile score (qui), the latter serving to capture the existence of “heavy tails” or the extent to which the nodal distribution adheres to the so-called 80:20 rule (Newman 2005). The quintile score is the sum of the values of the measure for the top 20% of the nodes divided by the sum over all the nodes. Thus, in a heavy tailed case where the top 20% of the nodes contain 80% of the measures the quintile score is 0.8, while if the distribution is less skewed with the top 20% of the nodes containing 20% of the measures the quintile score is 0.2. For example, if there are 10 nodes with degree 1,2,3,…,9,10, the top two nodes have degree 9 and 10, and contain (9+10)/(1+2+…+10)=0.35 which is far less than 80%, so this distribution is not heavy tailed, while the distribution 1,1,1, …,1,100 is heavy tailed with a quintile score close to 1.

The specific network measures used in this paper to assess and summarize the individual and consensus connectomes include: (1) fraction of nodes in the giant component (GIANT), (2) nodal degrees (DEG), (3) diameter (DIAM), (4) average path length (APL), (5) global efficiency (GEFF), (6) clustering coefficient (CLUST), (7) local efficiency (LEFF), (8) smallworldness (SW), (9) Girvan Newman modularity (MOD), and (10) betweeness centrality (CEN). The reader is referred to Rubinov and Sporns (2010) for a comprehensive discussion of these network metrics and their significance. The mean and standard deviation are calculated across the individuals for each network metric for both the functional and structural networks. Note that this is done for all network metrics discussed above, including dispersion statistics over nodes, e.g. the variance (over subjects) of the variance of degree (over nodes).

Stochastic Network Models

In the following analysis we consider a variety of stochastic network models. The first of these (#1-3 below) are standard models commonly used in connectome analyses, while the remaining models (#4-7) are motivated by the insights of Expert et al. (2011), Alexander-Bloch (2013) and represent novel extensions that capture geometric information about the network. They are:

1. The Erdos-Renyi model (ER) takes the average density measure of the networks in the group, p, as the key parameter. It then generates each edge in the network randomly with probability p.

2. The Consensus model (CON) is a probabilistic consensus where the probability of an edge between a given pair of nodes is chosen to be the empirical probability in the original group for that pair. Note that this captures the edge probabilities exactly but ignores correlations between edges. Nonetheless, one would expect this to provide an excellent fit for groups with small inter-network variations.

3. The Degree Distributed model (DD) creates a vector of degrees, where DEG(i) is the average degree (number of edges) for node i. It then constructs an edge between nodes i and j with probability min(q*DEG(i)*DEG(j), 1) where q is a normalization factor chosen so that the expected density of the network will be the same as the average density for the group. For the networks studied in the paper, this model creates networks where the average degree of each node is very close to the empirical average for the group at every node, something that has been shown to be extremely important in many models of real world networks (Newman 2009). (Note however that they are only approximately equal.)

4. The Geometric model (Geo) estimates the probability of edges between two nodes as a function of their (Euclidean) distance, f(d(i,j)) for some function f(d) where d(i,j) is the distance between nodes i and j. In analysis that follows, the function f(d) was computed by dividing the set of distances into 36 equal sized bins which provides a middle ground between accuracy and robustness due to small sample sizes.

5. The Geometric Hemisphere Models (GeoH) are computed similarly to the GEO models except the function f(d) is estimated separately for inter-hemispheric node pairs and intra-hemispheric pairs. This attempts to capture important structural effects, such as the effect of the corpus callosum on edge formation in the developing brain.

6. The Geometric Degree Distributed model (GDD) combines the GEO model's distance-based modeling with the DD model's degree-based modeling, which is expected to be important in some contexts (Expert et al. 2011) and seems natural for connectomes. This model has a similar weakness as the DD model, where one can get an incorrect density ratio. Unfortunately, on the empirical connectome data, this problem is significant (due to the stratification by distances) leading to noticeably reduced density ratios. To remedy this we developed the following model (#7):

7. The Normalized Geometric Degree Distributed model (NGDD) which computes the same probabilistic adjacency matrix as in the GDD but then rescales and truncates this matrix so that is has the correct density. (Algorithmically, one repeatedly multiplies the matrix by 1.01 and then truncates until the density is within 1% of its desired value.)

See Figure 1 for illustrative examples that highlight some of the differences of the above network models.

Note that our stochastic models are constructed from the entire group of networks and not specifically for each network individually as is commonly done when matching exact degree distributions using double edge swaps (Newman 2009). Using such individualized approaches are often powerful and easy to implement, but are difficult to interpret as a stochastic distribution over networks. For example, matching exact degree distributions using double edges swaps least to a stochastic model that only generates sets of degrees that exactly match one of the previously seen sets; however, one would expect different sets of degrees to arise if additional subjects were added a zero probability event in that model, but not unlikely in the class of models we use.

Importantly, as hinted at previously and as we shall discuss in more detail later, it turns out that all these models display far less variability than found in the actual empirical connectome data sets, specifically, the variability of the density ratio for the fixed threshold networks. This observed discrepancy is critical. However, we demonstrate how to effectively treat it by introducing a randomly chosen density ratio into each of the above stochastic network models: In particular, we first compute the empirical density ratio of the given group of networks and then for each network that we randomly generate we rescale it to have the chosen density ratio. We denote the variable-density versions of the above models with a V at the end of their acronym, e.g. ER becomes ER_V and GDD becomes GDD_V. (See Figure 2 for an illustration of this.)

For the analysis, we fit the parameters of each model to the average parameter of the data (groups of functional networks or structural networks) and then generate 40 networks at random from the model. This group of networks is then compared to the empirical group of networks. Note that unlike p* modeling (Simpson et al. 2011 and 2012) and the “energy maximization” approach in Vertes et. al. (2013), we directly fit the models based on the basic properties, including density, average degree distribution and distance between nodes, and not on more complex network measures, such as average path length or clustering coefficient. This is perhaps more natural, but also avoids over-fitting, as the evaluative measures differ from those used for fitting.

Statistics over Groups of Networks

In order to compare a pair of networks, we compute the normalized Hamming distance, which is the total number of edges that are in one network but not the other divided by the total number of potential edges, which is n(n-1)/2 for a network on n nodes (Banks and Carley1994). Note that this requires that the two networks have the same set of nodes, something that does arise in most brain network studies. Note that the concordance between nodes relies on the reliability of the parcellation into the requisite atlas. For standard resolution data, ∼100 nodes or so (as used in this paper), this is quite feasible. In addition, note that this metric is a true metric since it is the (scaled) matrix distance between the two adjacency matrices for the networks.

While the comparison of two networks is reasonably straightforward, the comparison between two groups is not. The most well known approaches compare the means or medians in some way (Simpson et. al. 2011). For example, one can compute the matrix difference between the averaged adjacency matrix or the Hamming distance between the consensus matrices for each group. Unfortunately, these measures do not capture the variability with the groups. In order to do that, we introduce two approaches.

The first is a simple heuristic that captures the basic variability in a natural manner. For a single group, we consider the average Hamming distance between all pairs of networks in the group, and denote this as the “span” of the group. Thus, a group with more variability will have a larger span. For two different groups, a base group and a secondary group (such as a comparison between the empirical and a randomly generated functional connectome), we define the “cross-span” to be the average distance between pairs of networks where one network is chosen from the base group and the other from the secondary group. If the cross-span is much larger than the span of the base group, then clearly the secondary group does not significantly overlap with the base group. Thus, we define the “span-ratio” of the secondary and base groups to be the ratio of the cross-span to the span (of the base group).

The second approach for quantifying variability of groups of networks is somewhat more complex algorithmically but allows for statistically rigorous analyses. This is the “cross-match ratio” and is a nonparametric similarity test of distributions (Rosenbaum 2005), which can be applied to any groups where one can compute the distance between any pair of objects in the groups. To compute the cross-match ratio, one considers the union of the networks in both groups and constructs a matching where all the networks are paired up in a way that minimizes the sum of the distances between all of the matched pairs. This can be computed efficiently using Edmond's blossom technique after affine transformation of the Hamming distances (Edmonds 1965). One then computes the fraction of pairs that cross the two groups, i.e. when the networks in the pair are not from the same group. One can compute the distribution of cross-match ratio exactly, under the null hypothesis, since the pairing is random if the two distributions are identical. This allows one to compute the p-values of the non-parametric test of identicality of the underlying distribution of groups, which we will use to rigorously compare groups of networks.

See figure 3 for a graphical explanation of the span-ratio and cross-match statistic for two examples.

Figure 3.

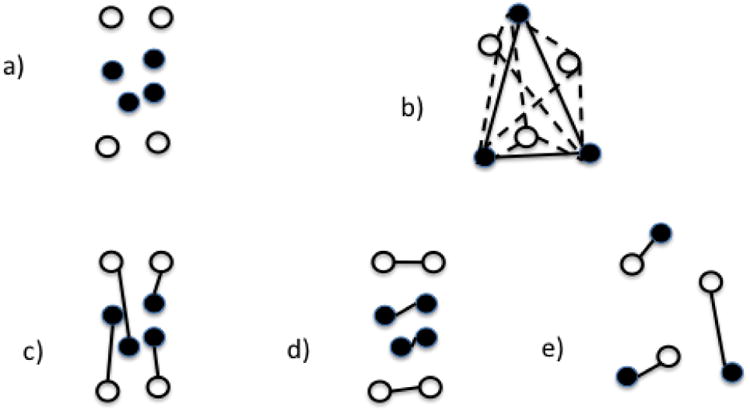
Schematic for group statistics. Filled disks represent single networks from a group of empirical networks while unfilled disks represent single networks from a group of a matched random network model, such as ER networks. The distance between disks represents their Hamming distances. a) An example where the mean of the two groups are similar but the empirical networks have significantly less variation between networks. b) Another example: the average length of the solid lines is the self-span of the empirical networks while the average length of the dashed lines is the cross-span of the two groups. c) A matching between the two networks which is not minimal. d) The minimum matching between the two groups, showing a cross-match of 0, since there are no edges between the two groups. e) A minimal matching for the groups in part (b), showing a cross-match of 1, since all edges join networks from different groups.

Results

In the following four sections we discuss the network measures (such as average path lengths or clustering coefficients) for all models except the CON models, which we discuss separately in the fifth section. We then return to measures over groups of networks, which use the cross-span ratios and cross-match statistic on the Hamming distances.

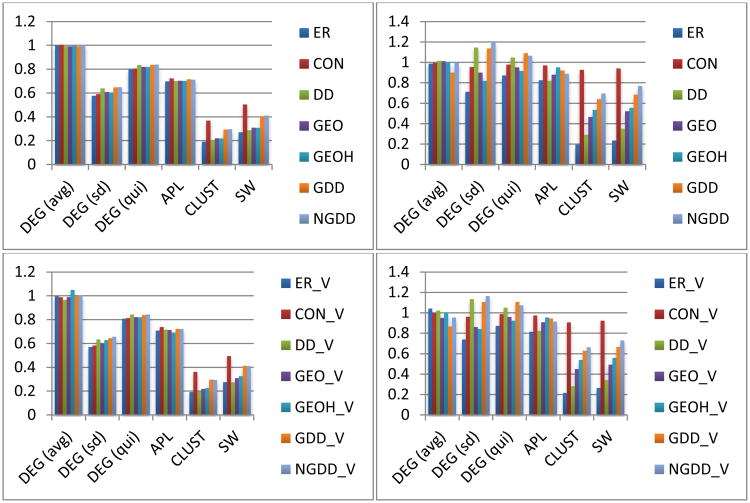
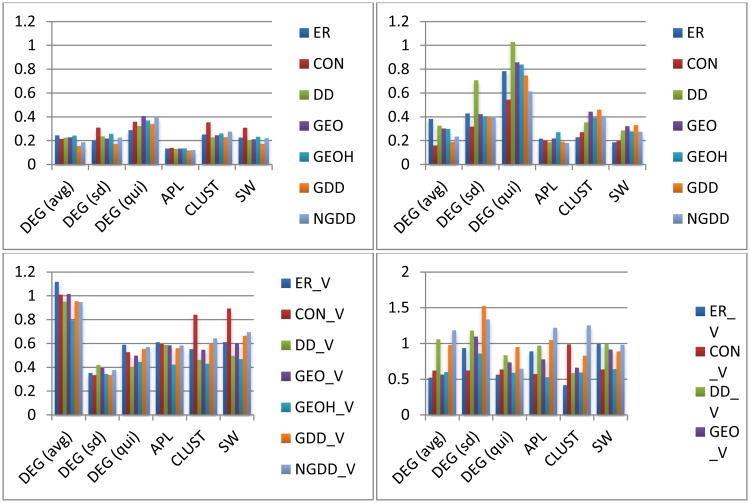
We will refer to Figures 4, 5 and 6, which contain the normalized measures for means and STDs, which allow for easy comparison, since the normalized measures are the ratios of the specific model measure to that for the data. (e.g. if the mean clustering coefficient for the data is 0.2 but for the model is 0.4 then we say that the normalized clustering coefficient for the model is 2.0, which is larger than 1, that maximum value for the un-normalized clustering coefficient.) We have also included Table 1, which contains the un-normalized means for the fixed threshold networks and stochastic models to provide a baseline. The full data tables can be found in the supplementary materials.

Figure 4.

Normalized selected network measures (means) for fixed threshold functional (left) and structural (right) networks. Note that the bottom row uses variable density random network models while the top uses fixed density random network models.

Figure 5.

Normalized selected network measures group standard deviations (SDs) for fixed threshold functional (left column) and structural (right column) networks. Note that the bottom row uses variable density random network models while the top uses fixed density random network models.

Figure 6.

Normalized selected network measures group standard deviations (SDs) for functional (left column) and structural (right column) fixed density networks. SDs for the average DEG are not shown as they are infinite, but labels are included for comparison with other plots.

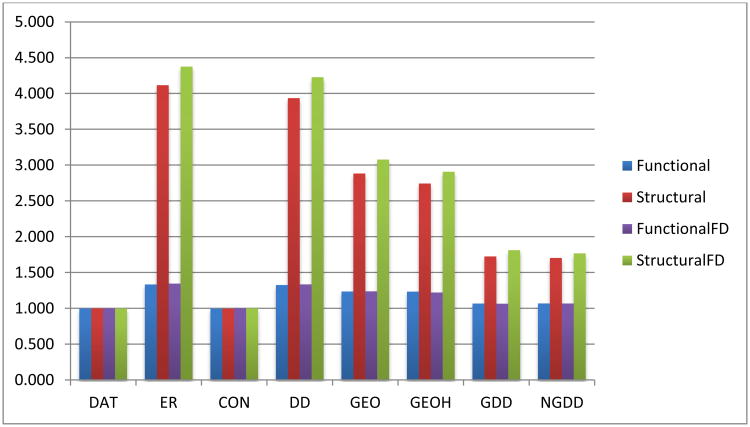
Table 1.

Average values and standard deviations (over the group) for network measures for functional connectomes (FN) and structural connectomes (SN) for both fixed threshold and fixed density (FD) networks.

	FN	FN_FD	SN	SN_FD
GIANT	0.985 (0.017)	1.00 (0.002)	0.987 (0.017)	1.00 (0)
DEG (avg)	9.00 (1.786)	8.00 (1.254)	9.000 (0)	8.00 (0)
DEG (sd)	4.864 (0.956)	3.661 (0.526)	4.892 (0.646)	3.691 (0.207)
DEG (qui)	1.873 (0.125)	1.749 (0.062)	1.872 (0.138)	1.754 (0.044)
DIAM	7.725 (1.516)	5.675 (0.848)	7.7 (1.536)	5.675 (0.468)
APL	3.262 (0.305)	2.836 (0.268)	3.238 (0.353)	2.795 (0.067)
GEFF	0.38 (0.035)	0.423 (0.03)	0.384 (0.025)	0.425 (0.006)
CLUST	0.516 (0.047)	0.484 (0.052)	0.516 (0.039)	0.495 (0.019)
LEFF (avg)	0.767 (0.021)	0.743 (0.024)	0.767 (0.021)	0.748 (0.009)
LEFF (sd)	0.106 (0.014)	0.096 (0.009)	0.102 (0.01)	0.096 (0.005)
LEFF (qui)	1.224 (0.04)	1.244 (0.021)	1.212 (0.028)	1.241 (0.016)
SW	0.16 (0.025)	0.173 (0.03)	0.16 (0.014)	0.177 (0.008)
MOD	0.525 (0.049)	0.483 (0.032)	0.513 (0.042)	0.482 (0.019)
CEN (avg)	0.025 (0.003)	0.023 (0.003)	0.024 (0.003)	0.022 (0.001)
CEN (sd)	0.026 (0.006)	0.036 (0.006)	0.027 (0.012)	0.036 (0.004)
CEN (qui)	2.77 (0.232)	3.483 (0.181)	2.759 (0.369)	3.5 (0.169)

Means of Network Measures (Functional Connectomes)

In the following note that the normalized measures (means) for fixed threshold networks are within 3% of those for the fixed density networks, so to simplify the presentation we will focus (in this section) on the fixed threshold networks for discussion as the main results apply to the other networks.

First, we consider the most basic property of networks, their degree distribution. As seen in Figure 4 the average degree matches closely (within ∼1%), as expected, since the average degree is essentially a fitting parameter in the models with the notable exception of the GDD models, which, as discussed earlier, have some definitional problems that are rectified in the NGDD (normalized) model. For the higher-order statistics, namely the standard deviation and quintile score, it is clear that none of the models are fully capturing the true diversity of nodal degrees of the empirical FNs, since all have smaller standard deviations (∼35% smaller) and quintile statistics (∼17% smaller) than the actual data. However, observe that adding either degree distribution information (DD) or geometric information (GEO) improves the result, and that the combination of the two (NGDD) yields the best match. Note too that there is little significant difference between the models with fixed density ratios and those with variable density ratios for matching the means.

One sees similar results for average path length, although in this case the DD models are the closest, but all have significantly shorter APLs (∼30%) than the functional network data. This is also true for global efficiency, which is closely related to APL, where the data has lower GEFF and modularity. This can be seen in the extreme for the clustering coefficient where the data has a value of about 0.51 while the models all have CLUST less than 0.16, again with NGDD the highest. Combining these two we see that the smallworldness of the functional connectome data is approximately 2.5 times larger than any of the models, providing further strong evidence that functional networks really are small world networks (Sporns and Zwi 2004).

This is also seen in the distribution of centrality (see the supplementary material) where the standard deviations are much smaller (∼60%) for all the models, with NGDD again the best; however, in contrast to the standard deviations, which capture diversity in nodal centralities, the models do a much better job of capturing the quintile statistic of the metrics (∼20% smaller), which reflects the extreme nodal centralities.

Means of Network Measures (Structural Connectomes)

As in the previous section, the normalized fixed threshold measures (means) are again within 3% of the normalized measures for the fixed density networks, so for ease of presentation we restrict our discussion in this section to the former.

For the structural networks the models appear to capture the means of the network measures better than for the functional networks as seen in Figure 4. For example, all models, except the ER models, seem to capture the standard deviations (∼20%) and quintile statistics (∼7%) of the nodal degrees reasonably well; however, in this case the models that build in degree distributions explicitly (DD, NGDD) produce too much nodal variability in degree distributions.

For the average path lengths, the models all underestimate the structural data by about 10%. Interestingly, the closest fit comes from the GEOH model which is ∼10% larger than the GEO model which suggests that the path length structure of the data depends on the physical hemispheres and the corpus callosum. This advantage of GEOH over GEO is seen in several other measures.

The models capture the clustering coefficients much better in the structural networks (∼30% smaller) than in the functional networks (∼70% smaller). In addition, here the importance of geometry is manifest, as CLUST is about 60% larger in the GEO model than in the DD model. However, combining the two in the NGDD model yields another 50% increase, showing the power of incorporating both influences. Combining this with the discussion on the APLs one sees that much of the smallworldness in the structural network appears to arise from the geometric structure, a common motivation in the discussion of small-world networks, going back to Milgram's original experiment and Kleinberg's analysis (Milgram 1967, Kleinberg 2000).

Standard Deviations of Network Measures

Next we consider the standard deviations of the metrics to understand the variability of the data and the models. Unlike the study of the means, just above, the variable density models differ significantly from the fixed density models when considering the SDs, as the networks generated by the fixed density models show far less variability in network measures than the empirical networks.

Note that we are focusing on the model variations (over different realizations of the random networks), which we signal by SD as opposed to the standard deviations, by node, which are specific measures for a single network. Thus, for example, one can consider the SD of the standard deviation of the nodal degree.

Standard Deviations of Network Measures (Functional Connectomes)

For the nodal distributions of the fixed threshold networks, one can see the advantage of the variable density models immediately from the average (by node) nodal degree by comparing the first and second rows in Figure 5. In this case the fixed density models have 80% smaller SDs than the data, while the variable density models are within about 10% of the data's SD. However, for the standard deviations and quintile statistics both classes of models are not very accurate, although the variable density models are better.

For the fixed threshold networks, this pattern repeats for many measures. For example SDs of the APL are almost 90% smaller for the fixed density models than the data while they are “only” about 50% smaller for the variable density models. For SDs of CLUST the comparable numbers are 75% and 45%. Interestingly, these combine so that the comparable numbers are 80% and 35% for the SDs of smallworldness. Overall, the SDs do not vary significantly among the variable density models but do vary significantly among the fixed density models.

For the fixed density networks, as seen in Figure 6, the results are similar to those for the fixed threshold networks (using fixed density models) with the obvious exception of the average DEG, since this is 0 for the fixed density networks by construction.

Standard Deviations of Network Metrics (Structural Connectomes)

For the fixed threshold structural networks the variable density models appear to model the SDs reasonably well and significantly better than the fixed density models (Figure 5). For example, the SD of the average degrees for the variable density models are within ∼10% of the data while the fixed density models differ by ∼80%. Even for the SDs of the standard deviations and quintile statistics of nodal degree, they are within ∼20% and 1% respectively compared to ∼70% and ∼30%. The results for SDs of other measures behave similarly, with the variable density models being much more accurate than the fixed density ones.

Interestingly for the fixed density structural networks some of the models seem to capture the SDs well (see Figure 6). In particular, the GEOH and the NGDD models are close for most measures, while the ER is quite inaccurate and the DD only somewhat less so.

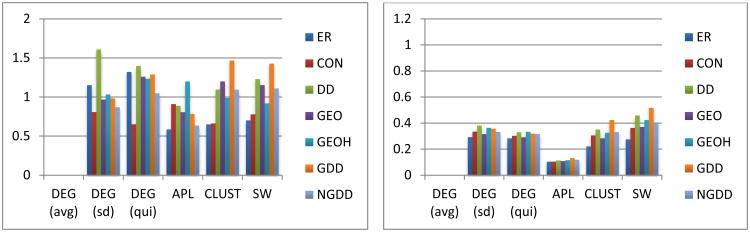
Consensus Networks

The consensus networks capture the exact probabilities for every edge without capturing the correlations. Thus, if the networks in the group do not vary too much then one would expect the CON model to capture at least the network measures. For the fixed threshold structural networks and the variable density models (Figure 4, second row) one can see this well as the CON model captures most of the means accurately, with most within 5% and all within 10%. For the fixed threshold functional connectomes (Figure 4, second row) the CON model is not nearly as accurate, with errors for the means of measures varying around 50% and more for most measures. The results are similar for the SDs where the errors for the fixed threshold structural networks vary from about 0-40% for most measures while those for the fixed threshold functional networks are mostly from 40-70%. For the fixed density functional networks the results are similar for the functional networks, while for the structural networks the fit is similar to that for the variable density models and much better than that for the fixed density models of the fixed threshold networks (see Figure 6).

Group Metrics

To understand the distribution of the entire group of networks we consider several metrics. The first is the average (Hamming) distance among the networks in a single group that we compare to the average (Hamming) distance between the networks in a pair of groups, where one group arises from the empirical data and the other from a model.

In the following, the results for the fixed threshold networks are quite similar to those for the fixed density networks, so we focus our discussion on the former.

First, we note that the self-span of the functional network data is about 0.135 while the self-span for the structural network data is about 0.044, while the self-spans of the models for the functional networks range from 1.28-1.75 without much difference between the variable density models and the fixed density ones (see supplementary materials). For the structural networks the models self-spans range from 0.042-0.174. The self-spans for the models of the structural networks vary more, ranging from 0.064 (NGDD) to 0.169 (DD_V) and 0.174 (ER_V). Interestingly the cross-spans for the models are all fairly close (<10%) to their self-spans.

As seen in Figure 6 the span ratios are minimized for the CON models with values of 1.00 to two decimal places for both structural and functional groups, with little difference between the variable and fixed density ratio models. Excluding the CON models the best fits are shown by the GDD and NGDD models with span ratio of about 1.07 for the functional network groups and 1.7 for the structural ones. The largest span ratios are for the ER and DD models with values of about 1.3 for the functional and 3.9 for the structural groups.

For the cross-match statistics, all p-values are <0.001, showing that all of the models generate groups of 40 networks that are easily distinguished from the subjects' networks. The CON_V models lead to the smallest t-values (∼2.9 functional and ∼1.8 for structural) and the CON and CON_V are the only models with any cross-matches at all.

Discussion

Means of Measures

The analysis of the network measures highlights the varying degrees of inaccuracies of all the well-known stochastic network models as well as the extensions introduced here. In general though we find that all models tend to capture the network measures for structural networks much more accurately than the functional networks. In part, this may be due to the structural networks having less variation, as seen in the strong fit by the consensus model and the small self-span of the structural data.

However, within these models our findings clearly illustrate the importance of including both distance and degree distribution information. The importance of incorporating degree distribution is well known (Newman 2003, 2009), while the importance of geometric information is less so, as network data sets often do not have geometric information, and moreover usually one does not have groups of networks on the same set of nodes, which is fundamental to the analysis.

However, none of the models succeed in capturing the clustering coefficient, which shows the significance of high clustering coefficients in connectome data, but also highlights a still unresolved deficiency in that these models are missing this key feature of brain networks. This is also seen to a lesser extent in the average path lengths. It is tempting to enforce higher CLUST and longer APLs in the models, but this is problematic. For the former, there are models which can fit any value of CLUST (Newman 2009) but these are constructed in a somewhat artificial manner (triangular clusters are explicitly added) that seems to overfit the data, while for the latter there do not appear to be known techniques (aside from p* models, discussed elsewhere in this paper) for adjusting the APL of a network model directly.

It is unclear how important it is to accurately model the intra- versus inter-hemispheric connectivity. For the APLs of the structural networks this appears to be significant, but for other measures this does not appear to be significant (e.g. Figure 4).

SDs of Network Measures

The SDs of the network measures attempt to capture the variability of brain networks, which is a fundamental but often overlooked consideration in modeling and analysis. Overall, the SDs do not vary significantly among the variable density models but do vary significantly among the fixed density models. This finding seems to suggest that much of the variability in measures arises from variability in density ratios, indicating the need to develop models with more intrinsic variability.

An interesting finding is that the for the fixed density functional networks, the fits for the SDs are similar to the fixed density models for the fixed threshold functional networks but for the fixed density structural networks the fits for the SD are similar to the variable density models for the fixed threshold structural networks

Group Metrics

Recall that the self-span is about 0.135 for the fixed threshold functional networks, 0.044 for the structural, and ranges from 1.28-1.75 for the models. To understand the significance of these distances, consider the probability that a randomly chosen edge in one randomly chosen network exists in another randomly chosen network of the same kind, which can be computed from the self-span using the mathematical properties of the Hamming distance. For the structural networks this probability is approximately 0.8; in the functional networks this probability is approximately 0.35. Thus, the existence of an edge in one structural network leads one to expect a similar edge in another structural network, but this statement is not true for functional networks. This helps explain the strong significance of the CON models for structural networks but their weaker fitting for the functional networks.

It is clear that none of the models generate groups that are close enough to be confused with the real data under rigorous statistical tests (e.g. cross-match), but nonetheless they provide reasonable approximations. In particular, the group metrics do show the value of including degree distribution and geometric information in modeling (and the normalization process used in extending the GDD model to the NGDD model improves the modeling in several respects).

Comparing the results from network measures to those from group metrics provides interesting insights. First, notice that even though the structural networks appear to be more accurately modeled than the functional ones for the network measures, the group metrics appear to show the opposite. Essentially, they show that due to the large variability in subjects' functional networks it is easy to construct models that are close in a relative sense, whereas the structural networks are so much less variable that any model that doesn't specify edge probabilities, like the CON model, can be easily distinguished from the data.

This can also be seen clearly in the data ER models, which have a large Hamming distance but tight network measures. This arises because many network measures depend on the statistics of the edge distribution, while Hamming distance depends in detail on the actual edge by edge distributions.

This leads to important questions on how best to model groups of brain networks, and draws clear the distinction between our approach and those using models which are fitted to the network measures, like the p* models (Simpson 2011,2012) and those in Vertes et. al. (2013).

Fixed density vs. fixed threshold networks

Our analysis included both fixed density and fixed threshold networks as the former is widely used, while the latter is becoming more popular. For the means of the network measures, there is very little difference in the evolution of stochastic models for fitting these as all network measures were within 3% of each other. Similarly, for the group measures the results for the different thresholding methods are also quite similar. However, the group SDs did differ between the fixed threshold and fixed density networks, which is surprising in contrast to the group measures which also depend heavily on variability but did not show these differences. In particular, for SDs the fixed density structural networks are more closely fitted by the models than the fixed density functional networks are fitted.

Future Directions

Our findings show many important directions for further study. Clearly, the development of better stochastic network models is an important first step. Are there natural models that capture the means and variations of empirical brain networks? Can we extend variable-density models like those introduced here to include other types of variability, such as randomized degree distributions? In addition, it would be interesting to combine our models with the approaches used in p* and energy based models. Would it, for example, be sensible or advantageous to choose the parameters for the heuristic models to match the network measures more accurately using the p* approach?

In addition, this work points out the additional need for a better statistical framework for analyzing groups of networks. Our first approach based on cross-spans appears to be a reasonable first step, but remains insufficiently precise to fully capture the details of the comparisons between groups of networks, while the exact statistical approach (the cross-match ratio) appears to be too precise, pointing out with statistical surety that the groups generated by the models are distinguishable from the data but failing to provide a good measure of which models are better.

Conclusions

To summarize, we have shown that random models of both functional and structural connectomes are improved when geometric information about the network is included alongside degree distributions. Moreover, to appropriately capture the empirical variability in the connectome data, one must explicitly incorporate additional variability into the model, as can be achieved by allowing density variations in the underlying stochastic networks. In this manner, our analysis underscores the importance of quantifying variability in groups of connectomes. This explicit analysis of variability is crucial for accurate modeling and should be included in connectome analyses. Lastly, we note that these new models highlight the smallworldness intrinsic in these networks, which is not captured even by the combination of a skewed degree distribution and local geometric structure, both contributors to smallworldness.

Figure 7.

Span-ratios for groups of functional and structural connectomes and the random network models for both fixed threshold and fixed density (FD) networks.