Classification of Multicolor Fluorescence In Situ Hybridization (M-FISH) Images With Sparse Representation

Abstract

There has been a considerable interest in sparse representation and compressive sensing in applied mathematics and signal processing in recent years but with limited success to medical image processing. In this paper we developed a sparse representation-based classification (SRC) algorithm based on L1-norm minimization for classifying chromosomes from multicolor fluorescence in situ hybridization (M-FISH) images. The algorithm has been tested on a comprehensive M-FISH database that we established, demonstrating improved performance in classification. When compared with other pixel-wise M-FISH image classifiers such as fuzzy c-means (FCM) clustering algorithms and adaptive fuzzy c-means (AFCM) clustering algorithms that we proposed earlier the current method gave the lowest classification error. In order to evaluate the performance of different SRC for M-FISH imaging analysis, three different sparse representation methods, namely, Homotopy method, Orthogonal Matching Pursuit (OMP), and Least Angle Regression (LARS), were tested and compared. Results from our statistical analysis have shown that Homotopy based method is significantly better than the other two methods. Our work indicates that sparse representations based classifiers with proper models can outperform many existing classifiers for M-FISH classification including those that we proposed before, which can significantly improve the multicolor imaging system for chromosome analysis in cancer and genetic disease diagnosis.

I. Introduction

Multicolor fluorescence in situ hybridization (M-FISH) is a combinatorial labeling technique developed for the analysis of human chromosomes [1], [2]. The technique has been used for the characterization of chromosomal translocations, the identification of cryptic rearrangements, and the study of mutagenesis, tumors, and radiobiology [3]. In this technology chromosomes are labeled with fluorescent dyes of different combinations and concentrations, which allows for the differentiation of each pair of chromosomes. A fluorescent microscope, equipped with a filter wheel is used to capture the chromosome images at different spectral channels or wavelengths. Each dye is visible in a particular wavelength and can be captured using a specific filter. Therefore, M-FISH signals can be obtained as multi-spectral or multi-channel images, in which a chromosome was stained to be visible (signed as “1”) or not visible (signed as “0”). For a number n, the number of Boolean combination is 2ⁿ. Hence, five spectrums are sufficient to distinguish the 24 classes of chromosomes in human genome. In addition to that, DAPI is used to counter stain each chromosome such that all of the chromosomes are visible in DAPI channel. By simultaneously viewing six different channel images, pixel-wise classification of chromosome is possible. This technique is also known as color karyotyping in cytogenetics [1]. Fig. 1 shows an example of M-FISH images of a male cell, where 22 autosomes and 2 sex chromosomes are classified from a 5-channel spectral image data and are displayed using 24 pseudocolors. For a normal cell, each chromosome should be painted with the same color. Otherwise, it indicates the presence of chromosomal abnormalities, which are often associated with certain genetic diseases or cancers.

Fig. 1.

The 24 classes of chromosomes are classified from the 5-channel spectral images; each class of chromosome is displayed with a different pseudocolor. This pixel-wise classification technique is called color karyotyping.

The successful detection of chromosomal abnormalities depends on accurate pixel-wise classification techniques. Even though many attempts have been made to automate image analysis procedure [4]–[9], the reliability of the technique has not yet reached the level for clinical application [8]–[11]. The sizes of the misclassified regions are often larger than the actual chromosomal rearrangements and chromosomal gain or lost, which may leads to incorrect interpretation by cytogeneticists. To improve the detection of chromosomal abnormalities for clinical diagnosis, accurate segmentation and classification algorithms have to be developed.

The algorithms for classification of M-FISH images can be categorized into two groups: the pixel-by-pixel classification [5], [7], [12]–[15] and the region-based classification [8], [16]–[20]. In the pixel-by-pixel classification algorithms, even with pre-processing and post-processing, the classification accuracy is still not high enough for clinical use (less than 90%) [4], [7], [9], [15], [20]. It was shown in [7] that the average accuracy of the pixel-by-pixel classification was only 68% with a standard deviation of 17.5%.

We have developed a number of classifiers for M-FISH classification. In [6] we developed Bayesian classifiers. Recently, we proposed the fuzzy c-means (FCM) [12], [13] and adaptive fuzzy c-means (AFCM) based methods [21]. We have tested these algorithms on M-FISH images from M-FISH data base [22] that we built, which have shown that they are promising for M-Fish image classification [12], [13]. However, those classifiers still cannot guarantee sufficient accuracy (classification is lower than 90%) that cannot be reliable for clinical use.

In recent years, sparse representations of signals/images have received a great deal of attentions in applied mathematics and signal processing community [23]–[26]. The sparse representation models are to search for the most compact representation of a signal in terms of linear combination of atoms in an over-complete dictionary. In general case, it is extremely difficult to compute the optimal representation [27]. However, when the optimal representation is sufficiently sparse, it can be efficiently computed by convex optimization [23]. Similar to the regularized version of the least squares solution (Lasso) in statistics [26], [28], the optimization process penalizes the L1-norm of the coefficients in the linear combination, rather than the directly penalizing the number of nonzero coefficients (i.e., the L0-norm).

Although the sparse representations have been used in many fields, to our knowledge, little work exists on their use for solving biological image classification. In this work, we applied the sparse representation model to chromosome classification with M-FISH imaging. The sparse representation based classification (SRC) algorithm was obtained by L1-minimization using Homotopy method [29]. The Homotopy method was originally proposed by Osborne et al. for solving noisy overdetermined L1-penalized least square problem [30]. Donoho et al. [29] applied it to solve the noiseless underdetermined L1-minimization problem

$$(\mathrm{P}1)\widehat{x}=\text{argmin}{\Vert x\Vert }_1\text{subject}\text{to}Ax=y,$$ (1)

and showed that Homotopy runs much more rapidly than general-purpose linear programs (LP) solvers when sufficient sparsity is present.

In this work, we applied the sparse representation based on Homotopy method to the pixel-wise classification of M-FISH images. Our results showed that sparse representation-based classification (SRC) method gave the best classification ratio (CR) among those three methods. In addition, results from using other sparse representation methods such as the Orthogonal Matching Pursuit (OMP) method [31], Least Angle Regression (LARS) method [32], were also compared. Statistical analysis showed that Homotopy method gave significantly better CR than that of OMP method and LARS method. This suggests that when using sparse representation based classifiers, the proper selection of computation methods of the sparse representations is important. Different computation methods can result in different accuracy.

II. Methods

A complete chromosome image classification process includes fluorescence image pre-processing, feature acquisition/selection, classification, and post-processing. In this work, our focus is to test the effectiveness of the proposed classifiers and compare their performances with other existing classifiers. To this end, no pre-processing (color compensation, background correction, noise filtering, etc.) or post-process (morphology process, joint segmentation-classification, etc.) were performed, which would otherwise further improve the overall classification accuracy.

A. Segmentation of Chromosome Images for Region of Interest

The AFCM method [34], [35] was applied to generate a mask from the DAPI channel. Only pixels within the mask were classified using the proposed sparse representation-based classification (SRC) methods.

B. Feature Normalization

Since each channel of the color images was acquired independently, normalization of these images should be favorable to remove the grayscale intensity differences caused by different fluorescence. FCM method was applied to find the intensity centers of chromosome region (upper center) and background (lower center). Then the images were stretched and normalized such that the intensities below the lower center are assigned to be 0; intensities that are higher than upper center are assigned to be 1; and intensities between the two centers were stretched to be between 0 and 1. After the normalization, each pixel has a feature as y_i = [y_i1, y_i2, y_i3, y_i4, y_i5]^T ∈ R⁵, where y_ij ∈ [0, 1]; i = 1, 2, … N; j = 1, …, 5; and N is the number of pixels in the image.

C. Sparse Representation-Based Classification (SRC) Algorithm

The basic problem in SRC is to use labeled training samples from c distinct object classes to correctly determine the class to which a new test sample belongs. We arrange the given n_i training samples from the i-th class as columns of a matrix A_i = [y₁, y₂, …, y_ni] ∈ R^m×n_i. In the context of M-FISH image classification, we have a set of grayscale images (5 channel/images for each set), corresponding to a vector v_j ∈ R^m, where j = 1, …, n_i, m = 5, and n_i is number of pixels to be used as training samples for the ith class. For the total c classes (c = 24 for the male and 23 for the female cell), A = [A₁, A₂, …, A_c] ∈ R^m×n will be the matrix of training samples, where $\mathrm{n}={\sum }_{\mathrm{i}=1}^{\mathrm{c}}{\mathrm{n}}_{\mathrm{i}}$ and m = 5.

For each class i, let δ_i: Rⁿ → Rⁿ be the characteristic function which selects the coefficients associated with the i-th class. For x ∈ Rⁿ, δ_i(x) ∈ Rⁿ is a new vector whose only nonzero entries are the entries in x associated with class i. Using only the coefficients associated with the i-th class, one can approximate the given test sample y as $\widehat{{\mathrm{y}}_1}=\mathrm{A}{\delta }_{\mathrm{i}}(\mathrm{x})$. We can then classify y based on these approximations by assigning it to the object class that minimizes the residual between y and $\widehat{{\mathrm{y}}_1}$:

$$\text{Identity}(\mathrm{y})=\mathrm{i}\text{subject}\text{to}\underset{i}{min}{\mathrm{r}}_{\mathrm{i}}(\mathrm{y})={\Vert \mathrm{y}-\mathrm{A}{\delta }_{\mathrm{i}}(\mathrm{x})\Vert }_2$$ (2)

where r_i(y) is the residual between y and $\widehat{{\mathrm{y}}_1}$, and ||*||₂ represents the L2-norm.

Sparse Representation-based Classification (SRC) algorithm:

Inputs: a matrix of training samples A = [A1, A2, …, Ac] ∈ Rm×n for c classes; and a test sample y ∈ Rm Normalize the columns of A to have unit L2-norm. Solve the L1 norm minimization problem (P1) defined by (1). Calculate the residuals ri(y) = ||y − Aδi(x)||2; Identity (y) = arg mini ri(y)

D. Homotopy Algorithm for Solving (P1)

From the SRC algorithm given in Section C, it can be seen that it is critical to correctly solve the L1-norm minimization problem (P1) defined by (1). Several methods have been developed [29], [31], [32] to find the optimal sparse representation for (P1), among which Homotopy method has been proven to have computational advantage in terms of speed [29]. Specifically, if the underlying solution has only k nonzeros, the Homotopy method reaches that solution in only k iterative steps. Donoho et al. proved that for coherent matrices A, where off-diagonal entries of the Gram matrix A^TA are all smaller than a positive M, and if k ≤ (M⁻¹ + 1) * N_c/2, where N_c is the number of columns of A, then Homotopy method has the k-step solution property [29]. In the case of M-FISH image classification, k = 5, N_c = 24 * 5 = 120; for any positive M, it will satisfy the condition given above, and consequently Homotopy has the k-step solution property. In addition to that, Homotopy based SRC also gave best classification accuracy for M-FISH image classification as tested in our work, which can be seen in Results section.

For the L1-minimization problem (P1), it is convenient to consider the unconstrained optimization problem instead:

$$(\mathrm{P}2)\widehat{\mathrm{x}}=\text{argmin}{\Vert \text{Ax}-\mathrm{y}\Vert }_2^2/2+\mathrm{\lambda }{\Vert \mathrm{x}\Vert }_1,$$ (3)

where λ is a non-negative coefficient. Homotopy method tries to find a pathway, which starts at large λ and x_λ = 0, and terminates when λ = 0 and x_λ converge to the solution of (P1).

Let f_λ(x) denote the objective function of (P2). By classical ideas in convex analysis, a necessary condition for x_λ to be a minimizer of f_λ(x) is that 0 ∈ ∂_xf_λ(x_λ), i.e., the zero vector is an element of the subdifferential of f_λ at x_λ. We calculate

$${\partial }_{\mathrm{x}}{\mathrm{f}}_{\mathrm{\lambda }}({\mathrm{x}}_{\mathrm{\lambda }})=-{\mathrm{A}}^{\mathrm{T}}(\mathrm{y}-{\text{Ax}}_{\mathrm{\lambda }})+\mathrm{\lambda }\partial {\Vert {\mathrm{x}}_{\mathrm{\lambda }}\Vert }_1,$$ (4)

where ∂||x_λ||₁ is the subgradient

$$\partial {\Vert {\mathrm{x}}_{\mathrm{\lambda }}\Vert }_1=\left\{\mathrm{u}\in {\mathrm{R}}^{\mathrm{n}}|\begin{array}{cc}{\mathrm{u}}_{\mathrm{i}}=sgn({\mathrm{x}}_{\mathrm{\lambda },\mathrm{i}}),& {\mathrm{x}}_{\mathrm{\lambda },\mathrm{i}}\ne 0\\ {\mathrm{u}}_{\mathrm{i}}\in [-1,1],& {\mathrm{x}}_{\mathrm{\lambda },\mathrm{i}}=0\end{array}\right\}.$$ (5)

Let I = {i : x_λ(i) ≠ 0} denote the support of x_λ, and call c = A^T(y − Ax_λ) the vector of residual correlations. Then the condition on the gradient expressed in (4) being zeros can be written equivalently as the two conditions:

$$\mathrm{c}(\mathrm{I})=\mathrm{\lambda }\text{sgn}({\mathrm{x}}_{\mathrm{\lambda }}(\mathrm{I})),$$ (6)

and

$$\mid \mathrm{c}({\mathrm{I}}^{\mathrm{c}})\mid \le \mathrm{\lambda },$$ (7)

In other words, residual correlations on the support of I must all have magnitude equal to λ, and signs that match the corresponding elements of x_λ, whereas residual correlations off the support must have magnitude less than or equal to λ. The Homotopy algorithm now follows from these two conditions, by tracing the optimal path x_λ that maintains (6) and (7) for all λ ≥ 0. The key to the successful implementation is that the path x_λ is a piecewise linear path, with a discrete number of vertices [32].

Homotopy algorithm:

Initial solution x0 = 0. For the l-th stage (l = 1, 2, …), compute an update direction dl by solving $$A_I^T{A}_I{d}_l(I)=sgn(c_l(I)),$$ (8) with dl set to zero in coordinates not in I, where $$I=\{j:\mid c_l(j)\mid ={\Vert c_l\Vert }_{\infty }=\mathrm{\lambda }\}$$ (9) Calculate the residual ${\mathrm{\gamma }}_l^{+}$ $${\mathrm{\gamma }}_l^{+}=\underset{i\in I^c}{min}\left\{\frac{\mathrm{\lambda }-c_l(i)}{1-a_i^T{v}_l},\frac{\mathrm{\lambda }+c_l(i)}{1+a_i^T{v}_l}\right\}$$ (10) where vl = AIdl(I), and the minimum is taken only over positive arguments. Call the minimizing index i+. Calculate the residual ${\mathrm{\gamma }}_{\mathrm{l}}^{-}$ $${\mathrm{\gamma }}_l^{-}=\underset{i\in I}{min}\{-x_l(i)/d_l(i)\},$$ (11) Again the minimum is taken only over positive arguments. Call the minimizing index i−. Calculate the residual rl $$r_l=min\{{\mathrm{\gamma }}_l^{+},{\mathrm{\gamma }}_l^{-}\},$$ (12) Update xl $$x_l=x_{l-1}+r_l{d}_l$$ (13) If ||cl||∞ = 0, terminate and xl is the solution of (P1); Otherwise, go back to step (2).

E. Classifier Training

Sparse representation based classifier was trained using randomly chosen samples from each of the 24 classes of the images (here we use male cell as an example; for female cell, it should be 23 classes).

First, an untrained classifier was built: twenty pixels were randomly selected from each class and fitted into the linear system Ax = y of sparse representation based classifier given by (2). In this work, y ∈ R⁵ is the sample vector, A ∈ R^5×480 is the untrained model matrix (the selected sample vectors will be columns of coefficient matrix A; for 24 classes with 20 samples from each class, A has the number of columns of 24*20 = 480). x ∈ R⁴⁸⁰ is the sparse solution of the linear system that is to be determined, which is sparse.

Each training sample vector y_i, i = 1, …, 480, was then classified by this classifier they built. Those that were not correctly identified were removed from the classifier model. Since the feature vector y ∈ R⁵, linear combination of five feature vectors (bases of R⁵ vector space) is sufficient to represent the vector in a given class. In other words, only five uncorrelated vectors are needed to build the final classifier. Therefore, the number of rows of A_i should be reduced to be 5, and |A_i| > 0, i = 1, …, 24.

When justifying if a sample vector is correctly identified or not, one could also take into consideration of sparsity concentration index (SCI) that was introduced in the following:

For the sparse representation based classifier, a valid training vector should have a sparse representation whose nonzero entries concentrate mostly on one subject, whereas an invalid vector has sparse coefficients spread widely among multiple subjects. To quantify this observation, we use the sparsity concentration index (SCI) that was proposed in [33] to measure how concentrated the feature vectors are on a single class in the dataset [33]:

$$\text{SCI}(x)=\frac{ck\ast {max}_i\frac{{\Vert {\mathrm{\delta }}_i(x)\Vert }_1}{{\Vert x\Vert }_1}-1}{c-1}\in [0,1]$$ (14)

where c is the number of classes. For a solution x̂ found by the SRC algorithm, if SCI(x̂) = 1, the feature vector y is represented using only vectors from a single class, and if SCI(x̂) = 0, the sparse coefficients are spread evenly over all classes. We choose a threshold τ ∈ [0, 1] and accept a test vector as valid if

$$\text{SCI}(\widehat{\mathrm{x}})>\mathrm{\tau },$$ (15)

and otherwise reject as invalid.

To summarize, for the class i, the selected sample vectors v_ij j = 1, …, 5, must satisfy the following three conditions to be valid sample vectors to fit into the model: 1. They can be correctly classified by the training model; 2. They satisfy SCI requirement given by (15); and 3. Let A_i = [v_i1, v_i2, …, v_i5], then its determinant |A_i| > 0.

F. Classification Using SRC Algorithm and ANOVA Analysis

After the classifier training, the coefficient matrix A of the sparse representation method given by (2) changed into A ∈ R^5×120 (24 classes * 5 basis vectors/class = 120), and the sparse solution changed into x ∈ R¹²⁰ correspondingly. Then a test vector y_j ∈ R⁵ is classified using the trained classifier, where j = 1, …, N and N is the number of pixels in the image. Only pixels within the region of interest were classified using the proposed SRC method. Results were given for each data set with mean and standard deviation for each method (see “Results” section).

In order to compare the performance of these different algorithms, one way ANOVA statistical analysis [36] was performed on the classification ratio (CR) obtained from SRC using different sparse representation computations: Homotopy, OMP, LARS. One way ANOVA analysis was also performed to compare classification ratio (CR) between Homotopy based SRC and the two existing methods: AFCM method and FCM method. P-values of the statistical analysis were given.

III. Results

A. M-FISH Database

A database consisting of 200 M-FISH-labeled human chromosome spread images has been established by Advanced Digital Imaging Research (ADIR) (Database website) to support this research. The database contains six-channel image sets recorded at different wavelengths. The specimens were prepared with probe sets from Applied Spectral Imaging (Migdal HaEmek, Israel), Advanced Digital Imaging Research (ADIR; League City, TX), Cytocell Technologies (Cambridge, U.K.), and Vysis (Downers Grove, IL). The database contains 200 spreads from 33 slides from five different laboratories. The specimens include 74 normal male spreads, 8 normal female spreads, 99 abnormal spreads, and 17 more that are of low specimen quality. There are 50 different chromosomal aberrations represented, including numerical abnormalities and structural arrangements. Spread quality ranges from excellent to very difficult. This comprehensive image database is a valuable source for M-FISH studies. In addition, the database includes a classification map, stored as an image file that was established by experienced cytogeneticists. This image is labeled so that the gray level of each pixel represents its class number (chromosome type). In addition, background pixels are 0, and pixels in a region of overlap are 1. This data file serves as ground truth to test the accuracy of M-FISH image classification algorithms.

B. Mask Generation

Adaptive Fuzzy C-means clustering methods (AFCM) have shown improved image segmentation results [34], [35], [37]–[40] when applying to MRI images. In this work, an AFCM was applied to DAPI channel to generate a mask, which was used for all other image channels. Only pixels within the mask were processed for the classification because they correspond to the chromosomes of interest. Fig. 2 gives an example of the DAPI channel image and the mask generated using AFCM. All the pixels outside the mask are in the background and can be considered to be in a separate class.

Fig. 2.

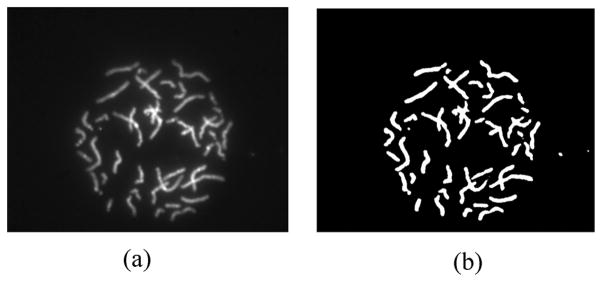
An example of a DAPI channel and the mask generated. (a) DAPI channel. (b) Mask for chromosome region.

C. Classification Results Using Different Methods

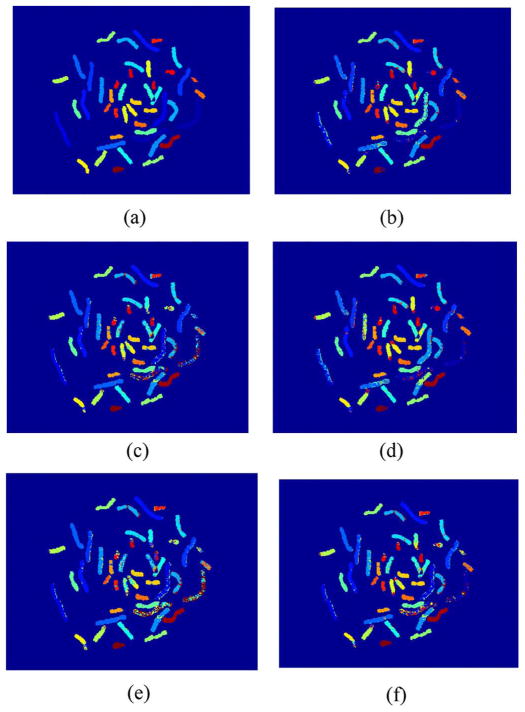
M-FISH images of 20 cells (10 male, 10 female) from the data base that we established [22] were tested. The proposed SRC algorithms using three different sparse representations (e.g., Homotopy, OMP, and LARS) were studied and compared. In addition, results of these SRC methods were compared with two other existing pixel-wise classification methods: FCM and AFCM method. Because we are testing the performance of the classifiers, there are no pre-preprocessing (color compensation, background correction, noise filtering, etc.) or post-process (morphology process, joint segmentation-classification, etc.) for those results, which would otherwise further improve the overall classification accuracy. Table I gives the CRs of SRC using different sparse representation computations: Homotopy, OMP, LARS, as well as the CRs of AFCM and FCM methods. Mean values and standard deviations were also provided. As an example, Fig. 3 shows the classification results using different methods (in the form of pseudocolor) on one set of M-FISH images.

TABLE I.

The CR of SRC Using Different Sparse Representation Computations: Homotopy, OMP, and LARS, and the Two Existing Methods Including AFCM and FCM

CR of SRC using Homotopy (%)	CR of SRC using OMP (%)	CR of SRC using LARS (%)	CR of AFCM (%)	CR of FCM (%)
82.01	76.86	71.97	74.83	79.16
72.41	69.76	58.00	61.18	69.89
81.87	50.28	77.23	77.68	43.26
78.38	52.46	69.53	72.73	55.73
58.15	59.66	59.47	61.69	52.04
78.38	58.23	61.32	61.67	60.89
85.84	62.02	66.81	67.79	64.63
71.77	69.03	63.32	65.24	70.41
56.23	70.17	57.26	60.62	72.47
76.88	91.85	64.29	67.67	92.45
64.28	56.08	61.46	62.02	58.56
63.58	64.44	67.64	71.04	64.56
78.88	74.88	74.39	77.75	75.85
79.24	74.31	75.15	76.85	74.48
74.38	71.52	69.92	72.73	71.86
70.88	67.32	66.94	67.44	70.21
73.93	64.15	68.50	69.98	66.59
69.29	62.34	67.11	70.32	63.45
72.54	66.02	65.97	68.75	69.35
86.74	82.20	76.75	80.11	82.33
Mean+std:	Mean+std:	Mean±std:	Mean±std:	Mean+std:
73.78 ± 8.39	67.18 ± 10.12	67.15 ± 5.98	69.40 ± 6.11	67.91 ± 10.97

Fig. 3.

M-FISH classification results of using different methods, which are displayed with pseudocolor. (a) Ground truth. (b) Result from SRC with Homotopy. (c) Result from SRC with OMP. (d) Result from SRC with LARS. (e) Result from FCM. (f) Result from AFCM.

D. Statistical Analysis to Compare CRs From Different Methods

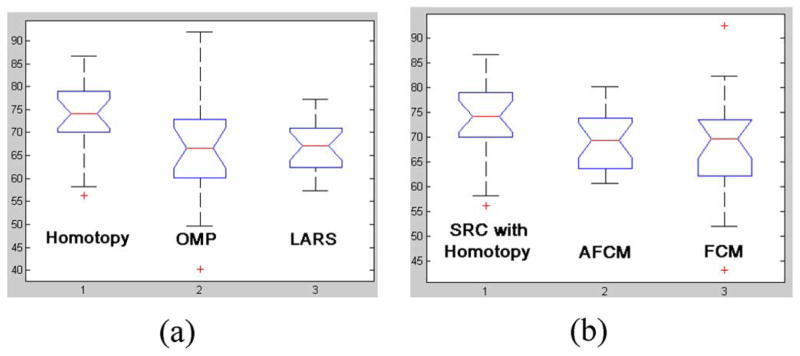
In order to compare the classification results of these different methods, one way ANOVA statistical analysis [36] was performed. P-values were given for each contrast. The smaller the p-value, the more significant the difference would be. P-value between Homotopy method and OMP method is 0.023, and the p-value between Homotopy method and LARS methods is 0.007. Thus, for the data we tested, we can conclude that Homotopy is better than OMP and LARS in M-FISH image classification with a confidence level over 95%. The p-values between Homotopy based classifier and AFCM method is 0.067, and is 0.065 when compared with FCM method. In other words, with a confidence level over 90%, Homotopy based classifier gives better classification ratio than AFCM and FCM for the data tested in this work.

Fig. 4 shows the box plot of results from each method, in which five most important sample percentiles were given: the sample minimum (smallest observation), the lower quartile or first quartile, the median (middle value), the upper quartile or third quartile, and the sample maximum (largest observation).

Fig. 4.

The box plots of M-FISH image classification ratios (CRs) using different methods (a) with different sparse representation methods: Homotopy, OMP, and LARS; (b) with Homotopy, AFCM and FCM.

IV. Discussion and Conclusion

In this paper, we proposed a sparse representation based M-FISH image classification algorithm. Three different optimal sparse representation methods, Homotopy, OMP and LARS, were compared for the classification of M-FISH images. The experimental results tested on the M-FISH datasets have shown that Homotopy based classifier is significantly better than the other two methods for the data sets we tested (p-values are 0.023 and 0.007 respectively). This suggests that proper selection of optimal sparse representation is essential to the classification result. Donoho et al.’s work also showed that Homotopy approach runs faster than general-purpose LP solvers [29]. Therefore, Homotopy based sparse representation classifier is a better choice for M-FISH image classification. In addition, SRC with Homotopy method was compared with two other existing pixel-wise M-FISH image classification methods, AFCM method and FCM method. Under the same processing sequence, (no preprocessing or post processing), SRC can give better classification ratio than AFCM and FCM methods can, although AFCM and FCM methods were proven to be effective in M-FISH image classification in our earlier work [12], [13]. Chromosome classification can be well formulated as the sparse representation; each sample in a chromosome class can be optimally represented by a five dimensional vector. We anticipate that this improved classification technique can be used to better characterize chromosomal abnormalities for cancer and genetic disease diagnosis.

Wright et al. proved that exploiting sparsity is critical for the classification of high-dimensional data [33]. In this paper, five channel images were employed for the classification tasks, which indicate that sparse representation is also effective for low-dimensional data.

Although the proposed Homotopy based sparse representation method gave the relatively highest classification accuracy, it hasn’t employed any pre- and/or post-processing steps. Some post processing methods such as the joint segmentation-classification proposed by Schwartzkopf et al. [7], and pre-processing methods such as the color compensation proposed by Choi et al. [9] can be incorporated to further increase the accuracy of classification. In addition, image segmentation to generate the mask was performed only on the DAPI channel; image segmentation method using multi-channel information such as proposed by Petros et al. [8], [19] can be used to further improve classification tasks. Finally, the use of more image features may also lead to an improved classification. For example, feature vectors including the neighboring information, such as first and second derivatives, central moment, etc., may help improve the classification accuracy.

Biographies

Hongbao Cao received the B.E. and M.S. degrees in BME from Tianjin University, Tianjin, China, in 2002 and 2005, respectively, and the Ph.D. degree in BME from Louisiana Tech University, Ruston.

He was a Postdoctoral Research Associate in the Department of Computer Science and Electrical Engineering, University of Missouri-Kansas City from November 2009 to August 2010. He is currently a Postdoctoral Research Associate in the Department of Biomedical Engineering Tulane University, New Orleans, LA. He has about 20 publications, and his research interests involve signal processing, image processing, pattern recognition, and computational modeling.

Hong-Wen Deng received the B.S. degree in ecology and environmental biology and studied two years of ecology and entomology at Peking University, China, and the M.S. degree in mathematical statistics and the Ph.D. degree in quantitative genetics from the University of Oregon, Eugene.

He was a Postdoctoral Fellow in the Human Genetics Center, University of Texas in Houston, where he conducted postdoctoral research in molecular and statistical population/quantitative genetics. He also served as a Hughes Fellow in the Institute of Molecular Biology at the University of Oregon. He previously served as Professor of medicine and biomedical sciences at Creighton University Medical Center, Professor of orthopedic surgery and basic medical science and the Franklin D. Dickson/Missouri Endowed Chair in Orthopedic Surgery at the School of Medicine of University of Missouri-Kansas City. He is currently the Chair of the Tulane Biostatistics and Bioinformatics Department and the Director of Center of Bioinformatics and Genomics. He is widely published with over 400 peer-reviewed articles, 10 book chapters, and 3 books. His area of interest is in the genetics of osteoporosis and obesity.

Dr. Deng is the holder of multiple NIH RO1 awards and recipient of multiple honors for his research.

Marilyn Li received her M.D. degree at Tongji Medical College of Huazhong University of Science and Technology, China, in 1983.

She is a Professor of Molecular and Human genetics, the Director of the Cancer Genetics Laboratory at Baylor College of Medicine, Houston, TX. She had her fellowship training in Clinical Cytogenetics and Clinical Molecular Genetics at the University of Pennsylvania/Children’s Hospital of Philadelphia. Prior to her appointment at Baylor College of Medicine, she served as the Director of the Tulane Clinical Cytogenetics Laboratory, Clinical Molecular Genetics Laboratory, Tulane Matrix DNA Diagnostic Laboratory, and the director of the Genomics Core Laboratory of Louisiana Cancer Research Consortium. Her primary research interest is clinical application of microarray technologies in cancer research and diagnosis.

Dr. Li holds American Board of Medical Genetics certification and is certified in Clinical Cytogenetics and Clinical Molecular Genetics. She is a fellow of the American College of Medical Genetics, the American Society of Human Genetics, the Southwest Oncology Group and the Children’s Oncology Group, the Association of Molecular Pathology, the American Society of Hematology, American Society of Clinical Oncology. She initiated, organized and is the president of the Cancer Cytogenomics Microarray Consortium, an international consortium whose mission is to facilitate the development and utilization of microarray-based technology for high quality, reliable cancer genetic testing in diagnostic laboratories. She is also the recipient of the 2010–2011 Luminex/ACMGF Award for the promotion of safe and effective genetic testing and services.

Yu-Ping Wang (SM’06) received the B.S. degree in applied mathematics from Tianjin University, China, in 1990, and the M.S. degree in computational mathematics and the Ph.D. degree in communications and electronic systems from Xi’an Jiaotong University, China, in 1993 and 1996, respectively.

After his graduation, he had visiting positions at National University of Singapore and Washington University Medical School in St. Louis, MO. From 2000 to 2003, he worked as a Senior Research Engineer at Perceptive Scientific Instruments, Inc., and then Advanced Digital Imaging Research, LLC, Houston, TX. In the fall of 2003, he returned to academia as an Assistant Professor of computer science and electrical engineering at the University of Missouri-Kansas City. He is currently an Associate Professor of biomedical engineering and biostatistics and bioinformatics at Tulane University, New Orleans, LA, and a member of Tulane Center of Bioinformatics and Genomics and Tulane Cancer Center. He is also a Visiting Professor at Shanghai University for Science and Technology, China, under the Eastern Scholarship Program. His research interests lie in the interdisciplinary biomedical imaging and bioinformatics areas, where he has about 100 publications.

Dr. Wang has served on numerous program committees and NSF/NIH review panels. He was a guest editor for the Journal of VLSI Signal Processing Systems on a special issue on genomic signal processing and was a member of Machine Learning for Signal Processing technical committee of the IEEE Signal Processing Society.