The Visual Input to the Retina during Natural Head-Free Fixation

Abstract

Head and eye movements incessantly modulate the luminance signals impinging onto the retina during natural intersaccadic fixation. Yet, little is known about how these fixational movements influence the statistics of retinal stimulation. Here, we provide the first detailed characterization of the visual input to the human retina during normal head-free fixation. We used high-resolution recordings of head and eye movements in a natural viewing task to examine how they jointly transform spatial information into temporal modulations. In agreement with previous studies, we report that both the head and the eyes move considerably during fixation. However, we show that fixational head and eye movements mostly compensate for each other, yielding a spatiotemporal redistribution of the input power to the retina similar to that previously observed under head immobilization. The resulting retinal image motion counterbalances the spectral distribution of natural scenes, giving temporal modulations that are equalized in power over a broad range of spatial frequencies. These findings support the proposal that “ocular drift,” the smooth fixational motion of the eye, is under motor control, and indicate that the spatiotemporal reformatting caused by fixational behavior is an important computational element in the encoding of visual information.

Introduction

Sensory systems have evolved to operate efficiently in natural environments. Therefore, linking the response characteristics of sensory neurons to the statistical properties of natural stimulation is an essential step toward understanding the computational principles of sensory encoding (Simoncelli and Olshausen, 2001; Hyvärinen et al., 2009). This step requires examination of the characteristics of both the natural environment and the motor behavior of the organism, as these two elements jointly contribute to shaping input sensory signals. In primates, small head and eye movements continually occur during the intersaccadic periods in which visual information is acquired and processed. These fixational movements directly impact the retinal stimulus and may profoundly influence the statistics of the visual input.

In observers with their heads immobilized—a standard condition for studying fixational eye movements—we recently showed that incessant intersaccadic eye drifts alter the frequency content of the stimulus on the retina; whereas low spatial frequencies predominate in natural images (Field, 1987), fixational eye movements redistribute the input power on the retina to yield temporal modulations with uniform spectral density over a wide range of spatial frequencies (Kuang et al., 2012). This finding has two critical implications for the encoding of visual information: it challenges the traditional view that this power equalization—also known as “whitening”—is accomplished by center–surround interaction in the retina (Srinivasan et al., 1982; Atick and Redlich, 1992; van Hateren, 1992); and it supports the general idea that the fixational motion of the retinal image acts as a mechanism for encoding a spatial sensory domain in time (Marshall and Talbot, 1942; Ahissar and Arieli, 2001; Greschner et al., 2002; Rucci, 2008).

Under more natural conditions, “fixational head movements,” the translations and rotations resulting from continual adjustments in body posture and physiological head instability, also contribute to retinal image motion (Skavenski et al., 1979; Ferman et al., 1987; Demer and Viirre, 1996; Crane and Demer, 1997; Louw et al., 2007; Aytekin and Rucci, 2012), and it is unknown whether an equalization of spatial power continues to occur. On the one hand, the smooth fixational motion of the eye is often assumed to be uncontrolled (Engbert and Kliegl, 2004; Engbert, 2012), and the superposition of fixational head and eye movements may decrease the precision of fixation and increase the velocity of the retinal image. These effects would reduce the extent of whitening resulting from fixational modulations and change their information-processing contribution. On the other hand, it has long been argued that ocular drift is also under visuomotor control (Steinman et al., 1973; Epelboim and Kowler, 1993; Kowler, 2011), and pioneering investigations have suggested some degree of compensation between fixational head and eye movements (Skavenski et al., 1979). Thus, in principle, adjustments in fixational eye movements could compensate for the normal presence of fixational head movements and still give spatial whitening of the stimulus on the retina. This issue has remained unexplored, and the frequency characteristics of the visual input to the retina under normal head-free fixation are as yet unknown.

In this study, we used simultaneous recordings of head and eye movements obtained by means of a custom device to examine the statistics of the retinal stimulus during normal head-free fixation. We show that fixational head and eye movements are coordinated in a very specific manner, resulting in a pattern of retinal image motion with frequency characteristics similar to those observed in subjects with their head immobilized. That is, with either head fixed or head free, temporal modulations on the retina equalize the spatial power of natural scenes.

Materials and Methods

Analysis of retinal motion under natural viewing conditions is challenging, as high-resolution measurements of eye movements typically require immobilization of the head. Here, we used data previously collected with the Maryland Revolving Field Monitor (MRFM), which, to our knowledge, is the only device with demonstrated capability of precisely recording microscopic eye movements during normal head-free viewing (Steinman et al., 1990). In this section, we focus on the procedures for reconstructing and analyzing retinal image motion. The apparatus, the procedures for data collection, and the experimental task have been described in previous publications (Epelboim et al., 1995, 1997; Epelboim, 1998) and are only briefly summarized.

To maintain a terminology similar to the one used in head-immobilized experiments, we will refer to the rotations of the eyes relative to a reference frame H fixed with the head (for the eye-in-the-head rotations, see Fig. 1) as eye movements. We will use the term “head movements” to denote the rotational and translational changes in the pose of the head (defined here as a rigid body H) relative to a standard reference position in an allocentric reference frame H^o. Head movements may be the consequence of neck rotations as well as movements of the torso. In head-fixed experiments, the smooth eye movements occurring during fixation on a stationary object are commonly referred to as “ocular drifts.” Extending this terminology, we use the term “retinal drift” (or simply “drift”) to indicate the intersaccadic retinal image motion present during fixation on one of the LED targets. Since the head is free to move in these experiments, retinal drift may result not only from eye-in-head rotations, but also from head movements.

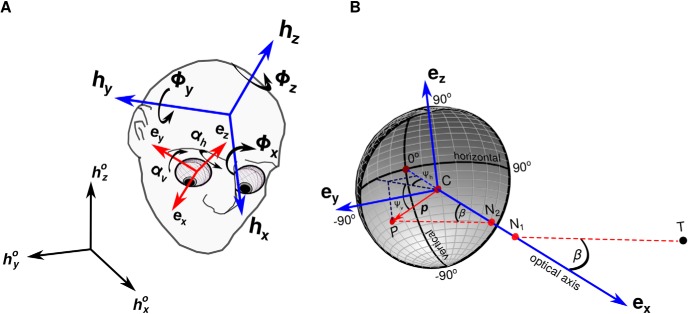
Figure 1.

Reconstruction of the retinal input. A, Head rotations were expressed by the Fick angles (yaw Φ_z, pitch Φ_y, and roll Φ_x) necessary to align a reference frame, H° = {h_x°, h_y°, h_z°}, established during an initial calibration procedure with a head-fixed frame, H = {h_x, h_y, h_h}. Eye movements, defined as eye-in-the-head rotations, were measured by the horizontal and vertical rotations, α_H and α_V, necessary to align H with an eye-centered reference frame E, oriented so that its first basis vector e_x coincided with the line of sight. B, Joint measurement of the orientation and position of the head enabled localization of the centers of rotations of the two eyes (C) and their optical axes (e_x). The retinal image was estimated by placing the eye model of Gullstrand (1924) at the current eye location. N₁ and N₂ optical nodal points, T target, P target's projection on the retina.

Subjects and task

Three human subjects participated in the experiments. Y.A. (a 63-year-old male) was naive about the goals of the original experiments and had only served in one prior oculomotor experiment. The other two subjects (R.S., a 70-year-old male; and J.E., a 30-year-old female) were the experimenters who collected the data. They were both experienced subjects and had participated in many previous oculomotor experiments. For the purpose of this article, however, these two experienced subjects can, in a sense, also be considered naive, as the analyses of retinal drift presented here were not part of the goals of the original experiments.

Observers sat normally on a chair and were asked to look sequentially, in a pre-established order, at four LEDs with different colors (the targets). The LEDs had diameter of 5 mm and were placed at fixed positions on a table (58.5 × 45 cm) in front of the subject. The positions of the targets were selected randomly and changed every five trials. Their distances from the observer's eyes varied between 50 and 95 cm, and their minimum separation was 4.5 cm. Subjects could move freely while remaining on the chair and were given ample time (6 s) to complete the task in each trial. The room was normally illuminated, and the targets remained clearly visible for the entire experimental session. Experiments were conducted according to the ethical procedures approved by the University of Maryland.

Apparatus

The orientation of the line of sight of each eye was recorded by means of the scleral search coil technique. Subjects had eye-coil annuli placed in their eyes [two-dimensional (2D) coils, eye torsion was not measured; Skalar Medical BV] and were surrounded by a properly structured magnetic field. In the traditional version of this method, amplitude measurements of the current induced in the eye coil enable estimation of the direction of gaze (Robinson, 1963; Collewijn et al., 1975). Amplitude estimation, however, gives precise measurements of eye rotations only with the head immobilized (Robinson, 1963; Houben et al., 2006); when the head is not restrained, lack of homogeneity in the magnetic fields causes measurement artifacts (Collewijn, 1977). To circumvent this problem, the MRFM uses an ingenious combination of three magnetic fields, which rotate at different frequencies in mutually orthogonal planes. This method has been shown to give precision higher than 1 arcmin even in the presence of considerable head and body motion (Rubens, 1945; Hartman and Klinke, 1976; Epelboim et al., 1995).

The measured eye coil angles give the gaze orientation in space. For measuring eye movements relative to the head, two additional coils were placed on the head of the observer. The angles given by these coils were converted into yaw, pitch, and roll angles—Φ_z, Φ_y, and Φ_x, respectively—according to Fick's convention (Haslwanter, 1995). The orientation of each coil was sampled at 488 Hz and digitally recorded with 12 bit precision. Because the objects were not at an infinite distance from the observer, retinal image motion was also influenced by head translations. Translations were measured by means of an acoustic localization system based on four microphones. This system estimated the position of a marker (a sparker on the subject's head) from the differences in the time of arrival of the sound at the microphones, an approach with an accuracy of ∼1 mm. Head position data were sampled at 61 Hz—a bandwidth sufficient for measuring the typically slow head translations of fixation—and interpolated at 488 Hz.

Preliminary calibration procedures conducted in each experimental session defined the room-centered reference frame H^o = {h_x^o, h_y^o, h_z^o} (Fig. 1A) with origin at the head marker and determined possible offsets in the placement of the coils. These initial calibrations also enabled estimation of the two vectors, r_o^L and r_o^R, which determined the positions of the centers of rotations of the two eyes relative to the position of the head-mounted sparker, s_o. The eye centers were assumed to be located 14 mm behind the surfaces of the cornea (Ditchburn, 1973).

Estimation of retinal image motion

For a given LED target, its instantaneous projection in the retinal image is determined by the position of the eye in space and the orientation of the line of sight. Therefore, to reconstruct the trajectories followed by the targets on the observer's retinas during a trial, we performed three successive computational steps at each time sample t. First, we estimated the position of each eye's center of rotation, c^L(t) and c^R(t), where L and R indicate the left and right eye, respectively. Second, we computed the coordinates of every LED target with respect to an eye-centered reference frame aligned with the line of sight. Third, we projected all the targets onto the retinal surface by means of a geometrical and optical model of the eye.

Step 1: eye positions in three-dimensional space.

This first step of the procedure is similar in concept, but different in implementation, to the method described by Epelboim et al. (1995). The trajectories followed by the centers of rotations of the two eyes (the eye displacements in Fig. 2C) were reconstructed on the basis of the three-dimensional (3D) position of the head marker s(t) and the instantaneous yaw, pitch, and roll head angles, Φ_z(t), Φ_y(t), and Φ_x(t). That is, at any time t during a trial, the eye displacements (i.e., the instantaneous 3D positions of each eye's center of rotation, c^L(t) and c^R(t)) were estimated by means of rigid body transformations of the subject's head relative to the room-centered reference frame H^o, as follows:

Here R_Φ (Φ_z, Φ_y, Φ_x) represents the Fick's angle rotation matrix defining the current head orientation relative to the reference orientation measured during the preliminary calibration procedure.

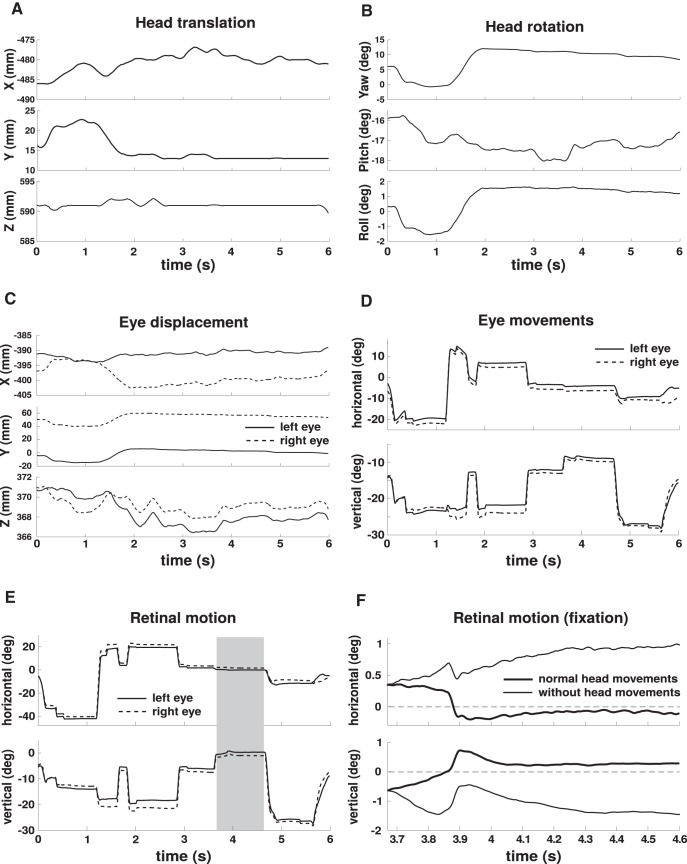
Figure 2.

Examples of head and eye movements and resulting image motion on the retina during an experimental trial. A, Head translations. B, Head rotations. Head movements were measured relative to a room-fixed Cartesian reference system, as shown in Figure 1. C, Eye displacements, defined as the translational motion of the eye resulting from head movements. Traces represent the spatial trajectories followed by the center of rotation of each eye. D, Rotational eye movements, defined as horizontal and vertical rotations of the eye within the head. E, Retinal image motion. Trajectory of the retinal projection of one LED target. F, Enlargement of a portion of the trace in E (shaded region). For comparison, the trajectory obtained by artificially eliminating head movements (i.e., by holding head position and orientation signals constant for the entire fixation interval) is also shown. In all panels, angles are expressed in degrees, and translations in millimeters.

Step 2: locating targets relative to eyes.

To compute the target positions with respect to an eye-centered reference frame, we first obtained the instantaneous head-centered reference frame H(t) = {h_x, h_y, h_z}. This coordinate system was computed by rotating the allocentric frame, H^o, by the measured Fick's angles (Fig. 1A), as follows:

Eye movements, defined as rotations of the eyes in the head, were given by the horizontal and vertical angles, α_h^L,R and α_v^L,R, of each eye's line of sight relative to H (see example in Fig. 2D). Rotating H by these two angles around h_z and h_y, respectively, brought h_x parallel to the line of sight and enabled the definition of an eye-centered reference frame E = {e_x, e_y, e_z}, as follows:

where R(α_h, α_v, 0) represents the corresponding rotation matrix (left/right indices omitted for simplicity of notation here and below). E was placed so that its origin coincided with the eye's center of rotation and was oriented so that its first vector, e_x, was aligned with the line of sight (Fig. 1A).

We then expressed the position of each target with respect to E. Given a target T at room-centered coordinates t, its position in eye-centered coordinates was given by the following:

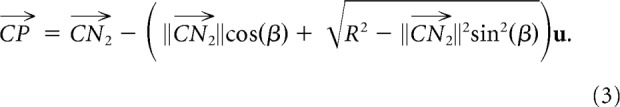Step 3: reconstructing the retinal image.

Given the instantaneous position of the eye center of rotation, c, and the eye-centered reference frame, it was possible to estimate the projection of each target on the retina. This was achieved by means of the eye model of Gullstrand (1924) with accommodation. In the schematic eye models of Gullstrand (1924), the retina as a spherical surface (radius, 11.75 mm) was centered at the center of rotation. It simulates the process of image formation as a two-nodal point optical system, so that a ray of light going through the first nodal point (N₁) exits the second nodal point (N₂) with a parallel path. The two optical nodal points are located on the line of sight at distances of 5.7 mm (N₁) and 5.4 mm (N₂) from the eye center.

The eye model was positioned so that its center of rotation C coincided with c(t) and its optic axis was aligned with the estimated line of sight (the basis vector e_x; see Fig. 1B). This enabled estimation of the vector $\overrightarrow{N_{1}T}$ and the angle β between $\overrightarrow{N_{1}T}$ and the direction of gaze e_x in Figure 1B. We then identified the position P of the retinal projection of the target relative to the eye center by means of the vector $\overrightarrow{CP}$. This vector is given by the sum of $\overrightarrow{C{N}_2}$ and $\overrightarrow{N_{2}P}$. Since $\overrightarrow{N_{2}P}$ is parallel to and in the opposite direction of $\overrightarrow{N_{1}T}$, we obtain the following:

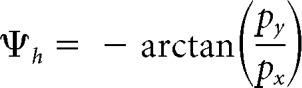where R is the radius of the eye, and u = $\frac{\overrightarrow{N_{1}T}}{\Vert \overrightarrow{N_{1}T}\Vert }$ is the unit vector in the direction of $\overrightarrow{N_{1}T}$.

Once $\overrightarrow{CP}$ = [p_x p_y p_z]^T was estimated, the instantaneous retinal position of the target was expressed in spherical coordinates by means of the horizontal and vertical angles Ψ_h and Ψ_v in Figure 1B, as follows:

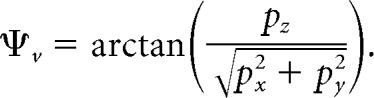In this way, the position marked by zero angles (i.e., Ψ_h = 0, Ψ_v = 0) corresponds to the center of the preferred retinal fixation locus measured during the calibration procedure (the center of gaze; the 0^o point in Fig. 1B at which the line of sight intersected the retinal surface). The retinal trace of a given target in a trial consisted of the 2D trajectories [Ψ_h(t), Ψ_v(t)] evaluated over the course of the entire trial. The distributions in Figure 5 were evaluated by translating each fixation trace along the retinal geodesic so that its first point coincided with the center of gaze. Note that because of the offset between the center of rotation C and the nodal point N₁ in the eye model of Gullstrand (1924), the use of a reference system centered at C implies a magnification in the velocity of the target in the retinal image relative to that measured in external visual angles. For small movements, like the ones occurring during fixation, this magnification is ∼50%.

Figure 5.

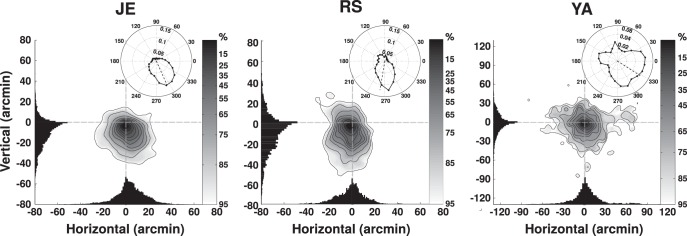
Precision of fixation. Two-dimensional distributions of displacements of the retinal projection of the fixated target. Retinal traces were aligned by positioning their initial point at the origin of the Cartesian axes. The marginal probability density functions are plotted on each axis. The insert panels give the probability of finding the retinal stimulus displaced by any given angle relative to its initial position. Each column shows data from one subject.

Retinal input analysis

In every trial, we estimated the trajectories of all targets on both retinas. For all the targets, the reconstructed retinal trajectories in a trial were jointly segmented into separate periods of fixation (the retinal drift periods) and saccades on the basis of the retinal velocity of the currently fixated target. The fixated target was selected binocularly as the target closer to cyclopean gaze, which we defined as the virtual line of sight going through the midpoint between the two eyes and the point of intersection of the lines of sight of the two eyes (or the point at minimum distance from these lines, if they did not intersect). This method ensured consistency between the fixation periods in the two eyes. Movements were categorized on the basis of the velocity of the fixated target because the various targets were located at slightly different distances from the observer and their instantaneous speeds on the retina were not identical during normal head movements.

Saccadic gaze shifts were defined as the periods in which (1) the instantaneous retinal speed of the target fixated at the beginning of the movement exceeded 12^o/s; and (2) its instantaneous acceleration exhibited a biphasic temporal profile with one peak before and one after the time of peak velocity. Retinal velocity and acceleration were estimated by temporal differentiation of the original traces. Saccade onset and offset were defined as the times at which the speed of the retinal projection of the presaccadic target became greater (saccade onset) and lower (saccade offset) than 4^o/s. Saccade amplitude was measured by the modulus of the angular displacement on the retina of this target. Consecutive saccades closer than 50 ms were merged together, a method that automatically excluded possible postsaccadic overshoots.

In this study, we focused on the characteristics of the head and eye movements occurring in the fixation intervals between saccades. To limit the impact of measurement noise in estimating the low velocities of fixational movements, intersaccadic segments in head and eye traces were filtered by means of a low-pass third-order Savitzky–Golay filter (Savitzky and Golay, 1964) before numerical differentiation. This local polynomial regression filter was designed to give a conservative cutoff frequency of ∼30 Hz. It was preferred over more traditional linear filters because of its higher stability during the initial and final intervals of each fixation segment, which enabled the use of larger portions of data. This approach also enabled direct comparison of the data presented here with the velocities previously measured in experiments with head immobilization. Head-fixed data were acquired by means of Generation 6 Dual Purkinje Image Eyetracker (Fourward Technologies) with the head immobilized by a dental imprint bite bar and a head rest, while subjects either maintained strict fixation on a dot or freely examined natural images.

To examine the characteristics of retinal drift and to allow for a direct comparison with our previous analysis under head-fixed conditions, we estimated the probability of retinal displacement, q(x,t) (i.e., the probability that the projection of the fixated target shifted on the retina by an amount x in an interval t; see Fig. 7). We summarized the overall shape of q(x, t) by means of the diffusion constant D, which defines how rapidly the dispersion of the displacement probability grows with time (D = < x^Tx >/4t). Since in the considered experimental task the lines of sight in the two eyes did not always exactly converge on the same target, estimation of q(x,t) was conducted over the intersaccadic intervals in which, in both eyes, a target was closer than 3° to the center of gaze, and its trajectory remained within a circular area as large as the fovea (1° diameter). This method ensured the selection of an identical fixation periods in the two eyes.

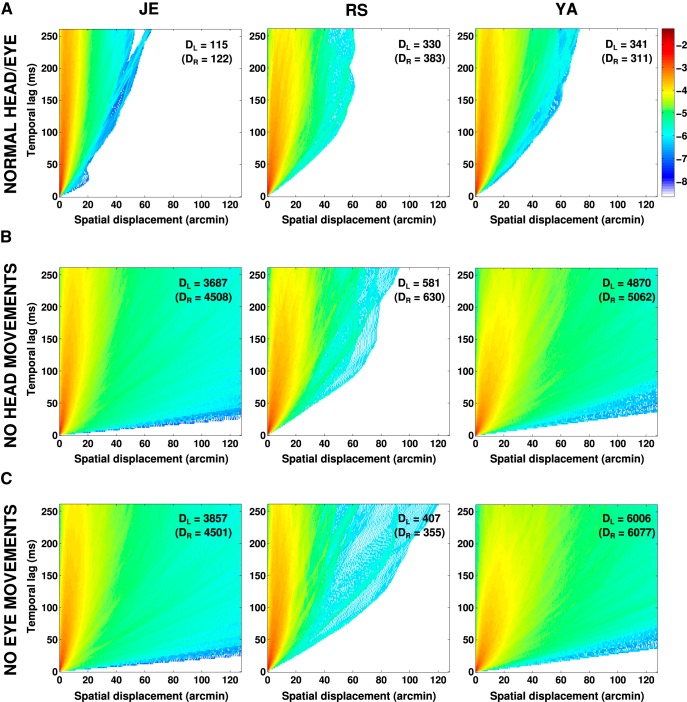
Figure 7.

Probability distributions of retinal image motion during intersaccadic fixation. In each panel, the color of a pixel at coordinates (x, t) represents the probability (in common log scale) that the eye moved by a distance x in an interval t. A, Probability distributions obtained during head-free fixation when both head and eye movements normally contributed to the motion of the retinal image. B, C, Same data as in A after removal of head (B) or eye (C) movements by replacing the original traces with equivalent periods of immobility. The numbers in each panel represent the diffusion constants measured in the two eyes of the Brownian process that best fitted (least squares) the distributions. Each column shows data from one subject.

The reconstructed retinal trajectories of the targets enabled estimation of the impact of head and eye movements on the frequency content of the visual input during natural fixation. In the absence of retinal image motion, the input to the retina would be an image of the external scene. However, fixational head and eye movements temporally modulate the input signals received by retinal receptors. These modulations transform the spatial power of the external stimulus into temporal power. The power redistribution of a small light source, like the LED targets used in this study, is well approximated by the Fourier transform Q(k, ω) of the displacement probability q(x, t) (see Fig. 8; k and ω represent spatial and temporal frequencies, respectively).

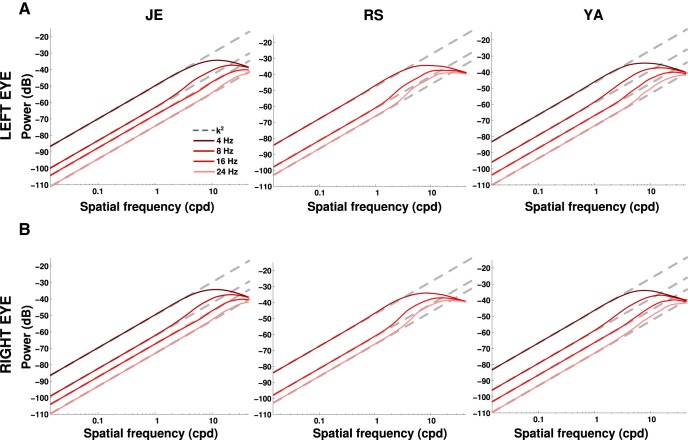
Figure 8.

Power redistribution in the retinal input resulting from fixational head and eye movements for an image consisting of a single point (the fixated LED target). In each panel, different curves represent different temporal frequency sections. Each column shows data from one subject; rows A and B show the two retinas. In all retinas, the power available at any temporal frequency increased proportionally to the square of spatial frequency (dashed lines).

More generally, Q(k, ω) also enables the estimation of how head and eye movements redistribute the spatial power of an arbitrary scene with spatially homogeneous statistics and spectral density distribution I(k). We have recently shown that, under the assumption that fixational drift is statistically independent from the retinal image, the power spectrum of the spatiotemporal stimulus on the retina, S, can be estimated as follows:

(see Kuang et al., 2012, their supplementary information). While the assumption of independence may not be strictly valid in restricted regions of the visual field—retinal image motion might be influenced by the stimulus in the fovea—it is a plausible assumption when considered across the entire visual field, as the estimation of the power spectrum entails.

The model in Equation 4 provides excellent approximations of the power spectra of visual input signals measured in head-fixed experiments (Kuang et al., 2012). We computed Q(k, ω) using the Welch method over periods of fixation >525 ms for subjects Y.A. and J.E. and >262 ms for subject R.S., who exhibited significantly shorter fixations. To summarize our results in two dimensions (space and time), probability distributions and power spectra are presented after taking radial averages across space (x = ‖x‖ and k = ‖k‖). As a consequence of the shorter time series for subject R.S., the 4 Hz section of Q is corrupted by leakage in this subject and is omitted in Figure 8. Estimation of how the fixational head and eye movements recorded in this study transform the spatial power of natural scenes was obtained by multiplying Q by the ideal power spectrum of natural images as in Equation 4 (i.e., by scaling Q(k, ω) by k⁻²; Field, 1987; see Fig. 9).

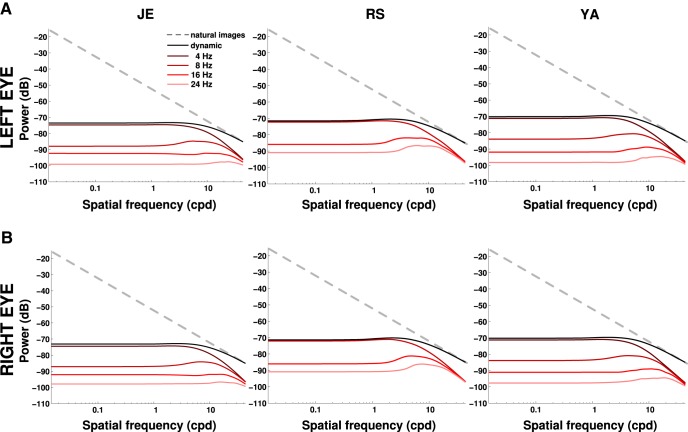
Figure 9.

Frequency content of the average retinal input during normal fixation in the natural world. The power of the external stimulus (natural images, dashed lines) is compared with the total power that becomes available at nonzero temporal frequencies because of fixational instability (dynamic, solid black line). The power distributions at individual temporal frequency sections are also shown. Each column shows data from one subject; rows A and B show the two retinas. Fixational head and eye movements whiten the retinal stimulus over a broad range of spatial frequencies.

Results

We reconstructed the spatiotemporal signals impinging onto the retina in a task in which observers looked naturally at a sequence of targets (a set of colored LEDs). Observers sat on a chair facing the targets but were otherwise free to move. The following sections summarize the characteristics of eye-in-the-head rotations (fixational eye movements) and head translations and rotations (fixational head movements) during fixation on the targets and the resulting image motion on the retina. Figure 2, to which we will periodically refer through the presentation of the materials, shows example traces of the head and eye movements recorded in the experiments and explains the approach followed by this study.

Fixational head and eye movements

Head movements, both translations and rotations, were measured relative to a room-centered reference frame defined during an initial calibration (see Materials and Methods). In the example trial considered in Figure 2, the head translated by ∼7 mm on the naso-occipital x-axis and by 8 mm on the intra-aural y-axis (Fig. 2A). As expected, given that the subject remained on the chair for the entire duration of the trial, movements in the vertical direction (the z-axis) were minimal. Because the targets covered a relatively wide angular field on the horizontal plane, head rotations occurred primarily around the vertical axis (yaw rotations) and were performed to shift gaze from one target to the next. Yaw rotations in this trial spanned a range of ∼13° (Fig. 2B). Rotations around the other two axes (pitch and roll) were also present, each covering a range of ∼2°.

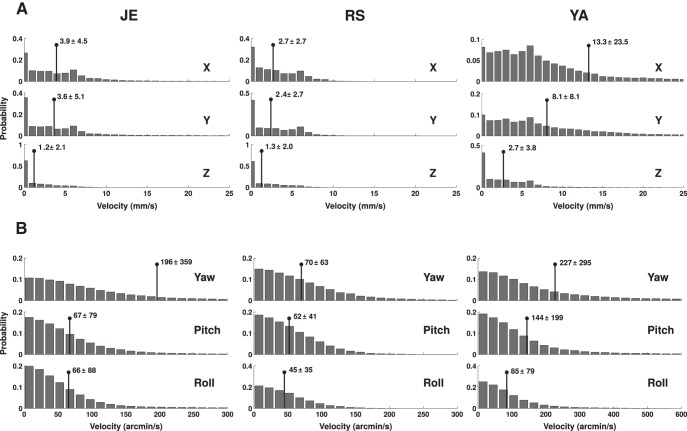
Measurements like the ones in Figure 2, A and B, were used to estimate the characteristics of head movements while subjects fixated on the targets (Fig. 3). Fixational head movements occurred in all 6 degrees of freedom. In agreement with previous reports (Crane and Demer, 1997; Aytekin and Rucci, 2012), the velocity of fixational head translations was for all subjects highest on the x-axis, intermediate on the y-axis, and minimal on the z-axis (Fig. 3A), probably reflecting the physiologically larger postural instability of the anterior–posterior axis (Paulus et al., 1984). Across subjects, the mean speed for head translations was 10 ± 8 mm/s. Conspicuous fixational head rotations also occurred on each degree of freedom (Fig. 3B). They were fastest around the yaw axis, intermediate around the pitch axis, and slowest around the roll axis, giving an average angular speed of ∼2^o/s (average ± SD across subjects: 112 ± 143 arcmin/s). Subjects differed in the velocity of head movements, but exhibited very similar motion patterns. Most notably, subject R.S. maintained a more stable fixation, moving his head significantly less than the other two subjects (p < 0.001, Kolmogorov–Smirnov test). His average translational and rotational speeds were >40% lower than those of subject Y.A. Still, even in this more stable observer, fixational head movements were significant, with average translational and angular speed equal to 5 mm/s and 56 arcmin/s, respectively.

Figure 3.

Fixational head movements. A, B, Distributions of instantaneous translational velocities along the three Cartesian axes (A) and instantaneous angular velocities for yaw, pitch, and roll rotations (B). Each histogram shows the characteristics of motion on an individual axis. Each column shows data from one subject. Numbers and lines in each panel represent the means and SDs of the distributions.

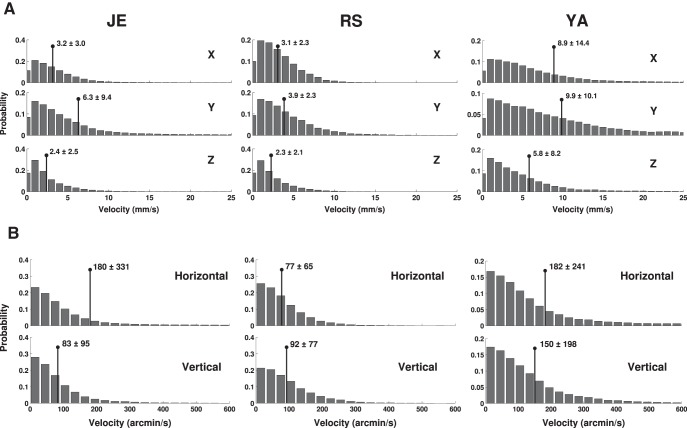
Under normal head-free viewing conditions, the eyes move in the following two ways: (1) they translate in space with the head because of head movements (eye displacements); and (2) they rotate within the head to redirect the line of sight (eye movements). We quantified linear displacements by reconstructing the 3D trajectory followed by the center of rotation of each eye. In the example of Figure 2C, the eye centers covered a distance of ∼2 cm, with a significant portion of the displacement taking place during fixation on the first two targets, in the interval between 1 and 2 s after trial onset. This change in position would, by itself, cause a large amount of motion in the retinal image, moving the retinal projection of a target at 50 cm from the observer by >2°. On average across trials, fixational head movements translated the two eyes in space by several millimeters during fixation (average displacement across subjects, 2.4 mm). The resulting average speed of eye displacement was 10.5 ± 5 mm/s (Fig. 4A). As expected because of the predominant yaw rotations, eye translations were more pronounced along the interaural y-axis, where they reached instantaneous velocities of many millimeters per second. But non-negligible linear velocities also occurred on the other two axes, particularly the x-axis.

Figure 4.

Fixational eye movements. A, B, Distributions of instantaneous translational (A) and rotational (B) eye velocities. Data refer to the displacements in the eye-center position caused by head movements in A and to eye-in-head rotations in B. Each histogram shows the velocity on 1 degree of freedom, with its mean ± SD reported in each panel. Each column shows data from one subject. Data refer to the right eye; the left eye moved in a highly similar manner.

Eye movements (i.e., eye-in-head rotations; Fig. 2D, example traces) were estimated on the basis of the signals given by the head and eye coils, which were both necessary to determine changes in the instantaneous directions of gaze relative to the head-fixed reference frame. Saccades were frequent in this experiment. Across observers, they occurred at an average rate of 2.4 saccades/s, ranging from 2 saccades/s for subject Y.A. to 2.7 saccades/s for subject R.S. Whereas saccades were frequent, microsaccades—defined as saccades with amplitudes of <30 arcmin—were extremely rare, a result that is in line with previous reports of both head-free (Malinov et al., 2000) and head-fixed studies (Collewijn and Kowler, 2008; Kuang et al., 2012) with tasks in which attention to fine spatial detail is not critical (but for examples of microsaccades in high-acuity tasks, see Ko et al., 2010; Poletti et al., 2013). A microsaccade occurred on average once every 4.4 s in subject J.E., and once every 10.4 s in subject Y.A. Microsaccades were virtually absent in subject R.S.

Even in the absence of microsaccades, the eyes moved considerably during fixation because of ocular drift, the smooth motion always present in the intervals between saccades. In all subjects, ocular drift reached velocities of several degrees per second on both the horizontal and vertical axes, with averages >1°/s (Fig. 4B). Across the six eyes considered in this study, the resulting 2D drift speed was on average 201 arcmin/s, a value approximately four times larger than the ocular drift speed we previously measured in a large pool of subjects during sustained fixation with the head immobilized (52 arcmin/s; p < 0.003; Mann–Whitney-Wilcoxon test; Cherici et al., 2012). This comparison should obviously be taken with caution, as the two sets of data were collected with different instruments and in different tasks. But the result is in agreement with those of previous studies suggesting that the fixational smooth motion of the eye is considerably faster when the head is free to move (Skavenski et al., 1979).

Retinal image motion

The results of Figures 3 and 4 show that considerable head and eye movements occur during the intersaccadic periods of fixation. What are the consequences of these movements on the input signal normally experienced by the visual system during natural head-free fixation?

To answer this question, we reconstructed the trajectories followed by the projections of the LED targets on the retina during the course of each trial (see example in Fig. 2E). These traces were obtained by means of a standard geometric/optical model of the eye (Gullstrand, 1924) properly placed at the estimated eye-center position in 3D space and oriented according to the estimated direction of gaze (Fig. 1B). The reconstructed retinal trajectories were the outcome of both head and eye movements. An example is given in Figure 2F, which compares the trajectory of the target fixated in a segment of the trace in Figure 2E to the one that would have resulted by artificially eliminating head movements (i.e., by maintaining head signals fixed for the entire fixation interval). In this example, as is typical, fixation was less stable in the absence of head movements, resulting in a considerably different trajectory of the stimulus on the retina.

Following the approach of Figure 2, we reconstructed the retinal trajectories of all the fixated targets and examined the precision of fixation by means of the resulting 2D distributions of displacement (Fig. 5). These distributions were obtained by aligning all the fixation segments by their initial point by means of parallel transport on the spherical surface of the retina (Shenitzer, 2002), so that they all started from the origin in Figure 5. These data show that subjects maintained accurate fixation in the intersaccadic intervals. All subjects exhibited approximately circular distributions with a tendency for drifting downward (Fig. 5, insets), a bias which was slightly more pronounced in observer R.S., possibly explaining the shorter fixation durations exhibited by this observer. Across observers, the average fixational area—defined as the area in which the gaze remained 95% of the time—was 4193 arcmin². As shown later, this area is much smaller (i.e., the precision of fixation was greater) than would be expected from the separate consequences of fixational head and eye movements.

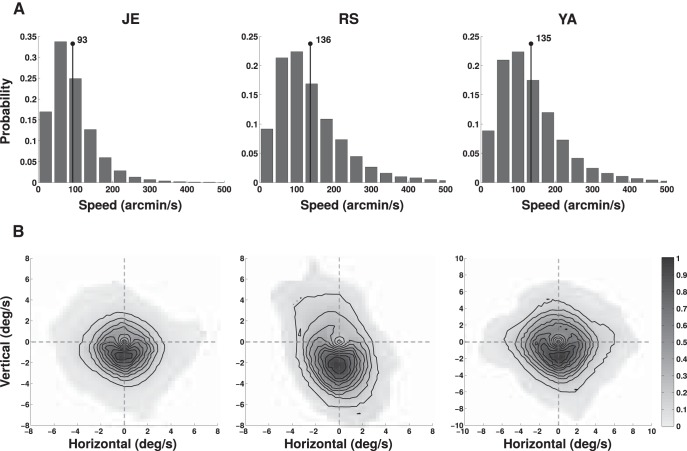
To understand how observers could maintain precise fixation despite continually occurring head and eye movements, we examined the velocity of retinal drift. The fixated target moved relatively fast on the retina. Two-dimensional velocity distributions were approximately circular (i.e., the projection of the target moved in all directions; Fig. 6B) with a slight preference for drifting downward. Speed distributions were broad in all observers, with an average speed across subjects of ∼119 arcmin/s (Fig. 6A). This value was significantly larger than the average speed of retinal drift that we previously observed under head immobilization (76 arcmin/s, taking into account the retinal amplification given by the Gullstrand, 1924, eye model; Cherici et al., 2012), a finding that confirms previous observations (Skavenski et al., 1979). But whereas the eye drifted approximately four times faster during normal head-free fixation, on the retina, the resulting speed of the fixated target was <60% higher than with the head immobilized. These comparisons suggest that, in head-free conditions, eye and head movements have largely canceling effects on retinal image motion.

Figure 6.

Velocity of retinal drift. A, Distributions of instantaneous drift speeds (the modulus of the retinal velocity vector). The numbers in each panel represent the mean speed values for each observer. B, Two-dimensional distributions of retinal velocity. The intensity of each pixel represents the normalized frequency that the fixation target moved with velocity equal to the vector given by the pixel position. Lines represent iso-frequency contours. Each column shows data from one subject.

With the speed distributions of Figure 6, the retinal projection of an initially fixated target would quickly leave the high-acuity region of the fovea if moving with uniform motion. This did not happen because drift changed direction frequently. To quantify this, we characterized the statistics of the retinal trajectory by means of q(x, t), the probability that the retinal projection of the fixated target shifted by a distance x in an interval t (Fig. 7A). In all six eyes, the variance of the spatial distribution increased approximately linearly with time (R² = 0.97), a behavior that is characteristic of Brownian motion. Consequently, the SD of the eye position increased only as $\sqrt{t}$, and the projection of the target remained within a narrow retinal region during the naturally brief periods of intersaccadic fixation.

For every observer, the diffusion constants of the equivalent Brownian motions (i.e., the proportionality between spatial variance and time) were similar in the two retinas and ranged from 115 arcmin²/s (subject J.E., left retina) to 383 arcmin²/s (subject R.S., right retina), which is in keeping with the slightly different mean retinal velocities of different observers. These values are much smaller than those expected from the independent effects of head and eye movements (Fig. 7B,C). Thus, despite the relatively high speed of fixational head and eye movements, the resulting distributions of retinal displacement were qualitatively similar to and only moderately broader than those previously measured when observers freely viewed natural images with their head immobilized (D = 63 arcmin²/s; note that D measures the rate of change in area).

It is important to observe that the displacement probabilities in Figure 7A resulted from a mutual compensation between fixational head and eye movements. To illustrate the importance of this compensation, Figure 7, B and C, shows the same probability density functions obtained when either head movements (Fig. 7B) or eye movements (Fig. 7C) were eliminated during the process of reconstructing retinal image motion. In these analyses, for each considered intersaccadic period, the recorded head or eye movement signals were substituted by equivalent periods of immobility (i.e., artificial traces with fixed position equal to those measured at the beginning of the considered fixation period). If fixational head and eye movements were independent, the diffusion constants in these two conditions should add up to give the diffusion constant measured when both head and eye movements contributed to image motion. In contrast, as is shown in Figure 7A, the diffusion constant of normal retinal motion was not only lower than this sum, but also lower than the diffusion constant for either head or eye movement alone.

In sum, these data extend the previous findings by Skavenski et al. (1979). They show that, during normal viewing of nearby objects, fixational head and eye movements partially compensate for each other to give a distribution of retinal displacements that resembles the one observed under head immobilization, a condition in which the eye drifts at much slower speeds. In the next section, we examine how the resulting motion transforms spatial patterns into temporal modulations.

Spectral characteristics of retinal input

If the observer did not move during fixation, the input signal impinging onto the retina would simply be an image of the external scene. Its spectral distribution would only depend on the frequency content of the scene, and its energy would be largely confined to the zero temporal frequency axis, as most of the scene is static. However, because of fixational head and eye movements, even a static scene yields a dynamic stimulus on the retina, a spatiotemporal input that also contains substantial energy at nonzero temporal frequencies. In other words, the observer's motor activity during the acquisition of visual information redistributes the power of the input stimulus across the spatiotemporal frequency plane away from the zero temporal frequency axis. This transformation is linear in space but not in time, since it is corresponds to sampling the scene through a moving window (effectively, a multiplication). It maintains the energy of the external stimulus at any given spatial frequency, but generates energy at temporal frequencies not present in the scene.

How did fixational head and eye movements redistribute the spatial power of the visual stimulus in the experiments? Considering, for simplicity, the LED targets as point-light sources, this space–time conversion can be directly estimated by means of the probability distributions of retinal displacement, the functions q(x, t) in Figure 7A. Specifically, the power that retinal drift makes available at any temporal frequency ω and spatial frequency k is proportional to the Fourier transform, Q(k, ω), of the drift probability distribution. Figure 8 shows that these redistributions were highly similar in the six retinas considered in this study. At all the examined nonzero temporal frequencies, temporal power increased by an amount approximately proportional to the square of the spatial frequency (Fig. 8, dashed lines). That is, normal fixational head and eye movements yielded temporal modulations on the retina, which enhanced high spatial frequencies with a square power law over a range larger than two orders of magnitude.

We then examined the consequences of the head and eye movements recorded in the experiments on the stimulus that would be present on the retina during fixation in the natural world. To this end, we used an analytical model of the power spectrum (Kuang et al., 2012, supplementary information). According to this model, under the reasonable assumption that retinal drift is statistically independent from the optical image of the external scene, the function Q can be regarded as an operator that transforms the spatial power of the external scene into spatiotemporal power on the retina. The spectral density of the retinal stimulus can then be estimated by direct multiplication of the power spectrum of the image with Q.

Natural scenes are characterized by a very specific distribution of spectral density, with power that declines proportionally to the square of the spatial frequency (Field, 1987). Note that the spatiotemporal transformation resulting from fixational drift (Fig. 8) tends to counterbalance this input distribution, as the amount of spatial power that retinal drift converts into temporal modulations increases inversely proportionally to the power available in natural scenes. The net result of this interaction is shown in Figure 9. In all six retinas, the spatial frequency enhancement given by fixational drift counterbalanced the scale-invariant power distribution of natural scenes, yielding temporal modulations with approximately equal power within a broad range of spatial frequencies. This power equalization (whitening) occurred at all nonzero temporal frequencies.

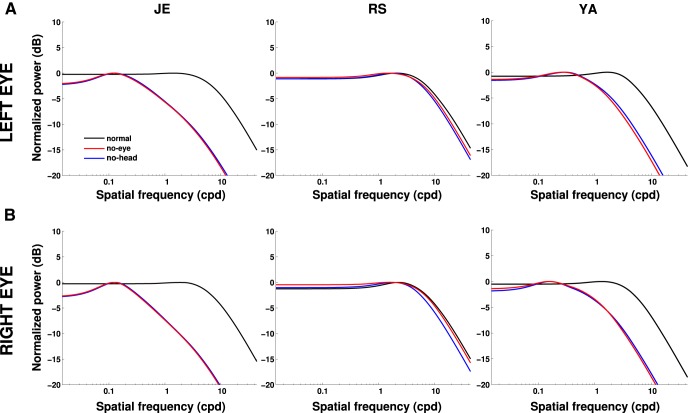
Figure 10 shows that the power equalization is a consequence of the way fixational eye movements compensate for head translations and rotations. These data represent the total temporal power present on the retina when we artificially eliminated head or eye movements. As in the analyses of Figure 7, B and C, for each considered fixation, we replaced head or eye movement traces by equivalent periods of immobility (i.e., artificial traces with fixed position equal to that measured at the beginning of the considered fixation period). In two of the subjects (J.E. and Y.A.), whitening was lost completely when head or eye movements were omitted from the reconstruction; in the third subject (R.S., the subject with the smallest amount of head instability), the range of whitening was reduced. Thus, during normal fixation in the natural world, incessant head and eye movements combine to whiten the visual input to the retina within the spatiotemporal frequency range at which humans are most sensitive.

Figure 10.

Effect of compensatory head and eye movements. The total power that becomes available at nonzero temporal frequencies because of the joint effect of head and eye movements (normal, replotted from Fig. 9) is compared with that obtained after artificial elimination of either eye (no eye) or head movements (no head). Each column shows data from one subject; rows A and B show the two retinas.

Discussion

Microscopic head and eye movements are incessant sources of modulation during the brief intersaccadic intervals in which visual information is acquired and processed. This motor activity redistributes the spatial power of the external scene into the spatiotemporal domain on the retina. Our results show that the redistribution present under natural head-free fixation counterbalances the average spatial spectral density of natural scenes in a manner similar to what we had previously observed under head-fixed conditions (Kuang et al., 2012): the redistribution removes predictable spatial correlations by equalizing power across spatial frequencies. Therefore, retinal drift whitens the visual input under both head-fixed and head-free viewing despite the large differences in eye movements present in the two conditions. These findings suggest that ocular drift is normally controlled to partially compensate for head movements to achieve a specific information-processing transformation.

Much research has been dedicated to unveiling the function of the fixational motion of the retinal image. It is well known that stabilized images—images that move together with the eyes—tend to lose contrast with time and possibly fade altogether (Ditchburn and Ginsborg, 1952; Riggs et al., 1953; Pritchard, 1961; Yarbus, 1967), a phenomenon commonly held as the standard explanation for the existence of microscopic eye movements. According to this traditional view, the physiological instability of fixation is necessary to refresh neuronal responses and prevent the disappearance of a stationary scene. However, it has long been questioned whether fixational jitter might play a much more fundamental role than preventing neural adaptation. Several theories have argued for a contribution of this motion to the processing of fine spatial detail (Averill and Weymouth, 1925; Marshall and Talbot, 1942; Arend, 1973; Ahissar and Arieli, 2001, 2012; Rucci, 2008). These theories differ in their specifics, but share the common hypothesis that the fixational motion of the retinal image is necessary for encoding spatial information in the temporal domain (i.e., for structuring, rather than just refreshing, neural activity).

Support for a contribution of fixational retinal image motion to temporal encoding comes from multiple experimental and theoretical observations on the perceptual consequences of fixational eye movements (Greschner et al., 2002; Rucci et al., 2007; Kagan et al., 2008; Ahissar and Arieli, 2012; Baudot et al., 2013). These movements are the sole contributor to retinal image motion when the head is immobilized, the standard laboratory condition for investigating small eye rotations. Under these conditions, experiments that eliminated retinal image motion have shown that fixational eye movements improve high spatial frequency vision (Rucci et al., 2007), an effect consistent with the way fixational modulations convert spatial energy into temporal energy in the retinal input. Furthermore, in observers with their head immobilized, a form of matching similar to that reported here for head/eye movements and natural images exists between ocular drift and the statistics of natural scenes (Kuang et al., 2012), showing, as discussed later, that fixational eye movements reformat natural scenes into a computationally advantageous spatiotemporal signal.

At first glance, the proposal that fixational eye movements are part of an active spatiotemporal coding process may appear challenged by the presence of fixational head movements, and by the changes in the characteristics of eye-in-head movements when the head is free to move. Involuntary head movements continually translate the eye in space during normal head-free fixation (Fig. 3), and ocular drift is much faster when the head is not restrained (Fig. 4). Both movements would, by themselves, alter the statistics of retinal stimulation, attenuating or even completely eliminating the equalization of input power (Fig. 7; for an analysis of the consequences of artificially enlarging eye movements, see also Kuang et al., 2012, their Fig. 3). The results of this study resolve these concerns. They show that the characteristics of the retinal input resulting from fixational head and eye movements are functionally similar to those of the signal given by ocular drift alone when the head is immobilized. In either condition, the ensemble of retinal drift trajectories resembles Brownian motion with a diffusion constant small enough to counterbalance the spectral density of natural scenes over the range of peak sensitivity of retinal ganglion cells. This outcome occurs because the more rapid eye movements in the head-free condition are anticorrelated with the fixational head movements, so that they largely neutralize the effects of the latter, maintaining the probability distribution of retinal displacements relatively unaltered.

In other words, our study shows that ocular drift (1) normally compensates for the fixational instability of the head, but (2) does so only in part, yielding residual motion with approximately Brownian characteristics on the retina. Both findings are in agreement with previous observations. Studies of the vestibulo-ocular reflex (VOR) have traditionally focused on much larger head movements than those on the microscopic scale that are considered here (but see Steinman and Collewijn, 1980; Raphan and Cohen, 2002; Angelaki and Cullen, 2008; Goldberg et al., 2012). However, it is known that reliable smooth pursuit in humans can be elicited with stimuli moving at much lower velocities than those resulting from fixational head movements (Mack et al., 1979). Indeed, partial oculomotor compensation of head instability has been previously observed in experiments in which subjects maintained strict fixation on targets at optical infinity while attempting to move as little as possible (Skavenski et al., 1979). In our study, observers looked at nearby objects, a frequent everyday condition in which head translations also matter. They did not attempt to remain immobile, and looked normally with frequent saccades separating brief periods of fixation. Our results show that partial fixational head/eye compensation extends to these natural conditions.

It is well known that oculomotor compensation is incomplete in the presence of both head translations and low-frequency rotations (Barr et al., 1976; Skavenski et al., 1979; Tweed et al., 1994; Paige et al., 1998; Medendorp et al., 2002), and various observations indicate that partial compensation is not just caused by limitations in motor control, suggesting that preservation of a certain amount of retinal image motion is a desired feature (Steinman, 1995; Liao et al., 2008). For example, the VOR gain varies with the distance of the fixation point (Paige, 1989; Schwarz and Miles, 1991; Crane and Demer, 1997; Paige et al., 1998; Wei and Angelaki, 2004). In addition, optical adaptation experiments found that subjects converge on their own idiosyncratic degree of compensation, even though, in doing this, they progressively modify the VOR gain so that the stimulus on the retina is stationary at some point during the course of adaptation (Collewijn et al., 1981). In keeping with these previous findings, our results strongly support the proposal that the function of ocular drift is the maintenance of a specific range of retinal image motion that facilitates the acquisition and processing of visual information.

While multiple factors, including pupil size and optical aberrations, contribute to the frequency content of the retinal stimulus, the transformation resulting from retinal drift is distinguished by its profound effects over a broad frequency range. Furthermore, the resulting spatially whitened temporal input to the retina has important implications for the understanding of visual and oculomotor functions. Equalization of power is equivalent to decorrelating in space. Thus, our results show that, during normal fixational motor activity, any pair of retinal receptors experiences uncorrelated luminance fluctuations over a broad spatiotemporal frequency range. It has long been argued that, in the early stages of the visual system, a fundamental goal of neural processing is reduction of the redundancy inherent in natural scenes (Attneave, 1954; Barlow, 1961). Lateral inhibition has been implicated in this process (Srinivasan et al., 1982; van Hateren, 1992) and has been proposed to be responsible for decorrelating responses (Atick and Redlich, 1992). However, these proposals rely on the traditional view of equating the retinal input to an image of the external scene. The results of our study show that, during normal fixation, the spatiotemporal signals impinging on retinal receptors are already whitened within the range of temporal frequencies at which ganglion cells respond best. This whitening occurs before any neural processing takes place. Thus, neural decorrelation, is not a viable theory to explain the filtering characteristics of receptive fields.

The results presented here suggest instead an alternative picture of early visual processing. Fixational head and eye movements, together, transform a static spatial input to the retina into the temporal frequency range in which neurons are most sensitive. This transformation treats spatial frequencies unevenly, equalizing power across space. With such a decorrelated input, the typical contrast sensitivity functions of retinal ganglion cells further enhance high spatial frequencies above and beyond what is required for redundancy removal, leading to an enhancement of the luminance discontinuities in the scene. Critically, this edge enhancement happens in the temporal domain: it occurs in the synchronous firing of retinal ganglion cells, yielding a temporal code that takes advantage of the notion that synchronous responses tend to propagate more reliably than asynchronous ones (Dan et al., 1998; Bruno and Sakmann, 2006).

This view has further consequences regarding the mechanisms of sensory encoding. It argues that information about fine spatial detail is stored not only in spatial maps of neural activity, as is commonly assumed, but also in the temporal structure of the responses of neuronal ensembles—whose dynamics are critically shaped by the fixational motion of the retinal image. Furthermore, it suggests that the process of edge detection, currently believed to occur in the cortex, begins in the spatiotemporal structure of neural activity in the normally active retina. More generally, it replaces the traditional view of the early visual system as a passive encoding stage designed to optimize the average transmission of information with the idea that neurons in the early pathway are part of an active strategy of feature extraction, whose function can only be understood in conjunction with motor behavior.