The Recurrent Case for the Renshaw Cell

Abstract

Although Renshaw cells (RCs) were discovered over half a century ago, their precise role in recurrent inhibition and ability to modulate motoneuron excitability have yet to be established. Indirect measurements of recurrent inhibition have suggested only a weak modulatory effect but are limited by the lack of observed motoneuron responses to inputs from single RCs. Here we present dual recordings between connected RC–motoneuron pairs, performed on mouse spinal cord. Motoneuron responses demonstrated that Renshaw synapses elicit large inhibitory conductances and show short-term potentiation. Anatomical reconstruction, combined with a novel method of quantal analysis, showed that the strong inhibitory input from RCs results from the large number of synaptic contacts that they make onto individual motoneurons. We used the NEURON simulation environment to construct realistic electrotonic models, which showed that inhibitory conductances from Renshaw inputs exert considerable shunting effects in motoneurons and reduce the frequency of spikes generated by excitatory inputs. This was confirmed experimentally by showing that excitation of a single RC or selective activation of the recurrent inhibitory pathway to generate equivalent inhibitory conductances both suppress motoneuron firing. We conclude that recurrent inhibition is remarkably effective, in that a single action potential from one RC is sufficient to silence a motoneuron. Although our results may differ from previous indirect observations, they underline a need for a reevaluation of the role that RCs perform in one of the first neuronal circuits to be discovered.

Introduction

Motoneurons constitute the “final common path” of the CNS (Sherrington, 1906). The information conveyed by their axons to muscle fibers is also transmitted to a specific type of interneuron, the Renshaw cell (RC) (Renshaw, 1946), through local collateral branches (Eccles et al., 1961). RCs in turn inhibit motoneurons (Granit et al., 1957), thus completing the circuit for recurrent inhibition (Eccles et al., 1961). The recurrent inhibitory loop was one of the first functional circuits described in the nervous system, and much is known concerning the physiology and morphology of RCs (Willis, 1971; Alvarez and Fyffe, 2007). However, despite the historical importance and our considerable knowledge of the circuit, we know very little about the role of RCs in motor control or about their synapses onto motoneurons.

There is contrasting evidence about the capacity of RCs to inhibit motoneuron activity. The location of RC contacts on motoneuron dendrites (Curtis and Eccles, 1959; Burke et al., 1971), the small evoked responses to RC activation (Van Keulen, 1981; Hamm et al., 1987), and small recurrent IPSPs suggest only a marginal inhibitory effect on cell conductances (Lindsay and Binder, 1991) and firing in motoneurons (Windhorst et al., 1978; Maltenfort et al., 2004). By contrast, although synaptic contacts from RCs are distal to those from Ia inhibitory interneurons, they are still located on proximal dendrites at short electronic distances from the soma (Fyffe, 1991). Because most glutamatergic inputs from primary afferents synapse onto proximal dendrites (Rotterman et al., 2014), RC terminals may be strategically located to shunt excitation, amplified by persistent inward currents (Bui et al., 2008). Indeed, pharmacological blockade of cholinergic neurotransmission produces profound effects on motoneuron firing during fictive locomotion (Noga et al., 1987). The impact of recurrent inhibition depends not only on how many RCs synapse onto individual motoneurones but also on the unitary effect of each RC on motoneuron excitability. To date, the only available estimates of synaptic responses evoked by a single RC (Van Keulen, 1981) suggest a minimal inhibitory effect on the motoneuron membrane potential. However, no study has reported definitive measurements of the change in conductance elicited by a single RC, nor the resulting shunt effect.

In this paper, we present recordings from connected pairs of RCs and motoneurons and determine whether RCs can exert an effective inhibition of motoneuronal activity. We evaluate the probability of release, the quantal size, and the number of release sites at the RC synapse onto motoneurons, by using a novel method for quantal analysis (Bhumbra and Beato, 2013). Anatomical reconstructions of recorded pairs confirm correspondence between the number of functional and anatomical release sites. The reconstructions are used to build a NEURON model for evaluation of the shunt level (Gidon and Segev, 2012). We extend the model to simulate motoneuronal spiking and to estimate the effects of RC inhibition on firing. Using paired recordings, we test whether activation of a single RC interrupts spike firing in motoneurons. Finally, we activate the recurrent circuitry using ventral root stimulation at an intensity that evoked inhibitory conductances of a size corresponding to that from the connection from a single RC. We combine the experimental and simulation data to determine whether the inhibitory capacity of RCs is sufficient to affect motoneuronal firing.

Materials and Methods

Spinal preparations were obtained from P8-P14 mice of either sex in which EGFP is expressed under control of the promoter of the neuronal glycine transporter GlyT2 (Zeilhofer et al., 2005). The transgenic strain was used to identify glycinergic neurons during paired recordings. All experiments were undertaken in accordance with the Animal (Scientific Procedures) Act (United Kingdom) 1986 and with the approval from the local Ethical Committee.

Animals were anesthetized with urethane 1.8 mg/kg intraperitoneally and perfused through the heart with ice-cold artificial CSF, identical to that used during recordings. The aCSF consisted of the following (in mm): 113 NaCl, 3 KCl, 25 NaHCO₃, 1 NaH₂PO₄, 2 CaCl₂, 2 MgCl₂, and 11 d-glucose. After decapitation, spinal cords were extracted according to standard procedures, involving ventral laminectomy followed by rapid dissection of the cord in oxygenated ice-cold aCSF (Beato, 2008).

Immunocytochemistry.

For experiments to determine the distribution of RCs at the developmental stage used for electrophysiology, 3 P9-P10 GlyT2-EGFP mice were perfused with 4% formaldehyde. The L5 spinal segment was removed and cut into 50-μm-thick transverse sections with a vibrating blade microtome (VT1000, Leica Microsystems). Sections were incubated for 48 h at 4°C in a mixture of primary antibodies consisting of rabbit anti-calbindin (1:1000, Swant), goat anti-VAChT (1:1000; Millipore), and guinea-pig anti-GFP (1:1000) (Takasaki et al., 2010). These were revealed with species-specific secondary antibodies raised in donkey and conjugated to DyLight 649 (1:500) or Rhodamine Red (1:100) (both from Jackson ImmunoResearch Laboratories), or Alexa-488 (1:500; Invitrogen). Sections were scanned with a Zeiss LSM710 confocal microscope (with Argon multiline, 405 nm diode, 561 nm solid state, and 633 nm HeNe lasers) through a 40× oil-immersion lens (NA 1.3), with the pinhole set to 1 Airy unit. z-stacks (1 μm separation) were scanned through the full thickness of the section, and these were analyzed with Neurolucida for Confocal (MBF Bioscience) to produce plots of cell distributions in the most ventral 200 μm of the gray matter.

Slice recordings.

For paired recording experiments, transverse 400-μm-thick slices were cut with a VT1000 vibrating microtome (Leica Microsystems) from the L5 segment in oxygenated ice-cold solution containing the following (in mm): 130 K-gluconate, 15 KCl, 0.05 EGTA, 20 HEPES, 25 d-glucose, 3 kynurenic acid, pH 7.4 (Dugué et al., 2005). In experiments involving ventral root stimulation, slices were cut obliquely at a 35° angle to the transverse plane, to preserve motoneuron axons and their connections (Lamotte d'Incamps and Ascher, 2008). Antidromic stimulation was delivered via a bipolar suction electrode filled with aCSF. We incubated slices at 37°C in normal extracellular solution for ∼45 min before electrophysiological recordings, which were performed at room temperature. Slices were continuously superfused at 5–8 ml/min with aCSF bubbled with 95% O₂/5% CO₂.

Whole-cell recordings from motoneurons were performed with an Axopatch 200B amplifier (Molecular Devices), whereas we used an ELC-03X amplifier (NPI Electronics) for interneuron current clamp and loose cell-attached recordings. Signals were filtered at 5 kHz, sampled at 50 kHz with an Axon 1440A interface (Molecular Devices), and acquired using Clampex 10 software (Molecular Devices). Electrodes were pulled with a P-1000 Flaming/Brown micropipette puller (Sutter Instruments) from thick-walled borosilicate glass GC150F capillaries (Harvard Apparatus). Electrodes for voltage-clamp recordings were pulled to a resistance of ∼0.5 MΩ and fire polished to a resistance of ∼1.5 MΩ. The resistance of electrodes used for current-clamp recordings was ∼4 MΩ.

The pipette solution for voltage-clamp recordings consisted of the following (in mm): 140 CsCl, 4 NaCl, 0.5 CaCl₂, 10 HEPES, 5 EGTA, 2 Mg-ATP, QX-315 Br 3, pH 7.3 with CsOH, and osmolarity of 290–310 mOsm. During paired recordings, motoneurons were voltage-clamped at −60 mV. In a subset of recordings, where recurrent inhibitory currents were recorded without blockers of glutamatergic transmission, we clamped the motoneurons at 0 mV and used a pipette solution consisting of the following (in mm): 140 Cs-gluconate, 4 CsCl, 2 CaCl₂, 10 HEPES, 5 EGTA, 2 Mg-ATP, 3 QX-315 Br, pH 7.3 with CsOH, and osmolarity of 290–310 mOsm (see Results). For current-clamp recordings from either interneurons or motoneurons, the pipette was filled with the following (in mm): K-gluconate 125, KCl 6, CaCl₂ 2, HEPES 10, EGTA 0.1, Mg-ATP 2, pH 7.3 with KOH, and osmolarity of 290–310 mOsm.

Cells were visualized with an Eclipse E600FN (Nikon) microscope through a 40× water-immersion objective equipped with a double port that allowed simultaneous visualization of infrared differential interference contrast images and EGFP fluorescence (detected through a laser scanning confocal unit D-Eclipse C1, Nikon). Motoneurons were identified by their position in the lateral motor column and by their soma diameter of at least 20 μm (Takahashi, 1992; Thurbon et al., 1998). The series resistance of 4–10 MΩ was compensated by 60%–80% and gave a 0.2–0.8 kHz corner frequency range (with a typical whole-cell capacitance of ∼200 pF). Recordings were abandoned if series resistance increased by >20%.

For paired-recording experiments on transverse slices, 3 mm kynurenic acid (Sigma) was added to the aCSF to block excitatory glutamatergic activity. While recording from a motoneuron, a spike was evoked in putative presynaptic EGFP-positive neurons in the loose cell-attached configuration (Barbour and Isope, 2000) with an ELC-03X amplifier, as described previously (Bhumbra et al., 2012). When a monosynaptic connection was established (revealed by a postsynaptic current time locked with the spike), the presynaptic interneuron was repatched with a new electrode and recorded in current-clamp configuration.

Spikes were evoked in the presynaptic cells every 9 s by application of a train of current pulses. The interval between spikes within each train was adjusted to maximize the degree of facilitation observed in postsynaptic responses. For quantal analysis experiments, the probability of neurotransmitter release was reduced by partially replacing extracellular calcium (between 0.5 and 2.0 mm) with magnesium. During experiments in which we tested for multivesicular release, we bath-applied the fast-unbinding glycine receptor antagonist SR-95531 (Sigma) at a concentration of 50 μm (Beato, 2008).

Anatomical reconstructions.

Electrodes used for patching both presynaptic and postsynaptic cells during paired recordings were filled with 0.25% biocytin to allow post hoc reconstruction. Slices were fixed in 4% formaldehyde for 12 h. They were incubated overnight in streptavidin conjugated to Rhodamine Red (1:1000; Jackson ImmunoResearch Laboratories) and scanned with the confocal microscope to allow reconstruction of labeled neurons with Neurolucida. The slice was then embedded in agar and cut into 50 μm serial sections. Each section was reincubated with avidin-rhodamine and rescanned to allow identification of processes deep within the slice that were not revealed in the initial scans. The interneuron axon could usually be identified unequivocally because it could be followed to its origin. However, in a few cases, axon collaterals of the interneuron were intermingled with those of the motoneuron; and to confirm its identity, we immunostained for EGFP (which was present in the interneuron axon, but not the motoneuron axon) as described above.

Electrophysiological analysis and simulations.

Estimation of the quantal parameters was performed using Bayesian quantal analysis (BQA) as described previously (Bhumbra and Beato, 2013). Like multiple-probability fluctuation analysis (Silver, 2003), BQA yields estimates of the quantal parameters from postsynaptic responses observed at different release probabilities. Our technique simultaneously models the profiles of every amplitude distribution of responses at all observed probabilities of release. This approach has the advantage that reliable estimates of the quantal parameters can be obtained from small datasets (Bhumbra and Beato, 2013).

Electrotonic analysis was performed based on the data acquired from the anatomical reconstructions of motoneurons, the location of visualized synaptic contacts, and the quantal size. We simulated the electrotonic properties of reconstructed motoneurons and the effects of inhibitory conductances by using the NEURON simulation environment (Hines and Carnevale, 1997). Each motoneuron reconstruction was imported as a Neurolucida file using NEURON′s graphical user interface and inspected for integrity. The reconstructed data, comprising the geometric configuration of neuronal segments represented as connected truncated cone frusta, were then exported into the native NEURON format. The Python application programming interface for NEURON (Hines et al., 2009) was used for subsequent electrotonic analysis.

The membrane properties of somal and axonal sections were modeled according to active Hodgkin–Huxley channel properties with all sections, including dendritic compartments, set to a fixed specific capacitance (C_m = 1 pF cm⁻²) and axial resistivity (R_a = 100 Ω cm). Active conductances for sodium and potassium channels were set to g_Na = 0.2 S cm⁻² and g_K = 0.035 S cm² (Dai et al., 2002) with respective reversal potentials of E_Na = 40 mV and E_K = −77 mV. The after-hyperpolarization was modeled using a voltage-dependent calcium conductance to activate a calcium-dependent potassium conductance, with peak values set to g_Ca = 0.03 mS cm⁻² and g_K(Ca) = 0.03 S cm⁻², respectively (Powers et al., 2012).

Passive leak conductances were modeled with a reversal potential of −70 mV, with the soma 50-fold leakier than the dendrites (Taylor and Enoka, 2004): g_soma = 500 μS cm⁻², g_dend = 10 μS cm⁻². Active conductances in dendrites at path distances 100–400 μm from the soma were included to simulate the effects of persistent inward currents according to a model described in detail previously (Booth et al., 1997). Briefly, the model comprises a voltage-dependent L-type calcium conductance that is inactivated by a calcium diffusion mechanism; the peak calcium conductance was set to g_Ca = 0.3 mS cm⁻² (Booth et al., 1997).

Inhibitory conductances were positioned according to the locations of contacts from the axon of the labeled RC and were functionally modeled by the sum of two exponentials, by using NEURON′s “Exp2Syn” function with rise and decay time constants of 0.5 and 2 ms, respectively, to mimic the decay kinetics of glycine receptors in physiological concentrations of chloride (Pitt et al., 2008). We matched the reversal potential for chloride to the resting potential membrane of the motoneuron in simulations (−70 mV). The mean somatocentric conductance at each release site was estimated by dividing the BQA estimate of the quantal size by the electromotive force based on a reversal potential of 0 mV and a voltage-clamped holding potential at −60 mV to correspond with the symmetrical chloride recording conditions used for experiments. We calibrated the magnitude of inhibitory conductances at individual release sites by using voltage-clamp simulations with the same magnitude of electromotive force for chloride (60 mV) to equate the total inhibitory conductance to the product of the mean somatocentric conductance and the number of release sites.

The “Impedance” class of NEURON was used to measure the electrotonic distances of the release sites from the soma and to evaluate changes in input resistances during the course of inhibition. Relative changes in input resistance have been used (Lindsay and Binder, 1991) to measure the shunt effects of recurrent inhibitory postsynaptic events in motoneurons. The measure, recently termed the shunt level (SL), quantifies the attenuating effect of inhibition on depolarizing inputs (Gidon and Segev, 2012). Input resistances were computed in all motoneuronal segments, and the SL was calculated by dividing the magnitude of the change in input resistance following the activation of inhibitory conductances, by the initial value.

For spike modeling analysis, we drove the modeled cells with depolarizing inputs characteristic of Group Ia afferents, with an average of five release sites from each input onto the motoneuron (Segev et al., 1990). Excitatory synapses were distributed to reflect the relative preponderance of Ia afferent synapses in proximal dendrites compared with more distal locations (Rotterman et al., 2014). For each motoneuron, 980 excitatory contacts arising from 196 independent inputs were distributed with a density inversely proportional to their path distances from the soma with a minimum of 100 μm. Excitatory conductances were modeled by using NEURON′s “AlphaSynapse” function with a decay time constant of 1 ms, a reversal potential of 0 mV, and a magnitude of 1 mS cm⁻².

Spike suppression analysis.

Using the oblique slice preparation, we performed current-clamp recordings of motoneurons and applied current steps to induce firing. Dual whole-cell current-clamp recordings were performed on pairs of motoneurons and RCs, identified by ventral root stimulation. While evoking spike trains in the motoneuron, a single spike or a train of 3 spikes were elicited in RCs to determine their inhibitory effect. We used a binless cumulative sum (CUSUM) technique to quantify the effect of inhibition on neuronal firing. Because standard CUSUM procedures (Ellaway, 1978) based on peristimulus time histograms are affected by the arbitrary choice of bin width, we avoided this dependence by using a modified procedure as described below.

For each sweep, the latency of every spike was expressed with respect to the time of the inhibition. We combined the latencies from all N sweeps into a single numerically sorted dataset of elements t_k (where the index k refers to the k^th spike latency) and size K (the total number of observed spikes) within the latency range −100 to 100 ms. The latencies t_k constituted the x-ordinate of the CUSUM plot. We evaluated the y-ordinate by using a normalized binless CUSUM calculation, based on the difference between the observed count n_k and the expected count n̂_k at the k^th latency t_k. By definition, the observed count comprised a set of unit increment integers n_k = [1,2,…,K]. The expected count n̂_k was based on the assumption of a constant spike frequency before the stimulation. If we define the total number of spike latencies occurring before the stimulation in all the sweeps as c, we can express the expected count by using the relation n̂_k = c(t_k + 100 ms)/100 ms. Finally, the binless CUSUM values were evaluated by normalizing the difference between the observed and expected counts by the number of sweeps as follows: CUSUM = (n_k − n̂_k)/N.

The size of the descent in the CUSUM plot was measured by fitting the period of inhibition with a scaled and offset hyperbolic tangent. We expressed the relative inhibition by dividing the amplitude of the descent by the expected spike count over the same period. An identical technique was used to measure the inhibitory effect observed from spike suppression recordings during ventral root stimulation.

Results

Identification of RCs

Figure 1A shows a representative section through the ventral horn from a perfusion-fixed P10 GlyT2-EGFP mouse, in which glycinergic interneurons can be identified by their EGFP expression (green). Glycinergic neurons are distributed throughout laminae VII-VIII but are largely excluded from motor nuclei. RCs are located in the ventral region of lamina VII and are characterized by the presence of cholinergic inputs from ipsilateral motoneuron axon collaterals (Alvarez et al., 2005). Although the location of RCs is well established, to date no study has quantitatively reported the proportion they represent among all inhibitory interneurons in different regions of the ventral horn. Consequently, we undertook a series of experiments to compare their distribution in relation to other EGFP-positive cells.

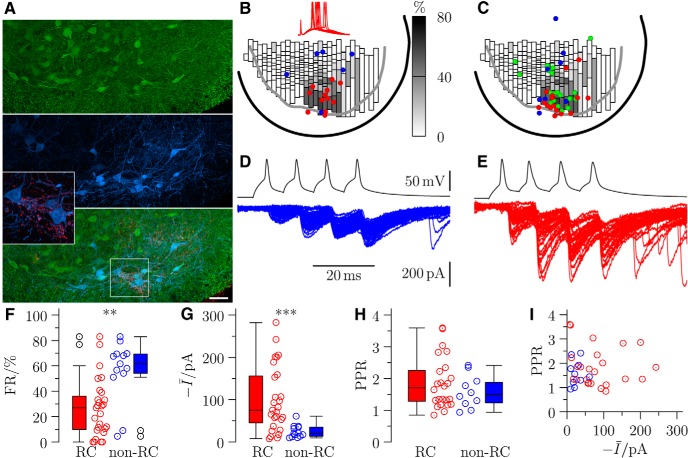
Figure 1.

Stimulation of RCs (identified by location, glycinergic phenotype, and synaptic input to motoneurons) evokes large motoneuronal responses. A, Immunocytochemical characterization of EGFP-positive (glycinergic) interneurons in a section from L5 of a perfusion-fixed P10 GLYT2-EGFP mouse, with calbindin immunoreactivity (blue) and VAChT terminals (red). Inset, Contacts between VAChT terminals and individual calbindin-immunoreactive cells (putative RCs). Scale bar, 100 μm. B, The proportions of EGFP-positive cells identified as RCs are represented in bins, each of which contains the same number of EGFP cells (15). This is overlaid with locations of EGFP-positive cells identified as RCs (red) and non-RCs (blue) by excitatory responses following ventral root stimulation; examples of EPSPs at threshold for evoking a spike are illustrated in the inset as red traces (the upward deflections preceding the responses are stimulus artifacts). C, A similar plot for the presynaptic interneurons from paired recordings, color-coded according to calbindin immunoreactivity (blue represents negative; red represents positive; green represents not tested). Representative traces are shown for motoneuron responses to spike trains evoked from a non-RC (D, blue), and an RC (E, red). Inhibitory postsynaptic currents are inward because motoneurons were voltage-clamped at −60 mV and recorded using a high chloride intracellular solution. Group data for responses to RCs (red) and non-RCs (NRC, blue) are represented as box-and-whiskers plots for the (F) failure rate (FR), (G) mean current (Ī), and (H) paired-pulse ratio (PPR). I, Scatter distribution of the PPR against the mean current. **p < 0.01; ***p < 0.001.

Several criteria have been used to identify RCs in previous anatomical studies. These include location, size, calbindin immunoreactivity, input from motoneuron axons (which can be revealed with antibody against VAChT), and the presence of large gephyrin-immunoreactive clusters on somata and proximal dendrites (Alvarez and Fyffe, 2007). Because distinctively large gephyrin clusters only develop between P10 and P14, we identified EGFP cells in the perfusion-fixed tissue as RCs based on the expression of calbindin and the presence of contacts from VAChT terminals (Alvarez et al., 1999) on their somata or dendrites (≥5 per cell). A dense plexus of VAChT terminals surrounded many of the calbindin-positive cells (Fig. 1A). Figure 1A (magnified boxed inset) highlights the presence of large VAChT terminals in contact with putative RCs.

We used these criteria to identify and count RCs in nine sections through the L5 region of spinal cords from 3 P9–P10 mice. The nonuniform distribution of glycinergic interneurons, with higher density in the dorsomedial area, complicates evaluation of the proportion of glycinergic neurons that are RCs in different regions. We therefore divided the ventral horn into 30 columns along the mediolateral axis and then subdivided each column in the dorsoventral axis into individual bins, so that each bin contained the same number of EGFP-positive cells (15). Bins were shaded with a grayscale value corresponding to the proportion of EGFP cells that were classified as RCs (Fig. 1B). This distribution confirms the known location of RCs in the most ventral region of lamina VII, where they comprise up to ∼80% of glycinergic interneurons.

In a separate series of experiments, we determined the proportion of glycinergic interneurons that could be functionally identified as RCs in different regions of the ventral horn. EGFP-positive cells were recorded in slices cut at a 35° angle to preserve motoneuron axons and their synapses with RCs (Lamotte d'Incamps and Ascher, 2008). We tested 18 cells, 12 of which were identified as RCs by the presence of a ventral root-evoked excitatory response. The locations of these functionally identified cells (Fig. 1B, red circles) confirmed that a high proportion of EGFP-positive cells within ∼150 μm from the ventral edge of the gray matter are RCs. An example of the typical excitatory response is shown in Figure 1B (inset), with an intensity of stimulation at threshold for evoking a spike. All of the cells recorded outside that area (blue circles) did not respond to ventral root stimulation. We therefore defined this region as the RC area.

Paired recordings

Because RCs are known to project to motoneurons within the same segmental level, we performed experiments in transverse slices to maximize the connectivity within the preparation. Paired recordings (n = 43) were performed on presynaptic glycinergic interneurons and postsynaptic motoneurons that were located in the ventrolateral nucleus of the ventral horn. Successful recordings were made in slices of the L5 spinal segments obtained from 35 animals. Figure 1C plots the locations of all recorded premotor interneurons in the ventral horn. Whereas the identification of RCs by the presence of VAChT puncta was effective in perfusion fixed tissue (Fig. 1A), VAChT immunostaining was unreliable in fixed slices. We therefore used calbindin immunoreactivity to confirm the identity of RCs among the recorded interneurons. From the 24 experiments in which the presynaptic interneuron could be recovered, 18 were located in the Renshaw area. Of this subset, 14 (red dots) were calbindin-positive, whereas calbindin was not detected in 4 cases (blue dots). The remaining EGFP-positive cells were lost during processing of the tissue and thus could not be tested (green dots). However, their position was determined from the low-magnification images captured during recordings.

Recent trans-synaptic viral tracing studies have shown that the majority of glycinergic premotor interneurons in the Renshaw region are calbindin-positive (Coulon et al., 2011). In combination with our findings in perfusion-fixed tissue, this suggests that there are very few premotor interneurons other than RCs in this region. Consequently, the combination of anatomical location of the interneuron, inhibitory phenotype, expression of calbindin, and the presence of a monosynaptic connection to a motoneuron constitute reliable criteria to confirm RC identity. The failure to detect calbindin in four of the interneurons in the RC area may reflect its washout to below detectable levels following whole-cell recordings. Because virtually all glycinergic premotor interneurons in this region are calbindin-positive (Coulon et al., 2011), we classified premotor cells patched within the Renshaw area as RCs (n = 30), even though calbindin immunoreactivity could not be tested in 12 and was not detected in 4. Interneurons outside this region were classed as non-RCs (n = 13), belonging to a currently unidentified population of premotor intrasegmental inhibitory neurons.

Representative voltage-clamped responses of motoneurons to spike trains (4 spikes with 10 ms interval) elicited from current-clamped presynaptic cells are shown for two different paired recordings in which the presynaptic interneuron was located outside (Fig. 1D) or inside (Fig. 1E) the RC area. Responses to non-RCs (blue) were characteristically small, with high failure rates (∼51% on the first pulse in this example) that decreased upon facilitation by repeated stimulation (to 0% in the example shown). By contrast, responses to RCs (red) were large and exhibited low failure rates, with responses increasing in size following multiple-pulse facilitation.

Group data from successful electrophysiological recordings are shown in Figure 1F–I for both RCs (n = 27) and non-RCs (n = 13). The mean failure rate (Fig. 1F) among RCs (26.6 ± 4.4%) was significantly less than for the non-RCs (56.3 ± 6.6%, Wilcoxon rank-sum z = −3.13, p = 0.002). This was associated with a larger mean current (including failures) in response to RCs (Fig. 1G; −99.9 ± 14.9 pA) compared with average responses to non-RCs (−24.9 ± 4.1 pA, z = 3.35, p < 0.001). Paired-pulse ratios were calculated for recordings in which multiple-pulse stimulation was performed. The paired-pulse ratios associated with inputs from RCs (1.85 ± 0.16, n = 24) and non-RCs (1.59 ± 0.16, n = 10) were not significantly different (Fig. 1H; z = 0.59, p = 0.558). There was no significant correlation of the paired-pulse ratio with the mean current (Fig. 1I) from RCs (Spearman's r = −0.19, p = 0.391) or non-RCs (r = 0.309, p = 0.411).

These results indicate that the synaptic input from RCs is large and characterized by fewer failures compared with inputs from non-RCs. Differences in amplitude may arise from disparities in the average response to the release of individual quanta of neurotransmitter because synaptic contacts from RCs are electrotonically close to the soma (Fyffe, 1991). However, a difference in quantal size alone cannot explain the lower failure rate observed from RC inputs. A reduced failure rate from RC inputs could result from an elevated baseline probability of release, an increased number of release sites, or a combination of both. If the baseline probability of release from RCs was high, then we may have anticipated reduced paired-pulse ratios compared with non-RCs, but no such differences were observed. To determine whether differences in synaptic responses result from differences in the probability of release or the number of release sites, we performed quantal analysis.

Quantal analysis

Quantal parameters were estimated by applying BQA (Bhumbra and Beato, 2013) to model the amplitude distribution of evoked inhibitory postsynaptic currents (eIPSCs) in different conditions of release probability. The probability of release was either reduced by decreasing the extracellular calcium ([Ca] = 0.5–2.0 mm) or increased by eliciting spike trains at different frequencies, adjusting the time interval between spikes (10–30 ms) to maximize facilitation and hence the range of probability of release. For each of these paired recordings, both cells were filled with biocytin for anatomical reconstruction.

A representative example of a RC–motoneuron pair is illustrated in Figure 2. Anatomical reconstruction (Fig. 2A) of the interneuron axon showed extensive projection into the motor nucleus. High-magnification confocal microscopy was used to localize axo-dendritic contacts. Nine contacts on the motoneuron were identified in this example; and although their locations were distributed across the dendritic tree, they tended to be positioned on proximal dendrites (Fig. 2A, a–e). Enlarged illustrations of the regions where contacts are located are shown in Figure 2B, alongside corresponding reconstructions of the axon and dendrite.

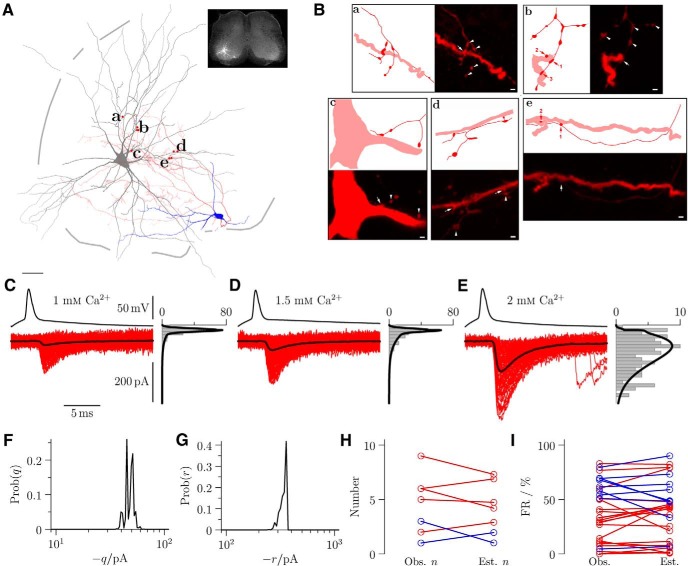
Figure 2.

Anatomical reconstruction corroborated estimates of the number of release sites (n) evaluated by quantal analysis of paired recordings. A, Reconstruction of an RC (blue represents soma; red represents axonal arborization) motoneuron (gray) pair, and the location of contacts. The position of the pair within the slice is shown at low power in the inset. B, Panels illustrate regions of synaptic contacts (arrows) projected from short series (7–48) of optical sections and schematic representations of the same regions (red represents interneuron axon; pale red represents motoneuron dendrite/soma) labeled in A. B, Illustration of only 1 of 3 contacts. Arrowheads indicate other noncontacting interneuron terminals in the field. Paired recordings showing the motoneuron responses are shown alongside their respective amplitude distributions observed during applications of extracellular calcium at concentrations 1 mm (C), 1.5 mm (D), and 2 mm (E). BQA yields probability distributions for the quantal size q (F) and maximal response r (G) and thus provides estimates of the number of release sites n. H, Plot illustrates correspondence between the observed (Obs. n) and estimated (Est. n) number of release sites (red represents RCs; blue represents non-RCs) and a similar comparison (I) of observed (Obs.) and estimated (Est.) failure rates (FR) provides further validation of the quantal analysis estimates. Scale bars: A, 50 μm; B, 1 μm.

For the motoneuron illustrated in Figure 2A, postsynaptic responses and their amplitude distributions are shown for different extracellular concentrations of calcium: 1 mm (Fig. 2C) and 1.5 mm (Fig. 2D), as well as at the control concentration of 2 mm (Fig. 2E). In control conditions, the failure rate was low (Fig. 2E; 2.1%) and the magnitude of currents was large (up to ∼500 pA). A reduction in extracellular calcium concentration (Fig. 2C,D) increased the failure rate with a concomitant decrease in the size of evoked responses.

BQA was applied with a binomial model to obtain posterior probability distributions for the quantal size q, the maximal response r (where r = nq and n is the number of release sites), and the total quantal coefficient of variation v; the medians of the distributions were used as best estimates. Posterior probability distributions are shown for the quantal size (Fig. 2F) and maximal response (Fig. 2G). The quotient of the estimates of the maximal response (r̂ = −370 pA) over the quantal size (q̂ = −48 pA) gave an estimate of n̂ = 7.7 for the number of functional release sites.

Of the 31 paired recordings that could be analyzed using BQA, seven were recovered for reconstruction (five RCs and two non-RCs). The anatomical number of contacts was similar to the functional estimates of the number of release sites (Fig. 2H). A paired Wilcoxon sign-rank test confirmed no statistically significant difference (z = 0.17, p = 0.866). We undertook a second validation of the BQA estimates by comparing the measured failure rate with that predicted from the BQA binomial model at the control calcium concentration (2 mm) following the first spike. A comparison of the estimated and observed failure rate (Fig. 2I) showed no statistically significant difference (sign-rank z = 1.23, p = 0.217), indicating accurate determination of quantal parameters.

Our method of quantal analysis assumes that the quantal size and number of release sites are independent of the probability of neurotransmitter release. Increases in probability by repeated presynaptic stimulation may cause partial postsynaptic receptor densensitization and thus underestimation of the quantal size. High probabilities may also lead to multivesicular release or vesicular depletion and thus confound estimates in the number of release sites. Although quantal analysis has yielded estimates of the number of release sites in agreement with those visualized anatomically at excitatory synapses (Silver et al., 2003; Biró et al., 2005), disparities between observed and expected values have been reported at inhibitory GABAergic synapses in the hippocampus (Biró et al., 2006). Such differences could have been due to the release of multiple vesicles from the same release site, which would cause the estimate of the number of functional release sites to be systematically higher than the number of physical contacts. Consequently, we performed a series of experiments to test for the presence of multivesicular release, to limit our quantal analysis to conditions in which only one vesicle is released at each site.

We tested for the occurrence of multivesicular release from premotor interneurons by bath application of high concentrations of SR-95531 during paired recordings. SR-95531 exhibits fast unbinding kinetics at glycine receptors (Beato et al., 2007) and can be used to detect changes in the concentration profile of neurotransmitter (Beato, 2008) that would occur if more than one vesicle is released from the same site (Tong and Jahr, 1994). We therefore measured the relative attenuation induced by SR-95531 at different probabilities of release.

Figure 3A–F shows a representative example of a paired recording where the addition of 50 μm SR-95531 resulted in an ∼60% attenuation of both the first and second IPSC compared with control (Fig. 3A,B). Increases in extracellular calcium from 2 to 4 mm (Fig. 3C) were associated with a reduced attenuation of ∼20% by SR-95531 for the first spike (Fig. 3D). Figure 3E, F shows the mean eIPSCs in control (black) and in the presence of SR-95531 (gray, scaled to the size of the control response to the first spike) for the two calcium concentrations. The recordings suggest that, although multivesicular release is absent at 2 mm following the second spike, it may occur in all spike-evoked responses at higher calcium concentrations.

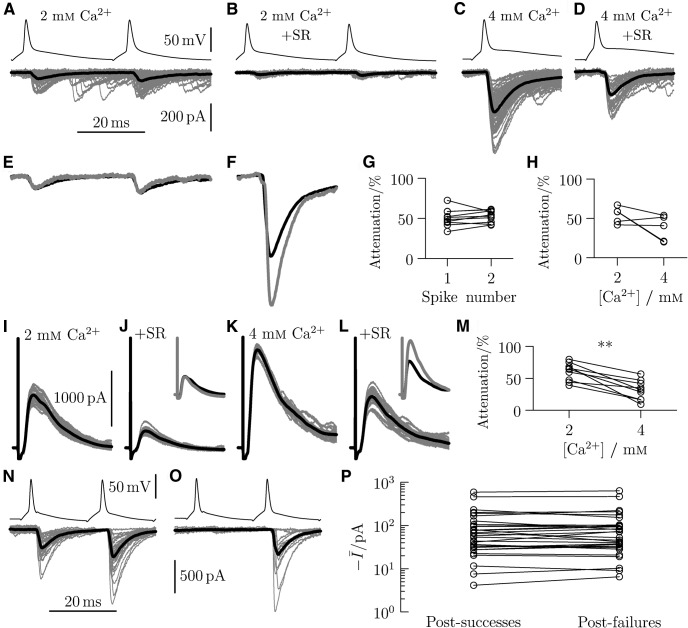
Figure 3.

Increases in extracellular calcium concentration >2 mm result in multivesicular release, and paired-pulse stimulation is not associated with presynaptic depletion or postsynaptic densitization. A, Representative paired recording ([Ca] = 2 mm) with motoneuron responses (mean response in black) attenuated by SR-95531 (B). Increases in calcium concentration ([Ca] = 4 mm; C) resulted in larger responses with a reduced relative attenuation (D). This is illustrated by scaling the mean response (black) by the relative attenuation (gray) at [Ca] = 2 mm (E) for the higher concentration (F). Group data are shown for the paired-pulse stimulation at [Ca] = 2 mm (G) and changes in calcium concentration (H). Ventral root stimulation resulted in recurrent inhibitory postsynaptic currents (I) that could be attenuated by SR-95531 (J). Increases in calcium concentration ([Ca] = 4 mm; K) reduced the relative attenuation (L) as illustrated by the scaled traces in J and I. M, Group data. **p < 0.01. A representative example of a dual recording with paired stimulation is shown to illustrate the similar sizes in the response to a second spike following successes (N) and failures (O) in response to the first. P, Group data.

Group data for the paired recordings in which we evaluated the relative attenuation of responses to the first and second spike (Fig. 3G) showed no systematic differences (Wilcoxon's sign-rank n = 10, z = −1.38, p = 0.169). The results are consistent with the absence of multivesicular release following the second spike. Although a similar comparison between the effects of 2 and 4 mm calcium (Fig. 3H) also showed no significant differences (z = 1.48, p = 0.138), there was heterogeneity in the effects of SR-95531, with three of five recordings showing reductions in relative attenuation as shown in the illustrated example (Fig. 3F). We therefore devised a separate series of experiments to test the effects of SR-95531, in 4 mm calcium, on the glycinergic input specifically from the RC population.

Using oblique slices (Lamotte d'Incamps and Ascher, 2008), we stimulated the disynaptic pathway of the recurrent inhibitory loop by antidromic stimulation of motoneuronal axons via a suction electrode applied to the ipsilateral ventral root. Motoneuron responses were recorded in 2 and 4 mm calcium in control conditions (without blockers of glutamatergic and cholinergic transmission) (Lamotte d'Incamps and Ascher, 2008) and in the presence of SR-95531. Inhibitory currents were isolated by voltage-clamping the motoneurons at the reversal potential for excitatory currents (0 mV).

Figure 3I–L illustrates a representative example of the effect of increases in calcium concentration on the attenuation of responses by SR-95531. In 2 mm calcium, responses to ventral root stimulation (Fig. 3I) were reduced by ∼60% in the presence of SR-95531 (Fig. 3J). Increasing the calcium concentration to 4 mm increased the magnitude of responses (Fig. 3K) but reduced the relative attenuation by SR-95531 (Fig. 3L) to ∼40%. Scaling the antagonist effect of SR-95531 in 2 mm calcium (Fig. 3J, inset) shows the reduction of the relative attenuation in 4 mm calcium (Fig. 3L, inset). Group results (Fig. 3M; n = 9) show a statistically significant reduction in the relative attenuation (Wilcoxon sign-rank z = 2.67, p = 0.008), consistent with multivesicular release at 4 mm calcium.

Paired-pulse facilitation of evoked responses during dual recordings could mask underlying neurotransmitter depletion or desensitization of postsynaptic receptors. The effects of both phenomena on short-term plasticity could confound estimates obtained from quantal analysis. We therefore analyzed paired recordings in which responses were evoked by pairs of spikes. A representative example is shown where currents evoked by a second spike following successful responses to the first (Fig. 3N) are compared with those following failures (Fig. 3O) from the same recording. Comparison of the traces shows no differences for the two conditions. Group data from paired recordings with multiple pulse stimulation recorded at 2 mm calcium (Fig. 3P; n = 30) showed no significant difference in the magnitude of responses to the second spike following successful or failed responses to the first (z = 0.06, p = 0.951). This comparison confirms that neither neurotransmitter depletion nor receptor desensitization occurred under our recording conditions.

Based on the results illustrated in Figure 3, we avoided the confounding effects of multivesicular release by conducting quantal analysis only on recordings in which the probability of release was either increased by facilitation using spike trains or decreased by reductions in calcium from the control concentration of 2 mm within a range that was sufficient for accurate estimation of both the quantal size and the number of release sites (Bhumbra and Beato, 2013).

We investigated whether motoneurons belonging to RC–motoneuron and non-RC–motoneuron pairs were located in different regions. The map of a spinal cord section at the L5 level illustrates the location of each of the recorded pairs (Fig. 4A). Motoneurons are indicated by circles, with the mean evoked response represented on a pseudo-color scale. Presynaptic interneuron locations are indicated by connecting lines, with connections from non-RCs and RCs illustrated on the left and right, respectively. Comparison of the two sides suggests no obvious differences in locations of the postsynaptic motoneuron groups. The vast majority of the motoneurons were located in the ventrolateral column, corresponding to lower limb muscles (Bácskai et al., 2014), with only two exceptions: one belonging to the medial and one to the dorsolateral nucleus.

Figure 4.

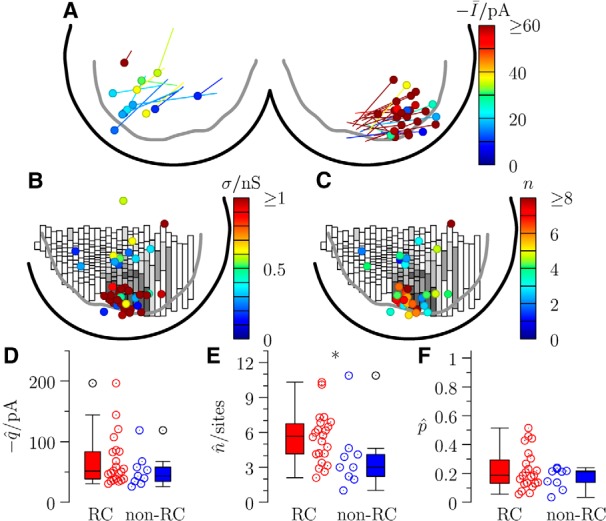
BQA demonstrates that the increased magnitude of responses for inputs from RCs compared with non-RCs is a result of a greater number of release sites. A, Location of all recorded pairs, with motoneurons represented by a circle. The lines terminate at the position of the corresponding presynaptic partner (non-RCs shown on the left and RCs on the right quadrant). The pseudo-color map shows the size of the mean evoked current in control for all pairs. B, Overlay of an adaptive bin histogram (Fig. 2B) with a pseudo-color plot of inhibitory conductances σ alongside a similar plot for the estimates for the number of release sites n (C). Box-and-whiskers are shown to compare the group data for inputs from RCs (red) and non-RCs (blue) by the quantal analysis estimates of the quantal size q (D), number of release sites n (E), and probability of release p (F). *p < 0.05.

Because motoneurons were recorded in voltage clamp, we calculated the inhibitory conductance by dividing the mean response by the electromotive force for chloride (−60 mV). The positions of the presynaptic interneurons and their respective evoked conductances in motoneurons are represented in Figure 4B. Large inhibitory conductances (>0.5 nS) are associated with interneurons clustered in the Renshaw area. An equivalent plot for the BQA estimates for the number of release sites (Fig. 4C) shows a similar distribution with a greater number (≥5) estimated for synapses from presynaptic cells in the same region.

Figure 4D–F shows the BQA estimates of the quantal parameters for the motoneuron inputs from RCs (n = 22) and non-RCs (n = 9). Although there were no significant differences in quantal size between the two groups (Fig. 4D; z = 0.98, p = 0.327), the number of release sites for the RCs was significantly greater (Fig. 4E; z = 2.24, p = 0.025). We also tested for differences in the probability of release calculated by dividing the mean response to the first spike at 2 mm calcium by the BQA estimate of the maximal response (i.e., p = ^μ/_r, where μ is the mean response and r = nq); no statistically significant differences were observed (Fig. 4F; z = 0.46, p = 0.648).

Quantal analysis thus confirmed that the increased conductance associated with inputs from RCs compared with those from other glycinergic interneurons is mostly the result of a greater number of release sites. Based on this observation, we considered whether release of transmitter from a single RC could exert a detectable effect on the subthreshold-depolarizing activity and spike firing of a postsynaptic motoneuron. The selective activation of purely excitatory pathways is not possible within the slice preparation because any form of extracellular stimulation (in either the white or gray matter) would inevitably result in simultaneous activation of excitatory and inhibitory fibers. Similarly, dorsal root stimulation would not only activate Ia afferents monosynaptically but would also induce disynaptic inhibition through Ia interneurons, thus precluding the isolation of the inhibitory effects of RCs on motoneuron firing. We therefore assessed the effect of the inhibitory inputs on motoneurons by using simulations based on the detailed anatomical reconstructions of the motoneurons, the location of the synaptic contacts, and the quantal parameters.

Electrotonic analysis and simulations

At rest, the activation of inhibitory conductances has little effect on the membrane potential because the reversal for chloride ions is close to the resting membrane potential. Opening of large inhibitory conductances, however, can reduce postsynaptic excitability by shunting. Measurements of the relative change in input resistance have been used previously (Lindsay and Binder, 1991) to quantify the shunt effects of recurrent inhibitory postsynaptic events in motoneurons. This measure, recently termed the SL, can be computed for different regions throughout the dendritic tree to study the regional effects of inhibitory conductances (Gidon and Segev, 2012). The SL is defined as the relative local change in membrane resistance during inhibition, and its value ranges from 0 (no shunt) to 1 (complete shunt).

We used the NEURON simulation environment (see Materials and Methods) to evaluate the SL throughout the dendritic tree and soma of the whole postsynaptic cell. SL measurements were based on the anatomical reconstructions of motoneurons, and we compared the shunt effects on motoneurons induced by inputs from individual RCs and non-RCs. An example of a shunt map is illustrated in Figure 5A for a reconstructed motoneuron with three closely spaced contacts located ∼300 μm from the soma and originating from a non-RC. The SL is represented on a pseudo-color scale alongside a corresponding graph plotting the SL against the distance from the soma. Although there is concentrated shunt effect in the region of the three synaptic contacts, it is mostly confined to the immediate area neighboring the postsynaptic dendritic region. Consequently, the SL is not substantial in the region of the soma.

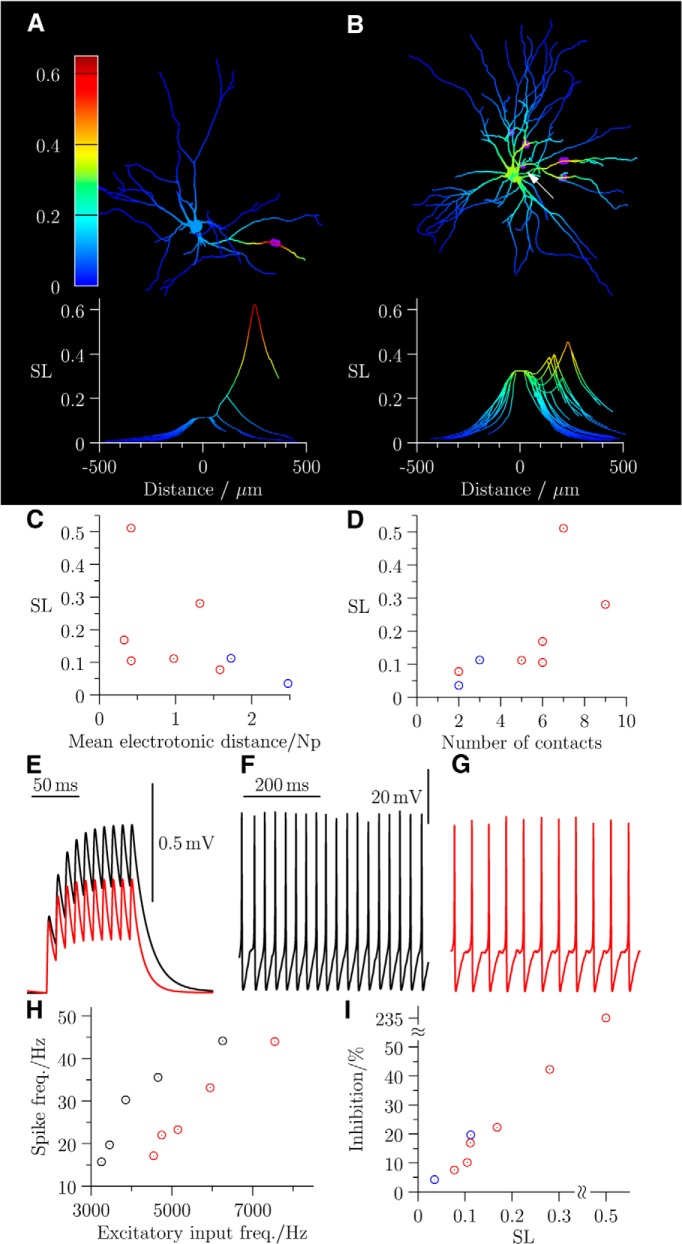
Figure 5.

Shunt level maps show that inputs from RCs exert a considerable shunt effect at the motoneuron soma compared with inputs from non-RCs. A representative shunt map with presynaptic non-RC contacts is shown (A) alongside a corresponding graph plotting the SL, again the distance from soma. A, A shunt map for the cell illustrated in Figure 2A with visualized RC contacts is shown illustrating a substantial effect at the soma. The somatic SL in RC (red) and non-RC (blue) inputs is plotted against the mean electrotonic distance (C) and number of synaptic contacts (D). E, A train of synaptic excitation at the location indicated by the white arrow in B results in evoked responses (black) that are attenuated by activation of inhibitory conductances (red). Multiple synaptic excitation (see Materials and Methods) at 4.7 kHz drives simulated firing (F) that is reduced in rate during inhibition (G). H, The input–output frequency relationship in the absence (black) and presence (red) of inhibition. I, The relationship between the inhibitory effect on firing and shunt level: red represents RCs; blue represents non-RCs).

Figure 5B shows the shunt map for the reconstructed motoneuron illustrated in Figure 2A with 9 presynaptic RC contacts. As observed for the shunt map in Figure 5A, the SL is maximal in the dendritic branches in the proximity of the inhibitory contacts. By contrast, however, the combined shunt effect from the inhibitory contacts distributed on the different dendritic branches is substantial at the soma, where there is a ∼30% shunt effect.

Shunt maps were generated for reconstructed motoneurons where the presynaptic interneurons were non-RCs (n = 2) and RCs (n = 6). Overall (n = 8), there was no statistically significant correlation of the shunt level computed at the soma with the mean electrotonic distance from the identified release sites (Fig. 5C; r = −0.59, p = 0.136). In contrast, a positive correlation was observed between the shunt level with the number of visualized contacts between interneuron boutons and motoneurons (Fig. 5D; r = 0.843, p = 0.007). The results suggest that the somal shunt effect is associated with the total number of synaptic contacts rather than variations in the distance of inhibitory contacts from the soma.

The SL is a measure of the modulatory effect of inhibitory shunting on excitatory inputs. Figure 5E illustrates voltage changes at the soma during a train of 10 impulses (100 Hz) from a single excitatory synaptic conductance (applied to the segment indicated by Fig. 5B, white arrow) in the absence (black) and presence (red) of the inhibitory conductances applied at the locations of the inhibitory contacts (Fig. 5B, purple circles). The depolarization induced by the excitatory train is clearly reduced during inhibition and indicates a potential effect of a single RC in modulating motoneuronal firing.

The modulatory effects illustrated in Figure 5B would result only from shunt inhibition because the membrane potential is very close to chloride reversal, resulting in a negligible electromotive force. Because inhibitory postsynaptic potentials would additionally affect motoneuron excitability at spike threshold, we performed spike simulations in which multiple synaptic excitation drove the motoneuron to firing threshold. Active conductances for spike generation in the soma and for persistent inward currents in proximal dendrites were both included in the model, and we simulated Ia afferent excitation to produce excitatory drive (see Materials and Methods). We measured the firing rate to determine the input–output relationship over different frequencies of synaptic excitation. For the motoneuron illustrated in Figure 5B, input excitation at 4.7 kHz resulted in firing at ∼36 Hz (Fig. 5F) that was reduced to ∼22 Hz in the presence of inhibition (Fig. 5G). Figure 5H illustrates that a comparison of the input–output relationship in the absence (black) and presence (red) of inhibition shows a shift to the right in the latter case. For the group data illustrated in Figure 5I, we quantified the relative inhibition by dividing the shift by the minimum input frequency required to generate firing (red represents RCs; blue represents non-RCs). A Spearman rank correlation test statistic (r = 1.00, p < 0.001) confirms a strong association between the shunt level and relative inhibition.

The results suggested that the inhibitory conductance activated by a single RC is sufficient to modulate the firing activity of motoneurons. Consequently, we undertook a series of experiments to confirm whether the effect of spike suppression could be observed in electrophysiological recordings.

Spike suppression recordings

In a subset of experiments on oblique slice preparations, motoneurons were patched using a K-gluconate-based solution (see Materials and Methods), without inclusion of sodium channel blockers. Putative presynaptic glycinergic interneurons were tested in the RC area using loose cell-attached stimulation while voltage-clamping the motoneuron at 0 mV to increase the electromotive force for chloride. Because slices were cut at an oblique angle, we were able to confirm the RC identity of the presynaptic interneuron in recorded pairs (n = 3) using ventral root stimulation.

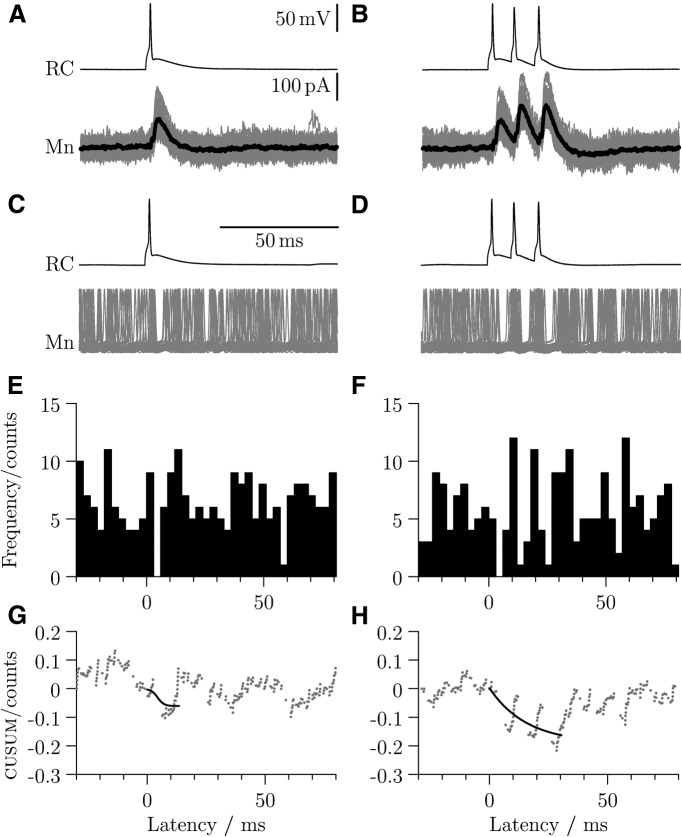
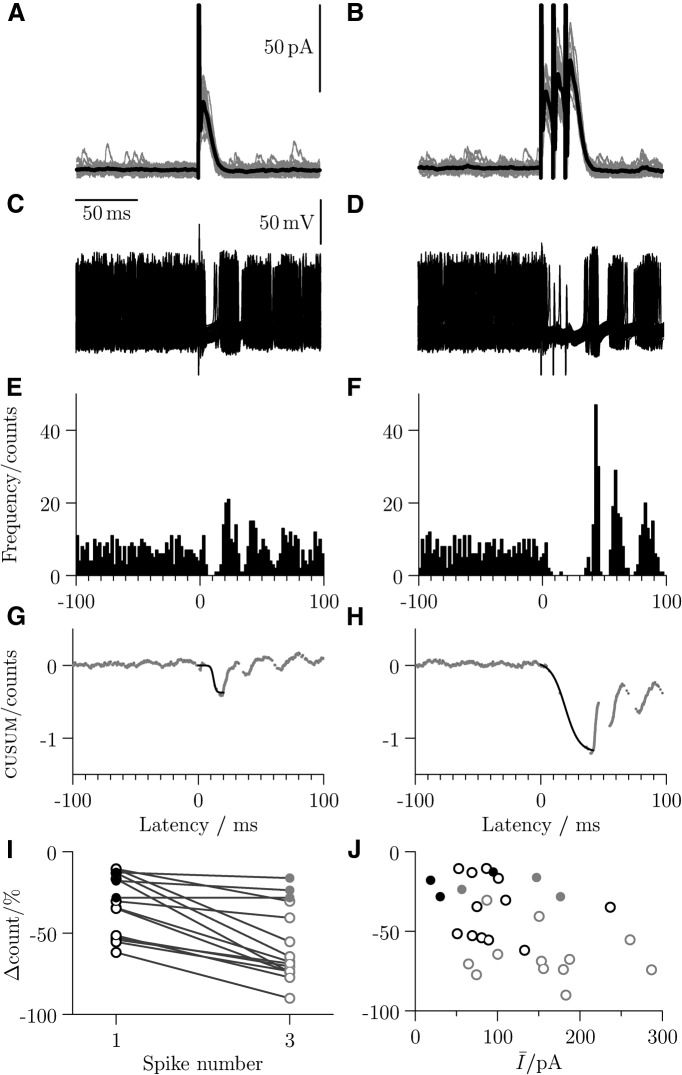
An example of a paired recording is illustrated in Figure 6, where a single spike or a train of three spikes (100 Hz) in the RC (Fig. 6A and Fig. 6B, respectively, top trace) induce monosynaptic IPSCs in the voltage-clamped motoneuron (bottom trace, mean current ∼120 pA). The motoneuron recording amplifier was then switched to current clamp, and steady-state firing was induced by somatic current application to elicit a firing rate of ∼40 Hz in the motoneuron. During steady firing, a single spike (Fig. 6C) or a train of three spikes separated by 10 ms (Fig. 6D) were evoked in the RC. Both single and multiple spikes produced a pause in motoneuron firing. Peristimulus histograms are shown in Figure 6E, F with corresponding binless CUSUM plots in Figure 6G, H. The sigmoidal fits used to measure the effects on firing rate (see Materials and Methods) are overlaid in black.

Figure 6.

Firing in a single RC can transiently interrupt spikes in a motoneuron. Paired recording from a RC (current clamp, top traces) and a motoneuron (voltage clamp, A, B, bottom trace; average trace in black). The motoneuron electrode contains a physiological concentration of chloride, and inhibitory postsynaptic currents evoked by one (A) or three (B) spikes are outward at 0 mV holding potential. Continuous spiking in the motoneuron is evoked by current injection and interrupted by firing in the RC (C, D). Corresponding peristimulus histograms (E, F) and CUSUM plots (G, H) show the extent of inhibition induced by a single spike and by a 100 Hz train.

In addition to the paired recordings, we obtained single recordings from motoneurons in oblique slices, and applied electrical stimulation to the ventral roots using suction electrodes to activate the recurrent inhibitory pathway selectively. Motoneurons were first recorded in voltage clamp at 0 mV holding potential to allow calibration of the stimulus intensity to correspond with the magnitude of inhibitory currents observed during paired recordings (typically <100 pA). By applying the same stimulus intensity calibrated during voltage-clamp measurements for subsequent current-clamp recordings, we ensured that the size of the inhibitory conductance was equivalent to that evoked by a single RC. Experiments were performed only on motoneurons that were not antidromically stimulated and that did not receive recurrent excitation from other activated motoneurons.

A representative example of the effects of recurrent inhibition on motoneuronal activity is illustrated in Figure 7. Traces of voltage-clamped responses are shown following stimulation of the ventral roots using one pulse (Fig. 7A) and three pulses with an interval of 10 ms (Fig. 7B). As for the paired recordings, firing in motoneurons was elicited by current injection to produce a steady spike rate of ∼40 Hz. Recurrent inhibition was evoked either as a single (Fig. 7C) or triple (Fig. 7D) impulse. While multiple pulse stimulation resulted in a more profound inhibition, both produced effective suppression of spikes.

Figure 7.

Recurrent inhibitory postsynaptic conductances of a magnitude equivalent to the input from a single RC is sufficient to suppress firing in motoneurons. Voltage-clamp traces following ventral root stimulation are shown for single-pulse (A) and three-pulse (B) activation (stimulus artifacts truncated; average trace in black). Current-clamp depolarizations induced motoneuronal firing, and ventral-root stimulation (C, D) suppressed spike occurrences (stimulus artifacts truncated). Corresponding peristimulus time histograms (E, F), and binless CUSUM plots (G, H) illustrate the extent of inhibition, with group data (I) illustrating the greater extent of inhibition following three stimulation pulses compared with one. J, A scatter of the inhibition (single-pulse black; three-pulse gray) against the mean current. Filled circles represent the inhibition measured from the paired recordings.

Peristimulus histograms for the two stimulation conditions are illustrated in Figure 7E, F with their corresponding binless CUSUM plots showing the fits used to measure the extent of decrease in the firing rate (Fig. 7G,H). For both conditions, the period of inhibition is followed by a rebound increase in firing and subsequent synchronization of spikes across sweeps.

Group data (n = 12) are shown in Figure 7I (open circles), which compares the inhibitory effect of a single and triple pulse. After including the corresponding data from the paired recordings (n = 3, filled circles), a statistical comparison that the inhibitory effect of the stimulus train was significantly greater than that of one pulse (Wilcoxon sign-rank z = 3.35, p < 0.001). Plotting the inhibitory effect against the mean current (Fig. 7J; first response in black, third response in gray), showed no significant correlation following single-pulse (black; Spearman's r = −0.235, p = 0.419) and three-pulse (gray; r = −0.329, p = 0.250) stimulation. Pooling both datasets together, however, yielded a statistically significant correlation (r = −0.435, p = 0.019). The results suggest that any underlying relation may be a consequence of the increase in number of pulses rather than differences within each of the datasets.

Discussion

In the present study, we have shown that motoneurons receive a strong inhibitory input from RCs, and that this is due to a large number of release sites. By developing an electrical model based on anatomical reconstructions, we have demonstrated that activation of a single RC induces a considerable somatic shunt that is sufficient to suppress motoneuron firing. Finally, we have experimentally confirmed the results of the simulations using recordings that show motoneuronal firing is suppressed by the input from a single RC and by selective activation of the recurrent inhibitory pathway.

RC identity

The combination of immunostaining for EGFP, calbindin, and VAChT in the perfusion-fixed spinal cord confirms the location of RCs (Alvarez et al., 1999) and that they represent the majority (60%–70%) of glycinergic neurons in the most ventral part of lamina VII. The few non-Renshaw glycinergic cells in this region belong to a currently unidentified interneuron population and are not necessarily premotor. Because presynaptic cells from paired recordings that were located in the RC area were both glycinergic and premotor and almost all of those tested were calbindin-positive, it is highly likely that these were RCs (Coulon et al., 2011). Misclassification between RC and non-RC groups could have affected only a very small number of cells. Indeed, misclassification would increase heterogeneity between groups and blur any differences. However, we observed significant differences in both the size of synaptic responses and the estimated number of release sites.

Number of release sites

Identification of synaptic contacts by light microscopy can potentially lead to false-positives from contacts not associated with synapses. In an attempt to confirm the presence of synapses, we reacted sections containing axo-dendritic contacts with anti-gephyrin antibody because the presence of postsynaptic gephyrin clusters is a reliable marker of glycinergic synapses (Todd et al., 1995). Although numerous gephyrin puncta were visible, they were either absent or extremely weak in recorded motoneurons, suggesting that gephyrin is washed out during long motoneuron recordings (often >3 h). This precluded confirmation of synapses with anatomical criteria. However, the consistent agreement between numbers of functional and anatomical contacts suggests that there was little or no systematic overestimation.

Slice preparation may sever branches of the interneuron axon or motoneuron dendrites and thus reduce the number of synaptic contacts. In particular, a few synapses from non-RCs onto distal dendrites of motoneurons may have been lost. However, the estimated number of release sites from RCs overlaps considerably with the range reported from anatomical studies (Fyffe, 1991) in the cat (1–9). Observed locations of synaptic contacts on proximal dendrites are also consistent with previous reports (Burke et al., 1971; Fyffe, 1991), and suggests that contacts were mostly preserved within slices. Even if a few contacts were lost, our computational simulations and spike suppression recordings showed that the activation of the synaptic input from a single RC is sufficient to suppress motoneuron firing.

A case for RCs

A number of studies in the cat have attempted to evaluate the capacity of RCs to inhibit motoneuronal activity. Cholinergic blockage of RC excitability produces only small increases in motoneuron activity evoked by peripheral nerve stimulation (Windhorst et al., 1978). Activation of heteronymous motor axons (Lindsay and Binder, 1991; Maltenfort et al., 2004) induces a 2%–3% decrease in motoneuron input resistance, indicating modest shunt effects. Recurrent postsynaptic potentials evoked by antidromic stimulation of homonymous motoneurons rarely exceed amplitudes of 3 mV (Hultborn et al., 1988). Because motoneurons have large cell bodies and dendritic trees (Cullheim et al., 1987) and RCs contacts are mostly located on dendrites (Fyffe, 1991), electrotonic distances would attenuate the effects of recurrent inhibition at the soma. Low-pass capacitive filtering by the motoneuron membrane would particularly affect glycinergic conductances, which have very fast kinetics (Pitt et al., 2008).

Previous studies are, however, limited by a number of factors. First, stimulation of peripheral nerves evokes different inhibitory responses when comparing homonymous (Hultborn et al., 1988) and heteronymous (Lindsay and Binder, 1991) activation. Second, antidromic stimulation also activates recurrent excitatory circuits (Ichinose and Miyata, 1998) between homologous motoneurons (Gogan et al., 1977), inducing simultaneous activation of excitatory and inhibitory recurrent pathways. The full magnitude of recurrent inhibitory postsynaptic potentials would thus be masked to an unknown extent by excitation. Finally, antidromic activation induces synchronized firing within motor pools, producing artificially synchronous patterns of summation of both recurrent excitatory and inhibitory inputs. It is therefore unsurprising that, when the effect of RCs was investigated in behaving animals (Noga et al., 1987), the blockade of RC activity by cholinergic antagonists substantially increased firing and bursting activity in motoneurons.

In our reduced preparation, at the single-cell level, we show that the substantial inhibitory effect of a Renshaw synaptic input on motoneuron excitability is due to a combination of large conductance changes (often >1 nS), the number of synaptic contacts (typically >5), and the location of synaptic contacts at short electrotonic distances from the soma. The degree of convergence of RCs onto motoneurons is presently unknown. In the light of our measurements of the effect of a single RC on motoneuron excitability, however, the inhibitory capacity of the intact recurrent circuit is likely to be substantial.

There is considerable overlap in the dendritic locations of Ia excitatory and recurrent inhibitory synapses onto motoneurons. As illustrated in Figure 5A, RC contacts may be strategically located to produce maximal shunt effects in proximal dendrites, in regions where the density of Ia afferent contacts is maximal (Rotterman et al., 2014). Furthermore, the amplification of synaptic currents by persistent inward currents occurs in the region of proximal dendrites where most calcium channels are located (Carlin et al., 2000), enhancing the inhibitory capacity of the recurrent circuitry (Hultborn et al., 2003).

Our simulations, based on the measured position of individual inhibitory synaptic contacts and on the known location and density of Ia afferent terminals (Rotterman et al., 2014) and voltage-gated dendritic conductances (Carlin et al., 2000), show that activation of a single RC reduces the depolarization elicited by single excitatory synaptic inputs, even with a near-zero electromotive force for chloride. Furthermore, activity in an RC can strongly shift the input–output relation of the motoneurons.

Role of recurrent inhibition

One of the first postulated functions of RCs was a simple role in preventing excessive discharges in motoneurons (Eccles et al., 1954). A more developed framework proposed that the recurrent circuitry served as a variable gain regulator of motor output (Hultborn and Pierrot-Deseilligny, 1979). This view is supported by observation of a nonlinear input–output relation across motor-pools, indicating that recurrent inhibition is not merely inducing a constant negative bias in motoneuronal signaling (Hultborn and Pierrot-Deseilligny, 1979).

RCs receive a strong convergent input from motoneurons that innervate functionally synergistic muscles (Ryall et al., 1971). Studies in cats indicate that the excitatory synapse from motoneuron collateral inputs to RCs is very reliable. Stimulation of single motoneurones can elicit action potentials in RCs and drive RC firing up to a frequency of 60 Hz (Ross et al., 1975, 1976). RCs can follow the rate of stimulation of motoneuron axon collaterals over the frequency range characteristic of motoneuron firing (Christakos et al., 1987), suggesting that the excitatory component of the recurrent feedback loop is not modulated by changes in the motoneuron activity pattern.

By contrast, the inhibitory synapse formed by the RC onto the motoneuron typically has a baseline probability of neurotransmitter release of <0.5. However, a paired-pulse ratio of ∼2 confers a large range for short-term plasticity. Although we did not specifically model the cumulative effects of multiple pulse facilitation in the simulations, our spike suppression experiments confirm that trains of action potentials in RCs have a larger and longer-lasting effect than single spikes on the pattern of motoneuron firing. The short-term plasticity of the RC–motoneuron synapse could therefore serve as a variable gain mechanism to modulate the bandwidth of motoneuronal signaling.

Ever since the discovery of RCs almost 70 years ago, there has been intense debate about the role they play in motor function (Windhorst, 1996). RCs cannot be regarded only as components of a feedback circuit because their axons are presynaptic to other classes of neuron in addition to α-motoneurons. Because RCs are also regulated by descending systems, other RCs, and various unidentified classes of interneuron, their role contributes to the complex operation of a neuronal network with changing dynamics.

Some mammalian motoneurons, such as those innervating muscles of the digits (Illert and Kümmel, 1999) or muscles of mastication (Shigenaga et al., 1989), are not subject to recurrent inhibition. However, recurrent inhibition acts on motoneurons supplying most limb (Hahne et al., 1988) and neck muscles (Brink and Suzuki, 1987), and the diaphragm (Lipski et al., 1985). Studies on spasticity have shown disruption of recurrent inhibition, which suggests that RCs are important for the normal function of motor systems that control posture and locomotion (Mazzocchio and Rossi, 1997).

The exact role of RCs remains unclear. It has been suggested that the strength of recurrent inhibition generated by RCs is insufficient to have a substantial effect on motoneuron firing (Lindsay and Binder, 1991), and one hypothesis proposes that RC inhibition modulates specific inputs to motoneurons, rather than acting within a closed-loop system (Fyffe, 1991). However, our results show that inhibitory inputs from RCs effectively reduce motoneuron excitability directly, and RCs therefore play a more important role in the coordination of motor activity than has hitherto been supposed.