Quantile Regression in the Study of Developmental Sciences

Abstract

Linear regression analysis is one of the most common techniques applied in developmental research, but only allows for an estimate of the average relations between the predictor(s) and the outcome. This study describes quantile regression, which provides estimates of the relations between the predictor(s) and outcome, but across multiple points of the outcome’s distribution. Using data from the High School and Beyond and U.S. Sustained Effects Study databases, quantile regression is demonstrated and contrasted with linear regression when considering models with: (a) one continuous predictor, (b) one dichotomous predictor, (c) a continuous and a dichotomous predictor, and (d) a longitudinal application. Results from each example exhibited the differential inferences which may be drawn using linear or quantile regression.

In developmental research we use data analyses to make sense of data to support or refute a theory. Through data analysis, we can determine if predictors are related to outcomes, and how strongly they are related. One advanced approach to data analysis called quantile regression has become popular in economics (e.g., Chernozhukov & Hansen, 2005). Quantile regression allows for the possibility that how important predictors are may be different depending on the quantile (a term that closely corresponds to percentile) of the outcome variable (i.e., whether they are low, average, or high on the outcome; Koenker & Bassett, 1978). Developmental science has also begun to see how useful quantile regression can be. For example, Reeves and Lowe (2009) studied the achievement gap in math skills, testing whether ethnicity and gender were predictive of math achievement. Using quantile regression, they were able to demonstrate that both ethnicity and gender were stronger predictors of math achievement for students low on math achievement. In other words, the achievement gap was larger, more present, for students at the low end of math achievement, and smaller for students with higher math ability scores.

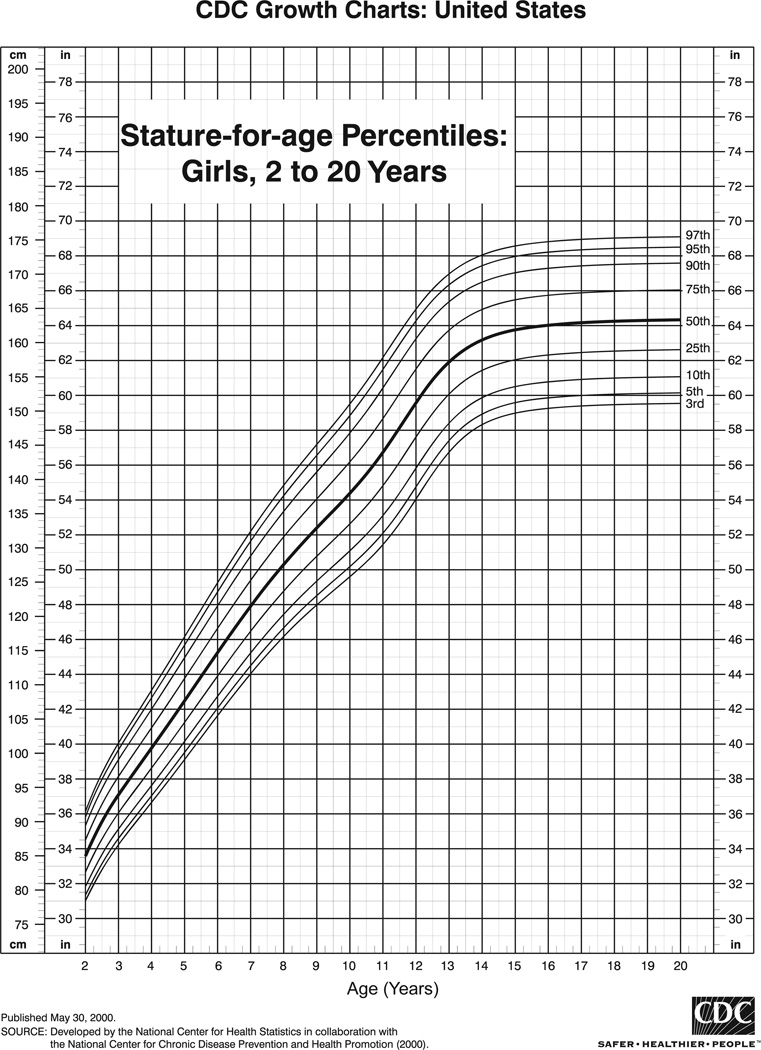
To conceptualize the utility of quantile regression, consider the example of the relations between girls’ age and height (Centers for Disease Control growth charts are presented in Figure 1). If you wanted to guess the relative ages of a group of young children that you have just met, a good strategy would be to look at how tall they are. The shortest child will probably also be the youngest child because younger children tend to be shorter than older children. This strategy will not work as well when you meet a group of teenagers or adults, because by this time, the strong correlation between age and height is not as strong as it is for children. The predicted height for a 6-year-old child is higher than that of a 5-year-old, and as such the slope is of the relation between age and height is large, but that slope is zero (no increase in height when age increases). In other words, the ability to predict a girl’s age from their height is dependent on the girl’s age.

Figure 1.

U.S. normative growth chart for height (stature) with age.

Statistically modeling the relation between age and height could be done a number of ways dependent on the question of interest. If one were interested in testing at what age and below that age might have a different relation with height than above a certain age level a segmented or piecewise regression could be used. In this instance, a cut-point on age (X) is selected (e.g., age 15), and then a series of models could be fit to test the extent to which different slopes exist for the relation between age and height when age > 15 versus age ≤ 15. Conversely, suppose the question was changed such that height was used to predict age. According to Figure 1, the piecewise regression would not be as useful because the cut point for the height (Y) is not as reliable as the one for age; all children stop growing around age 15, but children stop growing at a wide range of different heights. Using a quantile regression allows you to predict age from height, but conditional on the outcome of height.

For a question such as the relation between age and height, age has a very clear and well understood point where height is no longer predictive. Also, the designation of whether age or height is predictor or outcome is more readily interchangeable, and thus, the uniqueness of quantile regression may seem trivial; however, consider the aforementioned example of the gender-based achievement gap in math (Reeves & Lowe, 2009). It is fairly clear that math achievement should be predicted from gender rather than the reverse. The hypothesis tested by the authors’ study was that the differences between males and females on math achievement may vary depending on how good the students are at math. Because females often choose not to take higher level math courses, the gender gap may be wider at higher levels of math achievement; however, the cut point that will correspond to “high levels” of math achievement is unknown. For this question, a piecewise regression would not apply because only the outcome is continuous, and the predictor is dichotomous (male–female). The authors chose to use quantile regression because it allows for the estimation of the achievement gap between males and females at multiple points in the distribution of math achievement with no selected cut points and no constraints on the functional form of the relation across the distribution of math achievement. Using this method, the authors identified that the achievement gap was near zero for low levels of math achievement, but was much larger at the higher end.

Other recent applications of quantile regression have been used to study the relation between alphabet knowledge and home literacy (Petrill et al., in press), the relation between oral reading fluency and reading comprehension (Petscher & Kim, 2011), and effect of nonnormally distributed data on predictions of oral reading fluency (Catts, Petscher, Schatschneider, Bridges, & Mendoza, 2009). Petrill et al. (in press) hypothesized that a child’s alphabet knowledge can be considered a function of the home literacy environment because parents or caregivers who provide more opportunities to read books tend to have children who know more letters of the alphabet, but by definition, alphabet knowledge is a count variable, so the construct often demonstrates strong floor effects. Because the outcome in the Petrill et al. study was a skewed variable, the researchers chose to use quantile regression, and identified that the prediction of alphabet knowledge was near zero when the children knew only a few letters, but was much stronger once the children knew more than five letters. In a regression or conditional means model, the estimated relation would have been weaker due to the influence of the floor effect. Other studies in education and psychology found similar results. Petscher and Kim (2011) studied the relation between oral reading fluency and reading comprehension, and found that the correlation was near zero for those with low fluency (r < .10), but was strong for students with high oral reading fluency rates (r > .70). Similarly, Catts et al. (2009) found that quantile regression was useful for understanding associations between measures of oral reading fluency used for early identification in first grade with third-grade performance in oral reading fluency. The authors found much lower correlations for individuals with low third-grade oral reading fluency (r < .30) compared to individuals with stronger fluency skills (r > .60).

Given the potential ability of quantile regression to contribute to the field of developmental science research, the goals of this study are fourfold. First, we provide the reader with a conceptual and practical introduction to the technique of quantile regression by comparing it to multiple regression. Second, we discuss fundamentals of how quantile regression is estimated and compare it to multiple regression so that the reader can see the similarities and differences. Third, we demonstrate quantile regression using four illustrations of a simple quantile regression with a continuous predictor, a simple quantile regression with a dichotomous predictor, a multiple quantile regression, and a developmental quantile regression example. In each demonstration, comparisons to simple and multiple regression analyses are included, along with interpretations of the relevant parameters. Finally, we conclude with some considerations for best practice, with the hope that readers will begin to use this extension to address questions in developmental research.

Contrasting Linear and Quantile Regression

An implicit tenet of evaluating the relations among variables in developmental research is that the mean best summarizes the associations germane to specified research question. To this end, researchers in developmental psychology have relied statistical analyses rooted in providing average effects. Sample means, Pearson correlation coefficients, multiple regression coefficients, and estimates from longitudinal and structural equation models are always interpreted as the average effect from a substantive viewpoint. Although focusing on this particular statistical moment is useful and relevant to virtually all research studies, it is possible to conceptualize that, under many circumstances, the mean effect may not adequately characterize the underlying relations among variables.

Developmental psychology research includes the study of language, cognitive, social, and emotional development, among other things, all of which may frequently encounter data distributional issues such as normality violations. When skills such as early language development are studied, measures may yield skewed data distributions as a result of floor effects. Subsequently, statistical models that produce an average effect may mask other associations in the data which cannot be understood by a mean-based analysis. From a conceptual perspective, the scope of a research question regarding associations becomes broadened via quantile regression. While linear regression posits the question, “What is the relation between X and Y?” quantile regression extends this to, “For whom does a relation between X and Y exist?” as well as testing for whom a relation is stronger or weaker. Each of the studies and examples from the previous section highlighted how quantile regression yielded a more comprehensive evaluation of the relations between a predictor and the outcome at various points at the higher and lower end of what was being predicted.

It is worth noting a few specific distinctions between traditional linear regression and quantile regression. We alluded to the notion that quantile regression maintains a modeling advantage over linear regression as it pertains to non-normally distributed data. Variables in a linear regression are assumed to be normally distributed, and any violation of these assumptions may impact the associated statistical tests. Violations of normality are often of concern in linear regression, and are of particular concern in educational and developmental research. Studies in these fields often examine abilities or skills as they are first coming online or as they are approaching mastery. When studying skills that are first developing, such as language or play behavior in young children with autism (Charman et al., 2003) or word identification skills for kindergarten students (Wagner, Torgesen, & Rashotte, 1994), the scores will often show a floor effect in the sample, and demonstrate strong, positive skew. The opposite is true of examining mastery skills, as these will show ceiling effects. To correct for the problem of measurement, researchers may apply square root or logarithmic transformations to the data, dichotomize data to represent mastery or nonmastery, use a zero-inflated Poisson or negative binomial regression models, or ignore the potential violations of assumptions.

By contrast, quantile regression was designed, in part, to specifically model data where unequal variance exists (Koenker, 2005). Quantile regression is semiparametric in nature as it makes no assumptions about the distribution of the errors; thus, it is more robust to non-normal errors and outliers. It is also invariant to a monotonic transformation, such as logarithmic transformations, which is not possible for linear regression (Koenker, 2005). Most importantly, a particular benefit of quantile regression is that uses the full data set for estimating the relation between X and Y when fitting quantiles across the range of the dependent variables. Linear regression may achieve the goal of evaluating between variables by creating groups based on Y. This often occurs by the way of creating groups of 4 (quartiles), 5 (quintiles), 10 (deciles), or other numbers of groups based on the distribution of scores. Such procedures are often criticized (e.g., Heckman, 1979) for truncating the range of the outcome and resulting in parameter bias due to sample selection effects. Quantile regression overcomes such complications as the estimation of its model coefficients uses a weight matrix (see the next section) to include all of the sample data. Moreover, the standard errors for the coefficients at each quantile are estimated using bootstrapping the next (Gould, 1997).

Estimation

Given such prospective advantages of using quantile regression, we now turn our attention to elements of how multiple regression and quantile regression are estimated to show the similarities in process as well as the distinct elements of quantile regression. In linear regression, estimated values for an outcome, Y, is calculated based on the corresponding value for a predictor, X, and are found with

$$Y_i={\beta }_0+{\beta }_1{X}_i+{\epsilon }_i,$$ (1)

where β₀ is the intercept, β₁ is the slope, X_i is the score for individual i on independent variable X, and ε_i is the error term, which is assumed to be identically, independently and normally distributed with a mean of 0 and variance of σ². The relation of X with Y is estimated by minimizing the squared difference between the predicted value of Y and the observed value of Y (the sum of the squared error), and the result of the prediction equation can be represented by a single line through a scatterplot of points.

Similarly, quantile regression can be used to estimate the relation of X with Y at a given quantile within the distribution of Y through a process that involves: (a) identifying which sample scores for Y are associated with the selected quantile(s) of interest and (b) estimating the coefficient(s) for the independent variable(s). The relation between a given quantile (τ) and a selected score on Y occurs through a minimization process of the sum of absolute residuals (compared to the sum of squares in multiple regression), which is represented by the equation:

$${\widehat{Q}}_Y(\tau )=\underset{{\xi }_{\tau }\in ℝ}{\text{argmin}}\{\sum _{i\in \left\{i\right|Y_i\ge {\xi }_{\tau }\}}\tau |Y_i-{\xi }_{\tau }|+\sum _{i\in \left\{i\right|Y_i<{\xi }_{\tau }\}}(1-\tau )|Y_i-{\xi }_{\tau }\left|\right\},$$ (2)

where Y_i is the vector of independent variables, ξ_τ is the dependent variable, and τ is the quantile of interest. Positive residuals are given a weight of τ and negative residuals are given a weight of 1 − τ. For example, suppose 10 individuals were assessed on a measure of language development and the following vector of scores were obtained as follows:

• Y_i = (11 5 30 7 9 13 25 40 31 35).

To calculate which of the scores in the sample set corresponds to a selected quantile, such as .45 quantile, Equation 2 may be used to generate a weight matrix as in Table 1. The top row and left column of the matrix contain the vector of scores reported above, ordered by magnitude. Within the matrix, weights are calculated based on Equation 2. When considering the column for the score of 13, the 0 denotes that this is the selected score of interest (i.e., no weight is assigned). The weights above the 0 are calculated with (1 − τ) | Y_i − ξ_τ | from Equation 2, while the weights below 0 are calculated with τ | Y_i − ξ_τ | from Equation 2, where τ = .45, ξ_τ = 13, and Y_i are each of the other scores in the vector. When a score of 13 is compared to a score of 5 at the .45 quantile, the associated weight is calculated as (1 – 0.45) | 5 – 13 | = 4.40. Conversely, when a score of 13 is compared to 25 the calculated weight is 0.45 | 25–13 | =5.40. This process is repeated for each score in the vector, and the resulting weights are summed in each column. To determine which score in the sample set corresponds to the .45 quantile, one examines the sum of the weights; the ξ_τ with the smallest sum value represents the score aligned to the .45 quantile. In this illustration, the score of 13 corresponds to the .45 quantile as its sum (i.e., 54.20) is the smallest calculated value. This estimation process is repeated for any quantile the analyst is interested in testing. As another example, Table 1 shows that a score of 31 corresponds to the .75 quantile.

Table 1.

Quantile Regression Sample Weight Matrix for Estimated Quantiles at τ = .45 and τ = .75

Quantile
.45					ξτ
Yi	5	7	9	11	13	25	30	31	35	40
5	0	1.10	2.20	3.30	4.40	11.00	13.75	14.30	16.50	19.25
7	0.90	0	1.1	2.2	3.3	9.9	12.65	13.2	15.4	18.15
9	1.80	0.90	0	1.1	2.2	8.8	11.55	12.10	14.30	17.05
11	2.70	1.80	0.90	0	1.1	7.7	10.45	11.00	13.20	15.95
13	3.60	2.70	1.80	0.90	0	6.6	9.35	9.9	12.1	14.85
25	9.00	8.10	7.20	6.30	5.40	0	2.75	3.3	5.5	8.25
30	11.25	10.35	9.45	8.55	7.65	2.25	0	0.55	2.75	5.5
31	11.70	10.80	9.90	9.00	8.10	2.70	0.45	0	2.2	4.95
35	13.50	12.60	11.70	10.80	9.90	4.50	2.25	1.80	0	2.75
40	15.75	14.85	13.95	13.05	12.15	6.75	4.50	4.05	2.25	0
Sum	70.20	63.20	58.20	55.20	54.20	60.20	67.70	70.20	84.20	106.70
Quantile
.75					ξτ
Yi	5	7	9	11	13	25	30	31	35	40
5	0	0.50	1.00	1.50	2.00	5.00	6.25	6.50	7.50	8.75
7	1.50	0	0.5	1	1.5	4.5	5.75	6	7	8.25
9	3.00	1.50	0	0.5	1	4	5.25	5.50	6.50	7.75
11	4.50	3.00	1.50	0	0.5	3.5	4.75	5.00	6.00	7.25
13	6.00	4.50	3.00	1.50	0	3	4.25	4.5	5.5	6.75
25	15.00	13.50	12.00	10.50	9.00	0	1.25	1.5	2.5	3.75
30	18.75	17.25	15.75	14.25	12.75	3.75	0	0.25	1.25	2.5
31	19.50	18.00	16.50	15.00	13.50	4.50	0.75	0	1	2.25
35	22.50	21.00	19.50	18.00	16.50	7.50	3.75	3.00	0	1.25
40	26.25	24.75	23.25	21.75	20.25	11.25	7.50	6.75	3.75	0
Sum	117.00	104.00	93.00	84.00	77.00	47.00	39.50	39.00	41.00	48.50

Once the relation between observed scores and quantile for Y has been established via Equation 2, the association between Y and X at a given quantile can then be expressed with

$$Y_i={\beta }_0^{(\tau )}+{\beta }_1^{(\tau )}+{\mathbf{ϵ}}_i^{(\tau )}.$$ (3)

Equation 3 is structurally similar to that of Equation 1 (i.e., each includes the intercept, slope, and error parameters), with the noted addition of the superscript τ above the intercept, slope, and error parameters which denotes the quantile at which the equation is estimating the association. This means that for each specified quantile of interest for testing, a unique intercept, slope, and error term will be estimated. As previously noted, a distinguishing feature of quantile estimation is that no assumption is made about the distributional form for ${\mathbf{ϵ}}_i^{(\tau )}$ (e.g., normal, poisson) in Equation 3, while the corresponding ε_i in Equation 1 (typical linear regression) is assumed to be normally distributed. This critical difference allows quantile regression equations to be fitted to data with non-normal distributions without worries about an impact on parameter bias. Just as with linear regression, the results from a quantile regression from Equation 3 would be represented by a single line through a scatterplot of points; however, the distinction between the two approaches is that quantile regression would fit the line to the data as a function of the selected quantile while linear regression fits the line to the average for the entire distribution.

A distinctive feature of Equation 3 compared to Equation 1 bears mentioning as it pertains to how the slope coefficients from each model should be interpreted. Students who have taken linear regression classes have been taught that the interpretation of the effect of X on Y is such that for a unit increase in X, Y will increase by the coefficient associated with X. For example, if we have an equation for a linear regression as,

$$Y_i=2.5+1.2(X),$$

it is expected that Y will increase by 1.2 units for each unit increase in X. An alternative way to construct the interpretation is in terms of how much gap exists in Y when considering different values of X. To illustrate, it could also be stated that the X coefficient of 1.2 reflects the gap in estimated performance at the mean of Y for a student who is average on X compared to an individual who is 1 SD above the mean on X. Although this is a bit more complex than the traditional interpretation of a slope, it serves as a foundation to understand how the slope relates to the outcome in quantile regression. Now suppose we have two equations from a quantile regression that estimated the association between X and Y at the .25 and .75 quantiles:

$$.25\text{quantile}:Y_i=0.43+2.5(X);.75\text{quantile}:Y_i=1.57+0.82(X).$$

The interpretation of the slope coefficient for the .25 quantile (i.e., 2.5) is best stated as the gap in performance on Y at the .25 quantile for individuals who were average on X compared to individuals who were 1 SD above the mean on X was 2.5 units. Similarly, the interpretation of the slope at the .75 quantile (0.82) is stated as: the gap in performance on Y at the .75 quantile for individuals who were average on X compared to those who were 1 SD above the mean on X was 0.82 units.

This aspect of slope interpretation in quantile regression is necessary as it assists in avoiding confusion about the relations between the model coefficients in the analysis. It is tempting to use the traditional linear regression interpretation of a slope; however, this would potentially mislead an individual to think that at the .25 quantile, increasing the X by 1 unit leads to a predicted score of Y, which increases by 2.5 units. By increasing a score in Y by 2.5 units, an individual would no longer be at the .25 quantile, but would be at a higher quantile. Consequently, it is more appropriate to think and describe slope coefficients as reflective of gap performances in Y based on differences in performance on X.

Data Sources for Illustrations

In the remainder of this manuscript, we illustrate the utility of quantile regression using two publicly available data sets. For the first three examples, we demonstrate quantile regression with the High School and Beyond (HS&B) data. The data file contains a standardized measure of 10th-grade math achievement (M = 50, SD = 10) data on 7,185 students, as well as students’ socioeconomic status (SES; i.e., a standardized composite of parent education, parent occupation, and parent income; M = 0, SD = 1), and a dichotomous indicator reflecting if students were identified as minority (coded as 1) or not (coded as 0). We begin by illustrating two simple quantile regressions of math achievement on SES and minority status. This is done to highlight the differential substantive interpretations made when using a continuous predictor and a dichotomous predictor. Following these examples, SES and minority status will be simultaneously entered to demonstrate an example of multiple quantile regression, whereby the model estimates represent partial coefficients at each quantile (i.e., predictor relation to outcome controlling for other effects).

The developmental illustration stems from the U.S. Sustaining Effects Study (Carter, 1982), which collected data on up to 120,000 students twice a year from Grades 1 through 3. The specific data set used here is a reduced version of the companion data file for the HLM6 software package (Raudenbush, Bryk, Cheong, Congdon, & du Toit, 2004) and contains 1,721 students with math achievement scores that are on a developmental item response theory scale score metric (M = 0, SD = 1), as well as an indicator if the student was male or female, and an indicator if the student was Black or White. This developmental analysis uses the data to study the gap in math achievement between Black and White students at the fall and spring of Grades 1 and 2.

As part of the examples, we highlight selected results from a traditional linear regression analysis compared to quantile regression, and draw contrasts in the types of conclusions that may be reached by both techniques. Furthermore, we illustrate within quantile regression how to compare slope coefficients between quantiles, such that the researcher may test the extent to which point estimates for slopes may be statistically distinguished. We conclude our article with a description of best practices, including sample size considerations, multiple hypothesis testing, and future directions for this technique. In all illustrations, we used the quantreg and glm packages in SAS 9.3 (SAS Institute Inc., 2013).

Regression With One Continuous Predictor

Method Comparison

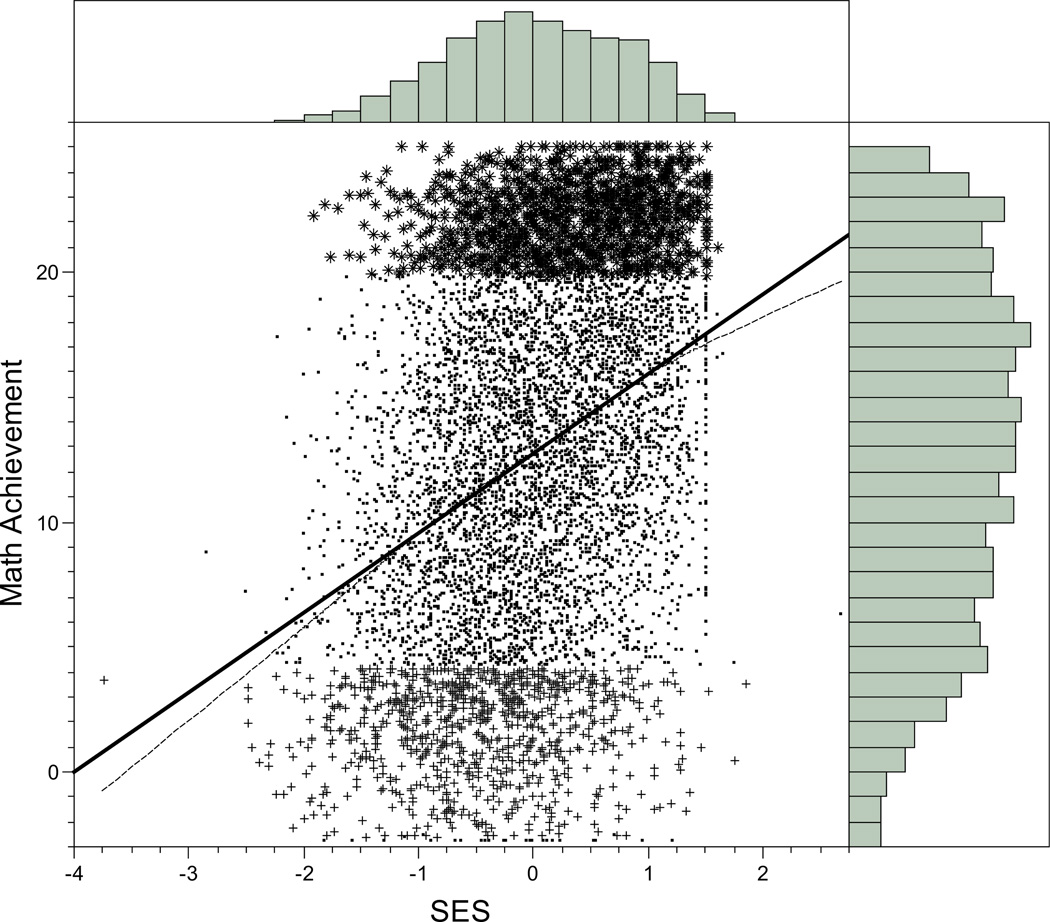
In our first illustration we consider differences in intercept and slope coefficients between linear and quantile regressions when regressing math achievement (Y) on a measure of student SES (X). As a preface to the analysis, we begin with a visual inspection of the data via histograms and scatterplots for the two variables. Figure 2 highlights that slight negative skew was found for both SES (X; −0.23) and math achievement (Y; −0.18), and that math achievement trended toward a platykurtic distribution (−0.92). Furthermore, the scatterplot demonstrates that the correlation between the two variables is moderate (r = .36). Two fit lines have been imposed on the scatterplot, with the solid line representing fit from a linear correlational analysis approach that yields a fit based on the means. The dashed line is a spline function, which is a useful mechanism for highlighting nonlinear patterns in one’s data. It can be observed that while the spline and linear fit lines overlap for part of the scatterplot, the spline function deviates from a linear fit closer to the tails of the two distributions, suggesting that the magnitude of the correlation between SES and math achievement may vary when, for example, SES scores are less than −1 or greater than approximately 1.5. Another piece of evidence from Figure 2 that corroborates this idea lies in the nature of the scatter itself. For math achievement scores on the y-axis less than 4 (i.e., the bold + symbols in the scatterplot) SES scores range from −3.5 to 2; however, for math achievement scores greater than 20 (i.e., the bold * symbols in the scatterplot), the range of SES scores is much narrower (−2 to 1.5). The restricted range of SES scores for high math achievement, and wider range of SES scores for low math achievement suggests that a different relation between the two variables may exist when math achievement is high compared to when it is average or low. In this case, quantile regression could further illuminate the extent to which such a differential relation exists.

Figure 2.

Scatterplot between socioeconomic status (SES) and math achievement with overlain histograms and both a regression fit line (solid) and spline fit line (dashed).

Moving from the simple correlation analysis to a regression model, the primary distinction between the specifications of two procedures is that the quantile regression allows the user to specify quantile, in this case the .10, .25, .50, .75, and .95 quantiles. It is via this design that the quantile regression estimates unique intercept and slope coefficients at each of the quantiles.

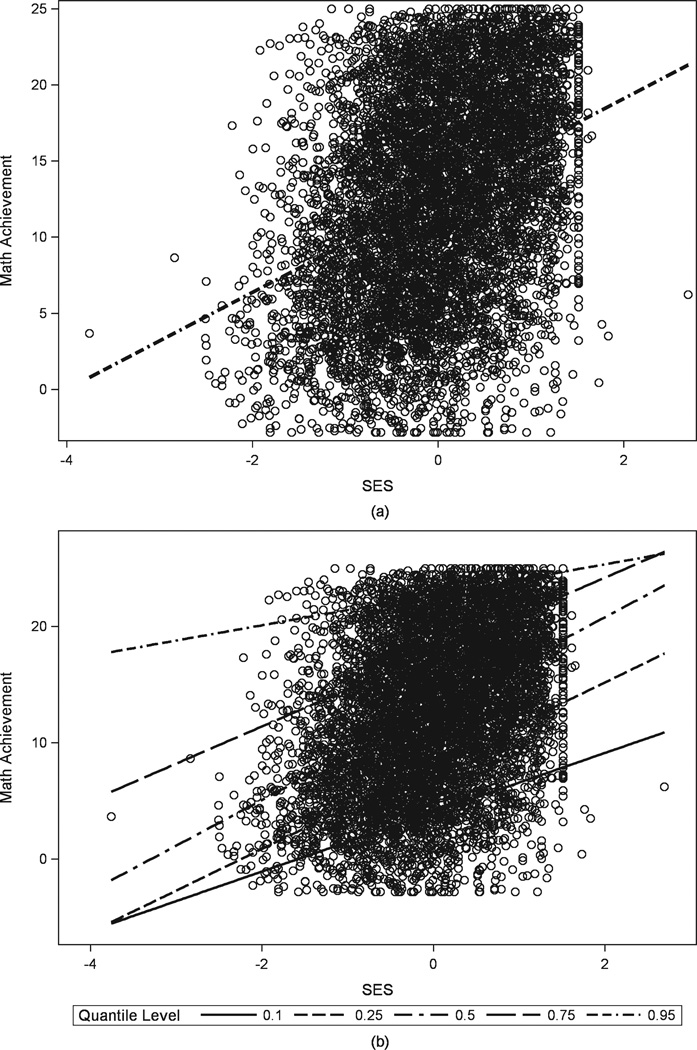
A graphical comparison of the results from the two procedures is provided in Figures 3a and 3b. Figure 3a displays the scatterplot of SES and math achievement with the linear regression line (identical to that in Figure 2), where the fit line represents the minimization of the sum of squared residuals. Figure 3b, by contrast, represents the results of a quantile regression on the same data. There are five fit lines presented in Figure 3b, representing the .10, .25, .50, .75, and .95 quantiles. Notice that the fit line for the .50 quantile (i.e., median) is very similar to the line representing the linear regression (Figure 3a). Conversely, the lines representing the .10 and .95 quantiles have slopes that are not as steep as that of the .25, .50, or .75 quantiles. As we hypothesized from the correlational analysis in Figure 2, this suggests that scores at the 10th and 95th percentiles of math achievement demonstrate a weaker relation between math achievement and SES compared to scores within the interquartile range of math achievement.

Figure 3.

Comparison of scatterplots and fit lines from (a) linear regression and (b) quantile regression from High School and Beyond data regression of math achievement on socioeconomic status (SES).

The specific intercept and slope estimates associated with these linear and quantile regression plots are reported in the upper portion of Table 2. Linear regression results are reported in the usual manner with the coefficients, standard errors, confidence intervals, t statistics, and p values. Model coefficients for this analysis indicated that for students with average SES (due to SES being a z score in the data set), their expected math achievement score was 12.75, and as SES changed by 1 unit, math was expected to change by 3.18 points. As a first comparison between linear and quantile regression, we focus on the .50 quantile (i.e., the median of the distribution of math achievement). When the data are multivariate normal, both methods will yield the same result; because the histograms in Figure 2 demonstrated deviations from normality, it was expected that the results would be similar, albeit not exact. The coefficients at the .50 quantile indicated that the expected math achievement score for an individual with average SES was 12.94, which closely corresponded to the intercept of the linear regression model. Similarly, the slope for SES at the .50 quantile (3.93) was closely aligned to that of the linear model (3.18), as were the standard errors, confidence interval bounds, t statistics, and p values. As we noted in the previous section on estimation, the slope coefficient should be interpreted differently in the quantile framework compared to what commonly occurs in linear regression. In this example, the slope coefficient of 3.93 reflects the gap in math achievement performance at the .50 quantile between an individual who is average with SES and one who is 1 SD above the mean with SES. Similarly, this interpretation could also be applied to the linear regression model whereby the 3.18 slope reflects differences in math achievement performance at the mean of math achievement between an individual who is average with SES compared to a student who is 1 SD above the mean with SES.

Table 2.

Comparison of Linear and Quantile Regressions of Math Achievement on SES and Math Achievement on Minority Status

				95% confidence Interval
Model	Parameter	Estimate	SE	LB	UB	t value	p value
Linear regression—Math achievement and SES
	Intercept	12.75	0.08	12.60	12.90	168.42	<.001
	SES	3.18	0.10	2.99	3.37	32.78	<.001
Quantile regression—Math achievement and SES
QR-10	Intercept	4.04	0.11	3.81	4.26	35.13	<.001
	SES	2.54	0.17	2.21	2.88	14.91	<.001
QR-25	Intercept	8.04	0.10	7.82	8.25	73.42	<.001
	SES	3.58	0.13	3.33	3.84	27.50	<.001
QR-50	Intercept	12.94	0.09	12.75	13.14	131.60	<.001
	SES	3.93	0.10	3.72	4.14	37.14	<.001
QR-75	Intercept	17.81	0.11	17.59	18.03	159.11	<.001
	SES	3.20	0.13	2.94	3.46	24.07	<.001
QR-95	Intercept	22.74	0.08	22.58	22.89	282.50	<.001
	SES	1.31	0.11	1.09	1.52	12.05	<.001
Linear regression—Math achievement and minority status
	Intercept	13.88	0.09	13.70	14.06	151.22	<.001
	Minority	−4.13	0.18	−4.47	−3.79	−23.58	<.001
Quantile regression—Math achievement and minority status
QR-10	Intercept	4.36	0.15	4.07	4.65	29.09	<.001
	Minority	−3.07	0.24	−3.55	−2.50	−12.75	<.001
QR-25	Intercept	8.79	0.15	8.49	9.10	57.03	<.001
	Minority	−4.28	0.20	−4.68	−3.88	−20.94	<.001
QR-50	Intercept	14.49	0.14	14.23	14.77	104.96	<.001
	Minority	−5.10	0.28	−5.65	−4.56	−18.41	<.001
QR-75	Intercept	19.33	0.14	19.06	19.60	140.93	<.001
	Minority	−4.52	0.27	−5.05	−3.98	−16.65	<.001
QR-95	Intercept	23.47	0.08	23.31	23.62	291.83	<.001
	Minority	−2.18	0.23	−2.62	−1.73	−9.55	<.001

Note. Boldface in the table is used to facilitate comparison of results. SES = socioeconomic status; LB = lower bound; UB = upper bound; QR-10 = quantile regression at the .10 quantile; QR-25 = quantile regression at the .25 quantile; QR-50 = quantile regression at the .50 quantile; QR-75 = quantile regression at the .75 quantile; QR-95 = quantile regression at the .95 quantile.

This initial comparison serves to show that when estimating the relation between SES and math achievement using either a means-based approach via linear regression, or a median-based approach, the results can be very similar given the nature of data distributions. With linear regression, however, the interpretation of the dynamic between math achievement and SES would cease at knowing that the effect of SES was 3.18, yet the specification of multiple quantiles allows for us to test whether that slope effect changes depending on one’s level of math achievement. In addition to estimating the relation at the .50 quantile, the model was specified to test for effects at the .10, .25, .75, and .95 quantiles, and the estimated slope coefficients across these selected points of the distribution are reported in the upper portion of Table 2. There are several points worth noting about the quantile-based estimates. First, the intercept values increase from 4.04 at the .10 quantile, to 22.74 at the .95 quantile, and this is a natural expectation of quantile regression. Because the analysis is conditional on score of the dependent variable, higher quantiles are associated with higher observed scores, and thus higher intercepts compared to intercepts at lower quantiles. Second, the slope coefficients for SES vary across the five selected quantiles, and in a manner that appears curvilinear. At the .10 quantile the SES slope was β = 2.54, which increases to β = 3.58 at the .25 quantile, and β = 3.93 at the .50 quantile, but then begins to decrease at the .75 quantile down to β = 3.20 and β = 1.31 at the .95 quantile. These between-quantile differences in slopes relate well to what was observed in Figure 3b. Just as the fit lines for the .10 and .95 quantiles demonstrated slopes that were not as steep as the other quantiles, so too are the actual coefficients for SES lower for the two quantiles.

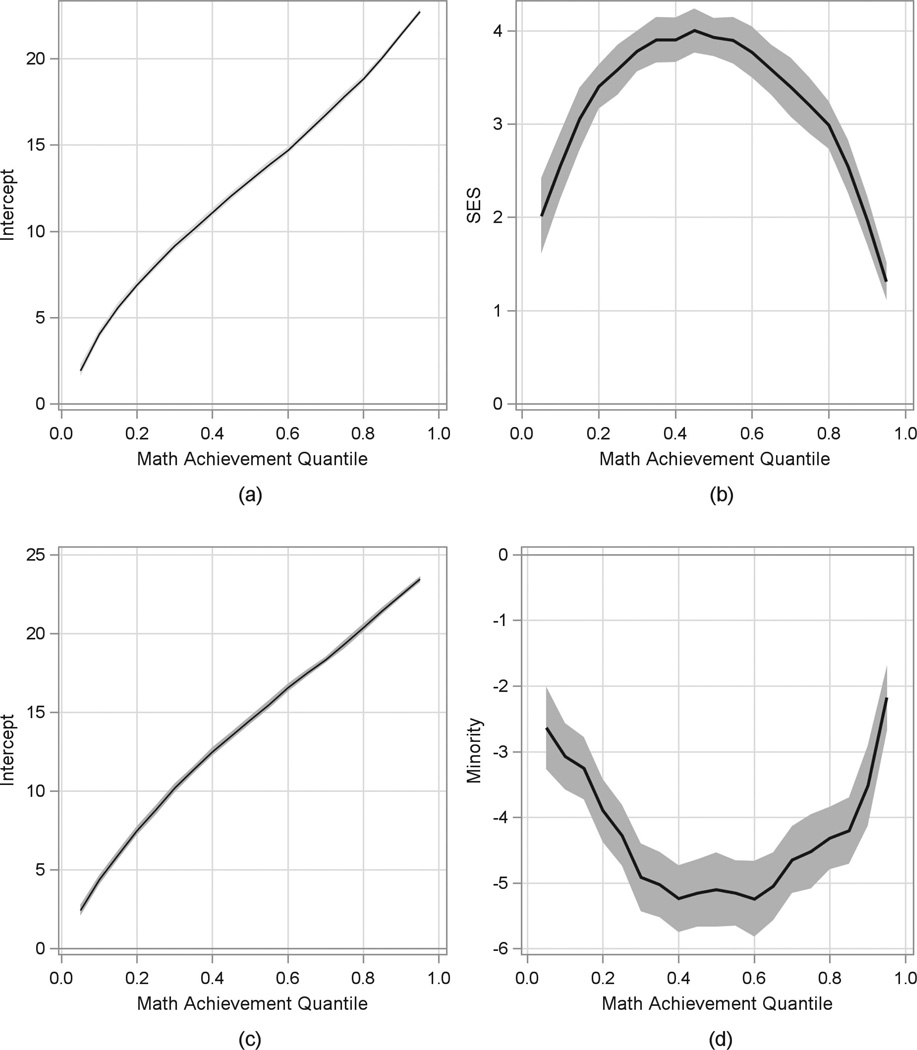
Plots

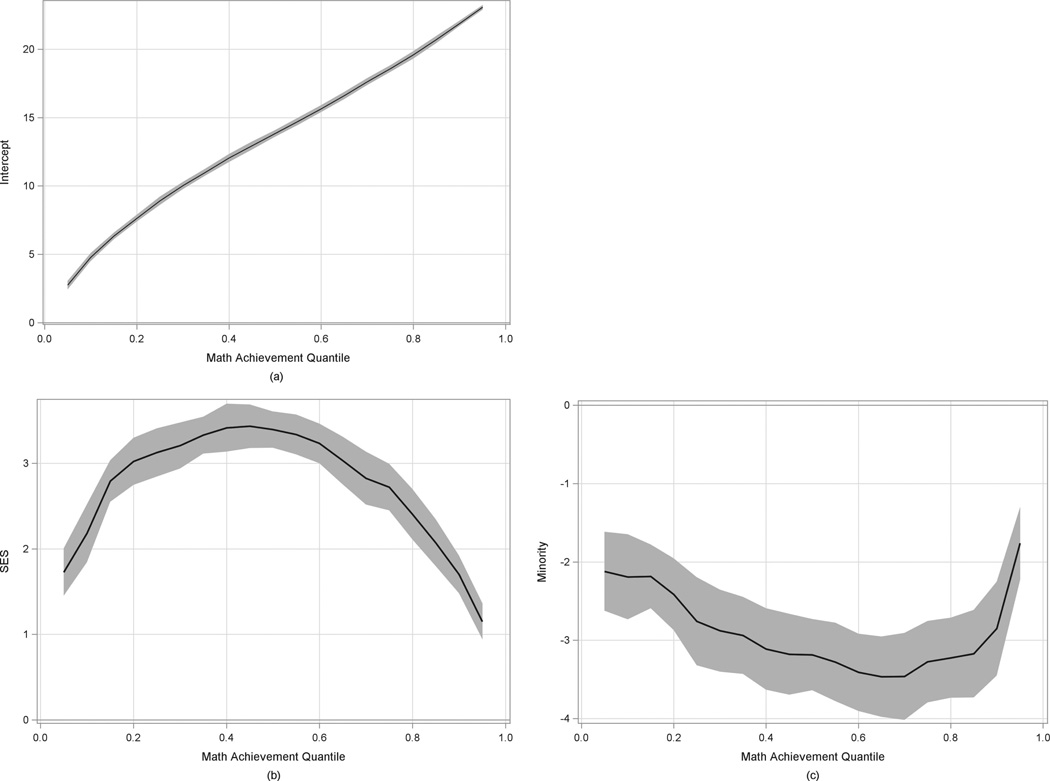
A useful way to summarize the intercept and slope coefficients is to generate a quantile process plot. The intercept portion of the quantile process plot (Figure 4a) displays the predicted math achievement score when SES is 0 (y-axis), which corresponds to the data presented in Table 2, conditional on the quantile of math achievement (x-axis). The intercept plot is self-referential, demonstrating that children at lower quantiles of math achievement have lower math achievement scores, and children at the higher quantile of math achievement have higher math achievement scores. A more useful plot to examine is the slope plot (Figure 4b), which contains SES on the y-axis and the math achievement quantile on the x-axis. The dark line reflects the estimated slope coefficient for SES conditional on the quantile of math achievement. At the lowest quantile (.01), the process plot shows that the coefficient for SES is approximately 2. By examining the pattern of this process plot, it is clear that as math achievement increases from the .01 quantile to the .50 quantile, SES becomes more strongly related to math achievement, with the SES coefficient increasing from approximately 2.0 to 4.0, and then begins to decline, such that the slope coefficient approaches 1 for those students with very high math scores. Although specific estimates may be difficult to ascertain from this plot, it is useful for quickly ascertaining patterns in the conditional Y–X relation that varies across quantiles. From this plot, we conclude that SES has the strongest relation with math achievement for those students who are in the middle of the distribution (i.e., between the .40 and .60 quantiles), but for students who have very high or very low math scores, SES does not maintain as strong of an association. This is quite different than the interpretation yielded from the linear regression. A contrast of the two approaches demonstrates that the relation between SES and math achievement was overestimated (predicted to be higher than is truly observed) in the 20th percentile and below, as well as the 80th percentile and above, while scores were underestimated for those individuals closer to the median of the distribution. The advantage of quantile regression is more readily observed with these data as it provides broader context to the effect of slope on math achievement.

Figure 4.

Quantile process plots for math on socioeconomic status (SES)—(a) math intercept, (b) SES slope—and math on minority status—(c) math intercept, (d) minority status slope.

Quantile Comparisons

A subsequent query that may arise when viewing the trend from Figure 4b is whether slope values across the quantiles are statistically differentiated from each other. For example, one could ask if the estimated slope coefficient of 2.54 at the .10 quantile (Table 2) is significantly different from the 3.93 slope coefficient at the .50 quantile. The between-quantile analysis uses a Wald test (Koenker & Bassett, 1978), which provides a χ² statistic with degrees of freedom, and p value for the test of differences. For a comparison between the .25 and .50 quantiles the results suggested that the estimated SES slope coefficients were significantly differentiated, χ² (1) = 7.45, p < .01, as were the differences between the .50 and .75 quantiles, χ²(1) = 32.79, p < .001, and the differences between the .25 and .75 quantiles, χ² (1) = 5.44, p < .05. As a whole, these findings suggested that the effect of SES on math achievement is statistically differentiated based on one’s math achievement; thus, we may infer that SES and math achievement have a smaller association when math achievement is very low or high compared to SES having a stronger association when math achievement was average.

Regression With One Dichotomous Predictor

Along with using quantile regression for predicting outcomes with a continuous independent variable, researchers often hypothesize that differences in an outcome may be explained by a categorical variable (e.g., examining gender differences, treatment group differences, etc.). Our second example tests whether minority students differ in math achievement from White students across the distribution of math achievement. Results from linear and quantile regressions of math achievement on minority status are presented in the lower portion of Table 2. For the linear regression model, the intercept value was 13.88, reflecting the mean math achievement for White students. The slope coefficient for minority students was negative and indicated that minority students, on average, had lower math achievement by 4.13 points. Quantile regression at the .50 quantile revealed that the mean predicted value of math achievement for a White student is 14.49, and that minority students, on average, had math scores that were 5.10 points lower. These values are comparatively similar to the linear regression, however, not exact due to the distributional characteristics of the dependent variable previously described. As was observed in the former example, the intercept coefficients expectedly increased across the quantiles, and in this model the slope coefficients also varied. At the .10 quantile the gap between White and minority students was 3.07 points, and increased to 4.28 at the .25 quantile and 5.10 at the .50 quantile, but then decreased to 4.52 points at the .75 quantile and 2.18 points at the .95 quantile. This pattern of different slope coefficients when plotted as a quantile process plot (Figures 4c and 4d) yielded a U-shaped pattern for minority status (Figure 4d), demonstrating that the gap between minority and nonminority students in math achievement was not uniform across the range of math scores. Although the gap was smallest when students had either very low (i.e., quantiles < .20) or very high (i.e., quantiles > .80) math achievement scores, performance closer to the middle portion of the distribution (i.e., the .40 to .60 quantiles) resulted in the largest the gap between White and minority students, evidenced by the minority slope coefficients of greater than −5.

The slopes from this model were compared across selected quantiles to test the extent to which the gap between White and minority students at the .50 quantile statistically differed from that observed at the other estimated quantile. Differences were analyzed using the same between-quantile approach in the first example, and results indicated that the math achievement gaps between at the .10, .25, .75, and .95 quantiles were all significantly smaller compared to differences at the .50 quantile: (a) .10 contrast, χ²(1) = 50.62, p < .001; (b) .25 contrast, χ²(1) = 12.55, p < .001; (c) .75 contrast, χ²(1) = 5.50, p < .05; and (d) .95 contrast, χ²(1) = 89.01, p < .001. With the dichotomous predictor the linear regression estimation demonstrated that, on average, there was a 3-point difference between students of minority status and nonminority status in math achievement. However, the quantile regression demonstrated the more complex relation: The 3-point differential was specifically representative of individuals with either low or high math scores, but that the gap ranged from 2 to 5 points based on their math achievement.

Multiple Regression

Our next illustration of the quantile regression technique extends the findings from the previous two examples to integrate the predictors into a multiple regression. Doing so allows an examination of the partial effects of SES and minority status when controlling for each other.

The results of the multiple linear and quantile regression analyses are summarized in Table 3; the linear regression demonstrated that the predicted math achievement score for a White student who was average on SES was 13.53. When controlling for the effect of minority status, SES had a positive relation with math, whereby the gap in math performance at the mean was expected to be 2.74 points between an individual with mean SES compared to 1 SD above the mean in SES. In addition, when accounting for SES, minority students scored 2.83 points lower than White students. At the .50 quantile, the predicted math achievement score for a student with nonminority status and an SES of 0 was 13.83, which was close to the estimated value for the linear multiple regression. The expected gap in math achievement at the .50 quantile between average SES and 1 SD above the mean in SES was expected to be 3.40 points when controlling for minority status. Similarly, when controlling for SES, the predicted math achievement score for minority students was −3.18 points lower than nonminority students (i.e., 10.65). Note the similarity of the solution at the .50 quantile to that of the multiple regression (top rows, Table 3). Furthermore, the slope coefficients at the .10, .25, .75, and .95 quantiles all displayed estimates that deviated from the mean value from the linear multiple regression and demonstrated patterns that were similar to when they were estimated in separate, simple quantile regression models.

Table 3.

Comparison of Linear Multiple and Quantile Regression

				95% confidence interval
Model	Parameter	Estimate	SE	LB	UB	t value	p value
Linear multiple regression
	Intercept	13.53	0.09	13.35	13.70	153.31	<.001
	SES	2.74	0.09	2.55	2.94	27.69	<.001
	Minority	−2.83	0.17	−3.17	−2.49	−16.35	<.001
Quantile multiple regression
QR-10	Intercept	4.79	0.13	4.52	5.05	35.95	<.001
	SES	2.18	0.16	1.86	2.50	13.35	<.001
	Minority	−2.19	0.27	−2.71	−1.67	−8.19	<.001
QR-25	Intercept	8.91	0.15	8.60	9.21	57.69	<.001
	SES	3.13	0.13	2.88	3.38	24.54	<.001
	Minority	−2.76	0.25	−3.26	−2.26	−10.87	<.001
QR-50	Intercept	13.83	0.13	13.59	14.07	112.81	<.001
	SES	3.40	0.11	3.17	3.62	29.94	<.001
	Minority	−3.18	0.25	−3.68	−2.69	−12.63	<.001
QR-75	Intercept	18.57	0.12	18.34	18.81	155.56	<.001
	SES	2.72	0.13	2.47	2.97	21.36	<.001
	Minority	−3.27	0.26	−3.79	−2.76	−12.49	<.001
QR-95	Intercept	23.06	0.09	22.90	23.23	272.88	<.001
	SES	1.15	0.09	0.96	1.34	11.65	<.001
	Minority	−1.76	0.24	−2.24	−1.28	−7.22	<.001

Note. Boldface in the table is used to facilitate comparison of results. SES = socioeconomic status; LB = lower bound; UB = upper bound; QR-10 = quantile regression at the .10 quantile; QR-25 = quantile regression at the .25 quantile; QR-50 = quantile regression at the .50 quantile; QR-75 = quantile regression at the .75 quantile; QR-95 = quantile regression at the .95 quantile.

Figure 5 shows the quantile process plots for the multiple quantile regression, including the intercept (5a), the slope coefficient for SES (5b), and the slope coefficient for minority status (5c). The plots of the two predictors in Figures 5b and 5c represent the partial slope coefficients for each variable when controlling for the other. An ancillary component of this model examined next was the extent to which the between-quantile comparisons demonstrated different results than the simple linear quantile regressions. In other words, how does the gap between minority and nonminority students in math achievement change when controlling for the effects of SES? First, when comparing Figure 4d (simple quantile for minority status) with Figure 5c (multiple quantile for minority status), it is clear from an evaluation of the scaling of the y-axis in both figures that minority gap in math achievement is not as strong after controlling for SES (range = 0 to −4) as it was when it was the only predictor of math achievement (range = 0 to −6). Quantile comparisons tests were used to determine if the observed differences across the distribution of math achievement were significant. The results of the between-quantile comparisons suggested the estimated coefficients at the .25, .50, .75, and .95 quantiles were not significantly different from one another, confirming that the achievement gap between students of minority status and nonminority status is stable across the distribution after controlling for SES. The effect of SES on math achievement was also comparatively weaker in the multiple regression (Figure 5b) than the simple regression (Figure 4b). However, even though the magnitude of the partial coefficient for SES was weaker compared to the simple regression model, the quantile comparisons indicated that significant differences across the distribution still existed between the 25 and .50 quantiles, χ² (1) = 4.15, p < .05; the .75 and .50 quantiles, χ²(1) = 27.80, p < .001; and the .50 and .95 quantiles, χ²(1) = 226.50, p < .001.

Figure 5.

Quantile multiple regression process plot with confidence limits.

Taken together, these results revealed several trends that would not have been directly observable using multiple regression. First, the simple linear regression demonstrated that a differential achievement gap existed between minority and nonminority students at different points of the outcome. Once SES was controlled, however, this differential gap no longer existed, which, in one sense corroborates the findings in the multiple regression in that the mean coefficient can generalize across the distribution of math achievement. From another perspective, it is important to note that without controlling for SES, the differential gap would still exist across the different points of the outcome, and multiple regression would have still assumed that the model coefficient remained the best estimate of predicting differences in math. Second, when controlling for minority status in the multiple regression the between-quantile analysis for SES was found to be significantly more strongly related to math achievement scores for moderate math achievement scores (the .4 to .6 quantiles) than it was of those students with higher or lower scores (Figure 5b).

Developmental Illustration

The preceding sections have served to familiarize the reader to quantile regression theory and estimation, with applied examples of simple and multiple quantile regression. A natural extension of the previous examples is to examine the extent to which the predictive relation between selected variables varies at different developmental phases. Using the previous HS&B data as a conceptual illustration, it is possible that the quantile relation between math achievement and minority status might vary at different points in time, such that the curvilinear shape from Figure 4d may change when measured at an alternative time point.

As the referenced HS&B data set lacks sufficient data for this longitudinal examination, we switch to the U.S. Sustaining Effects data set. Recall from earlier that while this study uses math achievement as an outcome, the metric of the score is different from HS&B in that the current data set uses a vertically scaled z score such that growth may be inferred over time. Here, we consider achievement differences in math achievement between Black and White students at four time points (i.e., fall and spring of Grade 1, fall and spring of Grade 2) using linear and quantile regression. Our previous illustrations of quantile regression have thus far demonstrated how we were able to compare intercept and slope coefficients between points on the distribution of Y. For this longitudinal application, we can further examine whether the relations between minority status and math achievement at a given quantile were different in magnitude at different data collection points, as well as examine whether a statistically significant difference in Black–White student achievement gaps in map between two specified quantiles varied across the four time points.

Linear Regression

Results for the linear regression of math achievement on the dummy-coded covariate representing Black and White differences for each of the four time points are reported in Table 4. The intercept value, representing the mean math achievement for White students, increased across each of the four administrations from −1.63 at the fall of Grade 1 (i.e., Math 1) to 0.75 at the spring of Grade 2 (i.e., Math 4). The coefficient for Black students at Math 1 was −0.34, indicating that their math achievement was, on average, lower than White students by .34 units. Across the remaining time points, it can be seen that the coefficient for Black students increases, suggesting that the gap in math achievement grows from the fall of Grade 1 (−0.34) to the spring of Grade 2 (−0.66).

Table 4.

Linear Regression Results for U.S. Sustaining Effects Study

				95% confidence interval
Outcome	Predictor	Coefficient	SE	LB	UB	t value	p value
Math 1	Intercept	−1.63	0.05	−1.74	−1.54	−31.98	<.001
	Black	−0.34	0.06	−0.46	−0.22	−5.55	<.001
Math 2	Intercept	−0.61	0.05	−0.71	−0.51	−12.36	<.001
	Black	−0.43	0.06	−0.55	−0.32	−7.35	<.001
Math 3	Intercept	0.18	0.05	0.08	0.29	3.36	<.001
	Black	−0.56	0.07	−0.69	−0.43	−8.56	<.001
Math 4	Intercept	0.75	0.06	0.63	0.87	12.42	<.001
	Black	−0.66	0.07	−0.80	−0.51	−8.99	<.001

Note. SES = socioeconomic status; LB = lower bound; UB = upper bound; Math 1 = fall, Grade 1; Math 2 = spring, Grade 1; Math 3 = fall, Grade 2; Math 4 = spring, Grade 2.

Quantile Regression

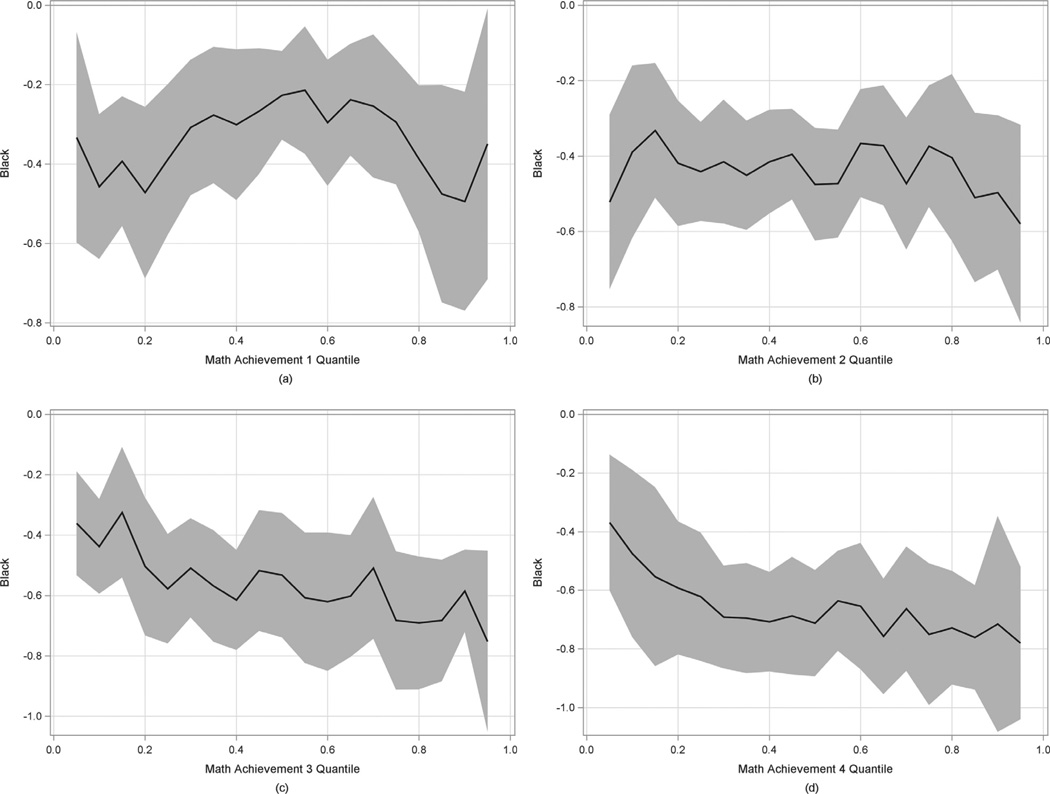
The results of the quantile regressions of Black–White student differences in math achievement are displayed in Figure 6 (6a = Math 1; 6b = Math 2; 6c = Math 3; 6d = Math 4), with estimates reported in Table 5. Model coefficients can be interpreted in the same way as those in the previous (simple dichotomous predictor) sections; however, we will briefly describe the results of the quantile regressions at each time point, followed by a comparison across the time points.

Figure 6.

Regression of math achievement on Black–White differences over four time points.

Table 5.

Quantile Regression Results for U.S. Sustaining Effects Study

					95% confidence interval
Outcome	Quantile	Predictor	Coefficient	SE	LB	UB	t value	p value
Math 1	QR-10	Intercept	−3.07	0.07	−3.21	−2.93	−42.60	<.001
		Black	−0.46	0.10	−0.66	−0.26	−4.47	<.001
	QR-25	Intercept	−2.41	0.07	−2.55	−2.28	−34.72	<.001
		Black	−0.39	0.10	−0.59	−0.19	−3.79	<.001
	QR-50	Intercept	−1.76	0.04	−1.83	−1.69	−46.91	<.001
		Black	−0.23	0.05	−0.32	−0.13	−4.61	<.001
	QR-75	Intercept	−0.94	0.06	−1.06	−0.82	−15.34	<.001
		Black	−0.29	0.07	−0.44	−0.15	−4.03	<.001
	QR-95	Intercept	0.46	0.14	0.19	0.74	3.31	<.001
		Black	−0.35	0.18	−0.70	0.00	−1.97	0.049
Math 2	QR-10	Intercept	−2.07	0.08	−2.23	−1.91	−25.28	<.001
		Black	−0.39	0.10	−0.59	−0.19	−3.78	<.001
	QR-25	Intercept	−1.38	0.05	−1.48	−1.28	−26.49	<.001
		Black	−0.44	0.06	−0.56	−0.32	−7.02	<.001
	QR-50	Intercept	−0.65	0.07	−0.78	−0.51	−9.23	<.001
		Black	−0.48	0.08	−0.63	−0.32	6.17	<.001
	QR-75	Intercept	0.06	0.06	−0.07	0.18	0.90	0.370
		Black	−0.37	0.08	−0.53	−0.22	−4.80	<.001
	QR-95	Intercept	1.49	0.13	1.22	1.75	11.19	<.001
		Black	−0.58	0.15	−0.88	−0.29	−3.86	<.001
Math 3	QR-10	Intercept	−1.56	0.06	−1.68	−1.43	−24.74	<.001
		Black	−0.44	0.09	−0.61	−0.27	−5.11	<.001
	QR-25	Intercept	−0.73	0.07	−0.86	−0.59	−10.17	<.001
		Black	−0.58	0.08	−0.74	−0.42	−7.10	<.001
	QR-50	Intercept	0.11	0.09	−0.07	0.29	1.25	0.212
		Black	−0.53	0.10	−0.73	−0.34	−5.44	<.001
	QR-75	Intercept	1.15	0.10	0.94	1.35	11.02	<.001
		Black	−0.68	0.11	−0.89	−0.47	−6.39	<.001
	QR-95	Intercept	2.43	0.13	2.17	2.69	18.03	<.001
		Black	−0.75	0.14	−1.02	−0.48	−5.41	<.001
Math 4	QR-10	Intercept	−0.89	0.11	−1.10	−0.67	−8.14	<.001
		Black	−0.48	0.13	−0.73	−0.22	−3.59	<.001
	QR-25	Intercept	−0.08	0.10	−0.27	0.11	−0.81	0.416
		Black	−0.62	0.12	−0.85	−0.39	−5.32	<.001
	QR-50	Intercept	0.79	0.07	0.64	0.93	10.65	<.001
		Black	−0.71	0.09	−0.88	−0.54	−8.18	<.001
	QR-75	Intercept	1.62	0.10	1.42	1.83	15.56	<.001
		Black	−0.75	0.12	−0.99	−0.51	−6.20	<.001
	QR-95	Intercept	2.81	0.13	2.57	3.06	22.35	<.001
		Black	−0.78	0.13	−1.04	−0.52	−5.91	<.001

Note. Boldface in the table is used to facilitate comparison of results. SES = socioeconomic status; LB = lower bound; UB = upper bound; QR-10 = quantile regression at the .10 quantile; QR-25 = quantile regression at the .25 quantile; QR-50 = quantile regression at the .50 quantile; QR-75 = quantile regression at the .75 quantile; QR-95 = quantile regression at the .95 quantile.

For Math 1, the intercept value was −1.76 compared to the −1.63 from linear, and the slope coefficient of −0.23 in the quantile model approximated that of the linear regression model (i.e., −0.34). However, the quantile regression showed that the gap between Black and White students had high dispersion in its differences. Note that in the quantile results for Math 1 that the gap between Black and White students decreases by half from the .10 quantile (−0.46) to the .50 quantile (−0.23), but then increases from the .50 quantile to the .95 quantile (i.e., −0.23 to −0.35). This trend is graphically displayed in Figure 6a and corroborates the data found in Table 5. To test these differences, empirical comparisons were made between slope coefficients of selected pairs of quantiles. Significant differences in the slope was observed between the .10 and .50 quantiles, χ²(1) = 743, p < .01, but no significant differences in the slope coefficient were estimated when the .50 quantile was compared to the .25, .75, or .95 quantiles. This indicated that at the fall of Grade 1, the gap between Black and White students’ math achievement was significantly greater for students who attained the lowest math achievement scores compared to those who were at the median, or close to the average performance level, where the gap was much smaller.

By the spring of Grade 1, the gap between Black and White students appeared to normalize across the distribution of math achievement (Figure 6b), such that the slope coefficient was approximately −0.40 at each quantile (Table 5). A pairwise comparison of quantiles concurred with this observation: no significant differences in the Black–White math achievement gap were found when the .50 quantile was compared to the others. Once students moved into Grade 2, the quantile regression highlights that the gap between Black and White students ranged from −0.44 at the .10 quantile up to −0.75 at the .95 quantile (Figure 6c). The significance of this change was confirmed via between-quantile comparisons tests: Effects were found when comparing estimates at opposing ends of the distribution, that is, .10 and .75 quantiles, χ²(1) = 4.45, p < .05. Finally, the achievement gap found in fall of Grade 2 continued through the spring (Figure 6d), whereby the math gap was much smaller for those students whose math scores were lower (e.g., a −0.48 difference at the .10 quantile; Table 5), compared to a larger gap when math achievement was higher (e.g., −0.78 difference at the .95 quantile).

Longitudinal Comparisons

Examining the results developmentally, the linear regression suggests a small but steady widening of the gap in math achievement between Black and White students from the fall of Grade 1 (−0.34) to the spring of Grade 2 (−0.66). The quantile regression results demonstrated substantial individual differences around each of these estimates. First, the estimates from the quantile regression at the median generally aligned in magnitude with those of the linear regression at each of the four time points, suggesting a slight widening of the achievement gap over time. If we focus instead on the low end of the distribution of math scores (i.e., the .10 quantile), the gap in math achievement at each time point as consistently about 0.40, suggesting no change in the achievement gap for students who score at the low end of math achievement. The opposite was true when we examined the results at the highest quantiles. While the gap increased by .32 z-score units for students at the median (i.e., −0.66 to −0.34), at the .75 quantile, the coefficient associated with math differences increased from −0.29 in the fall of Grade 1 to −0.75 in the spring of Grade 2 (i.e., a 0.46 increase in the gap). Thus, the extent to which Black students and White students differed in their math achievement scores over time was dependent on whether students were low (stability in gap over time), at the median (small increase in gap over time), or high (moderate increase in gap over time) in math achievement.

Discussion

Many questions about individual differences in the developmental and education sciences have traditionally been evaluated with linear regression-based methodologies. Such procedures allow for the discussion of the average effects existing within a sample. In this study, we have provided an overview of quantile regression, which extends the general logic and goal of linear regression to specific knowledge about individual differences conditional on the performance on the outcome. The illustrations highlighted that quantile regression possesses several advantages over linear regression. First, in the basic illustration of simple linear regression, the quantile process plots demonstrated that the relation between SES and math achievement in the HS&B data was not the same magnitude across all points of math achievement. Although the slope coefficient from linear regression was aligned to that found at the .50 quantile, the quantile regression revealed that SES was less related to math when math achievement was very poor or very good but was strongly related at approximately the 40th to 60th percentiles of math achievement.

Next, we demonstrated a multiple regression example of both minority status and SES as predictors of math achievement. Quantile regression revealed that after controlling for minority status, there were still significant differences in the strength of the relation of SES with math achievement. Furthermore, comparing the simple and multiple regression results was also illuminating. In the simple regression results, there were significant differences in the math achievement gap between minority and nonminority students at particular quantiles. Once SES was controlled for in the multiple regression these differences were no longer significant. Such an observation could not have been tested using multiple regression.

Finally, the developmental illustration demonstrated that it was possible to observe whether the relation between X and Y at a specific quantile of Y remains static over multiple assessment points. In our illustrative example, the linear regression suggested a moderate increase in the achievement gap between the fall of Grade 1 and the spring of Grade 2. The quantile regression results suggested that this relation was more complex. We found that the math achievement gap between Black and White students was about the same at each time point for those students with low math achievement. However, for those students with high math achievement, the achievement gap was much larger (almost double) in the spring of Grade 2 than it was in the fall of Grade 1. This finding highlights the fact that linear regression models are not capable of providing such targeted information about slope coefficients at different points in the distribution of scores.

Other Potential Uses

Although it did not happen in these particular examples, it is possible that a predictor identified as statistically significant in the linear regression may show a lack of relation at certain points when subset on the conditional distribution of the outcome. For example, even when a linear regression weight (slope or intercept) is statistically significant, it is still possible that the quantile regression results find nonsignificant relations between the predictor and the outcome at or below a given quantile. If such a pattern of results were observed, it would suggest that the predictor was important for the outcome in general but was not an important predictor of the lowest performers on the outcome. A similar result was found in the Catts et al. (2009) study mentioned in the Introduction: No relations between two reading skills were observed at the lowest quantiles. In the case of Catts et al., this finding was indicative of the floor effects found with the examined assessments. Such a result could also suggest that two qualitatively different groups of people exist (e.g., good and poor readers, high and low frequency of response, impairment and not impaired). This analysis would give the researcher an empirical basis to determine at what point in the distribution the qualitative change occurred.

Research questions in educational research are often examined using simple regression techniques. However, questions can often go beyond what can be answered in a standard regression framework. As previously noted, splitting a sample into two groups results in several potential limitations, including the sacrifice of statistical power from dividing the sample, and the fact that the results could differ depending on where the cut point is set. The use of quantile regression allows for the examination of questions of differential relations or importance without the problems associated with dichotomizing variables or splitting a sample into smaller subsamples.

Considerations for Best Practices

We conclude this article with a discussion of several ancillary considerations pertaining to planning a study using quantile regressions. Issues such as minimal sample sizes and estimation of effect sizes or practical importance are all common components of methodologies that should be addressed. Current research into minimal samples for quantile regression is limited. Most of the research pertaining to sample size is rooted in simulation work pertaining to potential new estimators for quantile regression and its impact on parameter estimates given a particular set of sample sizes (see Hardle, Ritov, & Song, 2010; Huber & Melly, 2011). A growing body of research has begun to develop permutation tests to improve Type I error rates (Cade & Richards, 1996, 2006), yet such studies do little to provide concrete recommendations for sample size beyond the general maxim that larger samples are desired compared to smaller. Koenker and d’Orey (1987) found that quantile regression may perform poorly at particular quantiles (e.g., > .70 quantiles) when the sample size at that place in the distribution is smaller. Similarly, Chernozhukov and Umanstev (2001) found that slope coefficients at the tails of the conditional distribution had wider confidence bands compared to the coefficients at the middle part of the distribution. Such findings suggest that when one is planning a study to use quantile regression, uniform sampling of individuals across the ability distribution will ensure that the conditional point estimates are equally precise the range of the outcome. In addition, when data are collected from small samples, individuals should consider the use of bootstrapping the parameter estimates or using a permutation test (Cade & Richards, 2006).

A second consideration for best practices pertains to the selection of the number of quantiles to be specified. Our focus in choosing quantiles in this study was to provide individual points that corresponded to a reasonable lower bound quantile (i.e., .10), values approximately corresponding to points in the interquantile range (i.e., .25, .50, .75), as well as a reasonable upper bound quantile (i.e., .95). In practice, the specification should be based on the sample size, the number of parameters in the number, and the distribution of the data (Cade & Noon, 2003). Catts et al. (2009), Logan et al. (2011), and Petscher and Kim (2011) used 19 selected quantiles ranging from .05 to .95 in intervals of .05. Applications of quantile regression in econometrics and biometrics have similarly used the 19 quantiles based on the inversion of a quantile rank-score test (Koenker, 1994; Koenker & Mochado, 1999). It is likely that basic applications can reasonably use the quantile points used in this study to broadly characterize phenomena in their data, and with larger samples the use of 19 (or greater) quantiles will add greater specificity to potentially differential estimation of slopes.

Third, when fitting a regression model, researchers are often interested in evaluating the goodness of fit for a sequence of models. In linear regression, this is typically done via the coefficient of determination (i.e., R²), which indicates how well the fitted regression line approximates the real data points. Model R² values are useful for not only examining the total explanatory power for a set of predictors but can be used to estimate how much unique variance a given independent variable explains within a set of predictors. Although quantile regression has, to date, contained little research on extensions of this statistic to the conditional median models, work by Petscher, Logan, and Zhou (2013) demonstrated that a pseudo-R² may be calculated for each quantile, with results showing comparable findings to the traditional linear regression R².

A final consideration for quantile regression concerns hypothesis testing for between-quantile slope coefficients. When multiple hypothesis testing occurs in data analysis, it is possible that the Type I error rate may become inflated. Traditional multiple hypothesis testing occurs when differences are being tested on one outcome for multiple groups, or when multiple outcome are being tested in multiple groups. It may be practically relevant to consider between-quantile coefficient testing as an instance of multiple hypothesis testing. When planning for a between-quantile analysis, it is likely the user both (a) a priori select the points in the distribution that to compare and (b) choose an appropriate method for hypothesis testing correction (e.g., linear step-up procedure). This will minimize the likelihood of capitalizing on chance data fluctuations when conducting these inferential tests.

Conclusions

Although the goal of this article is to introduce the reader to quantile regression through the illustration of simple and multiple regressions at one point in time, or across multiple, it is possible to see that conditional median modeling could illuminate other types of relations beyond what has been presented here. For example, our example of simple linear regression with a dichotomous variable could be extended to looking at treatment effects, evaluating how groups may differ along the distribution of a posttest score, yet more research is needed to develop upon ideas of power analysis, sample size, and effect sizes before more fully utilizing the strengths of quantile regression in treatment studies. In addition, it may be possible to extend these models to account for clustering effects (Geraci & Bottai, 2011) as well as other models that seek to explain individual differences. In summary, we believe that quantile regression fills a need in the developmental and educational research fields by providing the ability to examine correlations and partial correlations, along with their corresponding significance tests, as well as estimates of variance explained, all conditional on the score of the outcome without the potential disadvantages of dividing the sample into subgroups. Combined, these elements of the quantile regression technique make it a powerful tool that is particularly suitable for developmentally oriented questions.