A Maximum-Likelihood Approach for ADC Estimation of Lesions in Visceral Organs

Abstract

Accurate estimation of the apparent diffusion coefficient (ADC) of lesions in diffusion-weighted magnetic resonance imaging (DWMRI) is important to predict and monitor anti-cancer therapy response. The task of ADC estimation of lesions is complicated due to noise in the image, different variances in signal strengths at different b values and other random phenomena. In organs that have visceral motion, due to motion across scans, estimating the ADC becomes even more complex. To get rid of inaccuracies due to motion, only a single ADC value of the lesion is estimated, conventionally using a linear-regression (LR) approach. The LR approach is based on an inaccurate noise model and also suffers from other deficiencies. In this paper, we propose an easy-to-implement and computationally-fast maximum-likelihood (ML) method to estimate the ADC value of heterogeneous lesions in visceral organs. The proposed method takes into account the Rician distribution of noise in DWMRI. In the process, we also derive the statistical model for the measured mean signal intensity in DWMRI. We show using Monte-Carlo simulations that that the proposed method is more accurate than the LR method.

I. Introduction

Diffusion is the thermally-induced behavior of molecules moving in a microscopic random pattern in a fluid. Diffusion-weighted magnetic resonance imaging (DWMRI) is sensitive to this motion. The motion is quantified by means of an apparent diffusion coefficient (ADC) [1], [2]. Since cellular structures generally restrict water mobility, a change in the lesion anatomy in response to therapy results in a change in the ADC value of the lesion. In previous studies, the ADC value has been shown to be a positive indicator to tumor response to therapy, both pre-clinically and clinically [3]–[5]. However, for DWMRI to function as an imaging biomarker, it is critical to estimate the ADC accurately and precisely. To estimate the ADC, the lesion is scanned at multiple magnetic-gradient values (b values). From the scanned images, the signal intensity of the lesion pixels is determined, and using these intensity values, the ADC is computed. The task of ADC estimation is difficult due to the corruption of the diffusion-weighted (DW) images by noise, different variances in signal intensities at different b values [1], [6] and contamination due to flow artifacts and ghosting. In a visceral organ such as the liver, pancreas, or spleen, due to motion issues, this task becomes even more complicated.

There has been considerable research on ADC estimation in DW images. The suggested methods have targeted the problem of computing the ADC of the lesion on a pixel-by-pixel basis. This results in the computation of an “ADC map” of the lesion. The least-squares (LS) method has been one of the most popular methods for this task [7], [8], due to its speed and ease of implementation. However, the LS method can be biased, since it does not account accurately for the Rician distribution of noise in DW images [9], [10]. To overcome this issue, more rigorous schemes have been proposed. Sijbers et al. [11] have developed a maximum likelihood (ML) method for parameter estimation when the measurement data are Rician-distributed. Walker-Samuel et al. [10] have applied this method to compute the ADC of heterogeneous solid tumors in the brain. Bammer et. al. [12] have proposed a similar ML technique and also a modified LS method for ADC estimation. Kristoffersen et al. [13] have suggested another ML scheme for ADC estimation from averaged magnitude images.

While the suggested methods are very useful to compute an accurate ADC map of the lesion, they require that the images acquired at the different b values be perfectly registered with each other. In visceral organs, there might be movement of the organ across the different b value scans. Due to this movement, there is the possibility of mis-registration of the images at the different b values. Consequently, computing the ADC map on a pixel-by-pixel basis is potentially error-prone [5]. Thus, instead of computing an ADC map of the lesion, the mean signal intensity of the lesion, a parameter invariant to lesion movement, is determined at the different b values. Using the mean signal intensity, a single ADC value for the lesion is computed [5], [6], [14]–[17]. To compute this single ADC value, a linear-regression (LR) technique is currently used [5], [15], [16]. However, the LR technique is based on an incorrect noise model as we show later in the paper, and leads to inaccurate ADC computation.

In this paper, we investigate the problem of designing an accurate estimator to compute a single ADC value for a lesion in a visceral organ. Previously we had presented some strategies to estimate this single ADC value for homogeneous lesions using a ML approach [6], [18]. In this research, we further extend our work, proposing a significantly-improved ML approach that incorporates a more accurate model of the noise in the measured data and accounts for the heterogeneity in the lesions. In the process, we also develop a statistical model for the measured mean signal intensity in DWMRI.

II. Theory

A. Problem Formulation

Let N be the number of b values at which the lesion is imaged. Let b_i denote the b value for the i^th scan, for i = 1, 2, …, N. For the j^th lesion pixel at the i^th b value, let s_ij and m_ij denote the true signal magnitude and the noisy measured signal magnitude, respectively.

As we discussed earlier, computing an ADC map using the scans at the different b values is potentially error-prone for visceral organs. To circumvent this issue, the mean signal intensity of the lesion at the different b values is instead computed [5], [6], [15], [16]. Let us denote the true mean signal intensity of the lesion at b value b_i by s̅_i. For a particular lesion, the single ADC value a is required to satisfy the mono-exponential diffusion model,

$${\mathrm{s̅}}_i=K\text{exp}(-a{b}_i),$$ (1)

where K is another unknown parameter.

Let us denote the measured mean signal intensity at b value b_i by m̄_i. Therefore, ${\mathrm{m̄}}_i=\frac{1}{J}{\sum }_{j=1}^J{m}_{ij}$ where J is the total number of lesion pixels in the image. Let us denote the vector of measured mean signal intensities at the different b values, M̄ = {m̄_i, i = 1, …, N}. Our objective is to estimate the ADC value a, and the parameter K, accurately and precisely, given M̄.

B. Linear-Regression Approach

A common approach to get this single ADC value a is a linear-regression (LR) approach [5], [15], [16]. Let n_i denote the noise in the measured mean signal intensity at b value b_i. Thus, we can write

$${\mathrm{m̄}}_i={\mathrm{s̅}}_i+n_i=K\text{exp}(-a{b}_i)+n_i,$$ (2)

using Eq. (1). In the LR approach, we take the logarithm of both sides of the above equation:

$$\text{log}{\mathrm{m̄}}_i=\text{log}K-a{b}_i+\text{log}(n_i).$$ (3)

Using the least-squares-minimization technique, a and K are estimated. The issue with the method is that, since it is a least-squares technique, it is optimal when log(n_i) is normally distributed [19], which is not true in this scenario. Another issue with the LR method is that in DWMRI, at different b values, the variance of the measured signal is different [1], [6]. The LR method does not take this into account.

C. Maximum-Likelihood Approach

The basic objective of the ML approach is to obtain those values of {a, K} that maximize the probability of occurrence of M̄. Therefore, the ML approach requires an accurate and rigorous formulation of the probability model of M̄. We consider the general case of a heterogeneous lesion and investigate the characteristics of the MR noise corrupting the acquired image. The MR images are corrupted by Rician noise [9]. Therefore, at b value b_i, for the j^th lesion pixel, the probability model for the measured signal intensity m_ij is given by

$$pr(m_{ij}|s_{ij},{\sigma }_{\mathrm{r}})=\frac{m_{ij}}{{\sigma }_{\mathrm{r}}^2}\text{exp}\{\frac{-(m_{ij}^2+s_{ij}^2)}{2{\sigma }_{\mathrm{r}}^2}\left\}{I}_0\right(\frac{m_{ij}{s}_{ij}}{{\sigma }_{\mathrm{r}}^2}),$$ (4)

where σ_r is the Rician noise variance. We know that m̄_i is the sum of N Rician-distributed random variables, {m_ij, j = 1, …, J}. Under the assumptions that the noise is independent and identically distributed (i.i.d.) across all the lesion pixels, the signal-to-noise ratio (SNR) of each lesion pixel, i.e. s_ij/σ_r, is greater than 2.64 [9], [10] and the heterogeneity in the lesion is not very high, we can derive that pr(m̄_i) is normally distributed, and given by

$$pr({\mathrm{m̄}}_i|{\mathrm{s̅}}_i,{\sigma }_{\mathrm{r}},{\sigma }_i)=\sqrt{\frac{J}{2\pi {\sigma }_{\mathrm{r}}^2}}\text{exp}\{-\frac{{({\mathrm{m̄}}_i-{\mathrm{s̅}}_i-\frac{{\sigma }_i^2}{2{\mathrm{s̅}}_i})}^2}{2\frac{{\sigma }_{\mathrm{r}}^2}{J}}\},$$ (5)

where ${\sigma }_i^2$ is the sample variance of the lesion pixel intensities. The assumptions stated above were empirically validated on our dataset of lesion images.

The noise terms in the measurements at the different b values are independent of each other. Thus, we can write the complete probability model for M̄ as

$$pr(\mathbf{M̄}|\{{\mathrm{s̅}}_i,i=1,\dots ,N\},{\sigma }_{\mathrm{r}},\mathrm{\Sigma })=\prod _{i=1}^{N}pr({\mathrm{m̄}}_i|{\mathrm{s̅}}_i,{\sigma }_{\mathrm{r}},{\sigma }_i),$$ (6)

where Σ = {σ_i, i = 1, …, N}. Using Eq. (1), we substitute s̅_i to be K exp(−ab_i) in the above equation. Our objective is to compute the values of {a, K} that maximize the probability of M̄ given by Eq. (6). For computational efficiency, the logarithm of the probability is instead maximized. Upon simplifying, we determine that the ML estimates of {a, K} should minimize the log-likelihood function,

$$\lambda (a,K;\mathbf{M̄},\mathrm{\Sigma })=\sum _{i=1}^N{\{{\mathrm{m̄}}_i-K\text{exp}(-a{b}_i)-\frac{{\sigma }_i^2}{2K\text{exp}(-a{b}_i)}\}}^2.$$ (7)

III. Methods

A. In-Vivo Imaging and Implementation of the Algorithm

In the study at the Arizona Cancer Center, DWMRI is being used to monitor the therapeutic response in breast cancer patients with metastases to the liver [14]. Conventional T1 and T2-weighted imaging is performed at 1.5T, along with DW single-shot echo-planar imaging (DW-SSEPI) using b values of 0, 150, 300 and 450 s/mm². From the in-vivo study, we obtain a set of DW images for each lesion.

To determine the ADC of the lesion, the only inputs that our ML approach requires are M̄ and Σ. These quantities are obtained from the lesion images [20] and input to a quasi-Newton optimization technique [21] in MATLAB software to determine the values for a and K for which the maximum of the log-likelihood function (Eq. (7)) is obtained. We constrain this optimization to search only between reasonable values of the parameters. For the ADC value, we keep the initial guess of the ADC estimate as 2.0 × 10⁻³ mm²/s and the search space as between 0.1 to 5.0 × 10⁻³ mm²/s, to cover the range of values typically measured in-vivo [10]. The whole optimization task takes almost negligible time to run, and we thus have an easy-to-implement and computationally fast ADC estimator.

We cannot validate our algorithm using real data, since the true ADC value of the lesion is not known. Therefore, we instead perform Monte Carlo (MC) simulations to verify the accuracy of our algorithm. The dataset of lesion images obtained from in-vivo imaging is used in the MC study to determine the various parameters for lesion simulation.

B. Lesion Simulation and Experimental Setup

We simulate the DW data using Eq. 4 for b values of 0, 150, 300 and 450 s/mm², as in the in-vivo study. Both homogeneous and heterogeneous lesions are simulated. While simulating the lesion, we can vary the ADC value, the SNR, and the lesion size. We vary all these parameters based on the empirical values that we obtain from the dataset of real DW lesion images.

In every experiment, for a given ADC value, size and SNR of the lesion, we generate 100 instances of the lesion with different noise realizations. To quantify the performance of the ML and LR methods, we compute the ensemble mean square error (EMSE) between the true and estimated ADC values. The ESME is a common measure to quantify the performance of an estimation technique [19], and is defined as

$$\text{EMSE}=E\{{|â-a|}^2\},$$ (8)

where E{…} denotes the expected value of the quantity within the brackets and a and â denote the true and estimated ADC values, respectively. The expectation is over all noise and lesion-variations in the particular experiment.

IV. Experiments and Results

A. Homogeneous Lesion

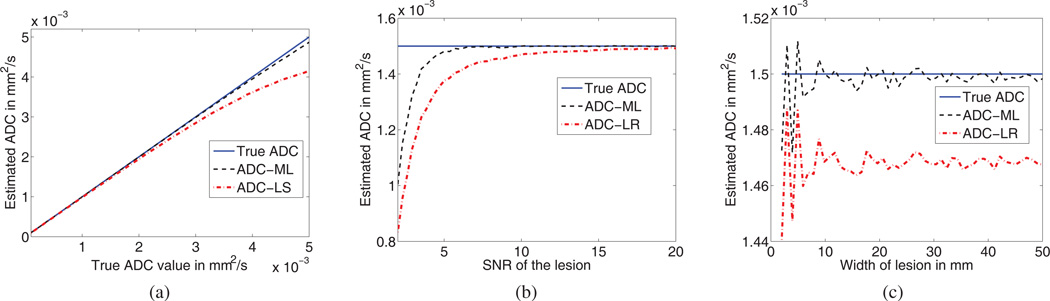
The set of experiments on homogeneous lesions were performed to study the performance of the ML and LR algorithms as the ADC value, the SNR and the size of the lesion were varied. In the first experiment, the ADC of the homogeneous lesion was varied between 0.1 × 10⁻³mm²/s and 5 × 10⁻³mm²/s [10]. The results of this experiment are shown in Fig. 1a. We observe that the ML approach is more accurate than the LR approach over the whole spectrum of possible ADC values of the lesion.

Fig. 1.

Comparing the accuracy of the ML approach with the LR approach for homogeneous lesions, as the (a) ADC (b) SNR and (c) size of the lesion is varied.

In the second experiment, the SNR of the lesion was varied, to study how the method performs as the standard deviation of the Rician noise in the DW images changes. The results of our experiment are shown in Fig. 1b. We observe that the ML approach is more accurate than the LR approach even when the SNR is low. This is an especially useful result, in light of the observation that typically DW images are low SNR images.

In the third experiment with homogeneous lesions, the width of the lesion was varied to account for different possible lesion sizes. The results of this experiment are shown in Fig. 1c. Again, the ML approach is more accurate than the LR approach over all lesion sizes.

The results of these three experiment are summarized in the first three rows of Table I. As the results show, the ML approach has the minimum EMSE for the three experiments.

TABLE I.

EMSE for the ML and LR estimation methods. The ADC is expressed in mm²/10³s.

Type of lesion	Parameter varied	ML	LR
Homogeneous	ADC	3.98	21.02
	SNR	4.36	8.68
	Size	3.48	5.26
Heterogeneous	ADC	11.20	22.60
	SNR	13.71	23.75
	Size	16.76	23.24

B. Heterogeneous Lesion

In the heterogeneous lesion model, the ADC values for the different pixels over the whole lesion are sampled from a normal distribution. The inspiration for this model is from the observation that in many studies [22], the histogram of ADC values of heterogeneous lesions typically form a Gaussian distribution.

In the first experiment, we varied the mean of the normal distribution of the ADC in the lesion from 1 × 10⁻³ mm²/s to 3 × 10⁻³ mm²/s. The standard deviation of the normal distribution was kept as 1 × 10⁻³ mm²/s. The second and third experiments were the same as the experiments for the homogeneous lesions in Sec. IV-A, except for the lesion being heterogeneous. The ADC of the different pixels were sampled from a normal distribution with mean 1.5 × 10⁻³ mm²/s and a standard deviation of 1 × 10⁻³ mm²/s. The results of these experiments are as summarized in the last three rows of Table I. We observe that the ML approach is more accurate than the LR approach for all the experiments.

V. Discussion and Conclusions

In visceral organs, a single ADC value of the lesion is computed. Currently an LR-based scheme is used for this purpose, but it suffers from various deficiencies. To solve this issue, in this paper, we have suggested a ML method that is based on the correct noise model in DWMRI, accounts for the heterogeneity in the lesion and also does not suffer from the other deficiencies of the LR method. In the process, we have derived the statistics of the mean signal intensity measurements in DWMRI. We have derived and implemented the ML method to estimate the ADC value of liver lesions. Also, we have performed a detailed MC study to compare the performance of the ML and LR methods for both homogeneous and heterogeneous lesions with different possible ADC values, SNRs and sizes. For the test cases, we have observed that the ML method is more accurate than the LR method.

The proposed ML algorithm is easy to implement and computationally fast. Often, slow computational speed and difficulty of implementation are significant impediments towards the practical use of an algorithm. Our ML method, while being accurate, takes almost the same execution time as the LR method. The ML approach is also convenient to use and does not require significant user interface. Segmenting the lesion using any semi-automated segmentation algorithm [20], [23] is sufficient to obtain all the required input data for the ML approach. The method does not require the user to mark a background region to obtain the Rician noise variance, as is required by some other methods [10], [12].

To summarize, we have derived, implemented and tested an ML approach to estimate the ADC value of lesions in visceral organs. The method is more accurate than the conventional LR approach, convenient to use, easy to implement and computationally fast. We are currently testing the performance of the ML approach with other heterogeneous lesion models.