Exciplexes versus Loose Ion Pairs: How Does the Driving Force Impact the Initial Product Ratio of Photoinduced Charge Separation Reactions?

Abstract

Many donor–acceptor systems can undergo a photoinduced charge separation reaction, yielding loose ion pairs (LIPs). LIPs can be formed either directly via (distant) electron transfer (ET) or indirectly via the dissociation of an initially formed exciplex or tight ion pair. Establishing the prevalence of one of the reaction pathways is challenging because differentiating initially formed exciplexes from LIPs is difficult due to similar spectroscopic footprints. Hence, no comprehensive reaction model has been established for moderately polar solvents. Here, we employ an approach based on the time-resolved magnetic field effect (MFE) of the delayed exciplex luminescence to distinguish the two reaction channels. We focus on the effects of the driving force of ET and the solvent permittivity. We show that, surprisingly, the exciplex channel is significant even for an exergonic ET system with a free energy of ET of −0.58 eV and for the most polar solutions studied (butyronitrile). Our findings demonstrate that exciplexes play a crucial role even in polar solvents and at moderate driving forces, contrary to what is usually assumed.

Photoinduced electron transfer (ET) reactions have been extensively studied for many years. This surge is motivated by the fact that ET is one the most fundamental, omnipresent elementary reactions in chemistry, physics, and biochemistry.¹⁻⁴ However, questions about the microscopic details of the quenching still remain, in particular, in solvents of low polarity. In these media, a photoexcited acceptor (A*) diffusively approaching a suitable electron donor (D or vice versa, i.e., D could be photoexcited) can be deactivated in a charge separation reaction either by forming a solvent-separated, loose ion pair (LIP) or by the formation of an excited-state charge-transfer complex (exciplex), which in the absence of intrinsic fluorescence emission is also referred to as a contact ion pair (CIP). While the LIP is formed at distances longer than or equal to the contact distance of A* and D, the exciplex formation typically involves tight stacking and a well-defined relative orientation,⁵⁻⁹ which can be inferred from the correlated motion of the donor and the acceptor in the complex.¹⁰ The solvent polarity strongly affects the quenching mechanism. In polar solvents, quenching occurs predominantly by distant ET, that is, by an ET process yielding directly the LIP. However, in nonpolar solvents, exciplex fluorescence is often observed, suggesting the contribution of the exciplex formation in the ET deactivation (the exciplexes can also result from secondary recombination of initially formed ion pairs; this question is addressed below).¹¹⁻¹⁸ Only a few exceptions to this empirical rule are known in the literature. For example, a CIP is dominantly formed by diffusive ET quenching of 9,10-dicyanoanthracene (DCA) by durene even in acetonitrile (quantum yield: 0.8).¹⁹

The primary quenching products are strongly affected by energetic parameters. The direct formation of free ions, partly at distances exceeding the contact distance, is expected to be significant for systems with larger driving force.^10,14,20,21 The experimental results for the DCA/durene system in acetonitrile indicated that with a free-energy change of ion formation of −ΔG^o_et = 0.25 eV, exciplexes are formed efficiently in the bimolecular quenching reaction from the AD* state, whereas in the case of 2,6,9,10-tetracyanoanthracene (TCA)/pentamethylbenzene (PMB) with −ΔG^o_et = 0.75 eV, an exciplex could not be detected.^22,23 Exciplex fluorescence was observed for several systems in acetonitrile when the −ΔG^o_et was in the range from −0.28 to +0.20 eV.^7,8 Yet, full ET is observed for the vast majority of donor–acceptor systems in acetonitrile.^7,8,13,23,24

Exciplexes, which are omnipresent in photochemistry, appear as intermediates in intra- and intermolecular photoinduced ET in solution.²⁵⁻²⁸ In general, exciplexes can be observed by their emission, which is, in the most favorable cases, spectrally well separated from the locally excited fluorescence.^11,19,23 Furthermore, under suitable conditions, this exciplex emission is sensitive to an external magnetic field.²⁹⁻⁴⁰ Magnetic field effects (MFEs) on exciplexes result from the interconversion of the singlet and the three triplet states of the radical ion pair (RIP) in equilibrium with the exciplex. The presence of an external magnetic field lifts the degeneracy of the three triplet states and, thus, reduces the rates of singlet–triplet conversion (S–T_±), which in these systems is induced by the hyperfine interaction (HFI).⁴¹⁻⁴⁵ This causes an increase of the population of the initial spin state in the presence of an external magnetic field. Due to the reversible conversion of the exciplex and the singlet RIP, the exciplex luminescence becomes magnetosensitive. Scheme 1 depicts a reaction scheme of the photoinduced ET processes of an exciplex-forming donor–acceptor system. The involved species can be uniformly described using a two-dimensional reaction coordinate, which comprises the interparticle distance and the solvent polarization expressed by the Marcus outer-sphere ET coordinate.³⁹ The horizontal arrangement of species in Scheme 1 corresponds to a curved trajectory on this two-dimensional reaction coordinate. The observation of the MFE on exciplexes is preceded by the formation of the singlet RIP, which can be formed via distant ET (1B; numbers are referring to reactions in Scheme 1) or by the dissociation of an exciplex (2) formed via reaction 1A. Note that the singlet and triplet RIPs can undergo charge recombination, yielding the ground state and the fluorophore triplet state, respectively. The singlet back ET to the ground state is typically located in the Marcus inverted region and, hence, is slow.⁴⁶⁻⁴⁸ Furthermore, because the exciplex dissociation is typically a slow process, the ions resulting from exciplex dissociation will be delayed with respect to the loose ions formed by direct ET. As a consequence, the MFE generated by the exciplex route will also be delayed. Thus, time-resolved studies of MFE of the exciplexes allow deduction of the initial quenching state (i.e., 1A versus 1B in Scheme 1). This methodology has been introduced in ref (40), and the interested reader is referred to this publication for additional details. There, a detailed study of the solvent polarity of the initial quenching products is given for a system with −ΔG^o_et = 0.28 eV. In the present work, we varied −ΔG^o_et in the range from 0.28 to 0.58 eV and the relative dielectric constant of the homogeneous solvent mixture of propyl acetate (PA)/butyronitrile (BN) in the range from 6 to 24.6. We have monitored the intensity decay of the exciplex luminescence in the presence and absence of an external magnetic field in time-resolved measurements and used a model allowing for reversibility between the exciplex and the RIP to simulate the experimental data. The driving force and solvent dependence on the mechanism of the fluorescence quenching reaction (1A versus 1B) were elucidated. We had expected that the most exergonic system deactivated exclusively via the LIP channel, in agreement with the discussion from above.

Scheme 1. Schematic Representation of the Species Involved in the MFE of the Exciplex Emission.

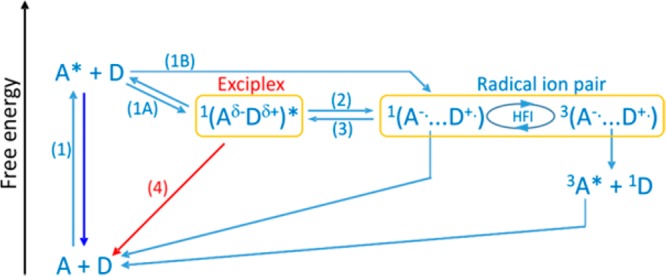
Photoexcitation (1), exciplex formation (1A), direct formation of the RIP via remote ET (1B), exciplex dissociation into RIPs (2), spin evolution by the HFI, re-formation of the exciplex from the singlet RIP (3), and exciplex emission (4). The blue and red arrows denote the (emissive) decay processes of either the locally excited fluorophore or the exciplex. The latter is detected in the experiment. Spin multiplicities are indicated by superscripts.

Solvent mixtures of PA (ε_r = 6) and BN (ε_r = 24.6) allow for a systematic variation of the relative dielectric constant ε_r in the range from 6 to 24.6 (295 K). The Pekar factor (1/n² – 1/ε_r = 0.459) of PA/BN mixtures, which governs the outer-sphere ET reorganization energy and, thus, the rate of ET processes, varies by only ±5% in the studied ε_r range.^1,3 The zero–zero energy E₀₀ is practically constant in the solvent mixtures used. For the studied donor–acceptor pairs, the driving force of the ET reaction −ΔG^o_et, the exciplex lifetime τ_E, and the zero–zero energy are reported in Table 1 (the solvent dependence of τ_E is illustrated in Figure S4 in the Supporting Information).

Table 1. Exciplex Lifetimes and Pertinent ET Parameters of the Studied Donor–Acceptor Systems^a.

A	D	E00/eV	–ΔGoet(εr = 13)/eV	τE (εr = 14)/ns	τE (εr = 22)/ns
Ant	DEA	3.29	0.58	20.5	5.9
MAnt	DEA	3.20	0.47	25.9	6.8
DMAnt	DMA	3.07	0.28	45.1	13.7

^aThe free-energy difference of ET −ΔG^o_et was calculated using the Rehm–Weller equation with Born correction assuming an interparticle distance of 6.5 Å⁴⁹ and an ion radius of 3.25 Å and ε_r = 13. The redox potentials of the compounds were taken from literature sources.⁵⁰ The lifetimes τ_E of the exciplex were extracted from the initial decay of the exciplex emission at ε_r = 14 and 22 in PA/BN mixtures. The 0,0 energy E₀₀ is practically independent of solvent composition in PA/BN mixtures. Abbreviations: Ant: anthracene; MAnt: 9-methylanthracene; DMAnt: 9,10-dimethylanthracene; DMA: N,N-dimethylanilne; DEA: N,N-diethylaniline.

Figure 1 depicts the absorption and emission spectra of anthracene in the absence and presence of N,N-diethylaniline. While the emission spectrum of the locally excited fluorophore is directly accessible from the spectrum in the absence of quencher, a model has to be employed to extract the exciplex emission,³⁹ for example, a sum of vibronic transitions with Gaussian band shape can be assumed.⁵¹

Figure 1.

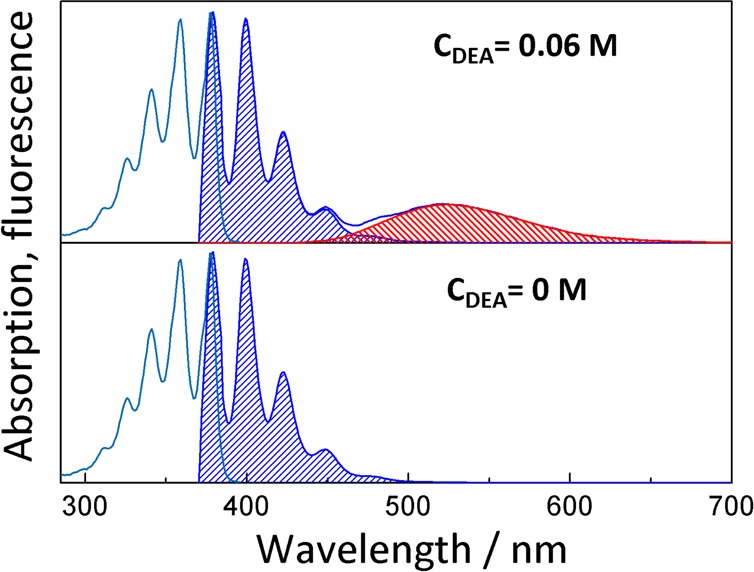
Absorption and emission spectra of anthracene in the absence (bottom) and presence (top) of 0.06 M N,N-diethylaniline. A mixture of PA/BN with a relative dielectric constant of ε_r = 12.1 was used as the solvent. The emissions of the locally excited fluorophore and the exciplex are shaded in blue and red, respectively.

When applying an external magnetic field (flux density B₀ = 62 mT), the delayed fluorescence intensity of the exciplex increases (see the Supporting Information for details on the steady-state measurements). Time-dependent measurements based on the time-correlated single photon-counting (TCSPC; a description of the experimental setup can be found in the Supporting Information) method reveal that all fluorescence time traces rise with a time constant of 1.8 ns, which, within the experimental error, is independent of the magnetic field. The decay kinetics are essentially nonexponential, reflecting the dissociation into solvent-separated ions and their recombination giving rise to a delayed component of the exciplex emission. This delayed component is enhanced upon exposure to an external magnetic field (see Figure 2 and Figure S1 in the Supporting Information). The difference in the exciplex fluorescence intensity ΔI(t) (lower panel in Figure 2) in the presence and absence of an external magnetic field is the time-resolved MFE (TR-MFE)

1

Here, I(t,B₀) and I(t,B₀ = 0) are time-dependent intensities of the exciplex in the presence and absence of an external magnetic field (upper panel in Figure 2). Prior to forming the difference according to eq 1, we matched the amplitudes of the two time traces within the first nanosecond after the excitation pulse, which is permissible on account of the fact that no significant MFE can be induced by the HFIs within this short time period. Integrating the time traces according to eq 2 with t_max exceeding the characteristic time scale of the MFE (formally t_max → ∞), the MFE χ_TR expected under steady-state conditions can be extracted from the time-dependent data

2

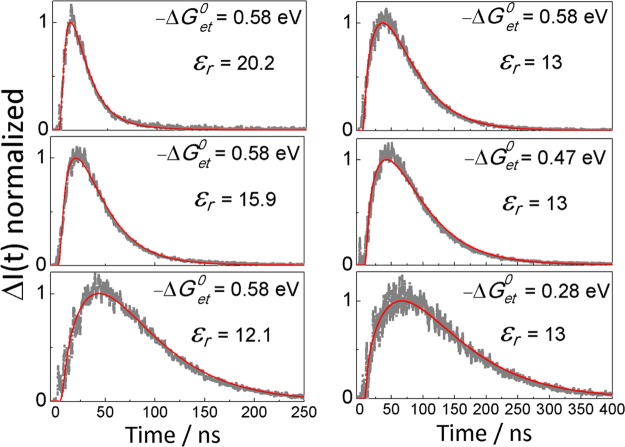
Here, t_max in the range from 250 to 500 ns was employed depending on the solvent polarity (see Figure 4 below).

Figure 2.

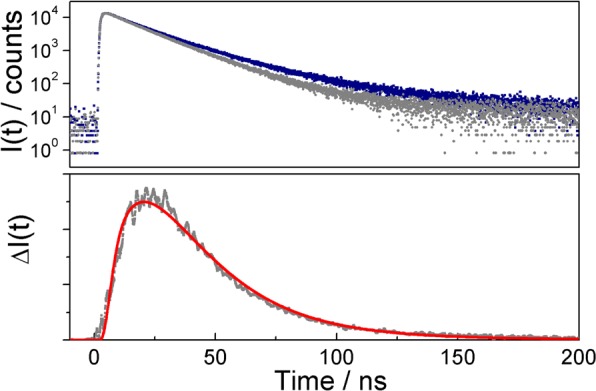
(Upper panel) Emission time trace corresponding to the exciplex of anthracene (2 × 10^–5 M) and N,N-diethylaniline (0.06 M) in a PA/BN mixture of ε_r = 15.9 in the absence (gray scatter plot) and presence (blue scatter plot) of a saturating external magnetic field (B₀ = 62 mT) observed with a 550 nm long-pass filter after excitation with a laser pulse at 374 nm. The delay fluorescence of the exciplex is enhanced in a saturating external magnetic field. (Lower panel) TR-MFE of the exciplex extracted from the experimental data (gray scatter plot) and its simulations (red, solid line).

Figure 4.

Experimental (gray scatter plots) and calculated (red solid lines) time-dependent MFEs. The left column shows data for the anthracene/N,N-diethylaniline system at different ε_r in PA/BN mixtures. The right column illustrates the driving force dependence of the TR-MFEs observed for the systems 9,10-dimethylanthracene/N,N-dimethylaniline (−ΔG^o_et ≈ 0.28 eV), 9-methylanthracene/N,N-diethylaniline (−ΔG^o_et ≈ 0.47 eV), and anthracene/N,N-diethylaniline (−ΔG^o_et ≈ 0.58 eV) at ε_r = 13.

The solvent dependence of the relative MFEs χ_TR as determined from the TR-MFE data by integration according to eq 2 is plotted in Figure 3 in comparison to χ_SS determined from steady-state measurements on an adapted fluorometer (see the Supporting Information for details).^38,39 Within experimental error, the two sets of MFEs agree, suggesting that all processes leading to the MFE under the experimental conditions indeed occur on a time scale smaller than t_max, that is, several hundred nanoseconds (for t_max → ∞, χ_TR and χ_SS naturally match). This finding emphasizes that bulk processes do not significantly contribute to the MFE under the employed experimental conditions and that it is appropriate to interpret the data in terms of isolated geminate RIPs.⁴¹ Bulk processes, for example, re-encounters of uncorrelated ions and processes involving fluorophore triplets (triplet–triplet pair or triplet–doublet pair processes), do not contribute significantly to the MFE. In fact, the experimental conditions have been chosen to minimize such effects (low light intensities and low fluorophore concentrations).

Figure 3.

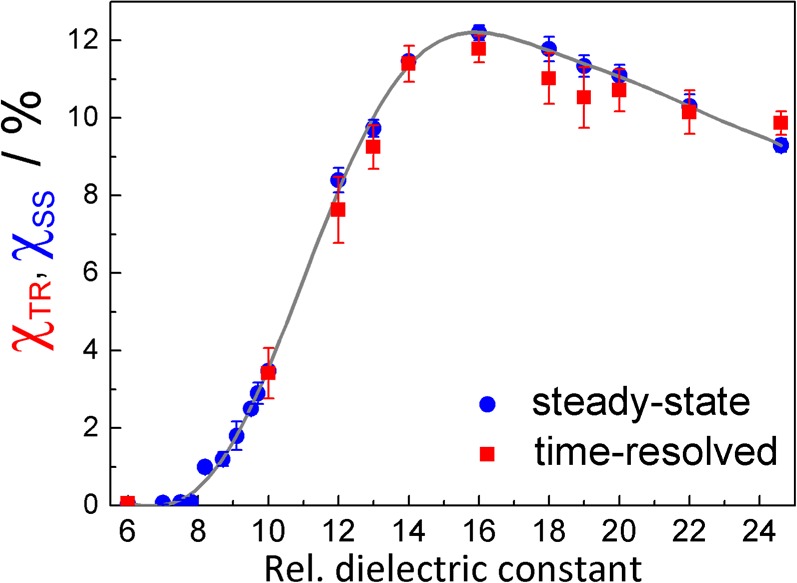
MFEs on the anthracene/N,N-diethylaniline exciplex determined from TR-MFE data using eq 2 (red filled squares) and from steady-state measurements (blue filled circles) in PA/BN mixtures of various relative dielectric constants ε_r.

As noted, the formation of RIPs via distant ET or via exciplex dissociation depends strongly on the properties of the solvent and the ET driving force. Figure 4 depicts the time-dependent MFEs at different relative permittivities and driving forces in PA/BN mixtures. The maximum of the TR-MFE occurs in the range from 10 to 70 ns after excitation, with the larger values occurring at lower permittivities and for the systems with a smaller driving force of ET, −ΔG^o_et. ΔI peaks at times where the delayed fluorescence contributes significantly and the intrinsic exciplex fluorescence is low. Thereafter, the effect decays and reaches the noise level of the experiment within 500 ns. Because the exciplex dissociation is usually a slow process, the ions resulting from the exciplex dissociation will be delayed with respect to those formed by direct ET. In solutions with higher polarity and more exergonic systems, the initial formation of RIP is favored. Thus, the TR-MFE reaches its maximum at shorter times.

The time evolution of the MFE depends on the parameters of the diffusive motion, the exciplex lifetime (τ_E), the exciplex dissociation quantum yield (ϕ_d = k_dτ_E, where k_d is the dissociation rate constant), the probability that the initial state (as prepared by the quenching reaction) is the LIP (ϕ_I; the probability that the initial state is the exciplex is thus 1 – ϕ_I), and the parameters governing the spin evolution (hyperfine coupling constants). Most of these parameters can be obtained from experiments or independently estimated. Making use of a model accounting for the exciplex dissociation, the spin evolution of the geminate pair, and its re-encounter⁴⁰ (see eq S1 in the Supporting Information), the parameter ϕ_I can be determined by fitting (in the least-squares sense) the theoretical model to the experimental MFEs. Figure 5 depicts the dependence of the dissociation quantum yield of the exciplex ϕ_d and the initial probability of the LIP state ϕ_I as a function of the relative dielectric constants of the solvent and the ET driving force for the systems studied. The ϕ_d values so obtained are close to those calculated from the dependence of τ_E on the solvent permittivity by assuming that for ε_r = 6, no exciplex dissociation occurs and that the radiative and nonradiative rates of the exciplex are constant within the polarity range studied.⁴⁰

Figure 5.

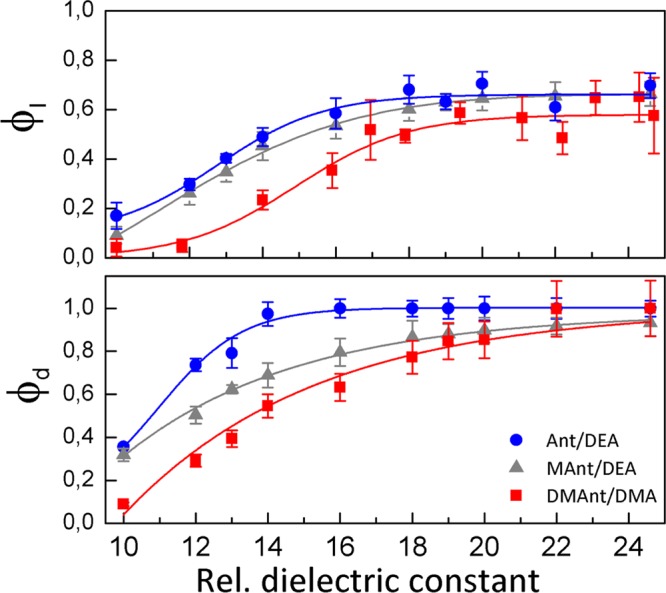
Solvent dependence of the initial probability ϕ_I of the LIP state (upper panel) and the dissociation quantum yield ϕ_d of the exciplex (lower panel) of the systems 9,10-dimethylanthracene/N,N-dimethylaniline (red filled squares), 9-methylanthracene/N,N-diethylaniline (gray filled triangles), and anthracene/N,N-diethylaniline (blue filled circles) in PA/BN mixtures. The solid lines provide a visual aid only; no physical model is implied.

From the data summarized in Figure 5, we infer that the exciplex quenching channel contributes at all studied permittivities, even for anthracene/N,N-diethylaniline, which exhibits the most exergonic ET among the systems studied (−ΔG^o_et ≈ 0.58 eV). As expected, the exciplex formation dominates at low permittivities (for ε_r < 15), and its significance increases with decreasing ET driving force. Interestingly, however, for all systems, ϕ_I levels off upon increasing the solvent dielectric constant (for ε_r > 15), and the exciplex channel contributes significantly even in neat BN (ε_r = 24.6). ϕ_d increases with increasing polarity of the solutions. At low polarity, the exciplex formation (pathway 1A in Scheme 1) is dominant. This is in qualitative agreement with the model introduced in ref (39), which predicts a more stabilized exciplex at low polarity of the solvent environment—essentially a consequence of the less shielded Coulomb interaction of A^– and D⁺ in low-permittivity solvents. The initial formation of the RIP is more favored in a polar solution, where the exciplex potential well is less pronounced and the excited-state population partly reacts through the LIP channel prior to assuming the well-defined mutual orientation necessary for forming the exciplex.

The fact that the direct formation of loose ions via full ET (pathway 1B in Scheme 1) is more significant for systems with larger ET driving forces is a consequence of the intrinsic ET rate constants increasing with driving force in the Marcus normal region.^52,53 Yet, even for the most polar solutions and the largest driving forces studied, the two types of ET reactions occur competitively. If the (long-distance) ET occurs faster than the diffusive approach of A* and D, the acceptor excited state is deactivated by full ET. On the other hand, if the diffusive approach giving rise to the favorable stacked configuration facilitating the exciplex is faster than the (more) distant ET process, the exciplex channel dominates. This also suggests that in solvents of comparable permittivity and ET parameters, the loose ion channel will gain significance with increasing solvent viscosity. Work along the lines of this supposition is underway. Apparently, for the low-viscosity solvent system studied here (η = 0.58 cP independent of composition), the diffusive approach to the stacking distance is fast enough for the exciplex formation to always contribute significantly, even for ε_r ≈ 20. Unfortunately, the approach detailed here cannot be easily extended to more polar solutions as a consequence of the low emissivity of the exciplexes/tight ion pairs at dielectric constants exceeding 25.

By systematically varying the solvent permittivity as well as the ET driving force and using a model that accounts for the initial charge-transfer state and the dissociation of the exciplex, we have been able to demonstrate that even in comparably polar solvents, a significant fraction of photoexcited donor–acceptor systems deactivates via direct exciplex formation instead of full charge transfer. For the studied systems, the initial RIP probability was always markedly less than unity. At low permittivities and less negative driving force (−ΔG^o_et ≈ 0.28 eV), the fluorescence is quenched predominantly by forming an exciplex. At higher polarity and for more exergonic charge separation processes, a LIP is the primary quenching product. Nonetheless, the exciplex formation remains important even for −ΔG^o_et ≈ 0.58 eV and ε_r = 24.6. While the relative importance of the LIP channel does increase with increasing driving force, we have only observed a very weak dependence of this kind. Even for the most exergonic system, the fraction of initially formed LIPs as a function of dielectric constant levels off at approximately 60%. This result shows that exciplexes play a crucial role even in polar solvents and at moderate driving forces, contrary to what is usually assumed (exciplex-only low-polarity solvents and driving forces below ∼0.4 eV). This conclusion has been reached based on TR-MFE data and the observation that the MFE originating from the exciplex (by dissociation into a RIP and its re-encounter) lags the MFE resulting from LIPs. We have thereby demonstrated that TR-MFEs on the exciplexes grant detailed insights into exciplex and RIP dynamics. The question of whether exciplexes can contribute to the charge separation process even in polar media is of relevance insofar as to date, no theoretical model is known that satisfactorily bridges the domains of diabatic, solvent-controlled outer-sphere ET and that of exciplex formation. The fact that the initial LIP fraction levels off with increasing solvent permittivity suggests that our findings extend to more polar solvents than are actually accessible by the current method, that is, well into the domain of polar solvent for which no exciplex emission is usually observable (already in BN, the exciplex emission amounts to only 0.2% of the original locally excited fluorophore emission at their respective maxima). This observation hints that CIPs could also be more relevant for the Rehm–Weller plot, where they could offer an explanation of one of the remaining paradoxes,^21,54−56 namely, the lacking reversibility of the ET for low driving forces. Clearly, this supposition is to be proven by methods other than that suggested here. In any case, it is clear that the microscopic details of the quenching step have important impacts on follow-up reactions of the transient species and, in particular, the efficiency of charge separation.

Supporting Information Available

Description of the experimental procedures and setups, additional spectra of emission decays and time-resolved MFEs, absorption and fluorescence spectra of 9,10-dimethylanthracene and 9-methylanthracene, a scheme of the TR-MFE setup, details of the computational methods, the solvent polarity dependence of the exciplex lifetimes of the studied systems, the solvent dependence of the association constant of the studied systems, and a compilation of the parameters used in the calculation of the results. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.