Beyond the functional matrix hypothesis: a network null model of human skull growth for the formation of bone articulations

Abstract

Craniofacial sutures and synchondroses form the boundaries among bones in the human skull, providing functional, developmental and evolutionary information. Bone articulations in the skull arise due to interactions between genetic regulatory mechanisms and epigenetic factors such as functional matrices (soft tissues and cranial cavities), which mediate bone growth. These matrices are largely acknowledged for their influence on shaping the bones of the skull; however, it is not fully understood to what extent functional matrices mediate the formation of bone articulations. Aiming to identify whether or not functional matrices are key developmental factors guiding the formation of bone articulations, we have built a network null model of the skull that simulates unconstrained bone growth. This null model predicts bone articulations that arise due to a process of bone growth that is uniform in rate, direction and timing. By comparing predicted articulations with the actual bone articulations of the human skull, we have identified which boundaries specifically need the presence of functional matrices for their formation. We show that functional matrices are necessary to connect facial bones, whereas an unconstrained bone growth is sufficient to connect non-facial bones. This finding challenges the role of the brain in the formation of boundaries between bones in the braincase without neglecting its effect on skull shape. Ultimately, our null model suggests where to look for modified developmental mechanisms promoting changes in bone growth patterns that could affect the development and evolution of the head skeleton.

Introduction

Craniofacial sutures and synchondroses articulate the bones of the human skull, forming boundaries that embody evolutionary, developmental and functional relations. Their presence or absence is used to identify homologous characters due to their deep evolutionary conservation (Hall, 1994; Depew & Simpson, 2006; Depew et al. 2008), their formation and obliteration timing are used to determine age in hominids (Cray et al. 2012; Falk et al. 2012), and their fibrous composition is important to distribute mechanical loads and stresses during the whole life of an individual (Herring, 2008). During ontogeny, the most important function of bone articulations in the skull is to act as primary bone growth sites (Opperman, 2000). For these reasons, suture formation is of particular medical relevance in humans, where disruption of normal suture patterns, for example due to premature fusion, often leads to malformations of the head and to brain injuries (Cohen & MacLean, 2000; Rice, 2008). In summary, insights on the development of suture patterns have broader applications in such disparate fields as taxonomy, functional morphology or pathological anatomy (Di Ieva et al. 2013).

Bone articulations in the human skull arise due to interactions between genetic and epigenetic factors that take place during skull late development (Moss, 2007; Sperber et al. 2010; Lieberman, 2011a). Epigenetic factors during suture formation are those originating not from the bone tissue itself, but from other tissues and cavities having a significant influence on the time, rate and direction of bone growth. The primacy of these epigenetic factors in skull development over autonomous genetic determination is the main claim of the functional matrix hypothesis (Moss & Young, 1960; Moss, 1968). Functional matrices include a variety of epigenetic factors, such as the presence of neighboring organs, surrounded cavities and the attachment of muscles, mediating in the morphogenesis of bones as well as their articulations to other bones in the skull (Lieberman, 2011a). According to this hypothesis, the position and shape of bones, as well as the formation of sutures, is fully determined by the functional needs of soft tissues and cavities that bones protect and support (Fig. 1). This hypothesis has been broadly used to explain many craniofacial disorders (Mulliken et al. 1989; Breitsprecher et al. 2002; Kikuchi, 2005) and some morphological features of the head (Festa et al. 2010; Richards & Jabbour, 2011), in particular the integration between brain growth and skull shape (Moss, 1975; Fields et al. 1978; Richtsmeier et al. 2006; Lieberman, 2011a; Richtsmeier & Flaherty, 2013). Other epigenetic factors that affect the formation of sutures include hormonal signals (Karsenty, 1999) and biomechanical mechanisms (Shwartz et al. 2012; Khonsari et al. 2013). In addition, external forces and movements related to functional matrices influence the internal complexity of sutures (Curtis et al. 2014).

Figure 1.

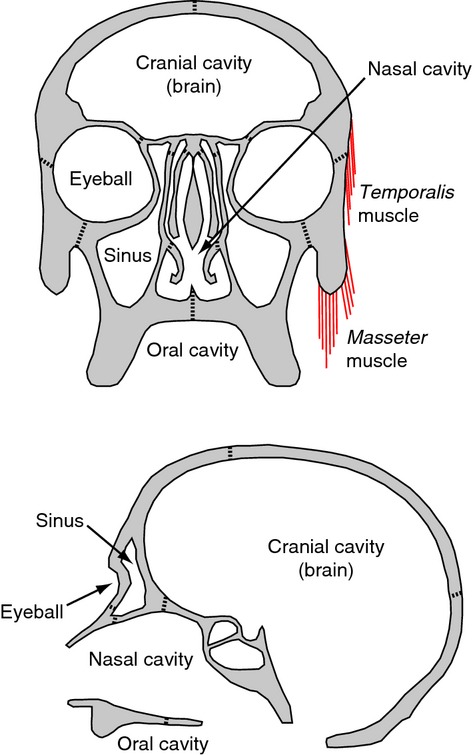
Schematic representation of functional matrices proposed for the human skull. Examples of functional matrices are the cranial cavity and the brain, the nasal cavity, the eyeballs, the maxillary sinuses, the oral cavity and head muscles, such as temporalis and masseter; these cavities and soft tissues have been suggested to mediate bone growth. Modified from Lieberman (2011a).

Despite the usefulness of the functional matrix hypothesis to explain the development and evolution of the human skull, several issues remain controversial (reviewed in Lieberman, 2011b; chapter 2). For instance, bones seldom participate only in one functional matrix and are influenced by many overlapping factors (Lieberman, 2011a). Consequently, studies on morphological integration and modularity that test for developmental modules in the skull often indicate that co-variation between skull parts blurs the boundaries among functional matrices (Cheverud, 1982; Sardi et al. 2004; Bastir et al. 2008; Singh et al. 2012). In addition, some morphological features of the human skull are invariant to the modification of the functional matrices they supposedly belong to (see Lieberman, 2011b; p. 53). Bone growth and suture formation, however, can take place even in the absence of brain growth or muscular activity (Nonaka & Nakata, 1984; Hirabayashi et al. 1988; Sugawara et al. 1999), probably due to cell-autonomous mechanisms (e.g. the Wnt regulatory network) that promote bone formation (reviewed in Zhang et al. 2009). As a result, the formation of boundaries among skull bones is a dynamical compromise between intrinsic genetic regulation of bone growth and the above-mentioned epigenetic factors.

The overall pattern of bone articulations has been formalized in studies about the morphological organization of the skull using anatomical network models (Rasskin-Gutman, 2003; Esteve-Altava et al. 2011; Rasskin-Gutman & Esteve-Altava, 2014). These models represent the bones and articulations of the skull as the nodes and connections of a network: 1s for presence and 0s for absence (Fig. 2). The entire skull is modeled using both the external and internal sutures among bones; this gives a precise description of how left and right counterpart bones connect to each other and to unpaired bones. In an evolutionary context, we used network models to quantify morphological complexity in tetrapod skulls, demonstrating that the reduction in the number of bones and articulations during evolution is a trend toward increase of morphological complexity (Esteve-Altava et al. 2013b, 2014; Esteve-Altava & Rasskin-Gutman, 2014). Using this approach we showed that the human skull is divided into two connectivity modules: one facial and one cranial (Esteve-Altava et al. 2013a). The facial module has a hierarchical organization composed of smaller blocks (i.e. groups of bones tightly interconnected) held together by the ethmoid, which acts as the bearing wall of the face. In contrast, the cranial module has a regular organization of connections, like the panels of a soccer ball. An independent analysis using geometric morphometrics demonstrated that these morphological modules also behave as units of allometric growth, thus suggesting that each module arises by different growth relations among bones (Esteve-Altava et al. 2013a). Therefore, because craniofacial sutures and synchondroses are sites of bone growth (Opperman, 2000), anatomical network models are also implicit models of growth relations (or co-dependences) among skull bones. The implication is that, even though these models are purely structurally defined, any statement about modularity and integration in anatomical network models in the skull is necessarily rooted in the dynamics of bone growth (Esteve-Altava & Rasskin-Gutman, 2014).

Figure 2.

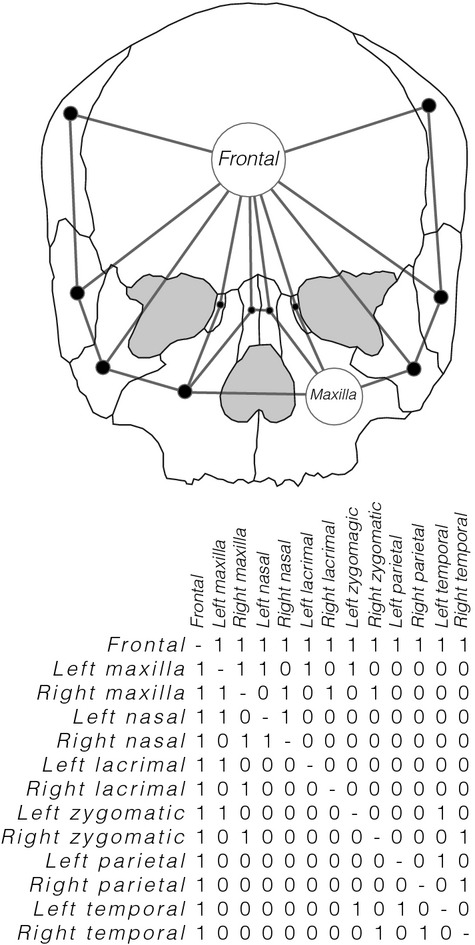
Simplified 2D example using only 13 bones of the abstraction process followed to build the human skull network (the actual 3D network has 21 bones and also captures internal articulations). The articulations among bones are coded as the connections among nodes in a network model in a binary adjacency matrix of presence (1) and absence (0) of articulation.

Here, we extend the use of anatomical network models by building an explicit null model to simulate the outcome of uniform, unconstrained growth for the formation of bone articulations in the human skull. By comparing bone connections in the null model vs. actual bone articulations in the human skull, we aim to test whether a particular bone articulation is either: (i) sufficiently explained by unconstrained bone growth; or (ii) necessarily explained by a specific modification of bone growth, presumably due to the induction of functional matrices. The proposed null model is based on geometric proximity assumptions, modeling the human skull as if it were a Gabriel network (Gabriel & Sokal, 1969). The Gabriel rule of linkage is used to formalize an idealized bone growth mechanism, in which bones grow in all directions with uniform speed – as if each node of the network was an ossification center that grows without constraints until it meets another growing edge, forming a bone articulation (Esteve-Altava & Rasskin-Gutman, 2014). Thus, the null model only predicts bone articulations that meet this primary assumption: uniform (in rate, direction and time) and unconstrained bone growth. For this reason, the null model will not predict bone articulations that arise due to changes in bone growth leading, for example, to irregular shapes, allometric growth or changes in the timing of ossification; this ensures that the null model is appropriate as a contrast model for the actual skull network. In this manner, this network null model (NNM) produces testable hypotheses about the modification of growth mechanisms acting specifically at each craniofacial suture and synchondrosis. Elucidating the nature and modification of these developmental mechanisms will need complementary empirical studies.

Materials and methods

A NNM of bone articulations

Our NNM of the human skull is a theoretical network in which we use the same number of bones as in the actual human skull, but nodes are connected following the Gabriel rule of linkage (Gabriel & Sokal, 1969) rather than using the actual connectivity pattern (Esteve-Altava et al. 2013a). The algorithm connects each pair of bones if, and only if, the sphere whose diameter is the line between both bones does not have any other bone within its volume. The input used to initialize the algorithm requires a set of spatial positions (i.e. 3D coordinates) for each bone. However, using the coordinates of the centroid for each bone would provide a tautological answer to the question we are asking. Instead, we have used the overall connectivity of the skull to calculate a virtual position for each bone, which renders coordinates for each bone position as related to the growth dependences it establishes with all others. To do this, we have performed a non-metric multidimensional scaling of the topological overlap (TO) similarity matrix of the human skull network (see Yip & Horvath, 2007 as an example of this type of approach in genetic networks). The Kruskal normalized stress index (Kruskal & Wish, 1978) was used to find the optimal number of dimensions (optimal dim = 3, stress = 0.06) of the virtual space that includes the bones of the human skull. These dimensions resemble the three body axes: anteroposterior, left–right and dorsoventral, forming a virtual space in which the coordinates of each bone are positioned.

What this means in biological terms is that we translate the growth relations among bones of the human skull network (Esteve-Altava et al. 2013a) into a set of relative positions of bones; as a consequence, distances among bones in the null model depend on sharing growth relations with the same neighboring bones. Because the main assumption of the model is that bone growth is uniform, these distances determine the connections among bones in the NNM. Therefore, we have used the TO (i.e. a measure of the number of common neighbors for each bone) as a proxy for the growth co-dependences among bones due to the spatial constraints imposed by each bone–bone articulation (Esteve-Altava et al. 2013a). The non-metric multidimensional scaling carries out isotonic regressions of the TO similarity matrix; this scaling technique is a non-parametric monotonic transformation that converts pairwise node (bone) similarity into Euclidean relative distances between two nodes within a virtual space (Borg & Groenen, 2005). Thereby, topological similarity among bones (size N × N) is scaled into virtual spatial coordinates of bones (size N × 3). The virtual position thus computed for each bone is used as the input of the Gabriel algorithm to build the NNM of the human skull. To further illustrate this method, we show a 2D toy example for only 10 bones, along with a simplified illustration of how an unconstrained model of growth determines bone connections in a NNM (Fig. 3).

Figure 3.

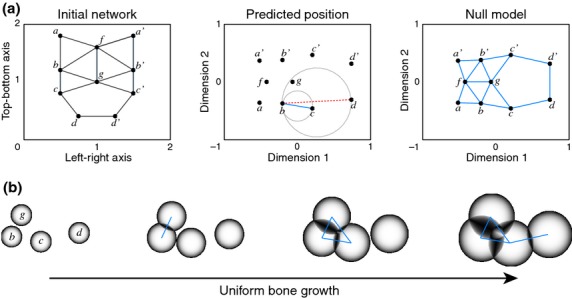
Two-dimensional toy example of the null model construction process for a 10-bone network intentionally connected using the Gabriel rule, in order to show the validity of the approach. (a) From an initial network model (left diagram) we measure pairwise bone similarity by their TO, which estimates common growth co-dependences among bones. A non-metric multidimensional scaling of these similarities yields a predicted virtual position for each bone (central diagram). Then, the Gabriel rule is applied to each pair of bones to establish whether they are connected or not; gray circles indicate how to apply the Gabriel rule to evaluate, for example, if bone b will be connected to bone c and/or d. In this case, bone b connects to bone c because there are no other bones within the circle; in contrast, bone b does not connect to bone d because bones c and g are situated within the circle. Thus, the Gabriel rule can be interpreted as the result of unconstrained bone growth (i.e. uniform rate, direction and timing) from the virtual position assigned to each bone. Finally, we obtain a null network model (right diagram), which can be compared with the actual network of the left diagram. Note that the dimensions of the virtual positions do not necessarily have the same scale and orientation as in the actual space, but all connections have been predicted correctly, as expected. Solid blue lines represent bone articulations predicted in the NNM; the dashed red line represents an example of a failure to establish a connection by the Gabriel rule. (b) Sequence illustrating the model of unconstrained growth in the vicinity of bone c; connections between two bones are established when the growing fronts meet. Nodes b, c, d and g in (b) refer to the same nodes in (a).

Analysis of the NNM

The organization of the NNM has been analyzed in order to compare it with that reported for the human skull (Esteve-Altava et al. 2013a). This was done to verify that the properties of the NNM were indeed like those of the actual human network, further ensuring its usefulness as a baseline comparative model. Thus, we have compared to what extent both networks were similar in: (i) structural complexity; (ii) hierarchical organization; and (iii) modularity. To do that it is necessary to compute a series of parameters, which we explain in detail below.

First, to analyze the complexity of the NNM we have quantified the following three parameters: density of connections (D), which quantifies the number of existing bone connections with respect to the maximum possible; mean clustering coefficient (C), which quantifies the arithmetic mean of the number of existing connections among the neighbors of each bone with respect to the maximum possible; and mean shortest path length (L), which quantifies the arithmetic mean of the number of connections required to interconnect any two bones in the network (for algorithm descriptions see Data S1).

Second, to evaluate the hierarchy (i.e. nested aggrupation of bones) of the NNM we have quantified the following parameters: connectivity distribution, P(k); and clustering coefficient distribution, C(k). The P(k) is the frequency of nodes with k connections, and the C(k) is the mean clustering coefficient of nodes with k connections; for practical reasons, we will use the cumulative P(k) in order to avoid statistical fluctuations due to a small number of nodes (Dorogovtsev & Mendes, 2003). Theoretically, the P(k) and C(k) in hierarchical networks should fit a power-law distribution, an instance of the Pareto distribution (Newman, 2005); in random networks, the P(k) fits a Poisson distribution and the C(k) is independent of the number of connections; and, in scale-free networks, the P(k) fits a power law and the C(k) is also independent of the node connectivity (Ravasz & Barabási, 2003; Wuchty et al. 2006).

Third, to identify meaningful morphological modules in the NNM, we have verified the presence of a small-world organization (Esteve-Altava et al. 2011, 2013a). This is so because the organization of connections in a small-world network lies somewhere between regularity and randomness (Watts & Strogatz, 1998); the heterogeneous patterns of connections in small-world networks promote the formation of modules (i.e. some nodes have more connections among themselves than to other groups of nodes). We have previously determined that the human skull network is small world and that it has two meaningful modules (Esteve-Altava et al. 2013a); in contrast, regular networks are not modular, whereas random networks can have modules by chance. To verify the presence of a small-world organization, we compared the clustering coefficient, C, and the shortest path length, L (described above), of the NNM with those of 10 000 random equivalent networks, which have the same number of nodes and connections but are rearranged at random. A network is small world if it fulfills the SW condition (Humphries & Gurney, 2008): (C/C_rand)/(L/L_rand) ≥ 0.012n^1.11, where C_rand and L_rand are the computed parameters for the random networks. Therefore, the NNM (with n = 21) will be small world if SW is greater or equal to 0.35.

To further characterize the modular structure of the NNM, we have carried out a hierarchical cluster analysis of the TO similarity matrix (Ravasz et al. 2002; Li & Horvath, 2007; Yip & Horvath, 2007). The TO between two bones is a measure of the number of shared connections to the same other bones (Esteve-Altava et al. 2013a): if TO = 1, two bones share all connections to the same other bones; if TO = 0, two bones lack common connected neighbors. Heuristically, we know that elements sharing connections to the same neighbors will tend to belong to the same module (Solé et al. 2006). This justifies the use of the TO similarity matrix as the input of a hierarchical cluster analysis; when performing this analysis, pairs of bones with higher TO will be grouped together in single branches until all bones form one single group and the outcome can be conveniently shown as a dendrogram. Each potential partition in the dendrogram is evaluated by quantifying an index of modularity (Q), which measures the strength of the modular organization in comparison to other possible random partitions (Newman & Girvan, 2004). The partition with the highest Q will identify the composition of each connectivity module in the NNM. The result of this analysis yields connectivity modules that are groups of bones with more connections among themselves than to other bones outside the group.

Further descriptions of network parameters and methods used in this study are available as Supplementary Information (see also Esteve-Altava et al. 2011, 2013a,b2013b; Esteve-Altava & Rasskin-Gutman, 2014). All algorithms have been scripted in Matlab.

Results

The NNM and the human skull network share the same basic organizational properties regarding their structural complexity, hierarchy and modularity. This similarity supports the use of the NNM as a baseline comparative model for the human skull; as expected by the assumptions, the null model and the human skull differ in the values for each network parameter.

Comparing their structural complexity (Fig. 4), the NNM has lower density of bone articulations (D = 0.25), lower clustering coefficient of bones (C = 0.51) and higher shortest path length among bones (L = 1.95) than the human skull (D = 0.3, C = 0.63, L = 1.74). Still, the values of C and L of the NNM are different from those expected in random equivalent networks (SW = 1.72), which indicates the presence of a small-world organization (SW ≥ 0.35). Regarding their hierarchical organization (Fig. 5), the NNM has an exponential P(k) (r = 0.95) and a power-law C(k) (r = 0.82), while both distributions fit a power law in the human skull (r = 0.98 and r = 0.89, respectively). These results indicate that both share similar hierarchical organizations.

Figure 4.

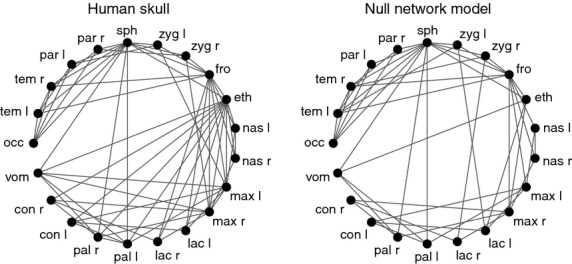
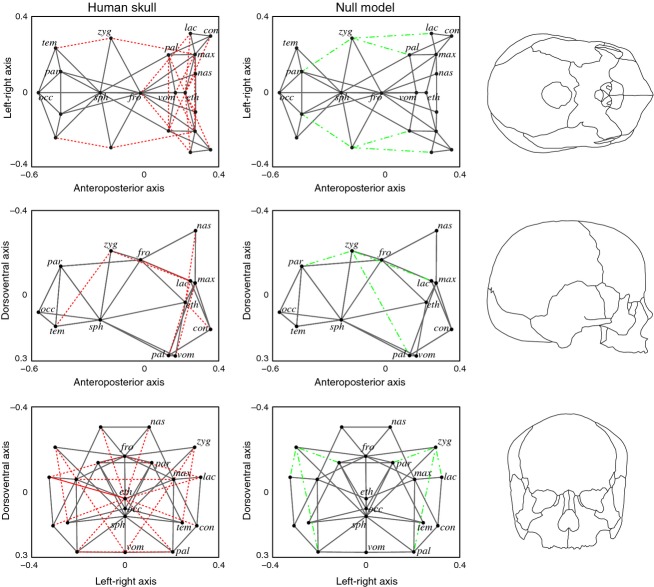
Circular representation of the human skull network and the NNM. In general, bones in the NNM are less connected than in the human skull; the most extreme case is the ethmoid, with 5 vs. 13 connections, respectively. Missing connections do not form in the NNM precisely because they deviate from the main assumption of the model: unconstrained bone growth. Labels: occ, occipital; tem, temporal; par, parietal; sph, sphenoid; zyg, zygomatic; fro, frontal; eth, ethmoid; nas, nasal; max, maxilla; lac, lacrimal; pal, palatine; con, inferior nasal concha; vom, vomer; l, left; r, right.

Figure 5.

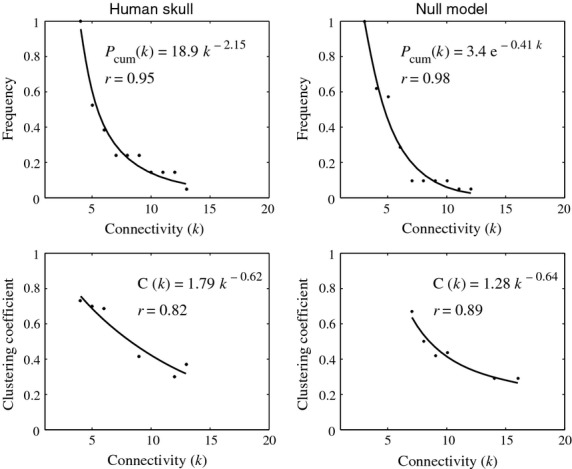
Connectivity distribution, P(k), and clustering coefficient distribution, C(k), of the human skull and the NNM. In the human skull network, P(k) and C(k) follow a power-law function, a type of right-skewed distribution in which a few bones have many connections and form many triangular motives, however many bones have few connections and participate in few triangular motives (Esteve-Altava et al. 2013a). In the NNM, the P(k) and C(k) also follow very similar right-skewed distributions, exponential and power law, respectively, which also indicate the presence of a hierarchical organization of bone connections.

Comparing their modularity (Fig. 6), the NNM shows a division in four modules (Q_max= 0.28): (i) left facial, composed of left palatine, lacrimal, nasal concha and maxillary bones; (ii) right facial, composed of right palatine, lacrimal, nasal concha and maxillary bone; (iii) central facial, composed of frontal, ethmoid and nasal bones; and (iv) cranial, composed of vomer, sphenoid, occipital, parietal, temporal and zygomatic bones. In contrast, the human skull is divided into two connectivity modules (Q_max= 0.27): (i) facial, composed of ethmoid, frontal, nasal conchas, lacrimals, maxillas, nasals, palatines and vomer; and (ii) cranial, composed of occipital, parietals, sphenoid, temporals and zygomatics. However, the four connectivity modules in the NNM still indicate a separation between facial and cranial regions; the formation of four modules instead of two is due to differences between predicted connections in the NNM and realized articulations in the human skull.

Figure 6.

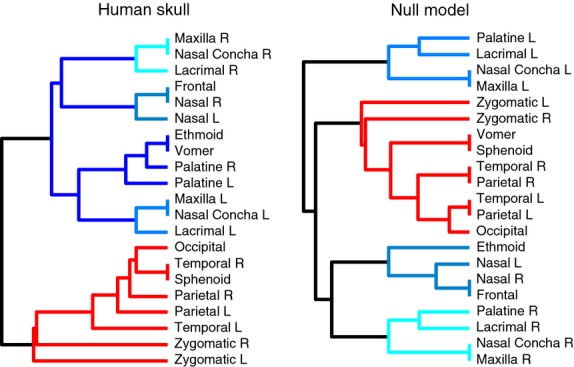
Connectivity modules identified in the human skull and the NNM. The general partition into cranial and facial modules is similar to the human skull network (Esteve-Altava et al. 2013a); however, in the null model, the unique facial module found in the human skull is split into three smaller modules. The connectivity modules in the NNM still support a separation between facial and cranial regions; the main difference being the bones that form each module, which is a consequence of differences between predicted connections in the NNM and realized articulations in the human skull.

A one-to-one comparison between predicted and realized articulations shows that most of them (72%) can be predicted correctly (Fig. 7, solid gray lines); therefore, these articulations are sufficiently explained using unconstrained bone growth as in the null model. The role of the functional matrices in the formation of these bone–bone articulations would be, at most, concomitant to a uniform growth of bones. In general, the NNM predicts well those articulations among bones in the cranial connectivity module: among sphenoid, occipital, temporal, parietal and zygomatic bones; but not the zygomaticotemporal suture. In contrast, facial articulations are less predictable by the NNM: (i) some involve the zygomatic bones; (ii) some connect maxillary and palatine bones in the midline; and (iii) some connect unpaired and paired bones within the face (Fig. 7, red dotted lines). Finally, the NNM predicts some connections that are absent in the actual human skull (Fig. 7, green dashed lines) whose formation would necessarily imply modifying bone growth patterns.

Figure 7.

Bone–bone articulations in the human skull and the NNM. In solid gray, predicted articulations by the NNM that occur in the actual human skull; in dotted red, non-predicted articulations by the NNM that occur in the actual human skull; in dashed green, predicted articulations by the NNM that are not realized in the actual human skull. Bones have been positioned in this virtual space according to their TO similarity and then connected according to the Gabriel rule in the NNM. The relative position of bones in the virtual space resembles the actual relative position of bones in the skull. We show each view with an actual skull outline. See labels in Fig. 4.

Discussion

The overall pattern of bone articulation of the null model is organized as in the human skull. Similarly to the actual skull (Esteve-Altava et al. 2013a), the NNM has a complex pattern of connections among bones, further characterized by a particularly interesting organization between randomness and regularity. Moreover, many bones have few articulations, while a few have many articulations; these highly connected bones participate in many more clusters (i.e. motifs of three interconnected bones) than the poorly connected ones. In addition, the NNM also has a modular organization of bones that discriminates between bones of the anterior facial region (facial connectivity modules) and the posterior cranial region (cranial connectivity module). Sharing such similarity of morphological organization supports the use of the NNM as a comparative baseline to explore the formation of craniofacial articulations in the human skull. In the following sections we compare both networks to analyze how functional matrices (i.e. cavities and soft tissues that mediate bone growth) differentially affect each bone–bone articulation.

Influence of functional matrices on the formation of facial sutures

The presence of functional matrices is especially important in the human face; these functional matrices include the oral cavity, the nasal cavity, the maxillary sinuses, the eyeballs and the masticatory muscles (Moss & Salentijn, 1969a,b1969b). At the same time, most differences in bone articulation between the null model and the human skull occur among facial bones, or bones of the cranial module that contact with facial ones such as the zygomatics. Indeed, the human skull deviates from the null model largely due to differences in the boundaries of the zygomatic bones.

On the one hand, zygomatic bones articulate to parietal and lacrimal bones in the null model, but these articulations do not occur during the development of the human skull. These articulations are wrongly predicted by the NNM precisely because the model does not take into account any constraints or local signals for non-uniform bone growth. Thus, our model suggests that, indeed, the growth of these bones must be constrained by external epigenetic factors. According to the functional matrix hypothesis (Moss, 2007), these factors could be the eyeball as well as the muscles that pass through the zygomatic arch (e.g. temporalis) and those attached to it (e.g. masseter). Together, the eyeball and the muscles of the zygomatic arch would modify greatly the morphology of the zygomatic bone preventing the articulation of the zygomatic to the lacrimal and the parietal bone. Furthermore, this key role of epigenetic factors mediating zygomatic morphology is further suggested by the observation that the absence of normal muscle contraction during late embryo development leads to different zygomatic deformations (Hall, 2010). The null model also predicts a connection between zygomatic and palatine bones that is absent in the human skull. This articulation is prevented by the presence of the maxillary bone, which fills the space between zygomatics and palatines rapidly due to its faster maturation rate (Buschang et al. 1983; Enlow & Hans, 1996; Bastir et al. 2006) and participates in the expansion of the sinus capsule (Moss & Greenberg, 1967; Smith et al. 2010). On the other hand, the null model does not predict the articulations of zygomatics to temporal and maxillary bones that naturally occur in the human skull. These bones would have to grow non-uniformly in order to establish these articulations. The same functional matrices that prevented the formation of articulations of the zygomatic to the lacrimal, parietal and palatine (i.e. eyeball, passing and attached muscles, and the expansion of the maxillary bone) might be responsible now for the particular irregular shape of the zygomatic that indeed allows its articulation with the temporal and maxillary bones.

Another group of articulations that the null model does not predict are midline connections between left and right maxillary and palatine bones, which make the hard palate of the skull. Thus, these articulations are not sufficiently explained by an unconstrained bone growth. Several forces would have to play a role for their formation; for example, by the nasal and oral cavities pushing these two bones to grow toward the midline in order to separate both functional spaces (Moss & Greenberg, 1967; Marazita & Mooney, 2004; Lieberman, 2011a).

Finally, the null model does not predict some articulations between unpaired and paired bones: frontal to lacrimals; vomer to maxillas; and ethmoid to inferior nasal conchas, lacrimals, nasals and palatines. All these bone articulations are structurally related to the organization of the facial skeleton surrounding the nasal cavity and the olfactory bulbs; thus, functional matrices are necessarily involved in the formation of these articulations as well (Bastir et al. 2011; Singleton, 2012).

Influence of bone growth relations on the formation of cranial sutures

In contrast to what happens in the facial skeleton, the null model successfully predicts most articulations among the bones of the braincase, which mainly occur within the cranial connectivity module (Esteve-Altava et al. 2013a). In accordance with the main premise of the null model, this result suggests that the sutural pattern in the braincase can emerge due to an unconstrained and uniform growth dynamics, that is, no additional processes need to be involved. In addition, this type of growth would also explain why the cranial connectivity module has a characteristic regular arrangement of bones (Esteve-Altava et al. 2013a). Furthermore, the only two bones showing exactly the same pattern of articulation in both networks, both in number and neighbors, are the sphenoid and the occipital. These two bones form the core of the cranial base, which has been reported as an evolutionary conserved developmental unit in tetrapods (McBratney-Owen et al. 2008). Moreover, this regular pattern of cranial sutures is also present in fishes such as the zebrafish (Quarto & Longaker, 2008). This result suggests that functional matrices nearby, such as the brain, do not constrain the establishment of their articulations, even though the shape and orientation of the cranial base in primates is highly integrated to facial size and cranial encephalization (Bastir et al. 2010; Bruner et al. 2014).

The brain and its dura mater are broadly recognized as epigenetic factors participating in the formation and maintenance of cranial sutures, as well as the shape of the cranial vault (Moss & Young, 1960; Smith & Tondury, 1978; Richtsmeier et al. 2006). Their prevalence, even over other epigenetic factors such as muscular movements and osteogenesis vs. apoptosis regulation (Pritchard et al. 1956; Ten Cate et al. 1977) is deeply rooted in mainstream explanations of the biology of craniofacial development and evolution (Lieberman, 2011b). However, brain size and cranial vault shape have co-evolved in hominins (Neubauer et al. 2009; Zollikofer & Ponce de Leon, 2010), suggesting that each influences the other's size and shape (Bruner, 2004; Bastir et al. 2011; Lieberman, 2011a). Indeed, evidence from studies on craniosynostosis suggests that the skull and the brain are so tightly integrated that there is no dominance of one over the other in shaping the final phenotype (Aldridge et al. 2005). Our conclusions regarding the lack of need to invoke extra forces to form the sutural pattern of the braincase might be seen as controversial. However, this conclusion by no means entails that other necessary forces imposed by the brain and related functional matrices have no effect in head development (Opperman et al. 1996; Morriss-Kay, 2001). Thus, processes of unconstrained bone growth would sufficiently explain articulations among neuro- and basicranial bones, whereas the growing brain would account for shape changes in cranial base and vault (Richtsmeier & Flaherty, 2013).

Conclusion

We have presented here a network growth model for the formation of bone–bone boundaries in the human skull, which has been built using information on growth co-dependences among bones captured in the anatomical network model of the human skull (Esteve-Altava et al. 2013a). This null model is indeed a simplification of the actual skull development in mammals, where two or more ossification centers fuse into individual bones during growth (Sperber et al. 2010, chapter 6), the timing of ossification of the face and the braincase is decoupled (Koyabu et al. 2014), and the growth of some bones is biased by the active presence of functional matrices, as we have shown here. We have focused our anatomical network analysis on our simplified model, which is able to correctly show more than two-thirds of the sutures of the human skull; thus, the model suggests that those articulations can be sufficiently explained by a process of unconstrained bone growth. We will develop, in future work, a model of growth that will include the multiplicity of ossification centers, as well as their dissociated developmental timing, in order to extend the use of anatomical networks to fully model head development. For the same reason, we are presently working on extending skeletal networks to include soft tissues, such as muscles and tendons, in order to cover more complex problems in head development using the anatomical network analysis framework.

In summary, our results suggest that the formation of bone articulations in the braincase does not need the concurrence of any other developmental process modifying bone growth, such as functional matrices; however, the influence of functional matrices during head development is necessary to form the articulations among facial bones surrounding functional spaces or acting as muscular attachments. In an Evo-Devo context, our results agree with the presence of two skull developmental modules (facial vs. basicranial), which show semi-independent allometric growth patterns (Esteve-Altava et al. 2013a), and decoupled patterns of heterochrony in bone ossification in mammals (Koyabu et al. 2014). We are aware that our conclusions underplay the role of functional matrices as sole actors to fully explain craniofacial skeleton development. We hope that these findings will motivate new experimental and theoretical studies on the role of genetic and epigenetic factors in the evolution and development of the head skeleton.

Supporting Information

Additional Supporting Information may be found in the online version of this article:

Data S1. Supporting methods.