Models of population-based analyses for data collected from large extended families

Abstract

Large studies of extended families usually collect valuable phenotypic data that may have scientific value for purposes other than testing genetic hypotheses if the families were not selected in a biased manner. These purposes include assessing population-based associations of diseases with risk factors/covariates and estimating population characteristics such as disease prevalence and incidence. Relatedness among participants however, violates the traditional assumption of independent observations in these classic analyses. The commonly used adjustment method for relatedness in population-based analyses is to use marginal models, in which clusters (families) are assumed to be independent (unrelated) with a simple and identical covariance (family) structure such as those called independent, exchangeable and unstructured covariance structures. However, using these simple covariance structures may not be optimally appropriate for outcomes collected from large extended families, and may under- or over-estimate the variances of estimators and thus lead to uncertainty in inferences. Moreover, the assumption that families are unrelated with an identical family structure in a marginal model may not be satisfied for family studies with large extended families. The aim of this paper is to propose models incorporating marginal models approaches with a covariance structure for assessing population-based associations of diseases with their risk factors/covariates and estimating population characteristics for epidemiological studies while adjusting for the complicated relatedness among outcomes (continuous/categorical, normally/non-normally distributed) collected from large extended families. We also discuss theoretical issues of the proposed models and show that the proposed models and covariance structure are appropriate for and capable of achieving the aim.

Introduction

In studies of large families, the family structures are usually complex and different, and the individuals may relate to each other in a range of ways. There may be considerable scientific value in assessing population-based associations of diseases with risk factors and estimating population characteristics such as disease prevalence and incidence in addition to testing genetic hypotheses. Since observations on family members are correlated, these results need to be adjusted. The commonly used adjustment method for relatedness in population-based studies is to use marginal models [1–3], in which clusters are assumed to be independent with a simple and identical covariance structure. In applying a marginal model to family data, clusters become families, and the assumption that clusters are independent with an identical covariance structure implies that families are unrelated with an identical family structure. For example, let y_ij denote an observed disease status (y_ij = 1, if diseased, and = 0, otherwise) of the jth member from the ith family, i = 1, 2, …, N; j = 1, 2, …, m. Then, the following marginal model is usually applied to assess population-based association of prevalence or cumulative incidence of the disease with its risk factors/covariates x₁, …, x_p,

$$\text{log}\left(\frac{P(y_{ij}=1)}{1-P(y_{ij}=1)}\right)={\beta }_0+{\beta }_1{x}_{ij1}+{\beta }_2{x}_{ij2}+\cdots +{\beta }_p{x}_{ijp},i=1,2,\dots ,N;j=1,2,\dots ,m,$$

where coefficients β₀, …β_p are unknown parameters, and the covariance/correlation structure among y_ijs from a family is assumed to be the same across all families and to follow some simple structures. The most often used covariance/correlation structures defined in the marginal model are the independent, exchangeable and unstructured structures [1, 2] (they have been accommodated in many statistical software packages such as SAS Process GENMOD, SAS software, SAS Institute, Cary, NC).

The independent and exchangeable correlation structures defined in the marginal model have the following forms:

$${\mathbf{R}}_{\mathit{\text{independent}}}=\left(\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)\text{and}{\mathbf{R}}_{\mathit{\text{exchangeable}}}=\left(\begin{array}{cccc}\hfill 1\hfill & \hfill r\hfill & \hfill \cdots \hfill & \hfill r\hfill \\ \hfill r\hfill & \hfill 1\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill r\hfill \\ \hfill r\hfill & \hfill \cdots \hfill & \hfill r\hfill & \hfill 1\hfill \end{array}\right).$$

On the other hand, if an extended family with, say, 8 members, is recruited based on “core sibs” in a family study and the 8 members are ordered as {father of core sibs, mother of core sibs, spouse of core sib 1, spouse of offspring 1 of core sib 1, core sib 1, core sib 2, offspring 1 of core sib 1, offspring 2 of core sib 1}, then the correlation matrix for outcomes collected from the 8 members should have the following form

$${\mathbf{R}}_{\mathit{\text{extended}}}=\left(\begin{array}{cccccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill *\hfill & \hfill *\hfill & \hfill \$\hfill & \hfill \$\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill *\hfill & \hfill *\hfill & \hfill \$\hfill & \hfill \$\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill *\hfill & \hfill *\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill *\hfill & \hfill *\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill *\hfill & \hfill *\hfill & \hfill *\hfill \\ \hfill *\hfill & \hfill *\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill *\hfill & \hfill 1\hfill & \hfill \$\hfill & \hfill \$\hfill \\ \hfill \$\hfill & \hfill \$\hfill & \hfill *\hfill & \hfill 0\hfill & \hfill *\hfill & \hfill \$\hfill & \hfill 1\hfill & \hfill *\hfill \\ \hfill \$\hfill & \hfill \$\hfill & \hfill *\hfill & \hfill 0\hfill & \hfill *\hfill & \hfill \$\hfill & \hfill *\hfill & \hfill 1\hfill \end{array}\right).$$

This is because spouses are usually unrelated, and father and mother relate to their children (the *s in the matrix) and their grandchildren (the $s) differently. Therefore, if the independent correlation structure is applied to the data collected from this kind of extended family, then it implies that all members in the extended family are unrelated while in actuality all members are related except the spouse of offspring 1 of core sib 1. On the other hand, if the exchangeable correlation structure is used, it implies that all members in the extended family are related to the same degree, and thus ignores those unrelated (more than half of correlations are zero as shown in R_extended) and those related to different degrees (those *s and $s). It is well known and has been reported in the literature using either theoretical proofs or simulations that treating related as unrelated or vice versa may either under- or over-estimate the variances of estimated parameters, which in turn may lead to false inferences about associations of the relevant outcome with its risk factors/covariates [2, 4].

The unstructured covariance structure defined in the marginal model has the following form:

$$\text{COV}=\left(\begin{array}{cccc}\hfill {\sigma }_{1,1}^2\hfill & \hfill {\sigma }_{1,2}\hfill & \hfill \cdots \hfill & \hfill {\sigma }_{1,m}\hfill \\ \hfill {\sigma }_{2,1}\hfill & \hfill {\sigma }_{2,2}^2\hfill & \hfill \cdots \hfill & \hfill {\sigma }_{2,m}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\sigma }_{m,1}\hfill & \hfill {\sigma }_{8,2}\hfill & \hfill \cdots \hfill & \hfill {\sigma }_{m,m}^2\hfill \end{array}\right),$$

where m is family size, {σ_i,j}s are unknown variance/covariance components, σ_i,j = σ_j,i, but σ_1,2 ≠ σ_1,3 ≠ ⋯ ≠ σ_1,m, σ_2,3 ≠ σ_2,4 ≠ ⋯≠ σ_2,m, …, σ_m−2,m−1 ≠ σ_m−2,m, and ${\sigma }_{1,1}^2\ne {\sigma }_{2,2}^2\ne \cdots \ne {\sigma }_{m,m}^2$. If the marginal model with the unstructured covariance structure is applied to the data collected from the abovementioned extended family (m = 8), then we need to estimate 36 (=8*(8+1)/2) unknown variance/covariance components in COV. This will be impractical if family size is large. Further, using the unstructured covariance structure in a marginal model also requires that we are able to uniquely order all members in each family in a way that is the same across all families (e.g., see the explanation about the “WITHIN” option in SAS Process GENMOD for details). However, it is difficult and sometimes impossible to order uniquely if families have different sizes or structures. Moreover, even when all recruited extended families have the same structure, if only a subset of the data is used in an analysis such as using the data collected from those aged 40–60 years only, then the numbers of the aged 40–60 members from different families may vary and so may the structures among the extracted members from different families.

Therefore, the current applicable covariance structures (independent, exchangeable and unstructured) used in a marginal model may not be optimal to describe the complicated relatedness, and the assumption of identical family structure may not be satisfied in larger extended families.

Let us take the Strong Heart Family Study (SHFS) [5] as an example. The SHFS was initiated in 1998 to identify genetic determinants of cardiovascular disease (CVD) in American Indians and to map and identify genes for CVD susceptibility. Families were recruited if they had a “core sibship” (a sibship with at least five living siblings, of whom three or more were original Strong Heart Study (SHS) [6] cohort members) and had at least 12 living offspring aged ≥15 years among the core sibship members. Each of the recruited families included the core sibship members, their parents (if alive), spouses, offspring, spouses of offspring, and grandchildren who were at least 15 years of age. A detailed description of the SHFS and SHS has been reported previously [5, 6] and published on the SHS web site (http://strongheart.ouhsc.edu). For example, 27 extended families were recruited in one of the centers of the SHFS. These extended families spanned four generations with the largest family size being 114 and the average size being 45. It is clear that family structures of these families are different and complicated. An application of the marginal model with either the independent or exchangeable covariance structure will lead to oversimplifying the complicated relationship among members in the extended families, while an application of the marginal model with the unstructured covariance structure will lead to estimating at least 6555 (=114*(114+1)/2) unknown variance/covariance components since the largest family size is 114. Moreover, because the families are recruited based on the “core sibship” and are not geographically distant from each other, it is not unusual for a recruited non-core member in a recruited family to be related to recruited members in other recruited families. This is often the case in family studies for populations such as American Indians, Alaska Natives or the Amish. Thus, the usual assumption that families (clusters) are unrelated (independent) in a marginal model may not be satisfied either.

Therefore, it is desirable and important to develop models to adjust for these kinds of complicated relatedness in order to assess the population-based associations and estimate population characteristics. This paper proposes such models for analyzing continuous or categorical, normally or non-normally distributed outcomes in “Models”, provides simulation and application examples in “Simulation and examples”, and discusses related theoretical issues in “Extension of the proposed models defined in (2.1) and (2.2)”, “Discussion”, and in the Appendix.

Models

Proposed model for a qualitative outcome

Let y_i = 1, if person i has an outcome of interest such as a disease, and =0, otherwise. We propose the following marginal model for assessing association of the prevalence or cumulative incidence of the disease with its risk factors/covariates x₁, …, x_p.

$$\text{log}\mathit{\text{it}}(P(y_i=1))=\text{log}\left(\frac{P(y_i=1)}{1-P(y_i=1)}\right)={\beta }_0+{\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+\cdots +{\beta }_p{x}_{ip},i=1,\dots ,m_1,m_1+1,\dots ,m_1+m_2,\dots ,n,{\mu }_i=P(y_i=1),\text{Var}(y_i)={\mu }_i(1-{\mu }_i),\text{Cov}(y_i,y_j)=2r_a\varphi (i,j)\sqrt{{\mu }_i(1-{\mu }_i)}\sqrt{{\mu }_j(1-{\mu }_j)},i\ne j,i,j=1,\dots ,n,$$ (2.1)

where logit(․) is called the logit link function, ϕ(i, j) is the kinship coefficient [7] between two individuals i and j, ϕ(i, j) = P{At any given locus, two randomly picked alleles, one from person i and one from person j are identity by descent}, 1 > r_a > 0, r_a and coefficients β₀, …β_p are unknown parameters, and the observations are ordered sequentially by families, that is, i = 1, …, m₁ denote the members in the 1st family, i = m₁ + 1, …, m₁ + m₂ denote the members in the 2nd family, etc., and n denotes the total number of participants in the study.

The covariance structure of the model defined by (2.1) is based on the classic biometrical model [7], where r_a denotes the component due to the additive effect, which is the major cause of resemblance between relatives. Following approach of the biometrical model, if the additive effects alone cannot adequately explain the data, a dominance component may be added [7]. That is, if necessary, we may use the following covariance structure in the model defined by (2.1)

$$\text{Var}(y_i)={\mu }_i(1-{\mu }_i),\text{Cov}(y_i,y_j)=(2r_a\varphi (i,j)+r_d{\mathrm{\Delta }}_7(i,j))\sqrt{{\mu }_i(1-{\mu }_i)}\sqrt{{\mu }_j(1-{\mu }_j)},i\ne j,i,j=1,\dots ,n,$$ (2.1a)

where r_a > 0, r_d > 0, r_a + r_d < 1, r_d denotes the component due to the dominance effect, which represents variance due to non-linear interaction between transmissible alleles and is contributed by individuals who share both alleles identical- by-descent [7], and Δ₇(i, j) is Jacquard’s coefficient [8], Δ₇(i, j) = P{The two alleles of person i at any given locus are identical by descent with the two alleles of person j at the same locus}. Both ϕ(i, j)s and Δ₇(i, j)s are directly calculated from the extended pedigrees of families ascertained in a family study since parents themselves may be related. For example, assuming parents are unrelated, it is well known that the kinship coefficient for two identical twins is 0.5; parent-offspring, 0.25; full sibs, 0.25; uncleniece, 0.125; etc. If there are no instances of inbreeding, no double cousins, and no twins in the pedigree, then Δ₇(i, i) = 1, ∀i; Δ₇(i, j) = 1/4, if i and j are full siblings; and zero otherwise. Many commercial software packages such as SAS Process INBREED (SAS software, SAS Institute, Cary, NC) and freely available software packages such as the PEDIG package [9] can be applied to calculate kinship coefficients between any two individuals based on their ascertained pedigree.

Compared to the independent, exchangeable and unstructured structures defined in the marginal model shown in the introduction, it is clear that the covariance structures in the proposed models defined by (2.1) or (2.1a) account appropriately for different degrees of relationship among family members. These covariance structures have at most two unknown parameters (r_a and r_d), and do not require that all members in each family be ordered in the same way across all families. The proposed covariance structure defines the relationship of outcomes collected from any two members in recruited families no matter how complicated and different the family structures are, or whether the families are related. The proposed model is also flexible for analyses that use only a subset of the data since the covariance structure for the subset can easily be composed from the corresponding sub-kinship matrix.

Proposed model for a continuous outcome

For a continuous outcome, y, such as cholesterol, the proposed model is

$$y_i={\beta }_0+{\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+\cdots +{\beta }_p{x}_{ip}+e_i,i=1,\dots ,m_1,m_1+1,\dots ,m_1+m_2,\dots ,n,\text{Var}(y_i)=\text{Var}(e_i)={\sigma }^2,\text{Cov}(y_i,y_j)=\text{Cov}(e_i,e_j)={\sigma }^{2}2r_a\varphi (i,j),i\ne j,i,j=1,\dots ,n,$$ (2.2)

where e_i’s denote random errors, 1 > r_a > 0, r_a denotes the component due to the additive effect, σ², r_a and coefficients β₀, …, β_p are unknown parameters, and the other notations are the same as those defined in (2.1). Similarly, if the dominance effect needs to be considered, we may use the following covariance structure in the model defined by (2.2)

$$\text{Var}(y_i)=\text{Var}(e_i)={\sigma }^2,\text{Cov}(y_i,y_j)=\text{Cov}(e_i,e_j)={\sigma }^2(2r_a\varphi (i,j)+r_d{\mathrm{\Delta }}_7(i,j)),i\ne j,i,j=1,\dots ,n,$$ (2.2a)

where r_a > 0, r_d > 0, r_a + r_d < 1, r_d denotes the component due to the dominance effect.

Extension of the proposed models defined in (2.1) and (2.2)

To extend the models defined in (2.1) and (2.2) to cover different kinds of outcomes in a family study and to allow for additional random effects such as random environmental effects, we follow the procedure for generalized linear mixed models [4, 10, 11].

Let Y = (y₁, …, y_n)^τ, x_i = (1, x_i1, …, x_ip)^τ, X = (x₁, …, x_n)^τ, B = (β₀, β₁, …, β_p)^τ, z_i = (z_i1, …, z_iq)^τ, Z = (z₁, …, z_n)^τ, U = (u₁, u₂, …, u_q)^τ, and e = (e₁, e₂, …, e_n)^τ, where y_i denotes the outcome variable observed in individual i with fixed covariates x_i and explanatory variables z_i that are associated with the random effects U, and U and the errors, e, are assumed to be independent. Assume that U has a mean zero O and covariance matrix Cov(U) = G (θ) that depends on an unknown vector θ; and given U, y_i will have means $E(y_i/\mathbf{U})={\mu }_i^{\mathbf{U}}$, variances Var(y_i/U), and covariance components

$$\text{Cov}(y_i,y_j/\mathbf{U})=\sqrt{\text{var}(y_i/\mathbf{U})}\{2r_a\varphi (i,j)\}\sqrt{\text{var}(y_j/\mathbf{U})},i\ne j$$ (2.3)

or

$$\text{Cov}(y_i,y_j/\mathbf{U})=\sqrt{\text{var}(y_i/\mathbf{U})}\{2r_a\varphi (i,j)+r_d{\mathrm{\Delta }}_7(i,j)\}\sqrt{\text{var}(y_j/\mathbf{U}),}i\ne j$$ (2.3a)

if the dominance effect is added, where 0 < r_a < 1 (or 0 < r_a, r_d < 1 and r_a + r_d < 1 if the dominance effect is added). Assume that ${\mu }_i^{\mathbf{U}}$ is related to ${\eta }_i^{\mathbf{U}}={\mathbf{x}}_i^{\tau }\mathbf{B}+{\mathbf{z}}_i^{\tau }\mathbf{U}$ by a link function $g({\mu }_i^{\mathbf{U}})={\eta }_i^{\mathbf{U}}$, with inverse h = g⁻¹. Then $\mathbf{\eta }={({\eta }_1^U,\dots ,{\eta }_n^U)}^{\tau }=\mathbf{X}\mathbf{B}+\mathbf{Z}\mathbf{U}$ and

$$E(\mathbf{Y}/\mathbf{U})={({\mu }_1^U,\dots ,{\mu }_n^U)}^{\tau }={(h({\mathbf{x}}_1^{\tau }\mathbf{B}+{\mathbf{z}}_1^{\tau }\mathbf{U}),\dots ,h({\mathbf{x}}_n^{\tau }\mathbf{B}+{\mathbf{z}}_n^{\tau }\mathbf{U}))}^{\tau }=h(\mathbf{X}\mathbf{B}+\mathbf{Z}\mathbf{U})$$ (2.4)

It is clear that if there are no random effects involved, the model defined by (2.1) is a special case of (2.4) when y is binomially distributed and the logit link function is used. The model defined by (2.2) is the one in which the identity link function is used and Var(y_i/U) = σ². Models in which outcomes have other distributions such as those belonging to the linear exponential family with respective link functions are also accommodated in (2.4) [4, 10, 11].

If all families are unrelated and have an identical structure, the estimation procedures for σ², r_a, r_d, θ, B and U in the models defined by (2.1), (2.2) or (2.4), the proofs for asymptotic properties of the estimators, and their statistical inferences follow those used in the generalized linear mixed models [4, 10, 11]. In the case where families in a study can be classified into unrelated subgroups, and families in each subgroup are unrelated and have identical structure, we show in the Appendix that similar approaches and asymptotic properties also hold. When families in a study are related and large and have different sizes and structures, and the number of families may be only moderate, it is difficult to theoretically prove the asymptotic properties of the estimated parameters from our models because families may be related. However, we showed by a simulation that the usual asymptotic properties also hold in this case no matter whether the families are related or with different family sizes or structures if the total number of members from all families is large enough even though the number of families may be only moderate (Appendix).

Simulation and examples

As mentioned in the introduction, it has been reported in the literature by either theoretical proofs or simulation methods that treating related observations as unrelated or vice versa may either under- or over-estimate the variances of estimated parameters, and thus may lead to false inferences about the significances of associations of a relevant outcome with its risk factors/covariates [2, 4]. To further confirm these uncertainties, we use a simulation to compare power of the proposed models with that of the marginal model with either the exchangeable or independent correlation structure in detecting significant associations of an outcome measure with its risk factors/covariates when correlation structure in a data is neither the exchangeable nor independent.

Let FPG_ij denote measured fasting plasma glucose (FPG) of the jth member in the ith family. The following proposed model (2.2) is used to simulate association of FPG with its seven risk factors/covariates: age, waist circumference (WAIST), body mass index (BMI), urinary albumin to creatinine ratio (UACR), insulin, low density lipoprotein (LDL), and triglycerides (TG),

$$\mathrm{F}\mathrm{P}{\mathrm{G}}_{ij}=-16.14+0.295{\text{age}}_{ij}+0.431\mathrm{W}\mathrm{A}\mathrm{I}\mathrm{S}{\mathrm{T}}_{ij}-0.894\mathrm{B}\mathrm{M}{\mathrm{I}}_{ij}+7.367\text{log}{(\mathrm{U}\mathrm{A}\mathrm{C}\mathrm{R})}_{ij}+4.115\text{log}{(\text{insulin})}_{ij}-0.065\mathrm{L}\mathrm{D}{\mathrm{L}}_{ij}+14.757\text{log}{(\mathrm{T}\mathrm{G})}_{ij}+e_{ij}.$$

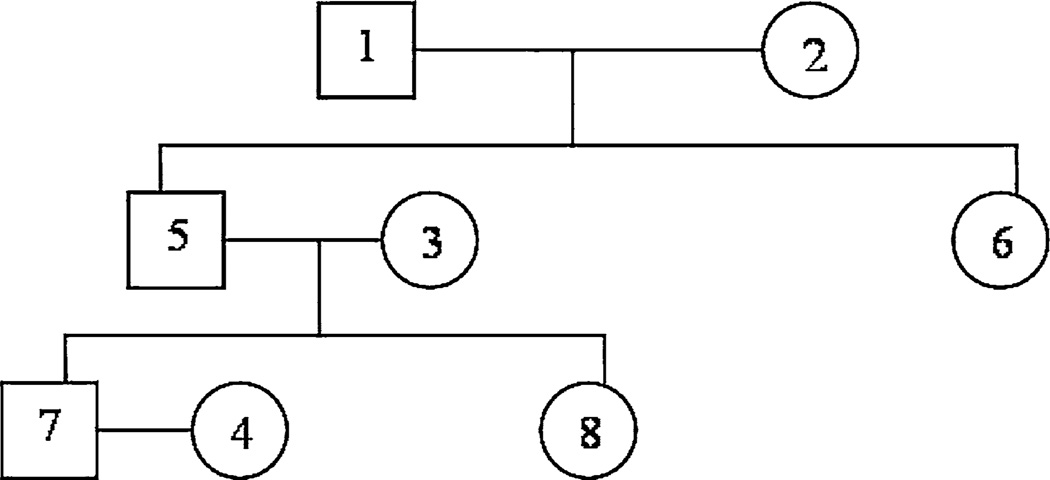
The families are those 50 unrelated extended families in which each family had 8 members ordered as {father of core sibs, mother of core sibs, spouse of core sib 1, spouse of offspring 1 of core sib 1, core sib 1, core sib 2, offspring 1 of core sib 1, offspring 2 of core sib 1}. Figure 1 shows the pedigree for the ordered 8 members. Assume FPGs observed from a family are normally distributed with Var(FPG_ij) = 1000 (or standard deviation of 31.6) and r_a = 0.5, then based on the definition of the covariance in (2.2) and the calculated kinship matrix Φ from the pedigree of the ordered 8 members, FPGs have the following correlation matrix

$$\text{Corr}(\mathrm{F}\mathrm{P}{\mathrm{G}}_{i․},\mathrm{F}\mathrm{P}{\mathrm{G}}_{i․})={\mathbf{R}}_1=\left(\begin{array}{cccccccc}\hfill 1& 0\hfill & \hfill 0& 0\hfill & \hfill 0.250& 0.250\hfill & \hfill 0.125\hfill & \hfill 0.125\hfill \\ \hfill 0& 1\hfill & \hfill 0& 0\hfill & \hfill 0.250& 0.250\hfill & \hfill 0.125\hfill & \hfill 0.125\hfill \\ \hfill 0& 0\hfill & \hfill 1& 0\hfill & \hfill 0& 0\hfill & \hfill 0.250\hfill & \hfill 0.250\hfill \\ \hfill 0& 0\hfill & \hfill 0& 1\hfill & \hfill 0& 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0.250& 0.250\hfill & \hfill 0& 0\hfill & \hfill 1\hfill & 0.250\hfill & \hfill 0.250\hfill & \hfill 0.250\hfill \\ \hfill 0.250& 0.250\hfill & \hfill 0& 0\hfill & \hfill 0.250& \hfill 1\hfill & \hfill 0.125\hfill & \hfill 0.125\hfill \\ \hfill 0.125& 0.125\hfill & \hfill 0.250& 0\hfill & \hfill 0.250& 0.125\hfill & \hfill 1\hfill & \hfill 0.250\hfill \\ \hfill 0.125& 0.125\hfill & \hfill 0.250& 0\hfill & \hfill 0.250& 0.125\hfill & \hfill 0.250\hfill & \hfill 1\hfill \end{array}\right),$$

where FPG_i. =(FPG_i1, …, FPG_i8)^τ denotes FPG collected from 8 members of the ith family, i=1, …, 50, and

$$\mathrm{\Phi }=\{{\varphi }_{ij}\}=\left(\begin{array}{cccccccc}\hfill 0.5& \hfill 0\hfill & \hfill 0\hfill & 0\hfill & \hfill 0.25& 0.25\hfill & \hfill 0.125& 0.125\hfill \\ \hfill 0\hfill & 0.5\hfill & \hfill 0\hfill & 0\hfill & \hfill 0.25& 0.25\hfill & \hfill 0.125& 0.125\hfill \\ \hfill 0& 0\hfill & \hfill 0.5\hfill & \hfill 0\hfill & \hfill 0& 0\hfill & \hfill 0.25& 0.25\hfill \\ \hfill 0& 0\hfill & \hfill 0\hfill & 0.5\hfill & \hfill 0& 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0.25& 0.25\hfill & \hfill 0\hfill & 0\hfill & \hfill 0.5\hfill & 0.25\hfill & \hfill 0.25\hfill & \hfill 0.25\hfill \\ \hfill 0.25& 0.25\hfill & \hfill 0\hfill & 0\hfill & \hfill 0.25& \hfill 0.5\hfill & \hfill 0.125& 0.125\hfill \\ \hfill 0.125& 0.125\hfill & \hfill 0.25\hfill & \hfill 0& \hfill 0.25& 0.125\hfill & \hfill 0.5\hfill & 0.25\hfill \\ \hfill 0.125& 0.125\hfill & \hfill 0.25\hfill & \hfill 0& \hfill 0.25& 0.125\hfill & \hfill 0.25& \hfill 0.5\hfill \end{array}\right).$$

Fig. 1.

Pedigree for the ordered eight members

For example, ϕ(father of core sibs, offspring 1 of core sib 1) = ϕ₁₇ = 0.125. When r_a = 0.8, FPGs have the following correlation matrix that has larger correlation coefficients

$${\mathbf{R}}_2=\left(\begin{array}{cccccccc}\hfill 1& 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.4& 0.4\hfill & \hfill 0.2\hfill & \hfill 0.2\hfill \\ \hfill 0& 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.4& 0.4\hfill & \hfill 0.2\hfill & \hfill 0.2\hfill \\ \hfill 0& 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0& 0\hfill & \hfill 0.4\hfill & \hfill 0.4\hfill \\ \hfill 0& 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0& 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0.4& 0.4\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & 0.4\hfill & \hfill 0.4\hfill & \hfill 0.4\hfill \\ \hfill 0.4& 0.4\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.4& \hfill 1\hfill & \hfill 0.2\hfill & \hfill 0.2\hfill \\ \hfill 0.2& 0.2\hfill & \hfill 0.4\hfill & \hfill 0\hfill & \hfill 0.4& 0.2\hfill & \hfill 1\hfill & \hfill 0.4\hfill \\ \hfill 0.2& 0.2\hfill & \hfill 0.4\hfill & \hfill 0\hfill & \hfill 0.4& 0.2\hfill & \hfill 0.4\hfill & \hfill 1\hfill \end{array}\right).$$

The parameters used in the simulation model are obtained from the SHFS data in order to make the model realistic and meaningful. It is clear that R₁ or R₂ contains three levels of correlations (e.g., 0, 0.125 and 0.25 in R₁), which is neither the exchangeable correlation (that assumes all correlation coefficients are the same and non-zero) nor independent correlation (that assumes all correlation coefficients are zero) structure defined in the marginal model. One thousand replicated simulated data sets, each including 400 simulated observations from the 400 members in the 50 unrelated extended families, were generated. For each of the 1,000 simulated data sets, the proposed model (2.2) and the respective marginal model with the exchangeable or independent correlation structure were applied separately to estimate the regression coefficients for the seven risk factors/covariates of FPG in these models. To estimate power of a model in detecting significant association of FPG with a given risk factor/covariate, say, WAIST, after adjusting for the other risk factors/covariates in the model, we tested the null hypothesis: H₀: “the coefficient for WAIST in the model” = 0, at a given significant level (type 1 error rate) α based on each of 1,000 simulated data. The empirical power of the model at the given significance level α in detecting the significant association of FPG with WAIST after adjusting for the other risk factors/covariates in the model was estimated as “the total number of the tests based on the 1,000 replicated simulated data sets where H₀ was rejected at the given significance level α “divided by 1,000. The same procedure was applied simultaneously for each of the seven risk factors/covariates in the model. Table 1 displays estimates of the empirical powers of the proposed model (2.2) and the marginal model with the exchangeable or independent correlation structure in detecting the significant association of FPG with each of its risk factors/covariates after adjusting for the other risk factors/covariates in the model at two different significance levels (α = 0.05 or 0.01) based on the 1,000 simulated data sets generated by using two different correlation matrices R₁ and R₂. For example, at the assumed correlation matrix R₁ and the given significance level α = 0.05, the estimated empirical powers of the proposed model (2.2) and the marginal model with the exchangeable or independent correlation structure in detecting the significant association of FPG with WAIST after adjusting for the other risk factors/covariates in the model are 0.611, 0.598 and 0.556, respectively. The power of the proposed model (2.2) is almost always greater than the power of the marginal model with either the exchangeable or independent correlation structure, and the differences between the powers increased with the correlation coefficients (those based on R₂ are larger than those based on R₁). Our simulation results indicated that using either simplified exchangeable or independent correlation structure in analyzing correlated data with more complicated correlation structures (e.g., those defined by R₁ or R₂) may either under- or overestimate the variances of parameters, and thus may lead to incorrect inferences about the significance of associations of an outcome with its risk factors/covariates. It may be expected that such uncertainty will be greater if simplified exchangeable or independent correlation structure is used in analyzing correlated data collected from the SHFS extended families that span four generations with the largest family size being 114 and the average size being 45.

Table 1.

Empirical powers of the proposed model (2.2) and the marginal model with the exchangeable (M-E) or independent (M-I) correlation structure in detecting the significant association of FPG with each of its risk factors/covariates after adjusting for the other risk factors/covariates in the model at two different significance levels (type 1 error rates) based on the 1,000 simulated data sets generated by using two different correlation matrixes R₁ and R₂

Correlation matrix	Risk factor/covariate	Significance level α = 0.05			Significance level α = 0.01
		Model (2.2)	M-E	M-I	Model (2.2)	M-E	M-I
R1	Age (year)	0.806	0.799	0.752	0.622	0.595	0.533
	Waist (cm)	0.611	0.598	0.556	0.392	0.373	0.318
	BMI (kg/m2)	0.461	0.446	0.409	0.254	0.250	0.212
	Log(TG) (mg/dL)	0.994	0.992	0.989	0.982	0.969	0.967
	Log(UACR)	1.000	0.999	0.999	0.999	0.999	0.999
	LDL (mg/dL)	0.282	0.272	0.237	0.113	0.115	0.098
	Log(Insulin) (µU/mL)	0.379	0.389	0.342	0.173	0.184	0.144
R2	Age (year)	0.946	0.849	0.776	0.815	0.662	0.541
	Waist (cm)	0.770	0.612	0.529	0.535	0.365	0.297
	BMI (kg/m2)	0.581	0.443	0.388	0.344	0.253	0.182
	Log(TG) (mg/dL)	1.000	0.996	0.986	0.997	0.969	0.946
	Log(UACR)	1.000	1.000	1.000	1.000	1.000	0.999
	LDL (mg/dL)	0.392	0.311	0.242	0.165	0.139	0.101
	Log(Insulin) (µU/mL)	0.565	0.443	0.369	0.346	0.224	0.166

BMI body mass index, LDL low density lipoprotein, TG triglycerides, UACR urinary albumin and creatinine ratio, Waist waist circumference

Table 2 shows results when applying the proposed model (2.2) and the respective marginal model with either independent or exchangeable correlation structure to one of the 1000 simulated data sets that used the correlation structure defined in R₁. We can interpret the results from the proposed model (2.2) in the same way as those from a conventional linear regression model since the proposed model (2.2) is a marginal model and the coefficients from a marginal model represent population averaged results [2, 4]. For example, based on the results from the proposed model (2.2) in Table 2, age, WAIST, log(UACR), log(insulin) and log(TG) were significantly and positively associated with FPG; while BMI and LDL were significantly and negatively associated with FPG. However, the results from the respective marginal models show that, besides the differences in the estimated coefficients, which maybe minor if the sample size is large [2, 4], some of the significant risk factors/covariates of FPG in the proposed model were no longer significant in the respective marginal models with either independent (age, log(insulin), and LDL) or exchangeable (age and LDL) covariance structures, reflecting uncertainty in inferences due to the simplification in correlation structures.

Table 2.

Marginal models for fasting plasma glucose on its risk factors/covariates based on the simulated data

Variable	Proposed model (2.2)			Marginal model with the exchangeable covariance			Marginal model with the independent covariance
	Coeff.	SE	P	Coeff.	SE	P	Coeff.	SE	P
Intercept	−15.448			−10.101			−12.443
Age (year)	0.217	0.101	0.0318	0.130	0.105	0.2200	0.170	0.112	0.1291
Waist (cm)	0.612	0.173	0.0005	0.555	0.187	0.0032	0.630	0.192	0.0011
BMI (kg/m2)	−1.380	0.449	0.0023	−1.304	0.386	0.0008	−1.357	0.495	0.0064
Log(UACR)	5.442	1.124	<0.0001	5.984	1.130	<0.0001	6.057	1.259	<0.0001
Log(Insulin) (µU/mL)	7.025	2.212	0.0016	5.514	2.167	0.0114	4.587	2.499	0.0672
LDL (mg/dL)	−0.098	0.042	0.0200	−0.058	0.048	0.2298	−0.062	0.047	0.1895
Log(TG) (mg/dL)	15.149	3.022	<0.0001	14.974	3.282	<0.0001	14.438	3.369	<0.0001

Coeff., regression coefficient; P, P value; SE, the standard error

Discussion

As indicated earlier, the proposed models are appropriate, capable, flexible and efficient for population-based association studies while adjusting for complicated relatedness in data collected from family studies with large extended families.

If outcomes are continuous and normally distributed, and families in a study are unrelated to each other and have an identical family structure, the proposed model defined in (2.4) with the identity link function is the variance components model used in pedigree analyses [7, 12, 13]. However, if outcomes are discrete or not normally distributed, the proposed model defined in (2.4) is different from those proposed models for correlated data in the literature. For example, for binary outcomes, the proposed Model (2.1) is different from those threshold models [14–16] or the generalized linear mixed model (GLMM) with a logit link function [17] or the mixed models on which family-based association tests (FBAT) are based [18, 19].

The threshold model for the disease outcome y_i (y_i = 1, if person i has the disease; and =0, otherwise) and its risk factors/covariates x₁, …, x_p is defined as follows. Let the random effects U = (u₁, u₂, …, u_n)^τ be normally distributed with

$$\mathrm{E}(u_i)=0,\text{Cov}(u_i,u_j)={\sigma }_a^{2}2\varphi (i,j),i,j=1,\dots ,n.$$

Assume given U, y_i, i = 1, …, n, are mutually independent, and

$$y_i=\{\begin{array}{ccc}1,\hfill & \text{if}\hfill & z_i\ge \vartheta ;\hfill \\ 0,\hfill & \text{if}\hfill & z_i<\vartheta ,\hfill \end{array}{\mathrm{\Phi }}^{-1}(P(y_i=1/\mathbf{U}))={\mathrm{\Phi }}^{-1}(P(z_i\ge \vartheta /\mathbf{U}))={\beta }_0+{\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+\cdots +{\beta }_p{x}_{ip}-\vartheta +u_i,i=1,\dots ,m_1,m_1+1,\dots ,m_1+m_2,\dots ,n,$$

where ϑ is the underlying threshold, z_i, i = 1, …, n, are the underlying random variables, and Φ⁻¹(․) stands for the inverse of the standardized cumulative normal distribution function, which is also called the probit link function in the GLMM.

The respective GLMM with a logit link function in this case is defined as follows. Assume given the same random effects U = (u₁, u₂, …, u_n)^τ defined above, y_i, i = 1, …, n, are mutually independent, and

$$\text{logit}(P(y_i=1/\mathbf{U})=\text{log}(\frac{P(y_i=1/\mathbf{U})}{1-P(y_i=1/\mathbf{U})})={\beta }_0+{\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+\cdots +{\beta }_p{x}_{ip}+u_i,i=1,\dots ,m_1,m_1+1,\dots ,m_1+m_2,\dots ,n.$$

The mixed model on which FBAT is based for the dichotomous phenotype y_ij of the jth offspring in the ith family is defined as follows. Assume given the random variable u_ij that codes for genotype of the jth offspring in the ith family at a particular allele, i = 1, …,m; j = 1, …, n_i, y_ij’s are independent and

$$\text{log}\mathit{\text{it}}(P(y_{ij}=1/u_{ij})=\text{log}(\frac{P(y_{ij}=1/u_{ij})}{1-P(y_{ij}=1/u_{ij})})+{\beta }_0+{\beta }_1{x}_{ij1}+{\beta }_2{x}_{ij2}+\cdots +{\beta }_p{x}_{ijp}+\gamma u_{ij,}$$

where x₁, …, x_p usually denote demographic or environmental effects, and u_ij are dependent on parental genotypes. FBAT based on this model tests the null genetic hypothesis H₀ : “no association in the presence of linkage”; or “no linkage and no association between a marker and the phenotype”, which is equivalent to testing whether the coefficient γ of the random variables equals zero, that is, H₀ : γ = 0.

It is clear that the proposed Model (2.1) is a marginal model while the threshold model and the GLMM model as well as the FBAT based model are mixed random effects models. It is known that a marginal model and a mixed random effects model can lead to different estimations and interpretations for the regression coefficients [2, 4]. In the proposed Model (2.1), the logit of the expectation E(I(y_i = 1)) = P(y_i = 1) was directly modeled with its risk factors/covariates x₁, …, x_p, and the covariance is directly defined through y_i’s themselves. Therefore, like the example of the proposed Model (2.2) shown in “Simulation and examples”, the estimated coefficients β̂₀, β̂₁, …, β̂_p for the risk factors/covariates from the proposed Model (2.1) can be interpreted in the same way as those estimated coefficients from a conventional logistic regression model since the coefficients from a marginal model represent population averaged results [2, 4]. While in the previous mentioned mixed random effects models, say, the GLMM model, the logit of the conditional (conditioning on the random effects U) expectation E(I(y_i = 1)/U) = p(y_i = 1/U) was modeled with both the fixed effects x₁, …, x_p and the random effect u_i, and the covariance is partially defined by the random effects U. Therefore, the estimated coefficients β̃₀, β̃₁, …, β̃_p for the fixed effects, x₁, …, x_p from these models are dependent on individual random effects u_is and the distribution of u_is by the definition of the conditional expectation and thus are individual- specific not population averaged [2, 4, 10, 17]. The Gibbs sampling method [20, 21] was usually used in fitting these mixed random effects models. Similar differences also exist between the proposed Model (2.4) and the GLMM models. Marginal models are appropriate when inferences about the population-average are the focus, which are what we focused in this paper and are usually the focus in population-based epidemiological studies; while a random effects model is most useful when the objective is to make inference about individuals rather than the population average [2, 4]. We adopted a marginal rather than random effects model approach for our covariance structure since we are interested only in assessing population-based associations of diseases with their risk factors/covariates and estimating population characteristics in epidemiological studies.

It is easy to verify that when families in a study are those unrelated pedigrees that contain only identical twins or only siblings without twins, the proposed models are equivalent to the marginal model with the exchangeable covariance structure that is often adopted in populationbased analyses [22].

Therefore, if families in a family study are unrelated and have identical structure, the covariance structure defined in the proposed models can be treated as an additional appropriate covariance structure to the existing covariance structures used in marginal models. If families in a family study are large and related, and have different sizes and structures like the extended families in the SHFS, the proposed models are most appropriate for and capable of handling this type of data for population-based analyses. The SAS macros for applying the proposed models will be available upon request.

Other marginal models for family data in the literature include the odds-ratio regression models [23] that model on each specific pair such as siblings or a parent-sibling pair, and the frailty models [24, 25] that take care of censored observations.

Abbreviations

BMI

Body mass index

CVD

Cardiovascular disease

FBAT

Family-based association tests

FPG

Fasting plasma glucose

GLMM

Generalized linear mixed model

LDL

Low density lipoprotein

SHFS

Strong heart family study

SHS

Strong heart study

TG

Triglycerides

UACR

Urinary albumin to creatinine ratio

WAIST

Waist circumference

Appendix

Case 1: Families in a study are classified into unrelated subgroups, and families in each subgroup are unrelated and have identical structure

This is the case for a family study in which we combined those related study families together to form an expanded family and then classified all such expanded families into different subgroups based on their structures.

Let Φ_l and n_l be the kinship coefficient matrix and the number of families associated to the subgroup l, respectively, l = 1, 2, …, S, S is the total number of subgroups of families in the study, and $M={\sum }_{l=1}^S{n}_l$. Let ${\mathbf{y}}_{l\nu }={(y_{\nu 1}^l,y_{\nu 2}^l,\dots ,y_{\nu m_l}^l)}^{\tau }$ denote the observed outcomes from the νth family in the subgroup l, ν = 1, 2, …, n_l, and f_l,ξ denote the density function of y_lν, where ξ denotes all unknown parameters. Suppose that S remains fixed, each of n_l tends to infinity, and n_l/M → λ_l > 0, ∀l. Let I^l (ξ) denote the information matrix corresponding to f_l,ξ and let

$$I(\mathbf{\xi })=\sum _{l=1}^S{\lambda }_l{I}^l(\mathbf{\xi }).$$

The likelihood L(ξ) is given by

$$L(\mathbf{\xi })=\sum _{l=1}^S\sum _{j=1}^{n_l}\text{log}{f}_{l,\mathbf{\xi }}({\mathbf{y}}_{lj})$$

and the likelihood equations by

$$\frac{\partial }{\partial {\xi }_i}L(\mathbf{\xi })=0,i=1,2,\dots ,w,$$

where w denotes the number of all unknown parameters. Then we have the following theorem:

Theorem 1 Suppose f_l,ξ for each l satisfies some general regular conditions [26], then with a probability approaching 1, there exist solutions ξ̂_M of the likelihood equations such that

1. ξ̂_M is consistent for estimating ξ.

2. $\sqrt{M}({\mathrm{\xi ̂}}_M-\mathbf{\xi })$ is asymptotically normal with (vector) mean zero and covariance matrix [I(ξ)]⁻¹.

The proof of this theorem for the model defined by (2.4) follows those of Theorem 6.1 in Lehmann [26] and those of the generalized linear mixed models [4, 10, 11].

The conditions used in the proof are reasonable because in a family study, the size of the largest expanded family must be finite since only several generations and certain individuals will be included. Therefore the number of different structures in recruited families in the study should be finite also. Assuming the finite family structures are distributed homogenously, it is expected that the number of families with each of these finite family structures will all be large if the study population size is large enough.

Case 2: Families in a study may be related and large, and have different sizes and structures, and the number of families may be only moderate.

It is difficult to theoretically prove the asymptotic properties of the estimated parameters from our models in this case because families may be related. However, we believe that the asymptotic properties also hold in this case if the total number of members from all families is large enough. To show that the asymptotic properties may still hold in this case, the following simulation study was conducted. We simulated data using the following model, which was derived from the SHFS data in order to make the coefficients realistic and meaningful, for the association of age and waist circumference (WAIST) with fasting plasma glucose (FPG):

$$\mathrm{F}\mathrm{P}{\mathrm{G}}_i=14.13+0.98{\text{age}}_i+0.53{\text{Waist}}_i+e_i,$$

where e_i‘s are normally distributed with mean zero and the covariance structure defined by the model in (2.2) with σ² = 2,043 and r_a = 0.3553 (or equivalently parameterized as ${\sigma }_a^2={\sigma }^2{r}_a=726,{\sigma }_{\epsilon }^2={\sigma }^2-{\sigma }_a^2=1,317$), and the kinship matrix that is derived from 653 individuals aged 30–65 in the 27 recruited families in the SHFS (since it is difficult to choose an appropriate 653-dimensional covariance matrix for related families with different family structures and sizes). We will show, by successively adding three more families in the simulation, that the asymptotic properties of the estimated parameters from our proposed model will hold no matter whether the included families are related or with different family sizes or structures if the total number of members from included families is large enough even though the number of families may be only moderate. Step 1: First, we simulated data for all members in the first three families based on the model and the sub-kinship matrix corresponding to these members, and then obtained a set of estimated parameters based on the simulated data. Next, we repeated this procedure 100 times and thus obtained 100 sets of the estimated parameters, then tested whether the 100 estimations of each parameter came from a normal distribution by using the Kolmogorov–Smirnov test. Similarly, in each successive step (Steps 2–9), we added three more families and performed the same simulation and analyses. The results from this simulation study are shown in Table 3. For example, at the last step, Step 9, we used the kinship matrix for all 653 members aged 30–65 in all 27 families. Means from the 100 estimates of intercept, coefficients of age and WAIST, ${\sigma }_a^2$ and ${\sigma }_{\epsilon }^2$ were 14.24, 0.986, 0.521, 717.68 and 1330.75, respectively. All of these means were quite close to the respective true parameters, 14.13, 0.98, 0.53, 726 and 1317 in the above model used in the simulation (actually, the true parameters all fell within the one-standard-error confidence intervals of the respective means). These estimated parameters were considered to have normal distributions based on the results from the Kolmogorov–Smirnov tests (all P > 0.1). Similar results also held even at the earlier steps such as Step 8 that included only 24 families but with 598 members. These results show that the asymptotic properties also hold in this case.

Table 3.

Results from the simulations for the asymptotic properties of the estimated parameters in the simulated model

Step	Families	No. of members in each family	Families used in each step	Total No. of members	Estimated σa (True σa = 726)			Estimated σε (True σε = 1,317)
					Mean	SE	P	Mean	SE	P
1	1,2,3	21,56,50	1–3	127	726.83	50.82	0.010	1303.48	42.00	0.060
2	4,5,6	22,9,26	1–6	184	710.14	39.58	0.141	1294.31	37.16	0.150
3	7,8,9	32,7,13	1–9	236	720.68	37.01	0.150	1332.18	33.05	0.150
4	10,11,12	14,14,42	1–12	306	709.98	41.20	0.150	1342.56	32.26	0.056
5	13,14,15	39,19,41	1–15	405	701.25	30.77	0.010	1332.58	28.06	0.150
6	16,17,18	17,2,10	1–18	434	723.13	28.79	0.150	1300.78	24.68	0.150
7	19,20,21	16,23,26	1–21	499	730.49	21.76	0.150	1319.40	20.04	0.150
8	22,23,24	50,14,35	1–24	598	712.68	22.51	0.150	1323.36	19.01	0.100
9	25,26,27	13,21,21	1–27	653	717.68	19.31	0.150	1330.75	15.57	0.150
Step	Families used in each step	Estimated intercept (True intercept = 14.13)			Estimated Coeff. of age (True coeff. = 0.98)			Estimated Coeff. of Waist (True coeff. = 0.53)
		Mean	SE	P	Mean	SE	P	Mean	SE	P
1	1–3	19.863	2.905	0.087	0.893	0.039	0.084	0.509	0.024	0.150
2	1–6	13.364	2.494	0.016	1.000	0.034	0.150	0.527	0.019	0.088
3	1–9	16.923	2.135	0.150	0.961	0.034	0.134	0.506	0.016	0.094
4	1–12	16.758	1.792	0.150	0.958	0.022	0.150	0.515	0.015	0.150
5	1–15	13.585	1.539	0.150	0.960	0.017	0.150	0.542	0.013	0.065
6	1–18	13.209	1.572	0.150	0.980	0.023	0.150	0.542	0.012	0.134
7	1–21	15.184	1.329	0.150	0.966	0.019	0.150	0.524	0.011	0.147
8	1–24	15.138	1.457	0.150	0.974	0.020	0.150	0.525	0.012	0.150
9	1–27	14.240	1.156	0.125	0.986	0.016	0.150	0.521	0.010	0.150

P, P value from Kolmogorov–Smirnov test for testing whether the 100 estimations of the parameter based on 100 times simulated data are from a normal distribution; Mean, mean of an estimated parameter based on the 100 estimations of the parameter; SE, standard error of an estimated parameter based on the 100 estimations of the parameter; Step, simulation step