Fast Reconstruction for Multi-channel Compressed Sensing Using a Hierarchically Semiseparable Solver

Abstract

Purpose

The adoption of multi-channel compressed sensing (CS) for clinical MRI hinges on the ability to accurately reconstruct images from an under-sampled dataset in a reasonable time frame. When CS is combined with SENSE parallel imaging, reconstruction can be computationally intensive. As an alternative to iterative methods that repetitively evaluate a forward CS+SENSE model, we introduce a technique for the fast computation of a compact inverse model solution.

Methods

A recently proposed Hierarchically Semiseparable (HSS) solver is used to compactly represent the inverse of the CS+SENSE encoding matrix to a high level of accuracy. To investigate the computational efficiency of the proposed HSS-Inverse method, we compare reconstruction time with the current state-of-the-art. In vivo 3T brain data at multiple image contrasts, resolutions, acceleration factors, and number of receive channels were used for this comparison.

Results

The HSS-Inverse method allows for > 6× speed-up when compared to current state-of-the-art reconstruction methods with the same accuracy. Efficient computational scaling is demonstrated for CS+SENSE with respect to image size. The HSS-Inverse method is also shown to have minimal dependency on the number of parallel imaging channels / acceleration factor.

Conclusion

The proposed HSS-Inverse method is highly efficient and should enable real-time CS reconstruction on standard MRI vendors’ computational hardware.

Introduction

In clinical applications of structural magnetic resonance imaging (MRI), there exists a multi-objective tradeoff between image quality, imaging time, and reconstruction time. Reducing imaging time for a given protocol is clearly beneficial from a cost perspective, and can also facilitate more detailed studies with the same patient throughput. Image quality tends to be a firm barrier placed by radiologists or researchers based upon requirements for data analysis. Finally, stringent hardware limitations exist for clinical FDA approved scanners. It is important to note that advances in MRI sequences and hardware continue to increase the computational burden for image reconstruction, e.g. large coil arrays, increased resolution, and multi-contrast studies. In this work, we investigate a highly scalable inverse algorithm intended to ameliorate the computational challenges associated with accurate compressed sensing (CS) reconstruction. As an alternative to reconstruction methods that repetitively evaluate forward CS / parallel imaging models, we introduce a technique for the computation of a compact inverse model solution. This is achieved by using a recently proposed Hierarchically Semiseparable (HSS) solver [1], which compactly represents the inverse encoding matrix to a high level of accuracy. Specifically, using a pre-specified level of accuracy the HSS solver will systematically compress parameters from a decomposition of the encoding matrix. When solving a 2D inverse encoding problem with N voxels, even optimized Cholesky decomposition based solvers such as [2] will require O (N^1.5) computation in the best case. When the encoding matrix has certain low-rank properties, the HSS method can achieve O (N). Under these conditions, the HSS scaling is less than the FFT complexity of O (N logN) while the optimized Cholesky is greater.

Sparse signal reconstruction has been introduced for MRI [3] as a method to improve imaging time through random under-sampling of k-space. By assuming a sparsity inducing L₁ image prior, the reconstruction problem can be formulated as an unconstrained optimization problem. This problem incorporates fidelity against the observed k-space samples with a penalty imposed on the sparsity prior. These methods have been shown to provide good image accuracy, but can significantly increase the computational burden for image reconstruction. This is especially evident with the inclusion of SENSE parallel imaging [4]. Several attempts have been made to reduce the computational requirements associated with sparse signal reconstruction [5-11]. These iterative techniques rely on repetitive evaluation of a forward CS+SENSE model. In this work, we propose an alternative approach that solves for the actual inverse of the encoding matrix using a direct (non-iterative) HSS solver.

In order to demonstrate the advantages of our HSS-Inverse approach we will focus on the popular Split Bregman (SB) [8] formulation. Here, the authors presented a relaxation method for L₁ penalties. The iterative SB approach produces a series of targets for the sparsity of the image. Each stage of the method involves solving an easier L₂ optimization and quickly updating the sparsity target. Our HSS-Inverse solver and several iterative CG approaches are embedded within the SB formulation for comparison. This allows for us to isolate the efficiency of solving the CS+SENSE model across consistent optimization problems. In order to accurately compare our method to state-of-the-art techniques, we will ensure optimized CG performance through the use of Jacobi pre-conditioning [9] and Geometric Coil Compression [11] where applicable.

In this work, we empirically verify the linear computational scaling shown in [1] with respect to the size of the system being solved. The linear scaling is demonstrated through CS+SENSE reconstructions across multiple image resolutions, based upon 32-channel 3T acquisitions. Specifically, our HSS-Inverse approach scales efficiently with the number of imaging voxels and minimizes the influence of acceleration factor / the number of parallel imaging channels toward the reconstruction time. This results in > 6× speedup over iterative methods even when they take advantage of state-of-the-art pre-conditioning [9] and coil compression [11] techniques.

Theory

As described in [3], CS reconstruction involves solving an inverse problem in order to match an observed subset of data under an assumed sparsity prior. Here, MR images are assumed to be sparse or compressible under a TV and/or Wavelet transformation. We begin by briefly reviewing optimization methods for CS reconstruction. We will then summarize the application of iterative CG based approaches and our HSS-Inverse technique within the reconstruction framework.

Compressed Sensing with Total Variation Penalty

The CS formulation for MRI, as presented in [3], is an unconstrained optimization problem involving penalty terms based upon assumed TV and Wavelet sparsity. By pre-defining penalty weights α and γ, the CS optimization estimates the true image x ∈ ℂ^N:

$$\widehat{x}=\underset{x}{\mathrm{arg\; min}}{\Vert F_{\mathrm{\Omega }}x-y\Vert }_2^2+\mathrm{\alpha }{\Vert {\mathrm{\Psi }}^{T}x\Vert }_1+\mathrm{\gamma }\mathit{TV}(x).$$ (1)

Here, F_Ω ∈ ℂ^M×N is the under-sampled Fourier operator that transforms the image x into k-space to match the observations y ∈ ℂ^M. Therefore, the acceleration factor is R = N/M. The data fidelity is measured using the L₂ metric to represent RMSE against the observations. Ψ is the Wavelet transform that is applied to the image x and the L₁ metric is used to promote sparsity in that domain. Similarly, the TV operator computes a finite difference across the image x to promote sparsity in this spatial smoothness domain. In this work, we will focus on the more general parallel imaging problem and for ease of illustration only consider TV sparsity. By introducing complex coil sensitivity profiles {C_i}_i=1,K, the SENSE parallel imaging model can be incorporated into the CS formulation [5, 7, 10]:

$$\widehat{x}=\underset{x}{\mathrm{arg\; min}}\sum _{i=1}^K{\Vert F_{\mathrm{\Omega }}{C}_{i}x-y_i\Vert }_2^2+\mathrm{\gamma }({\Vert G_{\nu }x\Vert }_1+{\Vert G_{h}x\Vert }_1).$$ (2)

Note that the TV operator has been re-written as a sum of horizontal and vertical finite difference operators G_h and G_ν. The SB approach from [8] relaxes the L₁ penalties through the iterative construction of L₂ targets:

$$\widehat{x}=\underset{x}{\mathrm{arg\; min}}\sum _{i=1}^K{\Vert F_{\mathrm{\Omega }}{C}_{i}x-y_i\Vert }_2^2+\mathrm{\beta }({\Vert G_{\nu }x-g_{\nu }\Vert }_2^2+{\Vert G_{h}x-g_h\Vert }_2^2).$$ (3)

The targets g_v and g_h can be updated simply using a soft thresholding truncation parameter ε. For example, g_ν ← max (|G_νx| − ε/2, 0) sign (G_νx). This operation is linear-time and thus the computational cost is dependent on the quadratic minimization shown in (3). The explicit solution of this minimization problem is:

$$\left[\underset{T_F}{\underbrace{\sum _{i=1}^K{C}_i^H{F}_{\mathrm{\Omega }}^H{F}_{\mathrm{\Omega }}{C}_i}}+\mathrm{\beta }\underset{T_s}{\underbrace{(G_{\nu }^H{G}_{\nu }+G_h^H{G}_h)]}}\right]x=\underset{b}{\underbrace{\sum _{i=1}^K{C}_i^H{F}_{\mathrm{\Omega }}^H{y}_i+G_{\nu }^H{g}_{\nu }+G_h^H{g}_h.}}$$ (4)

Here, we denote T_F as the Fourier operator which has been combined with the Laplacian operator T_S. We will refer to the inverse problem as the solution of $\underset{A}{\underbrace{(T_F+\mathrm{\beta }{T}_S)}}x=b$ or evaluating x = A⁻¹b. It is important to note that T_F, T_S, and the parameter β are constant with respect to the SB iteration and only depend on the protocol and coil sensitivity maps.

Figure 1 shows the flow diagram for three possible reconstruction scenarios. The Matrix Free and Matrix implementations [12] utilize an iterative CG based solver and the direct HSS solver [1] is used for our proposed HSS-Inverse method. As can be seen in Figure 1, the CG based methods require an evaluation of the forward CS+SENSE operator. For the Matrix Free method, the operator A is evaluated by looping across all coils and performing FFT / sensitivity operations. Alternatively, the Matrix method directly computes the operator A and removes this dependency on the number of parallel imaging channels. With the incorporation of channel compression techniques, the dependency of Matrix Free methods on the number of parallel channels can be reduced. Specifically, for the large array coils and Cartesian sampling used in this work, Geometric Coil Compression [11] can be effectively employed with only small loss in reconstruction accuracy. In the case of our HSS-Inverse method, a compact representation for the inverse operator A⁻¹ is formed using the HSS linear solver. This is accomplished by performing a structured factorization of the matrix A into lower diagonal L and diagonal D components: A = LDL^H. Here, many of the terms in L can either be inverted easily or represented using low-rank modeling. This allows for efficient evaluation of the inverse model.

Figure 1.

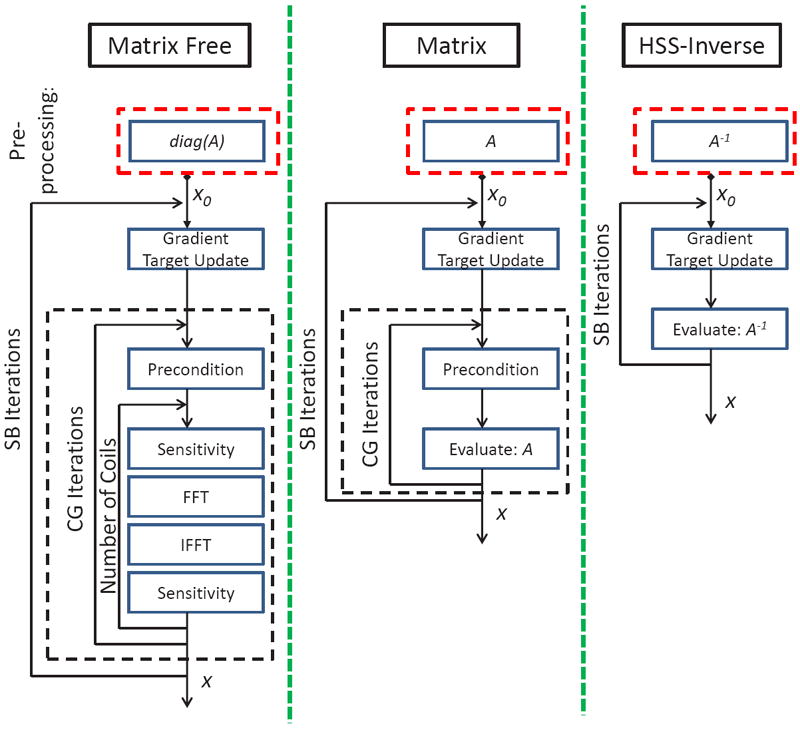
Split Bregman CS+SENSE implementations are illustrated. The required pre-computation is shown above the corresponding flow diagrams. The Matrix Free and Matrix methods rely on iterative CG solutions, while the HSS-Inverse method gives a direct solution for each Split Bregman iteration. The CG based approaches are optimized with the diagonal Jacobi pre-conditioner.

The impact of hierarchical compression can be clearly seen when comparing the HSS solver to optimized Cholesky based methods such as CHOLMOD [2]. Figure 2 shows the computational scaling of the algorithms with respect to image size. Here, the size of the matrix corresponds to the number of voxels in the 2D images, which range from 112 × 112 to 448 × 448. To put this in perspective, the largest image has 200K voxels and an explicit representation of the dense matrix A⁻¹ would require over 600GB of memory to describe the 40 · 10⁹ entries. Even if this matrix could be explicitly formed, the numerical evaluation would be extremely slow with a scaling of O (N²). Alternatively, the representations for A⁻¹ using CHOLMOD and HSS are much more compact and computationally efficient. The inverse evaluation time is shown for CHOLMOD and the HSS solver using a 10⁻⁶ tolerance across several relevant image sizes. The matrices are associated with a R = 3 acceleration and 32 receive channels. The difference between the O (N^1.5) scaling of CHOLMOD and the O (N) scaling of the HSS solver can be clearly observed. It is important to note that our HSS solver is implemented in MATLAB and the CHOLMOD solver we compared against is a highly optimized C++ implementation of [2]. It is expected that a highly optimized C++ implementation of the HSS solver will be faster for all image sizes. As we will demonstrate, the HSS evaluation of A⁻¹ has minimal dependency on the number of parallel imaging channels and the CS acceleration factor.

Figure 2.

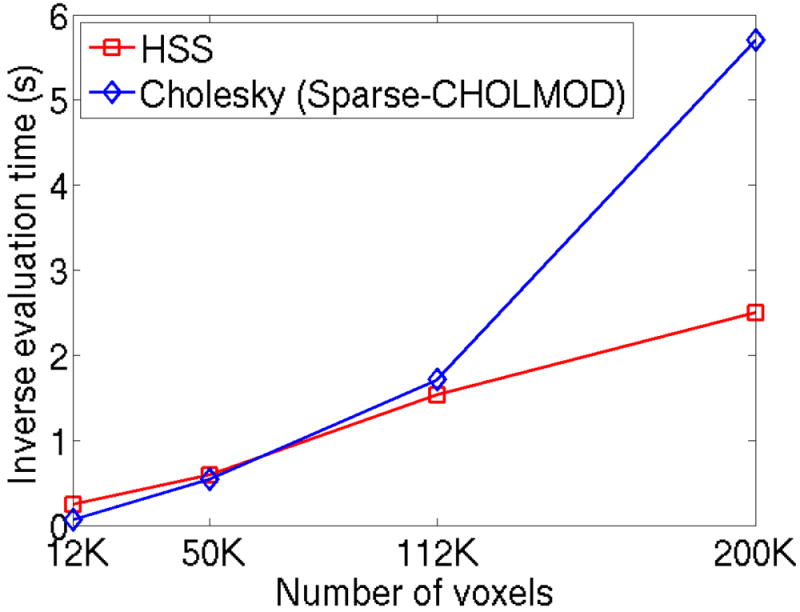
Computational scaling with respect to image size for non-iterative inverse methods. The time for a single inverse evaluation is shown for the optimized sparse Cholesky decomposition CHOLMOD and the HSS solver using a 10⁻⁶ tolerance. The matrix is associated with a R = 3 acceleration and 32 channels. The images range in size from 112 × 112 to 448 × 448.

Finally, the pre-computation trade-off for each method is shown above the respective flow diagrams in Figure 1. It is important to note that all of the CG methods can be optimized to exploit the Jacobi pre-conditioner, i.e. diag (A). Thus, the Matrix Free method computes the least information prior to reconstruction and HSS-Inverse pre-computes the most information (requiring an efficient representation for the inverse of the encoding matrix).

Methods

The focus of this work is on the application of a HSS solver for efficient Split Bregman reconstructions with SENSE parallel imaging. We evaluate the performance of our HSS-Inverse method against several CG based approaches to highlight the computational trade-offs for reconstruction. The computational scaling for all approaches are analyzed with respect to the image size and the number of parallel imaging channels. The image accuracy for all methods is computed as RMSE against the complex coil combined images from the fully sampled data. Therefore, our results include computational aspects for the algorithms and analysis of the methods using the acquired data. Exhaustive sweeps of TV and soft-thresholding parameters were performed for “best case” accuracy. In practice, methods such as [13, 14] could be used. As both the CG and HSS solvers have controllable accuracy, we choose a typical 10⁻⁶ criteria for all methods to ensure consistent results across the reconstructions.

In order to accurately compare the different CS approaches, multi-contrast in vivo data were acquired from a healthy volunteer subject to institutionally approved protocol consent. The data were acquired on a 3T Siemens Trio with the standard Siemens 32-channel head array coil. T2-weighted and Fluid Attenuated Inversion Recovery (FLAIR) images were acquired with a 224 × 224mm² FOV, across 35 slices with a 30% distance factor. The T2-weighted scan uses a Turbo Spin Echo (TSE) sequence with imaging parameters TR = 6.1s, TE=98ms, flip angle=150°, and a resolution of 0.5 × 0.5 × 3.0mm³, with a matrix size of 448 × 448. The FLAIR scan uses a TSE sequence with an inversion pulse and imaging parameters TR = 9.0s, TE=90ms, TI=2.5s, flip angle=150°, and a resolution of 0.9 × 0.9 × 3.0mm³, with a matrix size of 256 × 256. The fully sampled uncombined complex k-space data were retrospectively under-sampled for all computational experiments. In order to examine the computational scaling of the CS reconstruction algorithms, data sets of consistent size were generated across the multiple imaging contrasts. Where applicable, matrix sizes of 112 × 112, 168 × 168, 224 × 224, and 280 × 280 were constructed by down-sampling the coil data. We utilize these images to represent resolutions of 0.8, 1.0, 1.33, and 2.0 mm for the same FOV. In this work, data from two representative imaging slices will be used as test cases for the performance of the reconstruction methods. Sensitivity maps were created using JSENSE [15] estimation and used for all reconstructions. A 10^th order polynomial was used to fit the sensitivity profiles during the iterative JSENSE sensitivity map estimation. The polynomial fitting was performed only across a masked region of the brain.

We consider random under-sampling schemes based upon the method described in [3], where a variable polynomial density factor of 6 and a 1/R partial distance was used to generate each of the 1D under-sampling patterns. The results of the CS reconstructions are compared to the SENSE reconstruction using fully sampled data and the assumed sensitivity maps. In this work, our error metric is defined as the normalized root mean squared error against the SENSE images for any of the contrasts. All algorithms were implemented in MATLAB and numerical experiments were performed on AMD Opteron 6282 SE 2.6 GHz processors. MATLAB was run in single threaded mode to give accurate computational scaling for all of the methods. The standard MATLAB implementation of CG was used with the sparse Jacobi pre-conditioner. When investigating the impact of coil compression for CG based approaches, the Geometric Coil Compression MATLAB code associated with [11] was used. The MATLAB implemented HSS solver was provided through a request of the authors of [1]. Similar to the tree based FFT algorithm, the HSS solver used in this work can be easily made parallel for improved performance. We consider this to be future work for the proposed HSS-Inverse method.

Results

Figure 3 shows the HSS-Inverse reconstructed images and error for T2 and FLAIR imaging contrasts at resolutions of 0.8 × 0.8 × 3.0mm³ and 1.0 × 1.0 × 3.0mm³ respectively. In addition, Figure 3 illustrates the effect of channel compression on the reconstruction error. Figure 3(A) shows the R = 1 sensitivity combined images from the fully sampled 32-channel T2 data. The reconstructed images and error are shown below for 32 and 8-channel under-sampled data, assuming R = 3 and 4 accelerations respectively. The coil compression method [11] is used to project the 32-channel under-sampled data to 8 effective channels. This projection is also applied to the sensitivity maps. The dynamic range for the error images is scaled to 1=8 of the R = 1 images seen in Figure 3(A). Similar results are shown for the FLAIR images in Figure 3(B). When considering the original 32 channels, the R = 3 and 4 reconstructed T2 images had errors of 6.8%, 9.8% for the middle slice and 6.0%, 8.9% for the upper slice. The reconstructed FLAIR images had errors of 8.0%, 9.3% for the middle slice and 7.1%, 8.3% for the upper slice. Error for the 8-channel compressed reconstruction is measured against the fully sampled combination across the original 32 channels. Thus, this includes the error due to coil compression loss which was under 0.2% across all cases considered in this work. As alluded to above, the tolerance for the linear solvers used in each CS strategy leads to nearly identical reconstructions. Figure 4 shows the relative difference between the images reconstructed using the Matrix Free and HSS-Inverse methods. These extremely small differences are calculated by first subtracting the images and then scaling each voxel by the image intensity.

Figure 3.

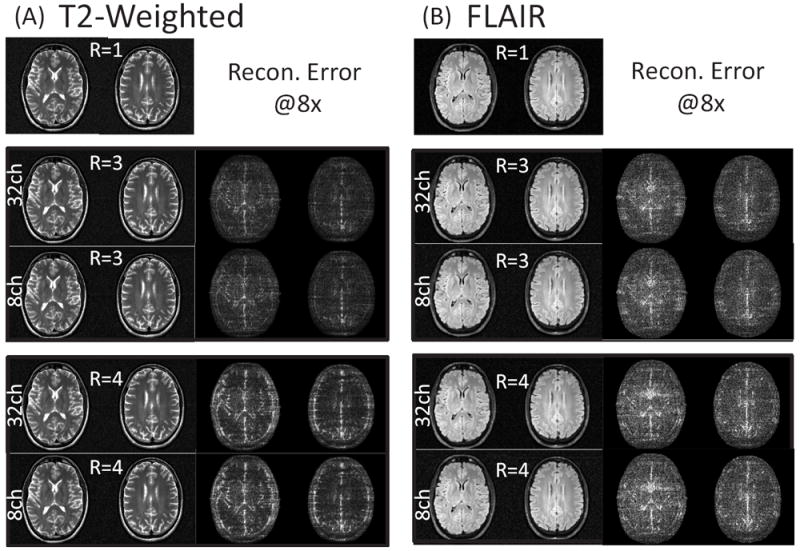
CS+SENSE reconstructed images and error for T2 and FLAIR imaging contrasts. The dynamic range for the error images is scaled to 1/8 of the fully sampled and sensitivity combined ground truth images. (A) shows the R = 1 sensitivity combined images for the T2 contrast at a resolution of 0.8 × 0.8 × 3mm³. The reconstructed images and error are shown below for R = 3 and 4 accelerations using either the coil compressed 8-channel under-sampled data or the full 32-channel data. Similar results are shown for the FLAIR images at a resolution of 1.0 × 1.0 × 3mm³ in (B).

Figure 4.

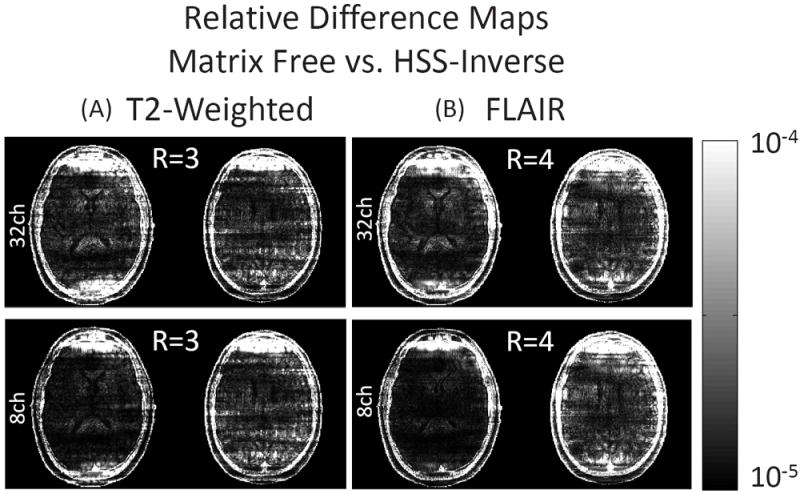
Relative difference in CS+SENSE reconstructed images for T2 and FLAIR imaging contrasts between the Matrix Free and HSS-Inverse methods. The relative difference is shown for R = 3 and 4 accelerations using either the coil compressed 8-channel under-sampled data or the full 32-channel data.

Figure 5 illustrates the computational scaling of several Split Bregman optimization techniques with respect to image size. The Matrix Free and Matrix methods rely on pre-conditioned CG to solve (4) and our HSS-Inverse method uses the HSS direct solver, see Figure 1 for algorithm flow-diagrams. In order to ensure consistent reconstruction error all numerical approaches assume a 10⁻⁶ tolerance for the solution (4). The times reported in Figure 5 correspond to 5 iterations of Split Bregman with a TV weighting β = 3 · 10⁻³ and soft-thresholding ε = 2 · 10⁻¹. The Jacobi pre-conditioner is used for all CG methods. The use of Cartesian optimized coil compression from 32 to 8-channels is explored for the Matrix Free method. The HSS-Inverse method had times of 1.1s and 5.4s for in-plane resolutions of 2 × 2mm² to 0.8 × 0.8mm². With the use of 4× channel compression the Matrix Free method became the best performing alternative to HSS-Inverse. It is important to note that the HSS-Inverse pre-processing time is not included in the reconstruction time since this calculation is independent of the acquired data and can be pre-computed. It is however noted that the model inversion time is small and increased linearly from 5s to 116s for these image sizes (and can be computed in parallel [1]).

Figure 5.

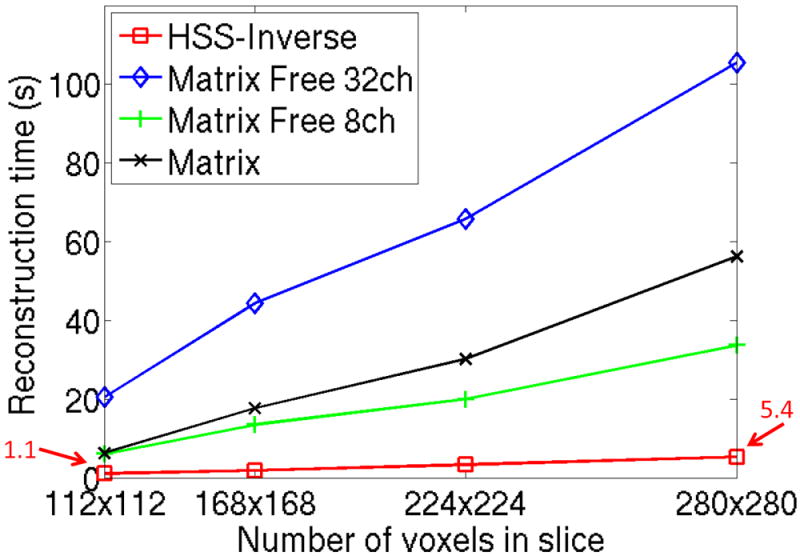
Computational scaling with respect to image size for CG and HSS based reconstruction methods, see Figure 1 for algorithm flow-diagrams. R = 3 acceleration is applied to the T2 weighted images. A 10⁻⁶ tolerance is assumed for all algorithms to ensure consistent final image error. All methods include 5 iterations of Split Bregman with a TV weighting β = 3 · 10⁻³ and soft-thresholding ε = 2 · 10−¹. The Jacobi pre-conditioner is used for all CG methods. The use of Cartesian optimized coil compression from 32 to 8-channels is explored for the Matrix Free method. The smallest and largest reconstruction times for HSS-Inverse are identified with arrows.

Finally, Figure 6 demonstrates the lack of dependence of the HSS-Inverse method on the number of parallel imaging channels and acceleration factor. Here, reconstruction parameters consistent with the results shown in Figure 5 are used. R = 2,3 and 4 accelerations are examined across in-plane resolutions from 2 × 2mm² to 0.8 × 0.8mm². The deviation in reconstruction time for HSS-Inverse was under 0.7s for all cases considered. This small deviation in time should be considered a constant based upon the numerical conditioning of the matrix A. The method from [1] automatically accounts for numerical stability in order to grantee accuracy for all possible linear system solutions. Alternatively, the Matrix Free computation time will increase linearly as the number of channels increases, see Figure 1.

Figure 6.

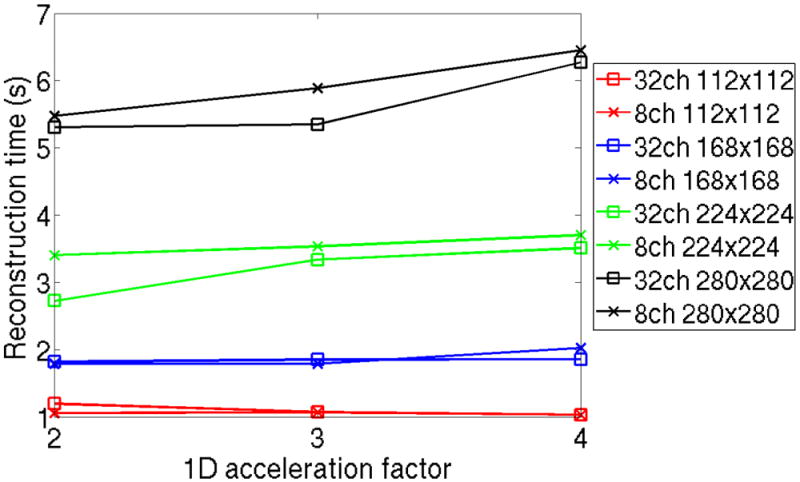
Computational scaling of the HSS-Inverse method with respect to the number of parallel imaging channels and acceleration factor. A 10⁻⁶ tolerance is assumed for 5 iterations of Split Bregman with a TV weighting β = 3 · 10⁻³ and soft-thresholding ε = 2 · 10⁻¹. Cartesian optimized coil compression is used to reduce from 32 to 8-channels. R = 2, 3, and 4 under-sampling is examined.

Discussion and Conclusion

In this work, we propose an efficient CS reconstruction strategy for MRI assuming SENSE parallel imaging. The proposed HSS-Inverse method exploits the fact that the Split Bregman framework produces a series of least squares problems with a fixed reconstruction operator. HSS-Inverse computationally outperformed all methods at all image sizes, with a reconstruction time of only 5.4s for a 280 × 280 image with 32 channels. When considering the full 32 channels, the speed-up of Matrix compared to Matrix Free reduced from 3.3× to 1.9× as the resolution increased. This is due to the superior computational scaling of the FFT operation for the Matrix Free method. Compression from 32 to 8 channels was required for the Matrix Free method to outperform the Matrix method at all of the resolutions. The speed-up for the 32-channel HSS-Inverse over the 8-channel Matrix Free increases from 5.7× to 6.3× when the in-plane voxel size was reduced from 2 × 2mm² to 0.8 × 0.8mm². This is a result of the linear scaling of [1] and the non-linear scaling for all other methods. In addition, we demonstrate minimal computational dependency with respect to both the acceleration factor and the number of parallel imaging channels for the proposed HSS-Inverse method. Given the dependence of the CG based Matrix Free method on channel count, we expect this speed-up to increase when considering larger array coils as additional compressed channels will be required for similar accuracy. It is important to note that the Matrix Free methods also utilize highly optimized FFT code and by re-implementing our MATLAB code into a lower level programming language we expect to see further improvement for the speed-up.

HSS solvers have been previously used to efficiently solve large-scale 2D and 3D problems in applied mathematics and physics. Linear-time scaling has been proven for many relevant 2D problems and O (n^4/3) scaling for 3D problems. In this work we have shown the applicability of this compact modeling strategy toward Split Bregman operators assuming 1D random under-sampling with in-plane resolutions up to 0.8 × 0.8mm². As was alluded to above, the efficiency of HSS-Inverse does not substantially change as the CS acceleration factor is increased which will ensure consistent reconstruction time regardless of the protocol. In addition, the HSS solver is non-iterative and the computational time should not be significantly affected by choice of CS penalty parameters. In the context of pre-specified MRI acquisition protocols, many factors for the HSS-Inverse method can be pre-computed and should enable clinically relevant reconstruction times, e.g. the computation of the inverse encoding matrix can be computed as part of a separate adjustment scan.

We have introduced the idea of compact representations for the inverse of CS+SENSE reconstruction operators. This is accomplished through the use of a non-iterative HSS numerical technique. The methods presented here should be applicable to many reconstruction operators that rely on locality of interactions, e.g. Wavelet transformations [16] and GRAPPA based parallel imaging [17, 18]. Finally, the proposed HSS-Inverse method should be amendable to computationally demanding applications such as cardiac imaging [10] wherein the problem size can become very large due to the additional time dimension.