Optimized Three Dimensional Sodium Imaging of the Human Heart on a Clinical 3T scanner

Abstract

Purpose

Optimization of sequence and sequence parameters to allow 3D sodium imaging of the entire human heart in-vivo in a clinically reasonable time.

Theory and Methods

A stack of spirals pulse sequence was optimized for cardiac imaging by considering factors such as spoiling, nutation angles, repetition time, echo time, T1/T2 relaxation, off-resonance, data acquisition window, motion and segmented k-space acquisition. Simulations based on Bloch equations as well as the exact trajectory used for data acquisition provided the basis for choice of parameter combinations for sodium imaging. Sodium phantom scanning was used to validate the choice of parameters and for corroboration with simulations. In-vivo cardiac imaging in six volunteers was also done with an optimized sequence.

Results

Phantom studies showed good correlation with simulation results. Images obtained from human volunteers showed that the heart can be imaged with a nominal resolution of 5 × 5 × 10 mm³ and with SNR>15 (in the septum) in about 6-10 minutes. Long axis views of the reformatted human heart show true 3D imaging capability.

Conclusion

Optimization of the sequence and its parameters allowed in-vivo 3D sodium imaging of the entire human heart in a clinically reasonable time.

Introduction

Tissue viability after an ischemic event is an important determinant in the decision to intervene with corrective measures (such as angioplasty or coronary bypass graft) in an effort to reperfuse the affected myocardial tissue (1). Sodium imaging provides a direct window into cell viability through altered functioning of the sodium pump. Under normal circumstances, the sodium pump maintains a gradient across the cell membrane whereby the extracellular concentration (~140 mmol/l) is much greater than intracellular concentration (~16 mmol/l) (2). After an ischemic event or an event that affects cell membrane viability, the intracellular concentration of sodium rises considerably (by almost threefold) resulting in a larger total sodium signal with MRI unless the area is completely occluded. Since sodium imaging provides a direct window into cell membrane viability, it can be an early and sensitive indicator in cancer, stroke and myocardial infarction (3,4).

Sodium nucleus has the second highest (second only to hydrogen) NMR sensitivity invivo. ²³Na has a lower gyromagnetic ratio (≅25% of ¹H) and lower in-vivo concentration. For example, concentration of sodium in healthy myocardial tissue is 43 mmol/l (1 liter of water = 111 moles of H⁺) (5). The signal from in-vivo sodium in myocardium is then about 12000 times lower than proton signal. Consequently, ²³Na imaging suffers from poor signal-to-noise ratio and increased scan times. A result of the lower gyromagnetic ratio is that B1 field required to induce nutation needs to be consequently higher (since α = γ∫ B1(t)dt). The sodium coil therefore typically has a higher B1 limit than the proton coil (B1 limit twice as high for ²³Na as ¹H for our coil). The excitation pulse is stretched by a factor of two to achieve the same nutation for sodium assuming operation at peak B1 to keep pulse duration at minimum. SAR increases proportionately as the square of the peak RF utilized. Therefore, SAR deposition in sodium imaging is approximately four times that in proton imaging.

Most techniques used to date rely on non-Cartesian trajectories to reduce echo time. For example, radial imaging has been used for studying the brain (6), heart (7), kidneys (8) and skeletal muscle (9). Boada et al. (10) have previously used a twisted projection technique for brain imaging while Ouwerkerk et al. (11) have presented a similar technique for cardiac sodium imaging. Few studies of 3D imaging of the heart have been done to-date. Pabst et al (12) used a spoiled gradient echo sequence to obtain 3D images of the heart in about 58 minutes. Similarly, Sandstede et al. (13) studied the time course of 23Na signal intensity after myocardial infarction using an ECG triggered 3D gradient echo sequence with a scan time of 30 min for six slices. A 3D radial projection technique was used by Jerecic et al (14) for cardiac imaging. Very recently, a stack of spirals has been used to perform sodium brain imaging at 7T (15).

To our knowledge, few studies have been done to optimize sequence and acquisition parameters especially for sodium cardiac magnetic resonance imaging. Lack of cardiac triggering leads to shorter acquisition time but triggering is typically employed (5,16) to reduce cardiac motion and blurring due to averaging of the systolic and diastolic phases of the heart (17). The need to perform triggering entails imaging in the non-steady state although constant rf excitation schemes can overcome this limitation. In this study, we first carried out a systematic optimization (for SNR/time) of pulse sequence parameters, including flip angle, echo train length (etl), echo time, repetition time, desired resolution and data acquisition window. Simulations were carried out to measure the point spread function (PSF) for a given acquisition based on the exact k-space trajectory of the spiral sequence. Simulation results were corroborated with results from imaging studies using a single channel sodium coil at 3T.

Theory

Case for Spiral Imaging

Spiral imaging (18-21) provides time efficient k-space coverage and has several advantages especially for sodium imaging. Chief among them are the possibility of reduced echo time (since the trajectory begins a k = 0) and reduced motion artifacts. In addition, the absence of off-resonant species such as signal from fat and the much reduced B₀ field inhomogeneity artifact (by virtue of gyromagnetic ratio being approximately 1/4 of ¹H) provide an ideal combination of circumstances for sodium imaging. Reduced off-resonance artifact allows for longer data acquisition windows. Motion artifacts are also much reduced as in proton imaging due to the inherent refocusing of gradient moments in spiral imaging. In addition, reduced gyromagnetic ratio (when compared with proton imaging) will lead to reduced dephasing of spins and therefore reduced artifacts. Previously described sodium imaging studies in the heart have used the 2D (7) or 3D radial (14) acquisition technique. While a true 3D radial technique (such as a cushball geometry) does enjoy the advantages of a very short echo time, it is not as efficient for k-space coverage. The volume scanned is spherical and prone to aliasing artifacts unless a large number of spokes are acquired. The geometry covered by 3D stack of spirals imaging is cylindrical which is conducive to complete cardiac coverage, especially when employing anisotropic resolution along the long axis. A longer scanning window has other advantages in that the percentage of time spent acquiring data per repetition time increases since duration of RF and crusher gradients stay roughly constant.

The k-space trajectory for spiral is defined by (22,23)

$$\mathrm{k}\left(\mathrm{t}\right)=\mathrm{A}\lambda \left(\mathrm{t}\right)\exp \left(\mathrm{j}\lambda \right(\mathrm{t})+\mathrm{jn}{\lambda }_0)$$ [1]

λ₀ is the spiral angle at the origin; λ₀ = 2π/N_s, where N_s is the number of spiral arms. λ(t) is the pitch of the spiral. A = k_max/(2πN_τ) where N_τ is the number of revolutions required to reach maximum pitch of λ(T_max) = 2πN_τ and j = √−1. The initial part of the spiral has constant angular velocity while the latter part is traversed with constant linear velocity. The function λ(t) = Ωt (1+t/T)^−1/2 describes such a spiral where T determines the transition from constant angular velocity (when t << T) to constant linear velocity (when t >> T). T is found by optimization such that the velocity and acceleration in k-space remain just within limits set by the gradient system.

Gradient Echo Variants

Two popular variations of gradient-echo imaging for the spiral trajectory are considered. The first (labeled as sequence A) is a gradient echo sequence where a large constant dephasing gradient (24) is applied after the acquisition and the phase encoding gradient is rephased after the echo (also known as SSFP-FID or FISP) while the second is the standard spoiled gradient echo similar to (A) except that RF spoiling is employed. This latter sequence is labeled sequence B in this work.

In the first case, a large but constant gradient is applied at the end of each TR while the RF pulses have the same phase. The large constant gradient provides a certain distribution of the phase φ of the transverse magnetization within a voxel. As shown by Buxton (25), if the gradient area is large enough, it is reasonable to assume that φ is distributed uniformly over the voxel. The resulting signal can then be calculated using the formulation from (26,27):

$$M(n+1)=\frac{1}{2\pi }\left[\int R_z\left(\phi \right)S(t,T1,T2)R_x\left(\alpha \right)\mathrm{d}\phi \right]M\left(n\right)+(1-E_1)M_0$$ [2]

R_z(φ) refers to the phase dispersion, R_x(α) is the rotation resulting from the RF pulse α, while S(t, T1, T2) corresponds to relaxation (see Appendix for detailed definitions); M(n+1) and M(n) are the magnetization values before and at the end of a given TR. E₁ = exp(−t/T1) and M₀ is the equilibrium magnetization. An optimized train of excitation angles is difficult to derive in this case. Unless TR >> T2, both longitudinal and transverse spins will contribute to the magnetization in the next TR.

The more familiar spoiled sequence (labeled as sequence B) employs a RF spoiling scheme such that the transverse magnetization at the end of each sequence is essentially zero. The magnetization evolution is given by

$$\begin{array}{cc}\hfill M_z(n+1)=& M_z\left(n\right)E_1\cos \alpha +(1-E_1)M_0\hfill \\ \hfill M_y(n+1)=& M_z\left(n\right)E_2\sin \alpha \hfill \end{array}$$ [3]

Flip angle

A constant flip angle train employed with the spoiled gradient-echo spiral scheme (sequence B) will lead to a filtering effect as the transverse magnetization varies from one TR to the next. To reduce this variation, an iterative scheme can be employed to derive the flip angle train (28) whereby

$${\alpha }_{n+1}={\sin }^{-1}\left[\frac{\sin {\alpha }_0\tan {\alpha }_n}{E_1\sin {\alpha }_0}+(1-E_1)\tan {\alpha }_n\right]$$ [4]

As noted, with sequence A, there is no standard solution to a constant magnetization. Consequently, a filtering effect can occur (based on T1 value) resulting in blurring.

Relaxation Effects

Sodium exhibits biexponential T2 relaxation with a short component (~0.5-3 ms) and a longer component (~20 ms) at 3T (29,30). Typically, 60% of the signal contribution comes from the short T2 species while the rest is from the longer T2 species (31). As an approximation, E₂ can to be replaced by a weighted sum of two bi-exponentials (E₂ = 0.6 × E₂₁ + 0.4 × E₂₂); where E₂₁ ≅ 1.5 ms and E₂₂ ≅ 20 ms. T1 value for sodium also shows some variation (~25-40 ms). For simulations, a value of 35 ms was used (32).

The 60:40 ratio of short and long T2 for sodium holds only in when motion of Na⁺ is restricted in some fashion, either by a gel matrix or charged macromolecules. For human in-vivo studies, the above ratio was modified to 15:85 (short:long T2) based on studies done in perfused ex-vivo rat hearts (33). Extracellular volume fraction in the normal myocardium is about 25%. The short T2 component in intracellular space is around 28% while it accounts for 11% of the extracellular sodium. Sodium concentration in ECV is 144 mmol/L and 16 mmol/L in intracellular space. Combining these factors gives a 15% contribution from short T2 and 85% from the long T2 species in-vivo.

Off-resonance

Given the low gyromagnetic ratio (γ_Na/γ_H = 0.26) of sodium, it follows that sodium imaging is less susceptible to off-resonance effects resulting from field inhomogeneity or susceptibility. In addition, motion related spin dephasing would also be reduced by the same factor (~ 4). In particular, chemical shift effects that occur from shielding of protons in lipid are absent in sodium imaging. The above observations make sodium imaging over a longer cardiac phase possible. In addition, spiral imaging will show reduced motion artifacts even with longer acquisition windows compared to rectilinear imaging. Assuming a variation of roughly ±50Hz (Figure 3 in (34)) across the left ventricle for proton imaging at 3T, this corresponds to a variation of just ±13Hz for sodium imaging. Thus, sodium imaging with a longer spiral acquisition window can be used when compared with traditional proton imaging.

Figure 3.

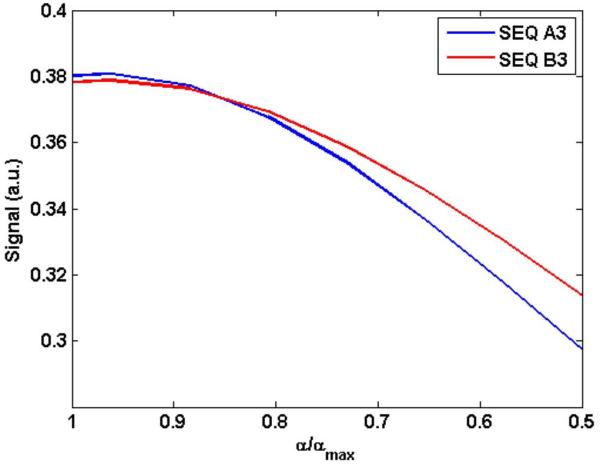
Simulated change in signal as a function of a change in the excitation angle as would be expected due to B1 inhomogeneity. A polynomial of order three was fit to get a smooth variation. α_max is the optimal flip angle as determined through simulations. TR = 40 ms for both sequences. The RF spoiled gradient echo sequence shows better B1 robustness compared with sequence A (SSFP-FID).

Motion

The quiescent period of the cardiac cycle (corresponding to diastole) can vary from 60 ms to about 300 ms (35). Since motion related dephasing follows the same principles as off-resonance, one would expect motion related artifacts to be lower by a factor of 4 in sodium imaging. Since resolution for sodium images is lower than proton images, partial volume effects will be present. However, cardiac motion is greater during systole, so there exists a trade-off between motion-related dephasing and increased acceptance window. Despite the use of a gating window, motion related blurring will result in an underestimation of signal and overestimation of infarct zone. Finally, by changing the order of spiral arms in a predetermined or random fashion coherent motion artifacts can be further reduced (36).

Methods

Excitation pulse

A modified 3D slab selective excitation pulse that allowed for a relatively short TE was used. The RF pulse was a truncated sinc-gauss with one left side lobe for shorter effective TE; pulse duration was 1.56 ms at a nominal angle of 70° for sodium imaging. The iterative solution (eq. [4]) for RF pulse train determination was introduced to determine the flip angles for echo train length in a realtime fashion.

Sequence Determination

To resolve which of the two choices ((A) or (B)) provides better signal, a simple 1-D Bloch simulation was performed. Bloch simulations were performed using equations [2], [3] and [4] with TR increases in steps of 5 ms from 15 ms to 50 ms. Since the echo time changes with the flip angle (due to pulse stretching), echo time recorded for a particular flip angle was used in the Bloch simulations. Three sequence variations were considered: (A) Constant gradient-echo dephasing with constant flip angle train (B) Spoiled gradient with constant flip angle train and (C) optimal flip angle train combined with sequence (B). To ascertain signal per unit time for segmented acquisition, the segmented acquisition during a cardiac cycle was set to a fixed value of 360 ms. Thus, for TR = 20 ms, the echo train length (etl) was 18, while with TR = 30 ms and TR = 40 ms, the etl was 12 and 9, respectively. To estimate the signal strength for each implementation, we considered the discrete Fourier transform of the transverse magnetization ([ℑ (M_y(nTR)], n=1,…,etl), which gives the filtered PSF. Peak of the PSF in turn provides knowledge of the signal strength achieved.

For each TR (changed in steps of 5 ms) for sequence (A) and (B), the flip angle was varied (in steps of 5°) to realize the maximum signal possible. Note that for the constant flip angle version of sequence B, the excitation angle does not necessarily correspond to the Ernst angle of α = cos⁻¹(exp(−TR/T1)). This is because the minimum TE changes with the excitation angle. For sequence B with varying flip angle along the etl, the maximum flip angle (at n = etl) was varied in steps of 5° to determine the maximum signal for a given TR.

B1 Inhomogeneity

Our current work used a single transmit-receive surface coil which results in considerable RF field inhomogeneity that is disadvantageous for clinical applications. As an alternative to correcting for it (which involves substantial acquisition time and post-processing), we modeled the B1 inhomogeneity resulting from a 50% drop from the prescribed angle for sequences (A) and (B). The achieved maximum value of PSF was then compared to the flip angle for (A) and (B). This provided an indication of the SNR drop to be expected for a 3D acquisition for slices away from the transmit/receive coil.

Imaging Resolution

To determine imaging resolution as a function of relaxation and field inhomogeneity, the exact spiral trajectory (based on equation [1]) was simulated in Matlab®. The segmented trajectory — where a fraction of the total number of spiral arms (given by etl) is acquired per cardiac trigger— meant that relaxation needed to be modified accordingly. Since the spiral arms were acquired in two shots (each shot duration = 360 ms), the k-space locations resulting from such an acquisition were modified to reflect the segmented nature of the acquisition. For example, magnetization for spiral arms 1,…,18 (for the case with 36 total arms) were calculated with initial magnetization M_Z = 1 for arm 1 and signal evolution for the 18 arms based on eqs. in [3]; M_z for arms 2-18 corresponded to recovered longitudinal magnetization from previous TR. Spiral arms 19,….,36 followed the same pattern with initial M_z for arm 19 being 1 (Figure 5). Exact imaging parameters were used to derive this PSF; values for TE, TR, T_acq and excitation angle were as recorded on the scanner. For example, for spiral sequence (B) with constant flip angle, when TR = 20 ms, spiral arms = 36 and flip angle = 35°, TE = 0.74 ms, T_acq = 15 ms and TFE factor (etl) = 18; when TR = 40 ms, spiral arms = 18 and flip = 40°, TE = 0.77 ms, T_acq = 35 ms, TFE factor = 9.

Figure 5.

Simulated k-space data for the exact spiral trajectory used for data acquisition. TR = 20 ms, TE = 0.74 ms, spiral arms = 36, echo train length = 18. Two shot acquisition and T2 relaxation effects can be easily perceived as the signal evolves from the center of k-space.

Off-resonance effects were simulated by introducing the factor (e^−iγΔB0^.t) where ΔB₀ is the field inhomogeneity. The magnetization was consequently modified using Δf = 13 Hz (value derived earlier). The signal obtained in k-space was then reconstructed using the gridding algorithm described by Jackson et al (37). Sampling density compensation was performed prior to gridding using a normalized density compensation factor calculated using (k_x(t).g_x(t)+k_y(t).g_y(t)). This was followed by a 2D inverse Fourier transform. The reconstruction was implemented in Matlab®. The FWHM (full width at half maximum) of the resulting PSF was used as an estimate for the final resolution, different from the nominal prescribed resolution.

Imaging

Phantom studies

All imaging was performed on a Philips 3T Achieva system equipped with a broadband amplifier with multinuclear capability. A surface coil with an integrated transmit/receive sodium coil and a transmit/receive ¹H coil (Rapid Biomedical GmbH, Rimpar, Germany) was used. Coil dimensions were 27 cm (R/L) × 28 cm (F/H) for the sodium transmit coil while the receive coil had dimensions of 18 ×18 cm. The Tx/Rx ¹H coil had dimensions 23.5 × 23.5 cm. The maximum achievable RF was 33 μT for the sodium coil and 13.5 μT for the proton imaging coil. A bottle containing 4% agar 150 mM NaCl gel was imaged using a 3D protocol (16 slices) with slices along the coronal direction parallel to the coil. Imaging parameters were FOV = 30 cm, ECG gated acquisition (60 bpm) over 360 ms of cardiac cycle, TR/TE corresponding to sequences A1-A3 and B1-B3 (constant flip and optimized flip); NSA = 16, prescribed resolution was 4 × 4 × 8 mm³, scan time 5:22. All comparison scans were performed in a single session since phantom positioning may otherwise result in variations in the measured SNR.

Human studies

Institutional review board approval was obtained for human studies. Six volunteers were imaged in the prone position with cardiac leads attached to the back. A double oblique scan was used to establish the left ventricular short axis as well as the long axis. Nominal resolution and imaging window of the cardiac cycle was kept constant at 5 × 5 × 10 mm³ and 360 ms, respectively. Other imaging parameters were: FOV ≈ 26 cm, α = 75°, TR/TE = 40/1.02 ms, T_acq = 35 ms, spiral arms = 18, TFE factor = 9, NSA = 22, number of overcontiguous slices = 18, scan time: 6-10 minutes (depending on heart rate). For comparison to reformatted (long axis) sodium images, long axis ¹H images were obtained using a single-slice, multiple phase segmented gradient echo sequence with the following parameters: FOV = 40 cm, TR/TE = 4.4/1.2 ms, α = 15°, partial k_y = 0.65, res = 4× 4×10 mm³.

SNR measurements

In order to prevent any background filtering from affecting SNR measurements, reconstructed images were converted to complex data format on the scanner. The files were read off-line in a Matlab® program and SNR measurements were carried out by placing ROIs in the object and the remote background. SNR was measured using standard formulation (S_ROI/σ_ROI where S_ROI is the signal in an ROI in tissue while σ_ROI refers to standard deviation of an ROI in the remote background).

Results

Phantom

Figure 1 shows the simulated and measured PSF with sequence A (SSFP-FID) for three different TRs (20, 30 and 40 ms) and constant flip angles 55°, 60° and 65°, respectively. The maximum in PSF was recorded for the given flip angles with the corresponding TR for the case when short:long T2 = 0.6:0.4. Measured SNR for the three cases obtained from the phantom study is shown as a square icon. The measured signal increased by 28.3% across the three TRs while the simulated signal increased by 31.3%.

Figure 1.

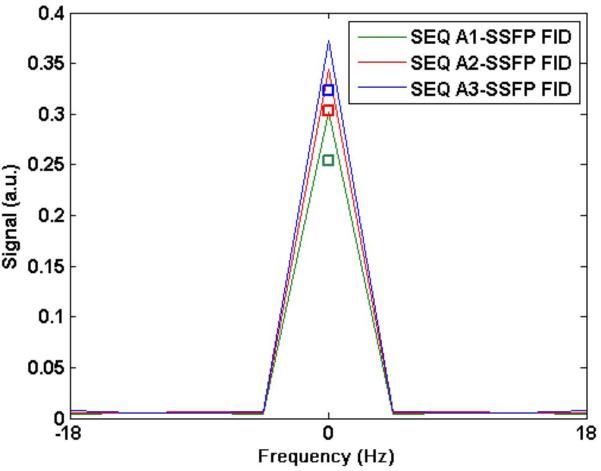
The signal resulting from sequence A (SSFP-FID) with three different TR times: (A1): TR = 20 ms, flip = 55°; (A2) TR = 30 ms, flip = 60°; and (A3) TR = 40 ms, flip = 65°. The square boxes near the corresponding peaks mark the measured SNR scaled to the value obtained from the simulated signal for sequence B3(opt) (see Figure 2).

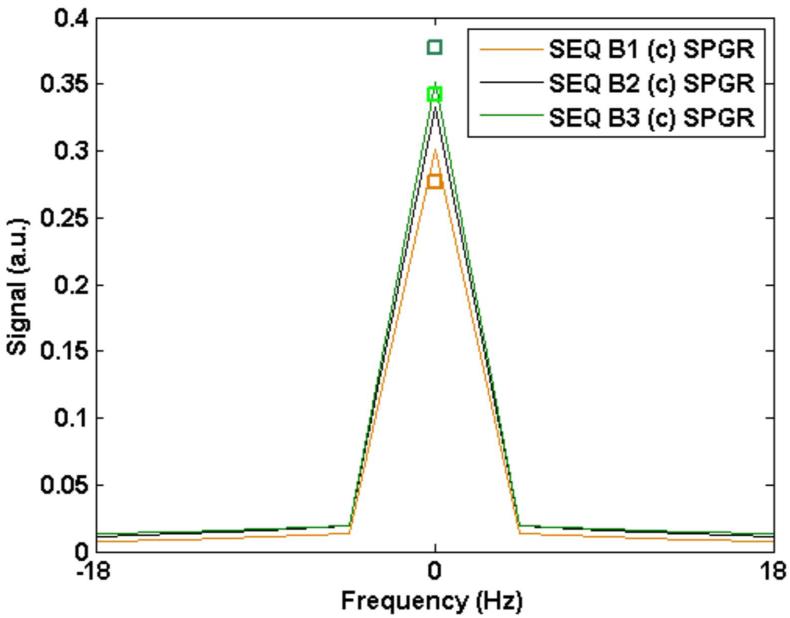
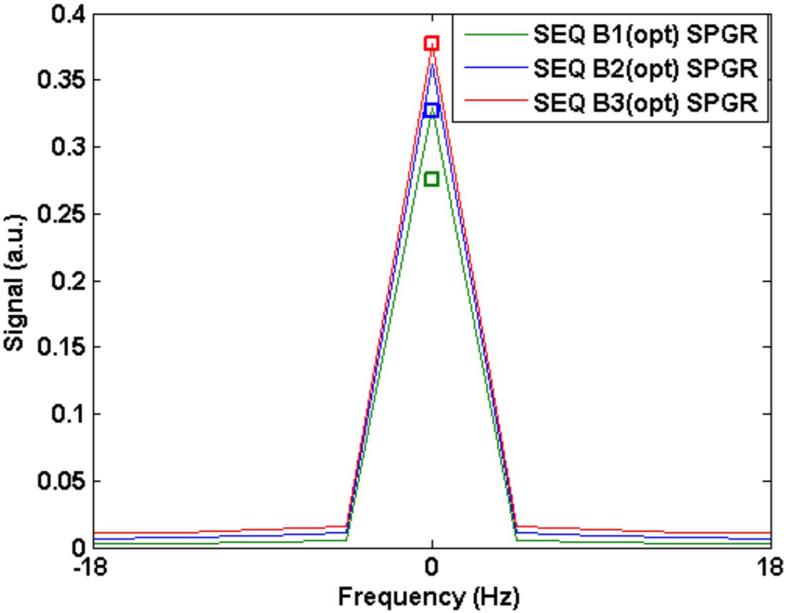
Figure 2 plots the simulated and measured PSF for sequence B (SPGR) with constant flip angle as well as with the optimized flip angle scheme described in the Theory section. Again, three sample cases are considered for illustrative purposes: (1) TR = 20 ms, flip = 35° (constant), flip = 45° (optimized train) (2) TR = 30 ms, flip = 40° (constant), flip = 50° (optimized) and (3) TR = 40 ms, flip = 40° (const), flip = 50° (optimized). A square icon indicated with each PSF shows the measured SNR for each case. For both Figures 1 and 2, values were scaled to the simulated value for sequence B3 (optimized) in order to provide a basis for relative comparisons between all values (simulated and measured). The difference in measured SNR between the constant and optimized train for each TR was minimal. The mean difference in measured SNR between the two cases (constant and optimized) for the three different TR sequences was 1.4% while the mean difference across the three sequences was 37%. The simulated difference across the three cases was 16.6%.

Figure 2.

A: The signal resulting from sequence B (SPGR) with an optimized flip angle scheme. Simulated signal from different TR times are shown: (B1): TR = 20 ms, flip = 45° (max); (B2) TR = 30 ms, flip = 50° (max); and (B3) TR = 40 ms, flip = 50° (max). The square boxes near the corresponding peaks mark measured SNR from the phantom scaled to the value obtained from the simulated signal for sequence B3(opt).

B: The signal resulting from sequence B (SPGR) with a constant flip angle scheme. Simulated signal from different TR times are shown: (B1): TR = 20 ms, flip = 35°; (B2) TR = 30 ms, flip = 40°; and (B3) TR = 40 ms, flip = 40°. The square boxes near the corresponding peaks mark measured SNR from the phantom normalized to the value obtained from the simulated signal for sequence B3.

These results show that for both sequences (A) and (B), longer TRs result in higher SNR. In addition, sequence B (SPGR) performs slightly better than sequence (A) at each TR (Figures 1 and 2). Of note, the flip angles corresponding to maximum signal strength are relatively higher with sequence (A) indicating higher SAR deposition.

Figure 3 shows simulated signal response for sequences (A) and (B) for flip angle variation from α_max to a lower value of 0.5×α_max. Figure 4 shows the measured SNR of slices obtained along the coronal direction (slices parallel to the coil with slice 16 being farthest from the coil). Both simulations and measurements indicate sequence B (SPGR) with constant or optimized flip angle train provides better robustness to B1 inhomogeneity than sequence (A). In addition, the signal provided by either the constant flip angle train or optimized train is very similar.

Figure 4.

Measured B1 inhomogeneity characteristics for the three sequences for TR = 40 ms. Measurements were taken in coronal slices parallel to the sodium coil. From the above, it’s apparent that sequence B3 (constant excitation or optimized train) provides better signal in the presence of RF inhomogeneity.

Relaxation and Off-resonance Effects

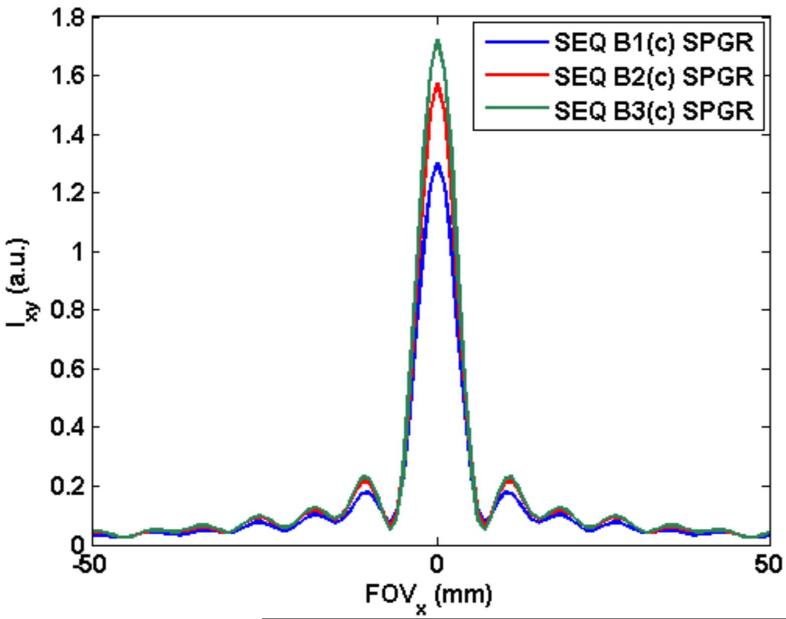
Since simulations and measurements showed that longer TR imaging provides better SNR per unit time, the upper limit on TR was determined. Typically, relaxation and off-resonance effects will result in a bound on the acquisition window (and therefore TR). Figure 5 shows the simulated k-space data for the spiral trajectory for sequence B1 with constant flip angle of 35°. Figures 6(A) shows the PSF for sequence B1 (SPGR), 6(B) shows the line profile through the PSF for the three sequences (B1), (B2) and (B3) with constant flip angles. The peak values for the PSF were 1.29, 1.59 and 1.72, respectively. This shows an improvement of about 37.5% (from TR = 20 ms to TR = 40 ms) which is close to the measured improvement of 34.5%. FWHM for sequences B1, B2 and B3 was equal at 6.8 mm while the nominal resolution was 4 mm. As described earlier, we consider a mean off-resonance of 13 Hz across the left ventricle. Simulations show that the peak of PSF deteriorates from 1.72 to 1.28 when TR = 40 ms while the peak deteriorates from 1.29 to 1.23 for the shorter TR of 20 ms. (FWHM stays the same at 6.8 mm.) This indicates that the relatively longer data acquisition of sequence B3 still outperforms the shorter acquisition of sequence B1 despite increased main field inhomogeneity related signal loss. Any further increase in TR (or a further increase in field inhomogeneity) provides diminishing returns as one gets a better response from shorter TR sequences. For example, for TR = 50 ms, the maximum value of the PSF (normalized for short duration differences) decreases from 1.73 to 1.09 due to the assumed inhomogeneity. We considered a TR of 40 ms as a reasonable compromise between increasing SNR versus off-resonance blurring and artifacts.

Figure 6.

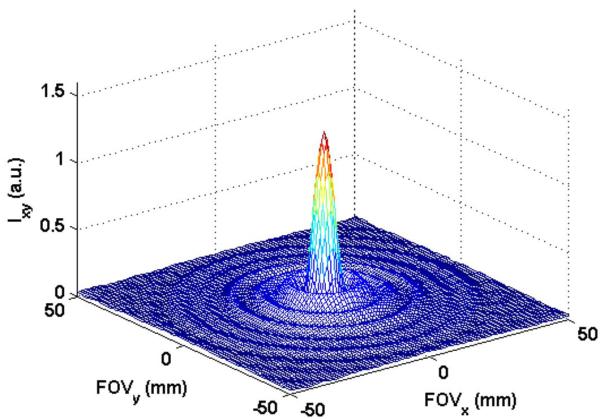
(A) PSF resulting from data acquired with sequence B1: TR = 20ms, flip angle = 35°, 36 spiral arms, echo train length = 18. Peak value of the PSF was 1.29. FWHM was 6.8 mm.

(B) Line profile through PSF (at y = 150 mm) resulting from data acquired with the three SPGR sequences B1: TR = 20 ms, flip angle = 35°, 36 spiral arms, echo train length (etl) = 18; B2: TR = 30 ms, flip angle = 40°, 24 spiral arms, etl = 12 and B3: TR = 40 ms, flip angle = 40°, 18 spiral arms, etl = 9. Peak values for PSF were 1.72, 1.59 and 1.29, respectively. FWHM was 6.8 mm for all three cases. Only the central 100 mm of FOV (= 300 mm) is shown.

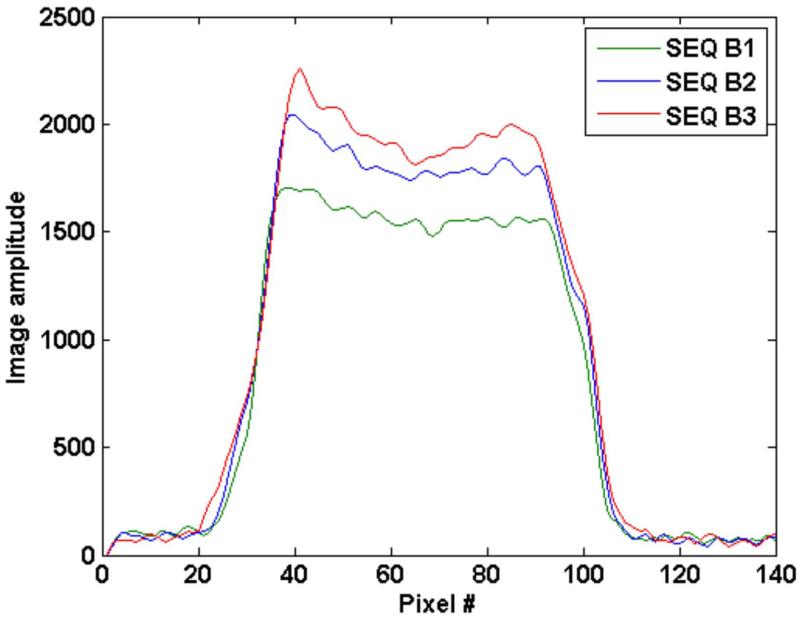
Figure 7 shows the line profile through the phantom reflecting the increased signal with increasing TR for SPGR sequence B1, B2 and B3. Note that no additional blurring is noticed (as at edges) with the increase.

Figure 7.

Line profile through image 5 (of 16 slices) for a NaCl/agar phantom obtained from three SPGR sequences B1, B2 and B3 with a constant flip angle train. Increased TR from B1 (TR=20ms) to B3 (TR = 40ms) does not result in increased blurring from T2 effects. Line profile was obtained by taking the mean of 20 line profiles (to reduce noise variation) around the center of the image.

In-vivo Imaging

In the in-vivo case with different ratio of short and long T2 sodium, simulations show a similar trend of increasing signal with increasing TR. The optimal TR based on off-resonance consideration is again 40 ms. However, the flip angle at which maximum signal is observed for the SPGR sequence with constant excitation angle was 75°. Using an optimal flip angle train gave maximum signal when the final angle was 80°. Maximum of PSF obtained by simulating along the spiral acquisition trajectory provided a slight edge for the constant flip angle case (~4% higher). When off-resonance was considered, PSF_max dropped by 25% for constant excitation SPGR sequence.

SSFP-FID sequence provided a slightly higher PSF_max at an optimal excitation angle of 90° (~2.6%) when compared with constant excitation angle SPGR. However, SSFP-FID suffers from greater signal reduction due to B₀ and B₁ inhomogeneity. As a result, sequence B3 (SPGR) with flip angle of 75° was used for in-vivo imaging. FWHM was the same for all sequences considered,

Imaging

Figure 8 shows the first 8 images (out of 16) obtained using the sodium phantom with sequence B3 (SPGR). The decrease in SNR with increasing distance from the coil is apparent. The measured SNR for the first 8 slices was 43.1 while is it was 33.5 across all 16 slices. Figure 9A shows sample short axis sodium images obtained from a volunteer. Figure 9B compares a reformatted long axis view of the sodium images with a corresponding long-axis ¹H image obtained at approximately the same cardiac phase. Both images are cropped and scaled to the same dimensions.

Figure 8.

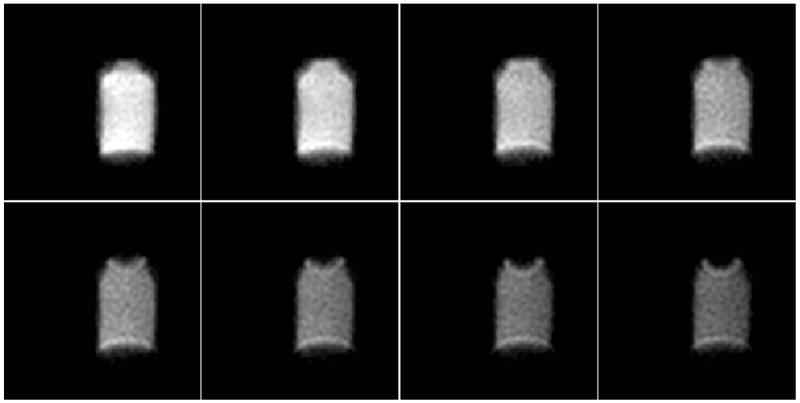
Eight contiguous slices (out of 16 slices) of the sodium phantom obtained using a 3D spiral sequence with optimized sequence values: TR/TE = 40/0.77 ms, 18 spiral arms with etl = 9, res: 4 × 4 × 8 mm³, NSA = 16. Total scan time: 5 min 22 s. All images with constant window/level = 1200/600.

Figure 9.

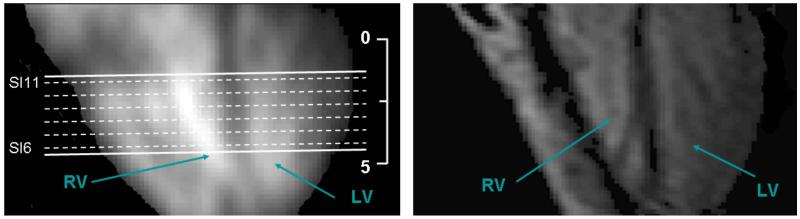
(A): Six (of 18) slices obtained along the short axis from a human volunteer (57 kg female) using the optimized 3D spiral sequence. True nominal resolution was 5 × 5 × 10 mm³ (reconstructed: 5 × 5 × 5 mm³). Total imaging time: 8:50. The images have been thresholded to reduce background noise.

(B): Reformatted view (long-axis) of the 18 slices (sodium imaging) shows the LV and RV. (Location of short axis images of figure 9(A) are shown as dashed lines on the long axis image.) The entire volume (of 90 mm from apex to base) was acquired in 8 min 50s. On right is the ¹H long axis image of a single slice (long axis view) acquired with the same volunteer. Ruler shows dimension in cm for both images.

The measured SNR in the septum over all slices where the septum was depicted for the six volunteers was 17±1.7.

Discussion

In-vivo sodium MRI requires extended scan times to realize sufficient SNR. In particular, sodium imaging of the heart requires efficient use of scanning time primarily to counter artifacts from patient motion (cardiac and respiratory motion, patient movement and patient-coil displacement) which typically increase with increasing scan time. Hence traversing the k-space in a fast, efficient manner is important. Since sodium T2 time is relatively short, a scan technique that is robust to motion and provides a short echo time is paramount. Stack of spirals imaging fulfills all the above criteria. Since the T1 of sodium is short (~ 25-40 ms), 3D scanning provides near theoretical √N advantage over corresponding N-slice 2D imaging. A favorable convergence of factors directly resulting from the gyromagnetic ratio (γ) of sodium being about one-fourth of γ for protons allows for extended data acquisition (of the order of T1 value) conducive to spiral imaging. Given the myriad number of combinations of possible MR parameters, Bloch equation simulations help to determine maximum predicted SNR in the setting of signal loss from relaxation effects, off-resonance and motion. Operating near the maximum B1 output of the sodium coil ensures lowest possible echo time. Counter-intuitively, constant excitation angle with a spoiled gradient-echo spiral performed better than an optimized flip angle train that aimed to keep magnetization constant from one repetition time to the next. On closer inspection, one can surmise that steady-state magnetization is achieved fairly rapidly for sodium since T1 ~ TR. As a result, a larger final excitation angle for the optimal excitation train results in marginally longer echo time and provides the constant flip angle train sequence a slight edge. A similar advantage is seen with relation to RF homogeneity; larger flip angles employed with sequence A resulted in more rapid fall off in excitation over a range of flip angles.

Relaxation and off-resonance can be studied by deriving the exact PSF. Although the absolute values of the PSF will change as a function of resolution, the relative PSF values depend only on relaxation properties, field inhomogeneity, excitation angle, echo time, repetition time and data acquisition window. For example, when in plane resolution was 5×5 mm², for TR = 40 ms, the maximum PSF ranged from 1.59 to 1.19 with Δf = 13 Hz. For TR = 20 ms, the PSF maximum ranged from 1.22 to 1.16, thus maintaining the trend. The FWHM was 7.9 mm for all TRs considered. While the FWHM does not change with off-resonance, PSF side lobes show increased amplitude and ripple effects. Note that the maximum PSF actually decreased from 1.72 to 1.59 when the spatial resolution changed from 4×4 mm² to 5×5 mm². This may be counterintuitive, but the signal is represented by the total volume under the PSF, approximated as PSF_max × (π × FWHM²/4); this gives a 25% higher value for the 5×5 mm² case versus 4×4 mm². Slice thickness was not considered in the optimization as it has no bearing on sequence parameters except for the total duration of the scan. Since each slice encoding is acquired in two shots, the number of slices will dictate the total scan time while 3D slab dimension (slice direction) affects the SNR. In this study, the number of spiral interleaves for a fixed TR was held constant. It’s possible to trade the number of interleaves with signal averages. For example, when TR = 40 ms, number of interleaves was fixed at 18 (etl = 9). If NSA is 16, number of interleaves could be increased to 36 (etl = 9) and NSA dropped to 8 to keep total scan time constant. Our simulations and phantom as well as in-vivo measurements showed minor changes resulting from such variations in combinations of interleaves and NSA. For example, three combinations of interleaves and NSAs were used (interleaves = 18, 9, 36; corresponding NSAs = 16, 32, 8). Maximum difference in SNR was 7% with the combination used in our experiments above providing the highest SNR. This is because in non-Cartesian sampling schemes such as radial or spiral imaging, increasing the number of spokes or interleaves acts as averaging since each spoke or arm is merely a rotated version of any other spoke or arm.

The contribution to total sodium signal from the faster relaxing sodium was calculated to be 15% based on studies in the reperfused rat heart. No studies on the ratio of fast to slow T2 contributions have been done in humans since toxic shift reagants are required to isolate the short and long T2 contributions. There is evidence that interspecies variation in the ratio does exist (38). A different ratio of (25:75) provided the same optimal solution although simulations showed a drop in signal of 11.6% over the (15:85) case as expected. ECV in infarcted myocardium can be much higher (~0.9 (39)). Accordingly, we studied the effect of the corresponding ratio (11:89) using simulations. Optimal solution (TR = 40ms, α = 75°) stayed the same while the signal was 2.85 times higher due to the much higher total sodium concentration as well as slightly increased concentration of long sodium T2 species. In addition, results obtained from phantom and volunteer studies were consistent with observations from simulations providing indirect support for the assumptions used in the simulations. In the six volunteers, the SNR for sequences B1, B2 and B3 was derived from ROIs placed on the ventricular septum. The SNR for B2 was 33% higher than for B1 and 47% higher for B3 compared to B1. Simulations showed increases of 20% (B2 vs B1) and 34% (B3 vs B1). Since RF inhomogeneity is a significant factor in the measured SNR, it is possible that the flip angle at which SNR is maximum can be different from the one derived through simulations. However, the difference is minor for a fixed TR and small changes in the excitation angle. For example, in phantom experiments, a flip angle of 55° (instead of 40°) resulted in a small drop in SNR (3%).

The relatively long echo time that was used will result in some loss of the sodium signal (about 25% of the total signal for the phantom and 12% in in-vivo imaging). The echo time was determined by two factors: (a) hardware limitation and (b) encoding scheme. Since the nutation angle is given by α = γ∫ B1(t)dt, the B1(t) field for sodium needs to be about four times that for proton imaging to achieve the same nutation angle. However, the peak B1 delivered by the ¹H coil is 13.5 μT while that delivered by the Na coil is 33 μT. This limitation means that the RF pulse is about 1.6 times longer for Na imaging than the corresponding pulse for proton imaging. Using a non-selective excitation pulse results in aliasing artifacts and minor reduction in scan time. Another factor that increased the echo time by ~0.3 ms was the need to perform k_z encoding with a stack of spirals. A k-space trajectory similar to the cushball radial imaging trajectory but with spiral arms for efficient coverage would result in a shorter echo time. A modified radial trajectory with longer data acquisition has been proposed recently (7). In addition, earlier works have looked at optimization based on T2 and field inhomogeneity effects for density adapted radial trajectory (40,41). However, as noted earlier, the stack trajectory may be better suited for cardiac geometry in that it covers a cylindrical space allowing for thicker slices along the long axis of the heart.

RF field inhomogeneity exacerbated by the use of a single channel surface coil resulted in a large variation in the measured SNR. For example, the SNR varied from 24.2 to 11.1 in the ventricular septum over all slices for a study subject. Previous studies have shown that the human eye is capable of discerning objects from the background with 100% certainty when the SNR > 5 (the Rose criterion (42)). The signal in the septum was well above this threshold for all volunteers. However, signal in the posterior wall away from the coil can fall below the threshold for slices. Improvements in coil design and correction techniques should overcome this deficiency. Total sodium concentration can only be determined when some technique for compensation of RF inhomogeneity can be employed.

One earlier work studied the advantage of retrospective (as opposed to prospective) gating for improving SNR (16). In our work, the window for the echo train to be played out was fixed at 360 ms. One would expect this time window to change with the heart rate. The number of spiral arms can be varied to change this window. For example, for TR = 40 ms and heart rate of 70 bpm, it would be possible to drop the number of arms by 1 (to 8) making the echo train time 320 ms. On the other hand, it could be increased to 400 ms with a lower heart rate. It is not clear whether using continuous non-triggered acquisition is beneficial. Our observations over a limited data set were inconclusive. In some subjects, image SNR with continuous scanning led to improved definition of the distal parts of myocardium. However, in other volunteers, non-triggered images exhibited greatly increased blurring and partial volume effects, negating any beneficial effects of improved SNR.

Earlier works on 3D sodium imaging of the heart have exhibited shortcomings. While 3D imaging of the heart was accomplished in 54 mins in (12), the work of (14) showed just one cardiac image from the 3D data set. TPI of the heart is more efficient (5); however, only a single slice with a hot color map overlaid on proton images makes it difficult to ascertain image quality (Figure 2 in (5)). A measure of the SNR was also not provided.

Conclusions

Simulations for optimization of parameters of a 3D stack of spirals sequence allows for the entire human heart to be imaged in about 6-10 minutes. To our knowledge, this work presents the first multiple cardiac sodium images from a full 3D set and the consequent reformatted images.

Appendix

$$R_z\left(\phi \right)=\left[\begin{array}{ccc}\hfill \cos \phi \hfill & \hfill \sin \phi \hfill & \hfill 0\hfill \\ \hfill -\sin \phi \hfill & \hfill \cos \phi \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$$

$$R_x\left(\alpha \right)=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \cos \alpha \hfill & \hfill \sin \alpha \hfill \\ \hfill 0\hfill & \hfill -\sin \alpha \hfill & \hfill \cos \alpha \hfill \end{array}\right]$$

$$S(t,T1,T2)=\left[\begin{array}{ccc}\hfill E_2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill E_2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill E_1\hfill \end{array}\right]$$