X-Ray Absorption Spectroscopy of Dinuclear Metallohydrolases

Abstract

In this mini-review, we briefly discuss the physical origin of x-ray absorption spectroscopy (XAS) before illustrating its application using dinuclear metallohydrolases as exemplary systems. The systems we have selected for illustrative purposes present a challenging problem for XAS, one that is ideal to demonstrate the potential of this methodology for structure/function studies of metalloenzymes in general. When the metal ion is redox active, XAS provides a sensitive measure of oxidation-state-dependent differences. When the metal ion is zinc, XAS is the only spectroscopic method that will provide easily accessible structural information in solution. In the case of heterodimetallic sites, XAS has the unique ability to interrogate each metal site independently in the same sample. One of the strongest advantages of XAS is its ability to examine metal ion site structures with crystallographic precision, without the need for a crystal. This is key for studying flexible metal ion sites, such as those described in the selected examples, because it allows one to monitor structural changes that occur during substrate turnover.

Introduction

Although x-ray absorption was described in the early 1900s (1–5), it was not until the advent of synchrotron light sources in the 1970s that x-ray absorption spectroscopy (XAS) began to realize its potential as a powerful structural tool. Synchrotron sources offer high-intensity light across a wide spectrum (up to ∼30 keV or 2 × 10⁸ cm⁻¹, λ = 0.4 Å), allowing application of XAS to a wide variety of elements. Synchrotron radiation provides several orders of magnitude more flux density than conventional vacuum tube sources and thus is especially suited to the study of dilute materials, such as metalloproteins in solution (6). XAS offers two key advantages for the study of metalloproteins. The most important of these is its ability to provide details regarding the local structure of a metal ion in frozen solution without the need for crystalline material, which facilitates the study of frozen reaction intermediates. The second advantage is its element specificity, which allows detailed studies of individual metal sites in heterodimetallic systems. Examples highlighting both advantages are discussed further below.

The application of XAS to metalloproteins has grown in frequency and sophistication with subsequent advances in monochromator (7–10) and detector design (11–15), and in the theory used to analyze the data (16–23). The technique itself has been reviewed extensively (6,24–26), along with the strategies associated with data collection (27). In this mini-review, we briefly discuss the physical origin of XAS before illustrating its application using dinuclear metallohydrolases as exemplary systems. The practicalities of data collection and analysis, specific to systems of this type, are addressed in the Supporting Material. The systems we have selected for illustrative purposes present a challenging problem for XAS, one that is ideal to demonstrate the potential of this methodology for structure/function studies of metalloenzymes in general. As the most commonly encountered metal ions in these systems are Zn(II) and Co(II) (as an in vitro replacement for Zn(II) or other biologically relevant metal ions), we will focus our discussion of the technique as applied to these ions.

Theoretical Background: The Physical Origin of XAS

XAS is a manifestation of the photoelectric effect, where incident light leads to ejection of a core electron, or photoelectron production. The onset of photoelectron production is accompanied by a rapid rise in absorption, referred to as an edge. The type of edge is determined by the principal quantum number associated with the initial state of the photoelectron, as illustrated in Fig. 1, with n = 1 (K shell) leading to a K edge and n = 2 (L shell) leading to an L edge. The L edge is split because a photoelectron that originates in the 2s orbital (L = 0, m_l = 0; L₁ edge) is different from one that originates in a 2p orbital (L = 1, m_l = 0, ± 1). The spin-orbit coupling of the 2p⁵ state that is generated from excitation of a 2p electron further splits the L edge into L₂ (m_l = 0, m_s = ¹/₂, m_j = ¹/₂) and L₃ (m_l = 1, m_s = ¹/₂, m_j = ³/₂) components. Because these are electronic transitions, they are governed by the same selection rules as optical absorption. Consequently, the probability of K-edge absorption is substantially higher than that of L-edge absorption. The degeneracy associated with the L₃ edge makes it twice as probable as L₂. Also indicated in Fig. 1 is the bound state 1s→3d transition that is common to open-shell, first-row transition metals (discussed below):

$$I_t=I_0\exp \left(-{\mu }_m\rho t\right)$$ (1)

$$A=\mu t=\ln \left(\frac{I_0}{I_t}\right)$$ (2)

At its most basic level, XAS is a simple Beer’s law absorption experiment, according to Eq. 1. The transmitted x-ray intensity, I_t, is directly proportional to the incident x-ray intensity, I₀, scaled by the element-specific mass absorption coefficient, μ_m (cm² g⁻¹), the density of the sample, ρ (g cm⁻³), and the sample thickness, t (cm). The absorbance can be expressed directly as the natural log of the incident intensity divided by the transmitted intensity (Eq. 2). However, the inherently low concentrations encountered in metalloproteins generally render the simple transmission measurement ineffective and one must resort to a more sensitive mode of detection, such as fluorescence.

Figure 1.

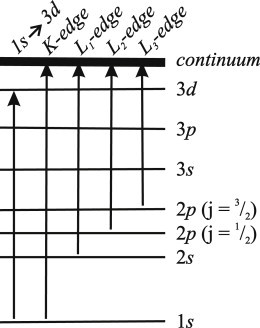
Electronic transitions associated with various x-ray edges.

Emission of a fluorescent photon is the dominant relaxation pathway for high-energy excitation. For lighter atoms of the second period, such as C or O, where the K edge is only a few hundred electronvolts, relaxation more commonly occurs by ejection of an Auger electron. However, for elements of the third period and beyond, where the K edge is greater than a few thousand electronvolts, Auger emission becomes less favorable. A simplified representation of the most common x-ray emission lines is shown in Fig. 2. Because emission occurs at a single, well-defined wavelength, the measurement of fluorescence excitation spectra allows one to use energy-dispersive (discriminating) solid-state detectors, which makes the application of XAS to dilute biomolecules substantially more accessible.

Figure 2.

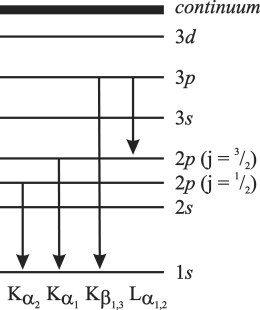
Simplified view of common x-ray emission lines.

A typical x-ray absorption spectrum, as shown in Fig. 3, can be divided into three distinct regions. Below the threshold (edge) energy of a given element (E₀), the incident x-ray photon has insufficient energy to cause core-electron ejection, and only background absorption from lighter elements in the sample matrix is observed. Historically, the region within approximately ±25 eV of the absorption edge (E ∼ E₀) is referred to as the x-ray absorption near-edge structure (XANES; the energy limits are somewhat arbitrary). This area of the spectrum is often called the near-edge x-ray absorption fine structure (NEXAFS) in the materials science literature, especially when dealing with lighter atoms. The extended x-ray absorption fine structure (EXAFS; E > E₀) region begins 20–50 eV beyond the absorption edge, continuing to higher energy. The acronym XAFS (for x-ray absorption fine structure) is often used in the literature as an umbrella term encompassing the fine structure associated with both the XANES and the EXAFS. The information content of the XANES and EXAFS is discussed in more detail in the following sections, and the methods necessary to extract this information are discussed in the Supporting Material.

Figure 3.

Example of an as-collected x-ray absorption spectrum at the Zn K edge.

XANES

The structure superimposed on the rising edge, observed in the XANES region of the spectrum, is due to transitions to unfilled molecular orbitals and continuum resonances, where the unbound final state is strongly perturbed by the electronic potentials of both the absorber and the surrounding atoms. Consequently, the shape and relative intensity of the XANES are indicative of the electronic structure and coordination geometry of the absorbing atom. Although investigators have made significant strides in developing the theory that describes the XANES (28–31), in practice, most still utilize this part of the spectrum as a fingerprint. The energy of the absorption edge effectively represents the metal ion’s ionization potential in the complex. Therefore, it is highly dependent on the oxidation state, typically shifting by ∼2 eV to higher energy per electron removed (24,32–35), and, to a lesser degree, on the composition of the donor set. The subtle differences in shape that accompany a change in environment are often more easily visualized by examining the derivative of the XANES (35).

For open-shell systems (d⁰–d⁹), bound-state transitions are often observed just below E₀. The 1s→3d transition that is typical of open-shell, first-row transition metals is forbidden by dipole selection rules. However, this transition is quadrupole allowed and therefore always exhibits some finite intensity. The 1s→3d transition becomes increasingly dipole allowed with increasing departure from centrosymmetry, due to greater mixing of the metal 3d and 4p orbitals. A quantitative comparison of XANES spectra requires prior normalization, which is usually accomplished by fitting a polynomial and scale factor to the data below and well above the edge (36), and scaling the result to match the atomic mass absorption coefficient (see Supporting Material for details) (37). The result of this procedure is an x-ray absorption spectrum whose edge jump is equivalent to that expected for a single atom in that environment.

Isolation of the 1s→3d transition from the rising absorption edge is typically accomplished by fitting a quadratic polynomial to the region immediately below the transition and an arctangent to the rising edge, above the transition, as illustrated in Fig. 4. The 1s→3d area is then calculated by numerical integration and divided by the mass absorption coefficient. In the case of Fe(II) and Fe(III) complexes, the intensity of the 1s→3d transition has been shown to be highly correlated with the metal coordination number, with the lowest intensity for six-coordinate Fe and the highest intensity for four-coordinate Fe (32,33). Similar correlations have been defined for Mn (38), Ni (39–41), and Co (see Fig. 4). The edge structure for Cu-containing systems is also diagnostic, but on a more complicated level. In contrast, as a closed-shell 3d¹⁰ ion, Zn(II) shows no pre-edge transitions, and only a slight dependence on coordination geometry and the composition of the donor set. In general, the first oscillation above the edge decreases in intensity relative to the white line, as the amount of sulfur donation increases (Fig. 5), and the white line increases with increasing coordination number.

Figure 4.

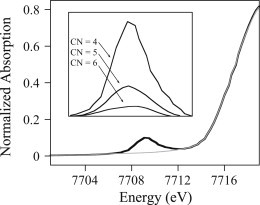
Co(II) XANES fit. Inset: trend in 1s→3d intensity for four-, five-, and six-coordinate Co(II).

Figure 5.

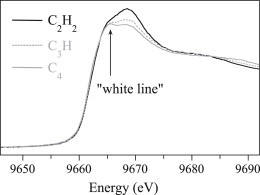
Four-coordinate Zn XANES spectra, with cys₂his₂, cys₃his, and cys₄ donor sets.

EXAFS

In contrast to XANES, the theory describing EXAFS is well established (16–23). As the energy of the incident x-ray photon increases, above E₀, the excess photon energy is converted to kinetic energy of the photoelectron. In K-edge spectroscopy, where the initial state is the absorbing atom’s 1s orbital, the ejected electron has an equal probability of propagating in any direction, allowing the photoelectron to be treated as a spherical wave with a characteristic de Broglie wavelength, λ = h/m_ev = 2hc/m_ev².

As the photoelectron radiates from the absorbing atom, there is a finite probability that it will encounter nearby atoms, scattering off of the nuclei. It is this scattering event that leads to modulation of the x-ray absorption coefficient, which arises from the interaction of the outgoing and backscattered photoelectron waves. The absorption coefficient is modulated by the amplitude of the backscattered photoelectron wave at the absorbing atom. As the incident x-ray energy is increased and the wavelength of the photoelectron is decreased, the outgoing and backscattered waves pass through regions of constructive and destructive interference. This results in local maxima and minima, respectively, in the absorption cross section (Fig. 6). When the photoelectron wavelength reaches an integer multiple of the absorber-scatterer interatomic distance, the outgoing and backscattered waves reinforce each other, enhancing the absorption cross section and resulting in a local maximum. As the two waves lose phase identity, they effectively cancel each other and a minimum in absorption is observed.

Figure 6.

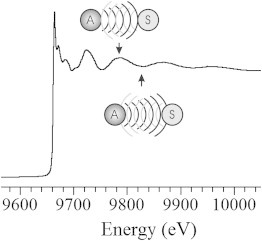
Phases associated with local maxima (top) and minima (bottom) in an x-ray absorption spectrum. Atom A represents the absorber, and atom S represents the scatterer.

The strength of the EXAFS lies in the precision and accuracy of the structural parameters that can be extracted from the data. This process (described in detail in the Supporting Material) entails background subtraction steps to first remove absorption by lighter elements and then the smoothly decaying atomic absorption of the atom of interest to isolate the oscillatory portion of the spectrum (the EXAFS), which contains the local structural information. The EXAFS amplitude is indicative of coordination number and scatterer size, whereas the frequencies report on absorber-scatterer distances, and a structural model is developed and tested by detailed curve fitting. The inherent distance resolution in any data set is limited by the energy range of the data (ΔR ∼ π/2Δk). Historically, the low signal/noise ratio at high k has limited EXAFS studies of metalloproteins to Δk ≤ 15 Å⁻¹, or ΔR ∼0.1 Å. Within this limit, it is extremely difficult to extract angular information for all but the simplest systems.

In practice, the accuracy of an EXAFS-derived average first shell bond length is ±0.02 Å for a group of similar scatterers, and this average first shell bond length has been shown to be a reliable indicator of coordination number (42) (better than the variable in curve fitting, which has an uncertainty of ±1). As shown in the Supporting Material, low-Z scatterers (nitrogen and oxygen) are difficult to distinguish from each other due to their similarity in size, but they are easily distinguished from larger atoms, such as sulfur. For the dinuclear examples discussed below, the analysis is complicated by the presence of multiple metal-binding sites (as a bulk technique, the EXAFS will measure the average coordination sphere), and for many studies, which hinge on detection of the metal-metal separation, it is further complicated by a background of multiple-scattering interactions from multiple coordinated histidines. A strategy for dealing with this complexity is outlined in the Supporting Material.

Application to Dinuclear Metallohydrolases

Dinuclear hydrolases encompass a vast array of enzymes with widely varying chemistry. Rather than attempt to review all cases that have been examined by XAS, we will restrict the following discussion to just a few in which XAS has made the most significant contributions. XAS has been used to study several aminopeptidases (N-terminal protein degradation) (43,44), AMP deaminase (nucleic acid metabolism) (45–47), prolidase (iminopeptidase) (48), DapE (bacterial peptidoglycan synthesis) (49), arginase (part of the urea cycle) (38,50), the acyl-homoserinelactone (AHL) lactonase (bacterial quorum sensing) (51,52), ZiPD (an RNA processing enzyme with phosphodiesterase activity) (53–56), and glyoxalase (detoxification of α-ketoaldehydes) (57,58). However, for the sake of brevity, we will focus our review on the use of XAS to study purple acid phosphatases (PAPs) and metallo-β-lactamases (MβLs).

PAPs

Phosphatases in general catalyze the hydrolysis of phosphate esters. There are a number of variations within this theme. For example, alkaline phosphatase is a nonspecific monoesterase, and its active-site structure has been examined by XAS (59). The dinuclear metal ion cluster in alkaline phosphatase is unusual in that it is not a cluster in the resting state (i.e., there is no bridge connecting the two catalytic Zn(II) ions). Only one of the two metal ions is required for enzymatic activity, and the other one dramatically enhances the turnover rate. Upon turnover, the product (inorganic phosphate) bridges the two metal ions. Mangani et al. (59) used EXAFS data to examine the effect of the population of the cocatalytic B site on the structure at the catalytic A site. Their study was one of the earliest to take direct advantage of the element specificity of XAS, along with the different binding affinities of the two catalytic sites. By comparing enzyme containing one equivalent of Zn(II) in the tighter-binding catalytic site (all Zn_A) with enzyme that had been preloaded with Zn(II) and supplemented with Co(II) (Zn_ACo_B), they obtained Zn K-edge EXAFS data that reported only on the local structure of Zn(II) in the A site. The data showed that the presence or absence of metal in the B site had no effect on the local structure of the A site.

By comparison, a considerably greater amount of mechanistic detail has been gleaned from EXAFS studies on PAPs, enzymes that hydrolyze a broad range of phosphorylated substrates (60,61). These enzymes are ubiquitous, having been isolated originally from bovine spleen (BSPAP), kidney bean (KBPAP), and porcine uterus (uteroferrin (Uf)). They have since been isolated from a number of other plant and animal species, including humans, where they have been suggested to play a role in iron transport, macrophage activation, and bone resorption. The active site common to all PAPs is a multiply bridged dinuclear center, which incorporates a pair of iron atoms in mammalian PAPs and a heterodinuclear Fe(III)-M(II) (M = Zn or Mn) cluster in plants.

XAS of bovine PAP was used very early on to determine that both metal ions were six-coordinate in a multiply bridged cluster (62), well in advance of the first crystal structure of any PAP (63). These initial studies further identified a directly coordinated phosphate, which was later shown to be bridging by crystallography (64), as illustrated in Fig. 7. The oxidation-state change, from Fe(II)/Fe(III) (pink) to Fe(III)/Fe(III) (purple), was confirmed by a 2 eV shift in the edge inflection, and the 1s→3d peak areas were used to confirm six coordination for both metal ions.

Figure 7.

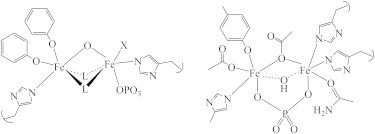
PAP active-site structure derived from XAS (left) and x-ray diffraction (1UTE, right).

EXAFS studies of the phosphate and arsenate complexes of the oxidized, diferric form of Uf provided strong evidence of the lack of a μ-oxo bridge, based on the lack of a short Fe-O distance, making Uf distinct from similar systems such as methane monooxygenase (65). The Fe-Fe distances observed (3.22 Å in the phosphate complex and 3.29 Å in the arsenate complex), together with Fe-P and Fe-As distances and associated angular constraints, were interpreted as arising from a bidentate bridging oxyanion. In the reduced form of the enzyme, the Fe-Fe distance increased to ∼3.5 Å, which was suggested to be indicative of a carboxylate shift, such that a bridging bidentate carboxylate in the reduced enzyme becomes a monodentate, nonbridging ligand in the oxidized enzyme to make room for the bridging oxyanion. These studies highlight one of the most important advantages offered by XAS, which is the ability to carefully monitor the oxidation state in redox active enzymes. As noted above, the edge position is indicative of the oxidation state, providing a sensitive internal reference.

Although similar studies of native Fe/Zn PAPs, such as those found in plants, have not yet been reported, several studies of a metal-substituted form of porcine PAP (Uf) have been performed. In one study, resting Fe(III)Zn(II) enzyme showed six-coordinate Fe and Zn sites with a metal-metal separation of ∼3.3 Å (66). Addition of phosphate left the primary coordination spheres and the metal-metal separation unchanged, with the appearance of a new outer-shell feature that could be attributed to metal-phosphorous scattering. The similarity of the M-P distances clearly showed that the phosphate bridges the two metals in a bidentate fashion (66). A later study showed that molybdate (MoO₄⁻) and tungstate (WO₄⁻), which inhibit the enzyme, formed similar bridging structures but with asymmetric cores, based on Zn-Mo(W) distances that were ∼0.4 Å longer than the associated Fe-Mo(W) distances (67). Together with electron paramagnetic resonance (EPR) and resonance Raman spectroscopy, XAS of the ternary complex of FeZnUf with phosphate and fluoride showed that F⁻ replaced a hydroxo bridge, based on contraction of the Fe and expansion of the Zn metal-ligand bond lengths (68). Based on these results, Wang et al. (68) suggested that the bridging hydroxide that is replaced by fluoride serves as the nucleophile in substrate turnover. More recent studies of the Fe(III)Ni(II) form of the enzyme supported this proposal (69). These four studies highlight the element specificity of XAS and its unique ability to examine both sites in a heterodimetallic center independently of each other, effectively doubling the available structural and mechanistic detail.

MβLs

The MβLs are a group of enzymes that confer bacterial resistance to penicillins and related β-lactam-containing antibiotics. These ubiquitous enzymes require one or two Zn(II) ions for catalytic activity and are generally unaffected by clinical inhibitors of the related serine β-lactamases (70,71). Approximately 50 MβLs have been reported, leading to their further classification into three subgroups (Fig. 8) (72,73). The B1 MβLs require two Zn(II) ions for full activity and prefer penicillins as substrates. They bind one Zn(II) in what is referred to as the Zn₁ (or 3H) site, which is made up of three histidine side chains and a solvent-derived ligand that bridges the two metal ions. The second Zn(II)-binding site, referred to as the Zn₂ (or DCH) site, consists of one histidine, one cysteine, a monodentate carboxylate, the bridging solvent, and a terminally bound water. The B2 enzymes require only one Zn(II) for full activity (they are actually inhibited by a second equivalent of Zn(II)), bind the catalytic Zn(II) in the Zn₂ site, and prefer carbapenems as substrates. The B3 enzymes, which prefer cephalosporins as substrates, generally require two Zn(II) ions for full activity, binding one Zn(II) in a canonical Zn₁ site and one Zn(II) in a modified Zn₂ site, where the cysteine is replaced by another histidine. Much of the mechanistic detail that has been derived for the MβLs has come from parallel studies of the native Zn(II) and Co(II)-substituted enzymes.

Figure 8.

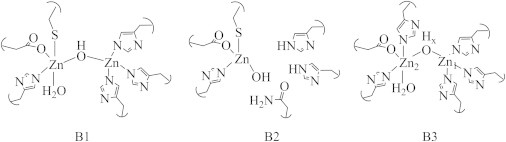
General structures for the three subclasses of MβLs.

Although there remains some debate regarding the physiologically relevant level of metal loading, it is widely accepted that all three subclasses are active with one equivalent of bound Zn(II), with the second equivalent improving the catalytic efficiency of the B1 and B3 enzymes. In light of these observations, the distribution of metal ions as the site is loaded and the individual role each plays in catalysis become critical issues for understanding the mechanism of antibiotic hydrolysis. The earliest application of XAS to the class B1 MβL from Bacillus cereus (BcII) identified the presence of sulfur in the zinc coordination sphere, but did not correlate this with metal loading (74). A later study of BcII containing 1.2 equivalents of Zn(II) showed fractional sulfur coordination (0.5 S per Zn), which was interpreted as partial occupancy of the Zn₂ site together with a small population of dinuclear enzyme (75). A subsequent study examined BcII containing one or two equivalents of Zn(II) and found that the first equivalent of metal was evenly distributed between the two metal-binding sites (76). XAS has also played a central role in a number of mutational analyses of BcII that were designed to delineate the factors that separate the MβL subclasses (77–79), but these studies are beyond the scope of this review.

It has since been shown that the minor differences in the two microscopic binding constants for BcII lead to near-statistical scrambling of the metal ions, with the presence of fully loaded, dinuclear enzyme being detected at substoichiometric metal concentrations (80,81), as predicted by the earlier EXAFS studies. A recent EXAFS titration of both Zn(II)- and Co(II)-loaded BcII generalized these results and clearly showed the presence of dinuclear enzyme with as little as 0.5 equivalents of metal per protein regardless of the metal ion (82). Similar behavior was seen in the B1 MβL IMP-1, which clearly showed distributed metal binding with one equivalent of added Zn(II) (83). The lack of significant metal-metal scattering suggests that this is not reflective of cooperativity. In contrast, Co(II) binding does appear to be cooperative, with dinuclear enzyme (indicated by significant metal-metal scattering) observed with one equivalent of added Co(II). Aside from minor differences, the binding sites in native (Zn(II)-bound) and Co(II)-substituted BcII and IMP-1 appear to be the same. XAS was similarly used to establish the distributed binding of Co(II) by the B1 MβL NDM-1 (84).

Unlike BcII and IMP-1, the B1 enzyme CcrA from Bacillus fragilis binds both Zn(II) and Co(II) sequentially, first fully loading the Zn₁ (3H) site and then populating the Zn₂ site. This has been shown through a combination of EXAFS, UV-Vis, EPR, and NMR spectroscopies (85,86). Similar behavior has been observed for the B3 enzyme L1 from Stenotrophomonas maltophilia (87). In each of these cases, it was shown that the Co(II)-bound form is slightly different from the native Zn(II) enzymes. The Co K-edge EXAFS for each enzyme indicated an expanded coordination sphere relative to the corresponding Zn(II) enzymes, most likely reflecting the incorporation of an extra solvent ligand by each metal ion in the Co(II)-containing enzymes. The lack of metal-metal scattering suggested that the di-Co(II) enzymes were not bridged, as is commonly observed in studies of MβLs. Interestingly, the absence of a bridge does not appear to affect the catalytic ability of the enzymes.

Distinct from all of the above examples is the B1 MβL from Bacillus anthracis (Bla2), which showed different metal-binding behaviors depending on whether the metal added was Zn(II) or Co(II) (86). Whereas Bla2 was shown to bind Zn(II) sequentially, similar to what was found for CcrA and L1, it clearly bound Co(II) in an indiscriminate manner, loading each site equally regardless of stoichiometry, thus resembling BcII, IMP-1, and NDM-1. Although it shares 89% sequence identity with BcII, the B. anthracis MβL provides a unique example of how small changes in outer-sphere residues can alter the metal-binding properties of an enzyme and tune its selectivity. The above results are summarized in Table 1.

Table 1.

Metal-binding behavior of dinuclear MβLs defined by XAS

Enzyme	Zn(II) binding	Co(II) binding	Co(II) coordination expansion	Zn-Zn separation	Co-Co separation	References
BcII (B1)	Scrambled scrambled	Scrambled	no	3.42 Å 3.70 Å	3.55 Å	(74,75,81)
IMP-1 (B1)	scrambled	scrambled	no	3.39 Å	3.45 Å	(82)
NDM-1 (B1)		scrambled	no	3.38 Å	3.45 Å (ZnCo) 3.51 Å (CoCo) 3.56 Å (CoCd)	(83,90)
CcrA (B1)	sequential	sequential	yes	3.44 Å	not detected	(84,85)
Bla2 (B1)	sequential	scrambled	yes	3.44 Å	not detected	(85)
L1 (B3)	sequential	sequential	yes	3.42 Å	not detected	(86)

EXAFS data recorded for the B2 MβL imiS from A. veronii shed light on the mechanism of metal ion inhibition, whose origin had not been previously understood (88). In the presence of one equivalent of Zn(II), the EXAFS of imiS was clearly consistent with the metal site defined by crystallography, with the metal ion bound at the Zn₂ site, including one cysteine sulfur and one histidine. When the enzyme in the presence of two equivalents of Zn(II) was examined, it was found that the level of sulfur contribution to the Zn K-edge EXAFS was the same (1.0 S/Zn), suggesting that the inhibitory site also included a sulfur ligand. A scan of the primary sequence of imiS revealed that the active-site cysteine was the only cysteine in the protein. However, several methionine residues were identified, including one that resides in the middle of an α-helix that was later shown to be mobile during substrate turnover (89), directly across from a histidine on the surface of the protein. Mutation of this methionine to an isoleucine fully abolished metal ion inhibition in imiS. A survey of MβL primary sequences showed that this methionine is only present in the B2 subclass, with no analog in the unstructured loops of B1 and B3 enzymes.

Two recent applications (90) frame the two areas where XAS can provide particularly unique information. The first focused on the reaction of L1 with substrate, opening a new line of research in this area. Earlier EXAFS studies of L1 included its product complex with hydrolyzed nitrocefin and showed that after hydrolysis, the bound product rotated in the active-site pocket, forming an unanticipated Zn-S bond (Fig. 9) (87). The Zn-Zn separation increased by 0.2 Å (from 3.42 Å to 3.62 Å) upon formation of this product complex. A later EXAFS examination of L1, freeze-quenched after 10 ms of reaction with nitrocefin, showed an even longer metal-metal separation of 3.72 Å (90). Together, these observations show that the transfer of physical stresses imparted by protein-associated motions may aid in the ring-opening reaction catalyzed by dinuclear MβLs.

Figure 9.

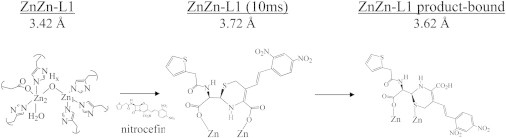
Variations in the structure of L1 during hydrolysis of nitrocefin, determined by EXAFS.

The second recent development involves the preparation of a series of homogeneous heterodimetallic forms of the B1 MβL NDM-1 (84). It was shown that by incubating the apoenzyme with one equivalent of either Zn(II) or Cd(II), followed by addition of one equivalent of Co(II), one can prepare heterodimetallic forms with fidelity, taking advantage of the similarity of the Zn₁ and Zn₂ sites’ affinities for Co(II) and their drastically different affinities for Zn(II), which loads the Zn₁ site, and Cd(II), which loads the Zn₂ site. This represents an important extension of the above studies because it affords the opportunity to exploit the element specificity of XAS, as described above for the mixed-metal phosphatases. A comparison of the four forms of NDM-1 (ZnZn, ZnCo, CoCo, and CoCd) showed nearly identical kinetic constants (within a factor of 5), and the metal-metal separations were shown to track nicely with the covalent radii of the metals involved, ranging from 3.38 to 3.56 Å (84,91) (see Table 1). Together, these two developments may enable investigators to study time-dependent local structure by specifically interrogating each side of an MβL dinuclear cluster independently in the same sample.

Conclusions

The above examples are not meant to comprise an exhaustive review, but rather to illustrate how XAS can contribute to the study of dinuclear hydrolytic enzymes. When the metal ion is redox active, XAS provides a sensitive measure of oxidation-state-dependent differences. When the metal ion is zinc, XAS is the only spectroscopic method that will provide easily accessible structural information in solution. In the case of heterodimetallic sites, XAS has the unique ability to interrogate each metal site independently in the same sample. One of the strongest advantages of XAS is its ability to examine metal site structure with crystallographic precision, without the need for a crystal. This is key for studying flexible metal sites such as those described above because it allows one to monitor structural changes that occur during substrate turnover. The metrical parameters provided by XAS are a critical link between solution and crystallographic structure, and allow for deeper interrogation of these systems using other techniques, as demonstrated above for Uf. For Zn(II)-containing systems, XAS may serve as the only available source of structural information in the absence of diffraction-quality crystals.

Supporting Citations

References (92–104) appear in the Supporting Material.