pH Alters PEG-Mediated Fusion of Phosphatidylethanolamine-Containing Vesicles

Abstract

Here, we examine the different mechanisms of poly(ethylene glycol)-mediated fusion of small unilamellar vesicles composed of dioleoylphosphatidylcholine/dioleoylphosphatidylethanolamine (DOPE)/sphingomyelin/cholesterol in a molar ratio of 35:30:15:20 at pH 7.4 versus pH 5. In doing so, we test the hypothesis that fusion of this lipid mixture should be influenced by differences in hydration of DOPE at these two pH values. An examination of the literature reveals that DOPE should be less hydrated at pH 5 (where influenza virus particles fuse with endosome membranes) than at pH 7.4 (where synaptic vesicles or HIV virus particles fuse with plasma membrane). Ensemble kinetic experiments revealed substantial differences in fusion of this plasma membrane mimetic system at these two pH values. The most dramatic difference was the observation of two intermediates at pH 5 but loss of one of these fusion intermediates at pH 7.4. Analysis of data collected at several temperatures also revealed that formation of the initial fusion intermediate (stalk) was favored at pH 7.4 due to increased activation entropy. Our observations support the hypothesis that the different negative intrinsic curvature of DOPE can account for different fusion paths and activation thermodynamics in steps of the fusion process at these two pH values. Finally, the effects of 2 mol % hexadecane on fusion at both pH values seemed to have similar origins for step 1 (promotion of acyl chain or hydrocarbon excursion into interbilayer space) and step 3 (reduction of interstice energy leading to expansion to a critical stalk radius). Different hexadecane effects on activation thermodynamics at these two pH values can also be related to altered DOPE hydration. The results support our kinetic model for fusion and offer insight into the critical role of phosphatidylethanolamine in fusion.

Introduction

Membrane fusion is one of the most fundamental processes in life and occurs when two separate lipid bilayers merge into a single continuous bilayer. Generally, membrane fusion is envisioned as a multistep process that proceeds from contacting bilayers through two semistable, nonlamellar lipidic intermediate states to a fusion pore (1). It occurs spontaneously only if the bilayers are highly curved and stressed at the point of their close contact (2) and the interbilayer space is dehydrated (3). Fusion proteins function in bending membranes and holding them in close contact (8), as well as in catalyzing lipid/water rearrangements for individual steps of the fusion process (5).

Membrane fusion is essential for lipid-sheathed viral entry. A specific viral fusion protein for each virus dictates the detailed mechanism of viral entry (e.g., entry via fusion with the cellular membrane or entry via a decrease of pH in the endosomal compartment). Apart from the requirement for a specific fusion protein, lipid composition plays a crucial role in membrane fusion (6,7). The lipid compositions of natural membranes are complex. In a previous study (8), we showed that an optimally fusogenic lipid composition (1,2-dioleoyl-3-sn-phosphatidylcholine (DOPC)/1,2-dioleoyl-3-sn-phosphatidylethanolamine (DOPE)/sphingomyelin (SM)/cholesterol (CH) in a ratio of 35:30:15:20) mimics the composition of mammalian membranes. Here, we report that fusion of this mixed-lipid system is quite sensitive to pH. Understanding the role of pH in fusion is especially important because influenza virus fuses with the endosome at pH 5, whereas HIV infection and all SNARE-mediated fusion take place at pH 7.4. The buffer pH could alter the phase behavior of this system or influence the physical properties of individual lipids in ways that might alter fusion. To our knowledge, no one has characterized the phase behavior of such a complex quaternary system. Without such a detailed analysis at different pH values, it is impossible to know precisely the extent to which phase separation might occur in our vesicles and how pH might influence this. However, we know that SM has a greater avidity than PC or PE for forming a liquid-ordered phase with CH (9), so such a SM/CH phase could reasonably occur to some extent in our small unilamellar vesicles (SUVs). This could explain their increased stability relative to PC/PE/CH SUVs (8). Since the choline headgroup of SM has a single pKa well below 3, we expect SM packing not to change significantly between pH 5 and 7.4, so the liquid-ordered phase, if it exists, should not be sensitive to pH. However, if such a phase separation were to occur, it would result in a liquid phase rich in DOPC and DOPE, both of which are fully miscible and fluid in the experimental temperature range, which is well above their phase transitions. Since the ionization of the PE headgroup does vary slightly between pH 5 and 7.4, we expect that the most pH-sensitive lipid in a DOPC/DOPE liquid phase is DOPE (10,11). Molecular-dynamics (MD) calculations suggest that a water hydration cage forms around the headgroups of zwitterionic PCs because of their methyl groups, whereas zwitterionic PEs (i.e., at low pH) engage in hydrogen (H)-bonding, either with other PEs or with water (12). Inter-PE H-bonding can occur between PEs in the same monolayer, but at low hydration it can span between monolayers, which is suggested to contribute an attractive component to interbilayer forces at low hydration (12,13). Also reflective of pH-dependent changes in PE hydration is the fact that PE has a distinct negative intrinsic curvature in bilayers at pH 5, as demonstrated by its distribution to the inner leaflet of egg PC/egg PE SUVs (14). Its negative curvature clearly decreases with increasing pH, since it distributes equally between the leaflets of sonicated 20–50 nm vesicles prepared at pD 11 (pH 10.3, with pD converted to pH (4)). Since the pKa of O-phosphoryl-ethanolamine is ∼10.2 (11), PE’s decrease in negative curvature with pH likely reflects an increasingly negatively charged headgroup as the pH increases, which could account in part for a change in hydration that would alter intrinsic curvature. As further evidence for the variation of PE hydration with pH, recent π-A isotherm measurements show that there is a significant drop in the average hydrated surface area of PE monolayers at the air-water interface at constant surface pressure between acidic (pH 5.0, 104 Å² /molecule) and neutral (pH 7.4, 92 Å² /molecule) pH (15). Even though PE remains roughly zwitterionic in this pH range (16), there should be some increase in the net PE headgroup charge in this range. This should lead to an increase in the average area per molecule due to simple electrostatic effects. The observed decrease in the mean surface area thus implies a change in PE headgroup hydration over this range, consistent with the increase in intrinsic curvature and the picture of PE headgroup hydration painted by MD (12). Based on these considerations, we envision PE at pH 5 as contributing to a highly ordered interface and interbilayer space in which PE-PE and PE-water H-bonding contributes to the observed negative intrinsic curvature (headgroup cross-section area < chain cross-section area) in lamellar structures. We expect that the contacting leaflets of our vesicles in the initial poly(ethylene glycol) (PEG)-aggregated state (state A in the kinetic schemes depicted below) should 1), be more weakly hydrated; 2), be somewhat farther apart; and 3), experience reduced positive curvature stress at pH 7.4 compared with pH 5. Here, we examine the hypothesis that these changes can account for the observed differences in fusion kinetics between low and neutral pH.

Materials and Methods

Materials

Chloroform stock solutions of DOPC, DOPE, and bovine brain SM were purchased from Avanti Polar Lipids (Birmingham, AL) and used without further purification. The concentrations of all the stock phospholipids were determined by a phosphate assay (17). Cholesterol was purchased from Avanti and then purified as previously described (18). A stock mixture of all lipids in the proper molar ratio was prepared in chloroform and spiked with small amount of ¹⁴C DPPC (Perkin Elmer, MA) so that the exact lipid concentrations could be determined by radiometry before experiments were conducted. We obtained 2-(4,4-difluoro-5,7-diphenyl-4-bora-3a,4a-diaza-s-indacene-3-dodecanoyl)-1-hexadecanoyl-sn-glycero-3-phosphoethanolamine (BODIPY530-PE), 2-(4,4-difluoro-5,7-diphenyl-4-bora-3a,4a-diaza-s-indacene-3-dodecanoyl)-1-hexadecanoyl-sn-glycero-3-phosphocholine (BODIPY500-PC) from Molecular Probes (Eugene, OR). Terbium chloride and N-[tris(hydroxymethyl)methyl]2-2-aminoethane sulphonic acid (TES) were purchased from Sigma Chemical (St. Louis, MO). PEG of molecular weight 7000–9000 (PEG 8000) was purchased from Fisher Scientific (Fairlane, NJ) and further purified as previously described (19). Dodecyl octaethylene glycol monoether (C₁₂E₈) was purchased from Calbiochem (La Jolla, CA). All other reagents were of the highest purity grade available.

Methods

Vesicle preparation

SUVs were prepared from a lipid mixture of DOPC/DOPE/SM/CH in a molar ratio of 35:30:15:20 in 10 mM TES, 100 mM NaCl, 1 mM EDTA, and 1 mM CaCl₂ buffer at pH 7.4 as previously described (20). We used an EDTA-buffered Ca²⁺ system to ensure that Ca²⁺ leached from the glassware would not add uncertainty to our results. Because the complexation constant for Ca²⁺ by EDTA is so large (K = [Ca₄EDTA]/[Ca]][EDTA] varies from ∼10⁴ at pH 5 to ∼10⁸ at pH 8), the amount of free Ca²⁺ is determined by the error limits of the measurements that are required to prepare the buffer and does not vary with pH or temperature (21).

Lipids mixing assay

Fluorescent lipid probes with fluorophores attached to their acyl chains (BODIPY500-PC and BODIPY530-PE; Molecular Probes, Eugene, OR) were incorporated into vesicles at 0.5 mol % each to measure lipid transfer between vesicles during PEG-mediated vesicle fusion, with a probe-containing/probe-free vesicle ratio of 1:4, as described in detail previously (1).

Contents mixing and leakage assays at pH 7.4

The Tb3+/DPA assay to measure contents mixing (CM) and leakage (CL) was performed according to the method described in Wilschut et al. (22) with some modifications (23).

CM and CL assays at pH 5

Mixing and leakage of the trapped contents of sonicated SUVs were monitored by the ANTS/DPX assay at pH 5.0 as described in detail elsewhere (1).

Structural fusion model and ensemble kinetics

We modeled our data in terms of a sequential four-state (three-step; Scheme 1) or three-state (two-step; Scheme 2) reaction, where each state is a thermodynamic ensemble of similar molecular arrangements (microstructures) (24). This is based on the structural model proposed by Siegel (25), although it is envisioned that the range of molecular microstructures that contribute to each thermodynamic state is much greater than that proposed in structural models. Although all steps of vesicle fusion are macroscopically irreversible in the presence of PEG, the second step is macroscopically irreversible even if PEG is removed (i.e., vesicle size increases in the absence of an aggregating PEG concentration) (26). In addition, lipids mixing (LM), CM, and CL are irreversible processes, further requiring the irreversible sequential treatment we developed previously (24). Our observations demand that CM, CL, and LM occur from t = 0 with no lag phase, thus requiring nonzero probabilities of CM (α_i), LM (β_i), and CL (λ_i) rates in different ensemble states of the fusion process. This is consistent with the expectation that each state in an ensemble kinetic analysis represents a multitude of different microstructures, in any one of which a transient leakage or intervesicle pore could form accompanied by mixing of lipids between vesicles. Observations of reversible or flickering pores as secretory (27) or model (28) systems evolve toward a final fusion pore support this view. In the accompanying diagrams, nV is the separated-vesicle state, A represents vesicles in contact within aggregates; I₁ is the semi-stable, initial intermediate state; I₂ is the semi-stable, second intermediate state; and FP is the final fusion-pore state. Scheme 2 shows the ensemble model in which the data are consistent with a single intermediate.

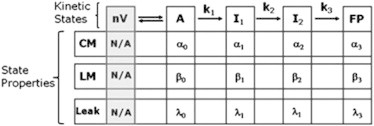
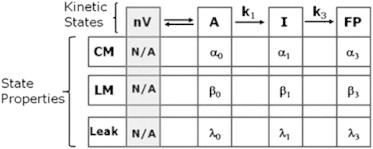
The rate constants for conversion between states are k₁, k₂, and k₃. The model can account for the time courses of five observables associated with PEG-mediated fusion (24), although the time courses of three basic observables (LM, CM, and CL) are sufficient to uniquely define rate constants that account for the other two observables (light scattering and the formation and disappearance of nonlamellar intermediates (29)) in all cases examined (24). In addition to the rate constants, the β_i, α_i, and λ_i values are required to define the probabilities of observing particular events in each state. Although this might seem to be an excessive number of parameters, experimental observations allow for elimination of some of them. The probabilities of CL and LM in the A state were negligibly small (i.e., α₀ = β₀ = 0), and a very small amount of LM takes place in the FP state (β₃ is assumed to be close to zero). Along with normalization conditions for the probabilities, this leads to three (k₁, k₂, and k₃) or two (k₁ and k₃) intrinsic rate constants and six ($\alpha ,\beta ,{\lambda }_0,\lambda ,{\lambda }_1,{\lambda }_2$) or five ($\alpha ,\beta ,{\lambda }_0,{\lambda }_1,{\lambda }_3$) extensive parameters to describe three independent observable time courses for three- or two-intermediate processes. In most cases, the observables are described by double exponentials, and four parameters are required to define an exponential. Thus, the parameters are not underdetermined.

Ensemble fusion kinetics compared with single-event analyses

Many labs follow fusion kinetics using single-event methods, which are now quite popular, as opposed to the ensemble kinetic model we used here and elsewhere (1,5). It is useful to relate the kinetic results obtained by these different methods. To obtain kinetics from single-event studies, one must record many traces of events that follow the initiation of fusion between docked membranes (vesicles attached to other vesicles or to membranes) and then analyze the time probability distributions (dwell-time distributions) to distinguish distinct events and obtain their characteristic times (rates). In two fairly recent studies, investigators performed such analyses and found, as did we, that at least two and maybe more events follow docking (30,31). In one particularly complete single-event analysis, biexponential dwell-time distributions with distinct preexponential factors defined fast and slow LM and CM events (31), consistent with assigning probabilities β_i and α_i to two evolving ensemble states. It is difficult to compare absolute rates of event evolution between different studies, as all experimenters design their systems to tune fusion rates to observable ranges. For instance, we use sufficiently low PEG concentrations to ensure that the fastest events we follow are roughly 10 times slower than the rate of PEG-mediated aggregation (i.e., docking), which is in the range of 0.3–10 s⁻¹ depending on the PEG concentration and mixing times (21,26). Although we cannot compare absolute rates between studies, if we compare relative rates for events within one study, we find that the fastest rates are roughly 10 times faster than the slowest rates, whether measured with dwell-time statistics or ensemble kinetics. Thus, the two experimental approaches for resolving fusion kinetics yield comparable results, although each has its own advantages and disadvantages. For our studies, in which we need to obtain rates of fusion events with considerable precision at multiple temperatures, the experiment-time advantages of ensemble kinetics weigh in favor of this method. In addition, ensemble rates can be interpreted in terms of ensemble activation thermodynamics as long as all elements of the ensemble evolve roughly in phase (i.e., assuming minimal ensemble broadening).

Transition-state thermodynamics

The methodology used to calculate the transition-state thermodynamics has been reported elsewhere (1), so we describe it only briefly here. If the initial and transition states for a process are in equilibrium, Eyring’s transition-state theory can yield information about the thermodynamics of the transition state relative to the initial state. We calculated the activation free energy of each step ($\Delta G_i^{\ast }$) using the equations $k_i=A{e}^{-\Delta G_i^{\ast }/k_{B}T};\Delta G_i^{\ast }=k_{B}T\ln \left(k_i/A\right)$, where k_i is the rate constant of different steps, and A is a preexponential factor. Here, A is an arbitrary constant (1) that does not take the classical Eyring form for gas-phase bimolecular reactions, because fusion is a complex process that does not have a simple reaction coordinate, such as the line along which two atoms collide in Eyring theory. This leads to the activation free energy having an arbitrary magnitude, although changes in activation free energy ($\Delta \Delta G_i^{\ast }$) have unambiguous units of kT. Plots of ΔG_i^∗ were fit to an empirical third-degree polynomial, and the coefficients of those fits are summarized in Table S1 in the Supporting Material. Activation entropy was calculated from these coefficients using the expression $\Delta S_i^{\ast }=-{\left[\delta \left(\Delta G_i^{\ast }\right)/\delta T\right]}_P$, with $\Delta H_i^{\ast }$ obtained as $\Delta G_i^{\ast }+T\Delta S_i^{\ast }$.

Errors in ΔG_i^∗ (Fig. 2) derive directly from errors in k_i values that are based on at least two time courses obtained at each temperature on each of three independently prepared samples. We must ask whether a third-degree polynomial is a reasonable function to describe our data. Ideally, the fitting function should be theoretically appropriate to describe the data, but it is impossible to know what function should theoretically describe a system as complex as the one we study. However, Taylor’s theorem posits that a convergent Taylor series can describe any function that is infinitely differentiable in a certain independent variable range. In the absence of phase transitions, thermodynamic state functions meet this requirement. The question is, is a third-degree Taylor series sufficient to provide a good approximation to ΔG_i^∗ over a narrow temperature range? To answer this, we seek to determine what thermodynamic predictions would result from assuming a third-degree polynomial, and whether higher-order polynomials or other functions might be more appropriate. The most obvious prediction is that ΔCp_i^∗ is linear in T. This is an eminently reasonable prediction, as even materials as complex as glass have heat capacities that are close to linear over a sufficiently narrow temperature range far from a transition, and our experimental temperature range is quite narrow. Next, an appropriate polynomial should have sufficient terms to describe the data, but no more, since excess terms would give ΔG_i^∗(T) features that are not supported by the experimental data. Although we cannot predict the appropriate temperature dependence of ΔG_i^∗, we see that a third-degree polynomial meets the criteria that it 1), is mathematically plausible in a narrow temperature range; 2), makes reasonable thermodynamic predictions for such a temperature range; and 3), is simple enough to avoid introducing thermodynamic features that are likely not inherent to the data, i.e., a complex dependence of ΔCp∗ on T.

Figure 2.

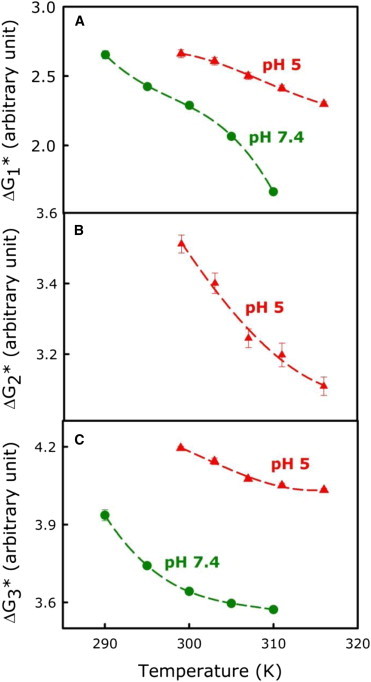
(A–C) Temperature dependence of the free-energy barrier for formation of the (A) I₁ state ($\Delta G_1^{\ast }$), (B) I₂ state ($\Delta G_2^{\ast }$), and (C) FP state ($\Delta G_3^{\ast }$) at pH 5.0 (red) and pH 7.4 (green). Data were fitted to a third-order polynomial and the parameters are shown in Table S1. To see this figure in color, go online.

Results

Fusion at pH 7.4 compared with pH 5

Fig. 1, A–C, show the time course of LM, CM, and CL, respectively, for 5% PEG-mediated fusion of DOPC/DOPE/SM/CH SUVs at pH 7.4 (green) and pH 5.0 (red) at 26°C. We fitted all three data sets (LM, CM, and CL) globally to a two-step/one-intermediate (pH 7.4) or three-step/two-intermediate (pH 5.0) sequential model to obtain the rate constant of each step, the rates of CL from each state, and the probabilities of LM and CM in each state. The single-intermediate model provided a good representation of the data at all temperatures (solid line through the plots in Fig. 1) at pH 7, whereas the two-intermediate model offered the best representation for the data at pH 5.0 (1). In addition to the observed loss of an intermediate, pore formation at pH 7.4 occurred earlier in the fusion process than at pH 5. Beyond this, the rates of intermediate and pore formation, as well as the extent of CM, all increased dramatically at pH 7.4 relative to pH 5. Table 1 presents the parameters that provide the best description of the data at pH 7.4 and pH 5.0 at one temperature (26°C). At both pH values, the total extent of LM (fLM) was greater than the extent of CM (fCM), meaning that not all of the initial intermediate microstructures that formed resulted in pore formation, a scenario we observed repeatedly. fLM was <0.67 at all temperatures (SUVs have roughly 2/3 of their lipid in the outer leaflet), meaning that the outer leaflets did not mix completely. We then measured LM, CM, and CL at various temperatures at both pH 7.4 and pH 5.0 to obtain the activation thermodynamics.

Figure 1.

(A–C) Effect of pH on the kinetics of (A) LM, (B) CM, and (C) CL during 5 wt % PEG-mediated SUV fusion at 26°C. Time courses are shown for pH 5 (red) and pH 7.4 (green). To see this figure in color, go online.

Table 1.

Ensemble Fusion Kinetic Parameters Derived from the Two-Intermediate Model

Temp = 26°C	k1 × 103 (s−1)	k2 × 103 (s−1)	k3 × 103 (s−1)	α1	α2	β1	λ0 ×104	λ1 ×104	λ2 ×104	λ3 ×104	fCM	fLM
pH 5.0	11.4 ± 0.56	2.71 ± 0.12	0.86 ± 0.09	0.12 ± 0.01	0.35 ± 0.03	0.54 ± 0.07	0.57 ± 0.02	0.33 ± 0.01	0.35 ± 0.01	NA	0.15 ± 0.02	0.45 ± 0.01
pH 7.4	21.5 ± 0.9	NA	2.22 ± 0.02	0.25 ± 0.01	NA	0.62 ± 0.01	3.81 ± 0.10	3.00 ± 0.05	NA	0.77 ± 0.23	0.26 ± 0.01	0.46 ± 0.02

Parameters were obtained by fitting LM, CM, and CL time courses to a sequential one-/two-intermediate model as described in the text. All experiments were performed on at least three independently prepared samples, with at least three time courses obtained each sample, and analysis was carried out on the combined time courses. The errors presented in the table are the parameter uncertainties from this combined analysis, although parameters from analysis of all experiments normally fell within this range of uncertainty.

Activation thermodynamics of PEG-mediated fusion of PC/PE/SM/CH SUVs at pH 7.4 versus pH 5.0

The activation free energy ($\Delta G_i^{\ast }$) refers to the difference in free energy between the initial states (A, I₁, and I₂) and transition states (TS1, TS2, and TS3). The activation free energies for different steps were calculated as mentioned above from rate constants obtained from experiments performed at five temperatures for each pH. These rate constants as well as extensive parameters are tabulated in Table 1 for data obtained at 26°C. Fig. 2 A shows the temperature dependence of $\Delta G_1^{\ast }$ for the formation of an initial intermediate at pH 7.4 (green) and pH 5.0 (red). $\Delta G_1^{\ast }$ was nonlinear with reciprocal temperature (i.e., the behavior was non-Arrhenius; plot not shown) and the activation enthalpy of step 1 thus varied with temperature, as would be expected for a process as complex as fusion. Fig. 2, B and C, show the activation free energies for step 2 ($\Delta G_2^{\ast }$) and step 3 ($\Delta G_3^{\ast }$), respectively, and these steps were also non-Arrhenius. A cubic was the simplest polynomial that could fit $\Delta G_i^{\ast }$ as a function of temperature for all three steps (coefficients given in Table S1).

The temperature dependences of activation entropy ($T\Delta S_i^{\ast }$; solid lines) and enthalpy ($\Delta H_i^{\ast }$; dotted lines) contributions are plotted in Fig. 3, A–C. For all three steps, a large positive $\Delta H_i^{\ast }$ is always partially overcome by a positive $T\Delta S_i^{\ast }$ to produce a smaller but still positive $\Delta G_i^{\ast }$. Thus, all three steps are entropically permitted, i.e., they would not occur were it not for a favorable entropy contribution. This enthalpy-entropy compensation is common in the activation thermodynamics of temperature-induced conversion between a configurationally less diverse but enthalpically favored ensemble to a state defined by a larger ensemble of enthalpically less favorable microscopic configurations. It is clear that aside from there being an extra step for fusion at pH 5.0, both initial intermediate formation and pore formation are more favorable at pH 7.4 ($\Delta G_i^{\ast }$ at pH 7.4 < $\Delta G_i^{\ast }$ at pH 5.0 for both steps). Both $\Delta H_i^{\ast }$ and $T\Delta S_i^{\ast }$ depend on temperature, meaning that there is a heat-capacity change ($\Delta C{p}_i^{\ast }$; slope of $\Delta H_i^{\ast }$ versus temperature), whose temperature dependence is shown in Fig. 3, D–F. Interestingly, the shapes of the $\Delta H_i^{\ast }$ and $T\Delta S_i^{\ast }$ plots with temperature are completely opposite for pH 7.4 and 5.0, and consequently the activation heat capacity for both steps increases with increasing temperature at pH 7.4 but decreases with temperature at pH 5.0.

Figure 3.

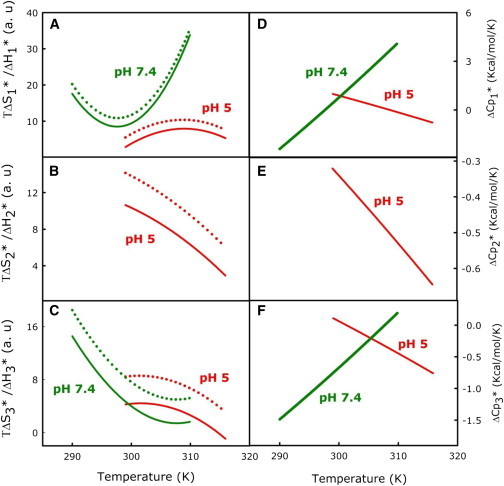
(A–C) Temperature dependence of $\Delta H_i^{\ast }$ (dotted line) and $T\Delta S_i^{\ast }$ (solid line) for formation of the (A) I₁ state, (B) I₂ state, and (C) FP state at pH 5.0 (red) and pH 7.4 (green). (D–F) Temperature dependence of $\Delta C{p}_i^{\ast }$ for formation of the (D) I₁ state, (E) I₂ state, and (F) pore at pH 5.0 (red) and pH 7.4 (green). To see this figure in color, go online.

Effect of hexadecane on the activation thermodynamics of PEG-mediated fusion at pH 7.4 versus at pH 5.0

The $\Delta \Delta G_i^{\ast }$ values obtained in the presence of 2 mol % hexadecane (relative to lipid) are plotted against temperature at pH 7.4 and 5.0 for all three steps in Fig. 4, A, D, and E. Hexadecane mostly catalyzed (i.e., produced a small negative $\Delta \Delta G_i^{\ast }$) the first and second steps of the fusion process at both pH values, but was very slightly anticatalytic toward step 1 at high temperatures and pH 5.0. It was anticatalytic toward step 2 at all temperatures at pH 5. Hexadecane catalyzed step 1 at higher temperatures and pH 7.4, but was barely catalytic at lower temperatures. Hexadecane’s greatest influence was by far on step 3, where it was most catalytic at pH 5 and high temperatures. $T\Delta \Delta S_i^{\ast }$ and $\Delta \Delta H_i^{\ast }$ are plotted as a function of temperature for TS1, TS2, and TS3 formation in Fig. 4, B, D, and F, at the two different pH values. We show $\Delta \Delta C{p}_i^{\ast }$ for two pH values and all steps in Fig. S1, A–C. The signs and relative magnitudes of $\Delta \Delta H_i^{\ast }$ and $T\Delta \Delta S_i^{\ast }$ define whether the catalytic effect of hexadecane was entropic ($T\Delta \Delta S_i^{\ast }>\Delta \Delta H_i^{\ast }$ > 0) or enthalpic ($\Delta \Delta H_i^{\ast }<T\Delta \Delta S_i^{\ast }$ < 0).

Figure 4.

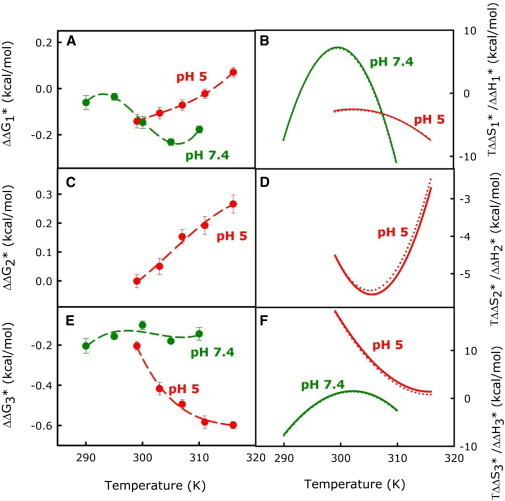
(A–F) The 2% hexadecane-triggered changes in activation free energy ($\Delta \Delta G_1^{\ast }$), entropy ($T\Delta \Delta S_1^{\ast }$), and enthalpy ($\Delta \Delta H_1^{\ast }$) of PEG-mediated fusion of PC/PE/SM/CH SUVs at pH 5 (red) and 7.4 (green) are plotted versus temperature: (A) $\Delta \Delta G_1^{\ast }$ and (B) $T\Delta \Delta S_1^{\ast }$ (solid line) and $\Delta \Delta H_1^{\ast }$ (dotted line) for formation of the I₁ state, (C) $\Delta \Delta G_2^{\ast }$ and (D) $T\Delta \Delta S_2^{\ast }$ and $\Delta \Delta H_2^{\ast }$ for formation of the I₂ state, and (E) $\Delta \Delta G_3^{\ast }$ and (F) $T\Delta \Delta S_3^{\ast }$ and $\Delta \Delta H_3^{\ast }$ for formation of the final fusion pore (FP). To see this figure in color, go online.

Discussion

As noted in the Introduction, we hypothesize that the aforementioned changes in PE hydration and charge with pH can account for the observed differences in fusion of DOPC/DOPE/SM/CH (35:30:15:20) SUVs with pH. Based on the considerations raised in the Introduction, we predict that the contacting leaflets of our vesicles in state A should 1), be more weakly hydrated; 2), be somewhat farther apart; and 3), experience reduced positive curvature stress at pH 7.4 compared with pH 5. In this section, we argue that these predictions can account for our results.

First step: initial intermediate formation

Based on transition-state thermodynamic properties, we previously proposed that the transition state for initial intermediate formation (TS1; Fig. S2) involves hydrocarbon-water contact in the space between closely juxtaposed bilayers (1,5). MD simulations based on simplified coarse-grained (32) or full-atomistic potentials (33) predict that individual acyl chains protrude into the water space in TS1, which is consistent with our proposal based on activation thermodynamics. Consistent with this model, the first derivatives of the transition-state free energy behave similarly at pH 7.4 and pH 5 (ΔH₁^∗ > TΔS₁^∗ > 0; Fig. 3 A), i.e., the transition state provides primarily an enthalpic barrier that is overcome in part by a favorable entropic contribution. This means that at both pH values, the transition state consists of a broad ensemble of enthalpically similar microstructural configurations compared with an A state that consists of a small number of enthalpically favorable microstructures. Compared with pH 5, the decreased negative intrinsic curvature and increased interbilayer repulsion predicted at pH 7.4 should reduce outer-leaflet curvature stress and increase interbilayer water. These effects should make acyl-chain protrusions into the interbilayer space in TS1 more enthalpically unfavorable. Thus, ΔH₁^∗ at pH 5 is expected to be smaller than that observed at pH 7.4 (∼6–9 compared with ∼10–40 in Fig. 3 A). Of course, the units of ΔH₁^∗ are arbitrary, and we may not be able to compare values determined at two pH values unless the preexponential factor of Eyring’s expression for k₁ is the same at both pH values (1). To avoid this complication and better understand the differences between step 1 at these two pH values, we turn to the curvature of the free energy versus temperature. At pH 7.4, ΔCp₁^∗ is the reverse (<0 at low temperature and >0 above a critical temperature, ∼297 K) of that observed at pH 5 (>0 below and <0 above a critical temperature, ∼308 K; Fig. 3 D). According to our model of TS1 (1), the positive ΔCp₁^∗ at low temperature and pH 5 results from a small interbilayer distance occupied by strongly ordered water in state A compared with an increased water-hydrocarbon contact and weakly ordered water in TS1. At pH 7.4, the increased interbilayer distance and more weakly ordered water near DOPE headgroups (12) should increase the heat capacity of state A, accounting for the negative ΔCp₁^∗ at low temperatures. The expected decrease in weakly ordered water in state A with increasing temperature can account for the large positive ΔCp₁^∗ at high temperatures, which also accounts for the large positive TΔS₁^∗ and the increased rate of I₁ formation (reduced ΔG₁^∗) at pH 7.4. Thus, whether we consider the first (ΔH₁^∗ and TΔS₁^∗) or second derivatives of ΔG₁^∗ (ΔCp₁^∗), the difference in the activation thermodynamics of step 1 between pH 5 and 7.4 is consistent with the expected change in DOPE hydration relative to pH 5.

Loss of an intermediate state and fusion-pore formation at pH 7.4

The increase in pH from 5 to 7.4 led to significant changes in fusion kinetics beyond step 1: 1), loss of the second step of the three-step process that is inherent to our originally proposed ensemble kinetic model of PEG-triggered SUV fusion (24) (Fig. S2); 2), a small increase in k₃; and 3), a decrease in the probability of CM (α₁) before FP formation. We argue that expected changes in DOPE hydration can also account for these effects. However, before we offer support for this argument, it is worthwhile to consider in more detail the likely nature of pore formation.

The first and last steps of the fusion process cannot be described by materials-based calculations because they involve changes in system topology and thus require exposure of water to hydrocarbon, which can only be treated with the use of molecular models. However, materials-based calculations at successive free-energy-minimized geometries along a reaction coordinate (stalk radius as defined in Fig. S2) can appropriately model the process of converting the initial intermediate (stalk or I₁ as already discussed) to a final transition state (TS3) that leads to an FP state (2). The transition state (TS2) between I₁ and I₂ has roughly the trans-membrane contact (TMC) geometry described by Siegel (25) and illustrated in Fig. S2. This occurs at the smallest stalk radius at which unfused trans leaflets make contact. Siegel refers to any geometry having a larger stalk radius than the TMC as an extended TMC (ETMC; Fig. S2). The ETMC geometry has a region of hemifused bilayer that is comprised of cis leaflets of the original vesicles and forms a diaphragm between unjoined compartments (Fig. S2). Both the TMC and ETMC geometries have extreme negative curvature stress as well as unfavorable interstice energy at their edges, where cis leaflets have merged (Fig. S2). The interstice energy reflects a geometric mismatch between the lamellar hemifused diaphragm of the ETMC and the lamellar regions of the unfused SUVs. In this materials view, a less negative intrinsic curvature (characteristic of PE at pH 7.4) somewhat destabilizes the I₁ state, severely destabilizes the I₂ state, and increases the transition-state barrier between I₁ and I₂ (see Fig. 4 B of Malinin and Lentz (2)). This makes the I₂ state so unstable at pH 7.4 that it disappears as a detectable free-energy minimum, and I₁ transforms directly to an ETMC geometry characteristic of the transition state leading to pore formation (TS3). This provides a materials-based explanation for the disappearance of the I₂ intermediate at pH 7.4, although a material-based model can never define the molecular nature of fusion-pore formation.

We have no certain molecular-level understanding of fusion-pore formation. The view that a stalk can transform directly into a pore has also been put forward based on Monte Carlo (34) or self-consistent field (SCF) (35) simulations of block copolymers with hydrophobic and hydrophilic ends. Although they are based on an extremely simplified model, block copolymer simulations provide the best available approximation to understanding pore formation on a microscopic scale. The stalk geometry predicted by these simulations is not Siegel’s cylindrically symmetric geometry that we used in our previous materials-based calculations (2), but rather is elongated or worm-like and more of a distorted ETMC than Siegel’s stalk. In these simulations, a leakage pore forms at the stalk edge because of movement of cis (hemifused) leaflet lipids into trans leaflets and then transforms into a fusion pore. In a block copolymer SCF simulation, Lee and Schick (36) used a mixture of lamellar-forming and hexagonal-forming diblock lipids to model fusion of a very highly curved vesicle with a planar membrane. This simulation predicted the evolution of an initial I₁-like intermediate to an I₂-like intermediate via a free-energy profile that is remarkably similar to that predicted by the materials calculations (2). A recent MD study of very highly curved vesicles with a highly artificial composition (37) also predicted Siegel’s TMC and ETMC geometries. In 80% of these simulations, the authors reported that cis leaflet lipids from one vesicle moved into the cis leaflet of another to account for fusion pores. However, in 20% of the simulations, trans-cis lipid inversion occurred and thus accounted for the formation of leakage pores (35). Although diblock simulations offer a discrete-particle view of pore formation, we cannot confuse this with a molecular view that might be obtained from atomistic MD simulations. However, they capture the essence of the materials-based free-energy profile (2) that we have shown to be consistent with our ensemble kinetic measurements (1). They also predict the intermediate-state microstructural heterogeneity that is necessary to account for the probabilities of CL (λ_i), intervesicle CM (α_i), and LM (β_i) that are required by our ensemble kinetic model (24). Next, their prediction of interleaflet lipid movement is consistent with our proposal that coordinated lipid fluctuations into the unfavorable interstice space of the stressed circumference of the ETMC geometry can account for the transition-state thermodynamics of fusion-pore formation from the I₂ state at pH 5 (1). Finally, both continuum calculations and discrete block copolymer simulations predict that fusion pores form via an ETMC geometry with an unstable periphery (see Fig. S2). For this reason, we focus on the ETMC geometry when discussing pore formation.

Because of the disappearance of the I₂ intermediate at pH 7.4, pore formation occurs via distinctly different paths at these two pH values (I₁ ➞ TS3 at pH 7.4 and I₂ ➞ TS3 at pH 5). However, both a continuum calculation and discrete diblock simulations predict that both processes occur via expansion of an intermediate with ETMC-like geometry. We thus persist in referring to the rate constant for FP-state formation at both pH 5 and pH 7.4 as k₃ with a transition state of TS3 in the continuum calculation. Next, we consider a picture of pore formation in terms of expansion and free energy of the ETMC geometry, since this can be related to the observed activation thermodynamics.

Second and third steps: conversion of ETMC intermediates to an FP state

At both pH 5 and 7.4, step 3 is entropically allowed (Fig. 3 C). Our previously proposed molecular model for pore formation views measured transition-state thermodynamics as resulting from coordinated multiple lipid fluctuations into interstice regions (1). This is analogous to the predictions of discrete block copolymer simulations in that interleaflet lipid transfer necessarily occurs via interstice space. These fluctuations are enthalpically unfavorable, but bending stress reduces this unfavorability and fluctuations are inherently entropically favorable. Coordinated fluctuations of both cis and trans leaflet lipids into interstice space should become increasingly common as the stalk radius increases, since the circumference of the ETMC diaphragm increases as the square of the radius (5). The exact stalk radius (r_S2) that defines the I₂ free-energy minimum (see Fig. S2) is determined by a trade-off between bending and interstice free energies (2). There is no clear distinction between the I₂ and TS3 ensembles structurally: they both have ETMC geometries and differ only in the stalk radii to which they correspond (see Fig. S2). We refer to TS3 as corresponding to a range of stalk radii that are both larger than r_S2 and sufficiently large that local correlated lipid fluctuations will become either so numerous or so large that they will more likely decay to a local pore that destabilizes the ETMC diaphragm, than return to the intact ETMC geometry. For convenience of discussion, we have defined a critical stalk radius (r_S^∗) that characterizes this distribution (1,5). According to this view, whatever promotes expansion of r_S from r_S2 toward r_S^∗ will promote fusion-pore formation. Although it is necessarily empirical, this description relates the thermodynamics of I₁ and I₂ evolution with increasing r_S (2) to the activation thermodynamics of pore formation, which we can measure.

According to this description, ΔG₃^∗, TΔS₃^∗, and ΔH₃^∗ at pH 5 are the differences in free energy, entropy, and enthalpy between ETMC geometries at r_S2 and r_S^∗, with r_S^∗ > r_S2, whereas ΔG₃^∗, TΔS₃^∗, and ΔH₃^∗ at pH 7.4 are the differences in free energy, entropy, and enthalpy between the stalk geometries at r_S ≿ 0 and the ETMC geometry at r_S^∗. Because ΔH₃^∗ and TΔS₃ correspond to such different processes at the two pH values, it is difficult to compare these quantities directly. The principal effects of moving from the stalk to ETMC geometry are a very substantial increase in unfavorable interstice free energy and a smaller decrease in unfavorable bending free energy (2). Since it is difficult to break these free energies into energy and entropy contributions, it is difficult to compare the very large ΔH₃^∗ and TΔS3 values observed at pH 7.4 with the smaller values observed at pH 5. We thus turn to the temperature derivative of these quantities (ΔCp₃^∗) for an interpretation. Cp is proportional to σ_E², i.e., to the square of the width of the energy distribution. At pH 5, ΔCp₃∗ compares Cp in the TS3 transition state to that in I₂ intermediate state. The number of closely spaced energy states in TS3 should be greater than in I₂ (positive TΔS₃^∗), but the decrease in ΔCp₃∗ with increasing temperature (Fig. 3 F) indicates that microstructural energies are more densely spaced in TS3 than in I₂, accounting for a negative thermal contribution to ΔCp₃∗. On the other hand, the positive ΔCp₃∗ at the lowest temperatures at pH 5 suggests that the exposure of water to hydrocarbon during coordinated lipid fluctuations is more extensive in TS3 than in I₂ (2). However, hydrophobic effects normally decrease with temperature, revealing the expected negative thermal heat-capacity change for transitioning from I₂ to TS3. At pH 7.4, ΔCp₃^∗ starts out negative and becomes increasingly positive with increasing temperature, exactly the opposite of the behavior seen at pH 5 (Fig. 3 F). Given the dramatic free-energy increase experienced when I₁ expands to a TMC or ETMC geometry (Fig. S2) (2), we expect very widely spaced energy states in I₁, leading to a low heat capacity that increases during the transition to TS3. The observed negative ΔCp₃^∗ at low temperatures must therefore reflect a configurational heat-capacity contribution to the I₁ state at low temperatures that could derive from water-hydrocarbon contact in I₁, which is favored by reduced bending free energy and disfavored by increased interstice free energy (2). With increasing temperature, we expect the influence of water-hydrocarbon interactions to diminish and reveal the aforementioned expected positive thermal contribution to ΔCp₃^∗. Thus, the results we obtained at pH 7.4 (increasingly positive observed ΔCp₃^∗ and very large TΔS₃^∗) and pH 5 (increasingly negative ΔCp₃^∗) support our proposal that pore formation involves a direct I₁-to-TS3 conversion at pH 7.4 and an I₂-to-TS3 conversion at pH 5. Since the change in the nature of pore formation (I₁ ➞ TS3 at pH 7.4 and I₂ ➞ TS3 at pH 5) can be explained in terms of a change in DOPE headgroup hydration, we conclude that the observed changes in activation thermodynamics for step 3 also could derive from this change in DOPE hydration.

In addition to the loss of the I₂ intermediate, increase in k₃, and change in activation thermodynamics that we observed at pH 7.4 relative to pH 5, we observed a substantial increase in the extent of CM (f_CM) at pH 7.4 relative to pH 5 (from 0.15 at pH 5 to 0.26 at pH 7.4; Table 1), but a decrease in the fraction of CM that occurs prior to formation of an FP (i.e., α = 0.25 at pH 7.4 compared with α₁+α₂ = 0.47 at pH 5; Table 1). The extent of LM (f_LM) was little influenced by the change in pH. According to our materials-based calculations, the less-negative intrinsic curvature associated with PE at pH 7.4 will destabilize the I₁ state (2), resulting in a greater probability that coordinated lipid fluctuations will occur to form pores and thus explain the increased f_CM at this pH. On the other hand, the reduced negative intrinsic curvature destabilizes I₁ less than it does ETMC structures with larger stalk radii (2), explaining why the probability of coordinated lipid fluctuations into interstice space would increase less in I₁ (α₁ = α) than in TS3 (α₃ = 1 − α > α).

Comparing the effects of hexadecane on transition-state thermodynamics at pH 5.0 and pH 7.4

We previously monitored the influence of hexadecane on fusion and bilayer structure as a means of gaining insight into the mechanisms of action of fusion-promoting peptides (5,39). Hexadecane is a known interstice-filling agent (40). Hexadecane has different influences on fusion and bilayer structure at low and high temperatures, and we have proposed that this is consistent with hexadecane adopting different conformational ensembles in the bilayer at these temperature extremes, i.e., being aligned with acyl chains at low temperatures but becoming increasingly disordered and occupying interstice space with increasing temperature (1,5,39). Here, we ask whether this proposal is consistent with its influence on fusion activation thermodynamics at both pH 5 and 7.4.

First step

We focus on the difference in hexadecane’s influence at pH 7.4 versus pH 5. This influence is small at both pH values (Fig. 4 A), so we stress qualitative differences rather than small quantitative differences. The two most obvious differences are that 1), hexadecane is catalytic at all temperatures at pH 7.4, but inhibitory at higher temperatures at pH 5; and 2), the curvature of ΔΔG₁^∗ at pH 7.4 changes from concave up at low temperatures to concave down at high temperatures, whereas that at pH 5 remains concave down at all temperatures. The consequences of the latter difference are seen in the different behaviors of ΔΔH₁^∗ and TΔΔS₁^∗ at the two pH values (Fig. 4 B). Acyl-chain excursion into the interbilayer space is less likely to occur at pH 74 than at pH 5, where DOPE curvature is more negative and outer-leaflet positive curvature stress is increased relative to pH 7.4. Hexadecane’s ability to replace acyl chains in the hydrophobic space apparently further promotes acyl-chain excursion (ΔΔH₁^∗ < 0 at all temperatures). Hexadecane’s inhibitory influence at pH 5 is due to TΔΔS₁^∗ being more negative than ΔΔH₁^∗ at higher temperatures (Fig. 4 B). Another view of this is that ΔΔCp₁^∗ goes from slightly positive at low temperatures to negative with increasing temperature. This is easily understood in terms of hexadecane promoting acyl-chain protrusion into the interbilayer space. This promotes water-hydrocarbon contact (ΔΔCp₁^∗ ≿ 0) at low temperatures, but this influence is overcome by its ability to increase the density of states in TS1 with increasing temperature at higher temperatures (ΔΔCp₁^∗ < 0).

At pH 7.4, hexadecane’s catalytic influence persists at all temperatures, but changes from enthalpic at low temperatures to entropic at intermediate temperatures, and to enthalpic again at high temperatures. ΔΔCp₁^∗ at pH 7.4, also in contrast to pH 5, progresses smoothly from very positive at low temperatures to very negative at high temperatures. Because PE is less rigidly hydrated and the interbilayer distance is greater at pH 7.4, the ability of hexadecane to promote acyl-chain protrusion is less impeded by the strongly ordered interfacial water present at pH 5.

In summary, even though k₁ is greater at pH 7.4 than at pH 5 (Fig. 2 A), the catalytic influence of hexadecane is still greater at pH 7.4 because PE’s weaker hydration at this pH allows hexadecane’s ability to enhance acyl-chain protrusion to have a greater influence on the rate of step 1.

Third step

In contrast to step 1, the influence of hexadecane on k₃ was catalytic at all temperatures at both pH values, but its catalytic influence was greater at pH 5 than at pH 7.4 (Fig. 4, E and F). As already noted, the process of FP state formation is quite different at these two pH values, which makes it more difficult to compare the influences of hexadecane. Step 3 at pH 5 corresponds to conversion of I₂ with ETMC geometry at r_S2 to TS3 with ETMC geometry at r₂^∗. We discuss the pH 5 effects first. Hexadecane’s substantial catalytic influence at pH 5 increases with temperature (Fig. 4 E) due to a decreasing enthalpic barrier along with increasing entropic catalysis (Fig. 4 F). A negative ΔΔCp₃^∗ implies that hexadecane either increases the width of the energy distribution in I₂ or decreases it in TS3. Given its positive TΔΔS₃^∗, it must increase the number of energetically closely spaced microstructures in TS3 and decrease the Cp of this state. Hexadecane reduces the interstice energy (13), in large part because of its ability to fill the interstice space at the circumference of intermediate structures (1,2) (see Fig. S2). Adjustment of the bilayer structure to accommodate this region of bilayer mismatch exposes water to hydrocarbon, so the interstice free energy has a substantially negative entropy component. Thus, the change in activation thermodynamics associated with the presence of hexadecane at pH 5 is consistent with it lowering the interstice energy of I₂ (a positive TΔΔS₃^∗ effect), which promotes expansion of r_S2 toward r_S^∗ (positive ΔΔH₃^∗ and negative ΔΔCp₃^∗) (2,5).

At pH 7.4, we propose that step 3 involves the conversion of I₁ at r_S ≿ 0 to an unstable ETMC geometry (unstable I₂) that proceeds directly to TS3 at r_S2^∗. Because the effect of hexadecane on ΔG₃^∗ was very small at pH 7.4, it is more difficult to interpret than its effect at pH 5. Indeed, the largest qualitative difference between hexadecane’s influence at pH 5 and 7.4 is the fact that it was very slightly enthalpic at the lowest temperatures, very slightly entropic at intermediate temperatures, and then very slightly enthalpic again at higher temperatures at pH 7.4, but always enthalpic at pH 5. This variation with temperature is reminiscent of hexadecane’s influence on step 1, which we attributed to a variation of its conformational ensemble with temperature. Although we do not think it appropriate to make a detailed interpretation of hexadecane’s small temperature-dependent effects on fusion at pH 7.4, we suggest that its effects may represent a trade-off between its ability to align with acyl chains and increase positive curvature at lower temperatures and its ability to lower the interstice energy at higher temperatures. At pH 7.4, where bilayer hydration and curvature stress are reduced, our interpretation is that it becomes more difficult to discern these competing influences (one on lamellar structures and one on interstices). These contrasting influences are also seen in the influence of hexadecane on bilayer properties at pH 7.4, where the abilities of hexadecane to occupy the bilayer free volume and limit water penetration into the bilayer are both maximal at intermediate temperatures, but for different reasons (i.e., variation in the control bilayer properties with temperature versus variation in the effects of hexadecane with temperature; see Fig. 4, C and D, in Sengupta et al. (39)).

In summary, despite a difference in the pathway to pore formation, the influence of hexadecane on pore formation at both pH 5 and pH 7.4 is proposed to result mainly from its influence on interstice energy. However, reduced hydration at pH 7.4 likely allows hexadecane’s influence on bending energy to play a larger competing role than it does at pH 5.

Conclusions

We propose that different fusion kinetics and activation thermodynamics for initial intermediate formation during PEG-mediated fusion are due to differences in DOPE hydration at pH 5 and pH 7.4.

Loss of the second intermediate at pH 7.4 is likely due to reduced outer-leaflet curvature stress (reduced negative intrinsic curvature of DOPE) destabilizing the I₂ intermediate, so that the initial intermediate transits directly via an ETMC geometry to the stalk radius (r_S^∗) that defines the final transition state (TS3) for pore formation.

Hexadecane promotes initial intermediate formation by the same basic mechanism (i.e., promoting acyl chain or hydrocarbon invasion of the interbilayer space) at both pH 5 and pH 7.4, but differences in DOPE hydration dictate whether this is reflected in entropic stabilization of the TS1 transition state or in enthalpic destabilization of the initial A state.

Hexadecane promotes pore formation at both pH values by reducing interstice energy and promoting expansion of the ETMC geometry toward a critical stalk radius (r_S^∗).