Infrared and Visible Absolute and Difference Spectra of Bacteriorhodopsin Photocycle Intermediates

Abstract

We have used new kinetic fitting procedures to obtain IR absolute spectra for intermediates of the main bacteriorhodopsin (bR) photocycle(s). The linear algebra-based procedures of Hendler et al. (2001) J. Phys. Chem. B, 105, 3319–3228, for obtaining clean absolute visible spectra of bR photocycle intermediates, were adapted for use with IR data. This led to isolation, for the first time, of corresponding clean absolute IR spectra, including the separation of the M intermediate into its M_F and M_S components from parallel photocycles. This in turn permitted the computation of clean IR difference spectra between pairs of successive intermediates, allowing for the most rigorous analysis to date of changes occurring at each step of the photocycle. The statistical accuracy of the spectral calculation methods allows us to identify, with great confidence, new spectral features. One of these is a very strong differential IR band at 1650 cm⁻¹ for the L intermediate at room temperature that is not present in analogous L spectra measured at cryogenic temperatures. This band, in one of the noisiest spectral regions, has not been identified in any previous time-resolved IR papers, although retrospectively it is apparent as one of the strongest L absorbance changes in their raw data, considered collectively. Additionally, our results are most consistent with Arg82 as the primary proton-release group (PRG), rather than a protonated water cluster or H-bonded grouping of carboxylic residues. Notably, the Arg82 deprotonation occurs exclusively in the M_F pathway of the parallel cycles model of the photocycle.

Introduction

The basic steps of light-driven proton transfer across the membrane by bR have been established (reviewed in ref. ¹). This accomplishment depended heavily on FTIR analyses performed in many laboratories. These earlier studies typically produced difference spectra, each nominally between an individual photoproduct and the unphotolyzed BR state, but which in actuality contained varying amounts of contamination from other intermediates. In the absence of the ability to truly separate each species kinetically, various enrichment procedures were used to obtain these difference spectra, such as trapping based on temperature and pH manipulations, and the use of mutants. There is no question that the photointermediate difference spectra published by various laboratories were truly enriched in the designated species. Furthermore, the general agreement in the results obtained from the different laboratories is reassuring. However, because at any point in the photocycle there is always a mixture of intermediates, and it has been shown that the photocycle can change with pH, temperature, and mutation, the degree of admixture of the intermediates in the difference spectra shown in earlier publications can not be quantified.²

The unique feature of the current work is that it is the first to calculate absolute IR spectra of isolated intermediates, each of which rises and decays according to a well-defined kinetic model that matches the observed data over broad spectral ranges.³ In addition, the original method described for visible spectroscopy has been adapted to yield corresponding IR spectra. Whereas previous IR difference spectra have been referenced to ground-state BR, we can now present transitional difference spectra involving only pairs of sequential intermediates. While we confirm most of the previous findings about bR photointermediates, we have gained some important new information and insights, in particular with regard to the controversial identity of the proton release group (PRG), which is responsible for net proton loss to the external medium during the transition from L to M. Specifically, our results are most consistent with Arg82 as the primary proton-release group (PRG), rather than a protonated water cluster or H-bonded grouping of carboxylic residues.

The specific kinetic model used to obtain these results was the parallel cycles model of Hendler et al. based on heterogeneous ground states rather than the more traditional homogeneous reversible, single cycle model.³ Reasons for this are presented below.

Methods

1. IR spectroscopy

Time-resolved IR measurements were made with a Bruker Equinox 55 spectrometer using a Globar™ source, an open aperture and a KBr beam splitter. The IR light was limited to λ<3950 cm⁻¹ by using a broadband interference filter (Bruker Optics, Billerica, MA) before the sample chamber. This filtering also kept the laser flashes from interfering with the reference HeNe laser signal. After the sample compartment, the light was again filtered (Bruker Optics, Billerica, MA) with a cutoff of 1866 cm⁻¹. The CaF₂ sample windows (Biotools Jupiter, FL) limit the light to above about 1050 cm⁻¹. Together these filters and windows allow single sided interferograms to be collected with sparse sampling (8× undersampling), corresponding to the Nyquist limit for a final spectrum between 1974 cm⁻¹ and 988 cm⁻¹, i.e. between 1/8 and 1/16 of the reference HeNe laser wavenumber. The throughput of the instrument in DC mode was cut to a maximum of 0.2 in the rapid scan check signal spectrum mode for the background spectrum without protein present using screens and a 10-mm masking aperture fitted to the sample cell. This mask is formed from a piece of aluminum, 2 by 3 inches that fits in the IR and visible transmission holder. The aperture serves to mask the sample and prevent light that does not go through the bR sample from reaching the detector. The pot on the Kolmar photovoltaic HgCdTe detector was used to zero the unmodulated light for the background spectrum with only the CaF₂ windows. An instrument gain of 4 was used. Laboratory vibrations of the interferometer mirror were limited to 3.5 nm as measured using the Bruker Opus software. Prior to obtaining the transmission (T) spectrum for the sample, a similar, but empty, CaF₂ sample holder was used to obtain the 100% T spectrum that was used to convert T of the sample to A (absorbance). The data were collected at 4 cm⁻¹ by coadding 100 flashes at each of 499 laser crossings to create single sided interferograms. The data were Fourier transformed using a Blackman Harris 3 term apodization, 2 levels of zero filling and a Mertz 32 cm⁻¹ phase correction.

2. Visible spectroscopy

For a complete description of the spectrometers used and the visible optics, see reference ⁴. The basic system uses two separate spectrographs, one covering a range of about 390 nm to 521 nm and another from about 553 nm to 681 nm with a resolution of 2.9 nm. With appropriate lenses, the light is focused through a beam-splitter and then directed to the entrance slits of the two spectrographs. The gap between 521 nm and 553 nm is to minimize the amount of laser light at 532 nm that can enter the spectrophotometers. To further reduce the amount of stray laser light, a 532 nm, “StopLine” notch filter (Kaiser Analytical Systems #30249) was employed in addition to two “RazorEdge” short and long wave pass “Semrock” filters (Rochester, NY) placed at the respective entrance slits of the two spectrometers.

3. Description of purple membrane (PM) sample and cell holder

PM was isolated from the ET1001 strain of Halobacterium salinarum by the procedure of Oesterhelt and Stoeckenius,⁵ as modified by Mukhopadhyay et al.⁶ The purified PM was suspended in H₂O at a concentration of 5 mg/ml. There is a major difference between the sample preparation used here and the one previously described. In the earlier case, the sample was a 3 ml aqueous suspension of PM in a 1 × 1 × 4 cm visible cuvette. In the current work the sample was a nearly dried film of PM with a thickness of <0.5 μm between two CaF₂ discs (BioCell, BioTools, Jupiter, FL.). A stock suspension was made from 50 parts of the PM suspension, 2 parts 50 mM potassium phosphate buffer at pH 7.1, and 1 part 50 mM H₃PO₄. The reason for adding H₃PO₄ to the phosphate buffer is described below under “pH control”. The bottom CaF₂ disc had a diameter of 50 mm and a thickness of 5 mm. A circular groove with a diameter of 25 mm, a depth of 3 mm and a width of 1.5 mm surrounded the central sample platform. The top disc was a lid with a diameter of 50 mm and a thickness of 5 mm. Fifty μL of the stock suspension was placed in the center of the sample platform and dried with a gentle stream of dry nitrogen over the course of about 30 minutes to form an irregular disk-shaped film, on average about 11 mm in diameter. When assembled, the two discs were tightly clamped together in a custom-made holder. The path length between the CaF₂ discs in the sample compartment was 120 μm.

4. pH control

The maximum amount of H₂O that can be present in the IR sample is < 0.5 μL. Therefore, the 50-μL sample must be taken to near dryness by a gentle current of N₂ blown across its surface. As the sample dehydrates, the concentrations of bR and buffer salts undergo a significant increase and the pH changes. To determine the final pH and fix it at 7.1, we used the following procedure. Fifty μL of a suspension of bR and 2 μL of 50 mM potassium phosphate buffer at pH 7.1 were placed in the center of the CaF₂ cell in the absence of H₃PO₄. A micro-combination glass pH electrode contained in a 4 cm 16 gauge hypodermic needle (Micro Electrodes, Inc., Bedford, NH model MI-4144 E Tip) was placed at the bottom of the droplet. This electrode requires only 1 mm depth of immersion. The electrode was connected to a pH meter and a Kipp and Zonen BD41 strip chart recorder. The starting pH of sample was 7.1. As drying proceeded, the pH rose and approached an asymptote of about 7.5 just before dryness. With the addition of 1 μL of 50 mM H₃PO₄ to the initial 50- μL sample, the final pH ended up instead near 7.1.

5. Determination of water content of sample

The molar extinction coefficient for H₂O at 1643.5 cm⁻¹ for a 1 cm light path at 25° C is 21.8.⁷ This absorbance is on the shoulder of the Amide I peak which is centered near 1658 cm⁻¹. The presence of water increases the height of the absorption peak for Amide I and raises the apparent ratio of Amide I to Amide II (1545 cm⁻¹) absorbances. For dried bR, we find an Amide I/Amide II ratio of 0.975. The ratio of absorbance at 1643.5 cm⁻¹ to the Amide I peak at 1658 cm⁻¹ in the dried sample is 0.700, and the ratio of the 1643.5 cm⁻¹ absorbance to the Amide II peak is 0.681. Because the contribution of a small amount of H₂O to the peak for Amide II at 1545 cm⁻¹ is considered negligible, the absorbance for zero H₂O content is taken as 0.681 × Amide II absorbance. The absorbance due to H₂O in the hydrated sample is taken as the absorbance at 1643.5 cm⁻¹ minus (0.681 × Amide II). (There could be a small error to this linear approximation, due to the expected decrease in mosaic spread of the purple membrane sheets as water is added to the dried film. This would result in an increase in the absorbance of amide I at 1658 and 1643 cm⁻¹, relative to amide II and water, as peptide C=O bonds become aligned increasingly away from the normal to the plane of the sample. This means that the formulas given here could overestimate the water content of the sample, especially for high values of that content. For the relatively low amounts of water that we used, this effect is expected to be small, compared to other components in the error, such as the assumption that the extinction coefficient of water in our protein film matches that of bulk water.) The absorbance due to H₂O can be expressed in μl per cm² by dividing by 1.206, which is the absorbance for 1 μl per cm², or 10 μm-thick, film of H₂O. The ratio of Amide I/Amide II absorbances is thus a good indicator of the degree of hydration of the sample.

6. Maintenance of proper sample hydration

The assembled cell with its sample, as described above, was sealed using ParaFilm™ and allowed to equilibrate for about 18 hours before data were collected. During the experiment which lasts nearly 4 h and during which the sample is irradiated with about 55,000 laser flashes, some loss of the initial water content occurs. However, we maintain the proper hydration of the sample during the course of the IR measurements by using the outer ring of the bottom disc as a reservoir that maintains an osmotic equilibration with the sealed sample. For example, if the osmotic strength in the reservoir is too low, H₂O tends to evaporate from it and condense on the sample, leading to over-hydration. Conversely, if the osmotic strength of the reservoir is too high, the sample dehydrates. By trial and error, we have found that 7 μL of 500 mM K₃PO₄ in the reservoir (a concentration that is expected to clamp the relative humidity in the range of 95–98%, extrapolated from data on monobasic and dibasic phosphate salt solutions)⁸ maintains the hydration of the sample within the narrow limits of inadequate hydration for normal photocycle activity and over-hydration that interferes with the Amide I absorption and leads to excessive noise at those frequencies that approach zero transmittance. The procedure for finding these conditions was to determine the range of ratios of Amide I/Amide II and μL H₂O/cm² that led to an S/N ratio that best permitted fitting of kinetic constants to the time-resolved IR data. Using the reservoir contents and our sample as described, it was found that Amide I/Amide II ratios between 1.1 and 1.4 and H₂O contents between 0.1 μL and 0.5 μL per cm² were maintained during the entire experiment.

7. Data collection

The same sample and photolysis setup was used for sequential visible and IR acquisitions. Controls for 100 % transmittances were obtained using a separate clean (empty) CaF₂ cell. Photocycles were initiated by 3.3 mJ/cm² pulses of 532nm light per ~8 ns flash produced by a Surelite I-10 Continuum Nd:YAG laser. Samples were light-adapted using the visible Xenon arc lamp light source for at least 20 min, as well as ~2000 warm-up flashes, prior to each set of data acquisitions. Digitized detector signals were collected in the following sequence of temporal spacings after the master experiment trigger: 40 @ 125 μs, 410 @ 5 μs, 200 @ 10 μs, 125 @ 30 μs, 100 @ 150 μs, and 75 at 1000 μs. This timing schedule was set with an in-house-built sampling clock generation device to allow the IR spectrometer to sample at the same timing schedule as the visible spectrometer. This device was based on an MAX II FPGA (Altera Corp., San Jose, CA) which is interfaced to a QuickUSB module (Bitwise Systems, Goleta, CA) to provide a way for the user to program the sampling schedule. This schedule is stored in the FPGA’s internal non-volatile flash memory. Upon receiving a trigger, the FPGA generates a pulse stream according to the schedule. The device uses an internal 10 MHz master clock which means the output pulses are not completely synchronous to the incoming trigger (100 ns jitter between triggers). The photolysis laser was fired at sample # 59. This allowed the collection of 58 dark spectra covering a time range of 5 ms, which were averaged for the ground state spectrum.

As described in the “General Procedure” below, visible spectra were taken both before and after a series of IR spectra. Prior to taking the kinetic visible spectra of the bR sample, the 100% T and 0% T control spectra were acquired. This sequence required the removal of the empty cell from the sample holder, the subsequent insertion of the sample cell, and finally the reinsertion of the empty cell. Although the fixed sample holder allowed very little freedom of motion for the orientation of the CaF₂ cell, the slightest difference could result in a subtle change in the amount of light passing through the beam splitter to the two spectrographs. This is sometimes evident as a small offset between the low and high wl regions obtained from the two visible spectrographs.

8. General Procedure

Using the same sample, 200 visible kinetic profiles of spectra were collected and averaged before and after collecting 100 co-added IR kinetic profiles of spectra in order to verify that the kinetics were not altered during the many thousands of laser flashes used to collect the IR data. For example, to collect 400 IR spectra, the schedule would be:

$$[\text{vis\#1}-\mathrm{IR\#1}-\mathrm{vis}\#2];[\mathrm{vis}\#3-\mathrm{IR\#2}-\mathrm{vis}\#4];[\mathrm{vis\#5}-\mathrm{IR\#3}-\mathrm{vis}\#6];[\mathrm{vis\#7}-\mathrm{IR\#4}-\mathrm{vis}\#8]$$

The kinetics before obtaining the IR spectra are the average of the 800 spectra in odd numbered vis data and the kinetics after obtaining the IR spectra are the average of 800 spectra in the even numbered series.

For the data described here, there were a total of 22 repeats of collections of 100 IR spectra (i.e. 2200 repeats at each laser crossing). Each of these runs was preceded and followed by the collection of 200 (averaged) visible kinetic spectra. All of the repeat “before” spectra were averaged and fit to seven exponentials. The same was done for all of the “after” spectra. Table 1 shows the average of the “before” and “after” of all visible spectra were obtained by averaging the two sets just described and is referred to as “avgavg”. The 7^th exponential is a minor component generally seen and considered to originate from a small amount of residual dark-adapted ground state rather than an intermediate in the light-adapted photocycle. Including it improves the fits of the 6 exponentials recognized as part of the true kinetic cycle. The first 6 kinetic constants shown in Table 1 vary within ± 10 % of the average of the before and after laser- exposures, which is well within variations normally reported in the literature and show that the sample was not significantly altered by the laser irradiations used during the IR acquisitions.

Table 1.

Fitted time constants, in ms, before and after acquisition of IR data.

	before	after	avgavg
1	0.004	0.004	0.004
2	0.054	0.044	0.049
3	0.145	0.128	0.136
4	0.478	0.452	0.470
5	2.12	1.91	2.04
6	4.60	4.26	4.51
7	12.3	18.0	14.9
Σsq.	9.98×10−4	2.81×10−4	5.80×10−4

9. Comparison of IR and visible data

The time course for BR turnover seen at 1526 cm⁻¹ in the IR is the same as that found using the characteristic indicator for BR in the visible at 568 nm (Supporting Information). The maximum absorbance decrease at 1526 cm⁻¹, observed at 0.25 ms, was about 2% of the starting absorbance of 0.428; this absorbance change was 28 times the size of the noise for the 800 averaged measurements. The maximum absorbance decrease at 568 nm, observed at 0.32 ms, was about 21% of the starting absorbance of 0.479 at 568 nm, or 1050 times the noise for the 200 averaged visible measurements. The greater noise in the IR data was largely due to the greater dark noise of the HgCdTe detector as opposed to the Si photodiode.

10. Computational approach

As previously described,³ raw spectral/kinetic data are contained in a matrix A whose columns correspond to spectra acquired at different times after initiation of a photocycle by an actinic laser pulse. The rows correspond to time courses of the absorbance at particular wavelengths (or wavenumbers). This A matrix can be deconvoluted into a model-specific matrix D which contains the absolute spectrum for each intermediate in the photocycle and a companion matrix Y which contains the corresponding real time course for the growth and decay of each spectrum in A, such that,

$$\mathbf{A}=\mathbf{DY}.$$ [1]

The matrix Y is obtained by mixing the fitted exponentials using a model-specific mixing matrix as described in ref. ³ and its supporting information. The unique kinetic model on which these procedures are based is described by a set of ordinary differential equations. Once Y is known, the absolute spectra are obtained by using Y⁺, the pseudoinverse of Y, in the formula

$$\mathbf{A}={\mathbf{DY}}^{+}.$$ [2.]

Equation 2 can be used for any kinetic model, including the two types most commonly hypothesized for bR (homogeneous reversible and heterogeneous parallel unidirectional).

However, as discussed in ref. ³, there are two essential requirements for calculating a Y matrix, which can then be used for testing any proposed kinetic model; 1. The model must be specifically stated by a series of ordinary differential equations. 2. The numeric values of all required kinetic constants must be provided. There are two essential criteria for accepting the tested model; 1. The eigenvalues of the J-matrix, which contains the kinetic constants,³ must be equal to the kinetic macro constants obtained by fitting exponentials to experimental data. 2. Each obtained absolute spectrum, (i.e. each column of D), should show only one Gaussian shaped peak with a maximum absorbance at the expected characteristic location, and each transitional difference spectra between pairs of successive intermediates should clearly show the disappearance of the precursor accompanied by the appearance of the product.

Over the past 25 years, publications from many laboratories have presented evidence in favor of parallel cycles emanating from different ground states.^{2, 3, 9–16} Hendler and coworkers have pointed out many experimental observations that can not be explained by a homogeneous sequential linear cycle.^{2, 10, 13, 14} Most important, when using short (~10 ns) laser pulses for actinic excitation of bR, the yield of any particular photointermediate produced from a homogeneous ground state is expected to rise linearly at low intensities, and then to exhibit a saturation curve with an exponential behavior. That is, the photoproduct yield as a function of incident pulse energy E (in photons per cm²) should be in proportion to [1- exp(-kE)], where k is a constant dependent on the bR extinction coefficient and quantum yield. All models that are based on a single homogeneous bR ground state should thus be single-exponential for the yield of any photoproduct as a function of E. However, the observed energy saturation curves for M_total, M_F, and M_S all require two exponentials for fitting, and thus require two distinct bR ground states, with either different extinction coefficients or (as better supported by experimental evidence) different quantum yields for photoproduct formation.¹⁷

In spite of the foregoing incontrovertible evidence for heterogeneous (parallel) cycles, we have also sought to apply equation [2] to homogeneous models with reversible steps, just to see what would result. The literature is rich with many varieties of homogeneous reversible single-cycle models (RHM) from many laboratories. However, we could find only one published model¹⁸ that met the two requirements for testing listed above. When tested with our visible spectral data, this model failed both requirements for acceptance listed above. Specifically, the absolute spectra for both M and N were contaminated with each other, and L and O showed considerable negative absorbances. The peak absorbance for O was at a wavelength much shorter than 640 nm. The transitional difference spectra did not show the clean conversion of precursor to product as in our Fig. 3 below. Finally, the eigenvalues of the J-matrix did not match the fitted macro constants (data not shown).

Figure 3.

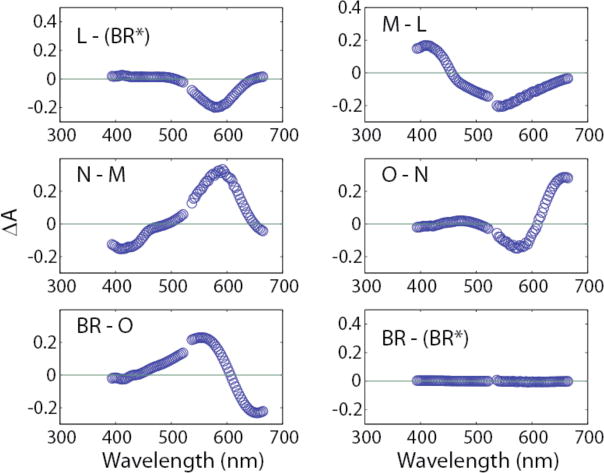
Transitional difference spectra obtained by subtraction of absolute spectra shown in Fig. 3. For example, the L-(BR*) spectrum is for the (BR*) ╜ L transition.

Results obtained from applying the same RHM to the IR data recapitulated the mixing of intermediates evident in the visible spectra. Even the earliest transitional difference spectrum, nominally L-BR, showed evidence of admixture. For example, instead of an isolated single-Gaussian negative band COOH band from protonated Asp96 at 1741 cm⁻¹, which is computed quite cleanly with the parallel-cycles model (see below), the use of an RHM results in the L-BR difference spectrum showing additional strong positive side-bands near 1750 and 1736 cm⁻¹. The latter are indicative of additional structural changes of carboxylic acids, most likely occurring as a result of contamination by other intermediate(s). Other spectral regions likewise show additional complexity when the RHM is used instead of the parallel cycles model. With later photointermediates, the evident admixture is even more apparent. That is, with the RHM there is always a larger number of Gaussian bandshapes visible in the 1700–1800 cm⁻¹ spectral region. This region is expected to represent protonation changes of one or two carboxylic acids at each stage of the photocycle (data not shown).

As noted above, the S/N ratio for IR data is much lower than that for visible data, making it much more difficult to obtain accurate kinetic fits. The photocycle must have the same kinetic time course whether it is monitored by visible or IR light. Therefore, once the model-specific time courses in Y are determined from the visible data, the absolute IR spectra in D can be determined from the raw data in the IR version of A, by using equation 2. This allows us to capitalize on the high S/N ratio obtained from the visible data in order to obtain clean absolute IR spectra.

The parallel cycles model

In the heterogeneous, parallel cycles model deduced by Hendler et al.,³ there are two different linear sequential pathways for the photointermediates to return to the ground state.

$$\begin{array}{l}{\mathrm{BR}}_{\mathrm{F}}\ast \to {\mathrm{L}}_{\mathrm{F}}\to {\mathrm{M}}_{\mathrm{F}}\to \mathrm{N}\to \mathrm{O}\to \mathrm{BR}\\ {\mathrm{BR}}_{\mathrm{S}}\ast \to {\mathrm{L}}_{\mathrm{S}}\to {\mathrm{M}}_{\mathrm{S}}\to \mathrm{BR}\end{array}$$

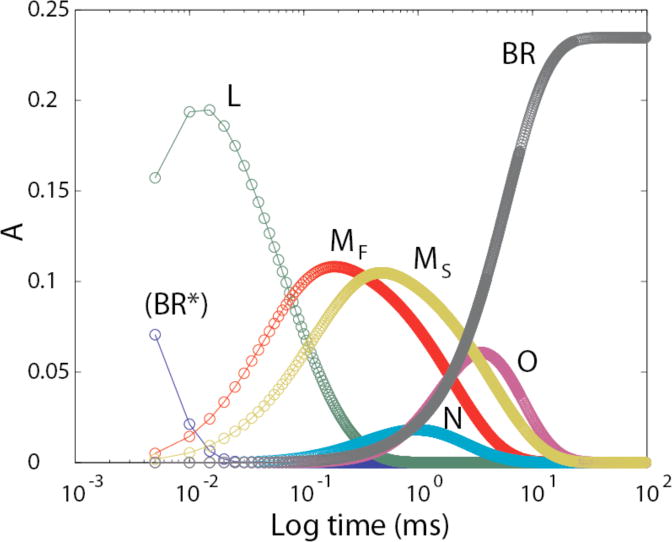
The subscripts F and S refer to the decay time constants (τ) for the two M intermediates. At pH near 7 and T near 20 °C, the faster, M_F, has a τ of ~2 ms and the slower, M_S, ~5 ms.³ Changing the intensity of actinic light alters the relative amounts of activated bR that proceed through the two different pathways. In the Discussion section, we point out how this phenomenon may allow the cell to adapt to different growth conditions. Because of the paucity of data points in the first 30 μs, we were unable to obtain a dependable IR absolute spectrum for L_F, and therefore the undivided (averaged) L intermediate was used.

Our time resolution does not allow us to separate the (BR_F^*) and (BR_S^*) states nor to isolate the combination of the two, which we designate (BR*). The initial state we do isolate consists essentially of the unphotolyzed state(s) that give rise to the distinct parallel photocycles. BR (without the asterisk) indicates the structure of the asymptotically-approached final product, many milliseconds after photolysis. Below we show that the spectra we have obtained for (BR*) and BR are essentially the same.

This information is provided in order to avert two erroneous inferences from our figures; (1) that the BR* → L transition occurs in a single step with a τ of 4.2 μs; and (2) that the absolute spectrum we label as (BR*) corresponds to an electronic excited state. In fact, we have not temporally resolved the excited state of bR, which is what BR* traditionally designates. In the text and figures, we will consistently use parentheses, e.g. (BR*), to convey that although BR* is the species that begins the thermal decay reactions that we are kinetically fitting, we have not isolated its spectrum. With higher time resolution, it becomes possible to isolate intermediates that we are missing here. For example, with data from Xie et al obtained at 1 μs time resolution,¹⁹ the 2-cycle model was confirmed and it was possible to also isolate the absolute spectrum for the K intermediate.²

Representation of a model with all intermediates in a simple linear sequence

All previously published TR-FTIR analyses were based on a photocycle originating from a homogeneous ground state and proceeding through a linear sequential sequence, which in its simplest form is,

$$\mathrm{BR}\ast \to \mathrm{L}\to \mathrm{M}\to \mathrm{N}\to \mathrm{O}\to \mathrm{BR}.$$

To compare results from our data with these previous publications, we have combined the time courses for L_F and L_S, and for M_F and M_S in our Y-matrix, which in effect is the same as using the undivided species. Analyses using this set of spectra based on unitary L and M intermediates are shown first.

Results

Statistical data for fitting the visible data to 7 exponentials are shown in Table 2 below. The sum of squares, errors, and dependency values are all very low, indicating a valid fit to the data with no superfluous exponentials.

Table 2.

Quality of fits to kinetic constants. Sum of squares = 0.00058044

k (ms−1)	errors§	dependencies¶	τ = k−1 (ms)
238.5	1.6	1.1	0.00419
20.34	0.27	2.1	0.04917
7.338	0.13	2.2	0.1363
2.129	0.058	1.8	0.4697
0.4905	0.0030	1.6	2.039
0.2216	0.0014	2.6	4.512
0.0673	0.0054	2.4	14.85

^§Standard error in the estimate of each k. There is a 68% confidence level that the true value of k lies within ± the listed error.

^¶For a proper fit, the required number of parameters (i.e. exponential amplitudes and rate constants) must be provided. Too few parameters lead to large errors and non-random residuals. Too many cause errors of a different kind. The residuals become deceptively better, while the errors become quite large. The superfluous parameters typically provide two redundant exponentials to fit a single kinetic event, so that there is no unique solution for the two affected rate constants. Perturbations in the value of one of the extra parameters results in compensatory changes in the value of its partner(s). Therefore, when all of the parameters are fit simultaneously, the errors for the redundant constant(s) will be large. However, if all parameters but the redundant one are held constant, its error will be greatly reduced. The dependency value is defined as the ratio of the error for one fitted parameter when none of the other parameters is held constant, to the error when all others are held constant. Dependency values have a lower bound of 1, and no upper bound. Values below 10 indicate the absence of any significant redundancies in the parameters. Values above 10 indicate possible problems. Values above 50 provide a strong indication that too many parameters are being used to fit the data set.

Part 1. Isolation of Spectra Using Unitary L and M intermediates

Visible Spectra

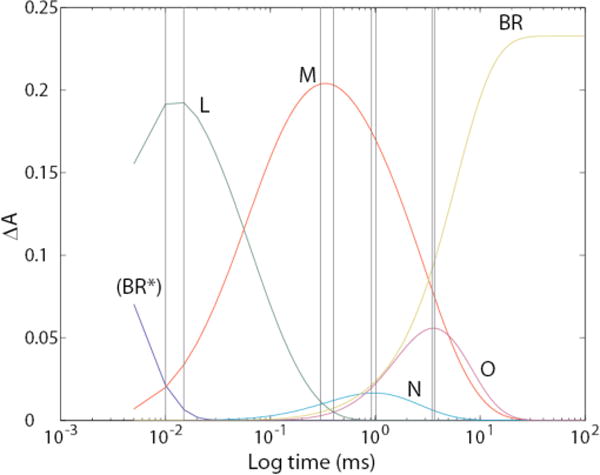
Using the kinetic data in Table 2 above, the model-dependent time course for each intermediate is shown in Fig. 1.

Figure 1.

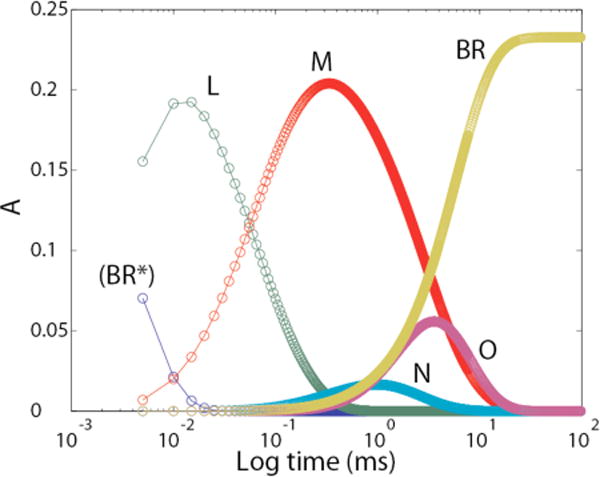
Time courses for photocycle intermediates according to the unitary cycle model shown in “Experimental Procedures”. The time courses for L_F and L_S were merged, as were those for M_F and M_S.

Using these time courses (Y) in equation 2 produced the absolute visible spectra shown in Fig. 2. The main thing to note is that the isolated spectra show single broad Gaussian shapes with maximum absorptions that are characteristic of the individual intermediates. The negative absorbances seen for intermediates M, N, and O in the 450–500 nm region, (i.e. near the gap between the two separate spectrographs for the low and high wavelength regions) arise from our use of two separate spectrometers with a gap between 521 nm and 537 nm to minimize the effect of scattered 532 nm light from the laser. As explained above under “Methods—Data Collection”, this procedure led to a small offset in the absorbances of the two spectrometers. The subsequent optimization procedures, used for determining the fraction of turnover while minimizing residuals for absorbances (i.e. amplitudes at a large number of wavelengths for five spectra) in regions away from the peaks, produced a “best-fit” solution with slight incursions into negative territory. Absolute spectra obtained using the same model and procedures with data collected from a single spectrometer showed no negative absorbances (see figure 8 in reference ²). Note also that the Y matrix is determined only from the model-dependent J matrix (Fig. 1) and the quality of fits to the macroscopic kinetic constants (Table 2), and not by the calculated visible spectra. Therefore, the IR spectra (see below) were not at all affected by the baseline offset that was present in the visible data.

Figure 2.

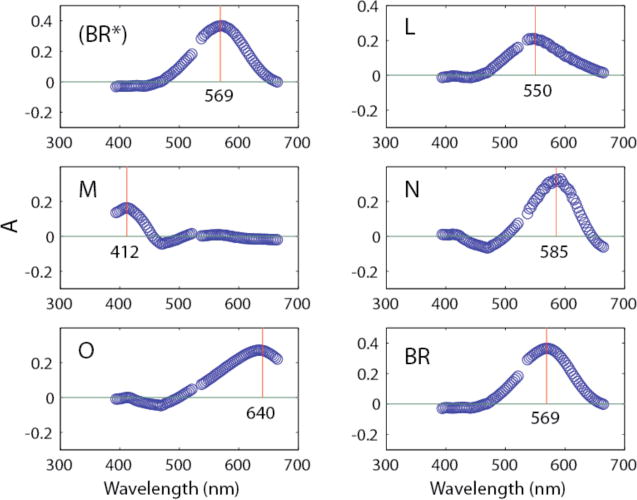
Isolated visible absolute spectra obtained from raw data using equation 2. The vertical lines indicate peak locations in nm as designated in the figure.

Figure 8.

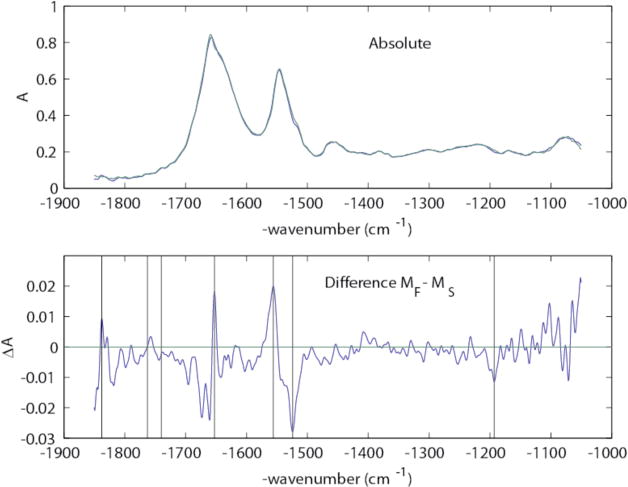
Upper panel: Absolute IR spectra for M_F (blue) and M_S (green). Lower panel: Difference spectrum between M_F and M_S, with vertical marker lines at 1838, 1763, 1740, 1654, 1556, 1524, and 1192 cm⁻¹.

Transitional difference spectra (TDS) obtained by subtracting sequential absolute spectra shown in Fig. 2 cleanly show each precursor as negative Gaussian trough and the accompanying product as a Gaussian peak (Fig. 3). With the higher time resolution of the data of Xie et al.,¹⁹ the same parallel-cycles model used here led to the isolation of the absolute spectrum for the K intermediate.²

Infrared Spectra

Using equation 2, with matrix A containing the raw time-resolved spectral IR data and the Y matrix obtained from the visible spectra (and represented by the plots in Fig. 1 above), produced the absolute IR spectrum for each intermediate, analogous to the absolute visible spectra in Fig. 2. All of the features in each spectrum therefore followed the appropriate time course shown in Fig. 1. The absolute spectra of individual intermediates are relatively uninformative, i.e. all appear to the naked eye to be nearly identical, and are not shown. TDS between successive intermediates were also obtained by subtracting these absolute spectra pairwise, analogous to Fig. 3; and these are shown in Fig. 4 below. In the IR spectral range, the combined strength of large numbers of invariant background absorption bands, i.e. those unaffected by photolysis, is very large. Thus, such TDS are needed in order to recognize important structural and liganding changes accompanying the transformation of each intermediate to its product.

Figure 4.

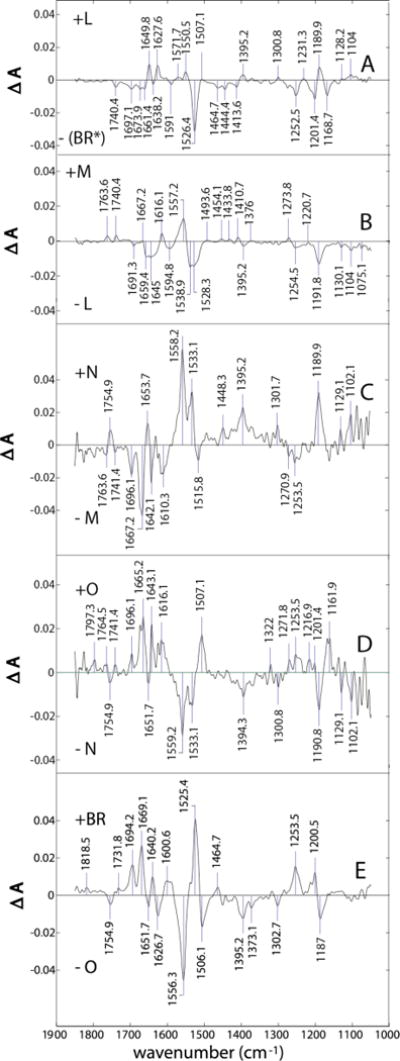
Difference spectra for (from top to bottom) the (BR*)╜L, L╜M, M╜N, N╜O, and O╜BR transitions.

The same kinetic profiles were found using either characteristic IR or visible markers for BR and the M intermediates (Supporting Information). For the intermediates L, N, and O, we found no single, unique IR markers. This is because the frequencies changed in concert with more than the single intermediate (not shown). The Supporting Information also includes difference spectra of the M, N, and O intermediates with respect to (BR*), i.e. ground-state difference spectra (GDS), which will be recognized as analogous to previously published TR-FTIR spectra of these intermediates.

Part 2: Isolation of Spectra With Separate M_F and M_S intermediates

Visible Spectra

Figure 5 shows the fitted time courses. This figure is the same as Fig. 1, except for the separation of the time courses for M_F and M_S.

Figure 5.

Time courses for photocycle intermediates according to the parallel-cycle model shown in “Experimental Procedures”, with divided M intermediates but still a unitary L intermediate (L_F and L_S summed).

The corresponding isolated absolute visible spectra are shown in Fig. 6 and difference spectra in Fig. 7.

Figure 6.

Isolated visible absolute spectra obtained from raw data using equation 2 and separate time courses for M_F and M_S. The vertical lines indicate peak locations in nm as designated in the figure.

Figure 7.

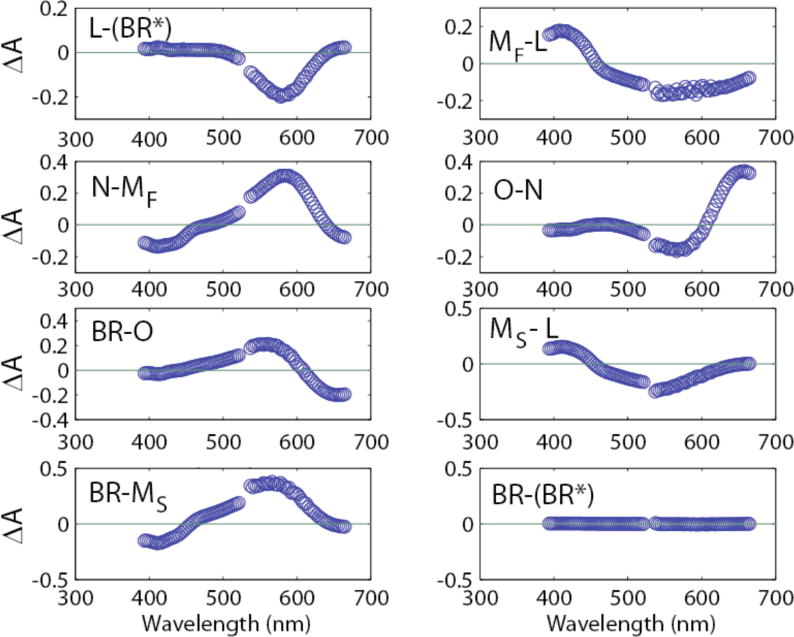
Transitional difference spectra obtained by subtraction of the absolute spectra shown in Fig. 6. For example, the L-(BR*) spectrum is for the (BR*) ╜ L transition.

Figure 6 should be compared to Fig. 2. The only difference is that in Figure 6, separate time courses for M_F and M_S were used which allowed the obtaining of separate spectra for these intermediates instead of a combined spectrum as seen in Fig. 2. As described in the Experimental Section, two separate spectrometers are used for the lower (<521 nm) and upper (>553 nm) wavelength regions, causing a small discontinuity in the mid region before and after the gap. In Fig. 2, this resulted in small negative dips in the intermediates, M, N, and O which were not seen in data obtained from a single spectrometer.² Splitting M into M_F and M_S exaggerates the aberration by introduction of more parameters to be fit. Both M_F and M_S show distinct prominent Gaussians for the M intermediate. Addition of the two spectra equals the single spectrum for M shown in Fig. 2. With the same procedures used here and described in reference ³, data were collected from a single spectrometer under nine different conditions of pH from 5 to 9, and temperature from 10° C to 30° C.² In some of these cases three and four different forms of M intermediate, each rising from L, were present. In all cases the central regions for M, N, and O were close to zero. The TDS in Fig. 7 (compare to Fig. 3) clearly show the expected disappearance of a single Gaussian for the precursor accompanied by the appearance of a Gaussian for the product, consistent with the sequential photocycle steps for the parallel cycle model used. The two forms of M were formed from L in two separate kinetic transitions. This is consistent with the IR results presented below (Fig. 9).

Figure 9.

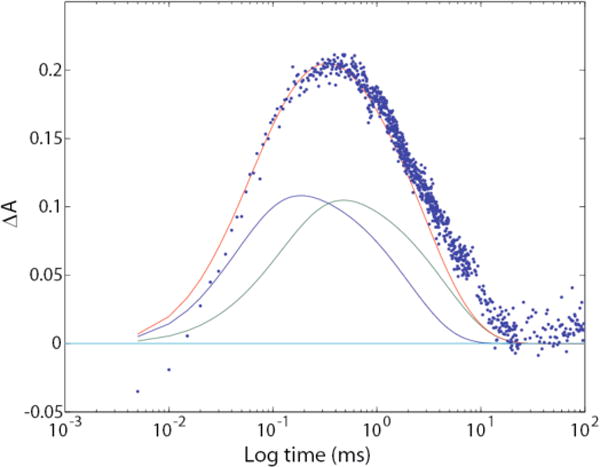
Comparison of time course for IR absorbance at 1763 cm⁻¹ (blue dots) with the fitted visible (410 nm) time courses for M_F (blue line), M_S (green line), and combined M_F and M_S (red line), computed from the visible data by using the parallel-cycles model. The y-axis scale applies directly to the fitted visible data; the measured IR data were multiplied by 390 in order to superimpose them.

Infrared Spectra

As described in Parts 1 and 2 above, absolute IR spectra were obtained from the raw data using equation 2 and the separated time courses for M_F and M_S shown in Fig. 5. TDS were obtained by subtraction of the appropriate absolute spectra for precursors and products. To the naked eye these are essentially the same as shown in Fig. 4 and not reproduced here.

However, Fig. 8 shows that although the IR spectra for M_F and M_S are quite similar, there are a number of clear differences, especially in the Amide I and Amide II regions and near 1763 cm⁻¹. Rather than speculate about the significance of these vibrational difference bands here, we will explore them further in future work.

Figure 9 shows that the protonation and deprotonation of Asp85 are associated with the formation and decay of both forms of M (i.e. both formed in L╜M transitions). This is apparent from the time-dependent growth and decay of the characteristic ~1760 cm⁻¹ signal for the protonated amino acid (blue dots). If the protonation of this carboxylate occurred in only one of the two forms, the dots would be skewed either to the M_F (blue line) or M_S (green line) curve instead of enveloping the sum of these two curves (red line). It should be noticed that the return of the blue dots to the baseline level is slightly delayed compared to that of the time profile for the decay of the combined M intermediates (red line). This is because Asp85 is still protonated in the O intermediate, which decays slightly after M_S (Fig. 5). This finding is the predicted result for a photocycle that is heterogeneous and consists of two separate parallel cycles.

Additional support for parallel cycles comes from the clear detection of two spectrally distinct transitions for the formation of M from L, one corresponding to a unimolecular rate constant near 40 μs and the other near 125 μs, as shown in Figs. 5 and 7, and in previous work.³ In the homogeneous photocycle, there is only one step where M₁ is formed from L.

Discussion

A major focus of the current study is the nature of the proton release group (PRG). This is defined here as a species that loses one of its protons to the extracellular medium when the M (or at least the M_F) intermediate is formed from L, and that reprotonates only after M (or M_F) decays, using protons that come from groups lying more toward the interior side of the membrane. The three major hypotheses for the PRG are that it is either (a) a protonated cluster of water molecules lying near Arg82; or (b) the hemi-protonated pair Glu(192/204), sharing a single proton in a strong H-bond affected by the position of Arg82; or (c) Arg82 itself.

The general consensus is that crystallographic studies are unlikely to reveal directly the protonation state of these PRG candidates, and that more direct information about them is likely to come from IR and/or NMR spectroscopy. One of the main goals of TR-FTIR measurements is to provide a clearer definition of the PRG, through careful kinetic analysis of these PRG candidates’ structures during the photocycle.

There is very good agreement among laboratories that 6 exponentials are required to fit the transitions seen during the normal photocycle at pH near 7 and temperature near 20 °C. The τ values are close to 0.005, 0.05, 0.13, 0.5, 2, and 5 ms, which we also observe (see Table 2). A low amplitude seventh exponential with a τ above 10 ms is sometimes seen.³ Using the IR data, we have no trouble in fitting the 0.005-ms τ, which we attribute to the formation of L, nor the constants near 2 and 5 ms for the decays of M_F and M_S. On occasion, we see the very slow exponential thought by many to emanate from a small amount of dark-adapted bR. A τ near 0.5 ms, which we attribute to N decay, is rarely seen. Instead of two separate constants near 0.05 and 0.13 ms, which we attribute to the decays of L_F and L_S, respectively, in the IR we see a single τ near 0.08 ms. Fits very much like these were reported by Müller et al.²⁰ The constant near 0.5 ms was not fit and a single value was reported for the constants near 0.05 and 0.13 ms, with the comment that it carried a high standard deviation. We are aware of only two cases where it was reported that all of the constants fit with the visible data were independently fit using the IR data,^{21, 22} but statistical data for errors and dependencies were not shown. In our approach, the fitting of time constants was based only on the more dependable visible data. These constants were then used to determine the time courses for growth and decay of each intermediate, from which we obtained the corresponding absolute spectrum. Verification that the same kinetics were being observed in the IR and visible data sets was based on overlapping plots using characteristic IR wn’s and wl’s for the two data sets (Supporting Information).

A. Band assignments and interpretations

Changes in protonation states of donors and acceptors: For interpretation of protonation changes, we focus on the 1800–1500 cm⁻¹ spectral region, since it is most sensitive to proton-binding changes of key ionizable groups in bR. An expanded presentation of this region is shown in Fig. 10, corresponding to the TDS in Fig. 4 and in Fig. 11.

Figure 10.

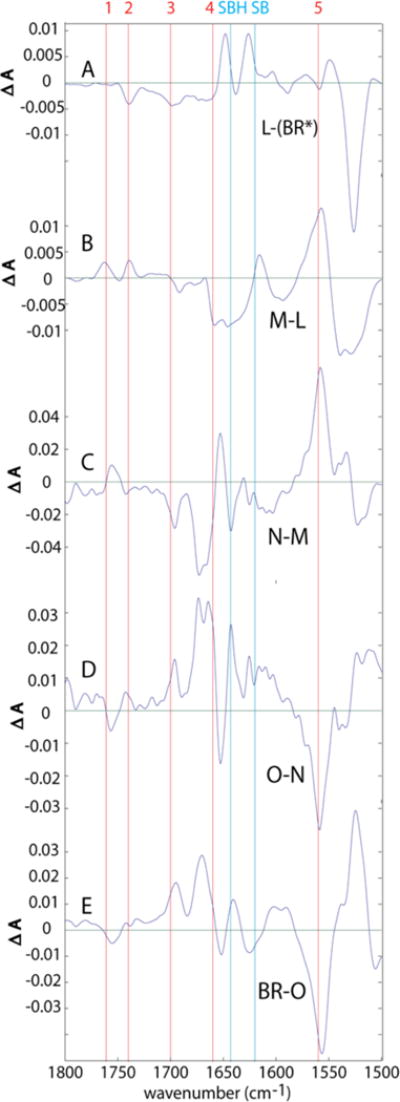
Transitional difference spectra (TDS) where “unitary” forms of L and M are used.

Figure 11.

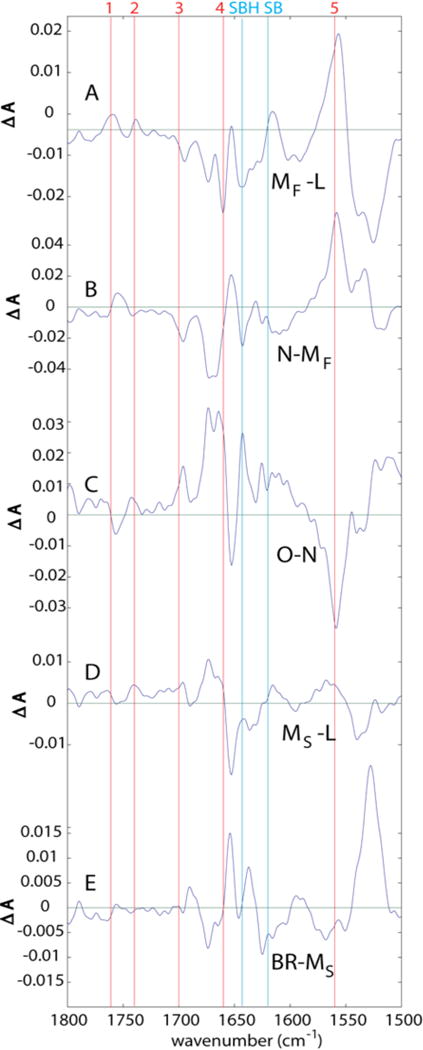
Transitional difference spectra (TDS) where separated M_F and M_S intermediates are used. The L-(BR*) and BR-O difference spectra in this case are identical to the top and bottom panels of Fig. 10, respectively, and are therefore not repeated.

In all of the TDS in Figs. 10 and 11, the frequencies of the major amino acid proton donors and acceptors are marked by numbered, red vertical lines and are assigned as listed in Table 3 below. Frequencies for the Schiff base are marked by vertical, cyan lines.

Table 3.

Frequencies of marker bands for groups changing protonation state, as labeled in Figs. 10 and 11.

	Frequency (cm−1)	References
1. Asp85 COOH§	1761 (in M)	23
Asp85 COOH	1755 (in N and O)	30, 32–34
2. Asp96 COOH	1740	23, 30, 33
3. Glu (194/204) COOH	1700	24–26
4. Arg82+	1660 (range 1652–1680)	27–29
5. Arg82 (neutral)	1560 (range 1554–1566)	27–29
6. SBH%	1639 (in BR)	30, 31, 35
SBH	1645 (in L and N)	24, 36
SBH	1628 (in O)	30, 31
7. SB%	1620	30, 31

^%SBH and SB designate the protonated and unprotonated Schiff base, respectively.

In Figures 10 and 11, the cyan line marked SBH is at 1643 cm⁻¹, which is an average for the protonated Schiff base frequency in BR, L, M, and N. The 1628 cm⁻¹ value for O is not separately marked.

⁺1560 and 1660 cm⁻¹ are used as averaged estimates for the deprotonated and protonated Arg82, respectively.

^§For the Asp-85 COOH group, line 1 is marked at 1761 cm⁻¹.

A complication, however, is that the frequency range from 1700 – 1550 cm⁻¹ is shared with Amide I and Amide II. This introduces confusion as to whether peaks or troughs in this region are due to changes in protonation for amino acid side chains, or to changes in secondary structure, or to both occurring simultaneously.

This is a significant problem for defining a marker band for Glu(194/204), whose COOH frequencies nearly coincide with a much larger band at ~1695 cm⁻¹. The latter band, however, is insensitive to 5-[¹³C]-glutamic acid labeling of bR,²⁴ or mutation at either of these residues,²⁶ and so is more likely to represent an amide I band of a β-sheet or -turn. The only band assignable to a Glu COOH vibration, based on appropriate sensitivity to deuteration,²⁴ as well as 5-[¹³C]- glutamic acid labeling²⁵ and site-directive mutation,^{24, 26} is a weaker, broader band centered at 1700 cm⁻¹ that appears most prominently as a negative band in the (BR*) → L difference spectrum (marked by line #3 in Fig. 10A). This 1700 cm⁻¹ trough in low-temperature (BR*) → M difference spectra was first assigned to a specific Glu (residue 204) based on its sensitivity to the E204D and E204Q mutations.²⁴ However, subsequent kinetic FTIR measurements called into question this assignment, by showing that change of this band in the E204Q and E204D mutants could have resulted purely from secondary effects.²⁶ In the same work, no alternative explanation was provided for the previously-observed isotope sensitivity of the 1700 cm⁻¹ band in low-temperature spectra, to both deuterium exchange²⁴ and ¹³C-glu labeling.²⁵ We therefore suggest here, as alternative possibilities, that (1) the 1700 cm⁻¹ trough may include components of both Glu194 and Glu204 COOH groups, or (2) this trough may represent a single vibration involving coupling of these two COOH groups. We indicate these possibilities, with intentional ambiguity, by designating this marker band “Glu(194/204)”.

The problem of overlap with amide group vibrations is biggest for Arg82 and the Schiff base group, for which the vibrational frequencies coincide most closely with those of Amide I and Amide II. The IR intensity for the SB band is also generally much weaker than for the SBH band.³⁷ Fortunately, it is possible to rely on resonance Raman spectra, rather than IR alone, for the assignment of protonation states of the Schiff base group in various intermediates.

Arg82 protonation changes remain most controversial, in part due to the enormous lowering in pK_a that they would require or proton release, and in part due to the lack of clear support from NMR spectroscopy.²⁹ We can only make assignments of peaks #4 and #5 to Arg82 with confidence in the M intermediate, and even in this intermediate, only 30–50% of the intensity change at these positions is attributable to Arg82; the rest is more likely due to concomitant changes in amide I and amide II vibrations. Thus, when we label peaks at positions #4 and #5 in spectra of other intermediates besides BR and M, their assignment to Arg82 is only one of several possibilities.

Even in the well-assigned M-BR difference spectrum, somewhat less than half of the band intensity at each position assigned to Arg82 (#4 and #5) shows the expected ¹⁵N isotope sensitivity.²⁸ However, because the differential absorbance changes at positions 4 and 5 are ample (e.g. as in our Fig. 10B or 11A), the ¹⁵N-sensitive component of those bands is sufficiently large to be attributed to a stoichiometric change in protonation state of Arg82. The L-(BR)* difference spectrum (as in Fig. 10A) was obtained from the same isotope-labeled and control samples, but showed no detectable sensitivity to [¹⁵N]-arginine labeling. Due to a limited measurement time range in that earlier work, spectra of the later intermediates, N and O, were not obtained from the isotope-labeled sample.

For the M intermediate, there was no ambiguity in this interpretation of the IR peaks assigned to Arg82 as arising from a change in its protonation state, based on comparison to model compounds. This is in stark contrast to the ¹⁵N-NMR chemical shifts, which for deprotonated guanidines fall along an overlapping continuum with signals from protonated, but strongly H-bonded, guanidinium ions.²⁹ In IR spectra of model guanidine compounds, even very strong H-bonding of the protonated form always upshifts the pair of strong C-N stretch vibrations between 1600 and 1700 cm⁻¹, and never gives rise to a strong downshifted band near ~1550 cm⁻¹, where deprotonated guanidines have a strong characteristic vibrational frequency corresponding to line #5 of Table 3.

B. Structural changes during the photocycle

Below we first discuss the photocycle according to the prevailing view of a unitary unbranched photocycle described above with certain important differences. Next, we discuss new information based on the separated intermediates M_F and M_S. In the parallel-cycle model, the pathway for return to the BR state differs in the separate M_F and M_S routes. As explained further below, it was not possible to obtain an authentic IR absolute spectrum for L_F, and we therefore examined the parallel photocycles model using undivided L.

i.) Protonation changes using unitary L and M intermediates

(BR*) → L

In this transition (Fig. 10A), there are no significant changes in the protonation states of either Arg82 (lines #4 and #5) nor of the SB. The prominent features from 1550–1500 cm⁻¹ are attributed to changes in Amide I and II vibrations as well as to chromophore isomerization (unmarked peak near1550 cm⁻¹; and trough near 1526 cm⁻¹).

However, the trough corresponding to deprotonation of the Asp96 COOH group (line #2, Fig. 10A) is somewhat larger than in corresponding low-temperature difference spectra.^{23, 33} More important, the accompanying positive band near 1748 cm⁻¹ that is seen in BR → L difference spectra obtained at cryogenic temperatures^{23, 33}, and that has been interpreted as resulting from an environmental change near Asp96, is not observed in the corresponding room-temperature spectra in Fig, 10A. That is, with careful kinetic decomposition at room temperature, there is no positive higher-frequency component to balance the decrease in absorbance at 1740 cm⁻¹.

An explanation is needed to account for the uncompensated trough at position #2. It is implausible, that the integrated absorbance of this non-H-bonded carbonyl group might somehow drop by 50–100% of its initial value when L is formed, without any change in its frequency. Extinction coefficients of aliphatic COOH carbonyl stretches do not vary much, at most ~30% upon formation of a strong H-bond.³⁸ Furthermore, the change in extinction coefficient in model compounds is always an increase upon H-bond formation, and never a decrease as would be needed to account for the depletion band at 1741 cm⁻¹ in Fig. 10A. The hypothesis that a mere H-bonding perturbation could produce such a huge drop in the Asp96 carbonyl group’s integrated intensity, that it would be impossible to observe a positive band at some other frequency within the characteristic COOH region, is without precedent.

Likewise, the possibility that a change in direction of the C=O bond could lead to a polarization-induced depletion of intensity for Asp96 is also remote. For our sample geometry, such polarization-induced intensity changes could account for our observations only if the Asp96 C=O bond switched from being aligned mostly within the membrane plane in BR, to mostly perpendicular to this plane in L, and then back to its original alignment in M. However, crystal structures of BR consistently show that the carbonyl of Asp96 is already aligned largely out of the membrane plane in the unphotolyzed state. More important, crystal structures of L (e.g. 1EOP, 2NTW, and 1VJM in the crystallographic data bank) do not indicate any substantial further shifting of the C=O bond towards the membrane perpendicular. Rather, they show a shift of at most 10–15° in the C-O bond vectors of the Asp96 side chain. Thus polarization effects cannot likely explain the large 1742 cm⁻¹ negative band that we and others consistently observe in low-temperature BR → L difference spectra.

A key to answering the conundrum of the absence of the positive peak near 1748 cm⁻¹ may be another positive band, in a frequency region not usually associated with carboxylic acids. This is the positive band at 1650 cm⁻¹ in the BR → L difference spectrum (just to the left of the line marked SBH in Fig. 10A). This peak is substantially larger than in corresponding low-temperature (BR)* → L difference spectra.^{23, 25, 33} This much stronger positive intensity for the band 1650 cm⁻¹ is retrospectively visible in all previously-published time-resolved TR-FTIR spectra of the (BR)* → L transition (see e.g. references ^{22, 28, 32}, and ³⁹). However, this has not been noted in prior discussions, most likely because this band lies very close to the absorption maximum for the strong background water/Amide I bands. It is notoriously difficult to obtain a high degree of photometric accuracy in this spectral region. Indeed, there is nearly a 2-fold variability in the size of the 1650 cm⁻¹ positive band in published time-resolved TR-FTIR difference spectra of the BR→L transition.^{22,28,32, 39} This is attributable to samples of varying uniformity in their thickness, and possibly to temperatures ranging from 0–25°C. The intensities of all of these bands are, however, well outside the much narrower range of what is seen in low-temperature BR → L difference spectra (e.g. refs ^{23, 33}, and ⁴⁰), in which the peak near 1650 cm⁻¹ never rises significantly above the 0-absorbance baseline.

The 4 most likely interpretations for the 1650 cm⁻¹ positive band’s consistent appearance in time-resolved, but not low-temperature, BR → L difference spectra are: (1) it could be due to a protonated, but highly-perturbed, Asp96 side chain; (2) it could be due to a deprotonated, highlyperturbed Asp96 side chain; (3) it could be due to an entirely different group that gains a proton (temporarily) from nearby Asp96 when L is formed; or (4) it could represent an amide I vibration that is altered by a protein conformational change occurring when L is formed at physiological temperatures, but not at cryogenic temperature. Possibility 4 seems rather unlikely, given that there are no large concomitant differences in the amide II region between low-temperature and physiological temperature L spectra. Possibilities 1 and 2 are given some credence by the by the fact that, in low-temperature BR → L difference spectra obtained from samples labeled with ¹³C-aspartic acid, the bandshape at 1650 cm⁻¹ undergoes one of the largest perturbations in the entire spectrum (see Supporting Information of reference ²⁵). This suggests moreover that, even at cryogenic temperatures, formation of L causes a portion of the Asp96 carbonyl intensity to shift downward in frequency to ~1650 cm⁻¹, rather than upward to 1748 cm⁻¹. On the other hand, the first two explanations are both made more difficult by the fact that 1650 cm⁻¹ would be an unprecedented frequency for an aspartic (or other carboxylic) acid—too low for the carbonyl of protonated COOH, and too high for either of the CO stretches of unprotonated COO⁻. Furthermore, TR-FTIR spectroscopy of the D96N mutant do not show a significant alteration of the size of the band at 1650 cm^−1.39

For a deprotonation of a carboxylic acid group, a strong positive band near 1560 cm⁻¹ due to the asymmetric C-O stretch, and a weaker band between 1300–1400 cm⁻¹ due to the symmetric stretch, are expected. Candidate bands for such Asp96-COO⁻ bands were detected in earlier publications, but not discussed much recently, largely because the idea of Asp96 deprotonation in L did not fit with the consensus mechanism for BR. The most significant of the earlier observations is the sensitivity, to both isotope labeling and site-directed mutagenesis at Asp96, of a substantial component of the positive band near 1560 cm⁻¹. (In our spectrum in Fig. 10A, this band is seen just to the left of marker band #5). A portion of the intensity in this 1560 cm⁻¹ band clearly shifts upon ¹³C-labeling of aspartic acid side chains in low-temperature L-BR difference spectra (see Supporting Information of reference ²⁵). This same band also weakens in the D96N mutant, as seen most clearly in time-resolved FTIR spectra measured at 1.4 μs after photolysis of bR (compare Figs. 1 and 2 in ref. ³⁹). The weaker symmetric Asp-COO- stretch band is not as clearly assignable in the L spectrum. Several candidate bands between 1300 and 1450 cm⁻¹ have shown the expected sensitivity to ¹³C-labeling of aspartic acids.^{25, 40} However, none of them has ever been observed to shift when Asp96 was mutated. The symmetric Asp-COO- stretch band may simply be too weak to observe reliably in the L-BR spectrum.

Protonation change of Asp96 during this step of the photocycle is not a part of extant models for the proton pump mechanism. This deprotonation, or some other unprecedented structural perturbation, is apparently fully reversed in the subsequent L → M step (see below), and may therefore be mechanistically relatively unimportant. On the other hand, this IR-detected structural change, which is likely to be unobservable in X-ray crystal structures until methods for obtaining them in time-resolved fashion at room temperature are developed, could provide an important new clue in understanding the proton pump mechanism.

L → M

In this transition (Fig. 10B), protonations of Asp85 (#1) and Asp96 (#2) are accompanied by deprotonations of Arg82 (#4 and #5), and SB (cyan lines). This is consistent with the simultaneous transfer of a proton from the Schiff base to Asp85 and release of a proton from Arg82 to the external medium. The simplest explanation for the appearance of the Asp96 positive band in the L→M spectrum, along with negative intensity near 1650 cm⁻¹, is that both represent a reversal of the structural changes involving Asp96 that occurred upon formation of L (see above).

It is also significant that there is no change in line #3 at 1700 cm⁻¹, despite the clear depletion of intensity in the nearby 1695 cm⁻¹ band. The latter is likely due to an Amide I vibration, rather than Glu(194/204), since in FTIR difference spectra, in the M – BR difference spectrum, this band shows no effect upon 5-[¹³C]-glutamic acid labeling,²⁵ or mutation of these residues.²⁶ Thus, there is no evidence in the L → M transition (Fig. 14B) for any change in protonation state of Glu(194/204). This is in complete agreement with earlier conclusions.²⁶

Figure 14.

The time course of integrated absorbances from 1850 cm⁻¹ to 1800 cm⁻¹, (black trace) has been scaled and superimposed on the time courses for the intermediates in the photocycle.

M → N

In this transition (Fig. 10C), there is a peak in the position for unprotonated Arg82 (#5). However, there is no clear indication of a compensatory loss at the position for protonated Arg82 (#4). In the absence of ¹⁵N labeling such as was available for the Arg82 features in the M spectrum,²⁸ interpretation of these features is ambiguous. It is possible that there could be some further degree of deprotonation of Arg82 at this stage of the photocycle. However, it seems more likely that changes in other components of Amide II may be responsible for the feature at position #5. In this transition, the proton lost by Asp96 is used for the reprotonation of SB as shown by IR,³² and by resonance Raman.⁴¹ Our observations thus agree with the consensus view that the only protonation change during the M → N transition is the transfer of a proton from Asp96 to the Schiff base group.

N → O

In this transition (Fig. 10D), there is some evidence for partial reprotonation of Arg82 (#4 and #5), although here again the interpretation of these features as due to Arg82 as opposed to amide I and II is ambiguous due to the lack of specific ¹⁵N isotope labeling data.

Formation of O also appears to be accompanied by partial loss of protonation in Asp85. Up to this point, the proton on the Asp85 –COOH, which originated on the SBH, has not been transferred to another acceptor and the proton lost from the PRG in the L → M transition has not been replaced. We identify for the first time this particular step of the photocycle as the one where the transient deprotonation of Arg82 might begin to be reversed, possibly through partial (~20%) proton transfer from Asp85. This is somewhat different from the consensus view that Asp85 is as fully protonated in O as in N or M. Our clear observation of simultaneous IR signals attributable to a fractional decrease in protonation of Asp85 in O, accompanied by partial reprotonation of Arg82, is consistent with the view that Arg82 is the PRG.

O → BR

(Fig. 10E) Although there is a trough near the position for deprotonated Arg82 (#5), there is no compensatory rise at the location for protonated Arg82 (#4). Therefore, it is likely that if any reprotonation of Arg82 is occurring during this stage of the photocycle, additional changes near 1661 cm⁻¹ due to amide I alterations must be masking them.

ii.) Altered protonation steps obtained when the analysis distinguishes M_F and M_S intermediates

The pathway containing M_F is the same as described above for the unitary M intermediate, except that in the L → M_F transition (Fig. 11A), the baseline under Asp85 is lower, and the extent of deprotonation of Arg82 is substantially greater. (Note also the 20% larger y-axis scale in Fig. 11 than in Fig. 10).

L → M_S

This transition (Fig. 11D) is similar to both the L → M transition shown in Fig. 9B and the L → M_F transition shown in Fig. 11B, with respect to the protonations of Asp85 and Asp96. There is a major difference, however, in the deprotonation of Arg82. The signals at positions #4 and #5, associated with deprotonation of Arg82, are both much smaller in the L → M_S transition (Fig. 11D) than in the L → M transition (Fig. 10B). Actually, in the L → M_S transition, there is no evidence whatsoever for Arg82 deprotonation. The L → M transition of Fig. 10B thus presents an average depiction of two distinct species that have very different behaviors with regard to this particular amino acid side chain. Previous spectra of the two M intermediates also indicated that the negative signal at position #4 (1660 cm⁻¹) was significantly attenuated in the later form of M, there designated M₂. ⁴² However, in that work, no significant change at position #5 was observed between M₁ and M₂.

We conclude that a proton is not released to the external medium at this step in the M_S pathway, as it is in the M_F pathway. This is consistent with a number of other reported observations that are reviewed below. Additionally, there is evidence for partial protonation of Glu(194/204) in Fig. 11B.

M_S → BR

Fig. 11E indicates that this terminal resolved step in the M_S decay pathway is different than the terminal O → BR step in the M_F pathway (Fig. 10E). There appears to be a deprotonation of Asp85 (line 1 in Fig. 10E), which could represent proton transfer to the extracellular medium. The presumed protonation of the SB can also possibly be discerned in a positive band near 1636 cm⁻¹ (at bit lower frequency than expected), and negative band near 1625 cm⁻¹ (a bit higher than expected). The only other significant changes are in the Amide I and Amide II regions.

C. Attempt to obtain separate absolute IR spectra for L_F, and L_S

Because of the very small time constant for the rise of L_F, there is a paucity of time points collected for this intermediate. In spite of this, it has been possible to collect separate visible spectra for both L_F and L_S (Fig. 7 of Ref. ³). Using the more extensive visible data obtained here, we obtained a less noisy spectrum for L_F, but, its shape was not Gaussian (not shown). Because of this, we decided not to rely on the associated absolute IR spectrum for L_F and instead to use the absolute IR spectrum of the undivided L species.

D. Identity of the PRG

1. Model with a protonated water cluster as the PRG

Traditionally, the PRG has been considered to be a single amino acid side chain that releases the proton to the external surface of the PM, prior to the final release to the external bulk medium. During the past 20 years, an alternative view has arisen that a Zundel-like water cluster is a more likely candidate for the role of PRG. The many papers supporting this view are both theoretical and experimental.^{26, 43–48}

The strongest experimental support for a protonated water cluster as PRG is that of Garczarek et al.⁴⁸ In this work, the IR spectral signature of the protonated water cluster is an absorbance continuum from 1900 cm⁻¹ to 1800 cm⁻¹ observable in an M – BR difference spectrum shown in their Fig. 2. They determined that under their conditions (pH 7 and T 20–23 °C), a time range of 300–400 μs would produce a relatively clean M – BR difference spectrum.

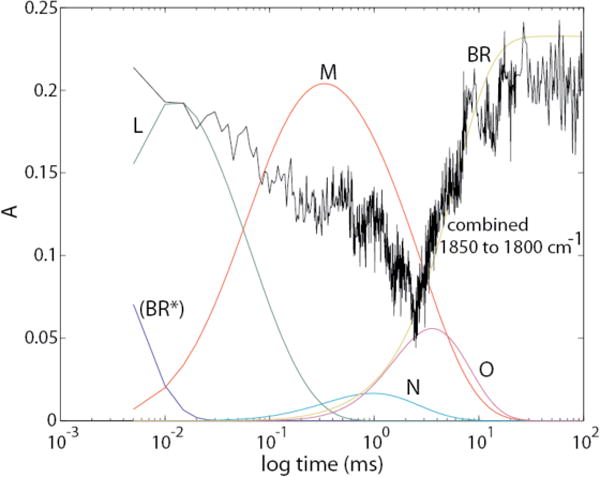
Our measurement conditions are the same as used by Garczarek et al.⁴⁸ Therefore, as a starting point in our consideration of this hypothesis, we sought to reproduce the findings of Garczarek et al.⁴⁸ using our data. Figure 12 shows that the range of 300–400 μs is indeed ideal for obtaining an enriched M – BR difference spectrum.

Figure 12.

Time courses, obtained from our data, for growth and decay of photocycle intermediates. The pairs of vertical lines show ranges where time samples were averaged.

We used this approach, instead of the more precise photointermediate difference spectra obtained by our procedures, in order to obtain spectra directly comparable to those of Garczarek et al.⁴⁸ The range of 300 to 400 μs included raw spectra digitized at 21 distinct time points. Based on Fig. 12, the resultant Mmix-BR difference spectrum contains about 5% N and 2 % O.

In addition to the pooled spectra for obtaining the Mmix – BR spectrum, we also included similar time ranges (i.e. sums of 21 spectra around the maximum for each of the peaks for the N and O intermediates) in order to obtain enriched Nmix – BR and Omix – BR difference spectra. For L, which peaks at 12 μs, we were able to pool only 2 spectra at 10 and 15 μs in order to obtain the enriched Lmix – BR difference spectrum. In Fig. 13, we present all four of these difference spectra obtained by subtracting the pre-flash spectrum of BR from all of the enriched intermediate spectra.

Figure 13.

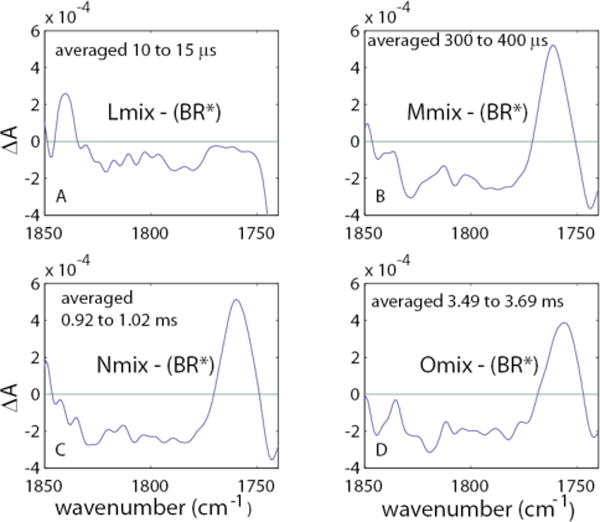
Averaged continuum difference spectra relative to the ground state, using our data. The designations Lmix, Mmix, Nmix, and Omix refer to the fact that these spectra are not the pure spectrum of each intermediate, but contain the spectra of other intermediates as shown in Fig. 12.

These difference spectra should be compared to the range of 1850–1800 cm⁻¹ shown in Fig. 2 of ref. ⁴⁴. The restricted frequency range we use is consistent with that of Garczarek et al.,⁴⁶ who pointed out overlaps of signals from some water configurations induced by laser-related heating that were not part of the Zundel-like water cluster. At any rate, if the continuum absorbance from 1900 cm⁻¹ to 1800 cm⁻¹ is truly emanating from the water cluster, the region from 1850 cm⁻¹ to 1800 cm⁻¹, which includes the maximum amplitudes, should also serve as a signature for the continuum absorbance.

Fig. 14 shows the integrated continuum spectrum from 1850 cm⁻¹ to 1800 cm⁻¹ as a function of log (time), superimposed on the time courses of all intermediates.

This figure is similar to that seen by others,^{25, 48} in that the continuum absorbance signal is most positive in the BR state. Therefore, any GDS, i.e. any IR difference spectrum referenced to BR, will be negative in this frequency range.

Figure 15 shows TDS for the conversions from L through M, N, and O en route back to the ground state, each calculated in two different ways. One used the averaged Lmix, Mmix, Nmix, and Omix shown in Fig. 13 and the other used the pure photointermediate spectra obtained as described here. The main observation is that in both cases, the signature IR spectrum for the continuum has disappeared.

Figure 15.

Transitional difference spectra for sequential conversions of L to M to N to O. The vertical red lines at 1761 cm⁻¹ indicate the position for protonated Asp85 in the M intermediate. The panels on the left contain mixtures of intermediates as shown in Fig. 12.

Whereas in Mmix, the contamination is relatively small, in Nmix, N is only a minor component (see Fig. 12). The panels on the right use the isolated intermediates as in Figs. 10 and 11.

2. Model with Glu194/204 as the PRG

It has recently been proposed that a hemi-protonated pair of glutamate side chains (Glu194/204), sharing their single ionizable proton nearly equally, serves as the PRG.⁴⁹ This hypothesis was supported with the assertion that the carbonyl band(s) of this hemiprotonated pair in the BR state have not been observed in difference spectra, because they would be expected to lie well below the heavily-investigated 1700 cm⁻¹ region. However, this does not adequately account for the actual observation of a negative band in the (BR*) – L difference spectrum at 1700 cm⁻¹, as in Fig. 1 (top), that has been clearly assigned to a protonated Glu204 and/or −194, as listed in Methods. This band in time-resolved (BR*) → L difference spectrum has been shown sensitive to mutation of Glu204 to Asp.²⁴ Furthermore, in low-temperature L – BR difference spectra, this 1700 cm⁻¹ band is sensitive to 5-[¹³C]-Glu substitution (see Supporting Information of reference ²⁴). The 1700 cm⁻¹ frequency for this Glu(194/204) band is very typical for fully-protonated H- bonded carboxylic acid dimers. The observation of such a negative band, assignable to Glu204, in L -BR difference spectra argues that if there is a strongly-H-bonded Glu(194/204) pair, it is fully protonated, rather than hemi-protonated, in the BR state. Furthermore, the results shown in Figs. 10–11 indicate that, if either or both of these two Glu residues deprotonate(s) during the photocycle, it is most likely when L is formed, not M. Such kinetic behavior is not consistent with what is expected for the PRG.

In summary, the IR data, taken together, argue strongly against a hemi-protonated Glu(194/204) pair as the PRG. The evidence is more equivocal, as to whether a fully-protonated Glu194/204 pair might participate in the PRG.

3. Model with Arg82 as the PRG

Figure 16 shows the integrated spectrum from 1655 cm⁻¹ to 1665 cm⁻¹ (in black) for protonated Arg82⁺ as a function of log (time) superimposed on the time courses of all intermediates (shown in color). This superposition shows that change at this wavenumber starts in the early part of L (i.e. L_F), and the absorbance reaches its low point at the time the L → M transition is complete. This behavior is entirely consistent with Arg82 functioning as the PRG.

Figure 16.

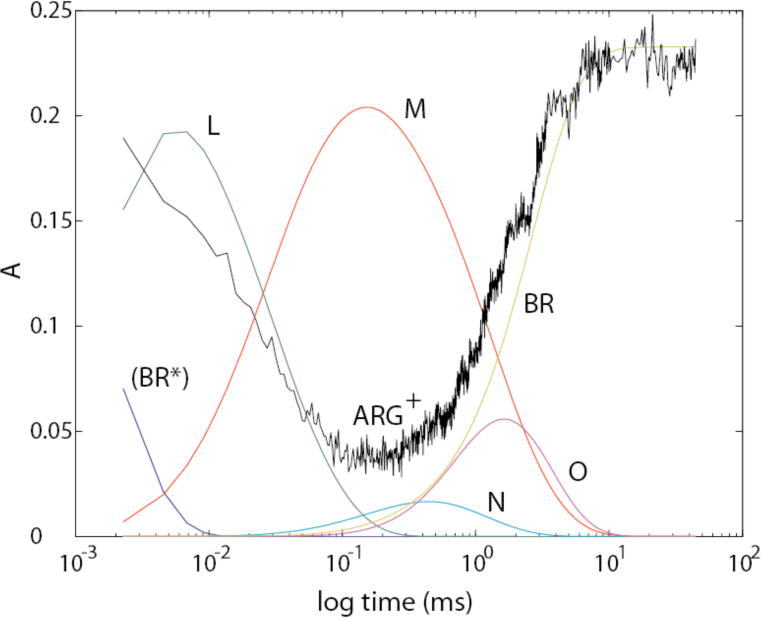
The time course of integrated absorbances from 1655 cm⁻¹ to 1665 cm⁻¹ (black trace), attributable largely to protonated Arg82, has been scaled and superimposed on the time courses for the intermediates in the photocycle.

The ¹⁵N isotope dependence of the Arg82 band in the M-BR difference spectrum led to the conclusion that this group undergoes a major structural change, mostly likely deprotonation, when M is formed. ²⁸ The absence of similar isotope labeling in spectra of the later intermediates prevents us from identifying, with any certainty, at which step(s) the Arg82 structural change is reversed. However, the time course of the recovery of the 1661 cm⁻¹ negative band is most closely aligned with the N → O transition (Fig. 16). Additionally, of the 3 distinct structural transitions that we observe during the decay of M, namely M→ N (Figs. 10C, 11B), N → O (Figs. 10D, 11C), and O → BR (Fig. 10E), the N→O transition shows the strongest coincident signals (positive absorbance change at marker band 4 and negative absorbance change at marker band 5) that would be expected for the Arg82 structural reversal. This suggests that if Arg82 does indeed deprotonate in M as concluded previously,²⁸ then it most likely reprotonates during the N → O step.

4. Comparison to other recent work

Morgan et al.⁵⁰ have recently obtained data under slightly different temperature conditions, and performed kinetic analyses using the unidirectional kinetic model of Chizhov et al.⁵¹ As discussed in the Introduction above, no strictly linear model can correctly describe the bR photocycle. Therefore no such model can lead to the isolation of accurately-separated absolute spectra for each of the known intermediates of the photocycle. In addition, Morgan et al. based their pH studies on the assumption that the same kinetic model applies at pH 7 and 5. This assumption has also been shown to be invalid.^{2, 14}

Nevertheless, Morgan et al. concluded that there is a pH dependence of a very small component, centered near 1885 cm⁻¹, that is part of a larger pH-invariant negative continuum absorbance band extending over most of the spectral region above 1600 cm⁻¹. They attributed the small component centered near 1885 cm⁻¹ to a protonated water cation serving as the PRG. This assignment also relied on this band’s similarity in frequency to a vibrational band previously seen in isolated protonated water clusters.⁵² In fact, the substantially narrower bandshape and greater intensity of the latter observed band call into question the significance of the similarity in frequency. The only isotope dependency observed for the 1885 cm⁻¹ band detected by Morgan et al. ⁵⁰ was ¹H/²H substitution, which is very non-specific. Broad continuum bands in this frequency region have also been observed for a variety of other H-bonded groups present in bR, such as carboxylic acids (e.g. see figure 1c in ref. ⁵³).

Morgan et al.⁵⁰ also challenged the validity of the assignment of the 1661 cm⁻¹ trough to protonated Arg82 (as indicated in Table 3). This was also based on their calculated “M-minus-BR” spectra, in which there did not appear to be any difference in the size of this band for ¹H and ²H samples. However, Morgan et al.⁵⁰ made both their ¹H and ²H measurements of the M – BR spectra at room temperature, rather than at 0°C as in Xiao et al.²⁸ As a result, the size of the 1661 cm⁻¹ negative band in the ¹H spectrum of Morgan et al.⁵⁰ is already substantially smaller than the 1661 cm⁻¹ negative band reported for the corresponding M – BR spectrum in Xiao et al., ²⁸ or in other time-resolved FTIR difference measurements made at 0°C. ³⁷ The ¹H/²H sensitivity of the 1661 cm⁻¹ band in Xiao et al.²⁸ cannot reasonably be assessed except under measurement conditions that successfully reproduce its large undeuterated intensity.

On the other hand, the much more complicated kinetic behavior at lower temperatures, the absence of a pure M state at any time during the photocycle, and (most importantly) the slowing of all the photocycle steps in ²H₂O, all make it a challenge to perform any kind of direct comparison of the size of the 1661 cm⁻¹ band in ¹H and ²H samples, even at 0°C. This is why no effort has been made in the current work to obtain data from deuterated samples, nor from samples at 0°C. (The comparison is much easier for ¹⁴N and ¹⁵N samples, because this type of isotope labeling does not significantly affect the photocycle kinetics. Unfortunately, ¹⁵N-arginine-labeled samples are expensive and complicated to produce, and were therefore also unavailable for the current work.)

Specifically, the “M minus BR” spectrum for the ²H sample (but not the ¹H sample) in Morgan et al.⁵⁰ was computed by subtracting 30% of a fitted kinetic spectrum believed to be mostly due to N. This subtraction could also have altered the trough size at 1661 cm⁻¹. The 30% subtraction factor was generated based on the presumption that deuteration should not have any effect on the size of a different trough, near 1670 cm⁻¹. This rather arbitrary assumption exemplifies the difficulties of trying to compare photointermediate spectra obtained for samples (e.g. ¹H/²H samples) that exhibit significantly different kinetic behavior, especially without performing a complete kinetic analysis in order to obtain pure spectra of individual species. Curiously, and somewhat contradictorily, kinetic plots of the raw (unfitted) data in ref. ⁵⁰ show clearly that the 1661 cm⁻¹ trough does in fact lose ~ 20% of its maximum time-dependent intensity upon ²H substitution.

Finally, any interpretation that the 1661 cm⁻¹ band is insensitive to ¹H/²H substitution requires a molecular vibrational assignment that can still account for this band’s observed sensitivity to ¹⁴N/¹⁵N isotope substitution.²⁸ Protein and lipid vibrations that are close (~20 cm⁻¹) to this frequency and that involve N atom(s) are not sensible alternate assignments, since these all also involve at least 1 exchangeable proton on the nitrogen.

D. Mechanistic implications of findings reported here

With respect to the homogeneous, linear sequential photocycle using intact L and M intermediates, our data agree with most of the major tenets of the consensus view. Additionally, our data support previously reported evidence for the transient deprotonation of Arg82 in the M state, and its reprotonation in the N-O transition, making this residue the most likely candidate for the PRG. ²⁸

The difference spectra based on the parallel-cycles model yielded new findings regarding the L→M_F transition in the M_F pathway in a comparison with the L→M_S transition in the M_S pathway. In the L→M_F transition, we saw a large deprotonation of Arg82, whereas in the L→M_S transition we saw none. This says that protons are released from Arg82 during L decay in the M_F pathway, but either not at all or at a later photocycle stage in the M_S pathway. Our data with the parallel-cycles model thus provide support for the view that Arg82 could be the PRG, and also that the PRG functions very differently in the two parallel photocycles.

This finding is consistent with, and helps to explain, a number of published observations which are briefly summarized below.

1. It has been shown that intermediates of the M_F pathway show markedly different laser energy saturation behavior compared to the intermediates of the M_S pathway.

2. Measurements of the membrane potential (Δψ) accompanying laser-induced proton transport correspond to the saturation curve for M_S. (not MF).

3. Proton ejection is depressed as pH is lowered with an apparent pK_a of ~5.8. ^55,56 A pH titration shows that the ratio of fraction M_F/M_total decreases and that of MS/M_total increases with a pK_a of ~6.5.⁵⁷ FTIR signals due to Arg82 deprotonation are reduced when the pH is lowered to 4.²⁸ indicating that the transient arginine deprotonation does not occur under pH conditions where M_S is known to predominate.

4. When an existing Δψ is too high to support proton release to the external surface, as in whole cells of H . Salinarum, essentially all energy is in the form of Δψ, ⁵⁸ and the fraction of M_S /M_total is very high. Titration with the protonophore CCCP collapses the Δψ, and leads to the formation of ΔpH as the fraction of M_F/M_total rises and that of M_S /M_total falls.⁵⁹

There is no way that a homogeneous, single cycle system could account for the changes in relative turnover amounts of M_F and M_S elicited by changes in pH, membrane potential, and light intensity as listed above, nor in the change in relative amounts of M_F and M_S elicited by changes in membrane polarity.^{57, 60} It is not only that the relative amount of these two intermediates change, but the relative amounts of the M_F → N → O and M_S → BR pathways change accordingly.

E. The path for proton flow in bR

In concluding that a protonated water cluster (a Zundel cation) is unlikely to serve as the PRG, we do not mean to imply that such a water cluster and associated proton wire can not play an essential role in the overall vectorial transport process linked to bR turnover. In fact, we think that the water molecules shown in the crystal structure for bR very likely do play a role in the energy-driven vectorial transport of protons, in particular on time scales other than those expected for protonation changes in the PRG. However, in order to identify this separate role, we need a new characteristic IR signature.

On the other hand, the findings presented here provide strong support for the deprotonation of Arg82 in the L → M transition. This negates one of the reasons cited by Garczarek et al.⁴⁸ for pursuing the idea of the water complex as the PRG for the L → M transition. They stated that there is no evidence for the deprotonation of a carboxylic acid in this step, but omitted the possibility that some other type of amino acid side chain deprotonates. One reason why they may have missed the deprotonation of Arg82, which is clearly shown in our data, is that their water content was far above the 0.1 to 0.5 μL/cm⁻² range used in our work. The strong water peak at 1643 cm⁻¹ overlaps the signature absorbance for protonated Arg82 near 1660 cm⁻¹. The high absorbance caused by this increases noise and decreases the ability to discern small changes in signal. In any reasonable attempt to consolidate all hard evidence in a picture that includes a role for the water molecules, Arg82 must also be considered as one of the key players.

Our proposed path for the flow of protons from the aqueous cytoplasmic medium across the membrane to the external surface of the PM, associating each proton transfer with a step from the single cycle homogeneous photocycle, and not including steps too fast to be observable is, thus

$$\begin{array}{l}{\mathrm{H}}^{+}\to \mathrm{Asp}96\to \mathrm{SB}\to \mathrm{Asp}85\to \mathrm{Asp}82\to {\mathrm{H}}^{+}\\ [\mathrm{N}\to \mathrm{O}][\mathrm{M}\to \mathrm{N}][\mathrm{L}\to \mathrm{M}][\mathrm{N}\to \mathrm{O}][\mathrm{L}\to \mathrm{M}]\end{array}$$

We recognize that there is not agreement on the step using Arg82, but in order to proceed, we use this as the PRG based on the findings reported here and in other publications.^{27, 28} As pointed out in ref. ²⁰, Arg82 is not in H-binding contact with bulk water either in the BR or M state. Therefore, the H⁺ release pathway must involve intermediate transfers to and from other groups such as Glu(194/204) and/or an H-bonded network, such as a water cluster. The proton from Arg82 is thus released first to other acceptor(s) in the membrane, from which it rapidly diffuses into the bulk medium.

The M_F pathway of the heterogeneous parallel photocycle is essentially the same as shown above; with the exception that M is replaced by the separate M_F. As shown in the Results section, the extent of Arg82 deprotonation is even greater in this case than when the unitary M state is used.

The M_S pathway of the heterogeneous parallel photocycle presents an entirely different situation. There are no detectable N or O intermediates, and Arg82 is not deprotonated during the L→M_S transition. In fact, our data lead to the conclusion that Arg82 is not involved in the events of the M_S pathway. At this time, we are not prepared to be specific, about the route from Asp85 to the external surface, but the involvement of Glu194 and/or 204 as well as water clusters seems most likely.

Abbreviations

TR-FTIR

Time-resolved Fourier transform infrared spectroscopy

bR

bacteriorhodopsin protein

BR

ground state of bR

BR*

photon-activated BR (authentic spectrum not isolated here)

M_F

form of M-intermediate which decays through the O-intermediate on its return to the ground state with a time constant near 2 ms at pH near 7 and T near 20 °C

M_S

form of M-intermediate that decays directly to the ground state with a time constant near 5 ms at pH near 7 and T near 20 °C.

M_tot

sum of M_F and M_S

SVD-lsq

Singular value decomposition based on least squares analysis

PRG

proton release group

PM

purple membrane

Δψ

membrane potential

τ

time constant

wn

wave number

wl

wave length

TDS

transitional difference spectrum between a pair of photointermediates

GDS

ground-state difference spectrum, between a photointermediate and BR

RHM

reversible homogeneous model for the bR photocycle