Making yttria-stabilized tetragonal zirconia translucent

Abstract

Objective

The aim of this study was to provide a design guideline for developing tetragonal yttria-stabilized zirconia with improved translucency.

Methods

The translucency, the in-line transmission in particular, of 3 mol.% yttria-stabilized tetragonal zirconia (3Y-TZP) has been examined using the Rayleigh scattering model. The theory predicts that the in-line transmission of 3Y-TZP can be related to its thickness with grain size and birefringence the governing parameters. To achieve a threshold value of translucency, the critical grain size of 3Y-TZP was predicted for various thicknesses (0.3 – 2.0 mm). The threshold value was defined by a measured average in-line transmission value of a suite of dental porcelains with a common thickness of 1 mm. Our theoretical predictions were calibrated with one of the very few experimental data available in the literature.

Results

For a dense, high-purity zirconia, its in-line transmission increased with decreasing grain size and thickness. To achieve a translucency similar to that of dental porcelains, a nanocyrstalline 3Y-TZP structure was necessitated, due primarily to its large birefringence and high refractive index. Such a grain size dependence became more pronounced as the 3Y-TZP thickness increased. For example, at a thickness of 1.3 mm, the mean grain size of a translucent 3Y-TZP should be 82 nm. At 1.5 mm and 2 mm thicknesses, the mean grain size needed to be 77 nm and 70 nm, respectively.

Significance

A promising future for zirconia restorations, with combined translucency and mechanical properties, can be realized by reducing its grain size.

1. Introduction

Yttria-stablized Tetragonal Zirconia Polycrystal (Y-TZP) has been used as a dental restorative material for over a decade [1]. While it is still the strongest and toughest ceramic ever used in dentistry, its aesthetics—in particular, its translucency—remains as a major drawback. The opacity of zirconia becomes a problem especially when placing an anterior crown or shortspan fixed dental prosthesis in the presence of other anterior natural teeth. In this case, the reflectance and light scattering do not always appear natural. In order to create space for a porcelain veneer thick enough to cover the opaque zirconia core and to match the optical properties of the adjacent natural dentition, a substantial reduction of tooth structure is required. In addition, in an effort to prevent veneer chipping [2–5] and delamination [6–8], monolithic zirconia is often used in full arch restorations, posterior crowns and fixed dental prostheses [9–16]. In these cases, the opacity of zirconia can pose a problem.

After a decade of research and development, some progress has been made in improving the translucency of Y-TZP (e.g. increase the density of zirconia and eliminate the alumina sintering aid). However, close examinations have revealed that unless it is thin (< 0.5 mm), the so-called commercial translucent Y-TZP restorative materials remain predominantly opaque. Beyond such phenomenon lies a critical question: how do we improve the translucency of Y-TZP? To answer this question, we must begin with the interactions of light and solids.

Light, x-rays, and heat are all part of electromagnetic waves; each is characterized by a specific range of wavelengths. X-rays have a wavelength typically in the range of 0.01 to 10 nm, while visible light lies between 400 nm (violet) and 700 nm (red). Under daylight conditions, the normal human eye is most sensitive to a wavelength of 555 nm, leading to a perception that green light, at this wavelength, is far “brighter” than the light at other wavelengths.

When light proceeds from air into a solid, part is reflected, part is absorbed, but part may be transmitted. Reflection occurs at the interfaces between the solid and air. Absorption happens when a photon of light transfers its energy and momentum to a valence band electron, excites the electron, across the band gap, into the conduction band. Naturally, these excitations with the accompanying absorption can take place only if the photon energy is greater than that of the band gap. The band gap of Y-TZP is around 5.2 eV and 6.0 eV according to the theoretical calculation and experimental determination, respectively [17]. Both values are much greater than the maximum energy 3.1 eV associated with the minimum wavelength 400 nm of visible light, suggesting that no significant adsorptions occur over the visible region of the spectrum. The question then arises: what makes an inherently transparent Y-TZP material opaque? In the following section, we examine the light transmission properties of Y-TZP.

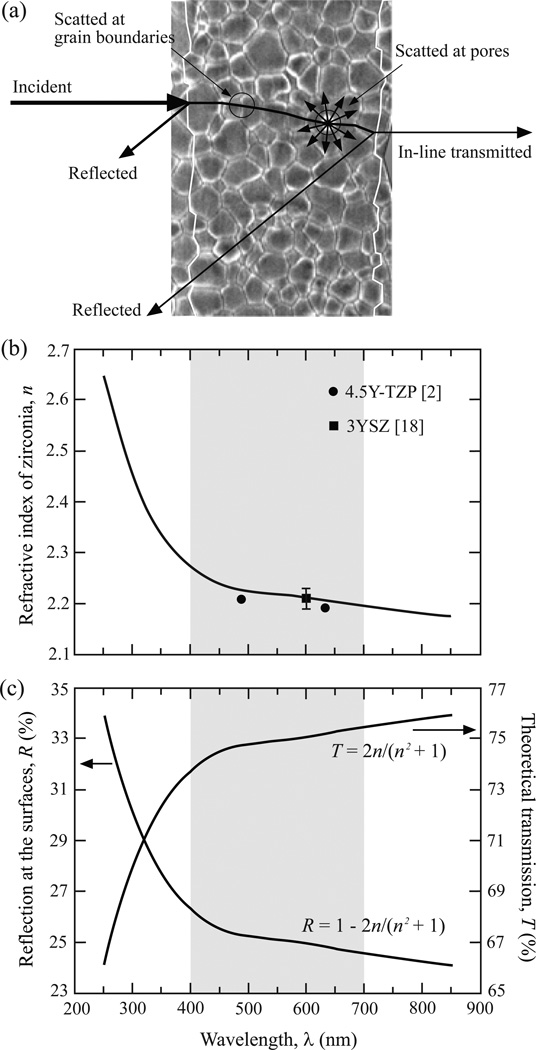
Light that transmitted into the interior of Y-TZP may experience interior reflection and refraction; the phenomenon is termed as scattering. This internal light scattering may result from several sources, including pores, impurities, defects, and grain boundaries (Fig. 1).

Figure 1.

The interactions of light and zirconia. (a) Schematic of light transmission through tetragonal zirconia. Losses in intensity of the incident light are due to reflection at zirconia surfaces, and scattering by optical birefringence and at pores. Wavelength dependence of (b) the refractive index of tetragonal zirconia, and (c) theoretical transmission and reflection (at the surfaces).

The influence of pore size and pore population on light scattering in zirconia has been examined by a number of authors [18–20]. It was found that pore sizes in the range of 200 – 400 nm (typical of the current dental zirconia) and pore populations as low as 0.05% can significantly relegate the translucency of Y-TZP. The dental community is well-aware the deleterious effect of porosity on zirconia translucency. Measures, such as high sintering temperatures (1510 – 1550 °C) coupled with prolonged dwell time (up to 6 hrs) (BruxZir, Glidewell, Newport Beach, CA), have been taken to ensure a respectable density.

Impurities that have different refractive index than zirconia (e.g. alumina sintering additives) can dampen the translucency of Y-TZP [21]. (The index of refraction for alumina and zirconia, at 600 nm wave length, is n = 1.76 and n = 2.21, respectively.) In this case, scattering of light occurs when a light beam travels across the two phase boundaries. To achieve a better translucency, some dental manufacturers have eliminated the light-scattering alumina sintering aids (e.g. Glidewell, Newport Beach, CA and 3M ESPE AG, Seefeld, Germany).

Point defects, such as oxygen vacancies, can form in the Y-TZP lattice, thus, absorbing light [22]. This is especially the case for Y-TZPs sintered in reduced atmosphere or a controlled environment. Post-sintering heat treatment in air is, therefore, necessary to diffuse oxygen back into crystal lattice, eliminating the oxygen vacancies [22–25].

Finally, tetragonal zirconia crystal is birefringent, meaning that the index of refraction is anisotropic in different crystallographic directions [18,21]. In polycrystalline Y-TZPs, birefringence results in the discontinuity of the refractive index at the grain boundaries if the adjacent grains do not have the same crystallographic orientation. This causes both reflection and refraction at grain boundaries, leading to diversions in the incident beam and thus reductions in light transmittance.

There has been a large volume of literature concerning the transparency/translucency of yttria-stabilized zirconia (YSZ); most of which has been focusing on the development of transparent cubic YSZ (fully stabilized with 8 mol.% or more yttria), due primarily to its isotropic refractive index property and thus the absence of scattering from birefringent grain boundaries [20,25–29]. The problem is that the strength of fully stabilized cubic zirconia can only attain one-half to two-thirds of that of partially stabilized tetragonal zirconia [18]. Few studies have investigated the translucency/transparency properties of 3 mol.% Y-TZP [18,19,21,22]. The findings suggest that nanocrystalline 3Y-TZP may potentially exhibit both desirable translucency and mechanical properties [30,31]. The challenge, however, lies in the fabrication of such high-quality nanocrystalline structures with little to no porosity and defects.

Several authors went on to predict the desirable grain size of 3Y-TZP for obtaining a good translucency/transparency using light-scattering models [18–20]. Following a pioneering theoretical treatment on the transparent property of alumina [32], Krell et al. [19] used the Rayleigh-Gans-Debye (RGD) scattering model to predict the dependence of translucency on the grain size of 3Y-TZP. However, these authors later discovered that the RGD approximation works perfectly for alumina (example see ref. [32]) but not 3Y-TZP, due to a large birefringence of 3Y-TZP relative to alumina [18]. Klimke et al. used the Mie scattering model—a solution of Maxwell’s equations for electromagnetic waves—to elucidate the translucency of 3Y-TZP [18]. However, only limited cases—two ceramic thicknesses (0.5 mm and 1.0 mm) at two wavelengths of the incident light (500 nm and 640 nm)—were examined. In addition, the Mie solution involves infinite series, which requires numerical simulation using computer codes, and thereby is not preferred over its approximations—the RGD or the Rayleigh scattering model.

In this study, we used a more straight forward Rayleigh scattering model—an approximation of the more general Mie scattering model—to systematically examine the effects of grain size, refractive index, birefringence, and layer thickness on the in-line transmission of 3Y-TZP. The transmittance of electromagnetic waves in the visible light range was investigated. The design philosophy in producing translucent 3Y-TZP restorative ceramics with excellent mechanical properties and phase stability through microstructural tailoring has been proposed.

2. Theory

2.1. Rayleigh approximation

The main factors that limit the translucency of a solid—apart from reflection and absorption—are scatting from pores, impurities, defects, and grain boundaries. For a dense, high purity and nonabsorbing 3Y-TZP, the Rayleigh approximation can be used to estimate its translucency (in-line transmission, T_IT) based on light scattering at grain boundaries due to the birefringence [18]:

$$T_{IT}=(1-R)\mathit{\text{exp}}\left\{\right(-\frac{129{\pi }^4{r}^3}{18{\lambda }^4}\left){\left[\frac{\Delta n_{\mathit{\text{ave}}}(2n+\Delta n_{\mathit{\text{ave}}})}{2}\right]}^{2}t\right\}$$ (1)

where Δn_ave is the average birefringence, n is the refractive index, 2r is the grain diameter, t is the thickness of 3Y-TZP, λ is the wavelength of the incident light, and R is the loss due to reflection at the solid surfaces. Note: Klimke et al., in the Eq. (2) of their original paper, had left out a negative sign in the exponents of the natural base. The first term of the exponential function (Eq. 1) signifies the dominance of ceramic grain size, while the second term emphases the importance of birefringence in anisotropic crystals.

Eq. 1 describes, in a very succinct way, the interrelation between the in-line translucency and ceramic thickness with grain size and birefringence the governing parameters. In design of highly translucent ceramics, it is crucial to keep their grain size small, especially for ceramics with a high refractive index and large birefringence such as 3Y-TZP.

2.2. Applicable range for the Rayleigh scattering model

Any meaningful application of the Rayleigh scattering model requires knowledge of its range of validity. Strictly speaking, Rayleigh scattering describes the elastic scattering of light by insulating particles much smaller than the wavelength of the incident light. In the case of propagation of light through polycrystalline 3Y-TZP, the criterion for Rayleigh scattering is:

$$\frac{2\pi rn}{\lambda }<1$$ (2)

where r is the radius of the 3Y-TZP grain, n is the refractive index, and λ is the wavelength of the light. Accordingly, the upper threshold of 3Y-TZP grain size, which satisfies the criterion for Rayleigh scattering, can be estimated using Eq. 2. Consider the shortest (370 nm) and the longest (750 nm) wavelengths that the human eye recognizes, the maximum grain size for Rayleigh scattering ranges from 50 nm to 110 nm.

2.3. Index of refraction

The refractive index is arguably the most important optical property of a material; it generally varies with the wavelength of light n(λ). We use one of the very few comprehensive refractive index data available for zirconia (http://refractiveindex.info/), and plot it as a function of wavelength in Fig. 1b (solid curve). The shaded area represents the visible light region (λ = 400 – 700 nm). As one can see, the refractive index of zirconia, n, increases drastically as the wavelength approaches the UV regime (< 400 nm), but gradually decreases as the wavelength enters the visible spectrum and beyond. The n – λ curve is then calibrated against experimental data from the literature. Individual data points of various symbols in Fig. 1b are experimental data for 3Y-TZP (square [33]) and 4.5Y-TZP (circles [17]). The measured n values for 3Y-TZP sit on the n – λ curve, whereas those for 4.5 Y-TZP lie just below the n – λ curve. It has been reported that, for a given wavelength, n decreases as the Y₂O₃ content increases [17]. This observation agrees with the fact that the n values for 4.5Y-TZP determined by French et al. [17] are slightly lower than the n – λ curve for 3Y-TZP, which boosts the confidence on the n(λ) data utilized.

As alluded to in our Introduction, when light strikes a solid, some will be reflected. If the incident light is normal to the solid surfaces, the loss of reflection, R, at the front and back faces of a solid is given by $R=1-\frac{2n{n}_{\mathit{\text{air}}}}{n^2+{n_{\mathit{\text{air}}}}^2}$, where n and n_air are the refractive indices of solid and air, respectively. Using the n(λ) data for 3Y-TZP from Fig. 1b and n_air ≈ 1 for air in the visible range, the loss due to reflection at both the front and back surfaces of Y-TZP can be predicted by $R=1-\frac{2n}{n^2+1}$, and results are plotted in Fig. 1c. Assuming no scattering from the grain boundaries and pores and no absorption occurred, the maximum theoretical transmission, T, of 3Y-TZP can be estimated by $T=1-R=\frac{2n}{n^2+1}$ (Fig. 1c). In the visible spectrum (shaded area in Fig. 1c), 3Y-TZP has a higher refractive index value relative to other dental ceramics. For instance: alumina (n ~ 1.76) [32], lithium disilicate (n ~ 1.55 [34]), leucite (n ~ 1.51 [35]), and porcelain (n ~ 1.50 [35]). As a result, 3Y-TZP exhibits a high surface reflection and a low light transmission relative to other dental ceramics, especially in the short wavelength region.

2.4. Birefringence in zirconia

Y-TZP has an anisotropic crystal structure, which causes different refractive indices in different crystalline directions. This optical anisotropy, or birefringence, can create discontinuity of the refractive index (Δn) at the grain boundaries if the crystal orientations of the adjacent grains are not the same, which in turn results in light scattering. Unfortunately, reliable experimental data on Δn for 3Y-TZP is not readily available. By comparing the tetragonal unit cell of zirconia to monoclinic and cubic lattices, Krell et al. [19] predicted that the maximum Δn_max value for 3YTZP should lie between 0.035 and 0.050. Assuming the 3Y-TZP grains are randomly orientated, the average birefringence can be estimated by Δn_ave = 3/2 Δn_max [32]. This theoretical prediction is in line with the experimentally determined Δn_max = 0.030 for 4.5Y-TZP reported by French et al. [17]. Thus, a range of Δn_ave = 0.020 – 0.033 appears appropriate to cover the possible variations in birefringence of 3Y-TZP.

3. Results

3.1. Predictions from the Rayleigh scattering model

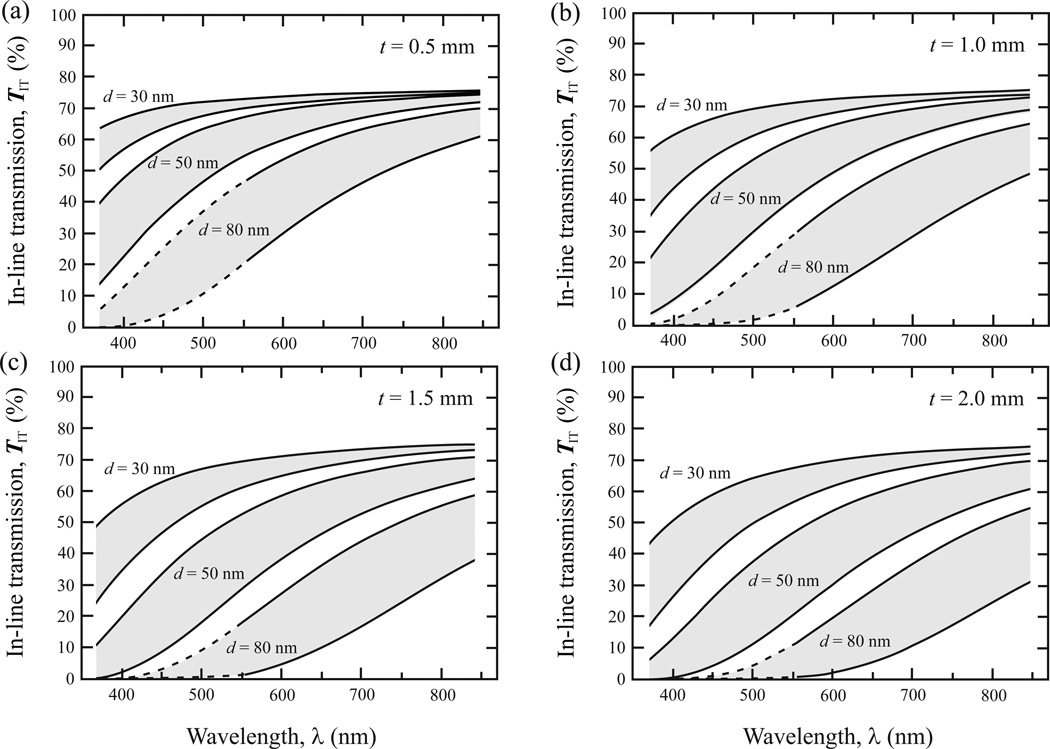
In-line transmission, T_IT, of Y-TZP with various grain size and plate thickness as a function of wavelength λ has been predicted using the Raleigh model (Eq. 1). The results are presented in Fig. 2. The grain sizes examined were 30, 50 and 80 nm; the thicknesses investigated were pertinent to those of dental restorations (0.5, 1.0, 1.5, 2.0 mm). The in-line transmission was given in a range with the upper and lower bounds corresponding to a lower and higher average Δn_ave value 0.020 and 0.033, respectively. Regions bounded by two dashed lines (i.e. 3Y-TZP of 80 nm at shorter wavelengths) were extrapolations of the theoretical prediction, due to the violation of the criterion for Rayleigh scattering. T_IT increased as the wavelength increased; however, it decreased as the grain size and zirconia thickness increased. For grain size of 30 nm, T_IT remained greater than 50% for thicknesses up to 2 mm at wavelengths between 500 and 600 nm, suggesting that an ultra-fine grain (<30 nm) 3Y-TZP is essentially transparent. However, the transmittance decreased significantly as the grain size increased.

Figure 2.

Predicted in-line transmission as a function of wavelength for 3Y-TZP with various grain sizes and layer thicknesses. Predictions were made using the Rayleigh scattering model (Eq. 1) with an average birefringence Δn_ave = 0.020 – 0.033. Regions bounded by two dashed lines were extrapolations of the theoretical prediction, due to the violation of the criterion for Rayleigh scattering.

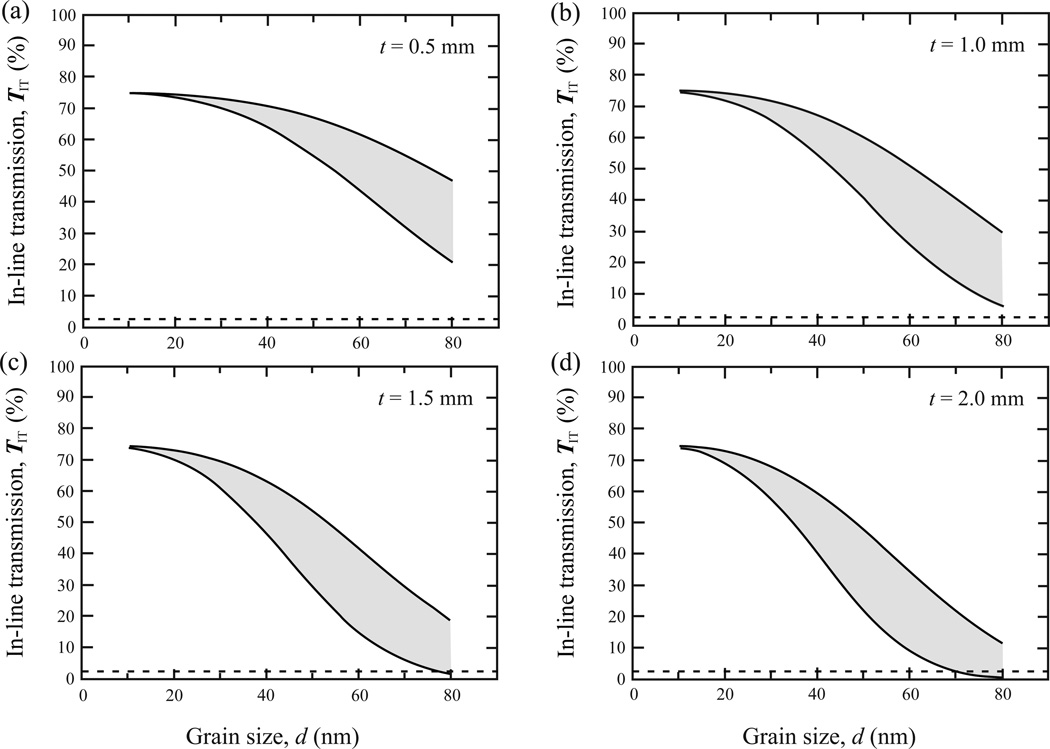
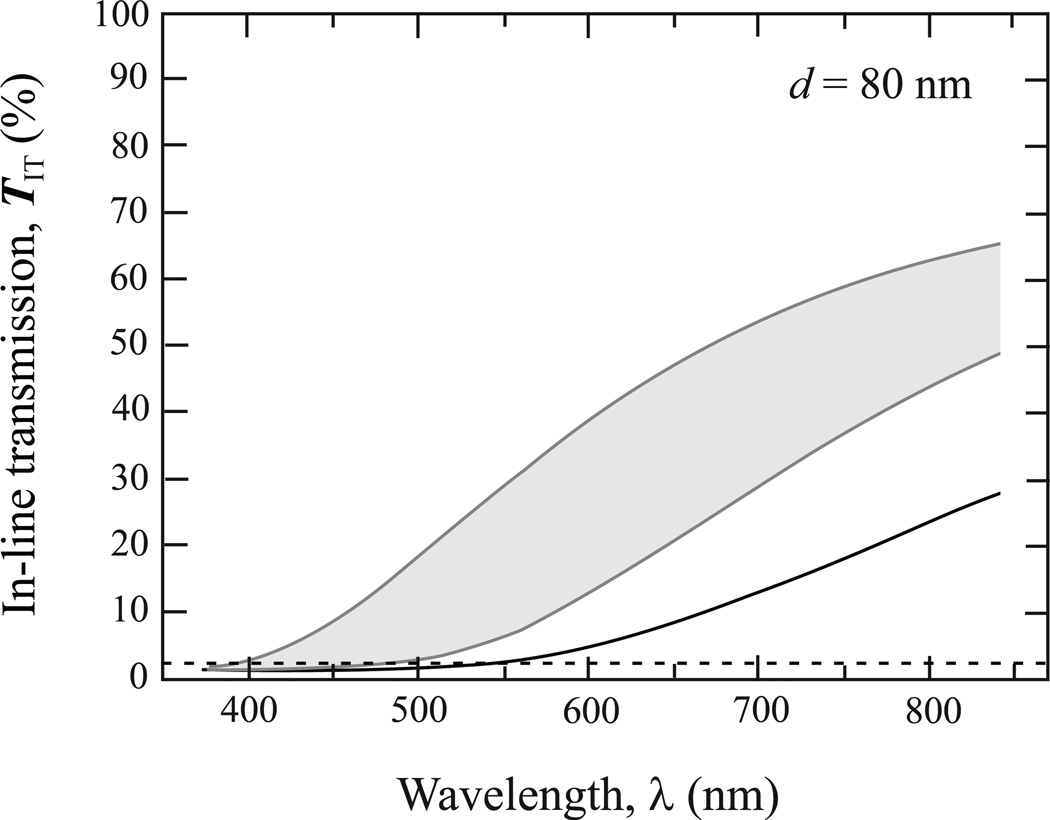
To demonstrate the effect of grain size on light transmittance, in-line transmissions of 3Y-TZP are plotted as a function of grain size for various thicknesses at a wavelength of 555 nm (Fig. 3). We chose 555 nm wavelength because it is most sensitive to the human eye. Our prediction of T_IT vs. d for 1 mm thick 3Y-TZP using a simple Rayleigh scattering model (Fig. 3b) is almost identical to that estimated using a more complex Mie scattering model (see solid curves in Fig. 16 of ref. [18]), which validates our analysis. Here, let T_IT = 2.5% be the minimum requirement for a desirable translucency. This assumption is based on our experimental measurements on a suite of commercial translucent porcelains (1 mm in thickness), where the T_IT values have varied between 2 – 3 % at a wavelength of 555 nm. In another words, the 2.5% T_IT threshold ensures that the translucency of a 1 mm thick 3Y-TZP plate is equivalent to that of dental porcelains as perceived by human eye. For reference, the T_IT value of a current translucent 3Y-TZP of 1 mm thickness (Zpex, Tosoh Corporation, Tokyo, Japan) is merely 0.5% at 555 nm. It is important to note that for t < 1 mm, zirconia plates remain essentially transparent for grain size up to 80 nm (Figs. 3 and 4). However, at larger thicknesses, t = 1.5 and 2 mm, in order to retain a good translucency, the average grain size of 3Y-TZP needs to be 80 nm or finer.

Figure 3.

The dependence of in-line transmission on the grain size for 3Y-TZP with various thicknesses at a wavelength of 555 nm. Predictions were made using the Rayleigh scattering model (Eq. 1) with an average birefringence Δn_ave = 0.020 – 0.033. Note: the dashed horizontal line at T_IT = 2.5% represents a measured average in-line transmission value of various dental porcelains with a common thickness 1 mm at a wavelength of 555 nm.

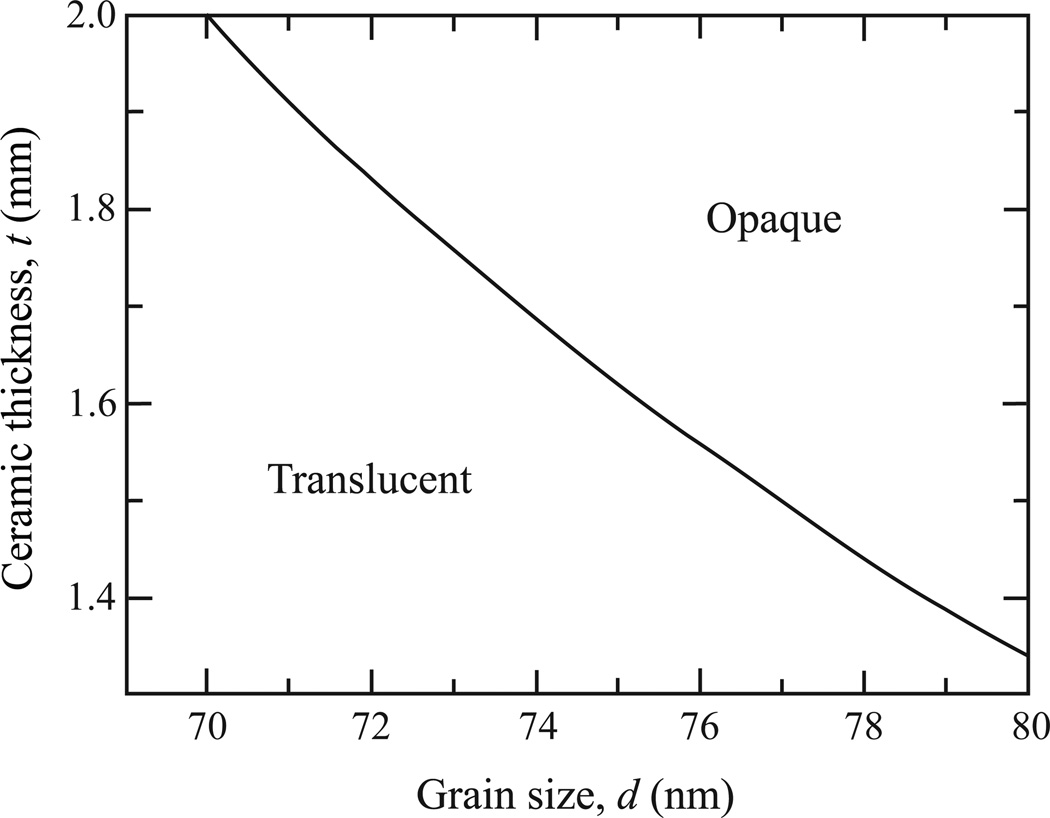
Figure 4.

Contours of threshold in-line transmission values for 3Y-TZP at 555 nm wavelength plotted on axes layer thickness (t) and grain size (d). Predictions were made using the Rayleigh scattering model (Eq. 1) with an average birefringence Δn_ave = 0.033.

To better illustrate the dependence of translucency on grain size and layer thickness, Fig. 4 shows the transmittance contour for 3Y-TZP obtained using Eq. 1 and Δn_ave = 0.033 at a wavelength of 555 nm. The boundary between the translucent regime (lower-left hand corner) and the opaque region (upper-right) is drawn based on the minimum criteria of 2.5% in-line transmission for translucency. It is evident that, in order to maintain a respectable translucency, demands for a finer grain size become increasingly crucial as the ceramic thickness increases.

3.2. Experimental validations using published data

To facilitate a direct comparison between the theoretical prediction and experimental measurement, the in-line transmission of a nanocrystalline 3Y-TZP across the visible spectrum predicted by the Rayleigh scattering model (Eq. 1) is presented in Fig. 5, together with a set of experimental data from ref. [21]. The 3Y-TZP specimens examined have a common mean grain size of d = 80 nm and thickness t = 1 mm. In our theoretical analysis, an average birefringence Δn_ave = 0.020 – 0.033 was used; estimated T_IT values are shown in a bold grey-shaded zone. Experimentally, using a commercial 3 mol.% yttria-stabilized ZrO₂ powder (YZ-3Y, Tosoh Corporation), nanocrystalline 3Y-TZP was fabricated using the spark plasma sintering (SPS) method in vacuum [21]. The sintered 3Y-TZP disks were heat-treated at 900 °C for 4 hrs in air. In-line transmission was measured according to the method described by ref. [28]; data are replotted in Fig. 5 (solid line). The theoretically predicted T_IT values are higher than those measured experimentally across the visible spectrum. The discrepancy between theoretical prediction and experimental data will be addressed in detail in Section 4 (Discussion).

Figure 5.

Comparison between the theoretically-predicted and experimentally-measured in-line transmission values for nanocrystalline 3Y-TZP as a function of wavelength. The 3Y-TZP examined have a common mean grain size d = 80 nm and thickness t = 1 mm. An average birefringence Δn_ave = 0.020 – 0.033 was used in theoretical prediction, whereas the experimental data was obtained from ref. [21]. Regions bounded by two dashed lines were extrapolations of the theoretical prediction, due to the violation of the criterion for Rayleigh scattering. Again, the dashed horizontal line at T_IT = 2.5% represents a measured average in-line transmission value of various dental porcelains with a common thickness 1 mm at a wavelength of 555 nm.

4. Discussion

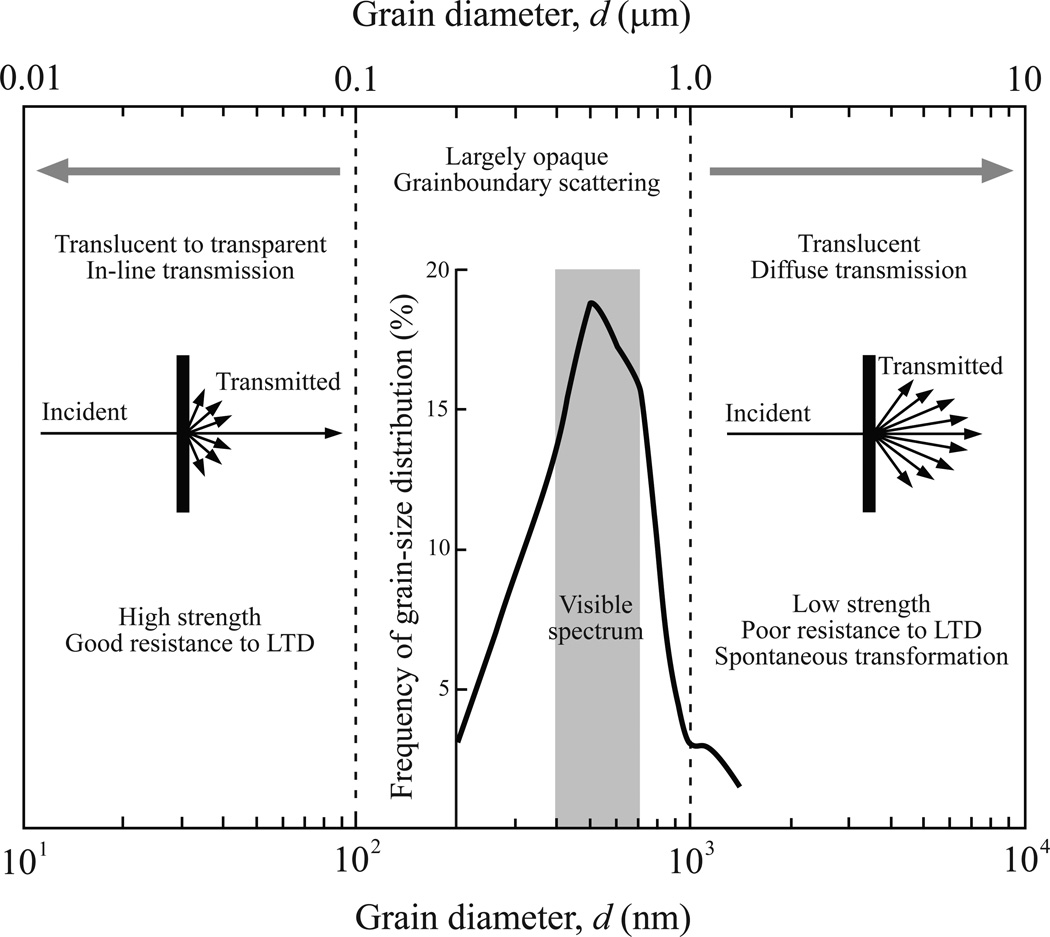
The most significant sources that hinder the translucency of 3Y-TZP are light scattering at the grain boundaries, pores, and secondary phases. Measures have been taken by the dental industry and elsewhere to reduce the porosity and to eliminate sintering additives, such as alumina. As a result, the modern dental zirconia has come a long way with its ever-increasing translucency (e.g. Lava Plus, Ivoclar Zenostar, Noritake Katana, and many more). However, careful examination revealed that commercial zirconia restorative materials, including all major brands, remain essentially opaque when their thicknesses approach 1 mm or greater. This is because of light scattering at the grain boundaries, due to the large birefringence of tetragonal zirconia crystals and the size of these tetragonal grains. The mean grain size of the current commercial zirconia varies from 0.2 to 0.8 µm; an example of the grain size distribution of a widely used commercial dental zirconia (Bruxzir, Glidewell) is shown in the central panel of Fig. 6, where the average grain size is 0.6 ± 0.2 µm with over 85% grains ranging between 0.3 and 0.8 µm. Studies have shown that 3Y-TZP of such a mean grain-size range possesses low translucency for thicknesses greater than 1 mm [18,19].

Figure 6.

Design diagram for developing 3Y-TZP with both excellent translucency and promising mechanical properties. Note: translucency in fine grained materials is achieved by a high in-line transmission (left panel), whereas that of coarse grained microstructures is attained by a high diffusion transmission (right panel). LTD stands for low temperature degradation.

The traditional way to minimize grain-boundary light scattering is to increase the grain size, leading to less encounter of a light beam with the grain boundaries as it travels through the material [36]. Thus, high translucency of coarse-grained ceramics relies on a diffuse-transmission mechanism (see the right panel of Fig. 6) [32]. By the same token, thinner ceramic permits more light transmission, simply due to fewer light/grain-boundary interactions. A successful example is the development of translucent coarse-grained alumina (mean grain size of 15 – 30 µm and about 90% translucent at a thickness of 1 mm), which was used extensively as the arc tube of high-temperature, high-pressure sodium-vapour lamps [36,37]. However, coarse-grained structures compromise the strength of ceramics [38,39]. In addition, the grain-size threshold for spontaneous phase transformation from tetragonal (t) to monoclinic (m) in 3Y-TZPs is around 1 µm [40,41], suggesting that if the vast majority of tetragonal grains are above 1 µm, then the simultaneous t → m transformation upon cooling from the sintering temperature can diminish the strength of 3Y-TZP. The grain coarsening approach is, therefore, not a suitable route for producing translucent 3Y-TZP.

A much more effective approach to increase the translucency of 3Y-TZP is to reduce its grain size. Here, high translucency is realized by a high in-line transmission (see the left panel in Fig. 6) [32]. Our analysis has demonstrated that to achieve a translucency that is comparable to dental porcelains, the mean grain size of 3Y-TZP should be about 82 nm (for 1.3 mm thickness), 77 nm (for 1.5 mm), and 70 nm (for 2 mm). Our findings are supported, with some discrepancies, by the experimental observations from ref. [21] (Fig. 5). In fact, at a slightly less translucency level, i.e. T_IT = 2% at 555 nm wavelength (which is about 80% of the translucency of porcelain), the grain size of 3Y-TZP can be ~120 nm [18], which is nearly half the size of the current fine 3Y-TZP (e.g. LAVA Plus, average grain size 250 nm).

During the development of this manuscript, 3M ESPE presented an experimental translucent zirconia at the 2014 AADR Annual Meeting in Charlotte, NC (Abstract #796). This experimental zirconia was fabricated from a 7.10 wt.% yttria-stabilized zirconia powder and sintered at 1400 °C for 1 hr dwell time. The resultant microstructure consisted of 75% tetragonal zirconia and 25% cubic zirconia with an average grain size of 150 nm. Typically, 3Y-TZP stabilized with 5.18 wt.% yttria contains 90% or more tetragonal zirconia; a higher yttria content tends to increase the amount of cubic phase in zirconia [41]. The better translucency of this new experimental zirconia was achieved by the combination of a relatively fine grain size and the introduction of cubic zirconia (with an isotropic refractive index to avoid scattering from the grain boundaries). A similar approach was adopted for the development of a new translucent zirconia (Zpex Smile) by Tosoh Corporation, where an even higher yttria concentration (9.32 wt.%) was utilized. Again, the improved translucency was achieved by the introduction of cubic zirconia. However, such a tetragonal-cubic hybrid zirconia is weaker and more brittle compared to its tetragonal counterpart (e.g. the average flexural strength and fracture toughness of Zpex Smile are 609 MPa and 2.4 MPa m^1/2, respectively). For the stronger 3Y-TZP to attend a similar translucency, its grain size needs to be further reduced, due to a large birefringence associated with tetragonal zirconia.

The discrepancy between the theoretical prediction and experimental data revealed in Fig. 4 warrants further elaboration. The higher translucency predicted by the Rayleigh scattering model relative to that observed from the experiments may be accounted for by the following reasons. Firstly, the Rayleigh scattering model substantially simplifies the microstructure of 3Y-TZP by assuming that all grains are spherical in shape and have an identical diameter. Secondly, ceramics are “optically” inhomogeneous, consisting of pores, defects, etc. The presence of porosity, even at an exceptionally low content (e.g. 0.01%) with exceedingly small size (e.g. 100 nm or so), can reduce the translucency by 50% [42]. The detrimental effect of pore size and pore content on ceramic translucency becomes more significant in materials with a high refractive index, such as zirconia, and at short wavelengths. This is due to a steep increase of the refractive index near the UV region (Fig. 1b). Finally, the material reported by Zhang et al. [21] is fabricated by SPS in a reduced environment. Consequently, the material contains a high concentration of oxygen vacancy, which acts as light scattering centers. Although post sintering heat treatment in air can put some oxygen back into 3Y-TZP crystals, such a treatment also introduces porosity to the material, owing to the coalescence of vacancies in large concentrations at high temperatures [43]. It is, therefore, crucial to optimize the heat treatment condition to reduce the oxygen vacancies while avoiding the introduction of porosity.

We acknowledge that the Rayleigh scattering model can only confidently predict the in-line transmittance of 3Y-TZP with grain sizes smaller than 80 nm. For grain sizes significantly larger than 80 nm, one needs to use the grain-size independent Mie scattering model. However, the Mie scatting model is more complex, requiring computer simulation.

5. Conclusions

This study aims to provide a guideline for designing dental zirconia with both excellent translucency and promising mechanical properties. The design philosophy for a translucent, high-strength tetragonal yttria-stabilized zirconia is to keep its grain size small, ideally under 100 nm, owing to its large birefringence and high reflective index relative to other dental ceramics. Unfortunately, reliable experimental data on translucency and mechanical properties of nanocrystalline 3Y-TZP are scarce, due primarily to the challenges in synthesizing these materials with little to no defects (i.e. pores and oxygen vacancies). One way to circumvent this problem is to “substitute” some tetragonal zirconia grains with optically isotropic cubic zirconia particles to relegate grain boundary light scattering. The trade-off of this approach is that the cubic zirconia is weaker and more brittle than its tetragonal counterpart.

Highlights.

• The translucency of 3Y-TZP has been examined using the Rayleigh scattering model.

• The in-line transmission of 3Y-TZP increased with decreasing grain size and thickness.

• To achieve a translucency similar to porcelains, a nanostructured 3Y-TZP was needed.

• At 1.3 mm thickness, the mean grain size of a translucent 3Y-TZP should be 82 nm.

• At 1.5 mm and 2 mm thicknesses, the mean grain size needed to be 77 nm and 70 nm.