Bayesian Random Threshold Estimation in a Cox Proportional Hazards Cure Model

Abstract

In this paper, we develop a Bayesian approach to estimate a Cox proportional hazards model that allows a threshold in the regression coefficient based on a threshold in a covariate, when some fraction of subjects are not susceptible to the event of interest. A data augmentation scheme with latent binary cure indicators is adopted to simplify the Markov chain Monte Carlo implementation. Given the binary cure indicators, the Cox cure model reduces to a standard Cox model and a logistic regression model. Furthermore, the threshold detection problem reverts to a threshold problem in a regular Cox model. The baseline cumulative hazard for the Cox model is formulated non-parametrically using counting processes with a gamma process prior. Simulation studies demonstrate that the method provides accurate point and interval estimates. Application to a data set of Oropharynx cancer patients suggests a significant threshold in age at diagnosis such that the effect of gender on disease-specific survival changes after the threshold.

1. Introduction

This paper is motivated by a data set of patients with Oropharynx cancer. The clinicians suspect that gender is a prognostic factor for disease-specific survival. However, the Kaplan Meier curves of females and males overlap at early times and cross during the follow-up, which suggests no difference in survival between males and females. But for a cohort of young patients, males tend to have worse survival than females. This seems to indicate a potential threshold in the age of diagnosis such that the gender effect is different below this threshold than above it. Further inspection of the data reveals that the Kaplan Meier survival curve levels off to about 0.7. The stable plateau at the tail may be taken as empirical evidence of a cured fraction. The use of standard survival analysis for detection of the threshold may be inappropriate since not all patients will die of Oropharynx cancer. To this end, we propose a survival model that allows for a threshold in the age of diagnosis to investigate a potential interaction between age and gender when a fraction of patients are cured.

Motivated by the Oropharynx cancer data set, but not limited to it, this model has broad application in biomedical studies. For example, physicians will rely on a threshold in a biomarker or combination of biomarker signatures to guide the choice of therapy for an individual patient. The therapy targeting a specific biomarker generally will work effectively for patients when that biomarker is highly expressed, and thus it is convenient to find a threshold in the biomarker such that therapy should only be given to those patients with the biomarker levels exceeding the threshold. In general, better characterizing cancers at the molecular level will lead to more efficient treatment, and methodology to improve estimates of a threshold point will help this characterization.

Several authors considered a Cox model with an unknown threshold in the covariate. Liang et al. [1] and Pons [2] proposed approaches which can be used to study the model as described in the motivating example if no cure fraction is present in the data, where the influence of a covariate z₁ (e.g. gender) jumps at a certain threshold of z₂ (e.g. age). Luo and Boyett [3] studied a model where a constant is added to the regression on a covariate z₁ after a threshold in z₂. In this model, the baseline hazard changes after the threshold. Jensen and Lutkebohmert [4] and Kosorok and Song [5] considered a Cox-type regression model with a piecewise linear functional form of the covariates. However, the above models are not appropriate when a cured fraction is present in the population.

Othus et al. [6] estimated a threshold in a covariate in the cure model setting. They assume that there is a threshold in a covariate z₂, where a sudden jump or fall occurs in the hazard value or cure probability. But their model is restricted to a simple binomial-exponential mixture model, in which a binomial model is used to estimate the cure rate and exponential distribution is used for the conditional survival. In this paper, we extend the threshold detection problem to a more general cure model in which a logistic regression is used to evaluate the effect of covariates on the cure rate and a standard proportional hazard model is used for the conditional survival. This mixture cure model (without threshold detection) has been studied by many authors [7, 8, 9], and they use EM type algorithms to compute the maximum likelihood estimates. We build on this previous research to implement a Bayesian estimation method for the Cox Proportional Hazards Cure Model, and extend it to allow a threshold in the regression coefficients. We will show that applying Bayesian methods in the mixture cure rate model is straightforward. Using a data augmentation scheme, the latent cure indicators are updated. As we demonstrate below, conditional on these indicators, the cure model reduces to a standard Cox model and a standard logistic regression model. Furthermore, our ultimate goal of detecting a threshold is simplified to a threshold problem in the regular Cox or logistic regression model.

The rest of the article is organized as follows: Section 2 outlines the model; Section 3 presents the Bayesian estimation and evaluation of model fit; Section 4 provides simulation studies; the analysis of the Oropharynx cancer data is presented in Section 5; the paper ends with a discussion in Section 6.

2. Model Description

The survival time, T, is assumed to be T = υT* + (1 − υ)∞, where υ is an indicator of whether a subject will eventually (υ = 1) or never (υ = 0) experience the event, and T* denotes the failure time if the subject is not cured. S(t|υ = 1) is the conditional survival function for patients who will experience the event, often called the latency distribution. The marginal survival function is S(t) = c + (1 − c)S(t|υ = 1), where c = P(υ = 0).

We consider a Cox proportional hazard model in the latency part of the cure model. Similar to Liang, Self and Liu (1990) and Pons (2003), a threshold, τ, could be present in a time-independent covariate z₂ and the effect of z₁ changes after τ, specifically,

$$\Lambda (t|z_0,z_1,z_2,\tau ;\upsilon =1)={\Lambda }_0(t)exp\{{\beta }_0{z}_0+{\beta }_1{z}_1\mathrm{I}(z_2\le \tau )+{\beta }_2{z}_1\mathrm{I}(z_2>\tau )\}$$ (1)

where I(z₂ ≤ τ) is a generic indicator function, which takes value of 1 if z₂ ≤ τ. β₁ represents the effect of z₁ for z₂ ≤ τ, and β₂ represents the effect of z₁ for z₂ > τ. z₀ is a vector of baseline covariates. Let β = (β₀, β₁, β₂) and z̃(τ) = (z₀, z₁ I(z₂ ≤ τ), z₁ I(z₂ > τ)), and z₀ could include z₂, but is distinct from z₁. Λ₀(t) is an unspecified cumulative baseline hazard function. S(t|z̃(τ), υ = 1) = exp{−Λ(t|z̃(τ), υ = 1)}.

A cure fraction c is modelled by a logistic regression or a probit model. In logistic regression, $c(x)=P(\upsilon =0|x)=\frac{exp(\gamma x)}{1+exp(\gamma x)}$, and the vector of covariates x includes the intercept. In a probit model, c(x) = Φ(γx), and Φ is the CDF of a standard normal distribution. These models can be extended to include a threshold in a covariate similar to that in the latency model.

3. Bayesian Estimation and Model Selection

In practice, we observe (t_i, δ_i, x_i, z_i), and i = 1, ⋯, n, where t_i, denotes the observed survival time for the i^th patient, δ_i is 0 if t_i is censored and 1 otherwise and z_i = (z_0i, z_1i, z_2i) is a vector of covariates that may associate with the risk of experiencing the event, and x_i is a vector of covariates associated with the chance of cure. x_i and z_i could be identical.

It follows that, υ_i = 1 if δ_i = 1, but if δ_i = 0, υ_i is unknown and it can be one or zero. The probability that a censored patient will eventually experience the event is given by

$$p_{{\upsilon }_i}=P({\upsilon }_i=1|x_i,z_i,T>t_i)=\frac{(1-c(x_i))S(t_i|z_i,{\upsilon }_i=1)}{(1-c(x_i))S(t_i|z_i,{\upsilon }_i=1)+c(x_i)}$$ (2)

In Bayesian sampling, a data augmentation algorithm, described by Smith and Roberts [10] and Diebolt and Roberts [11], arises naturally for estimating the missing data, which in this case is an indicator of whether the patient is cured or uncured. A vector of υ = (υ₁, ⋯, v_n) is introduced as a vector of latent Bernoulli random variables. For patient i with δ_i = 0, υ_i ∼ Bernoulli(p_υi). Conditional on the vector of (υ₁, ⋯, υ_n), the model reduces to the standard Cox model for patients with υ_i = 1. In the incidence part, the model reduces to the standard logistic regression model, in which the vector of (υ₁, ⋯, υ_n) is regressed on covariates (x₁, ⋯, x_n).

3.1. Bayesian Inference

We formulate the standard Cox model using counting processes ([12]). Let N_i(t) be the number of events occurred up to time t. Let λ_i(t) be the intensity function of N_i(t), i.e. E(dN_i(t)|ℱ_−t) = λ_i(t)dt, where dN_i(t) is the increment of N_i over the small time interval [t, t + dt). If subject i experiences the event during this interval, dN_i(t) will take the value 1, otherwise dN_i(t) is 0. ℱ_−t represents the available data just before time t. Then the proportional hazards model takes the form λ_i(t) = Y_i(t)λ₀(t) exp{βz̃_i(τ)}, where Y_i(t) is one if subject i is under observation at time t and zero otherwise.

The counting process increments dN_i(t) in the time interval [t, t + dt) are assumed to be independent Poisson random variables with means λ_i(t)dt = Y_i(t) exp{βz̃_i(τ)}dΛ₀(t), where dΛ₀(t) is the increment in the cumulative baseline hazard function during the time interval [t, t + dt). Given υ, the formulation for the latency applies only to patients with υ_i = 1.

The time intervals are constructed based on the ordered distinct event times, {s_j; j = 1, ⋯, J}, where J is the total number of distinct times, s_J is the maximum observed event time, and s_J+1 is infinity. The observed data D is assumed to be available within these intervals, such that D = {ℛ_j, 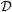_j, z_i, j = 1, ⋯, J; i = 1, ⋯, n}, where ℛ_j is the risk set and 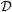_j is the event set in interval [s_j, s_j+1). Let θ = (β, dΛ₀(j), j = 1,⋯, J), the likelihood function for the above model is

$$L(\mathit{\theta },\tau ;\mathit{\upsilon }=1)=\prod _{j=1}^J{G}_j,$$

where

$$G_j=exp\{-\sum _{i\in {\mathcal{R}}_j}d{\Lambda }_0(j)exp\{\beta {\stackrel{\sim }{z}}_i(\tau )\}\}\prod _{i\in {\mathcal{D}}_j}d{\Lambda }_0(j)exp\{\beta {\stackrel{\sim }{z}}_i(\tau )\}$$ (3)

The gamma process is used as a prior for the cumulative baseline hazard function Λ₀ [13]. That is ${\Lambda }_0\sim \mathcal{\text{GP}}(c_0{\Lambda }_0^{\ast },c_0)$, where ${\Lambda }_0^{\ast }$ is often assumed to be a known parametric function. For example, ${\Lambda }_0^{\ast }=\eta y^{k_0}$ corresponds to the Weibull distribution, and c₀ represents the degree of confidence in this prior guess. The prior distribution for β ∼ MVN(μ₀, Σ₀), where μ₀ and Σ₀ are pre-specified.

In this study, τ is a parameter to be estimated from the data. Let z₂₍₁₎ < z₂₍₂₎ < ⋯, < z_2(K−1) be distinct ordered values of z_2i, i = 1, ⋯, n, and z_2(K) is the largest value of z₂. We propose to sample τ in two steps. The first step follows the work of Carlin et al. [14] and Lange et al. [15], in which the threshold is treated as a discrete variable in an application to simple regression models and Poisson processes. We first sample τ from a categorical distribution taking the value z_2(k) with probability π_k; that is,

$$\tau \sim \text{Multinomial}(1,({\pi }_1,\cdots ,{\pi }_k,\cdots ,{\pi }_{K-1}))$$ (4)

$${\pi }_k=\frac{L(\mathit{\theta },z_{2_{(k)}};\mathit{\upsilon }=1)}{{\sum }_{k=1}^{K-1}L(\mathit{\theta },z_{2_{(k)}};\mathit{\upsilon }=1)}$$

Given the intervals, the distribution of τ is assumed to be continuous with a uniform distribution, z₂₍₁₎ < τ < z_2(K). Thus having obtained a draw of z_2(k) in step one, we will sample τ from Uniform [z_2(k), z_2(k+1)] in the second step, which will result in a continuous posterior distribution of τ.

As an alternative to the above Gibbs sampling approach, we can directly consider τ as a continuous variable, and the conditional posterior density of τ can be written as

$$\tau \propto \prod _{j=1}^J{G}_j\mathrm{I}(min(z_2)<\tau <max(z_2))$$

We use the Adaptive Metropolis algorithm [16] to sample τ. Specifically, we consider the proposal distribution given at iteration l by

$$Q^{(l)}(\tau \ast ,.)=(1-B)\mathrm{N}(\tau \ast ,{2.38}^2{\sigma }_{\tau }^{(l)})+B\mathrm{N}(\tau \ast ,{0.1}^2)$$

where τ* is a candidate value for τ simulated from proposal Q^(l)(τ*,.). ${\sigma }_{\tau }^{(l)}$ is the empirical estimate of the variance of the target distribution based on the entire history up to lth iteration. As suggested in Roberts and Rosenthal [16], we take B to be 0.05.

When no threshold is present in the model, τ is not identifiable [17]. It is possible to estimate the existence of a threshold in a mixture model as described by Skates et al. [18], in which Reversible Jump MCMC was used to move between a linear model with no threshold and a model with a threshold. But in our more complicated setting of a Cox model with a cured fraction, we have considered two other strategies to evaluate the presence of a threshold. First, we use model selection criteria to compare the models with and without a threshold. Second, we constrain τ in the range (min(z₂), max(z₂)), and let the non-identifiability be reflected in the posterior distribution of τ and β₂ − β₁. Our goal is to identify a sharp estimate of τ when the data clearly indicate a threshold. When the data do not clearly indicate a threshold, estimates of τ would have large uncertainty, and the contrast parameter of β₂ − β₁ would be close to zero.

We can thus carry out the following hybrid Gibbs sampling scheme:

1. Sample υ_i ∼ Bernouli(p_υi) for patients with δ = 0, where p_υi is defined as in (2).

   Steps 2-4 are applied for patients with υ_i = 1.

2. Sample from

   $$P(\beta |\tau ,{\Lambda }_0,D)\propto \prod _{j=1}^J{G}_{j}exp\{-\frac{1}{2}(\beta -{\mu }_0){\sum }_0^{-1}(\beta -{\mu }_0)\}$$

   using Random Walk Metropolis algorithm as developed by Haario et al. [19].

3. Sample Λ₀(j), j = 1, ⋯, J as

   $$d{\Lambda }_0(j)\sim \mathcal{G}(c_0\eta (s_{j+1}-s_j)+d_j,c_0+\sum _{i\in {\mathcal{R}}_j}exp\{\beta {\stackrel{\sim }{z}}_i(\tau )\})$$

   where d_j is the number of events in [s_j, s_j+1).

4. Sample τ as defined in (4), or sample τ using the Adaptive Metropolis algorithm as developed by Roberts and Rosenthal [16].

5. Sample γ using Random Walk Metropolis algorithm [19] in the logistic regression model. For a probit model, the truncated normal sampling approach proposed by Albert and Chib[20], can be used. A multivariate normal prior was used for γ.

6. Update $S(t_i|{\stackrel{\sim }{z}}_i(\tau ),{\upsilon }_i=1)=exp\{-{\sum }_{j=1}^J{Y}_i(s_j)d{\Lambda }_0(j)exp\{\beta {\stackrel{\sim }{z}}_i(\tau )\}\}$ and $c(x_i)=c_i=\frac{exp(\gamma x_i)}{1+exp(\gamma x_i)}$, and update p_υi as a function of c(x_i) and S(t_i|z̃_i(τ), υ_i = 1). If there is no covariate in the incidence model, we can estimate the cure rate c by a logistic regression model with just an intercept or simply averaging over the indicator variables υ₁, ⋯, υ_n.

3.2. Model Selection

We computed two Bayesian model comparison criterions for selecting the best model. To alleviate the concern that the standard Deviance Information Criterion (DIC) measure ([21]) does not properly reflect the correct effective number of parameters in mixture models, Celeux [22] recommended a modified DIC, termed DIC₃, which estimates D(E[θ|y]) using the posterior mean of the observed likelihood averaged across the cured and uncured subjects. Specifically,

$${\text{DIC}}_3=-\frac{4}{m}\sum _{l=1}^m\{\sum _{i=1}^{n}log{f}^{(l)}(y_i)\}+2\sum _{i=1}^{n}log\{\frac{1}{m}\sum _{l=1}^m{f}^{(l)}(y_i)\},$$

f^(l)(y_i) is approximated by

$${\{(1-c_i^{(l)})\sum _{j=1}^J{\mathit{\text{dN}}}_i(s_j)d{\Lambda }_0^{(l)}(j)exp\{{\beta }^{(l)}{\stackrel{\sim }{z}}_i({\tau }^{(l)})\}{S}^{(l)}(t_i|{\stackrel{\sim }{z}}_i(\tau ),{\upsilon }_i=1)\}}^{{\delta }_i}\times {\{c_i^{(l)}+(1-c_i^{(l)})S^{(l)}(t_i|{\stackrel{\sim }{z}}_i(\tau ),{\upsilon }_i=1)\}}^{1-{\delta }_i}$$

where m is the number of draws of the posterior distribution. $c_i^{(l)}=\frac{exp({\gamma }^{(l)}{x}_i)}{1+exp({\gamma }^{(l)}{x}_i)}$, $d{\Lambda }_0^{(l)}(j),{\beta }^{(l)}$, and S^(l) (t_i|z̃_i(τ), υ_i = 1) are the values of the parameters for the lth draw.

The log-pseudo marginal likelihood (LPML) ([23]) is a cross-validated leave-one-out measure of a models ability to predict the data. It is valid for small and large samples and does not suffer from a heuristic justification based on large sample normality. LPML is defined based on the conditional predictive ordinate (CPO) statistic for the ith observation, and CPO_i is given by CPO_i = f(D_i|D⁽⁻ⁱ⁾), where D_i denote the ith observation, and D⁽⁻ⁱ⁾ denote the data with ith observation deleted. The log of the product of the CPO statistics under a given model is the LPML statistic for that model, $\text{LPML}={\sum }_{i=1}^{n}log{\text{CPO}}_i$. The model with larger LPML is preferred. A Monte Carlo approximation of CPO_i is given by Chen et al. [24]: $\text{LPML}=-{\sum }_{i=1}^{n}log\{\frac{1}{m}{\sum }_{l=1}^{m}1/f^{(l)}(y_i)\}$.

4. Simulations

Simulation studies were conducted to evaluate the proposed approach. All simulations consist of 1000 experimental replications, each with sample size of n = 200 or n = 400. Survival times, T, are generated from a logistic-exponential mixture model, where c(z) = (1 + exp(−γ₁ − γ₂z₁ − γ₃z₂))⁻¹, and S(t|υ = 1; z) = exp{−exp(β₀z₂ + β₁z₁I(z₂ ≤ τ) + β₂z₁I(z₂ > τ))t}. In this formulation, the baseline hazard function is constant with a rate of one. z₁ and z₂ are fixed by design. z₁ = 0.5 for half of the sample size and z₁ = −0.5 for the other half, and the covariate z₂ is generated from uniform[0,10]. The τ is assumed to be 3, 5, 7, or 15 in which no threshold is present. Each subject is followed up until at most time = 5. Censoring times C are generated from an exponential distribution with censoring rate of 4.5. The data for each observation are (t, δ, z₁, z₂), where t = min(T, C, 5). With the choices of the parameters listed in Table 1, the expected censoring proportion including those cured is around 0.54 and the observed cure rate is around 0.43.

Table 1. List of parameters used in simulation and performance statistics.

Parameter	True	Mean(ESE)a	SSEb	MSEc	CP d	Mean(ESE)	SSE	MSE	CP
		n = 200				n = 400
τ	5	5.01(0.98)	0.72	0.52	95	5.00(0.39)	0.39	0.15	96
β0	0.05	0.05(0.04)	0.04	.002	95	0.05(0.03)	0.03	.001	94
β1	-1	-0.98(0.50)	0.51	0.26	95	-0.97(0.29)	0.29	0.08	95
β2	1	1.02(0.40)	0.40	0.16	94	1.00(0.24)	0.23	0.05	95
γ1	0.2	0.21(0.35)	0.36	0.13	95	0.22(0.24)	0.25	0.06	93
γ2	0.5	0.57(0.35)	0.36	0.13	94	0.52 (0.24)	0.24	0.06	93
γ3	-0.1	-0.11(0.06)	0.06	.004	95	-0.10(0.04)	0.04	.002	93
β2 − β1	2	2.00(0.64)	0.63	0.40	96	1.97(0.37)	0.37	0.14	97
τ	7	6.65(1.03)	0.80	0.77	96	6.96(0.39)	0.37	0.14	95
β0	0.05	0.05(0.04)	0.04	.002	95	0.05(0.03)	0.03	.002	95
β1	-1	-1.00(0.44)	0.44	0.19	96	-0.97(0.23)	0.24	0.06	94
β2	1	0.98(0.53)	0.60	0.36	94	1.01(0.31)	0.31	0.10	95
γ1	0.2	0.21(0.35)	0.36	0.13	95	0.22(0.24)	0.25	0.06	93
γ2	0.5	0.58(0.35)	0.36	0.14	94	0.53(0.24)	0.24	0.06	94
γ3	-0.1	-0.11(0.06)	0.06	.004	95	-0.10(0.04)	0.04	.001	94
β2 − β1	2	1.98(0.70)	0.75	0.57	96	1.98(0.38)	0.39	0.15	96
τ	3	3.56(1.33)	1.00	1.32	96	3.15(0.58)	0.59	0.37	95
β0	0.05	0.05(0.04)	0.04	.002	96	0.05(0.03)	0.03	.001	94
β1	-1	-0.89(0.75)	0.84	0.71	93	-0.93(0.41)	0.41	0.17	94
β2	1	1.03(0.41)	0.43	0.19	96	0.99(0.22)	0.25	0.06	95
γ1	0.2	0.20(0.35)	0.35	0.12	95	0.21(0.24)	0.25	0.06	93
γ2	0.5	0.55(0.36)	0.37	0.14	94	0.50(0.24)	0.24	0.06	94
γ3	-0.1	-0.10(0.06)	0.06	.004	95	-0.10(0.04)	0.04	0.00	93
β2 − β1	2	1.91(0.86)	0.94	0.89	97	1.93(0.46)	0.49	0.25	95
τ	No	4.89(2.81)	1.36	–	–	4.89(2.86)	1.40	–	–
β0	0.05	0.05(0.04)	0.04	.002	95	0.05(0.03)	0.03	.001	94
β1	-1	-0.97(1.01)	1.03	1.06	97	-1.03(0.79)	0.79	0.62	98
β2	-1	-0.99(0.85)	0.94	0.89	98	-1.01(0.63)	0.81	0.66	97
γ1	0.2	0.21(0.35)	0.35	0.13	94	0.22(0.24)	0.25	0.06	94
γ2	0.5	0.58(0.35)	0.36	0.14	94	0.55(0.24)	0.24	0.06	94
γ3	-0.1	-0.11(0.06)	0.06	.004	95	-0.10(0.04)	0.04	.002	93
β2 − β1	0	-0.02(1.45)	1.42	2.01	95	0.02(1.13)	1.15	1.31	96

^aaverage of the posterior means over 1000 data sets (average of the posterior standard deviations over the 1000 data sets)

^bstandard deviation of the posterior means across 1000 data sets

^cmean square error

^dcoverage of the 95 percentage highest posterior density (HPD) interval

The models were implemented in R. A Multivariate t-distribution with a degree of freedom of 3 was used as the proposal density in the random-walk Metropolis algorithm in sampling β and γ. The proposal density centered at the previous value, and the covariance was adaptive as developed by Haario [19], which uses the empirical covariance from an extended burn-in period. We proposed two algorithms to estimate the threshold. We found that the Adaptive Metropolis algorithm in Step 4 perform better than the discrete algorithm. For the rest of this article, the Adaptive Metropolis algorithm in Step 4 is used. Patients who survive after the last observed survival time are considered as cured in the estimation procedure. We observed that the chain mixes well. The priors are quite vague relative to the likelihood: a vector of 0's is the prior mean of β and γ; Σ₀ is the prior covariance matrix with 100 on the diagonal for β and γ; In the gamma process prior, ${\Lambda }_0^{\ast }$ is assumed to have an exponential distribution (k₀ = 1) with η = 0.1 and c₀ = 0.1, namely, dΛ₀(j) ∼ (0.1 × 0.1(s_j+1 − s_j), 0.1). The value of 0.1 for η underestimates the true value of η, but a small c₀ of 0.1 gives large uncertainty about this η.

With a burn-in of 5000 iterations, an additional 10000 iterations were used for inference. Results from Table 1 indicate that the proposed model accurately estimates the true values of all the parameters regardless of different values of τ. The accuracy is further improved when sample size is increased to n = 400, as evidenced by significantly reduced standard deviations and MSE given about 95% coverage probability.

In the last scenario where no threshold is present in z₂, the mean of τ is around 5 which is in the middle of the range z₂ from 0 to 10, but with large standard deviations (ESE ≈ 3). The reason is that τ is constrained to be in the range of z₂ in each Gibbs sampling step, thereby leading to an average z₂ to be the estimate of τ, and the standard deviation is increased when n is increased to 400. Furthermore, the hypothesis of no threshold is strengthened by testing the contrast of β₂ − β₁ (the point estimates are very close to zero: -0.02 with n = 200 and 0.02 with n = 400;). From 1000 experimental replications, the 95% HPD intervals of the contrast include zero for about 95% of the times.

As a rule of thumb, if two models differ in DIC by more than three, the one with smaller DIC is preferred as the best fitting [21]. Based on both DIC₃ and LPML, threshold models are preferred to the models which ignore the threshold (called non-threshold model) when a threshold is truly present. For example, when τ = 5, 88% (based on DIC₃) and 80%(based on LPML) of the time the threshold model is chosen over the non-threshold model. In all cases studied, the correct models are chosen more frequently when n is increased to 400. When there is truly no threshold, DIC₃ tends to prefer the simpler non-threshold model, evidenced by the non-threshold model chosen over the threshold model 92% (100%-8%) of the time. In contrast, LPML seems to have no penalty for more complicated models; half of the time the threshold model is chosen although no threshold is present. In addition, using three as a threshold for DIC₃ comparisons seems to yield reasonable type I and II errors.

Normal priors for β and γ are routinely used in the regression models. In this application, we adopted very vague priors for these parameters (relative to the likelihood) in the above simulation studies and the oropharynx cancer example in the next section. However, the posterior distribution of τ could be sensitive to the gamma process prior. This prior consists of an initial estimate of the cumulative baseline hazard function ${\Lambda }_0^{\ast }$, and a precision c₀. In reality, an exponential distribution of ${\Lambda }_0^{\ast }$ is used mostly for convenience. It is easy to have a prior guess on the average event rate and assume it to be constant in the study period. Therefore, it is important to evaluate the robustness of the exponential distribution in the proposed model. For this purpose, we repeated the above simulation when τ = 5, and generated the baseline hazard function from three Weibull distributions: Scenario I: Weibull(0.9, 1.33), Scenario II: Weibull(1.1, 0.8) and Scenario III: Weibull(1, 1), where a is a scale parameter and b is a shape parameter in Weibull(a, b). In all the three scenarios, the average rate is one. We then applied the proposed model using an exponential distribution for ${\Lambda }_0^{\ast }$ with a rate equal to 1 (the same as the true rate) or 0.1 (much lower than the true rate). We also varied the degree of confidence in the prior guess by considering c₀ = 0.01, 0.1, 5, and 10.

As shown in Table 3, the exponential prior (when k₀ = 1) works well even when the hazard function is not exponential, and using the Weibull distribution did not improve the performance even when the parameters in the Weibull prior are the same as the truth. The independent assumption between the disjoint intervals in the posterior inference makes the parametric form of the hazard function less important and the rate per interval more important. As expected, when η is incorrectly specified (e.g. η = 0.1), a large precision, c₀, resulted in considerably increased bias, ESE and MSE.

Table 3. Performance of τ under different gamma process priors.

Scenario	Priora			Mean(Bias)b	ESEc	MSEd	CPe
	η	k0	c0
I	0.1	1	0.01	4.97 (0.45)	0.90	0.48	95
	1	1	0.01	5.00 (0.04)	0.90	0.49	95
	0.1	1	0.1	4.99 (0.11)	0.91	0.47	95
	1	1	0.1	5.00 (.001)	0.90	0.50	95
	0.1	1	5	4.93 (1.47)	1.08	0.50	97
	1	1	5	5.02 (0.36)	0.90	0.47	96
	0.1	1	10	4.84 (3.16)	1.13	0.59	96
	1	1	10	5.00 (.008)	0.91	0.44	96
	*0.9	1.33	0.1	4.99 (0.12)	0.88	0.46	96
	*0.9	1.33	5	5.00 (0.09)	0.79	0.52	94
II	0.1 1		0.01	4.99 (0.11)	1.06	0.55	96
	1	1	0.01	5.00 (0.04)	1.05	0.54	96
	0.1	1	0.1	1.99 (0.23)	1.07	0.50	96
	1	1	0.1	5.00 (0.09)	1.05	0.52	96
	0.1	1	5	4.89 (2.20)	1.15	0.54	97
	1	1	5	5.02 (0.34)	0.98	0.53	96
	0.1	1	10	4.83 (3.42)	1.17	0.69	97
	1	1	10	5.01 (0.26)	0.95	0.50	95
	*1.1	0.8	0.1	4.99 (0.24)	1.05	0.51	96
	*1.1	0.8	5	5.01 (0.17)	1.05	0.58	97
III	0.1	1	0.01	4.99 (0.21)	0.97	0.49	96
	*1	1	0.01	5.00 (0.08)	0.97	0.54	96
	0.1	1	0.1	5.01 (0.07)	0.98	0.52	95
	1	1	0.1	4.99 (0.23)	0.98	0.51	95
	0.1	1	5	4.92 (1.75)	1.11	0.53	97
	*1	1	5	5.01 (0.28)	0.93	0.53	95
	0.1	1	10	4.82 (3.43)	1.14	0.60	97
	*1	1	10	5.00 (.007)	0.92	0.50	95

^ascenarios denoted by * are those when the prior matches the true distribution

^baverage of the posterior means over 1000 data sets (bias is defined as |(Mean − 5)/5 × 100|)

^caverage of the posterior standard deviation over 1000 data sets

^dmean square error

^ecoverage of the 95 percentage HPD interval

5. Oropharynx Cancer Example

We now elaborate on and analyze the data from the motivating example in Section 1. The data was collected from 220 patients with Oropharynx cancer enrolled in the University of Michigan Head and Neck Cancer Specialized Programs of Research Excellence during the years 2003 to 2008. Of the 220 patients, 84 died, 55 of whom died from oral cavity cancer, and the remaining 136 were alive at the end of follow-up. Of the 220 patients, 36 are female and 184 are male; 11 patients had stage II, 37 had stage III and 172 had stage IV. The mean age is 58 (range from 22 to 86). A K-M survival curve (Figure 1) for the whole data set has a level region beyond about 60 months, which may indicate the appropriateness of a cure model. Patients who survive after the last observed survival time are considered as cured in our mixture model, which effectively eliminates the problem of lack of identifiability [25].

Figure 1. Kaplan Meier disease-specific survival plots for all ages.

The priors for β and γ are the same as in the simulation studies. They are very vague relative to the likelihood. To construct a reasonable prior for the baseline hazard, we fit our proposed model using data from all head and neck cancer patients excluding the Oropharynx cancer patients (n = 256), we obtained an estimate of 0.1 for the baseline hazard rate of η assuming the hazard is constant over time (a similar strategy was used in Ibrahim et al. [26] to construct a prior for the baseline hazard rate). We then set c₀ to be 0.01 to reflect the uncertainty of our estimate of the hazard rate in the Oropharynx population. The prior for the other parameters are the same as in the simulation studies. With a burn-in of 20000 iterations, an additional 20000 iterations were used for inference. We observed that the chain mixes well and the results are robust to different choices of the initial values.

As shown in Table 4, there is no difference in disease-specific survival between females and males when age is not considered (see Model 1). However, a significant gender effect is revealed when the analysis is conditional on age. Model 2 indicates an interaction between gender and age in the latency and Model 3 provides an estimate of a threshold in age such that the gender effect changes after the threshold. Both DIC and LPML favor models that considered the interaction between age and gender (see Table 5). Model 1 has significantly higher DIC and lower LPML than other models. Although Model 2 has slightly lower DIC than Model 3, the two models are considered to fit the data equally well using the cutoff of three (the choice of three is good in terms of the desired error rates as shown in the above simulation studies). The slightly higher LPML in model 2 seems to suggest that fitting the interaction using the continuous age is better than dichotomizing the age, however, a threshold can be important in clinical practice as emphasized in the introduction. We are willing to trade a little bit of goodness of fit of the model for a useful application, and this slight sacrifice is negligible in terms of the pseudo Bayes factor for comparing Model 2 to Model 3, defined as PBF₂₃ = exp(LPML₂ − LPML₃) = 2.7 ([27]). In Model 3, the point estimate of τ is 65, and males have significantly better prognosis in disease-specific survival for patients younger than τ, and females have significantly better prognosis for patients older than τ (95 % HPD interval of the contrast β₂ − β₁ is (1.8, 7.4)). Figure 2 presents the switched gender effect conditional on the point estimate of the threshold. This significant gender effect will not be detected when a threshold model is not considered.

Table 4. Parameter estimates and performance statistics for the Oropharynx cancer example.

	Covariate	Mean	SE	95% HPD
Model 1: Mixture cure model
Latency	Sex (F vs M)	-0.16	0.54	(-1.23, 0.85)
	Age	-0.003	0.02	(-0.04, 0.03)
	Stage	-0.13	0.42	(-0.92, 0.74)
Incidence	Sex(F vs M)	0.28	0.56	(-0.83, 1.45)
	Age	-0.008	0.02	(-0.04, 0.03)
	Stage	-0.34	0.49	(-1.24, 0.68)
Model 2: Mixture cure model with an interaction
Latency	Sex(F vs M)	0.002	0.56	(-1.02, 1.08)
	Age	0.001	0.02	(-0.03, 0.03)
	Stage	0.13	0.44	(-0.71, 1.03)
	Sex × Age	-0.18	0.05	(-0.28, -0.09)
Incidence	Sex(F vs M)	0.28	0.52	(-0.78, 1.30)
	Age	-0.01	0.02	(-0.04, 0.03)
	Stage	-0.20	0.45	(-1.10, 0.66)
Model 3: Mixture cure model with a threshold
Latency	Threshold (τ)	65	7	(51,75)
	Sex(age≤ τ)(F vs M)	1.50	0.73	(0.04, 2.91)
	Sex(age> τ)(F vs M)	-2.92	1.38	(-5.45, -0.17)
	Age	0.001	0.02	(-0.03, 0.04)
	Stage	0.03	0.45	(-0.78, 0.95)
Incidence	Sex (F vs M)	0.35	0.52	(-0.61, 1.36)
	Age	-0.008	0.02	(-0.04, 0.02)
	Stage	-0.26	0.44	(-1.04, 0.67)

Table 5. Model Comparisons.

Models	DIC3 (pD)	LPML
Model 1	795(66)	-470
Model 2	780(65)	-464
Model 3	783(66)	-466
Model 4	788(66)	-467
Model 5	794(66)	-475
Model 6	781(66)	-464
Model 7	783(66)	-465

Figure 2. (a) Kaplan Meier disease-specific survival plots for patients younger or equal to 65 (point estimate of τ) (b) Kaplan Meier disease-specific survival plots for patients older than 65.

To validate the presence of a cure fraction, we fitted the data using a regular Cox regression model with a threshold in age (called Model 4), namely, a Model 3 without the incidence part. A considerably increased DIC₃ of 788, compared to Model 3, indicates that the model with a cure fraction is a good choice. Without the cure fraction, we did not find a clear threshold in age, as evidenced by a large 95 % HPD interval in τ ranging from 28 to 85. The gender effect before and after the τ is estimated with a large variance caused by the large uncertainty in estimating τ (results not shown).

In this application, we also considered three other models to evaluate the potential threshold of age in incidence. Model 5 assumes a threshold in the incidence rather than in the latency. A large DIC of 794 and a large 95 % HPD interval of τ from age 27 to 86 supports the absence of a threshold in age in the incidence. Model 6 adds an additional interaction of age and gender in incidence to Model 2. The interaction in the incidence is not significant, the 95 % HPD interval of the interaction is (-0.05, 0.13), and both the DIC and LPML are very close to Model 2. Based on Model 3, Model 7 updates the parameters in the logistic regression given each realization of the threshold in latency. That is, Model 7 assumes the same threshold in latency exists in incidence. Again the gender effect is similar before and after the threshold in incidence, and both the DIC and LPML are very close to Model 3. The two stable plateaus in the KM curves are not statistically different in both Figure 2(a) and Figure 2(b), which seems to further confirm that no threshold is present in the incidence. The results for Model 6-7 were not shown since the parameter estimations are similar to Model 2 and 3 respectively.

6. Discussion

In this paper, we develop a Bayesian approach to estimate a Cox Proportional Hazards Cure Model and extend the Cox model to allow a threshold in the regression coefficient. Personalized therapy is the future of oncology drug development. Dichotomizing a continuous biomarker is a common practice in clinical research because it facilitates a decision to be made about which therapy to give, and is easy to include in protocols. Compared to other methods in finding the optimal threshold for categorizing continuous variable by maximizing some likelihood function or test statistic [28, 29], our method has the advantages of 1) taking into account the sampling variation in estimating the threshold, as well as other parameters in the model that depend on the variable threshold; 2) obtaining a distribution of the threshold; 3) adjusting for other prognostic variables when estimating the threshold; 4) directly testing the absence or presence of a threshold; 5) evaluating the assumption of a sudden jump of a covariate at the threshold by comparing to a model with an interaction term using model selection criterions.

The introduction of the latent Bernoulli cure indicators greatly facilitates the MCMC algorithm. Given the indicators, the latency and incidence can be evaluated separately using standard methods, and the threshold detection problem reverts to a problem in the Cox model. Chen et al. [30] noted that Bayesian inference for a mixture cure model requires proper priors to avoid the possibility of improper posterior distributions. We avoid this issue by using very mildly informative but proper priors.

In this study, we are interested in a threshold in the latency. We found that the MCMC algorithm had high autocorrelation and slow convergence when we tried to estimate a threshold in both latency and incidence for the same covariate. If the threshold in the latency model is your primary interest, you can simply update the parameters in the logistic regression given each realization of the threshold in latency, as describe in Model 5 in the oropharynx cancer example.

In this paper, we have used a mixture cure model in which covariate effects are separately considered for incidence and latency, and thus the the threshold effect on covariates can also be considered separately on incidence and latency. We believe that a covariate that is important for long-term incidence may not be important for latency and vice versa. We did not consider this threshold detection problem in the Bounded Cumulative Hazard cure model [30, 26, 31, 32, 33]. But it would be a nice alternative cure model if you believe that a covariate is equally important in both latency and incidence.

The parameter estimates (point or interval estimates) are calculated using the MCMC iterations from the proposed model rather than based on asymptotic approximation as in frequentist approaches. Moreover, estimates of the contrast β₂ − β₁ can be calculated easily to evaluate the existence of a threshold. This ad-hoc way of testing presence or absence of a threshold combined with the model selection criterions works well in our study.

In this application, we estimate a threshold in a continuous variable such that the effect of a dichotomized variable changes before and after the threshold. With some modification of the design matrix X, this method can be used to estimate a changepoint in a covariate as described in Jensen and Lutkebohmert [4], where the covariate effect has a piecewise linear functional form. Extensions to multiple threshold detection using Reversible Jump MCMC [34] will be the subject of future research.

Table 2. % of times threshold model is chosen over non-threshold model.

Selection Criterior	n	τ = 3	τ = 5	τ = 7	No threshold
DIC3a
	200	75	88	86	8
	400	97	100	100	6
LPML
	200	75	80	80	50
	400	86	93	93	50

^aIn DIC₃, threshold model is selected if its DIC₃ is less than the non-threshold model by more than three.