Use of radial density plots to calibrate image magnification for frozen-hydrated specimens

Abstract

Accurate magnification calibration for transmission electron microscopy is best achieved with the use of appropriate standards and an objective calibration technique. We have developed a reliable method for calibrating the magnification of images from frozen-hydrated specimens. Invariant features in radial density plots of a standard are compared with the corresponding features in a “defocused” X-ray model of the same standard. Defocused X-ray models were generated to mimic the conditions of cryo-electron microscopy. The technique is demonstrated with polyoma virus, which was used as an internal standard to calibrate micrographs of bovine papilloma virus type 1 and bacteriophage ΦX174. Calibrations of the micrographs were estimated to be accurate to 0.35%–0.5%. Accurate scaling of a three-dimensional structure allows additional calibrations to be made with radial density plots computed from two- or three-dimensional data.

1. Introduction

Magnification calibration in transmission electron microscopy (EM) is essential to obtain accurate specimen dimensions. Nominal magnification values displayed on most microscopes only approximate the actual magnifications of recorded images. More accurate values may be obtained with the use of appropriate external or internal calibration standards. Common standards include polystyrene latex spheres [1], replica gratings [2], catalase platelet crystals [3] and tobacco mosaic virus (e.g. ref. [4]). Polyoma virus [5] and bacteriophage T4 [6] have also been used as standards.

Unreliable measurements of dimensions typically result when biological specimens are prepared by conventional techniques such as negative-staining and metal-shadowing [5,7]. Fine details and internal features of specimens are altered or lost when they are embedded in stain or coated with metal, and this can change the specimen's appearance and size. In addition, biological samples are often distorted because surface tension effects cause shrinkage as the sample dehydrates. Cryo-electron microscopy (cryoEM) and low-irradiation procedures help preserve and protect the native structure of biological specimens and also avoid many of the artifacts associated with the more conventional preparation procedures (see refs. [8–10] for reviews). Some highly ordered, crystalline specimens have been shown to be preserved in two and three dimensions to atomic or near-atomic resolution with these techniques [11–15].

The use of polyoma virus as an internal or external calibration standard in frozen-hydrated preparations was previously described [5,16]. In this method, the icosahedral polyoma virus, whose diameter was accurately determined by X-ray crystallography [17], was used to calibrate micrograph magnification. The measured diameters of several different spherical viruses corresponded well with measurements of the same viruses made with X-ray crystallographic and solution scattering techniques. The main disadvantage of this technique is that particle–solvent boundaries must be identified in order to measure diameters. Circularly averaged images of individual particles or a circularly averaged image of an aligned set of several particles were used to estimate diameters. Several factors make it difficult to precisely identify such boundaries: (1) the density of the vitrified solution, which surrounds the particle, must be known accurately; (2) features of three-dimensional objects may be concealed in projection because densities at different radii are superimposed; (3) viral surfaces are not uniform because various features extend to different radii; (4) low-irradiation images of frozen-hydrated, biological specimens are characterized by high noise levels and low contrast; and (5) densities are modulated by effects of the microscope contrast transfer function (CTF).

Here we describe in detail a more objective procedure to determine magnification in images of frozen-hydrated specimens [18]. Radial positions of features inside the particle periphery that can be characterized as invariant are calibrated with this method. Such features are identified in radial density plots of three-dimensional maps determined by image reconstruction and X-ray crystallographic methods. Corresponding features in the two types of maps are scaled to give maximum correlation, which calibrates the original micrograph. This, in turn, permits calibration of radial density features in two-dimensional, circularly averaged images and also the calibration of other micrographs that include a sufficient number of images of the standard. We demonstrate how the procedure is implemented with bovine papilloma virus type 1 (BPV-1) and bacteriophage ΦX174 (ΦX174) by using polyoma virus as an internal standard. Certain aspects of the method are illustrated with model images.

2. Materials and methods

2.1. Cryo-electron microscopy

Purified samples of two papovaviruses, polyoma and BPV-1, and a bacteriophage, ΦX174, were kindly provided by colleagues (acknowledgements). As outlined previously [5], polyoma was mixed separately with BPV-1 and ΦX174 before freezing rapidly in liquid ethane and recording micrographs. The two micrographs we analyzed were recorded at ~ 1.6 μm (BPV-1) and ~ 1.3 μm (ΦX174) underfocus, at 80 kV, and at nominal manifications of 36 000 × (BPV-1) and 49000 × (ΦX174) in a Philips EM420 electron microscope (Philips Electronics Instruments, Mahwah, NJ) equipped with a Gatan anticontaminator and a Gatan 626 cryotransfer holder (Gatan Inc., Warrendale, PA). Defocus values were determined from the spacing of the Thon rings in a computed Fourier transform of a small region of the carbon film [19] and by visual inspection of the micrographs.

2.2. Image processing

Selected micrographs of BPV-1/polyoma and ΦX174/polyoma were digitized at 25 μm intervals and two reconstructions of polyoma and one each of BPV-1 and ΦX174 were computed according to established procedures (e.g. refs. [20–22]) with only minor modification. We initially located the center (origin) of each particle by a cross-correlation method [5] in which each particle image, after Fourier filtering to remove high-frequency noise, was correlated with an average of all images in the data set (section 2.4 describes how the average was computed). Three-dimensional reconstructions computed from the BPV-1 micrograph were calculated to 2.9 nm resolution from six BPV-1 and 21 polyoma particle images, respectively. Twenty-five ΦX174 and 11 polyoma images from the ΦX174 micrograph were used to compute reconstructions to 2.1 and 2.5 nm resolution, respectively. The four reconstructions were computed at slightly higher resolutions than the limits determined on the basis of R-factor calculations [23] in order to help eliminate Fourier series termination effects. All image processing and calibration (see below) steps were programmed in FORTRAN and run on a VAX/VMS computer (Digital Equipment Corp., Model 8550, Maynard, MA). Digital images were displayed and photographed as described previously [23].

2.3. CTF treatment of X-ray data

The polyoma virion structure, determined by X-ray crystallography to 2.25 nm resolution [24], served as the standard for calibrating our polyoma reconstructions. The X-ray virion map was Fourier-transformed to compute a set of structure factor amplitudes and phases [25], which were multiplied by theoretical microscope CTFs to simulate various levels of defocus. The CTFs were based on the following relationship:

$$\text{CTF}(\nu )=A\text{sin}[\chi (\nu )]+B\text{cos}[\chi (\nu )],$$ (1)

where A and B are treated as constants, ν is spatial frequency (in nm^–1), A sin[χ(ν)] is the contribution from phase contrast, and B cos[χ(ν)] is the contribution from amplitude contrast [26]. A and B were adjusted to give 7% amplitude contrast, a value typical for frozen-hydrated specimens [26]. The phase shift, χ, due to objective lens defocus, Δƒ, and spherical aberration, is given by

$$\chi =(2\pi {\lambda }^{-1})\left[\frac{1}{2}(\Delta f){\theta }^2-\frac{1}{4}{C}_{\mathrm{s}}{\theta }^4\right],$$ (2)

where λ is the electron wavelength (4.18 pm for 80 kV), C_s is the spherical aberration coefficient (2.0 mm for the Philips EM420), and θ is the scattering angle (= λν, in radians). For the purpose of these calculations we neglected effects of beam incoherence, axial astigmatism and inelastic scatter. We applied several CTFs to the X-ray data, with defocus values ranging from 0.4 to 3.2 μm (positive values of Δƒ correspond to underfocus settings of the objective lens). We computed “defocused”, polyoma X-ray maps by Fourier synthesis of the CTF-modulated structure factors [25].

2.4. Spherically averaged and circularly averaged radial density plots

The unmodified and “defocused” X-ray maps, and the two polyoma reconstructions were spherically averaged about their origins, where the icosahedral 5-, 3-, and 2-fold axes intersect. Plots of the spherically averaged density (SAD) were computed from each average. SAD plots were also computed for the BPV-1 and ΦX174 reconstructions and for an earlier BPV-1 reconstruction, which was computed from 77 independent images [23].

Radial plots of circularly averaged density (CAD) were computed for each of the BPV-1, ΦX174 and the two polyoma image averages. Each image average was formed as follows. An initial average was computed from a straight summation of all the particle images in a data set, with no adjustments for misalignment of origins. This average was circularly symmetrized about the best centrosymmetric origin [5]. That result, with its known origin, was used as a correlation reference to locate the center of each individual image [5]. These particle images were then summed with the refined origins in register to form a second average and subsequent circular average. Additional cycles of origin refinement, followed by averaging and circular averaging, essentially resulted in no significant changes for the resultant average image.

2.5. Magnification calibration

Characteristic features deemed to be invariant were identified in SAD and CAD plots of the calibration standard. For polyoma, we selected the region encompassing radii of ~ 18–26 nm, which corresponds to the protein capsid.

We scaled the two polyoma reconstructions to the “defocused” X-ray maps by comparing the corresponding regions of the SAD plots. Each SAD plot, ρ′(r), from each reconstruction was rescaled to give a new radial density distribution, ρ′(r), according to the following expression:

$$\rho \prime (r)=W\rho (Mr)+C,$$ (3)

where W is a weighting constant that adjusts the relative scale of densities (contrast), M is a linear, radial scale factor that adjusts the relative magnification, and C is a constant term that adjusts the average density. A least-squares-fitting routine was used to refine W, M, and C in search for an optimum fit between the two SAD plots.

2.6. Estimation of errors

Assuming that errors in the radial plots have a normal (i.e. Gaussian) distribution and that the residual sum of squares obeys the chi-square statistic, it is possible to estimate approximate errors for values of the parameters found by the fitting procedure, and in particular, for the radial scale factor, M. The error estimate for M was used in the evaluation of the total calibration error, which also included errors in unit cell size (from determination of the X-ray crystallographic structure) and microdensitometer step size. We estimated unit cell size error by measuring the average reciprocal lattice spacings from an X-ray diffraction photograph of red clover mosaic virus crystals. Errors due to variations in X-ray wavelength and missettings of crystal-to-film distance were insignificant compared to the errors in measuring the lattice spacings. The microdensitometer we used (Optronics International Inc., Model C-4100, Chelmsford, MA) was calibrated by scanning a photographic contact image of a reticle and comparing distances measured on the digitized image to distances measured on an optical comparator (Nikon, Model C profile projector). We calculated the total calibration error by using “propagation of errors” equations [27].

3. Results

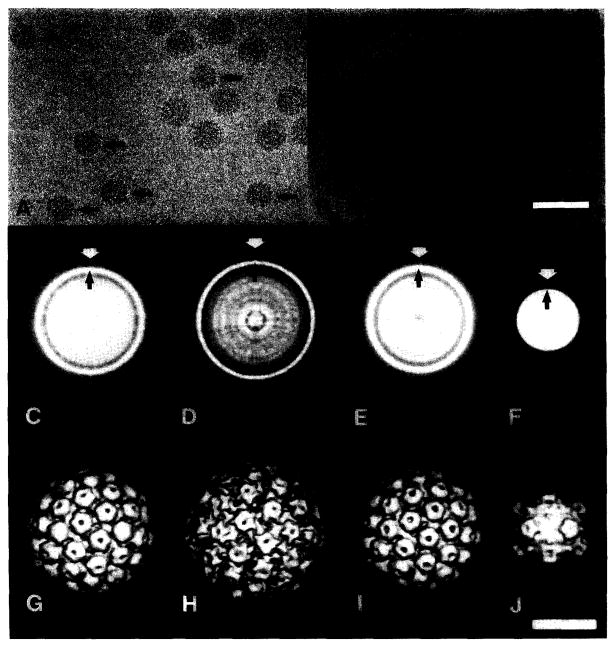
Polyoma was used as an internal standard to calibrate images of BPV-1 (fig. 1A) and ΦX174 (fig. 1B). The papovaviruses (BPV-1 and polyoma) all have nearly circular profiles, indicating that the external morphology of the virions is approximately spherical and the particles are well preserved in the frozen-hydrated state. BPV-1 and polyoma appear similar although BPV-1 is distinguished by its slightly larger size. The smaller size and distinct morphology of ΦX174 clearly distinguishes it from polyoma.

Fig. 1.

Use of polyoma virus as an internal standard in unstained, frozen-hydrated preparations: (A) Mixture of polyoma and BPV-1. Polyoma (arrows) is distinguished from BPV-1 by its slightly smaller size. (B) Mixture of polyoma and ΦX174. Several empty ΦX174 particles are also present. Apical caps on the ΦX174 particles may be observed as faint projections on the capsid periphery. (C–F) CAD images (in reverse contrast) of polyoma (C) and BPV- 1 (D) from image (A), and polyoma (E) and ΦX174 (F) from image (B). CAD images were computed from averages of 43 (C), 10 (D), 12 (E), and 57 (F) particle images. White arrows identify approximate particle edges used to calibrate magnification according to the method of Olson and Baker [5]. The bright rings (black arrows) correspond to the highest density peaks near the inner radius of the capsid shell. The CAD image of ΦX174 (F) is distinct from the papovavirus CAD images (C–E) because the apical caps, the density feature at maximum diameter (white arrow), gives rise to a faint ring. The average radius of the shell's inner wall (black arrow) is the most prominent CAD feature at higher radii. (G–J) Surface-shaded views (along icosahedral two-fold axes) of polyoma (G) and BPV-1 (H) computed from 21 and 6 particle images, respectively (from (A)), and polyoma (I) and ΦX174 [28] (J) computed from 11 and 25 particle images, respectively (from (B)). Bar = 100 nm (A, B) and 25 nm (C–J).

3.1. Diameter measurements

Although circularly averaged density (CAD) images of the virions appear uniform and have smooth profiles (figs. 1C–1F), they illustrate the difficulty in defining outer boundaries of the particles from radial density averages of two-dimensional or three-dimensional data. In contrast to the CAD images, reconstructed density maps of the virions (figs. 1G–1J) reveal that each has a strikingly bumpy topography, with features at significantly different radii. Distinction of such surface features is lost in the CAD image. Consequently, it is difficult to measure the particle diameter precisely. For example, the external diameter of ΦX174 ranges from 12.4 nm at the icosahedral two-fold symmetry axes to 16.8 nm at the apical caps on the five-fold axes [28]. Whereas a good estimate of the mean diameter of the ΦX174 shell is relatively easy to measure from a CAD image, the maximum diameter at the apical caps is much more difficult to measure because the ring of density corresponding to this feature is weak and diffuse in the CAD image (fig. 1F, white arrow). In the absence of three-dimensional data (fig. 1J) or prior knowledge of the ΦX174 structure, it is possible that the diffuse ring surrounding the particle could be overlooked.

The diameter of polyoma was measured in different ways, but all methods we tried proved unreliable because they ultimately depended on knowing the location of the particle–solvent interface (fig. 2). These methods included the use of CAD plots generated from image averages (figs. 1C and 1E), direct measurements from the three-dimensional maps (figs. 1G,1I and 2), and spherically averaged density (SAD) plots computed from the reconstructions (discussed below). Because these methods all failed to give consistent diameter measurements, we found it necessary to adopt a different strategy. This involved identifying invariant features in the object at radii beneath the external surface and accurately calibrating them with a known standard, which was obtained from X-ray crystallography.

Fig. 2.

Measurements of particle diameters from the three-dimensional reconstruction of polyoma shown in fig. 1G. This illustrates the difficulties encountered in defining the particle–solvent boundary. (A) Planar sections through the reconstruction, perpendicular to an icosahedral three-fold axis of symmetry. (This is where interparticle contacts were found in crystals used for X-ray diffraction experiments [17].) The centers of the four sections are at radii of 23.9, 24.6, 25.3 and 26.0 nm (left to right). The choice of which section contains protein density at highest radius depended on how the data were displayed (e.g. positive versus negative contrast, color versus black-and-white, and contrast-enhanced look-up tables). (B) Contoured, grey-level display of an equatorial section (left) from the reconstruction. The section passes through the axes of adjacent pentavalent (arrow identifies the icosahedral five-fold axis) and hexavalent capsomeres. The arc is drawn at a radius of 24.8 nm and corresponds to the interparticle packing distance determined by X-ray crystallography [17]. Low-magnification views of the reconstruction are shown in a central section (far right, top; in the same orientation as left) and surface-shaded representation (far right, bottom; particle rotated 90° about a horizontal axis). The line in the shaded view indicates the plane of the equatorial sections. Bar = 25 nm (A) and 5 nm (B).

3.2. SAD versus CAD plots

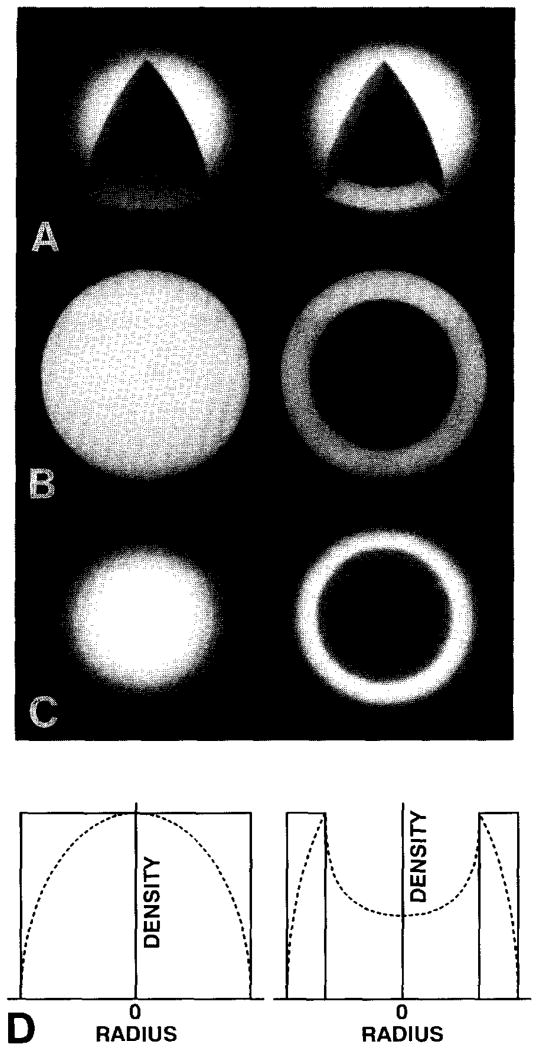
The fundamental difference between CAD plots from two-dimensional images and SAD plots from three-dimensional structures arises from the superposition of object densities at different radii that occur in projected images (fig. 3). The intensity at a particular radius, r, in a CAD plot is a projected sum of object densities at radii within the object greater than or equal to r. The origin of a CAD plot (r = 0) thus contains contributions from all densities in the view direction including density above and below the particle. An SAD plot, in contrast, is computed directly from the three-dimensional density map. Therefore, the value at a radius, r, in the SAD plot is just the mean particle density at that particular radius.

Fig. 3.

Solid sphere (left) and spherical shell (right) models of uniform density used to illustrate the properties of CAD and SAD plots. (A) Surface-shaded views cut open to reveal solid core of sphere and empty core of shell. (B) Equatorial sections of (A). (C) Projected images of (A). (D) SAD (———) and CAD (- - - - - -) plots of (A) and (C), respectively. Peak values in the corresponding CAD and SAD plots were normalized, which artificially reduces the absolute scale of the CAD plot relative to the SAD plot.

Positions of peak values in SAD and CAD plots need not correspond or be correlated in any simple way, especially for complex models (figs. 3 and 4). In a simple, spherical shell of uniform density (fig. 3, right column) the CAD plot shows a single peak corresponding to the inner radius of the shell, whereas the SAD plot of the same model is a simple, binary function (uniform density within the bounds of the shell and zero density elsewhere). This simple illustration shows how SAD plots can provide a more accurate measure of the radii of specific features compared to CAD plots.

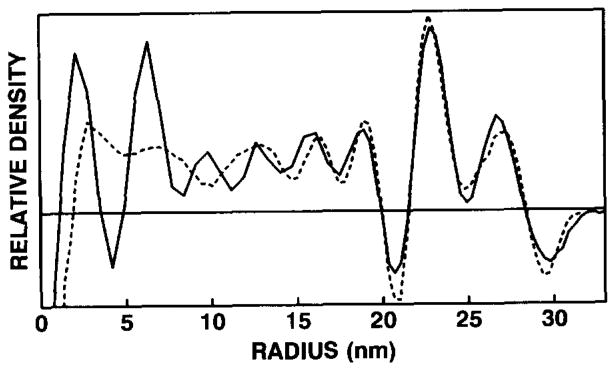
Fig. 4.

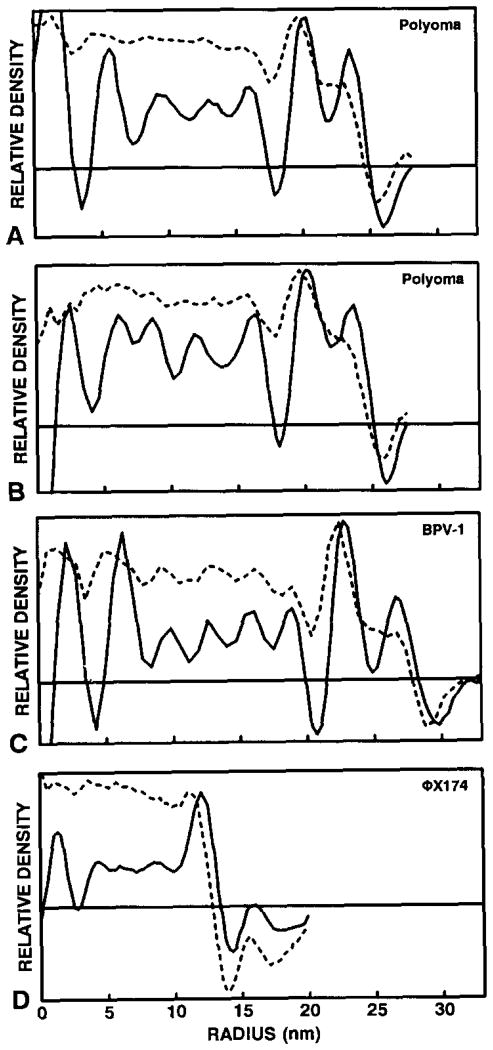
Comparisons of calibrated CAD (- - - - - -) and SAD (———) plots of polyoma from BPV-1 (A) and ΦX174 (B) micrographs, and BPV-1 (C) and ΦX174 [28] (D). The highest peak values of each CAD/SAD pair in the region ~ 18–26 nm for polyoma, ~ 21–30 nm for BPV-1, and ~ 10–14 nm for ΦX174 were normalized. Note the differences between SAD and CAD, especially in the capsid region (compare to fig. 3). Large fluctuations in the SAD plots near the origin are artifacts generated by the Fourier Bessel procedures used to compute the three-dimensional reconstructions. The horizontal line in each graph represents the zero density level.

For cryoEM images of spherical viruses such as polyoma, BPV-1 and ΦX174, we found that SAD in the capsid region is reliable for calibrations (fig. 4). For polyoma this occurred in the region between radii ~ 18–26 nm (figs. 4A and 4B).

3.3. Calibration of EM standard with a “defocused” X-ray standard

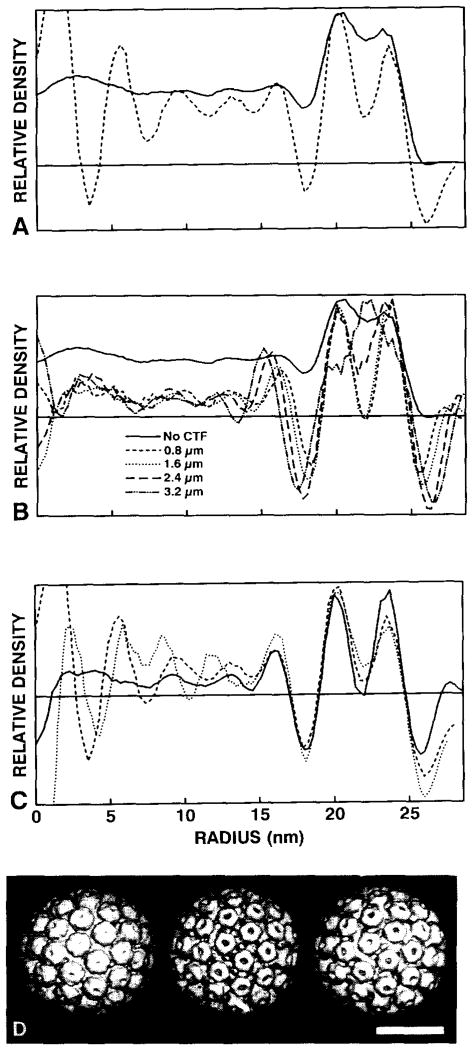
The polyoma standard was calibrated with the 2.25 nm resolution structure of polyoma virions solved by X-ray crystallographic methods [24]. We found, however, that a direct calibration of the polyoma EM and X-ray data (fig. 5A) was unreliable because the EM densities are modulated by the effects of the microscope contrast transfer function (CTF) [19,26]. We obtained a better calibration when the X-ray model was treated as if it was imaged in the electron microscope. Structure factors computed from the X-ray model were multiplied by various theoretical CTFs for a range of defocus values. SAD plots for the modified X-ray models (fig. 5B) remained essentially unchanged over a wide range of defocus settings that encompassed the defocus values we used to record the two images that were analyzed (figs. 1A and 1B). Features in the polyoma SAD plots that seem most sensitive to changes in defocus levels occur at the two troughs (r = 17−18 and r = 25−27 nm) which correspond to the strong Fresnel fringes that occur in regions where the average particle density varies sharply (e.g. at the outer particle surface and in the gap between the protein shell and the nucleohistone minichromosomc [21]). However, the position of the two peaks at r ≅ 20 nm and r ≅ 24 nm and the trough at r ≅ 22 nm remain relatively unchanged for underfocus values of 0.8 and 1.6 μm (fig. 5B). The SAD plots of the two polyoma reconstructions compared well when calibrated with the “defocused” X-ray model (in the region r = 18.8−24.9 nm; fig. 5C). Surface-shaded representations of the “native” and “defocused” X-ray models also illustrate the better correspondence of the “defocused” X-ray model with the EM reconstruction (fig. 5D). Only at high levels of defocus (e.g. ≥ 2.4 μm) does the “defocused” X-ray model differ substantially from the EM model (fig. 5B).

Fig. 5.

Comparison of polyoma EM and X-ray data. (A) SAD plots computed from “native” X-ray model (———) and EM reconstruction (- - - - - - -) (from the BPV-1 micrograph, fig. 1A) data, showing marked differences in the two types of data. The highest peak values in the capsid region (r = 18−26 nm) were normalized. (B) SAD plots of the X-ray model at various underfocus levels: native (———) (no CTF applied). 0.8 μm (- - - - - -), 1.6 μm (· · · · · ·), 2.4 μm (– – –), and 3.2 μm (–··–··–), showing the effects of treating the X-ray data with theoretical CTFs. The highest peak values in the capsid region were normalized. (C) SAD calibrations of two polyoma reconstructions ((- - - - - -) from the BPV-1 micrograph, and (· · · · · ·) from the ΦX174 micrograph) with the 1.6 μm underfocused X-ray model (———). Calibrations were made by comparing densities in the capsid region from r = 18−26nm. (D) Surface-shaded views (along two-fold axes of symmetry and contoured at comparable density thresholds) of the “native” (left) and 1.6 μm underfocused (middle) X-ray models, and the polyoma reconstruction (right) obtained from the ΦX174 micrograph. Bar = 25 nm. The “defocused” X-ray map resembles the reconstructed EM map more closely in appearance and SAD than does the unaltered structure. The horizontal line in each graph represents the zero density level.

3.4. Calibrations of micrograph magnifications

The magnifications of the BPV-1 (35 660 ± 140) and ΦX174 (49120 ± 230) micrographs (figs. 1A and 1B) were determined on the basis of the calibrated polyoma reconstructions. The error in the magnification value was approximately 0.35%–0.5% in each instance. The SAD plot of the 6-particle BPV-1 reconstruction (fig. 4C) was then used to calibrate the magnification of a micrograph used for an earlier 77-particle BPV-1 reconstruction [23] (fig. 6).

Fig. 6.

SAD plots showing the calibration of a 77-particle, BPV-1 reconstruction [23] (- - - - - -) with the 6-particle BPV-1 reconstruction (———). The two plots were calibrated for density values at radii between 21.4 and 28.4 nm. The poor correlation of densities at r < 19 nm, corresponding to the nucleohistone core, is consistent with the notion that the core components are not organized with icosahedral symmetry [21]. The horizontal line represents the zero density level.

A reliable calibration of a reconstruction automatically calibrates the corresponding CAD plot. Positions of characteristic features in CAD plots of the standard can therefore be used to calibrate micrograph magnifications just as features in SAD plots were used. To test this, we used the polyoma CAD plot from the BPV-1 micrograph (fig. 4A) to “recalibrate” the ΦX174 micrograph. In addition, we used the BPV-1 CAD plot (fig. 4C) to recalibrate the BPV-1 micrograph that was used to compute the 77-particle reconstruction [23]. Our results were identical within error limits to those obtained by the SAD calibration (data not shown).

For underfocus values between 0.4 and 2.0 μm, we found the calibration procedure to be insensitive to the level of defocus imposed on the polyoma X-ray model. The final calibrations reported here were performed with the polyoma X-ray model “underfocused” by 1.6 μm, which is approximately the defocus level in each image we analyzed (figs. 1A and 1B). Underfocus levels of 0 (no CTF applied), 2.4 and 3.2 μm gave scale factors greater than the error of those between 0.4 and 2.0 μm (fig. 5B). There also was no significant difference in the scale factor when the contribution of amplitude contrast to the CTF was varied between 7% and 13%.

4. Discussion

We have found that invariant features in radial density plots computed from cryoEM data can be used to give a reliable calibration of micrograph magnification. For the spherical viruses we have studied, the region corresponding approximately to the central portion of the icosahedral protein shell provides the most accurate data for calibration. This method offers several advantages over previously described techniques: (1) inaccuracy arising from uncertainties in defining particle–solvent boundaries is minimized; (2) two-dimensional (CAD) data can be used for calibrations once a three-dimensional map of the standard has been properly calibrated; (3) it is relatively insensitive to CTF scaling parameters (e.g. the levels of micrograph defocus and the ratio of amplitude to phase contrast); (4) calibrations can be performed with a small number (< 10) of particle images; (5) errors of measurement are reduced when averaged data from randomly oriented particles are used; and (6) the absolute error of calibration is minimized as a consequence of excellent specimen preservation, the use of accurate standards (e.g. from X-ray crystallographic data), and the use of objective correlation methods. Our technique does require computation of at least one three-dimensional reconstruction of the EM standard and also requires an accurate and compatible standard to compare to the three-dimensional reconstruction.

4.1. Calibrations with CAD plots

One significant advantage of our technique is that once a three-dimensional reconstruction of the EM standard is available and is calibrated with a compatible X-ray or other standard, the CAD plot is automatically calibrated. This CAD plot can then be used to calibrate the corresponding CAD plots of the standard computed from other micrographs. For example, our calibrated polyoma, BPV-1, or ΦX174 CAD plots could now be used as standards for other calibrations. Furthermore, it is possible to compute an SAD plot from the CAD [29], thus bypassing the need for a three-dimensional reconstruction. However, we believe that an initial calibration based on three-dimensional data will provide more reliable results.

4.2. Effect of data-set size

Our method appears to work well even for small data sets. The 6-particle BPV-1 reconstruction (fig. 1H) gave an SAD plot that matched quite well the SAD plot of a previously computed 77-particle reconstruction [23] (fig. 6). With any data set, however, it is important that representative images from particles in random orientations be used; otherwise, the CAD or SAD plots may be biased or it may be impossible to compute a three-dimensional reconstruction to adequate resolution.

4.3. Errors in the calibration measurement

The method we describe does not rely on subjective measurements of the calibration standard and thus reduces the magnitude of the calibration error. Data averages such as CAD, SAD and three-dimensional reconstructions are used, and these greatly suppress random errors arising from noise in the data. Also, the correlation procedure provides an objective means of scaling data. The largest uncertainties in our calculations, which ranged between 0.2% and 0.4%, were the result of errors in measuring the unit cell dimension of the X-ray crystallographic standard and from errors in scaling. The overall error of our calibrations was approximately 0.35%–0.5%, which is a significant improvement over the levels of errors inherent in more subjective procedures.

4.4. Compatibility of EM and X-ray standards

When comparing an EM and X-ray crystallographic standard, it is assumed that particle dimensions are identical in the frozen-hydrated and crystalline states. Evidence that the native dimensions of biological macromolecules are well preserved even after rapid cooling to liquid nitrogen temperatures and exposure to low doses of electrons is well documented [11–15,30,31]. The pitch of tobacco mosaic virus as measured by X-ray diffraction was found to be identical in frozen-hydrated samples [5]. Therefore, we are confident that the structure of polyoma seen by EM is well preserved and is comparable to the structure seen with X-rays. Consequently, a single calibration of the polyoma structure from cryoEM images in one micrograph can be used to calibrate the cryoEM images of polyoma in any other micrograph.

The compatibility of the EM and X-ray standards establishes the success level of our technique. Best results are obtained if the X-ray model is treated as if imaged (defocused) in the electron microscope, before it is compared to the EM data (fig. 5). In addition, we found that errors in the calibration procedure may be generated if the data being compared are not compatible. For example, we calibrated the ΦX174 micrograph (fig. 1B) on the basis of the known X-ray structure of ΦX174 [32]. The magnification value we obtained was 2% higher than that obtained using the polyoma X-ray standard. This discrepancy may be attributed in part to differences in the ΦX174 EM [33] and X-ray [32] structures. Though both structures were computed from “empty” capsids that contain up to 20% of the single-stranded DNA genome, only a small fraction of the DNA was included in the X-ray model and some of the protein density was not modeled in the X-ray map. In contrast, all polyoma structures used in this study were computed from data obtained with full virions, and the X-ray model included spherically averaged density for the nucleohistone core. Comparison of SAD plots showed much better compatibility between the polyoma data compared to that between the ΦX174 data.

4.5. Selection of invariant regions in radial density plots

Successful calibrations also require that suitably invariant regions be correlated in SAD or CAD plots. For each of the viruses we examined, the most invariant features in the plots occurred in regions that encompass the central portion of the icosahedral protein shell. Regions at low radii, corresponding to the viral cores, or at high radii, corresponding to the exterior surface in contact with solvent, were not included in the correlations because features in these regions are more sensitive to defocus effects (Fresnel fringes) and noise (non-icosahedrally symmetric density distributions). Indeed, Stewart [31] urged caution in defining particle boundaries from defocused images of frozen-hydrated samples. Simple diameter measurements are definitely affected by the defocus level (fig. 5B). As defocus increases, so does the measured particle diameter. Defocus within reasonable limits for cryoEM (~ 0.4–2.0 μm) does not, however, significantly change the positions of peaks of density in SAD or CAD plots for regions within the protein capsid (fig. 5B). Note, however, that the application of a CTF to X-ray model data did slightly change the positions of the two peaks in the polyoma capsid relative to the unmodified data (fig. 5B). This reiterates the need to compare data that are compatible. A reasonable estimate of the defocus level for a micrograph can thus be used to get an accurate magnification calibration.

4.6. Use of other standards

The calibration method we describe is not restricted to the polyoma standard and is readily adapted to the use of other spherical standards. For example, a number of plant viruses such as cowpea mosaic virus, tomato bushy stunt virus and southern bean mosaic virus are easier and cheaper to obtain than an animal virus such as polyoma, and the structures of all these viruses are known to atomic resolution [34]. The technique could also be modified accordingly to enable non-spherical standards such as the helical tobacco mosaic virus to be used to calibrate magnification.

5. Conclusion

Our calibration method can be used to calibrate both new and previously solved structures. In addition, the method could be implemented along with procedures designed to compensate for differences in magnification within the same micrograph or between separate micrographs [35,36]. This would provide a way of reducing systematic errors when image data are combined.

Finally, we note that although our method provides an accurate calibration of image magnification, accurate measurements of particle dimensions require that the image data first be corrected for effects of the microscope CTF. Such corrections are typically difficult to achieve in practice because of ambiguities in measuring the exact defocus and astigmatism levels in noisy micrographs, and in knowing the relative contributions of amplitude and phase contrast, beam coherence, and inelastic scattering. Excellent correlations between X-ray and CTF-corrected EM data have recently been obtained with energy-filtered images of tobacco mosaic virus [37,38]. Thus, if possible, calibrations and measurements should be made from CTF-corrected, energy-filtered EM data.