Distortion-product otoacoustic emission reflection-component delays and cochlear tuning: Estimates from across the human lifespan

Abstract

A consistent relationship between reflection-emission delay and cochlear tuning has been demonstrated in a variety of mammalian species, as predicted by filter theory and models of otoacoustic emission (OAE) generation. As a step toward the goal of studying cochlear tuning throughout the human lifespan, this paper exploits the relationship and explores two strategies for estimating delay trends—energy weighting and peak picking—both of which emphasize data at the peaks of the magnitude fine structure. Distortion product otoacoustic emissions (DPOAEs) at 2f₁−f₂ were recorded, and their reflection components were extracted in 184 subjects ranging in age from prematurely born neonates to elderly adults. DPOAEs were measured from 0.5–4 kHz in all age groups and extended to 8 kHz in young adults. Delay trends were effectively estimated using either energy weighting or peak picking, with the former method yielding slightly shorter delays and the latter somewhat smaller confidence intervals. Delay and tuning estimates from young adults roughly match those obtained from SFOAEs. Although the match is imperfect, reflection-component delays showed the expected bend (apical-basal transition) near 1 kHz, consistent with a break in cochlear scaling. Consistent with other measures of tuning, the term newborn group showed the longest delays and sharpest tuning over much of the frequency range.

I. INTRODUCTION

Hearing changes throughout the human lifespan due to maturation and aging of both peripheral and central auditory structures and processes. In newborns, for example, otoacoustic emission (OAE) amplitude and growth functions, suppression tuning curves, and deviations from cochlear scaling all show immaturities that have been attributed to incomplete development of the outer, middle, and inner ears, the latter most notably in the apical half of the cochlea (Prieve, 1992; Smurzynski, 1994; Abdala, 1998; Abdala and Keefe, 2006; Abdala and Dhar, 2012; Prieve et al., 2013). Studying how mechanical filtering in the cochlea changes during development may help disentangle the peripheral and central contributions related to maturation of hearing in humans. Conversely, during aging, various aspects of the auditory system become less efficient, showing reduced capability. Among noted aging effects are degradations in audiometric thresholds, cochlear nonlinearity, and speech perception in noise (Dubno et al., 1984; Gordon-Salant, 2005; Abdala and Dhar, 2012). Understanding and isolating the effects of aging on the mechanics of the cochlea in contrast to declines in neural processes would be helpful in developing a comprehensive model of auditory aging and potentially helpful in intervention.

Otoacoustic emissions provide a noninvasive window on peripheral auditory mechanics that can be applied to address these issues. Consistent relationships between OAE delays and cochlear frequency tuning have been demonstrated in several species (Shera et al., 2002, 2010; Bergevin and Shera, 2010; Joris et al., 2011).¹ The logic underlying these relationships builds on the observation that cochlear delay and frequency tuning are linked through filter theory, which holds that sharper tuning requires longer delays (e.g., Shera and Guinan, 2003). In addition, cochlear delays have been related to reflection-source OAE latencies both through empirical correlations and via the theory of coherent reflection (Zweig and Shera, 1995; Shera et al., 2008).²

Here, we apply measurements of the reflection-source component of the 2f₁−f₂ distortion product otoacoustic emission (DPOAE) to estimate OAE delays and cochlear tuning in humans. Our principal objectives are twofold: (1) to explore proposed signal processing and data analysis strategies for extracting reliable delay trends from OAE data (Shera and Bergevin, 2012) and (2) to generate preliminary estimates of reflection-source DPOAE delay and cochlear tuning for age groups representing seven decades of the human lifespan.

II. METHODS

A. Subjects

Subjects included 184 individuals categorized into seven age groups: 15 premature and 30 term neonates; 19 six-month-old infants; 27 teens; 41 young-adult, 20 middle-aged adult, and 32 elderly adult subjects. Detailed demographic data are provided in Table I. All newborns passed a neonatal hearing screening at birth with click-evoked auditory brainstem responses at 35 dB nHL. Thirty-two young adults were tested initially with the standard protocol and 9 additional adults (18 ears) were tested to extend the high-frequency range. For teen and adult subjects, air conduction hearing thresholds were established prior to DPOAE tests using a standard Hughson-Westlake audiometric procedure between 0.25 and 8 kHz. Teen, young-adult and middle-aged subjects had ≤15 dB hearing level (HL) audiometric thresholds. Some elderly adults showed thresholds outside of the normal range of hearing but within the expected guidelines for individuals in this age category (Gordon-Salant, 2005).

TABLE I.

Demographic and test details for each age group.

Age Group	n	Sex		Ear		Age
		M	F	R	L	mean	range
Premature neonate	15	5	10	8	7	34.2 wks	24–36
Term neonate	30	15	15	26	4	39.2 wks	37–42
Infant	19	9	10	19	0	6.4 mos	6–8
Teen	27	14	13	17	10	15 yrs	13–17
Young adult	41	9	32	19	22	22 yrs	19–27
Middle-aged	20	4	16	12	8	48 yrs	41–61
Elderly	32	10	22	16	16	68 yrs	63–73

B. DPOAE Protocol

Newborns were tested at the Infant Auditory Research Laboratory within the University of Southern California + Los Angeles County Medical Center Neonatology Unit. DPOAEs were measured in a sound-attenuating isolette providing between 25–40 dB of attenuation (Eckels ABC-100). Newborn testing was always conducted by a pair of researchers; one attended to the newborn throughout the entire test, watching for movement and probe slippage, while the other implemented the data collection program. If a spike in noise was noted on the spectral display of the ear canal microphone signal, or baby movement was observed, the sweep was manually stopped, rejected in its entirety, and re-initiated.

Six-month-old infants were tested at a satellite laboratory at the University of Washington (set up by C.A. and P.L.). Their hearing was screened with click-evoked OAEs and data were collected during natural sleep within a double-walled IAC sound-attenuating chamber. Whereas adult subjects were tested at both the House Research Institute (HRI) and Northwestern University (NU), teens were tested exclusively at HRI. Non-infant subjects were awake during testing and seated comfortably in a padded armchair within a double-walled IAC sound-attenuating chamber. Unless one ear had markedly higher DPOAE levels, the test ear was chosen at random. Laboratories in the different centers had comparable data-acquisition hardware and software; protocols were matched across sites, and all testers received similar training.

Primary tones and frequencies f₁ and f₂ were presented at 65 and 55 dB sound pressure level (SPL) (L₁,L₂) using a fixed f₂/f₁ ratio of 1.22. Tone frequencies were logarithmically swept upward at 8 s/octave between 0.5 and 4 kHz for a total of 24 s per sweep. (In a sample of young adults, data from this standard three-octave range were later supplemented with an additional octave spanning the interval 4–8 kHz using a sweep rate of 24 s/octave.) Between 6 and 16 sweeps contributed to each average. Calibrated stimuli were delivered to each subject after compensating for the depth of probe insertion (Lee et al., 2012). This allowed us to approximate the desired SPL across frequency at the tympanic membrane and, thereby, reduce the effects of standing waves. In newborns, measurement of the half-wave resonance in 20 ears provided a reference depth insertion; compensation was applied equally to all neonates based on this normative measure.

C. Signal processing and instrumentation

DPOAEs were recorded using a Macintosh laptop controlling a MOTU 828 Mk II audio device (44.1 kHz, 24 bit). The output of the MOTU was appropriately amplified and fed to either MB Quartz 13.01 HX drivers (NU) or Etymotic Research ER-2 tube phones (HRI, UW). The output of the drivers was coupled to the subjects' ears through the sound tubes of an Etymotic Research ER10B+ probe microphone assembly.

DPOAE level and phase estimates were calculated using the least-squares-fit (LSF) algorithm described by Long et al. (2008). In the LSF technique, models for the primary tones (at f₁, f₂) and DPOAE of interest (at 2f₁−f₂) are created and signal components are then fit to these models by minimizing the sum of the squared residuals between the data and the model within a series of specified analysis windows. Following Long et al. (2008), our implementation of the LSF technique used 500-ms analysis windows shifted in overlapping 50-ms steps. (To maintain roughly the same analysis bandwidth and resolution for the young-adult extension, we adopted a 1000-ms analysis window and increased the step size to 150 ms at frequencies above 4 kHz.) At the standard 8 s/octave sweep rate, the 500-ms window corresponds to a bandwidth of $\frac{1}{16}$ octave, spanning 22 Hz at 0.5 kHz and 177 Hz at 4 kHz; at the slower 24 s/octave rate used for the young-adult extension, the bandwidth corresponding to the 1000-ms window is $\frac{1}{24}$ octave, with a span varying from 117 to 234 Hz over the 4–8 kHz range. Our choice of analysis step size resulted in DPOAE estimates with a resolution of 160 frequencies/octave, corresponding to frequency intervals ranging smoothly from 2.2 Hz up to 17.4 Hz across the standard 3-octave range (0.5–4 kHz) and up to 34.7 Hz at 8 kHz for the young-adult extension. The noise floor was estimated by taking the difference between adjacent sweep pairs and applying the LSF to this difference. Extracted DPOAE phase at 2f₁−f₂ was corrected for phase variation of the primaries by subtracting 2ϕ₁−ϕ₂, where ϕ_1,2 are the measured phases of the stimulus tones at f_1,2. Finally, the DPOAE phase ϕ_DP was unwrapped by sequentially subtracting 360 degrees from all points beyond identifiable discontinuities.

matlab-based software (developed by C. Talmadge and adapted by P.L.) was used to separate the distortion- and reflection-source components of the measured DPOAE based on their respective phase-gradient delays (Long et al., 2008). Prior to computing the inverse FFT (IFFT), the complex DPOAE pressure measured in the frequency domain was multiplied by a moving Hann window in overlapping 50-Hz steps. The bandwidth of the window was increased as the square root of frequency (i.e., a power law with exponent 0.5); the bandwidth varied from 400 Hz at 0.5 kHz to 800 Hz at 2 kHz and up to 1600 Hz at 8 kHz. Rectangular time-domain filters were applied to the IFFT of each windowed segment to recursively extract the target component. A search range of −2 to 10 ms was applied to extract the distortion-source component; the time-domain filter was centered at the time of maximum energy within the window. Signal energy appearing after the windowed distortion-source component was identified with the reflection-source (or R) component. Additionally, a reflection-specific noise floor was calculated by processing the noise floor calculated in the ear canal through the same filters used to extract the R component. After transforming the extracted time-domain components back to the frequency domain using the FFT, the spectral magnitude, phase, and noise floor for the distortion- and reflection-source components were computed. Data segments equal to half of the length of the analysis window were eliminated at the low- and high-frequency boundaries to remove edge effects caused by the time-windowing process. Long et al. (2008) have shown that the DPOAE components extracted using this method generally match those obtained using other, independent unmixing procedures (e.g., suppressor tones).

D. Analysis

1. Calculating delays

Once the reflection-source component was extracted at all desired frequencies using the IFFT analysis, its phase-gradient delay was calculated as τ_R(f) = −dϕ_R/df, where ϕ_R is the R-component phase in cycles. To relate tuning to delay, it is helpful to express both quantities in dimensionless units (Shera and Guinan, 2003). Delay can be expressed in dimensionless form by calculating the equivalent number, N, of periods of the stimulus frequency; in these natural units, the delay can be compared to the dimensionless quality factor, or Q, defined as the ratio of center frequency to tuning bandwidth (Shera et al., 2010). Thus, we used the dimensionless R-component delay, N_R, defined as N_R = fτ_R(f), in all subsequent analyses.

2. Determining delay trends

Group trend lines for the N_R delays were computed using locally linear regression, also known as loess smoothing (Cleveland, 1993; Shera and Bergevin, 2012). Both coordinates were log-transformed before finding the trend; log-transforming the ordinate is necessary to equalize the variance across frequency. The loess fitting parameters λ and α specify the degree of the local fitting polynomial and the size of the moving window as a constant number of octaves, respectively. We used local linear regression (λ = 1) and a window size of α = 0.75 octaves. Whereas values of α greater than 1 octave smoothed the data excessively, values less than 0.5 octave produced results that were sensitive to local, subject-dependent variations in the data and were therefore regarded as not representative of the trend.

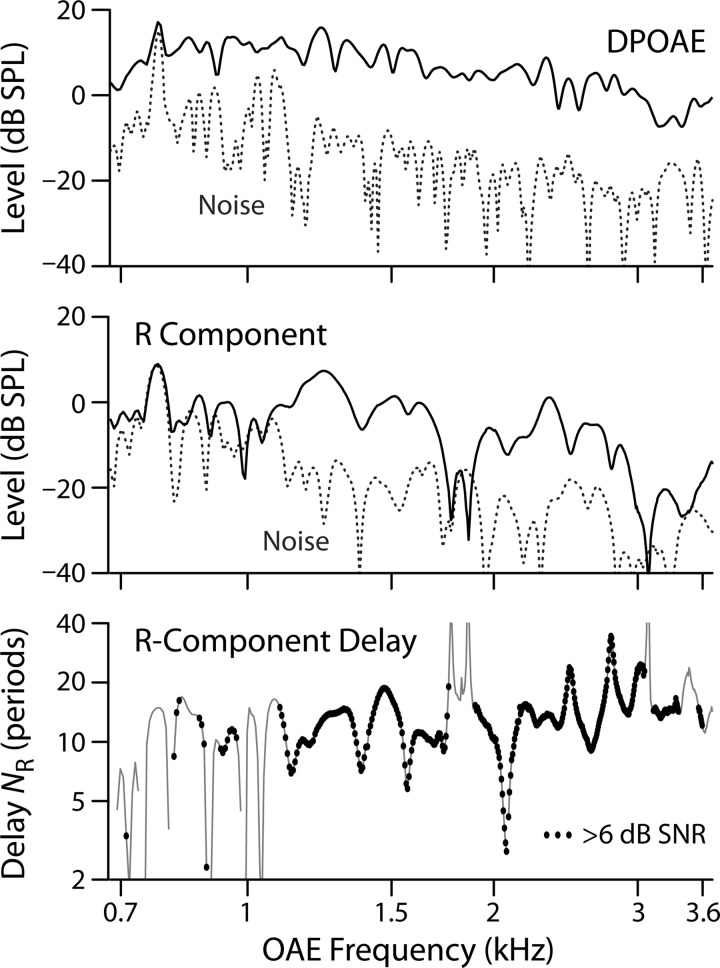
To ensure adequate SNR for the computation of the N_R delay trends, we eliminated delay values whose R-component magnitude was less than 6 dB above the reflection-specific noise floor. Figure 1 shows an example of the data-selection process for one young-adult subject. The small black dots in the bottom panel show data points that passed the SNR-based cleaning; segments of the thin black line without dots represent data that failed the SNR criteria and were therefore excluded from subsequent analysis.

FIG. 1.

Calculating delays in one young-adult subject. (Top) DPOAE level (black line) and noise floor (dashed line). (Middle) IFFT-separated reflection (R-component) level (black line) and R-component-specific noise floor (dashed line). (Bottom) R-component delay expressed in periods as N_R. Only data points whose R-component levels are at least 6 dB above the R-component noise floor are used to estimate the delay trend. The black dots represent accepted values; segments where only the thin black line is visible did not meet the SNR criterion.

We conducted exploratory tests to determine whether our SNR criteria provided adequate immunity from noise. Increasing the criterion for the R-component SNR to either 9 or 12 dB left the resulting loess trends almost unchanged. However, because the higher SNR criteria eliminated more data, they increased the 95% confidence intervals for the groups with fewer subjects, such as the premature newborns, and we therefore settled on the 6 dB SNR criterion. We also explored whether imposing an additional selection criterion based on the SNR of the total DPOAE from which the R component was extracted (e.g., DPOAE SNR > 6 dB) might improve the result but found no significant differences.

Loess smoothing was performed using two strategies found to be most effective in recent work: Energy weighting and peak picking (Shera and Bergevin, 2012). Both methods emphasize data at the peaks of the magnitude fine structure, although in different ways, and both were combined with SNR-based exclusion as described above.

A. Energy weighting.

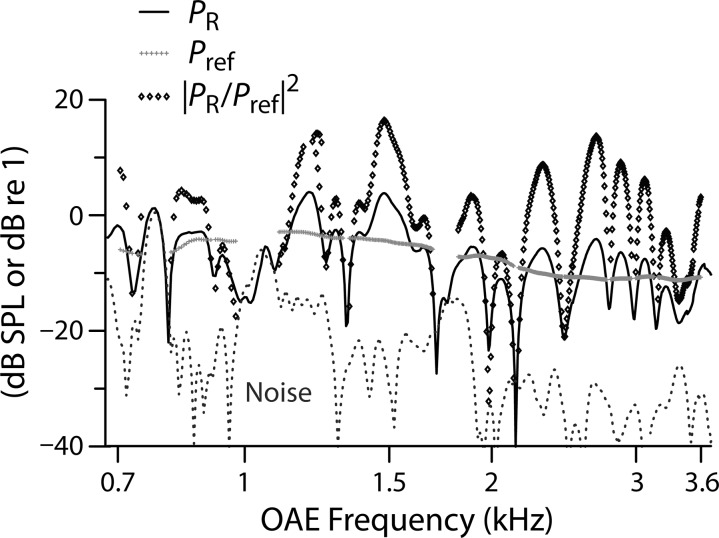
During the loess smoothing, delay values were weighted according to a measure of local R-component energy. Specifically, the values of N_R were weighted by the function |P_R/P_ref|,² where P_R is the complex R-component pressure and P_ref is the value of |P_R| averaged over a one-octave band about each data point (ignoring data not satisfying the SNR criterion). Figure 2 illustrates the energy-weighting procedure in another young-adult subject. The light gray points display estimates of P_ref obtained using the octave-wide window. Because the data analyzed here were collected in vivo (versus in silico in Shera and Bergevin, 2012) and in challenging subject groups (i.e., infants and elderly individuals with less than ideal SNR), we initially questioned whether a one-octave P_ref window would provide an appropriate estimate of local energy; in regions with poor SNR, where many data points may be excluded, P_ref can be sparse and fragmented. To explore this, we varied the size of the P_ref window to determine whether a smaller (i.e., more localized) window would improve the fits. Generally, we found little effect of window size except at the very edges of the domain, where the loess trend is intrinsically more uncertain due to the absence of flanking data.

FIG. 2.

Energy-weighting procedure illustrated in another young-adult subject. During the computation of the loess trend, delay values are weighted by R-component energy, defined as |P_R/P_ref|.² The solid and dashed lines show the R-component level (P_R in dB SPL) and noise floor, respectively. The gray symbols show the level of the local reference pressure, P_ref, obtained by smoothing the R-component level. The diamonds give the local energy |P_R/P_ref|² (in dB re 1).

B. Peak picking.

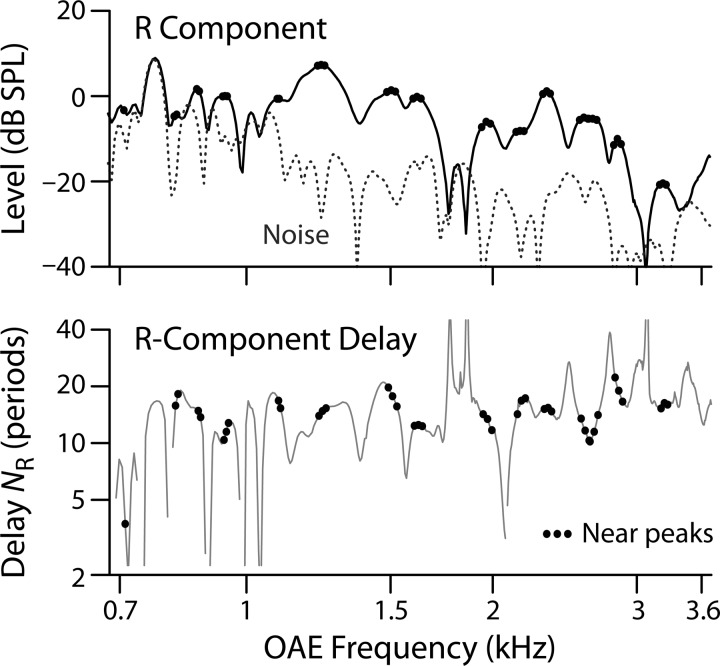
Motivated by the observation that model values of SFOAE delay closest to the known trend occur at frequencies near peaks in magnitude fine structure, Shera and Bergevin (2012) explored a second method for extracting delay trends. As shown in the top panel of Fig. 3, the peak-picking method selects only delay values that straddle local amplitude maxima (peaks) while ignoring the rest. To help reduce spurious maxima due to noise, emission levels were mildly smoothed (with Savitzky-Golay filters) prior to identifying the peaks. The corresponding N_R values are shown in the bottom panel. Peak picking eliminated about 90% of the data in each group.

FIG. 3.

Peak-picking procedure illustrated using data from one elderly subject. When computing the loess trend, only delay data (bottom panel) near local maxima in the R-component level (top panel) are employed. In both panels, data at frequencies straddling the magnitude peaks are marked with small dots.

3. Deriving estimates of tuning

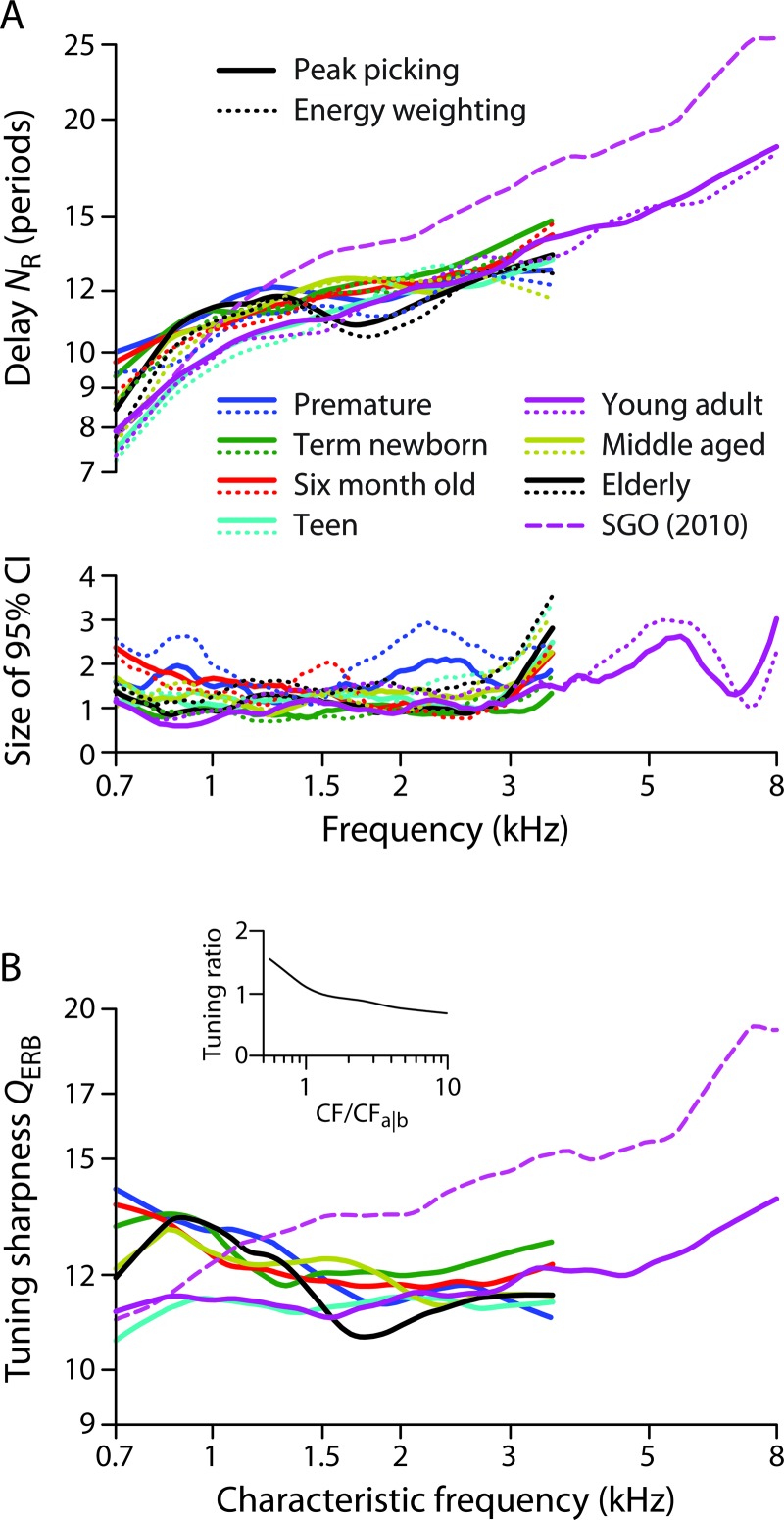
We used the delay trends for each age group to generate corresponding estimates of cochlear tuning by means of the tuning ratio obtained from non-human laboratory animals. The tuning ratio, r, quantifies the covariation of reflection-emission delay and auditory-nerve (AN) tuning and is defined as r = Q_ERB/N_SFOAE, where Q_ERB = CF/ERB (with CF the characteristic frequency and ERB the equivalent rectangular bandwidth obtained from AN tuning curves); and N_SFOAE is the analog of N_R obtained from SFOAEs (Shera et al., 2010). The tuning ratio we employed [see Fig. 5(B), inset] represents an average of tuning ratios derived from SFOAE and AN measurements in cat, guinea pig, and chinchilla (Joris et al., 2011). By using the tuning ratio derived from laboratory animals, we assume that r varies relatively little across mammalian species, consistent with previous results (Shera et al., 2010). We derive tuning estimates for each of our seven age groups using the formula Q_ERB(CF)= r(CF/CF_a|b) N_R(f)|_f = CF. The subscript a|b denotes the approximate boundary between the apical and basal regions of the cochlea (Shera et al., 2010). Delay data derived from human and non-human mammals show a slope discontinuity or bend at frequencies mapping to a region near the midpoint of the cochlea; the characteristic frequency of this bend point, CF_a|b, varies from species to species. Our value of CF_a|b was derived from the approximate location of the low-frequency bend in the human delay functions collected here; its value, between 1 and 1.2 kHz, is consistent with those reported elsewhere (Shera et al., 2010; Abdala et al., 2011a; Keefe, 2012).

FIG. 5.

(A) N_R delay trends lines (top) and 95% CIs (bottom) for seven age groups coded by color (see legend). Only the young-adult group shows an extended frequency range. The solid lines show the trends obtained using the peak picking algorithm; the dotted lines show trends obtained by energy weighting. The delay trend previously obtained from SFOAE data (dashed line SGO) is shown for comparison (Shera et al., 2010). (B) Estimates of the sharpness of tuning Q_ERB obtained as described in the text from the N_R trends in panel A (peak picking only) and the tuning ratio shown in the inset.

III. RESULTS

A. Delay trends

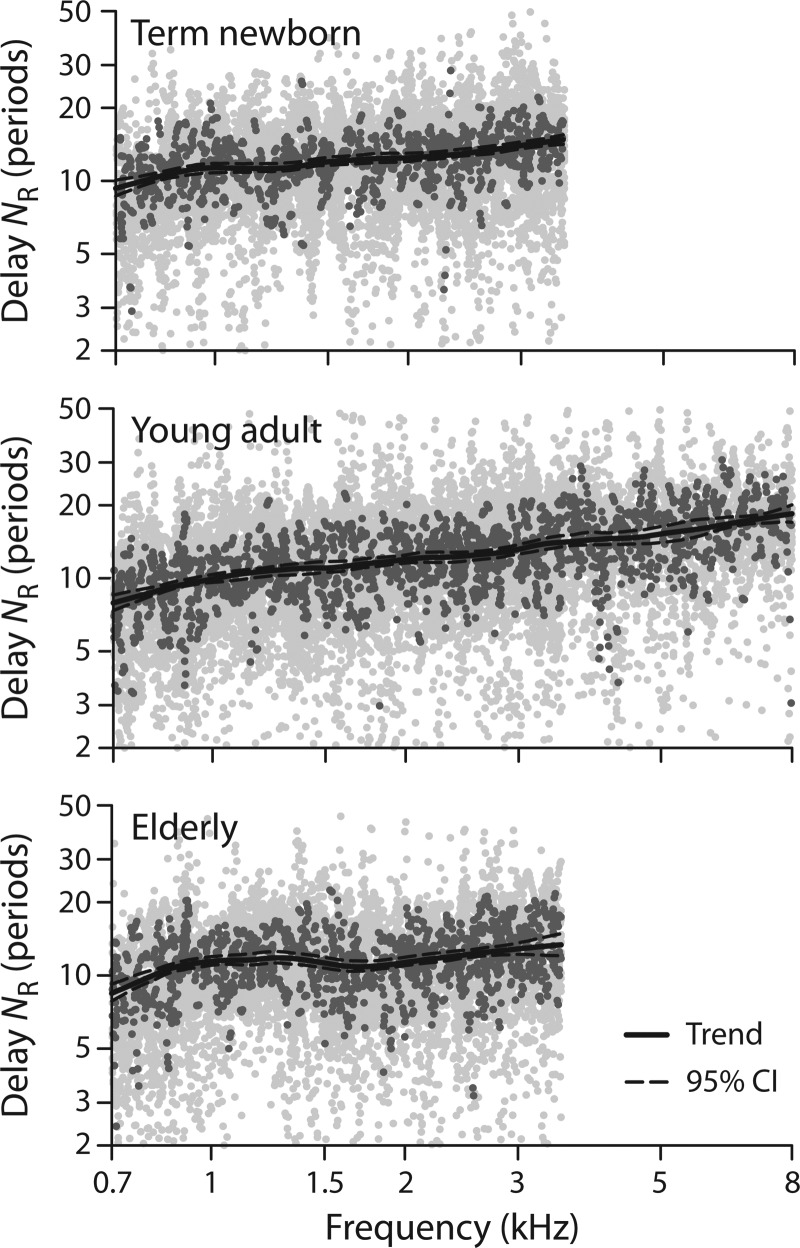
Figure 4 shows the emission delay data (dots) from a representative three of the seven age groups together with their loess trends (solid lines) computed using the peak-picking algorithm. The data points used to estimate the trend (i.e., at frequencies corresponding to magnitude peaks) are shown using darker gray dots and constitute between 8% and 11% of the total, depending on the group. The dashed lines show the 95% confidence intervals (CI) for the trend estimated using resampling on the individual subjects within the group. The young adult data in the middle panel include an extension of frequency to 8 kHz. In this group, 18 additional ears tested after initial data collection provide a wider frequency range for the fit.

FIG. 4.

R-component delays and trends for three age groups: Term newborns, young adults, and elderly adults. In each panel the light gray dots show all values of N_R that satisfied the SNR criterion; the dark gray dots show the values selected by the peak picking algorithm, and the solid lineshows the resulting loess trend. The 95% confidence bounds on the trend are shown by the dashed lines. The young-adult data are shown over an extended frequency range through 8 kHz.

Figure 5(A) shows the trends for each of the groups, coded by color. The solid lines show trends obtained using the peak picking algorithm, and the dotted lines those obtained using energy weighting. Whereas the trends obtained with energy weighting are based on all available data, those obtained via peak picking employ only about 10%. The sizes of the corresponding 95% confidence intervals for the trend are plotted in the lower panel. We note a few principal observations: (1) The peak picking and energy weighting algorithms produce nearly identical trends in all groups, consistent with in silico results (Shera and Bergevin, 2012). The two methods do yield small systematic differences, with the trends from energy weighting generally falling slightly below those from peak picking. (2) The confidence intervals in all groups are typically small, with the largest CIs found in the groups with poorer SNR. As expected, the CIs increase somewhat at the edges of the measured frequency range, where loess smoothing algorithm is less well constrained. In part, the increase at low frequencies also reflects the relative paucity of data in this region, where the SNR is generally worse and the effects of the data selection criteria more severe. As with the trends themselves, the CIs obtained using the two algorithms are similar, despite the difference in sampling, consistent with previous results on in silico subjects (Shera and Bergevin, 2012). Overall the CIs obtained using peak picking are somewhat smaller, despite being based on a much smaller fraction of the data. (3) All age groups show an increase in N_R with frequency. The increase is most clearly visible in the young adults; in this group, mean delay in periods varies by a factor of about 2.4 (from 8 to 19) across the nearly 4-octave range of the data. (4) To varying degrees, all age groups display a bend in the N_R slope located around 1 kHz. This bend is consistent with previous reports of a transition between apical- and basal-like OAE behavior at this frequency in humans (Shera and Guinan, 2003; Shera et al., 2010; Abdala et al., 2011a,b; Dhar et al., 2011; Abdala and Dhar, 2012; Keefe, 2012). (5) As shown by comparison with the dashed line in Fig. 5(A), the N_R trends are similar but not identical to the N_SFOAE trend derived from SFOAEs (Shera et al., 2010). Whereas the N_R trends for most groups are somewhat larger than the N_SFOAE trend at frequencies below the bend near 1 kHz, the N_R trends are consistently smaller than N_SFOAE above the bend. A consequence is that the N_R trends are slightly flatter across frequency and have a shallower bend, crossing the N_SFOAE trend near the apical-basal transition. As a slight exception to this rule, the teen and young-adult trends have somewhat shallower bends but do not intersect the N_SFOAE trend. Perhaps significantly, the N_SFOAE trend derives from SFOAE data collected on young adults.

B. Tuning estimates

We used the N_R trends for each age group to obtain corresponding otoacoustic estimates of the sharpness of cochlear tuning, Q_ERB(CF). The Q_ERB values were computed using the tuning ratio r(CF/CF_a|b) shown in Fig. 5(B) (inset) and a transition frequency CF_a|b of 1 kHz, as estimated from the location of the bend in the N_R trend. The tuning ratio we employed represents an average derived from SFOAE and auditory-nerve measurements in cat, guinea pig, and chinchilla (Joris et al., 2011). By applying the same tuning ratio for each age group, we implicitly assume that the tuning ratio does not vary systematically with age. The data of Fig. 5(A) suggest that the value of CF_a|b is relatively stable over the lifespan.

The resulting otoacoustic values of Q_ERB(CF) derived from DPOAE R-component delays are shown in the main panel of Fig. 5(B). For simplicity, the figure only shows estimates derived from N_R trends obtained via peak picking; those obtained with energy weighting are similar. The tuning estimates have broad similarities and intriguing differences, both across age groups and compared to estimates obtained using SFOAEs. Although the estimated Q_ERB values for the teens and young adults are relatively flat below 3 kHz (with the young adult values subsequently increasing from about 11 to 14 at higher frequencies), the tuning estimates in the other groups are more variable but generally decrease with frequency over their more limited range. Mathematically, these features reflect the shallow bends near CF_a|b characteristic of the N_R trends. By contrast, the estimates of Q_ERB(CF) obtained from the N_SFOAE trend increase monotonically throughout the measured range in a manner reminiscent of the Q values measured from auditory-nerve fibers. Since the form and parameters of the tuning ratio are assumed identical across groups, the conversion to Q_ERB(CF) preserves the relationships between the N_R trends evident in Fig. 5(A) (e.g., the N_R and Q_ERB curves for the elderly group dip below the others near 1.5–2 kHz).

IV. DISCUSSION

SFOAE delays have been used to provide estimates of human cochlear tuning (Shera et al., 2010). Our results indicate that the reflection (R) component of the DPOAE provides similar delay data for calculating tuning. Consistent with previous modeling work in silico (Shera and Bergevin, 2012), our in vivo results suggest that peaks in fine structure carry the most important information for estimating delay trends. Loess trends based on energy weighting and peak-picking usually agree and show generally overlapping CIs. The largest deviations between the methods (and among the various age groups) occur near the edges of test frequency range. In groups with decent SNR (i.e., those with many cooperative subjects and generally strong emission levels, such as young adults), analysis strategies such as peak picking and energy weighting may be unnecessary, and neither had much effect on the extracted trends. However, in groups with more biological and/or recording noise, such as the prematurely born neonates, both peak-picking and energy-weighting strategies produced smoother and presumably more representative trends (analysis not shown; see Shera and Bergevin, 2012).

Distortion-product R-component delays from the young adults appear similar to, albeit somewhat smaller than, previously reported SFOAE delays from the same age group. At least in part, the differences may be due to methodological factors. For example, the amplitude of the forward traveling wave whose reflection gives rise to the R component is uncontrolled in the DPOAE paradigm. (In the SFOAE paradigm, the probe level is typically held constant as measured at some location in the ear canal.) In addition, the presence of the primary tones in the DPOAE paradigm suppresses amplification and/or reflection near the 2f₁−f₂ place, potentially modifying the results. Indeed, obtaining a close correspondence between the DPOAE R component and SFOAEs at the same frequency entails the use of an f₁ primary “mimicker” during the measurement of SFOAEs (Kalluri and Shera, 2001). Finally, possible biases introduced by the swept-tone analysis, including parameters such as the durations of the LSF and IFFT windows, remain to be systematically investigated. Understanding the importance of these and other methodological differences requires further study.

To varying degrees, all age groups show a bend in their N_R delay trend near 1 kHz. Although the bend itself often appears shallower than that seen in SFOAE data, its location near the midpoint of the human cochlea matches nicely both with the location of the apical-basal transition obtained from SFOAEs (Shera et al., 2010; Abdala et al., 2011a; Keefe, 2012) and with the frequency characterizing deviations from scaling behavior seen in DPOAE distortion-component phase gradients (Dhar et al., 2011). Consistent with recent findings based on DPOAEs (Abdala et al., 2011b, Abdala and Dhar, 2012), the transition frequency appears stable over the lifespan.

Since the estimates of Q_ERB obtained here were derived using a tuning ratio assumed both independent of age and independent of the emission type being employed (whether SFOAE or R component of the DPOAE), the tuning estimates [Fig. 5(B)] reflect the same similarities and differences evident in the N_R trends [Fig. 5(A)]. Although the Q_ERB values therefore provide no additional information about variation across the lifespan, they do illustrate the procedure for estimating tuning while allowing us to highlight the assumptions used to obtain these estimates.

With the caveat that the assumptions underlying our estimates of cochlear tuning (e.g., the invariance of the tuning ratio with age and emission type) remain to be tested, we note that the Q_ERB values derived here from DPOAE R components share both similarities and differences with other metrics of tuning. Foremost among the differences are the large estimated Q_ERB values (Q_ERB > 12) and associated decline in Q_ERB with increasing frequency evident in most age groups at frequencies less than about 1.5 kHz. By contrast, the sharpness of tuning obtained from SFOAE measurements increases with frequency throughout the measured range, resembling the pattern seen psychophysically and in neural tuning curves from laboratory animals. The larger low-frequency Q_ERB values obtained in all groups except the teens and young adults reflect the longer R-component delays measured at these frequencies. Although the longer low-frequency delays may be related to the steeper DPOAE distortion-component phase gradients found at similar frequencies (Dhar et al., 2011), the origin and significance of these unexpected differences at low frequencies remain unclear.

At higher frequencies, the delay and Q_ERB trends evident in the two extremes of the lifespan are broadly consistent with trends seen in other metrics of phase slope. Although differences in tuning sharpness among individual groups are difficult to discern in Fig. 5(B), the term neonatal group produced Q_ERB values near the top of the pack over most of the frequency range, indicating relatively sharper tuning. [The term neonates (green line) were the most stable of infant groups, as judged both by the tight confidence intervals and the largest number of observation (n = 30). This group provided double the number of observations compared to the premature neonates, which also had more data points eliminated based on SNR criteria.] Sharper cochlear filtering in term neonates has been observed in other measures of tuning as well. For example, DPOAE ipsilateral suppression tuning curves are narrower in newborns compared to adults (Abdala, 1998). In addition, previous measurements of the total phase accumulation of the R component are also consistent with sharp cochlear filtering in neonates (Abdala and Dhar, 2012). Phase accumulation provides an average, non-frequency specific metric of tuning—the greater the total phase accumulation, the steeper the mean phase-gradient, which corresponds to a longer delay and narrower filters. Past work has shown greater R-component phase accumulation in neonates than adults, and the least phase accumulation in elderly subjects. The intermediate age groups (teens, young, and middle-aged adults) produced less clear accumulation trends.

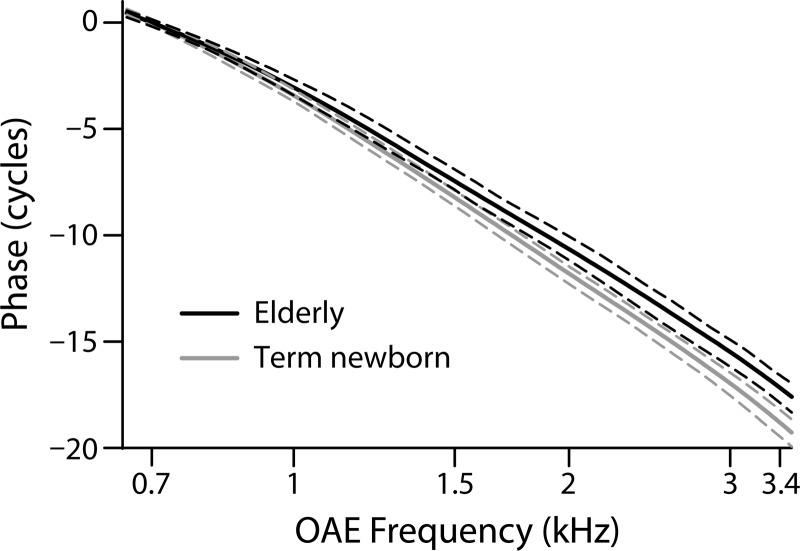
These previous results are consistent with patterns of total phase accumulation in our data. To compare our N_R and Q_ERB values with R-component phase trends, we calculated the phase accumulation between 0.7 and 3.4 kHz for all subject groups as a measure of average phase slope. Consistent with previous results, the elderly group showed reduced phase accumulation (shallower slope; mean = −16.97 cycles) and the term-born neonates showed the greatest accumulation (steepest phase slope; mean = −18.76 cycles). Figure 6 shows the phase trends for these two age groups along with their 95% confidence bounds. Although the phase trends for the other groups generally lie between these extremes, there is no consistent progression across age that holds at all frequencies. A one-way analysis of variance (ANOVA) found a significant effect of age across the seven groups (F = 2.63; p = 0.018). The main contributor to this age effect was the term newborn group; eliminating this group from the analysis rendered the age effect non-significant. Pairwise comparisons showed that the newborn-elderly difference in phase accumulation was the only significant age contrast (p = 0.0016, with the standard 0.05 significance level adjusted for multiple comparisons to 0.0024 using the Holm-Bonferroni method). Consistent with this result, the elderly group in our data showed shorter delays and lower Q values above 1.5 kHz compared to the neonates. It is at these higher frequencies where presbycusis often manifests first and where audiometric thresholds for one-third of our elderly subjects fell slightly outside of the normal range (i.e., 25 dB HL).

FIG. 6.

Phase trend lines (solid) and 95% CIs (dashed) for the term newborns and elderly groups coded by color (see legend). The phases are referenced to their value at 0.7 kHz, to allow comparison with the phase accumulation statistics discussed in the text.

The delay trend N_R provides frequency specific information and cannot easily be distilled into one convenient value, as we have done with phase accumulation. N_R changes across frequency, reflecting changes in the sharpness of filters along the cochlear map, among other factors. In addition, measurement noise and idiosyncratic spatial variations in OAE generation across subjects (i.e., micromechanical irregularity) presumably also contribute to the local fine structure. The fine structure in our N_R estimates across frequency makes its interpretation more complex, as is evident from data in Fig. 5(A). The phase accumulation metric considers only the starting and ending values of phase but cannot describe changes between these boundary frequencies. Despite these obvious differences, consistent trends are observed using both measures (N_R and phase accumulation) in the two groups (newborns and elderly) best representing the extremes of the age continuum.

Sharper neonatal tuning need not reflect a cochlear immaturity (for review, see Abdala and Keefe, 2012); rather, it can be explained by middle-ear inefficiencies in the forward transmission of stimulus tones through the immature neonatal ear, which produces reduced cochlear drive. The reduced drive, akin to lowered stimulus levels, activates optimal cochlear amplifier gain and associated sharp tuning. Although the sharper tuning in neonates might be explained by middle-ear effects, the hint of broadened tuning observed at high-frequencies in the elderly group is consistent with a cochlear source, possibly sensory cell damage and/or reductions in the endocochlear potential, both considered sequelae of aging and contributors to presbycusis (Lang et al., 2010). To refine studies of human cochlear tuning during maturation and aging, it would be most efficacious to measure SFOAEs, thereby eliminating the need for DPOAE component separation and providing a more robust reflection-source emission from which to measure delays.