Abstract
The origin of vocal registers has generally been attributed to differential activation of cricothyroid and thyroarytenoid muscles in the larynx. Register shifts, however, have also been shown to be affected by glottal pressures exerted on vocal fold surfaces, which can change with loudness, pitch, and vowel. Here it is shown computationally and with empirical data that intraglottal pressures can change abruptly when glottal adductory geometry is changed relatively smoothly from convergent to divergent. An intermediate shape between large convergence and large divergence, namely, a nearly rectangular glottal shape with almost parallel vocal fold surfaces, is associated with mixed registration. It can be less stable than either of the highly angular shapes unless transglottal pressure is reduced and upper stiffness of vocal fold tissues is balanced with lower stiffness. This intermediate state of adduction is desirable because it leads to a low phonation threshold pressure with moderate vocal fold collision. Achieving mixed registration consistently across wide ranges of F0, lung pressure, and vocal tract shapes appears to be a balancing act of coordinating laryngeal muscle activation with vocal tract pressures. Surprisingly, a large transglottal pressure is not facilitative in this process, exacerbating the bi-stable condition and the associated register contrast.
I. INTRODUCTION
The scientific and pedagogical descriptions of vocal registers became an active topic of discussion in the last half of the 20th century (Van den Berg, 1960; Vennard, 1967; Large, 1973; Hollien, 1974; Titze, 1988a; Švec et al., 1999) and continue to be pursued into this century (Miller and Schutte, 2005; Henrich, 2006; Roubeau et al., 2009). Attempts have been made to describe registers perceptually, acoustically, and physiologically. Perceptually, several distinct vocal timbres have been identified, with relatively sudden shifts between them that can vary somewhat with fundamental frequency, vowel, and lung pressure. One perceptual category is a voice with a light timbre, characterized acoustically by a predominance of first harmonic energy. It is often referred to as the falsetto voice, or falsetto register. In males, it is akin to the boy voice. In females, the child-adult distinction is less dichotic (with no separate labels) because pubertal voice changes are not as dramatic in females as in males. A second perceptual category is a voice with rich (heavy) timbre, characterized acoustically by an abundance of second and higher harmonic energy. This register is generally produced by adult males in speech. It has been called modal voice, or modal register (Hollien, 1974), suggesting a statistical “mode” or norm, at least in adult males. Chest register is a related label that may have its origin in sensations in the trachea or chest when a harmonically rich timbre is produced (Titze, 1988a). Females also produce this timbre, but to a lesser degree as measured by reduced spontaneous pitch jumps in register changes (Švec et al., 1999; Miller et al., 2002). Traditionally, females speak in a register that lies between the male modal and male falsetto registers in terms of harmonic energy produced at the larynx. The statistical mode, and hence modal register, may be slightly different for females than males. The vocalization most associated with stark and repeated register alternation is the alpine yodel (Frank and Sparber, 1972; Echternach and Richter, 2010).
Vocal fry, or pulse register, is a third perceptual category. This register is not mechanistically or spectrally unique, however. Sometimes a single long period exists, while at other times there is period doubling or tripling due to subharmonics (Švec et al., 1996). Perceptually, the fry register is based on the fact that below about 70 Hz, a signal with a temporal gap of energy in the lowest fundamental period is perceived as pulse-like (Bergan and Titze, 2001).
The interesting and often perplexing aspect of the modal-falsetto vocal timbre dichotomy is that it is not always predictable or controllable. A small change in muscular adjustment in the larynx, in lung pressure, or in vowel configuration can trigger a sudden change from one register to the other. Furthermore, the mixed register, also referred to as “voix mixte” in French literature, or simply “mix” in contemporary singing styles, seems to be less stable than either of the extreme registers in some individuals. While females have traditionally been less prone to register instabilities in speech because pubertal changes in vocal fold morphology are less dramatic than in males, recent trends in lower-pitched female voices are beginning to show register instabilities similar to those in many male voices (Wolk et al., 2012 for vocal fry; personal impression for use of male-like modal register by females).
What has confounded simple mechanical description of vocal registers is the fact that laryngeal muscle contraction, aerodynamics in the glottis, and acoustic pressures in the vocal tract can all contribute to the sudden shifts from one register state to the other. Hirano et al. (1970) were an early group of investigators to show that intentional changes in register are produced by differential activation of thyroarytenoid (TA) and cricothyroid (CT) muscles. Hsiao et al. (2001) showed that register transitions can be evoked in a canine model by stimulating the midbrain to obtain steady phonation (coordinated laryngeal muscle activity) and simultaneously modulating CT contraction with direct muscle stimulation. Titze (1988a) provided a conceptual framework of muscle balance in registration by including the possibility of acoustic interaction with the vocal tract. Kochis-Jennings et al. (2012) showed that as human subjects shifted from modal to mixed register, and from mixed register to falsetto, they decreased TA activation relative to CT activation.
Most of the recent investigations have focused on the influences of vocal tract pressures on registration (Neumann et al., 2005; Miller and Schutte, 2005; Titze, 2008; Echternach et al., 2011; Tokuda et al., 2010). Owing to the relatively narrow entry into the supraglottal vocal tract (the epilarynx tube) in comparison to the wider opening into the trachea, it is now understood that supraglottal acoustic pressures have a greater effect on registration than subglottal acoustic pressures. In the absence of a supraglottal tract, however, subglottal acoustic pressure plays a key role in registration (Zhang et al., 2006). The difference in vocal tract dimensions above and below the glottis was not known 25 yrs ago when this author hypothesized a framework on vocal registers based on subglottal interaction (Titze, 1988a). Magnetic resonance imaging of the vocal tract (Story et al., 1996) brought a lot of clarity to source-vocal tract interaction.
A complete causal description of vocal registers must take into account that registration can be controlled voluntarily (as in an artistic yodel), that its effect can be softened voluntarily by register “mixing,” and that involuntary shifts and instabilities in registration occur with lung pressure, F0, or vowel. For a review of register research in the previous century, see Titze (1994, 2000, Chap. 10), and for a review a decade further, see Henrich (2006).
It will be shown here that the mean medial surface orientation of adducted vocal folds can become bi-stable, meaning that many combinations of glottal air pressures are likely to cause one of two extreme adductory postures rather than a central one. An imbalance in stiffness of upper and lower portions of the layered vocal fold morphology can exacerbate this dichotomy of adduction. Although steady pressures will be used to calculate this mean adductory posture, oscillatory (acoustic) pressures are not excluded from triggering the instability. The definition of “bi-stable” used here is not the same as in nonlinear dynamics, i.e., that two stable attractors can co-exist in the same dynamic system (Guckenheimer and Holmes, 1983; Švec et al., 1999). Since oscillatory conditions are not described explicitly here, but rather mean adductory states that are expected to occur during oscillation, the topic of multiple attractors in self-sustained oscillation is postponed.
The mixed adductory posture to be described here was shown to be optimal for self-sustained oscillation in a vocal fold model (Titze, 1988b). It will be further shown here that mixed registration is achievable by balancing tissue stiffness and by reducing transglottal pressure. The task of balancing (or mixing) registration may therefore be a big part of voice training and voice therapy (Vennard, 1967; Miller, 1986; Titze and Verdolini Abbott, 2012). Males and females who habitually speak in mixed register seem to have worked out the laryngeal motor pattern to avoid the stark register contrast due to tension imbalances, but acoustic pressures above and below the glottis may still trigger register shifts.
II. A CRITERION FOR OPTIMAL ADDUCTION
Studies with physical models (Titze et al., 1995; Chan et al., 1997; Mau et al., 2011; Mendelsohn and Zhang, 2011), computer simulation models (Pickup and Thomson, 2011), and analytical calculations (Titze, 1988b; Lucero, 1998; Chan and Titze, 2006; Klemuk et al., 2010; Lucero et al., 2011; Fulcher et al., 2012) have shown that a near rectangular glottis (as viewed in the coronal plane) produces the lowest oscillation threshold pressure. (Direct measurement of this configuration in human subjects has not been reported.) If the configuration is exactly rectangular, the medial surfaces of the vocal folds are parallel, at least over a portion of the thickness of the vocal folds. This configuration is depicted in Fig. 1(b). When the top of the vocal folds is more adducted than the bottom, the glottis is referred to as convergent (with reference to the airstream, which moves from bottom to top). This is depicted in Fig. 1(a). When the bottom of the vocal folds is more adducted than the top, the glottis is said to be divergent [Fig. 1(c)]. A flat surface in any of these shapes is an idealization, however. There is usually some curvature on the medial surface (Hirano and Sato, 1993). To keep both a conceptual and a computational model of registers simple, the curvature is omitted in what follows. The loss of interpretive power with this assumption is that the bi-stable effects described here may not occur over the entire medial surface, but only a portion thereof.
FIG. 1.
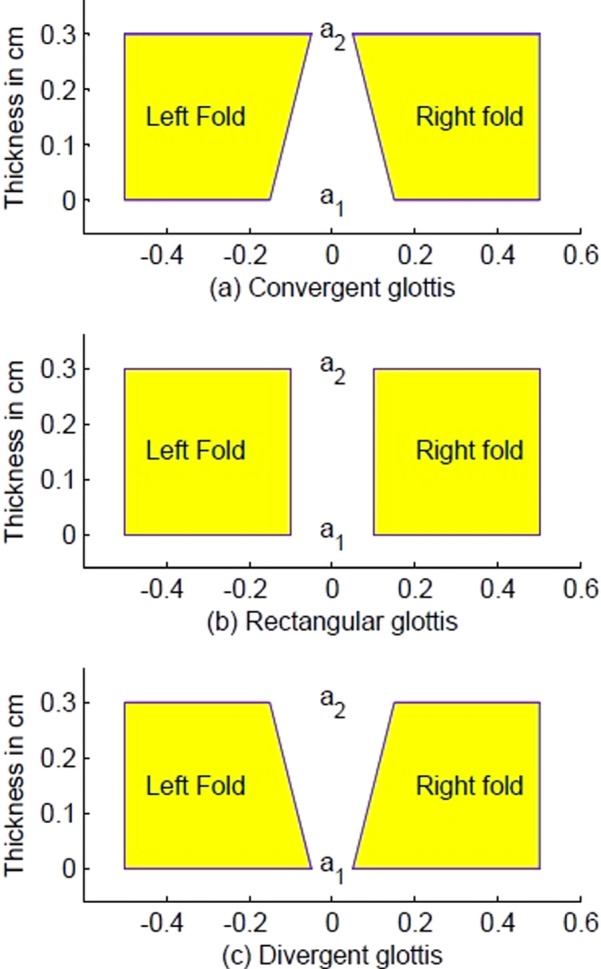
(Color online) Glottal shapes. (a) Top of the vocal folds more adducted than the bottom, glottis referred to as convergent; (b) vocal fold surfaces are parallel, glottis referred to as rectangular; (c) bottom of the vocal folds more adducted than the top, glottis referred to as divergent.
A measure of the glottal shapes in Fig. 1 is the ratio a1/a2, where a1 is the bottom cross sectional area of the glottis and a2 is the top cross sectional area of the glottis. For a rectangular glottis, a1/a2 = 1. A convergence angle can also be defined (Scherer et al., 2010),
| (1) |
where T is the effective (vibratory) thickness of the vocal fold.
Figure 2 is an abridged version of phonation threshold pressure data obtained from physical models (Titze et al., 1995; Chan et al., 1997) in which convergence angle and glottal half-width were varied systematically. Glottal half-width was defined as the distance from the glottal midline to the center (half-thickness) on the medial surface of the vocal folds. Note that for the three glottal half-widths shown, a −1° to 3° convergence angle has the lowest threshold pressure. Much of what follows in this paper is based on a hypothesis that a 0° or slightly convergent angle is a target for “easy” phonation in a mixed register. A brief review of how laryngeal muscles can be used to produce minimal adductory divergence or convergence is discussed next.
FIG. 2.
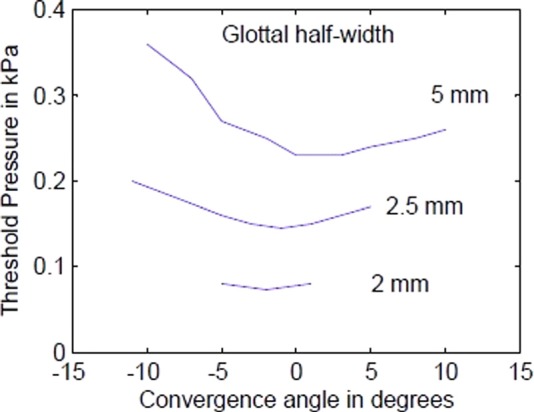
(Color online) Phonation threshold pressure versus convergence angle for three glottal half-widths.
III. REVIEW OF MUSCLE CONTROL OF ADDUCTION
The primary vocal fold adductory muscles are the lateral cricoarytenoid (LCA), the TA, and interarytenoid. The LCA adducts the vocal processes of the arytenoid cartilages, which bring the superior edges of the vocal folds together. Hence, the activation level of LCA is the main physiologic control variable for a2. The bottom of the vocal fold is adducted by the TA. Hirano (1975) demonstrated this with in vivo muscle stimulation, and similar results were reported by Berke et al. (1989) and Choi et al. (1993) with nerve stimulation. The medial surface of the vocal fold was imaged before and after stimulation. Thus, we can say that the activation level of TA is a reasonable predictor of a1. In terms of non-dimensional ratios, a1/a2 may be predicted by a TA/LCA activation ratio. Thus, without specifying an exact mathematical relation between vocal fold shape and muscle contraction, which would involve the biomechanics of all vocal fold tissue layers, one can say that Fig. 1(a) reflects LCA domination in adduction and Fig. 1(c) reflects TA domination in adduction. There is, however, saturation in the amount of medial surface control that can be obtained by muscle contraction. Fibers of the TA muscle are neither perpendicular to the medial surface nor exactly parallel (Hirano and Sato, 1993). Also, the compartmental arrangement between ligament and TA fibers is irregular. The important result is that over some portion of the vocal fold surface, a parallel contour can possibly be created. Over the rest of the vocal fold, some convergence or divergence is likely to remain. Hence, surface non-uniformity may limit one's ability to produce ideal thick, flat, and parallel surfaces. The so-called “vocal pads” of lions and tigers are the best evolutionary evidence of an ideal design for low phonation threshold pressure known to this author (Titze, 2012).
What role does CT activity play in registration? Its main function is anterior–posterior fiber stiffness regulation of the vocal fold tissue layers by vocal fold lengthening, but CT also plays a role in adduction. LCA and CT activity are often highly correlated in speech (Atkinson, 1978). One reason is that, when fundamental frequency is high and governed by tension in the vocal ligament (Van den Berg, 1960; Titze et al., 1988), amplitude of vibration is small. Smaller amplitude requires more adduction at the vocal processes to allow the vocal folds to reach contact in vibration. In addition, elongated vocal folds are retracted from the glottal midline because their cross sectional area is reduced. This retraction requires further LCA adduction, which adjusts the glottis toward a convergent shape if TA activity is not simultaneously increased (Hirano, 1975). In other words, bottom adduction may not follow top adduction of the vocal folds when CT is much more activated than TA (Berke et al., 1989). At the opposite extreme, if TA activation is strong and the ligament is lax due to little CT activation, a divergent pre-phonatory configuration can be the outcome. Adduction at the top is then weaker than adduction at the bottom. For mixed registration, it is hypothesized that the two extremes are avoided with appropriate muscle balance so that a near rectangular glottis is achieved and stiffness is balanced in the tissue layers. A small convergence angle is probably not detrimental, but large divergent or convergent angles are not conducive to low-threshold self-sustained oscillation.
The question now becomes, how are these adductory postures affected by glottal and vocal tract pressures? It will be shown that glottal driving pressures can undergo large variation with small changes in convergence angle when the vocal fold surfaces are in the near-parallel position. It is hypothesized that this can bring about a quantal shift in lower adduction, and hence in registration. To demonstrate this quantal shift, the approach taken here is to use the simplest possible fluid and tissue mechanical model to explain postural shifts in adduction by glottal pressures. The claim is that these shifts can be considered at least one origin of pressure-related modal-falsetto registrations, whereas gross register changes are associated with tension imbalance in the LCA-CT-TA muscle complex (Titze, 1994, 2000). The analysis is based on steady pressures in the glottis, given that these have been measured for specific convergence angles. It is understood, however, that in phonation all pressures have both an oscillatory and steady component, so that all variations in medial surface contour can occur within a glottal cycle.
IV. COMPUTATION OF MEDIAL SURFACE DISPLACEMENT BY GLOTTAL AIR PRESSURES
Computer simulation of vocal fold mechanics has reached a high degree of sophistication, involving three-dimensional geometry and multiple tissue layers (Titze, 2006; Mittal et al., 2011). Although a high level of complexity may be needed for quantitative refinement of registration (which is in fact contemplated for future studies), the essence of the phenomenon of interest here can be described by a very simple model. The value of such simplicity is complete repeatability (all equations are included herein) as well as analytic formulations that explicitly demonstrate relations between crucial variables. It is expected that quantitative refinement with high-dimensional models will confirm at least the basic trends.
Computation of medial surface displacement is divided into two parts. First, for heuristic purposes, the convergence angle will be held under control while glottal pressures are changed according to an ideal Bernoulli regime. Second, convergence will be allowed to vary according to two elastic restoring forces (upper and lower) in the tissues and the ideal Bernoulli assumptions will be replaced by empirically-derived pressure distributions reported by Scherer et al. (2010).
A. Controlled convergence angle and ideal Bernoulli pressures
Bernoulli pressure integration between two flat surfaces, developed in earlier work (Titze, 1988b, 2006, p. 356), resulted in a mean intraglottal pressure on the surfaces of the vocal folds as follows:
| (2) |
where ps is the subglottal pressure and pe is the pressure at the entry of the epilarynx tube (supraglottal pressure). Bernoulli energy conservation for incompressible flow was assumed in the glottis (no flow detachment from the surfaces or viscous energy losses) to obtain this simple formula. Flow separation in the form of a jet will be included in Sec. IV B. The medial surfaces of the vocal folds were assumed to be flat, as in Fig. 1, and no collision between the surfaces was assumed. These assumptions are severe and limit generality, but the result is heuristically important because it shows that the “Bernoulli Effect,” which has been widely used in explanations of vocal fold vibration for a long time, is present only in a weak form in glottal aerodynamics. More importantly, Bernoulli pressures play a role in self-sustained oscillation only if the divergence angle changes over the glottal cycle. As Eq. (2) shows, if a1/a2 is constant over the glottal cycle and the applied pressures are the same for glottal opening and closing, the intraglottal pressure cannot produce a push–pull driving force.
If a1/a2 is allowed to change, then for a convergent glottis (a1/a2 > 1.0), the mean intraglottal pressure is positive, assuming that both ps and pe are positive. The medial surfaces of the vocal folds can be separated when this pressure is applied. The separation is ultimately limited by elastic recoil of the tissues. For a divergent glottis (a1/a2 < 1.0), the Bernoulli intraglottal pressure may be positive or negative, depending on the magnitude of the supraglottal (epilaryngeal) tube pressure pe. If pe is near zero, divergence can cause a negative pressure, which will tend to pull the vocal folds together. Equilibrium is then reached in one of two ways, either by collision of the vocal folds, or by elastic recoil without collision if the vocal folds are initially spread widely apart.
Figure 3 shows plots of mean intraglottal pressure for ps = 1.5 kPa (horizontal line on top) and four values of supraglottal pressure Pe (0.0, 0.5, 1.0, 1.2 kPa). The area ratio a1/a2 is on the abscissa so that divergence is on the left side and convergence is on the right side. The area ratio is plotted logarithmically to maintain left–right symmetry in the spacing of area ratios, ranging from 0.1 to 10, with 1.0 being in the middle. The data points are from Scherer's M5 physical model (Scherer et al., 2010) with a minimum diameter of 0.08 cm. It is clear that the ideal Bernoulli pressures (solid lines) deviate substantially from the data, especially in the divergent region where flow separation from the wall occurs. Flow separation tends to reduce the slope of the p versus a1/a2 curves in the divergent region. Analytically, from Eq. (2), the derivative of p with respect to the a1/a2 ratio is (ps - pe) at the rectangular shape. This is obtained by differentiating p with respect to a1/a2 and then setting a1/a2 = 1. In other words, the slope of the pressure curves at the critical rectangular point (a1 = a2) is the transglottal pressure. (The slopes where the asterisks are plotted on the solid lines are the transglottal pressures ps-pe.)
FIG. 3.
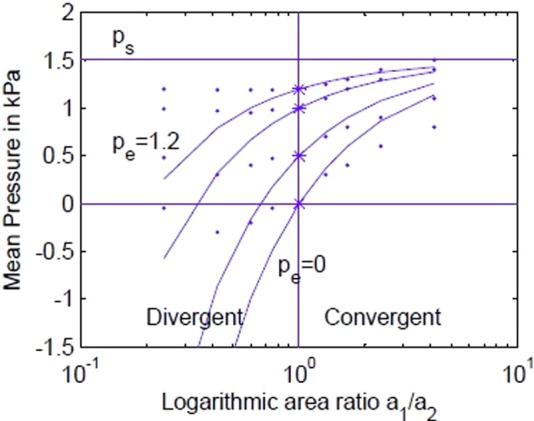
(Color online) Mean intraglottal Bernoulli pressure versus area ratio for 1.5 kPa subglottal pressure and four values of supraglottal pressure. Data points are from Scherer et al. (2010).
Figure 3 provides mild evidence for a quantal pressure slope change with a1/a2 when the Scherer data are considered. Although the slopes themselves are smaller than for the Bernoulli calculations, they show a quantal change around a1/a2 = 1.0. This change will be shown to become more abrupt when the vocal fold is partitioned into upper and lower parts.
Before abandoning the ideal Bernoulli pressures, it is instructive to ask what kind of steady (non-oscillatory) medial surface displacement they can produce. Consider an elastic recoil pressure for the entire vocal fold surface to be written as
| (3) |
where L is vocal fold length, T is vocal fold thickness, k is average vocal fold stiffness over the thickness, and x is the vocal fold separation that adds or subtracts from muscular adduction. Setting Eq. (2) to Eq. (3) for equilibrium and solving for x,
| (4) |
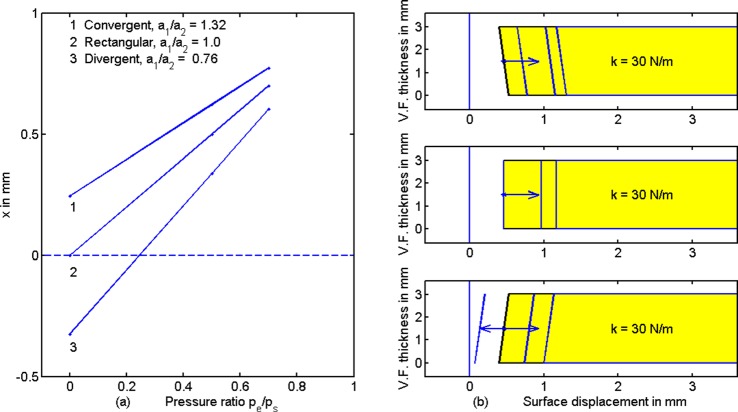
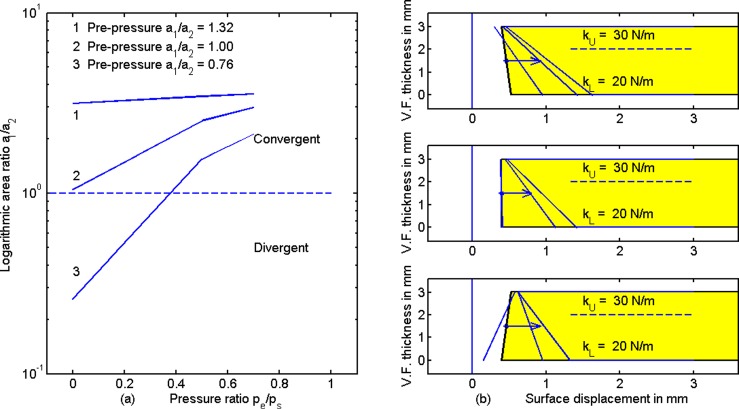
Figure 4(a) shows a plot of Eq. (4), the midpoint surface displacement x as a function of the supraglottal/subglottal pressure ratio pe/ps [last term in Eq. (4)]. Three specific area ratios a1/a2 are chosen for the three curves, 1 for convergence, 2 for rectangular, and 3 for divergence. Other constants are Ps = 1.0 kPa, L = 1.0 cm, T = 0.3 cm, and k = 30 N/m. Note that an increase in pe/ps drives all three shapes toward positive displacements x. The magnitude of this displacement is a fraction of a mm. Figure 4(b) shows coronal sections of the right vocal fold with their respective medial surface displacements. The vertical lines at the tail of the arrows are the medial surface positions before pressure was applied (equivalent to muscular adduction only). The remaining medial surface displacement lines are for pe/ps = 0, 0.5, and 0.7, increasing from left to right according to the arrow. (The rectangular shape has only two medial surface displacement lines because there is zero displacement for pe/ps = 0.) The Bernoulli Effect (negative displacement due to negative pressure) is seen in the bottom figure for a divergent glottis. Surface displacement x begins with a negative value (arrow pointing left), but trends toward positive values (vocal fold separation) when pe/ps is increased. This can create a potential instability in adduction. Specifically, reducing the transglottal pressure by making pe/ps > 0.25 flips negative displacement to positive displacement for this divergent surface [see also curve 3 in Fig. 4(a) for the 0.25 value].
FIG. 4.
(Color online) (a) Midpoint surface displacement x as a function of the supraglottal/subglottal pressure ratio pe/ps for three area ratios a1/a2, with Ps = 1.0 kPa, L = 1.0 cm, T = 0.3 cm, and k = 50 N/m. (b) Coronal view of right vocal fold medial surface displacements for convergent (top), rectangular (middle), and divergent (bottom) pre-pressure shapes. The tail of the arrows indicates no pressures applied (muscular adduction only). The remaining medial surface lines are for pe/ps = 0, 0.5, and 0.7.
With these preliminary trends, three simplifying assumptions will now be removed. First, flow detachment from the glottal wall will always be included; second, the area ratio a1/a2 will be allowed to change with the applied pressures; and third, the mean stiffness k will be replaced with an upper stiffness and a lower stiffness to represent a gradient in vertical tissue properties.
B. Glottal convergence angle controlled by air pressure and tissue elasticity
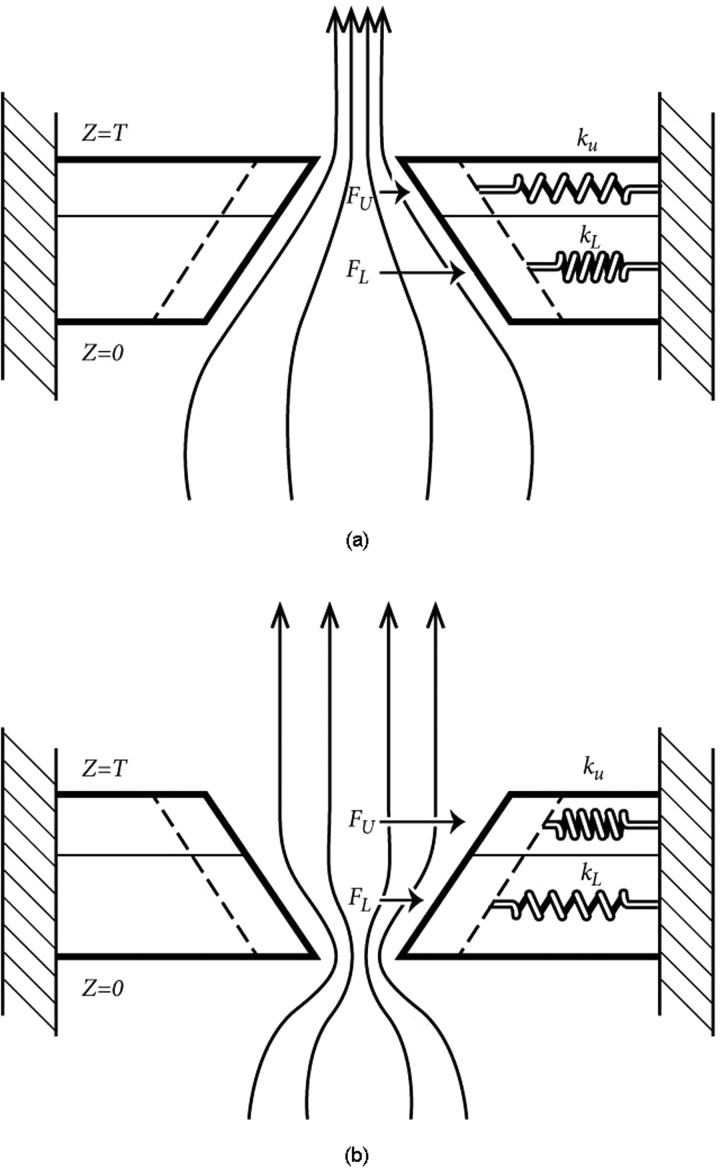
The vocal fold thickness was divided into a lower 2/3 portion and an upper 1/3 portion (Fig. 5). The lower portion was considered to represent primarily mucosal and TA muscle tissue, whereas the upper portion was considered to represent primarily mucosal and ligamental tissue. This division of tissue layers is obviously an oversimplification, but serves to create a vertical tissue stiffness gradient to show how medial surface orientation can be affected by glottal pressures with differential stiffness. A lower stiffness kL and an upper stiffness kU, in magnitude proportional to the surface thickness, were first assigned to produce a zero gradient,
| (5) |
| (6) |
The combined stiffness was equal to the total 30 N/m stiffness in Fig. 4. The stiffnesses are similar to the body stiffness used by Tokuda et al. (2010) for simulation of register shifts.
FIG. 5.
Two-spring model of the vocal folds for (a) a convergent glottis and (b) divergent glottis. Vocal fold mass is not relevant for static displacements.
Pressures on the lower and upper portions of the vocal fold surfaces, PL and PU, respectively, were derived from empirical data published by Scherer et al. (2010). These pressures replaced the ideal Bernoulli pressures and included the effects of flow separation, viscous losses, and turbulence losses. Figure 6 shows the pressure data as a function of area ratio a1/a2. The family of four curves on each sub-figure is for different minimum glottal diameters (0.02, 0.04, 0.08, and 0.12 cm), and the four separate sub-plots are for different transglottal pressures (1.5, 1.0, 0.5, and 0.3 kPa). A supraglottal pressure Pe was added to Scherer's data so that the subglottal pressure remained at 1.0 kPa. Note that the pressure PL on the lower portion of the vocal folds (solid lines labeled PL) shows the greatest rate of change (slope change) for small divergence (near a1/a2 ≈ 1.0). The slope stabilizes at a small convergence angle, which is desirable for low phonation threshold pressure. Little pressure change occurs on the upper portion of the vocal folds (dotted lines labeled PU). Thus, a preliminary observation is that pressure on the lower portion of the vocal folds may create a sensitive region for adduction between a divergent shape and a convergent shape. A second observation is that a smaller transglottal pressure (due to an increased supraglottal pressure) reduces the severity of the pressure change between divergence and convergence.
FIG. 6.
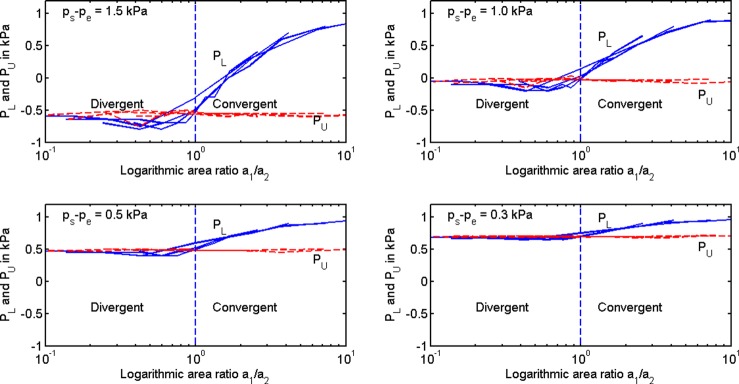
(Color online) Driving pressures on lower portion (PL) and upper portion (PU) of the vocal folds for different transglottal pressures listed in the upper left corner of each panel as measured by Scherer et al. (2010). The family of curves in each panel is for four different glottal diameters (0.02, 0.04, 0.08, 0.12 cm).
To test these preliminary observations further, mean equilibrium positions of the surface areas were calculated by setting the pressure forces equal to the elastic recoil forces from the upper and lower portions of the tissues,
| (7) |
| (8) |
where xL is the lower surface position, xU is the upper surface position, and xLO and xUO are the corresponding no-pressure positions. A substitution was made to relate mid-surface driving point variables to corner variables. Thus,
| (9) |
| (10) |
| (11) |
| (12) |
where left–right asymmetry was assumed in vocal folds of length L. With these substitutions, the equations above have two unknowns, a1 and a2.
The solution of Eqs. (5)–(12) is technically algebraic, but difficult to obtain analytically because there are nonlinearities and sampled data. A Newton-Raphson iterative solution is feasible by re-writing the equations as
| (13) |
| (14) |
Seed values for a1 and a2 are first set to a10 and a20, respectively, and then the values are corrected with increments Δa1 and Δa2 according to the Newton-Raphson approximations (Hildebrand, 1974, p.584)
| (15) |
| (16) |
where the partial derivatives and functions are evaluated numerically by forward and backward differences at the current approximation. The new approximations for a1 and a2 become
| (17) |
| (18) |
In the numerical method, the lower and upper driving pressures PL and PU are obtained from Fig. 6.
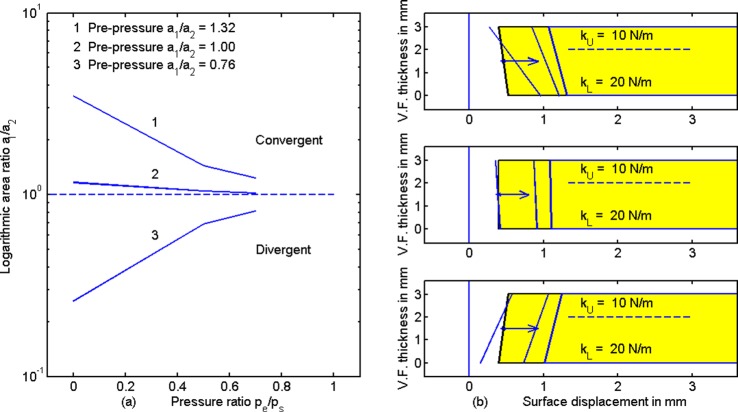
Figure 7 shows the surface displacements as a function of the pressure ratio pe/ps, similar to Fig. 4. These lines at the tail of the arrows are pre-pressure positions in Fig. 7(b) the same as in Fig. 4(b). For completeness, the following area values are given in mm2: a10 = 0.106 and a20 = 0.08 (top right); a10 = a20 = 0.08 (center right); a10 = 0.08 and a20 = 0.106 (bottom right). The upper and lower tissue stiffnesses are also shown on the right, along with the post-pressure surface displacement lines. Note that as the transglottal pressure ratio pe/ps is increased, convergent shapes become less convergent, divergent shapes become less divergent, and rectangular shapes remain rectangular. The area ratio a1/a2 (after pressure has been applied) is plotted logarithmically in Fig. 7(a). The trend toward a1/a2 = 1.0 for all lines speaks in favor of minimizing transglottal pressure to stabilize adduction in the near-rectangular glottal configuration, at least for the case where upper and lower stiffnesses are balanced (in humans with CT and TA activation).
FIG. 7.
(Color online) (a) Area ratio versus pressure ratio pe/ps and (b) medial surface tissue displacements for balanced upper and lower stiffness. Lines at the tail of the arrow show zero-pressure adduction.
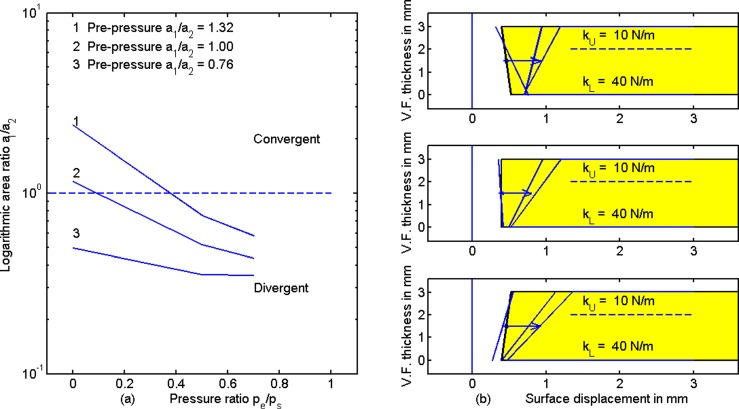
Figure 8 shows results for stiffening the bottom portion of the vocal fold from 20 N/m to 40 N/m, thereby creating a negative stiffness gradient from bottom to top. The same pre-pressure configurations were maintained as in Figs. 4 and 7. The stiffening at the bottom is a gross approximation to TA contraction in modal register. The most dramatic change from Fig. 7 to Fig. 8 is that all configurations now trend toward greater divergence when pe/ps is increased (left panel and arrows on the right panel). Assuming these modeling results capture the essence of vocal fold posturing, an increase in supraglottal pressure pe produces a strong push on the softer top portion of the vocal fold while the bottom is held in place due to greater stiffness. A bi-stable situation is noticed in the top right panel. A slightly convergent pre-pressure shape first becomes more convergent with positive ps and small pe/ps, but then becomes divergent for large pe/ps. To achieve and maintain a near rectangular glottis, a corrective action would be to set pe/ps to 0.4, a value that flips a convergent surface to a divergent one. Similarly, pe/ps = 0.2 flips a rectangular surface to a divergent one. For a pre-pressure divergent glottis, supraglottal pressure does not help to produce a rectangular shape (bottom right). An increase in LCA activation (top adduction) or CT activation (greater top stiffness) would likely be needed to square up the glottis.
FIG. 8.
(Color online) (a) Area ratio a1/a2 versus pe/ps and (b) medial surface tissue displacement for increased stiffness at the bottom portion of the vocal fold, as with TA contraction in modal register.
Figure 9 shows results for stiffening the top portion of the vocal fold, creating a positive tissue stiffness gradient from bottom to top (which is assumed to be related to stiffening the vocal ligament). This is presumably the case for falsetto register at high pitches. The general trend is that convergence increases with pe/ps for all configurations. In other words, a strong push is felt on the bottom of the vocal fold (which is soft) while the top is held in place due to greater stiffness. There is no corrective action with supraglottal pressure when the pre-pressure shape is either convergent (top right) or rectangular (middle). Only an increase in bottom stiffness (presumably with TA contraction) would help to square up the vocal folds. A new bi-stable situation is now seen for pre-pressure divergence (bottom right). A value of pe/ps = 0.4 flips a divergent surface to convergent surface.
FIG. 9.
(Color online) (a) Area ratio a1/a2 versus pe/ps and (b) medial surface tissue displacements for increased stiffness at the top portion of the vocal fold (as with a stiff ligament in high-pitched falsetto register).
In summary, vertical gradients in vocal fold stiffness (positive or negative) can set up conditions such that intraglottal pressures can produce dramatic changes in the medial surface contour. Some of these sudden changes can be mediated by adjusting the supraglottal/subglottal pressure ratio. Others require muscular action to reduce the stiffness gradient.
V. EMPIRICAL EVIDENCE FOR BI-STABLE ADDUCTION
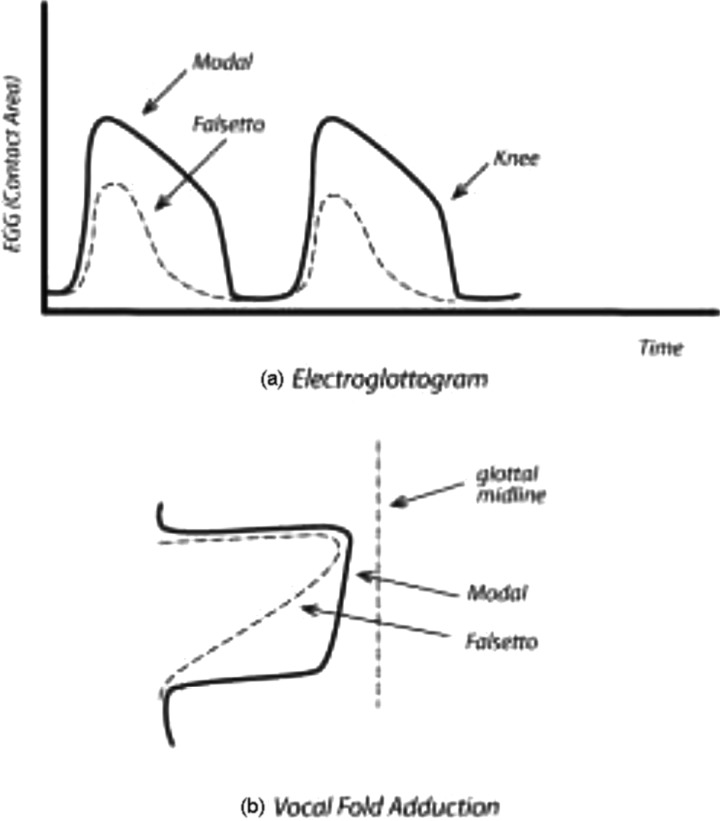
The best evidence for bi-stable adduction during vibration has been obtained with electroglottography (EGG). It measures the electrical conductance of tissues between two electrodes placed on opposite sides of the neck. The spatial distribution of the electric field in the larynx is complex (Titze, 1990), but modulations due to a time-varying airspace (the glottis) are detectable. In particular, the difference in upper and lower contact between the vocal folds is detectable by a “knee” in the declination of the EGG signal. Figure 10(a) shows typical EGG signals in modal register and falsetto register. Previous modeling of the EGG signal (Titze, 1989) has confirmed that this knee represents a rapid release of lower contact of the vocal folds. Visual observation by Hess and Ludwigs (2000) confirmed this.
FIG. 10.
Comparison of (a) electroglottogram signal for modal and falsetto register, and (b) vocal fold adduction sketch in modal and falsetto register.
An interesting observation is that the time course of the EGG signal, if rotated clockwise 90°, becomes an approximate facsimile of the medial surface of the vocal folds in coronal view [Fig. 10(b)]. This qualitative similarity between the temporal wave shape of the EGG and the spatial pattern of the medial surface is a result of the physical requirement that, for self-sustained oscillation, the bottom of the vocal fold must lead the top in phase. Thus, bottom contact generally leads top contact. Given that bottom contact increases with bottom adduction, it follows that a “squaring up” of the medial surface toward a rectangular shape will be reflected in a flattening of the top of the EGG signal. An exact quantitative equivalence in the shapes of the curves cannot be expected, however, because amplitudes of vibration (top and bottom) affect the contact area.
Documented changes in the EGG signal with perceived register change are numerous. To cite only a few, Roubeau et al. (1987, 2009) state that a change in laryngeal mechanism occurs when pitch is changed in glissando fashion (low to high or high to low). Modal register is labeled mechanism M1 and falsetto register is labeled mechanism M2 in their terminology. They note that the transition from modal register to falsetto register is characterized by a jump in frequency (albeit sometimes very small), a reduction of the EGG amplitude, and a change in the EGG wave shape as shown in Fig. 10. Salomão and Sundberg (2009) observed similar modal-falsetto differences in the EGG signal in male choir singers. The study by Hess and Ludwigs (2000) offers perhaps the most direct evidence of lower vocal fold contact being associated with the EGG-knee. They performed bidirectional stroboscopic trans-illumination of the glottis such that the vertical level of inferior opening was visible while the top margins were in contact. Their visual images were time-locked with the EGG signal. Miller et al. (2002) stated that a remarkably small interval of time (on the order of a vibratory cycle or less) is expended in the transition from one register to the other. This interval is much smaller than a deliberate muscular adjustment would require. The result suggests that a pressure-driven instability at the medial surface of the vocal folds may account for this rapid EGG change. Vilkman et al. (1995) attributed sudden register shifts and corresponding EGG changes to a “critical mass” concept, which translates to a release or activation of the lower part of the vocal fold by TA muscle contraction.
Some evidence for the possibility of register regulation by creating steady supraglottal pressures has been provided very recently by Alipour and Scherer (2012). They measured the steady ventricular pressure (the pressure directly above the vocal folds, which has been called pe here) in excised larynges when a steady subglottal pressure was applied. In one group of measurements, the ventricular folds were positioned with a narrow gap between them, and in another group, a wider gap was chosen. Results showed that the pe/ps ratio was about 0.2 for the wide gap and 0.6 for the narrow gap, with considerable variation across larynges. This study suggests that mean (steady) pressures can be maintained above the vocal folds to stabilize the glottal configuration. In addition, large supraglottal acoustic pressure fluctuations and large glottal configurational changes can occur under conditions of vocal fold oscillation. The pressures described here may then be thought of as quasi-static sequential states that occur at the medial surface during a glottal cycle.
VI. DISCUSSION OF CURRENT RESULTS IN LIGHT OF EMPIRICAL EVIDENCE
The current computational contribution to vocal registers, although highly simplified mathematically, encapsulates the primary observations that registers can change voluntarily or involuntarily, and that these changes can vary with lung pressure, F0, and vocal tract configuration. Given that LCA, CT, and TA muscle contractions shape the medial surface contour of the vocal fold during adduction and provide stiffness gradients in the layered morphology of the vocal folds, and given that there is an ideal target configuration (a nearly rectangular glottis with parallel medial surfaces), the voluntary component by muscle control has been represented (grossly) by both upper and lower adduction, and by upper and lower stiffness. An optimal adductory posture for efficient voice production is not necessarily achieved by every individual. Genetics and early speech habits may play a role in producing non-ideal adductory postures or stiffness gradients. Thus, for some people it may require some training to achieve optimal laryngeal adduction. Gross posturing often results in one of the extreme adductions, either a highly convergent or an excessively divergent pre-phonatory glottis. Phonation is theoretically possible with these extreme configurations, but at a higher cost in lung pressure. Ironically, higher lung pressure exacerbates the extreme adductory postures without a counteracting supraglottal pressure. Whereas a large transglottal pressure is desirable for driving airflow through the glottis, a small transglottal pressure is desirable for stabilizing the adductory posture.
As fundamental frequency is increased, stiffness in the lower part of the vocal folds (assumed to result from TA contraction) is gradually transferred to stiffness in the upper part of the vocal folds where the bulk of the vocal ligament resides. The stiffness in the ligament is increased by CT contraction. This transfer of stiffness between the TA muscle and the ligament (a positive stiffness gradient from bottom to top) can cause a change in the medial surface contour and therewith a register shift. The duration of glottal closure and the degree of vocal fold contact of the inferior portion of the vocal fold are affected by this shift in the surface contour, as evidenced by EGG. It has been shown here that supraglottal pressure can be used to mediate this re-distribution of tension and vocal fold contact.
VII. CONCLUSIONS
This study has not challenged the widely accepted and adequately researched concept that voice registers are physiologically under control of TA, LCA, and CT muscles. Contractions of these muscles leads to differential changes in stiffness of portions of the vocal folds, as well as differential changes in surface contours. Generally, LCA adducts the top of the vocal fold and TA adducts the bottom. CT contraction generally increases vocal fold length, thereby disproportionally stiffening the top of the vocal fold because the ligament has a steep stress-strain curve. TA contraction stiffens the bottom of the vocal fold, where less ligamental tissue resides between the mucosa and the muscle. The best validation of upper and lower adductory contrast (under vibration) has been vocal fold contact area, as measured by an electroglottographic signal.
The story of registers would end with the above physiological explanation, were it not for the fact that surface pressures on the vocal folds can alter the adductory state produced by the muscles. This paper has demonstrated, with a very simple computational model, how the medial surface configuration can change suddenly from convergent to divergent, and vice versa. This brings in the entire register dependence on F0, vocal tract configuration, and lung pressure. It has been shown here that both subglottal and supraglottal pressures can affect adduction by changing the net displacement of the medial surface and the convergence angle of the medial surface. The pressures have deliberately been kept steady (non-oscillatory) in this treatment, but assuming the usual quasi-steady flow assumption holds for glottal pressure distributions, loss of generality under self-oscillatory conditions is minimal. Inertial and compliant properties of the vocal tract can be included by making ps and pe time-varying and dependent on vocal tract acoustics. This will introduce the nonlinear dynamic effects such as pitch jumps, subharmonics, and hysteresis. The steady pressure analysis here was only the first step to establish causality between pressures and surface orientation. It was shown that intraglottal pressures are sensitive to both subglottal and supraglottal pressures. They vary abruptly around the 0° convergence angle. Generally, both adductory convergence and adductory divergence angles are reduced by lowering transglottal pressures, thereby creating less likelihood of a bi-stable state of adduction. If not mediated by stiffness-balancing of upper and lower portions of the vocal folds, or by reducing the transglottal pressure with a supraglottal back-pressure, a sudden register “break” can occur.
In singing, bi-stable adduction is either exploited (as in a yodel) or mediated with mixed registration. An argument has been made here that mixed registration is likely to have the lowest phonation threshold pressure because the vocal fold surfaces are only slightly convergent. To maintain this slight convergence over a wide range of pitches and vowels requires training for vocalists who have habituated one of the extreme registrations.
ACKNOWLEDGMENT
Funding for this work was provided by the National Institute on Deafness and other Communication Disorders, Grant No. 5R01DC012045-02.
REFERENCES
- 1.Alipour, F., and Scherer, R. C. (2012). “Ventricular pressures in phonating excised larynges,” J. Acoust. Soc. Am. 132(2), 1017–1026 10.1121/1.4730880 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Atkinson, J. E. (1978). “Correlation analysis of the physiological factors controlling fundamental voice frequency,” J. Acoust. Soc. Am. 63(1), 211–222 10.1121/1.381716 [DOI] [PubMed] [Google Scholar]
- 3.Bergan, C. C. , and Titze, I. R. (2001). “Perception of pitch and roughness in vocal signals with subharmonics,” J. Voice 15(2), 165–175 10.1016/S0892-1997(01)00018-2 [DOI] [PubMed] [Google Scholar]
- 4.Berke, G. S. , Moore, D. M. , Gerratt, B. R. , Hanson, D. G. , Bell, T. S. , and Natividad, M. (1989). “The effect of recurrent laryngeal nerve stimulation on phonation in an in vivo canine model,” Laryngoscope 99(9), 977–982 10.1288/00005537-198909000-00013 [DOI] [PubMed] [Google Scholar]
- 5.Chan, R., and Titze, I. R. (2006). “Dependence of phonation threshold pressure on vocal tract acoustics and vocal fold tissue mechanics,” J. Acoust. Soc. Am. 119(4), 2351–2362 10.1121/1.2173516 [DOI] [PubMed] [Google Scholar]
- 6.Chan, R. W. , Titze, I. R. , and Titze, M. R. (1997). “Further studies of phonation threshold pressure in a physical model of the vocal fold mucosa,” J. Acoust. Soc. Am. 101(6), 3722–3727 10.1121/1.418331 [DOI] [PubMed] [Google Scholar]
- 7.Choi, H. S. , Berke, G. S. , Ye, M., and Kreiman, J. (1993). “Function of the thyroarytenoid muscle in a canine laryngeal model,” Ann. Otol., Rhinol., Laryngol. 102(10), 769–776 [DOI] [PubMed] [Google Scholar]
- 8.Echternach, M., and Richter, B. (2010). “Vocal perfection in yodeling-pitch stabilities and transition times,” Logopedics Phoniatrics Vocology 35(1), 6–12 10.3109/14015430903518015 [DOI] [PubMed] [Google Scholar]
- 9.Echternach, M., Sundberg, J., Baumann, T., Markl, M., and Richter, B. (2011). “Vocal tract area functions and formant frequencies in opera tenors' modal and falsetto registers,” J. Acoust. Soc. Am. 129(6), 3955–3963 10.1121/1.3589249 [DOI] [PubMed] [Google Scholar]
- 10.Frank, F., and Sparber, M. (1972). “New resonance analytical knowledge of yodeling from the phonetic and voice training point of view,” Folia Phoniatrica 24(3), 161–168 10.1159/000263564 [DOI] [PubMed] [Google Scholar]
- 11.Fulcher, L. P. , Scherer, R. C. , and Waddle, J. M. (2012). “Phonation threshold pressure and the elastic shear modulus: Comparison of two-mass model calculations with experiments,” J. Acoust. Soc. Am. 132(4), 2582–2591 10.1121/1.4747618 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Guckenheimer, J., and Holmes, P. (1983). Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields (Springer-Verlag, New York: ). [Google Scholar]
- 13.Henrich, N. (2006). “Mirroring the voice from Garcia to the present day: Some insights into singing voice registers,” Logopedics Phoniatrics Vocology 31(1), 3–14 10.1080/14015430500344844 [DOI] [PubMed] [Google Scholar]
- 14.Hess, M. M. , and Ludwigs, M. (2000). “Strobophotoglottographic transillumination as a method for the analysis of vocal fold vibration patterns,” J. Voice 14(2), 255–271 10.1016/S0892-1997(00)80034-X [DOI] [PubMed] [Google Scholar]
- 15.Hildebrand, F. B. (1974). Introduction to Numerical Analysis, 2nd ed. (Dover Publications, Mineola, NY: ), Chap. 10, pp. 539–644 [Google Scholar]
- 16.Hirano, M. (1975). “Phonosurgery: Basic and clinical investigations,” Otologia Fukuoka 21(1), 239–262 [Google Scholar]
- 17.Hirano, M., and Sato, K. (1993). Histological Color Atlas of the Human Larynx (Singular Publishing Group, Inc., San Diego, CA: ), Chap. AC1, pp. 36–46; Chap. AH9, p. 20. [Google Scholar]
- 18.Hirano, M., Vennard, W., and Ohala, J. (1970). “Regulation of register, pitch, and intensity of voice,” Folia Phoniatrica et Logopaedica 22(1), 1–20 10.1159/000263363 [DOI] [PubMed] [Google Scholar]
- 19.Hollien, H. (1974). “On vocal registers,” J. Phonetics 2, 125–143 [Google Scholar]
- 20.Hsiao, T. Y. , Liu, C. M. , Hsu, C. J. , Lee, S. Y. , and Lin, K. N. (2001). “Inducing vocal register transition in an in vivo evoked phonation canine model,” J. Formosan Med. Assoc. 100(8), 543–547 [PubMed] [Google Scholar]
- 21.Klemuk, S. A. , Lu, X., Hoffman, H. T. , and Titze, I. R. (2010). “Phonation threshold pressure predictions using viscoelastic properties up to 1400 Hz of injectables intended for Reinke's space,” Laryngoscope 120(5), 995–1001 [DOI] [PubMed] [Google Scholar]
- 22.Kochis-Jennings, K. A. , Finnegan, E. M. , Hoffman, H. T. , and Jaiswal, S. (2012). “Laryngeal muscle activity and vocal fold adduction during chest, chestmix, headmix, and head registers in females,” J. Voice 26(2), 182–193 10.1016/j.jvoice.2010.11.002 [DOI] [PubMed] [Google Scholar]
- 23.Large, J. (Editor) (1973). Vocal Registers in Singing (Mouton, The Hague: ), pp. 1–153 [Google Scholar]
- 24.Lucero, J. C. (1998). “Optimal glottal configuration for ease of phonation,” J. Voice 12(2), 151–158 10.1016/S0892-1997(98)80034-9 [DOI] [PubMed] [Google Scholar]
- 25.Lucero, J. C. , Koenig, L. L. , Lourenço, K. G. , Ruty, N., and Pelorson, X. (2011). “A lumped mucosal wave model of the vocal folds revisited: Recent extensions and oscillation hysteresis,” J. Acoust. Soc. Am. 129(3), 1568–1579 10.1121/1.3531805 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mau, T., Muhlestein, J., Callahan, S., Weinheimer, K. T. , and Chan, R. W. (2011). “Phonation threshold pressure and flow in excised human larynges,” Laryngoscope. 121(8), 1743–1751 10.1002/lary.21880 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mendelsohn, A. H. , and Zhang, Z. (2011). “Phonation threshold pressure and onset frequency in a two-layer physical model of the vocal folds,” J. Acoust. Soc. Am. 130(5), 2961–2968 10.1121/1.3644913 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Miller, D. G. , and Schutte, H. K. (2005). “‘Mixing’ the registers: Glottal source or vocal tract?,” Folia Phoniatrica et Logopaedica 57(5–6), 278–291 10.1159/000087081 [DOI] [PubMed] [Google Scholar]
- 29.Miller, D. G. , Švec, J. G. , and Schutte, H. K. (2002). “Measurement of characteristic leap interval between chest and falsetto registers,” J. Voice 16(1), 8–19 10.1016/S0892-1997(02)00066-8 [DOI] [PubMed] [Google Scholar]
- 30.Miller, R. (1986). The Structure of Singing [Schirmer Books (NY) Cengage Learning, Stamford, CT: ], Chap. 9, pp. 115–131 [Google Scholar]
- 31.Mittal, R., Zheng, X., Bhardwaj, R., Seo, J., Xue, Q., and Bielamowicz, S. (2011). “Towards a simulation-based tool for the treatment of vocal fold paralysis,” Frontiers in Computational Physiol. Med. 2, No. 19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Neumann, K., Schunda, P., Hoth, S., and Euler, H. A. (2005). “The interplay between glottis and vocal tract during the male passaggio,” Folia Phoniatrica et Logopaedica 57(5–6), 308–327 10.1159/000087084 [DOI] [PubMed] [Google Scholar]
- 33.Pickup, B. A. , and Thomson, S. L. (2011). “Identification of geometric parameters influencing the flow-induced vibration of a two-layer self-oscillating computational vocal fold model,” J. Acoust. Soc. Am. 129(4), 2121–2132 10.1121/1.3557046 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Roubeau, B., Chevrie-Muller, C., and Arabia-Guidet, C. (1987). “Electroglottographic study of the changes of voice registers,” Folia Phoniatrica et Logopaedica 39(6), 280–289 10.1159/000265871 [DOI] [PubMed] [Google Scholar]
- 35.Roubeau, B., Henrich, N., and Castellengo, M. (2009). “Laryngeal vibratory mechanisms: The notion of vocal register revisited,” J. Voice 23(4), 425–438 10.1016/j.jvoice.2007.10.014 [DOI] [PubMed] [Google Scholar]
- 36.Salomão, G. L. , and Sundberg, J. (2009). “What do male singers mean by modal and falsetto register? An investigation of the glottal voice source,” Logopedics Phonatrics Vocology 34(2), 73–83 10.1080/14015430902879918 [DOI] [PubMed] [Google Scholar]
- 37.Scherer, R. C. , Torkaman, S., Kucinschi, B. R. , and Afjeh, A. A. (2010). “Intraglottal pressures in a 3D model with a non-rectangular glottal shape,” J. Acoust. Soc. Am. 128(2), 828–838 10.1121/1.3455838 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Story, B. H. , Titze, I. R. , and Hoffman, E. A. (1996). “Vocal tract area functions from magnetic resonance imaging,” J. Acoust. Soc. Am. 100(1), 537–554 10.1121/1.415960 [DOI] [PubMed] [Google Scholar]
- 39.Švec, J. G. , Schutte, H. K. , and Miller, D. G. (1996). “A subharmonic vibratory patter in normal vocal folds,” J. Speech Hear. Res. 39(1), 135–143 [DOI] [PubMed] [Google Scholar]
- 40.Švec, J. G. , Schutte, H. K. , and Miller, D. G. (1999). “On pitch jumps between chest and falsetto registers in voice: Data from living and excises human larynges,” J. Acoust. Soc. Am. 106(3), 1523–1531 10.1121/1.427149 [DOI] [PubMed] [Google Scholar]
- 41.Titze, I. R. (1988a). “A framework for the study of vocal registers,” J. Voice 2(3), 183–194 10.1016/S0892-1997(88)80075-4 [DOI] [Google Scholar]
- 42.Titze, I. R. (1988b). “The physics of small-amplitude oscillation of the vocal folds,” J. Acoust. Soc. Am. 83(4), 1536–1552 10.1121/1.395910 [DOI] [PubMed] [Google Scholar]
- 43.Titze, I. R. (1989). “A four parameter model of the glottis and vocal fold contact area,” Speech Commun. 8, 191–201 10.1016/0167-6393(89)90001-0 [DOI] [Google Scholar]
- 44.Titze, I. R. (1990). “Interpretation of the electroglottographic signal,” J. Voice 4(1), 1–9 10.1016/S0892-1997(05)80076-1 [DOI] [Google Scholar]
- 45.Titze, I. R. (1994, 2000). Principles of Voice Production (1994, Prentice Hall, Upper Saddle River, NJ: ); (2nd Printing, 2000, National Center for Voice and Speech, Salt Lake City, UT), Chap. 4, p. 100; Chap. 10, pp. 281–310 [Google Scholar]
- 46.Titze, I. R. (2006). The Myo-elastic Aerodynamic Theory of Phonation (National Center for Voice and Speech, Salt Lake City, UT: ), Chap. 9, pp. 253–284 [Google Scholar]
- 47.Titze, I. R. (2008). “Nonlinear source-filter coupling in phonation: Theory,” J. Acoust. Soc. Am. 123(5), 2733–2749 10.1121/1.2832337 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Titze, I. R. (2012). “Why lions roar like babies cry,” Phys. World 25(11), 52–53 [Google Scholar]
- 49.Titze, I. R. , Jiang, J. J. , and Druker, D. (1988). “Preliminaries to the body-cover theory of pitch control,” J. Voice 1(4), 314–319 10.1016/S0892-1997(88)80004-3 [DOI] [Google Scholar]
- 50.Titze, I. R. , Schmidt, S. S. , and Titze, M. R. (1995). “Phonation threshold pressure in a physical model of the vocal fold mucosa,” J. Acoust. Soc. Am. 97(5), 3080–3084 10.1121/1.411870 [DOI] [PubMed] [Google Scholar]
- 51.Titze, I. R. , and Verdolini Abbott, K. (2012). Vocology: The Science and Practice of Voice Habilitation (National Center for Voice and Speech, Salt Lake City, UT: ). [Google Scholar]
- 52.Tokuda, I. T. , Zemke, M., Kob, M., and Herzel, H. (2010). “Biomechanical modeling of register transitions and the role of vocal tract resonators,” J. Acoust. Soc. Am. 127(3), 1528–1536 10.1121/1.3299201 [DOI] [PubMed] [Google Scholar]
- 53.Van den Berg, J. W. (1960). “Vocal ligaments versus registers,” Curr. Prob. Phoniatrics Logopedics 1, 19–34 [Google Scholar]
- 54.Vennard, W. (1967). Singing: The Mechanism and the Technic (Carl Fischer Music Dist., New York: ), Chap. 4, pp. 52–143 [Google Scholar]
- 55.Vilkman, E., Alku, P., and Laukkanen, A. M. (1995). “Vocal-fold collision mass as a differentiator between registers in the low-pitch range,” J. Voice 9(1), 66–73 10.1016/S0892-1997(05)80224-3 [DOI] [PubMed] [Google Scholar]
- 56.Wolk, L., Abdelli-Berruh, N. B. , and Slavin, D. (2012). “Habitual use of vocal fry in young adult female speakers,” J. Voice 26(3), e111–e116 10.1016/j.jvoice.2011.04.007 [DOI] [PubMed] [Google Scholar]
- 57.Zhang, Z., Neubauer, J., and Berry, D. A. (2006). “The influence of subglottal acoustics on laboratory models of phonation,” J. Acoust. Soc. Am. 120(3), 1558–1569 10.1121/1.2225682 [DOI] [PubMed] [Google Scholar]