SUMMARY
To explore the link between bioenergetics and motor neuron degeneration, we used a computational model in which detailed morphology and ion conductance are paired with intracellular ATP production and consumption. We found that reduced ATP availability increases the metabolic cost of a single action potential and disrupts K+/Na+ homeostasis, resulting in a chronic depolarization. The magnitude of the ATP shortage at which this ionic instability occurs depends on the morphology and intrinsic conductance characteristic of the neuron. If ATP shortage is confined to the distal part of the axon, the ensuing local ionic instability eventually spreads to the whole neuron and involves fasciculation-like spiking events. A shortage of ATP also causes a rise in intracellular calcium. Our modeling work supports the notion that mitochondrial dysfunction can account for salient features of the paralytic disorder amyotrophic lateral sclerosis, including motor neuron hyperexcitability, fasciculation, and differential vulnerability of motor neuron subpopulations.
INTRODUCTION
Amyotrophic lateral sclerosis (ALS) is a fatal adult-onset neurodegenerative disorder characterized by a loss of motor neurons, leading to muscle wasting and weakness (Rowland, 2010). In ALS patients, however, not all motor neurons are equally susceptible to the disease process (Kanning et al., 2010). For instance, in ALS, motor neurons that innervate the fast-fatigable (FF) motor units are affected early whereas those that innervate the slow (S) motor units are affected late (Kanning et al., 2010). The basis for this differential susceptibility remains elusive, but an attractive possibility may lie in the variable bioenergetic needs of distinct subsets of motor neurons.
The human brain accounts for only ~2% of body mass, and yet utilizes ~20% of the O2 consumed by the body at rest (Harris et al., 2012). This disproportionally high energy requirement of the brain is attributed primarily to ATP-demanding processes in neurons. These include the maintenance of the resting potential, transport of metabolites along axonal or dendritic processes, synaptic function with neurotransmitter release, postsynaptic currents (Harris et al., 2012), and synaptic vesicle cycling (Rangaraju et al., 2014). In agreement with the theoretical brain energy budget model of Harris et al.(2012), we assume that reversing the ion flux and maintaining the homeostasis of ionic gradients across the plasma membrane and the endoplasmic reticulum (ER) are the most ATP-consuming processes in neurons.
Ion pumps are distributed over the entire cell membrane, but are particularly clustered in areas with high ion fluxes, such as the soma, the nodes of Ranvier, and at pre- and postsynaptic sites. Motor neurons are extremely active cells, continuously firing APs to maintain tonic posture or to generate the complex firing patterns needed for muscle contraction during specific movements. Motor neurons are large (in terms of membrane surface area) with long axons, adding to the metabolic burden that must be met by ATP produced both via oxidative phosphorylation and glycolysis (Hall et al., 2012; Rangaraju et al., 2014). Despite the large reservoir of neuronal ATP, especially at synapses (Rangaraju et al., 2014), reduced mitochondrial and/or glycolytic function will modify the electrical properties of motor neurons when ATP availability becomes insufficient to allow ion pumps to maintain the appropriate gradients. The relationships between electrical activity, changes in excitability, and intracellular machinery involving calcium (Ca++) and ATP are a focus of attention in the field of ALS pathophysiology (Fritz et al., 2013; Saxena et al., 2013).
We use a modeling approach to explore the link between electrical activity and susceptibility to degeneration due to insufficient levels of metabolic energy. We construct a realistic computer model that merges classical Hodgkin-Huxley type conductances and multi-compartmental modeling, including computations of ionexchange and energy requirements for ion pumps, with biochemical modeling of ATP production and consumption. Using this model, we find that a reduction in ATP availability can place motor neurons in a physiological state that leads to prolonged depolarization, massive influx of Ca++, and ultimately may cause cell death. We show that this process involves a positive feedback loop in which small deficits in available ATP lead to small ion imbalances that, in turn, cause a higher energy demand on the neuron, leading to worse imbalances. The energy production deficit can be localized to the axon terminal and still lead to a lethal cascade through a retrograde spread that ultimately reaches the entire cell. We also find that models built to match the more vulnerable (FF) motor neurons, enter this catastrophic cycle at milder bioenergetic deficiencies than models based on less vulnerable (S) motor neurons. Thus, this study provides theoretical evidence that bioenergetics may be a critical determinant of motor neuron differential susceptibility in ALS. We infer from our findings that any therapeutic strategies aimed at supporting bioenergetics may enhance the capacity of motor neurons to withstand pathological insults, thereby prolonging the life span of ALS patients.
RESULTS
A computer model linking electrical activity and ATP pathways
To explore the link between electrical and metabolic activities in motor neurons, we constructed a model that includes ion pumps and exchangers as well as metabolic pathways affecting ATP levels. The multi-compartmental neuron model was based on a Neurolucida reconstruction of a cat motor neuron (Alvarez et al., 1998), to which we added a 100 mm long unmyelinated axon (Figure 1A; Methods). The type and distribution of the ion conductances in the model are based on validated models and published voltage-clamp data (Araki and Terzuolo, 1962; Barrett et al., 1980; Powers et al., 2012), see also models from (Dai et al., 2002; Powers et al., 2012; Heckman and Binder, 1993).
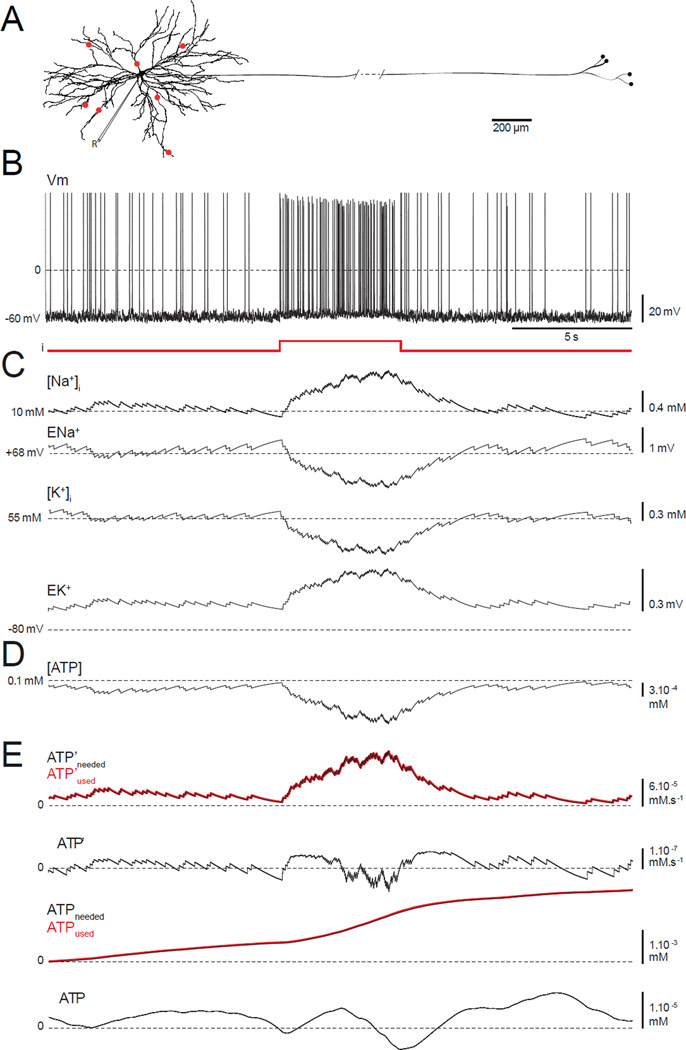
FIGURE 1. A model neuron combining conductance-based electrical activity, ion pumps, and pathways for ATP production and consumption.
(A) Model morphology based on Neuro Lucida reconstruction of a cat motor neuron. Red dots = synaptic inputs. “R” is for recording and shows where the measurements are made from.(B) Spontaneous membrane firing due to synaptic background. At 10 s, a 5 s depolarizing pulse is injected.(C) Evolution of the intracellular [Na+] ([Na+]i), the Na+ reversal potential (ENa+), the intracellular [K+] ([K+]i) and the K+ reversal potential (EK+).(D) Intracellular [ATP].(E) The amount of ATP used and needed per unit time, ATP’used (red line) and ATP’needed (black line). ΔATP’ is the difference between these quantities, ATPused and ATPneeded are their cumulative values, and ΔATP is the difference between ATPused and ATPneeded. ΔATP’ and ΔATP both fluctuate around 0, indicating that the model is stable.
We are interested in the energy demands for maintaining ion concentration gradients. Thus, the model includes the plasma membrane Na+/K+ ATPases and a series of Ca++ mechanisms: the plasma membrane Ca++ ATPase (PMCA), the sarcoplasmic Ca++ ATPase (SERCA), the plasma and mitochondrial Na+/Ca++ exchanger (NCX), and the Ca++ mitochondrial uniporter (MCU) (Methods). To drive the ATPases, we included a simple model of ATP production (Methods), and we modified the rate of this production to mimic pathological states.
Our multi-compartment model neuron consists of a 60 µm diameter soma, a complex dendritic tree, and an axon with distal branching (Figure 1A). Our first objective was to determine whether the model reliably reproduces the activity of a healthy motor neuron in vivo during tonic and phasic muscular movements. To mimic background synaptic input, we used a combination of excitatory and inhibitory drive (Methods) through synapses located at different locations on the dendrite (red dots, Figure 1A). Phasic activation of the motor neuron, such as that during voluntary movement, was reproduced by injecting a 1 nA current pulse into the soma. Under the influence of randomly generated background input, the model neuron fires at an average rate of 2–4 Hz, and with additional injected current the firing rate increases to 12–14 Hz (Figure 1B). Because we keep track of internal ion concentrations and included ion pumps in our model, we could monitor how ion concentrations return to baseline levels after high-frequency firing (Figure 1C). During high-frequency firing, the intra-neuronal Na+ concentration, [Na+], rises, causing the Na+ reversal potential, ENa, to decrease. Simultaneously, the [K+] decreases, and EK increases. These changes engage the Na+/K+ ATPase, which restores the baseline concentrations (Figure 1C). The energy required to drive this pump lowers [ATP] (Figure 1D) but, because we are modeling a healthy neuron, [ATP] rapidly returns to baseline through the conversion of ADP to ATP by the mitochondrial oxidative phosphorylation included in the model.
The “healthy” state of our model neuron can be revealed more clearly by comparing the rate of ATP consumption at any given time with the rate required for ion concentration homeostasis. To quantify this comparison, we computed the rate at which ATP is actually consumed by the Na+/K+ pump (denoted by ATP’used) and the rate at which ATP should be consumed to keep [Na+] at its baseline level of 10 mM despite the firing (denoted ATP’needed) (Methods). If we compute these quantities for the soma only, we find that ATP’used and ATP’needed overlap (red and black lines, first trace, Figure 1E), so ATP’needed - ATP’used (denoted by ΔATP’) is small (~10−7 mM.s−1) before, during and after the input current pulse (second trace, Figure 1E). Time integrals of the two ATP rates and their difference (denoted by ATPused, ATPneeded, and ΔATP; third and fourth traces, Figure 1E) show that the total amount of ATP consumed (ATPused) by the pump over the duration of the activity (right extremity of the plot) is 2.16×10−3 mM. Furthermore, the strong match between ATPused and ATPneeded and the small ΔATP value indicate that ATP production in the model neuron can fulfill the demands of repetitive firing. A larger positive ΔATP would have mean that the Na+/K+ pumps do not consume enough ATP to restore [Na+] and [K+] to their equilibrium values, possibly implying the existence of a bioenergetics problem. Longer simulations (not shown) indicate that, as in Figure 1, the model is stable, in that ion and ATP concentrations return to baseline after any stimulation, and the actual amount of ATP consumed always matches the computed amount necessary to drive the Na+/K+ pumps.
A deadly loop: Reducing ATP production increases ATP demand
To mimic a mitochondrial dysfunction, we reduced the steady-state ATP concentration ([ATP]ss) that our model neuron maintains. This reduces the rate at which the neuron can drive its Na+/K+ pumps. A reduction in [ATP]ss from 0.1 mM to 0.01 mM has no effect on the spontaneous firing pattern of the neuron over the time scale shown in Figures 1 and 2, but even a single injected current pulse identical to that shown in Figure 1, increases the peak ATP demand to a level beyond the capacities of the model neuron, introducing a metabolic instability (Figure 2B). After the current pulse shown in Figure 2A, [Na+] and [K+], as well as ENa and EK, do not return to baseline, but instead start to drift (Figure 2B). The root of this problem lies in the difference between the amount of ATP needed to drive the Na+/K+ pumps and the amount actually used. The curve for ATP’used is slightly offset compared to ATP’needed, resulting in a positive ΔATP’ after the pulse (Figure 2B). Similarly, over time, ATPused lags below ATPneeded resulting in an ever-increasing value of ΔATP (Figure 2B). Clearly, ATP production is not sufficient to satisfy the demands imposed by the Na+/K+ pumps. Thus, by the end of the time period shown in Figure 2, the neuron is in a state in which the ion pumps have failed to compensate for the Na+ accumulation and the K+ loss due to APs and, rather than being restored to equilibrium, the reversal potentials move toward 0. The model neuron is in an unstable elecrophysiological state triggered by the conjunction of lower [ATP]ss and a firing rate that exceeded a critical value.
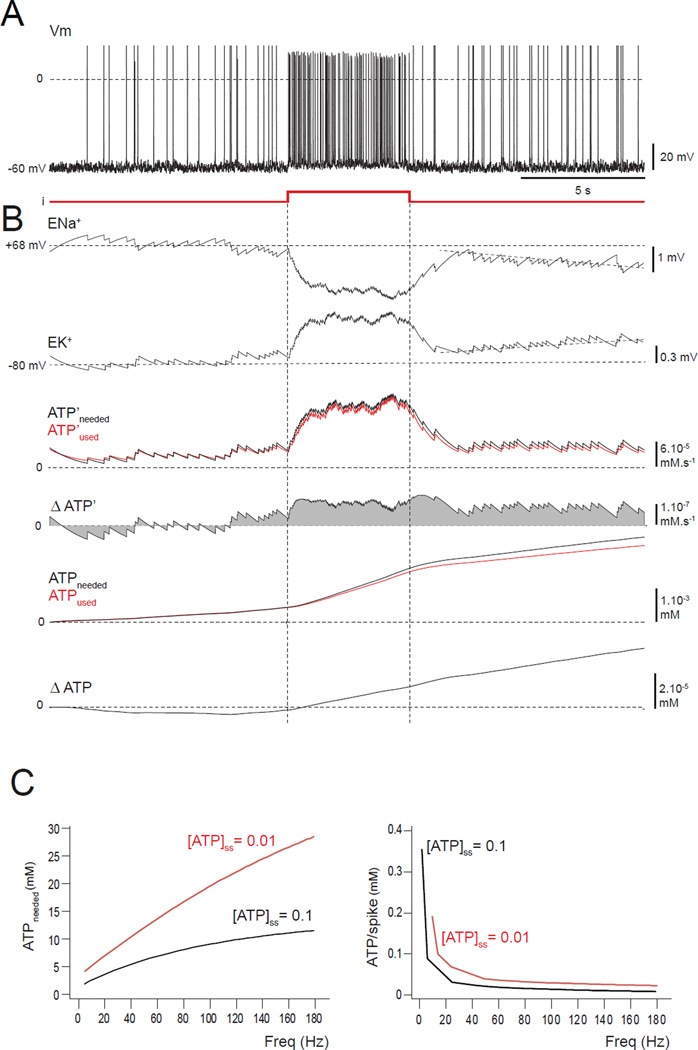
FIGURE 2. A neuron with a small ATP reduction is stable for low-frequency firing but a brief input pulse triggers instability.
(A–C) Model is set with a ten-fold reduction in [ATP]ss, i.e. 0.01 mM.(A) Spiking appears normal before, during and after a brief depolarizing pulse. (B) The reversal potentials ENa+ and EK+ start to drift (tilted dashed lines) from their stable values after the higher-frequency firing, indicating the triggering of an instability. The instability results from the difference between the ATP’used and ATP’needed (red and the black curves) after the pulse, the separation of ATPused and ATPneeded, the positive value of ΔATP’, and the increasing ΔATP. (C) For a total simulated run of 25 s, the amount of ATP needed by the entire neuron was measured for different firing frequencies. When the ATP level is normal ([ATP]ss = 0.1 mM; black curve), the ATP needed (left panel) is lower by a factor of about 3 than with a ten-fold reduction ([ATP]ss = 0.01 mM; red curve). Similar results were found for the ATP needed per AP (right panel). Note that APs are less costly for high-frequency firing.
To quantify this metabolic instability for the whole neuron, we plot the total cost in ATP of driving the pumps for the duration of a run similar to that of Figure 2 for different values of injected current that produce different firing rates during the period of stimulation. The black line in Figure 2C shows the result with the normal level of ATP production ([ATP]ss=0.1 mM), and the red curve corresponds to the lowered level ([ATP]ss=0.01 mM). In both cases, the ATP demand rises for increasing firing rate, but the demand for the model with lowered ATP is both higher and rises more rapidly (Figure 2C, left panel; note that these quantities are larger than those in Figure 2B, because they refer to the whole neuron, not just the soma). Interestingly, the ATP cost per spike (i.e. ATP cost divided by the number of spikes produced) declines as a function of firing rate, but it is always higher in the ATP-deficient model than in the “healthy” model (Figure 2C, right panel). Thus, a deficit in [ATP]ss makes the model neuron even less able to provide the energy required to recover from firing.
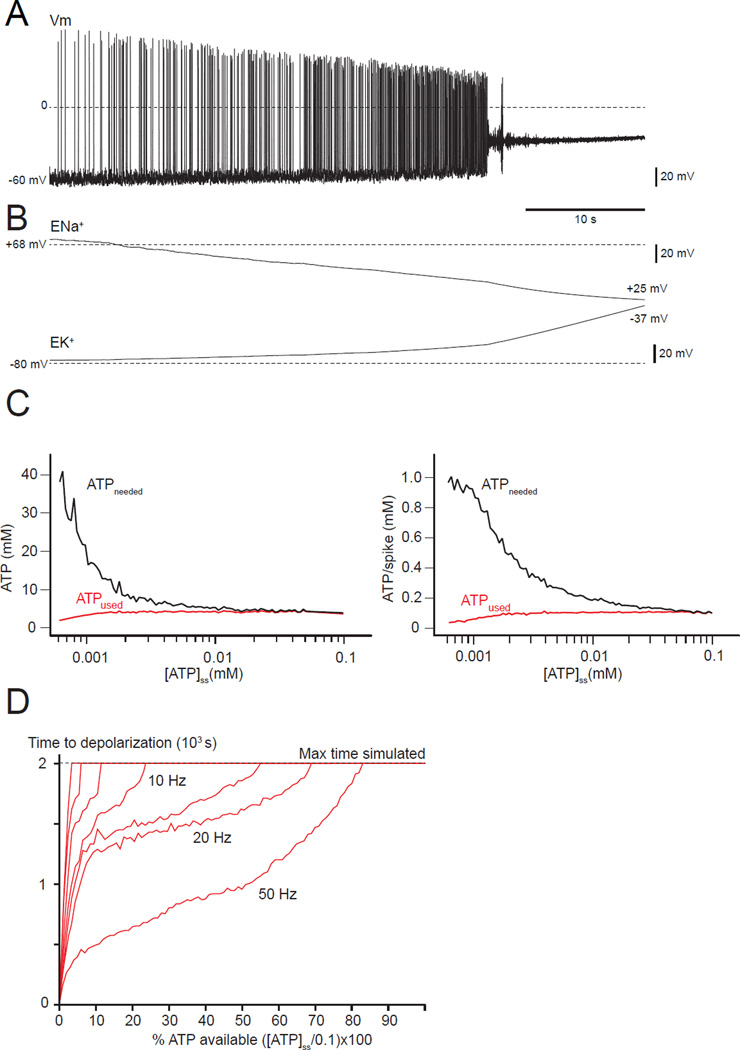
Next, we further reduced [ATP]ss to 0.001 mM, and simulated over a longer period of time (i.e. 50 s). The model neuron starts firing at the typical background rate, but then steadily depolarizes and fires increasingly rapidly as the reversal potentials ENa and EK start drifting toward 0 (Figure 3A). Eventually, the depolarization becomes so high that APs can no longer be generated because of inactivation of the fast Na+ conductance. The steadily increasing depolarization results from a rise in EK from −80 mV to −37 mV (Figure 3B). This decreases the outward K+ current, depolarizing the cell. Simultaneously, ENa falls from +68 mV to +25 mV, reducing the Na+ current and thus the height of the spikes. During this time, the rate of ATP consumed by the Na+/K+ pump falls further behind what is needed, resulting in an ever-growing total ATP deficit. Remarkably, ending the firing does not ameliorate the problem (Figure 3A), but instead the depolarized state further increases the energy demand. The cell is thus engaged in a vicious cycle in which depolarization opens most of the ion channels worsening the pump deficit, and the model neuron cannot recover spontaneously.
FIGURE 3. A deadly loop: A neuron with a severe deficit in [ATP]ss (0.001 mM) irreversibly depolarizes and further increases its energy needs.
(A) The membrane potential is unstable even for spontaneous activity, showing a progressive depolarization until APs stop due to sodium channel inactivation. (B) ENa+ and EK+ drift toward 0 as a consequence of the loss of ion gradients linked to the reduction in ATP-ase pumping. (C) ATPused and ATPneeded versus the ATP level ([ATP]ss). Lower [ATP]ss increases the amount of ATP needed (left panel), but not the amount used. The right panel shows the cost of a single AP for different levels of [ATP]ss. The amount of ATP needed for a single spike is greater when the ATP availability is lower.(D) Relationship between ATP deficit (x-axis), time to depolarization (y-axis) and average frequency firing (red lines between 10Hz and 50 Hz). The horizontal line at 2.0×103 s represents the longest simulations explored. Even for low ATP deficit, a depolarization can occur after a very long time, and is even more likely if the average firing rate is high.
We also compared the cost of running the Na+/K+ pump for 10 s across the entire neuron at a stable 5 Hz firing, and the cost per AP for different levels of [ATP]ss (Figure 3C). The less ATP the neuron produces, the higher the metabolic demand, illustrating the fundamental instability that leads to the depolarization block seen in Figure 3A. For this figure, we intentionally used an extreme ATP deficit that led to a complete depolarization as described in Figure 3A within 10 s. In a disease such as ALS, motor neuron death occurs years after birth (Kanning et al., 2010), so we explored the relationships between the time of occurrence of the potential deadly depolarization, the level of the ATP deficit, and the firing rate. The time at which depolarization block occurs depends on the ATP depletion and the firing rate (Figure 3D). Complete depolarization can occur for ATP depletion as small as 15% if the firing rate and therefore the ATP consumption are high enough. The maximum simulation time of 2,000 s (45 min run time) limited this exploration, but we extrapolate that, at a firing rate of ~20 Hz, a deadly depolarization could arise at times greater than 2,000 s for ATP depletions < 15%.
Neurons with a higher ATP demand are more vulnerable
Because the ATP cost of an AP is related to the membrane current, each neuron, having a particular morphology and set of intrinsic conductance, has its own energy demand. Energy profiles have been estimated theoretically and studied experimentally for neurons in different species or different parts of the brain (Hasenstaub et al., 2010). The energy cost per AP in vertebrates was found to differ by up to 10 fold, depending on the neuron type (Sengupta et al., 2010). We explore the hypothesis that there is a relationship between the vulnerability of a neuron to energy-related death and its energy consumption profile by constructing realistic models of FF and S motor neurons based on morphological reconstructions from Camera Lucida techniques and measured conductance distributions (Methods).
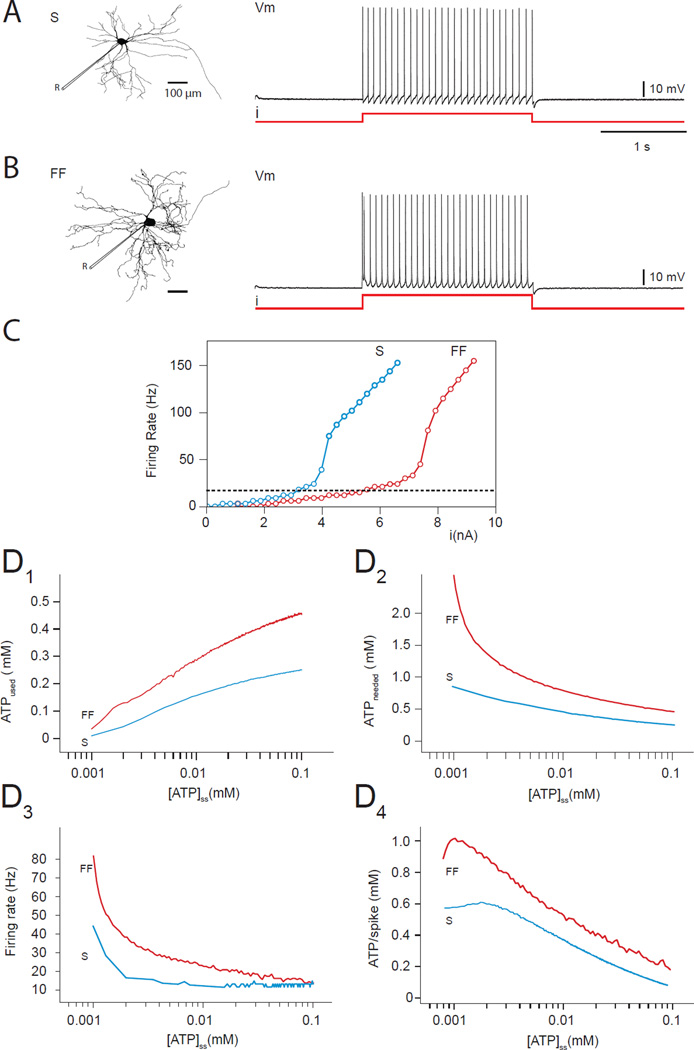
As indicated in Kanning et al. (2010), S motor neurons have a smaller soma and axon size, as well as less dendritic branching and fewer neuromuscular terminals than FF motor neurons (Figure 4A and 4B). Thus, S motor neurons have ~20% less cellular membrane than FF neurons and their electrical properties, characterized by the relationship between injected current and firing rate (Figure 4C) show a lower threshold than for FF motor neurons due to their higher input resistance and different distribution of active conductance (Button et al., 2006). Because of their lower threshold, S motor neurons are recruited earlier than FF motor neurons during muscle contraction (Kernell et al., 1999). To explore the effects of ATP availability in both cell types, we injected a 2s step of current tuned so that each cell fires at ~15 Hz (Figures 4A,B). We then reduced the ATP production capacity by lowering [ATP]ss in each compartment of both the FF and S models, and measured the relationship between [ATP]ss and ATP consumption. Figures 4D1 and 4D2 show the expected decreasing value of ATPused and increasing ATPneeded as a function of the decrease of [ATP]ss (see Figure 3C for comparison). Note that the energy demand on the FF motor neuron is considerably larger than on the S for a similar discharge. Not only is their basal requirement for ATP higher, FF motor neurons are also considerably more sensitive to ATP imbalances than S motor neurons, and thus more vulnerable to the instability seen in Figure 3. FF motor neurons fire more rapidly than S motor neurons (Figure 4D3), but their ATP demand is still greater when normalized to the number of APs emitted (Figure 4D4). These results suggest that even small differences in morphology and electrical properties can make neurons differently vulnerable to metabolic energy dysfunction, even if their firing rates do not differ appreciably.
FIGURE 4. FF motor neurons firing consume more than S neuron firing.
(A, B) Morphologies and firing patterns of S (A) and FF (B) motor neurons. “R” is for recording and shows where the measurements are made from.(C) Firing rate versus injected current for S (blue curve) and FF (red curve) neurons.(D) In both cell types, a reduction in [ATP]ss leads to a reduction in the amount of ATP used by the neuron (D1), but an increase in the amount of ATP needed (D2). The FF neuron both uses and needs more ATP than the S neuron and, in particular, its ATP needs are more sensitive to low levels of [ATP]ss. As [ATP]ss is reduced, both neurons depolarize and their firing rate increases (D3) with the FF neuron being more sensitive. As a consequence, the ATP needed for a single AP is higher for the FF motor neuron than for the S neuron (D4).
Local energy failure, hyperexcitability, and ectopic fasciculation-like potentials
Altered mitochondrial function in ALS is thought to occur early but also locally within motor neurons, associated with an early defect in the fast axonal transport (Bilsland et al., 2010). The latter may affect the mitochondria distribution, leading to abnormal accumulation of mitochondria in the soma and depletion in the axon (Knott et al., 2008). Analysis of mouse models of ALS has also shown that motor neuron death begins with distal axonal degeneration and dismantlement of the neuromuscular junction (Kanning et al., 2010). We thus investigated the consequence of a local energy failure in the distal axon, rather than the global deficits considered in previous sections.
To mimic the depletion of mitochondria in the axon, we produced a gradient of ATP availability by setting [ATP]ss to a normal value of 0.1 mM in the soma, but steadily reducing [ATP]ss away from the soma down to a value of 0.001 mM at the distal end of the axon (Figures 5A and 5B). Of note, we have assumed the ATP deficit originates from a mitochondrial defect, hence purposely omitting the contribution of glycolysis (Hall et al., 2012; Rangaraju et al., 2014).
FIGURE 5. Local energy failure results in local depolarization and a hyperexcitability.
(A) Morphology of the model with a 100 mm axon. “R” is for recording and shows where the measurements are made from.(B) We imposed values of [ATP]ss that decrease from 0.1 to 0.001 mM with distance down the axon.(C) Initially, depolarization of the soma triggers APs that travel from the soma to the distal axon (anterograde). Over time, instability arises, leading to distal depolarization and distally generated APs that travel back toward the soma (retrograde). When both ends (soma and distal) are firing, collisions occur (collision). (D) Over a longer time scale, repeated depolarization leads to AP block in the distal axon (green line) and depolarization of the soma (black line).(E) The cumulative ATP deficit (ΔATP) along the axonal length is positive distally but, for a time at least, the soma can remain balanced with ΔATP near zero.
The model neuron in the distally depleted state was activated using a step current injected into the soma to trigger somatic spikes that propagate in the usual anterograde manner to the distal axon, where they arrive after a conduction delay (Figure 5C, first third of run). As the firing continues, however, a local depolarization develops in the distal axon due to the local shortage of ATP. This depolarization is linked to a progressive but local reduction of the ion gradients and change in ENA and EK, as seen in previous figures. After ~10 s, the distal depolarization is sufficient to trigger APs that propagate from the distal axon to the soma (Figure 5C). Those retrograde-propagated spikes occasionally trigger a secondary spike in the soma, similar to an F-wave seen in EMGs, and collision phenomena also occur (Figure 5C). Distal, ectopic spike generation slowly increases in frequency as the worsening pump deficit increases the depolarization caused by the degradation of the reversal potentials. This distal hyperexcitability and the related events are reminiscent of fasciculation observed in ALS patients (de Carvalho and Swash, 2004).
If we look over a longer time interval (Fig 5D, upper panel), APs initiated at the soma initiate a local energy crisis in which the axon depolarizes, reaches the threshold for spiking, and fires APs at an increasing frequency until inactivation of the Na+ current stops spiking, though the axon remains in a depolarized state. The spatial profile of the ATP deficit, ΔATP, shows a large positive value (indicating an ATP deficit) in the region of the distal axon reflecting this problem (Figure 5E). Thus, local as well as global deficits in ATP production can produce neuronal pathological changes. This local energy failure combined with a spreading deficit and dysfunction provides a better model of motor neuron damage in ALS than the global scenario considered previously.
Local energy failure and global neuronal energetics
Problems caused by a local ATP deficit are likely to spread as highly concentrated ions diffuse from the affected region to nearby compartments and eventually throughout the neuron. An indication of this propagation can already be seen in Figure 5E, where positive values of ΔATP occur a considerably distance back from the end of the axon. We examined this issue further by running the model studied in the previous section for longer times.
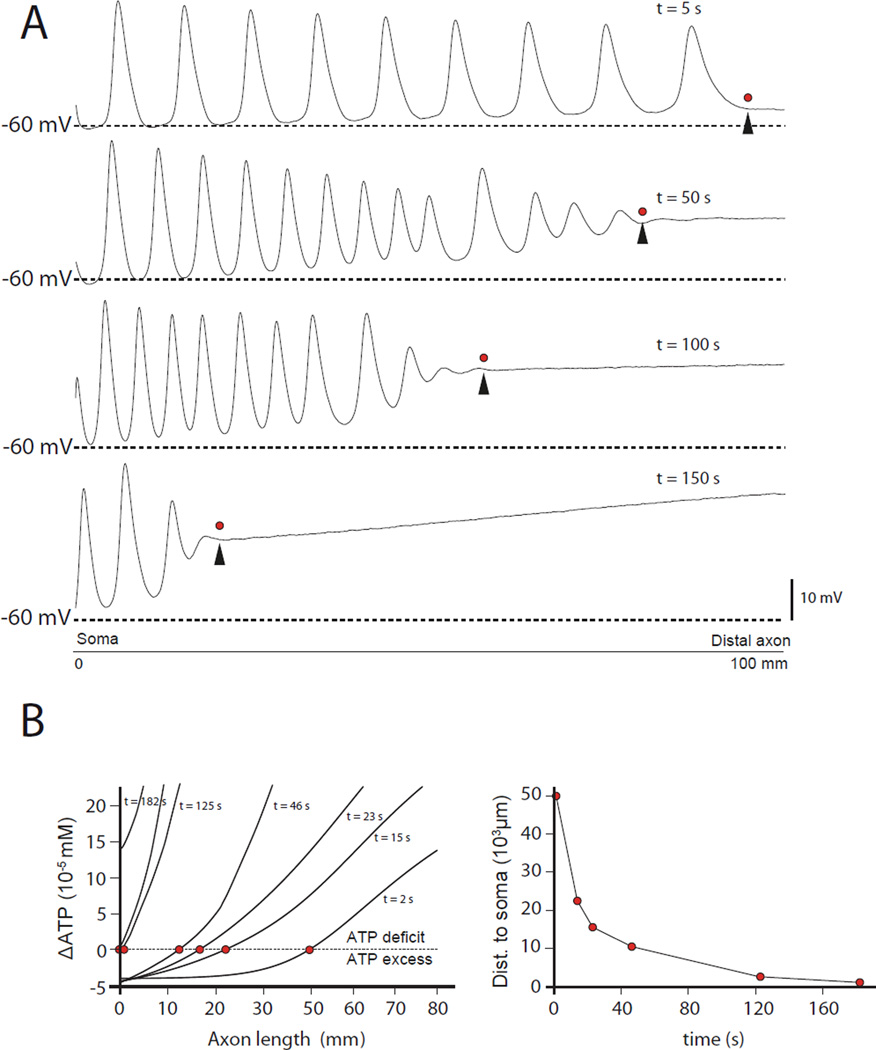
The top panel of Figure 6A shows a series of APs that originate in the distal axon (at the location of the arrowhead), and propagate antidromically (from right to left) back to the soma. These arise from the ATP deficit in the distal axon, as in Figure 5. Over time, the point along the axon where these spikes originate moves steadily inward toward the soma (Figure 6A). Regions of the axon more distal than the ectopic AP initiation zone are chronically depolarized. After 150 s, most of the axon is in this depolarized state (Figure 6A, bottom panel). Figure 6B (left panel) shows the evolution of the total ΔATP profile over time. The red dots indicate the zero crossing point (the equilibrium), which slowly moves towards the soma (Figure 6B right panel). These results show that an energy crisis initially localized at the distal end of the axon can propagate in a retrograde direction and ultimately spread to the whole neuron.
FIGURE 6. Spontaneous retrograde propagation of the distal depolarization towards the soma.
(A) Membrane potential along the axon. The distal axon initially generates APs locally (top panel, arrow head shows the initiation site) that move toward the soma (leftward). Over time, the initiation site moves inward along the axon (panels 2–4), with the membrane potential distal to the initiation site remaining steadily depolarized. (B) Left panel: Each curve is a profile of ΔATP at a given time, plotted against the distance to the soma. The red dots show the location of the zero values (balance between ATP needed and ATP used) along the axonal length. The right panel plots the balance point (red dots) location over time, indicating a spread of the ATP deficit from its distal origin towards the soma.
Consequences of ATP shortage for intra-cellular calcium dynamics
Regulation of cytosol [Ca++] involves many pumps and exchangers, some of which do not require ATP. We included three generic mechanisms of intracytosolic Ca++ regulation in our model: (1) P-type Ca++ ATPases, which pump Ca++ either into the ER, SERCA, or into the extracellular space, PMCA (Palmgren and Nissen, 2011); (2) mitochondrial and plasmatic NCX (Boyman et al., 2013), which extrude cytosolic Ca++ without ATP consumption (Berridge, 1998; Clapham, 2007; Grienberger and Konnerth, 2012); and (3) MCU, a specific Ca++ channel driven by the proton-motive driving force and hence depending on the mitochondrial transmembrane potential ΔΨ, but not on ATP (Raffaello et al., 2012; Williams et al., 2013).
In Figure 7A, we display [Ca++] after a 2 s simulation during which the model fired tonically under the influence of synaptic inputs (marked as red dots). Under standard conditions (Figure 7A1), the dominant Ca++ extrusion mechanism is the ATPases (both PMCA and SERCA). We studied the effect of bioenergetic impairment on cytosolic Ca++ by comparing different mitochondrial pathological situations parameterized by [ATP]ss and ΔΨ, operating under the premise that mitochondrial defects are the primary cause of ATP deficits. First, we emulated a defect in ATP production without alteration of ΔΨ on which MCU function depends (Williams et al., 2013) and as seen in an impairment in mitochondrial F0/F1 ATP synthase function (Schon and Przedborski, 2011). To do this, we reduced ATP production (either to [ATP]ss=0.001 in Figure 7A2 or [ATP]ss=0.01 in Figure 7B1) while maintaining ΔΨ at 180 mV. This modification reduces the fraction of Ca++ extruded by the Ca++ ATPases so that, in the more extreme case (Figure 7A2), it is no longer the leading mechanism of extrusion. Even with the smaller reduction in [ATP]ss (Figure 7B1), we see an increase in intracytosolic Ca++ despite the increased contributions of the NCXs and MCU (Figure 7B1). Second, we emulated a defect in bioenergetics in which both [ATP]ss and ΔΨ were reduced, as seen in many mitochondrial diseases (DiMauro and Schon, 2003). In this case, the increase in intracytosolic Ca++ is even more pronounced, and the relative contributions of ATPases and MCU are reduced while that of the NCXs increases (Figure 7B2). Third, we explored the consequences of removing mitochondria in one specific dendrite (marked by the arrow in Figure 7C). In this extreme case, this region of the neuron relies entirely on plasmatic NCX, causing a dramatic increase in intracytosolic Ca++ (Figure 7C).
FIGURE 7. Consequence of ATP deficit on the intracellular calcium concentration.
(A–C) Average [Ca++] after 2 s of tonic firing in the model driven by the synaptic inputs marked as red dots. The histograms show the relative contribution of each intra-cytosolic Ca++ regulation mechanism, with the Ca++ ATPases in red, the NCXs in green, and the MCU in blue.(A) Lowering the ATP availability mainly affects PMCA and SERCA, and leads to a large increase in the average [Ca++]. The ATPase deficit is not compensated by the intrinsic mitochondrial ATP-independent buffer mechanisms, the NCX exchanger or the MCU. (B) Although important, the MCU intrinsic mitochondrial buffer channel is not alone capable of compensating the loss of ATPase activity due to low ATP production, even for a smaller deficit than in A, with or without a modification of ΔΨ. (C) When mitochondria are removed entirely from a single dendrite (white arrow), the only buffering mechanism left is the NCX exchanger and it cannot preserve the Ca++ homeostasis in that region. Here histograms show Ca++ extrusion only in the affected compartment. (D) The dynamic range of the [Ca++] between the resting level and the peak level in some microdomain when an AP is fired for different [ATP]ss and ΔΨ, showing how mitochondria is essential for Ca++ homeostasis mainly through ATPase function and to a lesser extent, the NCX exchangers and the MCU.
With bioenergetics defects, hot spots of Ca++ accumulation arise, initially at the dendritic sites of synapses (Figure 7) but then spreading through the cell including the soma (which does not receive any synaptic input in this model). At first, the rise in [Ca++] occurs because of reduced Ca++ ATPase activity but, with the progressive loss of Na+ and K+ gradients and the induced depolarization, voltage-gated Ca++ conductances are activated, resulting in a large Ca++ influx. In addition, the rise in [Na+] slows the rate of Na+/Ca++ exchange and if [Na+] is high enough, the NCX pumps can even work in a reverse mode, actively pumping Ca++ into the cell.
As shown in Figure 7D, where ranges of [Ca++] from resting to peak are displayed for a number of levels of [ATP]ss, intrinsic mitochondrial buffering capacity and Ca++ dishomeostasis increases and spreads throughout the neurons as mitochondrial function is reduced. This occurs through reduction of ATPase pumps but also through MCU reduction, depending on the mechanism of mitochondrial failure (relative preservation of ΔΨ, through decoupling mechanisms, or loss of ΔΨ, through dysfunction in the respiratory chain complex upstream of the ATP synthase).
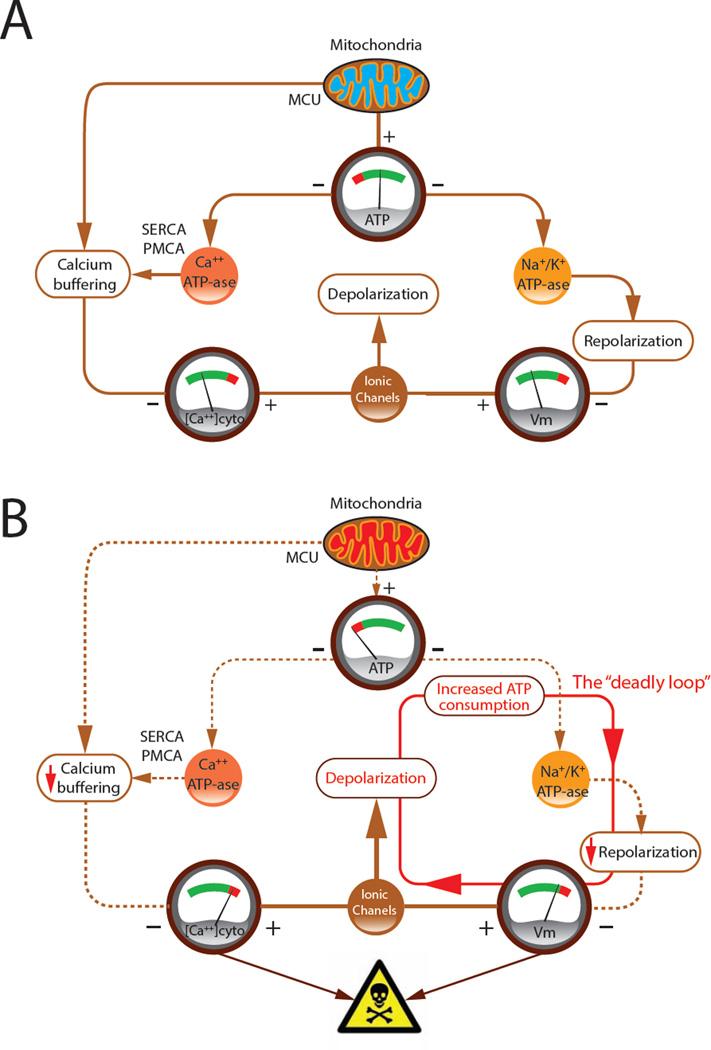
Our model indicates that under normal conditions, mitochondria maintain an adequate [ATP]ss that supports the activity of ATPases for membrane-potential homeostasis and the maintenance of a normal cytosolic [Ca++] (Figure 8A). Membrane-potential homeostasis contributes to Ca++ homeostasis by preventing excessive depolarization and extended periods of high-rate firing, both of which activate voltage-gated Ca++ conductances. Reduced mitochondrial ATP production causes a positive feedback loop in which membrane potential depolarization increases the rate of ATP consumption and of firing, leading to increased Ca++ influx (Figure 8B). This higher influx along with the reduced Ca++ ATPase activity due to the ATP shortage causes the cytosolic [Ca++] to rise. The end result is a deadly loop that we believe is likely to be lethal to the neuron.
FIGURE 8. A schematic diagram of the consequence of an ATP deficit.
(A) The effects of mitochondrial ATP production acting through ATPases on the resting membrane potential and intracellular [Ca++]. VGCC indicates voltage-gated Ca++ conductances. (B) Low [ATP]ss due to mitochondrial disfunction engages a positive feedback loop that leads to increased ATP consumption and even lower [ATP]. These problems lead to pathologically high [Ca++].
DISCUSSION
Computer modeling has advantages in putting together complex interacting mechanisms and in exploring consequences of specific parameter combinations. It is a particularly useful tool for visualizing the results of a basic underlying hypothesis. Our model combines classical Hodgkin-Huxley (1952) multi-compartment modeling with a description of some, but of course not all, of the important metabolic pathways linked to energy production, energy consumption and ion homeostasis. Although others have addressed the issue of the energy cost of firing in different types of neurons (Aiello and Bach-y-Rita, 2000, Hasenstaub et al., 2010, Venkateswaran, 2012) our work represents, to our knowledge, the first cell-based, biologically realistic computer model related to a neurodegenerative disease.
Because an ATP imbalance is pivotal for the pathogenic scenario we consider and oxidative phosphorylation produces most of the ATP in active neurons (Hall et al., 2012; Rangaraju et al., 2014), it is worth discussing the state of mitochondria in ALS. Striking morphological and functional alterations in mitochondria from postmortem spinal cord samples of sporadic ALS patients have been reported (Borthwick et al., 1999; Hirano et al., 1984; Sasaki and Iwata, 2007). ALS-causing genes in superoxide dismutase-1 (SOD1), TAR DNA-binding protein 43, and fused in sarcoma/translated in liposarcoma cause comparable mitochondrial abnormalities and altered distributions in mice (Tan et al., 2014). Furthermore, VCP/p97 mutations, which are found in ~2% of familial ALS patients (Johnson et al., 2010), can cause mitochondrial uncoupling and an ensuing decreased ATP production in patients’ fibroblasts (Bartolome et al., 2013). More speculative are the ALS-causing mutations in Optineurin (Maruyama et al., 2010) and SQSTM1 (Fecto et al., 2011) which, given the known biological functions of the corresponding gene products, could, respectively, affect mitochondrial movement and turnover by autophagy (Schon and Przedborski, 2011). In both instances, a local bioenergetics failure could occur because, with Optineurin mutations, normal mitochondria may not travel properly to the high-energy demand areas in the neurons, while with SQSTM1 mutations damaged mitochondria may be insufficiently eliminated. Finally, the hexanucleotide expansion repeat in C9ORF72 is the most common genetic cause of ALS (Majounie et al., 2012), but its effect on mitochondrial biology is thus far unknown. Nevertheless, [18F]fluorodeoxyglucose positron emission tomography revealed overt hypometabolism in brain areas of C9ORF72-ALS patients (Cistaro et al., 2014). Thus, even if ALS is not a mitochondrial disorder per se (Schon and Przedborski, 2011), mitochondrial dysfunction may be one of the earliest pathological events and one of the most common neuronal perturbations of the disease. Whether this apparent commonality reflects the convergence of very different ALS-causing factors or is merely a generic pathological response of compromised motor neurons will have to be clarified.
An ATP requirement for firing depends on the surface area of the membrane (i.e. the morphology of the neuron) and on the intensity of the ion currents, specifically Na+ and K+, flowing through the membrane. Thus, neurons with different intrinsic properties and morphologies have different energy requirements. Our estimates of the ATP requirement for motor neurons place them at the higher end of mammalian neurons but lower than invertebrate neurons (Niven and Laughlin, 2008; Sengupta et al., 2010). Here, we have compared two subtypes of motor neurons, namely FF and S, and have found that FF motor neurons consume, on average, more ATP for each AP. Another important factor is firing pattern. FF motor neurons usually fire in short-lasting high-frequency bursts, whereas S motor neurons fire at a slower pace for postural tasks (Burke, 2011). Thus, FF neurons have high peak needs of ATP, which is a factor that can trigger the first step of an energy crisis. The selective vulnerability to degeneration is probably the consequence of multiple features, but we propose that the higher the energy need, the more vulnerable the neuron.
We uncovered an unexpected consequence of reduced ATP production, the development of a pathological state in which, paradoxically, low ATP availability increases ATP consumption. This causes the cell to enter into a deadly feedback loop with reduced activity of Na+/K+ ATPase pumps and loss of Na+/K+ ion gradients leading to gradual depolarization. The consequence of this process is an increased ATP cost per AP, triggering a vicious cycle. Nevertheless, clinical manifestations emerge typically in adults despite the hypothesized early defects in bioenergetics. Relevant to this apparent temporal discrepancy are the following two considerations. First, as our model shows, the conditions contributing to or causing motor neuron death may be the result of transient, repeated imbalances between ATP needs and ATP produced. Over time, a recurring imbalance may be especially perilous to FF motor neurons since, according to our model, motor neurons with fast transient high-frequency firing involved in phasic movements may be at higher risk to enter in the pathophysiological loop described above than neurons firing at low frequency, such as S motor neurons. Second, as spinal motor neurons die in ALS, giant motor unit potentials can be recorded in affected muscles (Brown, 1973), reflecting the reinnervation of denervated muscle fibers by nearby surviving motor axons via collateral sprouting. This compensatory mechanism may also account for the delay in the emergence of the ALS phenotype. Interestingly, this clinically beneficial process could be bioenergetically catastrophic because, as the number of muscle fibers innervated by a single spared motor neuron increases, so does the imbalance between its ATP needs and its ATP production.
An energy crisis in motor neurons is more likely to begin in a localized microdomain of the cell. We have demonstrated that such a localized event, even at the distal end of the axon, can trigger hyper-excitability and generate ectopic APs. This phenomenon is reminiscent of fasciculation potentials, an early clinical hallmark of the disease (Mills, 2011), reflecting spontaneous discharges of single motor units. The origin of fasciculation potentials has been a source of intense debate since the early work of Denny-Brown and Pennybacker (1938). Many authors have emphasized the distal origin of fasciculation and the probable involvement of fluctuations in the ion gradients along the membrane (de Carvalho and Swash, 1998; Layzer, 1994; Roth, 1982). The current concept is that the sources of fasciculation vary in location over the duration of the disease, and we speculate that an initial distal hyperexcitability, linked to an energy failure and a loss of ion gradients, contributes to their production and distal-to-proximal spread (Desai and Swash, 1997; Kleine et al., 2008). In our model, this propagation is mainly due to depolarization that increases ATP demands in surrounding compartments. Although diffusion of ATP is limited, diffusion of ion species, such as Na+ or K+, plays an important role in the spreading of this local homeostasis failure. The local energy crisis thereby propagates to neighboring compartments, traveling from the distal axon to the soma. In the transgenic mutant SOD1 mouse model of ALS, the degenerative changes in the lower motor neuron pathway also follow a distal-to-proximal pattern (Kanning et al.). Although the model demonstrates this retrograde spread, the effect depends on ionic and ATP diffusion parameters and, more importantly, on the distribution of mitochondria within the neuron. The question of whether a distal energy crisis and the ensuing retrograde spread of ionic disturbances gives rise to a dying-back phenotype should be addressed experimentally.
Finally, we showed that Ca++ accumulation is an important byproduct of energy failure. This accumulation is the result of two processes, an increased influx of Ca++ through plasma membrane voltage-dependent Ca++ channels due to depolarization, and a reduced efficiency of PMCA and SERCA intracellular Ca++ uptake by the plasma membrane and the ER. Should the mitochondrial transmembrane potential be preserved, the low affinity, high capacity MCU might attenuate the rise in intracellular Ca++, but probably not in a spatially even manner because mitochondria cluster in both nerve terminals and dendrites in contrast to the ER which forms a dense anastomotic, tubular network throughout the neuron (Broadwell et al., 1984).
Intracellular Ca++ dyshomeostasis is likely to have pervasive negative consequences. In normal situations, increased cytosolic influx of Ca++ is short-lived and restricted to nanodomains such as presynaptic compartments, where it plays a key role in the physiological determination of the timing and efficiency of transmitter release (Vyleta and Jonas, 2014). However, a sustained, local increase in cytosolic Ca++ can, for example, activate and redirect CaMKII from the cytosol to the active zones, hence altering neurotransmission (Shakiryanova et al., 2011) and, in conjunction with a depletion of calpastatin, it can activate the calpain proteases promoting axon degeneration (Yang et al., 2013). Sustained increased cytosolic Ca++, upon reaching the soma, can modulate transcriptional programs, which, incidentally, may not all be pro-degenerative (Cho et al., 2013). Nonetheless, increased intracellular Ca++ has been linked to the activation of necroptosis (Nomura et al., 2014), a form of programmed necrosis that has been shown to drive the death of motor neurons in animal models of both mutant SOD1 and sporadic ALS (Re et al., 2014).
Finally, previous work has shown that internal Ca++ is tightly linked to the average firing pattern (LeMasson et al., 1993; Ross, 1989), which suggests another possible Ca++-related pathology. It is possible that mitochondrial dysfunction may distort the relationship between electrophysiological activity and Ca++ regulation in such way that compensatory mechanisms are inefficient (Saxena et al., 2013).
Several features of our model could guide future experiments. Beyond what has already been explored concerning reduced ATP production in ALS animal models, the model predicts changes in the reversal potential for Na+ and K+ ions, especially in regions where ATP levels are reduced. Techniques such as high definition microelectrode arrays coupled with micro-fluidics could, in principle, demonstrate the capacity of selective blockers of the ATP synthesis to trigger a spreading axonopathy. An interesting prediction is the relationship between overall firing activity and the progression of the degeneration. Overstimulation elicited with high KCl media or chronic electrical stimulation is predicted to accelerate the degeneration process, whereas reducing firing with tetrodotoxin or optogenetic techniques should delay it.
Our work presents a scenario linking mitochondrial perturbation, hyperexcitability of motor neurons, selective vulnerability, and Ca++ dysregulation in a biologically realistic computer model. Because of the importance of energy metabolism in neurons, previous work (Hasenstaub et al., 2010; Sengupta et al., 2010; Venkateswaran, 2012) has suggested that neurons are optimized to reduce energy costs. We suggest that ALS is, in part, a pathological example of energy-impaired homeostasis (Schon and Przedborski, 2011). Whether this feature is a key player in the degenerative process or a secondary consequence is an important topic for experimental investigation.
EXPERIMENTAL PROCEDURES
Neuron Model
Models were build using the NEURON® simulation package (V7.1, Linux version; (Hasenstaub et al., 2010; Hines and Carnevale, 1997). The simulations used an integration step size of 0.1 ms, but were checked with a reduced step of 0.01 ms. The model neuron used the Hodgkin and Huxley formalism. A 250 compartments model was constructed on the basis of a Neurolucida reconstruction of a cat motor neuron with a soma of 60 µ of diameter and 227 dendritic branches. The total surface area is 13,660 µm2 and the soma surface is 5,296 µm2. The ion channels included in the soma are the Na+ and K+ conductances for the production of APs, a passive K+ conductance (gNa+max=0.1mS/cm2; gK+max=0.05mS/cm2 ; gLeak=0.0001mS/cm2), a calcium L-type current (using the Goldman Hodgkin Katz permeability of 5×10−5 cm/s), a persistent Na+ current (gNa+Pmax=5×10−5mS/cm2), and a Ca++-dependent K+ conductance gKCa++ (gKCa++max=0.05mS/cm2). The axon consisted of a cylinder made from 1,000 compartments each 100 µm long and 1.2 µm in diameter, with the same Na+, K+ and leak conductances as the soma (gNa+max=0.01mS/cm2; gK+max=0.001mS/cm2; gLeak =10−4mS/cm2). The dendrites only had a passive conductance (gLeak =10−5 S/cm2). Synaptic inputs were located at seven random dendritic locations and modeled using the formalism developed by Destexhe et al. (1994; Sengupta et al., 2010) with the following parameters: GeMean=2–5nS; GeSigma=4nS; GeTau=3ms; GiMean=5–8nS; GiSigma=5nS; GiTau=7ms. In all compartment, [Ca++] is computed in a shell of 1 µm just beneath the membrane.
ATP Production
Within each compartment of the model, the action of mitochondria is assumed to operate toward maintaining baseline, steady-state concentrations of ATP, ATD and P ([APT]ss, [APD]ss, and [P]ss) at rates k0 and k1 through the equations
with k0 and k1=1/ms. Although ATP is regulated through the above equation individually in each compartment, it can diffuse among compartments with a diffusion coefficient Datp=3.6µm2/ms (Cullheim et al., 1987; Hubley et al., 1996). Similarly, ions such as Na+ and K+ diffused throughout the model neuron with a diffusion constant of Dion=30µm2/ms (Pohl et al., 1998). Ca++ diffusion, which is affected by many Ca++ binding protein, was set to DCa++=0.6µm2/ms (Saftenku and Friel, 2012). Under normal conditions, [ATP]ss=0.1 mM, but this value was reduced by a factor of 10 or 100 to model deficits.
Pumps
The plasma Na+/K+ ATPase pump is described by the kinetic scheme
where “pump” and “pumpworking” represent two different states of the pump, kp1 to kp4 are rate coefficients and i and o refer to inside and outside the neuron. At t=0, pump=pumpworking=0.01pmol/cm2.
The fast (NCX) Na+/Ca++ exchanger is driven by the Na+ gradient and is defined using the following kinetic scheme
This pump has been model using the same equation whether it is plasmatic or mitochondrial, and can work in a reverse mode if Na+ i is sufficiently high.
Two P-type ATPases have been implemented: PMCA that has a stoichiometry of 1 molecule of Ca++ for 1 molecule of ATP consumed and SERCA that has a stoichiometry of 2 molecules of Ca++ for 1 molecule of ATP. They both have a high affinity for Ca++. For PMCA:
and for SERCA:
Finally, the [Ca++] MCU flux is of the form (Williams et al., 2013):
where p0 is the open probability of the pore, gmcu is the MCU maximal conductance (3.10−6 mS), Δψis the mitochondrial transmembrane potential set to 180mV, is the [Ca++] Nernst reversal potential for the inner mitochondrial membrane, F the Faraday constant, z the Ca++ valence and V the cytosolic volume.
In all of these cases, there is a net transfer of charge associated with the ion exchanges, and the resulting current is included in the model along with the other membrane currents (except for SERCA, the mitochondrial NCX and the MCU for which the fluxes are not across the plasma membrane). At t=0, pmcapump = pmcapumpworking=0.1 pmol/cm2; secapump = secapumpworking = 20 pmol/cm2.
With time measured in ms and concentrations in mM, the parameters are: kp1=20, kp2=0.01, kp3=20, kp4=0.01, kp5=0.038, kp6=0.096, kp7=0.038, kp8=0.096, kp9=99.92, kp10=0.0023, kp11=99.92, kp12=00023, kp13=99.92, kp14=0.0024, kp15=99.92, kp16=00024
The quantity we label as ATP’used is the time derivative dATP/dt obtained from the kinetics of the Na+/K+ pump (equations 2 and 3), and ATPused is the time integral of this quantity. ATP’needed is computed as: where ina and iss are the actual and steady-state Na+ current densities, and Area is the surface area of the neuron.
FF and S Motor Neurons
To reproduce FF and S motor neuron differences, we used two morphologies downloaded from http://NeuroMorpho.Org, for the FF motor neuron: NMO_00913 from (Li et al., 2005) for the S motor neuron, NMO_00907 from the same authors. The S cell has an overall surface of 11,931.8 µm2, 47 bifurcations, and 111 branches whereas the FF cell has an overall surface of 66,311.6 µm2, 98 bifurcations, and 209 branches. Passive and active parameters where derived from (Dai et al., 2002); both neurons have fast Na+ (gNa) and a delayed rectifier K+ (gKD) conductances for the spike generation, Ca++ T-type (gCaT) and L-type (gCaL) conductances, a K+ A-conductance (gKA), a Ca++-activated K+ conductance (gKCa) and an h-current (gIh) in the soma. In the dendrites, the model includes a Ca++ L-type conductance and a Ca++-activated K+ conductance. The maximal conductances were derived from (Dai et al., 2002; Heckman and Binder, 1993) and fine-tuned to obtain a realistic i/f relationship (see Figure 4). Specific values for ATP production, ATPases and other pumps for both cells are as in the model described above. For all the specific values of the parameters as well as for the construction of the conductances, see the Supplementary Material.
The Ca++ concentrations shown in Figure 7 are derived from the Figure 1 motor neuron and are based on a 2 s simulation.
Supplementary Material
Acknowledgments
We are thankful to Michael Hines for his help and advice concerning the development of the bioenergetics model in NEURON. We are grateful to Chris Henderson and Franck Polleux for their insightful comments on the study. Financial supports are from Région Aquitaine and Neurocampus grants to GLM, NIH grant MH093338 to LA and NS042269-05A2, NS072182-01, NS062055-01A1 to SP, the U.S. Department of Defense grants W81XWH-08-1-0522 and W81XWH-12-1-0431 to SP, and by the Gatsby Foundation, the Swartz Foundation, and the Kavli Institute for Brain Science at Columbia University to LA, and Project A.L.S., P2ALS, Target ALS, the ALS Association, the Muscular Dystrophy Association/Wings-over-Wall Street, the Parkinson’s Disease Foundation to SP. GLM is recipient of a Pilot Grant from the Motor Neuron Center at Columbia University.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aiello GL, Bach-y-Rita P. The cost of an action potential. J Neurosci Methods. 2000;103:145–149. doi: 10.1016/s0165-0270(00)00308-3. [DOI] [PubMed] [Google Scholar]
- Alvarez FJ, Pearson JC, Harrington D, Dewey D, Torbeck L, Fyffe RE. Distribution of 5-hydroxytryptamine-immunoreactive boutons on alpha-motoneurons in the lumbar spinal cord of adult cats. J Comp Neurol. 1998;393:69–83. [PubMed] [Google Scholar]
- Araki T, Terzuolo CA. Membrane currents in spinal motoneurons associated with the action potential and synaptic activity. J Neurophysiol. 1962;25:772–789. doi: 10.1152/jn.1962.25.6.772. [DOI] [PubMed] [Google Scholar]
- Barrett EF, Barrett JN, Crill WE. Voltage-sensitive outward currents in cat motoneurones. J Physiol (Lond) 1980;304:251–276. doi: 10.1113/jphysiol.1980.sp013323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartolome F, Wu H-C, Burchell VS, Preza E, Wray S, Mahoney CJ, Fox NC, Calvo A, Canosa A, Moglia C, et al. Pathogenic VCP Mutations Induce Mitochondrial Uncoupling and Reduced ATP Levels. Neuron. 2013;78:57–64. doi: 10.1016/j.neuron.2013.02.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berridge MJ. Neuronal calcium signaling. Neuron. 1998;21:13–26. doi: 10.1016/s0896-6273(00)80510-3. [DOI] [PubMed] [Google Scholar]
- Bilsland LG, Sahai E, Sahai E, Kelly G, Kelly G, Golding M, Golding M, Greensmith L, Greensmith L, et al. Deficits in axonal transport precede ALS symptoms in vivo. Proc Nat Acad Sci USA. 2010;107:20523–20528. doi: 10.1073/pnas.1006869107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borthwick GM, Johnson MA, Ince PG, Shaw PJ, Turnbull DM. Mitochondrial enzyme activity in amyotrophic lateral sclerosis: implications for the role of mitochondria in neuronal cell death. Ann Neurol. 1999;46:787–790. doi: 10.1002/1531-8249(199911)46:5<787::aid-ana17>3.0.co;2-8. [DOI] [PubMed] [Google Scholar]
- Boyman L, Williams GSB, Khananshvili D, Sekler I, Lederer WJ. NCLX: The mitochondrial sodium calcium exchanger. J Mol Cell Cardiol. 2013;59:205–213. doi: 10.1016/j.yjmcc.2013.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broadwell RD, Cataldo AM, Cataldo AM. The neuronal endoplasmic reticulum: Its cytochemistry and contribution to the endomembrane system. II. Axons and terminals. J Comp Neurol. 1984;230:231–248. doi: 10.1002/cne.902300208. [DOI] [PubMed] [Google Scholar]
- Brown WF. Functional compensation of human motor units in health and disease. J Neurol Sci. 1973;20:199–209. doi: 10.1016/0022-510x(73)90030-0. [DOI] [PubMed] [Google Scholar]
- Button DC, Gardiner K, Marqueste T, Gardiner PF. Frequency-current relationships of rat hindlimb -motoneurones. J Physiol (Lond) 2006;573:663–677. doi: 10.1113/jphysiol.2006.107292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burke RE. Motor unit types: functional specializations in motor control. Tins. 2011:1–4. [Google Scholar]
- Cho Y, Sloutsky R, Naegle KM, Cavalli V. Injury-Induced HDAC5 Nuclear Export Is Essential for Axon Regeneration. Cell. 2013;155:894–908. doi: 10.1016/j.cell.2013.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cistaro A, Pagani M, Montuschi A, Calvo A, Moglia C, Canosa A, Restagno G, Brunetti M, Traynor BJ, Nobili F, et al. The metabolic signature of C9ORF72-related ALS: FDG PET comparison with nonmutated patients. Eur J Nucl Med Mol Imaging. 2014;41:844–852. doi: 10.1007/s00259-013-2667-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clapham DE. Calcium Signaling. Cell. 2007;131:1047–1058. doi: 10.1016/j.cell.2007.11.028. [DOI] [PubMed] [Google Scholar]
- Dai Y, Jones KE, Fedirchuk B, McCrea DA, Jordan LM. A modelling study of locomotion-induced hyperpolarization of voltage threshold in cat lumbar motoneurones. J Physiol (Lond) 2002;544:521–536. doi: 10.1113/jphysiol.2002.026005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Carvalho M, Swash M. Fasciculation potentials: a study of amyotrophic lateral sclerosis and other neurogenic disorders. Muscle Nerve. 1998;21:336–344. doi: 10.1002/(sici)1097-4598(199803)21:3<336::aid-mus7>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
- de Carvalho M, Swash M. Cramps, muscle pain, and fasciculations: not always benign? Neurology. 2004;63:721–723. doi: 10.1212/01.wnl.0000134609.56166.15. [DOI] [PubMed] [Google Scholar]
- Denny-Brown D, Pennybacker JB. Fibrillation and fasciculation in voluntary muscle. Brain. 1938;61:311–34. [Google Scholar]
- Desai J, Swash M. Fasciculations: what do we know of their significance? J Neurol Sci. 1997;152(Suppl 1):S43–S48. doi: 10.1016/s0022-510x(97)00243-8. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Mainen ZF, Sejnowski TJ. Synthesis of models for excitable membranes, synaptic transmission and neuromodulation using a common kinetic formalism. J Comput Neurosci. 1994;1:195–230. doi: 10.1007/BF00961734. [DOI] [PubMed] [Google Scholar]
- Fecto F, Yan J, Vemula SP, Liu E, Yang Y, Chen W, Zheng JG, Shi Y, Siddique N, Arrat H, et al. SQSTM1 Mutations in Familial and Sporadic Amyotrophic Lateral Sclerosis. Arch Neurol. 2011;68:1440. doi: 10.1001/archneurol.2011.250. [DOI] [PubMed] [Google Scholar]
- Fritz E, Izaurieta P, Weiss A, Mir FR, Rojas P, Gonzalez D, Rojas F, Brown RH, Madrid R, van Zundert B. Mutant SOD1-expressing astrocytes release toxic factors that trigger motoneuron death by inducing hyperexcitability. J Neurophysiol. 2013;109:2803–2814. doi: 10.1152/jn.00500.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grienberger C, Konnerth A. Imaging Calcium in Neurons. Neuron. 2012;73:862–885. doi: 10.1016/j.neuron.2012.02.011. [DOI] [PubMed] [Google Scholar]
- Hall CN, Klein-Flugge MC, Howarth C, Attwell D. Oxidative Phosphorylation, Not Glycolysis, Powers Presynaptic and Postsynaptic Mechanisms Underlying Brain Information Processing. J Neurosci. 2012;32:8940–8951. doi: 10.1523/JNEUROSCI.0026-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris JJ, Jolivet R, Attwell D. Synaptic Energy Use and Supply. Neuron. 2012;75:762–777. doi: 10.1016/j.neuron.2012.08.019. [DOI] [PubMed] [Google Scholar]
- Hasenstaub A, Otte S, Callaway E, Sejnowski TJ. Metabolic cost as a unifying principle governing neuronal biophysics. Proc. Natl. Acad. Sci. USA. 2010;107:12329–12334. doi: 10.1073/pnas.0914886107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman CJ, Binder MD. Computer simulations of motoneuron firing rate modulation. J Neurophysiol. 1993;69:1005–1008. doi: 10.1152/jn.1993.69.4.1005. [DOI] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT. The NEURON simulation environment. Neural Comput. 1997;9:1179–1209. doi: 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
- Hirano A, Nakano I, Kurland LT, Mulder DW, Holley PW, Saccomanno G. Fine structural study of neurofibrillary changes in a family with amyotrophic lateral sclerosis. J Neuropathol Exp Neurol. 1984;43:471–480. doi: 10.1097/00005072-198409000-00002. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol (Lond) 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubley MJ, Locke BR, Moerland TS. The effects of temperature, pH, magnesium on the diffusion coefficient of ATP in solutions of physiological ionic strength. Biochim Biophys Acta. 1996;1291:115–121. doi: 10.1016/0304-4165(96)00053-0. [DOI] [PubMed] [Google Scholar]
- Johnson JO, Mandrioli J, Benatar M, Abramzon Y, Van Deerlin VM, Trojanowski JQ, Gibbs JR, Brunetti M, Gronka S, Wuu J, et al. Exome sequencing reveals VCP mutations as a cause of familial ALS. Neuron. 2010;68:857–864. doi: 10.1016/j.neuron.2010.11.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanning KC, Kaplan A, Henderson CE. Motor Neuron Diversity in Development and Disease. Annu Rev Neurosci. 2010;33:409–440. doi: 10.1146/annurev.neuro.051508.135722. [DOI] [PubMed] [Google Scholar]
- Kernell D, Bakels R, Copray JC. Discharge properties of motoneurones: how are they matched to the properties and use of their muscle units? J Physiol (Paris) 1999;93:87–96. doi: 10.1016/s0928-4257(99)80139-9. [DOI] [PubMed] [Google Scholar]
- Kleine BU, Stegeman DF, Stegeman DF, Schelhaas HJ, Schelhaas HJ, Zwarts MJ, Zwarts MJ. Firing pattern of fasciculations in ALS: Evidence for axonal and neuronal origin. Neurology. 2008;70:353–359. doi: 10.1212/01.wnl.0000300559.14806.2a. [DOI] [PubMed] [Google Scholar]
- Knott AB, Perkins G, Schwarzenbacher R, Bossy-Wetzel E. Mitochondrial fragm. 2008 doi: 10.1038/nrn2417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Layzer RB. The origin of muscle fasciculations and cramps. Muscle Nerve. 1994;17:1243–1249. doi: 10.1002/mus.880171102. [DOI] [PubMed] [Google Scholar]
- LeMasson G, Marder E, Abbott LF. Activity-dependent regulation of conductances in model neurons. Science. 1993;259:1915–1917. doi: 10.1126/science.8456317. [DOI] [PubMed] [Google Scholar]
- Li Y, Brewer D, Burke RE, Ascoli GA. Developmental changes in spinal motoneuron dendrites in neonatal mice. J Comp Neurol. 2005;483:304–317. doi: 10.1002/cne.20438. [DOI] [PubMed] [Google Scholar]
- Majounie E, E Renton A, Mok K, Dopper EG, Waite A, Rollinson S, Chiò A, Restagno G, Nicolaou N, Simon-Sanchez J, et al. Frequency of the C9orf72 hexanucleotide repeat expansion in patients with amyotrophic lateral sclerosis and frontotemporal dementia: a cross-sectional study. Lancet Neurol. 2012;11:323–330. doi: 10.1016/S1474-4422(12)70043-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maruyama H, Morino H, Ito H, Izumi Y, Kato H, Watanabe Y, Kinoshita Y, Kamada M, Nodera H, Suzuki H, et al. Mutations of optineurin in amyotrophic lateral sclerosis. Nature. 2010;465:223–226. doi: 10.1038/nature08971. [DOI] [PubMed] [Google Scholar]
- Mills KR. Detecting fasciculations in amyotrophic lateral sclerosis: duration of observation required. J Neurol Neurosurg Psychiatry. 2011;82:549–551. doi: 10.1136/jnnp.2009.186833. [DOI] [PubMed] [Google Scholar]
- Niven JE, Laughlin SB. Energy limitation as a selective pressure on the evolution of sensory systems. J Exp Biol. 2008;211:1792–1804. doi: 10.1242/jeb.017574. [DOI] [PubMed] [Google Scholar]
- Nomura M, Ueno A, Saga K, Fukuzawa M, Kaneda Y. Accumulation of Cytosolic Calcium Induces Necroptotic Cell Death in Human Neuroblastoma. Cancer Res. 2014;74:1056–1066. doi: 10.1158/0008-5472.CAN-13-1283. [DOI] [PubMed] [Google Scholar]
- Palmgren MG, Nissen P. P-Type ATPases. Annu Rev Biophys. 2011;40:243–266. doi: 10.1146/annurev.biophys.093008.131331. [DOI] [PubMed] [Google Scholar]
- Pohl P, Saparov SM, Antonenko YN. The Size of the Unstirred Layer as a Function of the Solute Diffusion Coefficient. Biophys J. 1998;75:1403–1409. doi: 10.1016/S0006-3495(98)74058-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powers RK, ElBasiouny SM, Rymer WZ, Heckman CJ. Contribution of intrinsic properties and synaptic inputs to motoneuron discharge patterns: a simulation study. J Neurophysiol. 2012;107:808–823. doi: 10.1152/jn.00510.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raffaello A, De Stefani D, Rizzuto R. The mitochondrial Ca2+ uniporter. Cell Calcium. 2012;52:16–21. doi: 10.1016/j.ceca.2012.04.006. [DOI] [PubMed] [Google Scholar]
- Rangaraju V, Calloway N, Ryan TA. Activity-Driven Local ATP Synthesis Is Required for Synaptic Function. Cell. 2014;156:825–835. doi: 10.1016/j.cell.2013.12.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Re DB, Le Verche V, Yu C, Amoroso MW, Politi KA, Phani S, Ikiz B, Hoffmann L, Koolen M, Nagata T, et al. Necroptosis Drives Motor Neuron Death in Models of Both Sporadic and Familial ALS. Neuron. 2014:1–8. doi: 10.1016/j.neuron.2014.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ross WN. Changes in Intracellular Calcium During Neuron Activity. Annu Rev Physiol. 1989;51:491–506. doi: 10.1146/annurev.ph.51.030189.002423. [DOI] [PubMed] [Google Scholar]
- Roth G. The origin of fasciculations. Ann Neurol. 1982;12:542–547. doi: 10.1002/ana.410120607. [DOI] [PubMed] [Google Scholar]
- Rowland LP. Ameliorating Amyotrophic Lateral Sclerosis. N Engl J Med. 2010;362:953–954. doi: 10.1056/NEJMcibr0912229. [DOI] [PubMed] [Google Scholar]
- Saftenku EÉ, Friel DD. Combined Computational and Experimental Approaches to Understanding the Ca2+ Regulatory Network in Neurons. Springer Netherlands: Dordrecht; 2012. pp. 569–601. [DOI] [PubMed] [Google Scholar]
- Sasaki S, Iwata M. Mitochondrial Alterations in the Spinal Cord of Patients With Sporadic Amyotrophic Lateral Sclerosis. J Neuropathol Exp Neurol. 2007;66:10–16. doi: 10.1097/nen.0b013e31802c396b. [DOI] [PubMed] [Google Scholar]
- Saxena S, Roselli F, Singh K, Leptien K, Julien J-P, Gros-Louis F, Caroni P. Neuroprotection through Excitability and mTOR Required in ALS Motoneurons to Delay Disease and Extend Survival. Neuron. 2013;80:80–96. doi: 10.1016/j.neuron.2013.07.027. [DOI] [PubMed] [Google Scholar]
- Schon EA, Przedborski S. Mitochondria: The Next (Neurode)Generation. Neuron. 2011;70:1033–1053. doi: 10.1016/j.neuron.2011.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sengupta B, Stemmler M, Laughlin SB, Niven JE. Action Potential Energy Efficiency Varies Among Neuron Types in Vertebrates and Invertebrates. PLoS Comput Biol. 2010;6:e1000840. doi: 10.1371/journal.pcbi.1000840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shakiryanova D, Morimoto T, Zhou C, Chouhan AK, Sigrist SJ, Nose A, Macleod GT, Deitcher DL, Levitan ES. Differential Control of Presynaptic CaMKII Activation and Translocation to Active Zones. J Neurosci. 2011;31:9093–9100. doi: 10.1523/JNEUROSCI.0550-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan W, Pasinelli P, Trotti D. Role of mitochondria in mutant SOD1 linked amyotrophic lateral sclerosis. Mol Basis of Disease. 2014 doi: 10.1016/j.bbadis.2014.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venkateswaran N. Energetics based spike generation of a single neuron: simulation results and analysis. Front. Neuroenergetics. 2012;5:1–12. doi: 10.3389/fnene.2012.00002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vyleta NP, Jonas P. Loose Coupling Between Ca2+ Channels and Release Sensors at a Plastic Hippocampal Synapse. Science. 2014;343:665–670. doi: 10.1126/science.1244811. [DOI] [PubMed] [Google Scholar]
- Williams GSB, Boyman L, Chikando AC, Khairallah RJ, Lederer WJ. Mitochondrial calcium uptake. Proc Nat Acad Sci USA. 2013;110:10479–10486. doi: 10.1073/pnas.1300410110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Weimer RM, Kallop D, Olsen O, Wu Z, Renier N, Uryu K, Tessier-Lavigne M. Regulation of Axon Degeneration after Injury and in Development by the Endogenous Calpain Inhibitor Calpastatin. Neuron. 2013;80:1175–1189. doi: 10.1016/j.neuron.2013.08.034. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.