Influence of covariate distribution on the predictive performance of pharmacokinetic models in paediatric research

Abstract

Aims

The accuracy of model-based predictions often reported in paediatric research has not been thoroughly characterized. The aim of this exercise is therefore to evaluate the role of covariate distributions when a pharmacokinetic model is used for simulation purposes.

Methods

Plasma concentrations of a hypothetical drug were simulated in a paediatric population using a pharmacokinetic model in which body weight was correlated with clearance and volume of distribution. Two subgroups of children were then selected from the overall population according to a typical study design, in which pre-specified body weight ranges (10–15 kg and 30–40 kg) were used as inclusion criteria. The simulated data sets were then analyzed using non-linear mixed effects modelling. Model performance was assessed by comparing the accuracy of AUC predictions obtained for each subgroup, based on the model derived from the overall population and by extrapolation of the model parameters across subgroups.

Results

Our findings show that systemic exposure as well as pharmacokinetic parameters cannot be accurately predicted from the pharmacokinetic model obtained from a population with a different covariate range from the one explored during model building. Predictions were accurate only when a model was used for prediction in a subgroup of the initial population.

Conclusions

In contrast to current practice, the use of pharmacokinetic modelling in children should be limited to interpolations within the range of values observed during model building. Furthermore, the covariate point estimate must be kept in the model even when predictions refer to a subset different from the original population.

WHAT IS ALREADY KNOWN ABOUT THIS SUBJECT

• Modelling and simulation (M&S) is often applied as a design tool for pharmacokinetic and pharmacokinetic–pharmacodynamic bridging in paediatric research.

• When models are used for the selection of dose and prediction of drug exposure and/or effects in a new population the identification of influential covariates can play a major role in the accuracy of parameter estimates and subsequent predictions.

• The identification of the correct covariates in children is often complex due to the presence of correlations and co-linearity between covariates.

WHAT THIS STUDY ADDS

• Unless a mechanism-based model can be warranted, the use of a stepwise approach for covariate analysis is not recommended when small datasets are available.

• Extrapolation of the covariate effects beyond the parameter distributions explored during model building cannot be performed without bias and, consequently, lead to erroneous dosing recommendations.

• The covariate point estimate must be retained in the model when predictions refer to a population in which median or mean values differ from the population used during model building.

Introduction

Modelling and simulation (M&S) of clinical data represents a powerful approach for evidence synthesis and consequently for a more comprehensive interpretation of the data available at any point in time during the process of drug development. Ideally, it should also provide the basis for inferences and extrapolation of findings from a subgroup to the entire target population [1,2]. At present, regulatory bodies in Europe encourage the application of the M&S approach during drug development [3], as it may circumvent some practical and ethical difficulties in the evaluation of paediatric medicines. In fact, industry and academia have been developing and applying models under the assumption that non-linear mixed effects modelling methods are robust enough to enable the characterization of pharmacokinetics and pharmacodynamics even when sparse sampling and unbalanced data sets are used [4–8].

More recently, M&S has been applied as a design tool for pharmacokinetic and pharmacokinetic–pharmacodynamic bridging. In this case, the main objectives of such models include the selection of dose and prediction of drug exposure and/or effects in a new population, for which no data have been generated. In this context, the identification of influential covariates such as demographic characteristics can play a major role in the accuracy of parameter estimates and subsequent predictions. The assessment of the correct correlations between covariates and parameters is crucial, given that it will have direct implication for the dose selection in a new population with different demographic characteristics. In paediatric research, however, the identification of the correct covariates is often complex due to the presence of correlations and co-linearity between covariates. As shown by a previous investigation from Ribbing et al., competition between multiple covariates may further increase selection bias, especially when there is a moderate to high correlation between the covariates [9].

Different methods are available to select significant covariates during model building. The one most used is the stepwise covariate selection in which two processes, forward inclusion and backward elimination, are applied [10,11]. Alternative methods, such as genetic algorithms for covariate selection [12] and automated covariate model building [13,14] are also becoming more common, but have not been scrutinized to the same extent in pharmacokinetic research. In contrast to traditional data analysis, where the objective is primarily parameter estimation, models developed by stepwise covariate selection are also being used to predict drug exposure and consequently define the dose rationale in new patients, whose characteristics differ from the original patients in the trial.

Model-based predictions can be considered for a population with similar characteristics as the one under investigation during model building (interpolation) or for a new population beyond the covariate range explored during model building (extrapolation). Many examples are available in the published literature in which modelling has been applied to interpolate data [15–17]. Fewer examples exist however in which extrapolations are made to a population which does not share exactly the same characteristics or includes individuals beyond the range of values explored during model building. Yet, this is a common practice during the clinical development of compounds for paediatric indications, when typically exposures in younger age groups are predicted using pharmacokinetic parameter distributions obtained from the analysis of data in older children and vice versa. In fact, two recent publications by Cella et al. [18,19] showed the lack of predictive power of pharmacokinetic models when they are used for extrapolation purposes.

The current analysis has two main objectives. First of all, we want to define the feasibility and pre-requisites to use pharmacokinetic models as an extrapolation tool, i.e., to make predictions about a population in which the values of the covariates are beyond the covariate range explored during model building. Secondly, we investigate how parameter-covariate correlations should be expressed when a model is used for simulation purposes. From a methodological perspective, there are different ways to express the parameter-covariate correlation during covariate selection. Among other options, as shown in equations 1 and 2, we evaluate the impact of ‘centring’ on the median or the mean value of the covariate in the population. This approach is supposed to stabilize parameter estimation and facilitate the interpretation of the coefficients in the correlation.

(1)

(2)

In these equations P is the parameter, COV is the covariate, COV_median the median value of the covariate in the data set and θ₁ and θ₂ are the intercept and the slope, which describe the correlation between the parameter and covariate. In both equations the intercept and the slope are estimated during model building. In the first case (equation 1), the variation in the values of the covariate can cause instability in the estimation of slope and intercept. This contrasts with the second case (equation 2) as the intercept is centred on the mean values. For instance, for an adult population 70 kg is commonly used as the median value of body weight.

In addition to investigating the predictive performance of a pharmacokinetic model for extrapolation purposes, here we also evaluate whether the covariate point estimate should be retained in the model when extrapolations refer to a population in which the median or mean value differs from the one in the population previously analyzed or whether it should be adapted to reflect the covariate distribution of the new population.

Methods

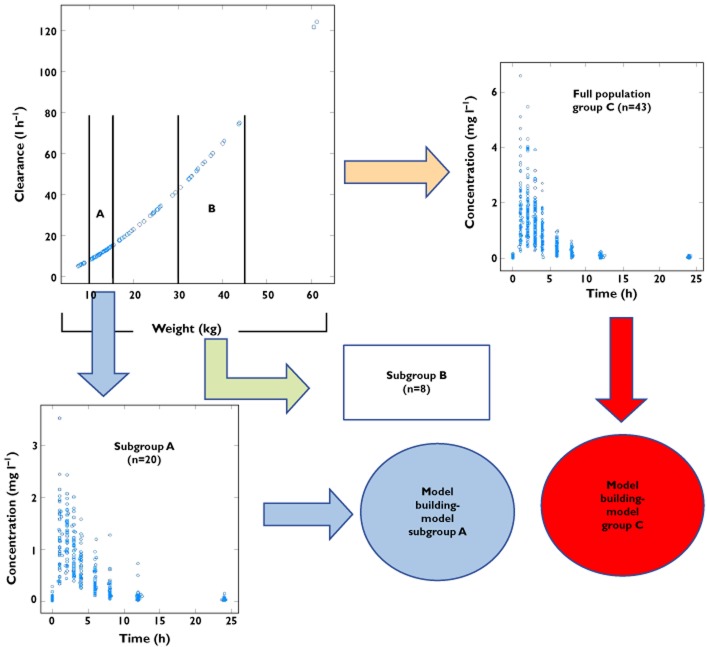
The different steps required for this investigation are summarized in Figure 1.

Figure 1.

Diagram depicting the steps of the investigation. Simulation of the pharmacokinetic profiles and subsequent model building using the data from a population of 43 children and from the two subgroups with differing body weight ranges. The simulation scenarios are based on a model in which clearance and body weight are exponentially correlated [i.e. CL = θ₁*(WT/WTMedian)**θ₂].

We would like to highlight that despite the potential role of demographic factors on multiple pharmacokinetic processes, e.g. effect of body weight on drug distribution and elimination, in this manuscript scenarios have been considered that enable the evaluation of covariate effects from a methodological perspective. Therefore, covariate effects were initially explored on a single parameter (i.e. clearance) to illustrate the impact of covariate distributions on the performance of hierarchical models when extrapolating across populations. Furthermore, readers are reminded that physiological correlations exist between parameters describing drug disposition, such as the correlation between clearance and volume. One should also take these interactions into account when assessing the consequences of data imbalance and censored covariate distributions.

Population demographics and hypothetical protocol

A group of 43 hypothetical paediatric patients with a weight range between 7.43 and 61.3 kg (median weight 14.2 kg) were sampled from a pooled dataset including demographic characteristics from three pharmacokinetic studies [20–22]. The sampling procedure was performed in such a way that the age and body weight distribution in the hypothetical population was balanced across the weight range of interest. The population size was based on a real-life case, in which a similar population of children was selected for the evaluation of the pharmacokinetics of lamivudine, an anti-retroviral drug widely used in HIV-infected children.

These patients were then treated with a hypothetical drug, given orally every 12 h. A total of eight plasma samples per subject was then simulated throughout the dosing interval. Using data from the overall population (group C), two subgroups were selected based on different body weight ranges. It is worth mentioning that, despite the fact that children are commonly stratified by age, body weight was used for the purposes of stratification in the simulations. This choice was based on the co-linearity between age and body weight. As shown in Table 1, the first subgroup (subgroup A) comprised 20 children with weight between 10 and 15.4 kg (median body weight 12 kg), whilst the second group (subgroup B) included eight children with weight between 30 and 45 kg (median body weight 37 kg).

Table 1.

Summary of demographic characteristics of the hypothetical population

	Subgroup A	Subgroup B	Group C (Full population)
Subjects	20	8	43
Median weight (kg)	12.5	35.05	14.2
Minimum weight (kg)	10.3	30.05	7.43
Maximum weight (kg)	15.4	43.8	61.3
Median age (years)	2.18	8.85	2.81
Minmum age (years)	0.99	8.1	0.42
Maximum age (years)	3.89	12.67	12.92

Predefined covariate effects

The pharmacokinetics of the compound were assumed to be described by a one compartment pharmacokinetic model with first order absorption and elimination. A base model previously developed by our group for lamivudine [23] was used for simulations.

Various scenarios were simulated, in which body weight was linearly and/or exponentially correlated to clearance and volume of distribution. Allometric scaling concepts were also taken into account, but the exponents were explored with values higher and lower than 0.75. Four different scenarios in which one covariate was significant were simulated, based on previously reported, realistic parameter-covariate correlations:

• Body weight linearly correlated with clearance (with a slope of 0.65)

• Body weight linearly correlated with clearance (with a slope of 1.5)

• Body weight exponentially correlated with clearance (with an exponent of 0.65)

• Body weight exponentially correlated with clearance (with an exponent of 1.5)

To ensure further insight to the impact of covariate effects on overall drug disposition taking into account known physiological changes associated with developmental growth and size, two additional scenarios were simulated in which a second covariate was incorporated into the model.

• Body weight linearly correlated with volume of distribution (with a slope of 1.8) and exponentially correlated with clearance (with an exponent of 0.65) [15]

• Body weight exponentially correlated with volume of distribution (with an exponent of 0.807) and exponentially correlated with clearance (with an exponent of 0.84) [23]

The relationship between parameter and covariate was described as follows:

(3)

(4)

In these equations, P is the pharmacokinetic parameter (in this case clearance or volume of distribution), WT is body weight and WT_median is the median of the body weight distribution in the population analyzed during model building. Equation 3 represents a linear relationship between the parameter and body weight with θ₁ and θ₂ as the intercept and the slope of the correlation, respectively. Equation 4 represents an exponential relationship between the parameter and body weight with θ₁ and θ₂ as the coefficient and the exponent of the correlation, respectively. The operator ** represents the exponentiation.

Analysis of simulated patient data: PK model and covariate criteria

The simulated plasma concentration datasets (full population and subgroup A) were subsequently fitted to a pharmacokinetic model according to standard model building criteria. All the available covariates, such as body weight, age and gender, were tested according to a stepwise covariate inclusion approach [24], i.e. the covariates were entered one by one into the population model. After inclusion of statistically significant factors into the model (forward selection), each covariate was removed one at a time (backward elimination). The likelihood ratio test was used to assess whether the difference in the objective function between the base model and the full (more complex) model was statistically significant. The difference in −2log likelihood (DOBJF) between the base and the full model is approximately χ² distributed, with degrees of freedom equal to the difference in the number of parameters between the two hierarchical models. Because of the exploratory nature of this investigation, an additional parameter leading to a decrease in the objective function of 3.84 was considered significant (P < 0.05). During the final steps of the model building stricter criteria were applied and only the covariates which resulted in a difference of at least 7.88 (P < 0.005) were kept in the final model. Model selection procedures also included standard diagnostic measures and internal validation based on visual predictive checks.

Model predictive performance: posterior predictive check (PPC)

In order to evaluate model performance, a posterior predictive check (PPC) was carried out. PPC operates under the basic assumption that if the model provides an adequate description of the data then the simulated data from the same model should mimic the essential features of the observed data. In this investigation, model performance was assessed by comparing the accuracy of area under the curve (AUC) estimates obtained for each subgroup, based (1) on the final model derived from the overall population and (2) by extrapolations to subgroup B (n = 8), using the model derived from subgroup A (n = 20). This was done for each scenario, as described previously. AUC estimation was performed by keeping the median body weight of the population analyzed during model building or by adapting the parameter correlation using the median body weight of the new population. Integration of the concentration–time data was performed according to the trapezoidal rule.

Results

In this paper, we summarize the results from two out of the six simulation scenarios proposed initially for the evaluation of covariate effects on the accuracy of model-based extrapolations. These scenarios are representative of the overall investigation, in that they capture the key issues regarding covariate model building and the use of a model-based approach for dose selection and extrapolation of pharmacokinetics across populations. In particular, we focus on the scenarios in which body weight is exponentially correlated with clearance according to an exponent different from 0.75, i.e. the value which is typically fixed in allometric scaling exercises. Tables 2 and 3 show the parameter values used for the initial simulations and the values estimated for subgroup A and for the full population (group C), including scenarios in which the exponent describing the correlation between weight and clearance is lower and higher than 0.75.

Table 2.

True and estimated parameter values for the simulation scenario in which body weight is exponentially correlated with clearance with a slope of 0.65

Parameter	True value	Estimated subgroup a	Estimated group c
Clearance (CL)
CL/F = θ1 × (BW/med)** θ2
θ1 (coefficient) (l h−1)	13.8	12.7	13.6
θ2 (exponent)	0.65	0.941	0.767
Volume of distribution (V) (l)	40.4	45.8	43.8
Absorption rate constant (Ka) (h−1)	2.8	4.8	2.7
Interindividual variability
ηCL/F	0.079	0.0836	0.0868
ηV/F	0.056	0.0236	0.0325
ηKa/F	0.331	0.267	0.227
Residual error (proportional)	0.03	0.02	0.003

Table 3.

True and estimated parameter values for the simulation scenario in which body weight is exponentially correlated with clearance with a slope of 1.5

Parameter	True value	Estimated subgroup a	Estimated group c
Clearance (CL)
CL/F = θ1 × (BW/med)** θ2
θ1 (coefficient) (l h−1)	13.8	10.7	13.7
θ2 (exponent)	1.5	1.31	1.60
Volume of distribution (V) (l)	40.4	40.9	42.2
Absorption rate constant (Ka) (h−1)	2.8	3.92	3.35
Interindividual variability
ηCL/F	0.079	0.092	0.076
ηV/F	0.056	0.022	0.036
ηKa/F	0.331	0.241	0.185
Residual error (proportional)	0.03	0.002	0.003

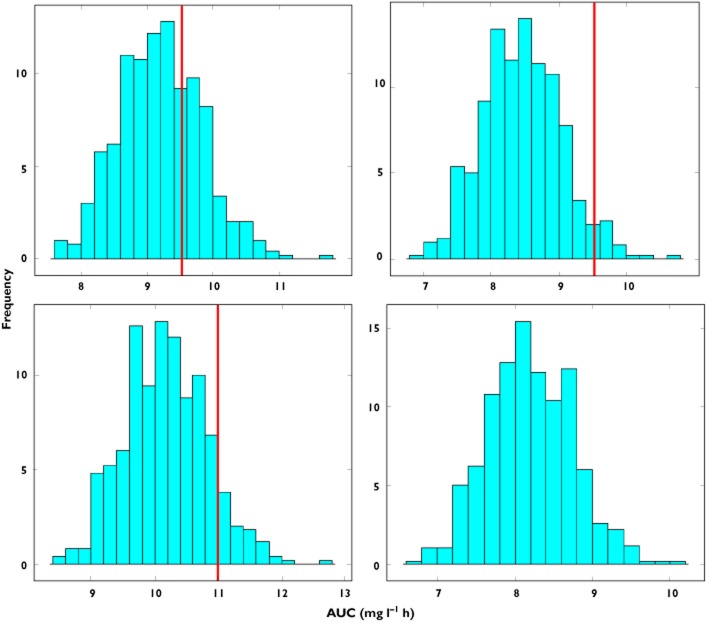
As shown in Figure 2, each pharmacokinetic model was validated using a visual predictive check. The models obtained from the full population (group C) and from the subgroup of children weighing between 10 and 15 kg (subgroup A) seem to predict accurately the observations. In contrast, in Figure 3 discrepancies are observed between the predicted area under the curve (AUC) for the children from subgroup B when using the model built with the data from subgroup A. Clearly, the model does not predict the parameter of interest accurately when the covariate range in the new population differs from the one of the original model. Moreover, as shown on the right panel of Figure 3, adjusting the median of body weight to the distribution of the new population did not result in any improvement in model performance.

Figure 2.

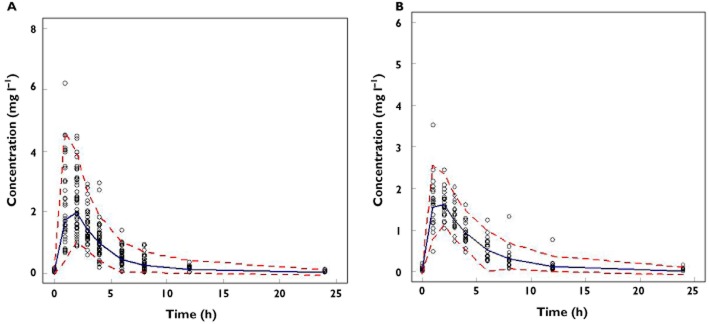
Visual predictive check of the models obtained from the fit of the simulated plasma concentrations of the children in the full population (group C) (A) in subgroup A (B) when body weight was exponentially correlated to clearance with an exponent of 0.65

Figure 3.

Predicted AUC distribution in subgroup B based on model parameter estimates obtained from data fitting of subgroup A. Upper panels show prediction distributions for an exponential correlation between clearance and body weight with an exponent of 0.65, whilst lower panels show prediction distributions for an exponent of 1.5. The line represents the true point estimate for AUC in the population. In the left panels the difference in the covariate distribution between subgroups A and B is not taken into account, with the median of the weight distribution in subgroup A being used in the simulations. In the right panels a shift is observed in the predictions when the covariate range of subgroup B is used in the simulations

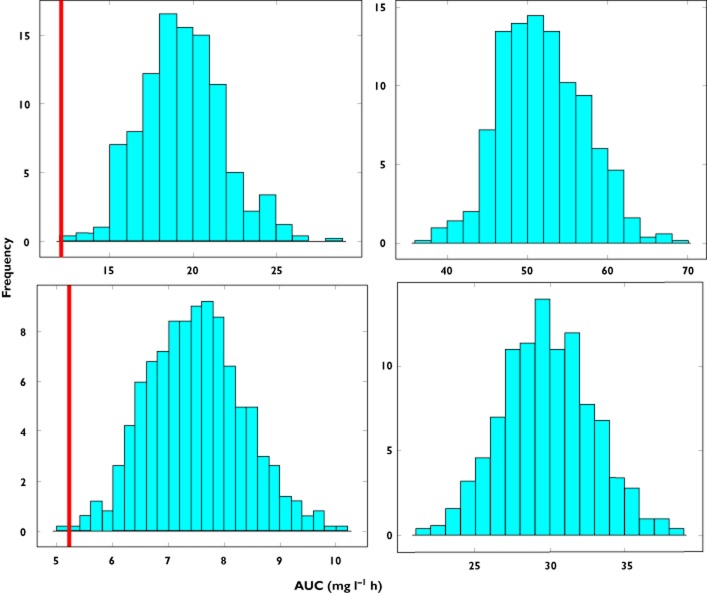
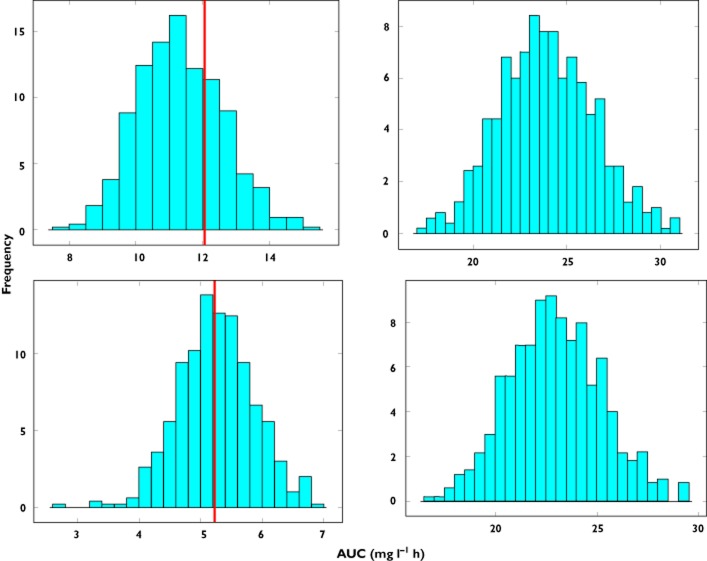
On the other hand, accurate predictions of the PK parameter of interest were obtained in each of the subgroups when using the model based on the full population data set (Figures 4 and 5). Furthermore, the model seems to perform well if the covariate point estimate is kept in the model (left panels). These results also show that accuracy in parameter estimates is warranted only when the model is used for interpolation purposes, i.e. when predictions encompass the range of covariate values used during the model building process. Interestingly, model performance deteriorates when the relation between clearance and body weight is adapted to reflect the covariate distribution in the new population. This happens irrespectively of the magnitude of the exponent which correlates body weight to clearance.

Figure 4.

Predicted AUC distribution in subgroup A based on model parameter estimates obtained from data fitting of the full population (group C). Upper panels show prediction distributions for an exponential correlation between clearance and body weight with an exponent of 0.65, whilst the lower panels show prediction distributions for an exponent of 1.5. The line represents the true value of AUC in the population. In the left panels the difference in the covariate distribution between group C and subgroup A is not taken into account, with the median of the weight distribution of subgroup C being used in the simulations. In the right panels a shift is observed in the predictions when the covariate range of subgroup A is used in the simulations

Figure 5.

Predicted AUC distribution in subgroup B based on model parameter estimates obtained from data fitting of the full population (group C). Upper panels show prediction distributions for an exponential correlation between clearance and body weight with an exponent of 0.65, whilst the lower panels show prediction distributions for an exponent of 1.5. The line represents the true value of AUC in the population. In the left panels the difference in the covariate distribution between group C and subgroup B is not taken into account, with the median of the weight distribution of subgroup C being used in the simulations. In the right panels a shift is observed in the predictions when the covariate range of subgroup B is used in the simulations

Whilst the assessment of covariate effects on a single parameter provides a straightforward measure of the impact covariates can have on model-based extrapolations, questions may arise about the physiological relevance of such an effect. It is therefore useful to demonstrate the overall impact of covariate distributions when covariate effects affect more than one parameter. Additional scenarios were considered in which body weight is exponentially correlated with both clearance and volume of distribution. As shown in Figure 6, similar results were observed in terms of predictive performance, i.e. discrepancies occur when extrapolations are based on model building based on subgroups of the overall population. In addition, model predictions are inaccurate when the relation between clearance and body weight is adapted to reflect the covariate distribution in the new population.

Figure 6.

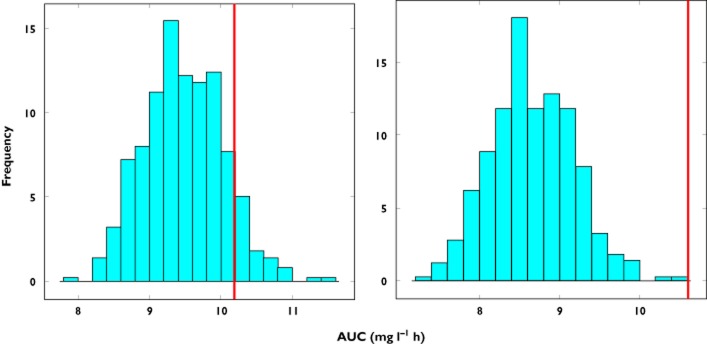
Predicted AUC distribution in subgroup A based on model parameter estimates obtained from data fitting of the full population (group C) for an exponential correlation between clearance and body weight with an exponent of 0.84 and an exponential correlation between volume of distribution and body weight with an exponent of 0.807. The line represents the true value of AUC in the population. In the left panel the difference in the covariate distribution between group C and subgroup A is not taken into account, with the median of the weight distribution of subgroup C being used in the simulations. In the right panel a shift is observed in the predictions when the covariate range of subgroup A is used in the simulations

Discussion

The main focus of our study was to investigate the role of demographic covariates during bridging and extrapolation of pharmacokinetic data across paediatric populations. Undoubtedly, the identification of influential covariate effects on pharmacokinetic parameters is crucial to ensure accurate dose selection or dose adjustment in a new population. This is particularly important during the planning phase of a bridging exercise, when pharmacokinetic models are used for simulation purposes. Ideally, the predictive performance of population models should be warranted before its application in paediatric therapeutic research and drug development. Here we have shown the potential for bias in model predictions when extrapolating data beyond the covariate range explored during model building, a common practice in industry and academic research, which relies on small sample sizes for the characterization of the pharmacokinetic properties of a compound. These findings emphasize the importance of meta-analysis and other techniques for evidence synthesis as the basis for any quantitative evaluation of pharmacokinetics and pharmacodynamics in children. From a methodological point of view we have also shown the relevance of ‘centring’ on the point estimate of the covariate distribution, which must be retained in the model when extrapolations are performed, irrespectively of the differences in the covariate distribution in the population or subgroup of interest.

Model-based extrapolation and interpolation

The current findings show that extrapolation to a new population beyond the covariate range explored during model building is not possible for exponential parameter-covariate correlations. These results appear to be in agreement with a previous publication which showed that, irrespective of whether extrapolation methods are to be applied during paediatric drug development, model predictions beyond the range of the data used for parameter estimation may be biased [18,19]. Adaptations or adjustments of parameter-covariate correlations to account for the covariate range of the new population do not improve model predictive performance. In fact, it appears that the further the median of the covariate of the new population deviates from the original one, the less accurate is the predicted AUC distribution (right panels, Figure 3). The only scenario which appears to yield accurate extrapolation from one group to another with different covariate values is when a linear correlation is used to describe the covariate effects (as shown in Figure 7).

Figure 7.

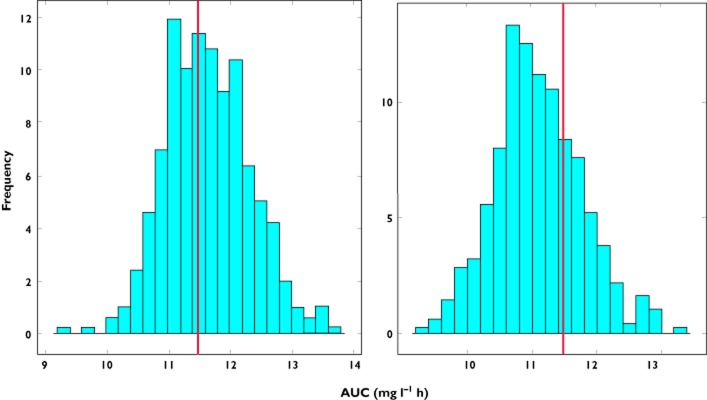
Predicted AUC distribution in subgroup B based on the model parameter estimates obtained from data fitting of subgroup A. The histograms show AUC predictions for a linear relation between clearance and body weight with a slope of 1.5. The line represents the true value of AUC in the population. In the left panel the difference in the covariate distribution between subgroups A and B is not taken into account, with the median of the weight distribution of subgroup A being used in the simulations. In the right panel a shift is observed in the predictions when the covariate range of subgroup B is used in the simulations

The (often physiologically-driven) exponential correlation between pharmacokinetic parameter and covariate is linked to non-linearities that cannot be predicted without a semi- or fully mechanistic approach to bridging or extrapolations beyond the evidence derived from the available data. From a statistical perspective, this issue could be handled by defining uncertainty in parameter estimation [25,26]. However this can potentially lead to wide parameter distributions, with little value for dosing recommendation purposes. It should also be noted that this bias cannot be eliminated by the identification of additional covariates. Extrapolation to a different population requires accurate estimation of the underlying parameter-covariate correlations, which in turn imposes the availability of data (likelihood) or alternatively, the use of priors that support inferences about the parameter distribution in a different population, including the magnitude and nature of the covariate effects in those conditions [27,28]. At present, our findings suggest that only interpolation is feasible when making use of non-linear hierarchical models to describe pharmacokinetics in children. Interpolations will be accurate independently of the nature of the parameter-covariate correlations.

Influence of sample size on predictive performance

In addition to the hurdles for the use of bridging and extrapolation across populations, another issue in the covariate analysis presented here was the limited sample size of the data available for model building, which may clearly lead to wrong covariate selection and inclusion bias. In some of the simulation scenarios evaluated here, the correct covariate (body weight) was identified when the full dataset was analyzed, whilst a confounding factor (age) or no covariate effects (results not shown) were detected when evaluating the small, imbalanced subgroup of children (n = 20). This problem, previously highlighted by Ribbing & Jonsson in their simulation study [9], emphasizes the importance of performing a stepwise covariate selection only when large paediatric datasets are available. If this is not the case, meta-analysis or different methods, such as the use of a genetic algorithm (GA) for covariate selection [12] or automated covariate model building [13], should be considered. GA is based on the mathematics of evolution, i.e. natural selection and survival of the fittest. The solution space can be seen as a population of all the possible models to be tested and the ‘fitness’ (based on objective function and penalty for less parsimonious models) is created for each model. Subsequently, the next generation of models is created, until the ‘best’ model is identified. The main advantage compared with the stepwise covariate selection is that GA eliminates subjective bias from covariate selection. Furthermore, this method also enables a more systematic analysis of confounders. With regard to automated covariate model building, one should bear in mind that (i) the covariate model is built for all parameters simultaneously, (ii) the covariate model is built within the modelling program, which allows better specification of significance levels used, (iii) it can appropriately handle covariates that varies over time and (iv) it is not dependent on the quality of the posterior Bayes estimates of the individual parameter values.

Recommendations on the use of models for simulation purposes

M&S represents a powerful tool to avoid unnecessary studies in the target population as well as facilitate the interpretation of the limited evidence available [29]. However, our findings underscore the importance of a careful and cautious use of models. Awareness about model assumptions and formal evaluation of the predictive performance of a model is required to avoid biased predictions, which in turn, could lead to wrong dosing adjustments in clinical practice.

The main recommendations from this investigation are listed below:

• Unless a mechanism-based model can be warranted, the use of a stepwise approach for covariate analysis is not recommended when small datasets are available. Instead, alternative (Bayesian) approaches should be considered for paediatric bridging and extrapolation.

• Extrapolation of the covariate effects beyond the parameter distributions explored during model building cannot be performed without bias, and consequently lead to erroneous dosing recommendations.

• Pharmacokinetic models can be used for simulation purposes only when the population of interest can be considered a subgroup of the initial population.

• The covariate point estimate must be retained in the model when predictions refer to a population in which median or mean values differ from the population used during model building.

Limitations

Two main limitations need to be acknowledged in our study. First, we have restricted the analysis to a fixed number of hypothetical patients. This choice was based on the need to assess whether the data set size might influence the final results. In addition, we have excluded potential confounders, which may not be random in a real population, such as bioavailability, co-medications, co-morbidities, etc. Here, the same bioavailability was assumed for the whole population of children and no drug–drug interactions. We also acknowledge that from a methodological perspective, one may wish to disentangle some of the issues presented here from potential artefacts due to approximate likelihood methods, as implemented in nonmem. Other algorithms, such as the stochastic approximation of the standard expectation maximization (SAEM) or Bayesian algorithms (Markov Chain Monte Carlo simulations) need to be further tested to evaluate whether the magnitude of the bias observed would be the same as with the first order conditional estimation method with interaction (FOCEI) algorithm applied during this investigation [30].

In summary, model performance appears to be independent of the nature of the parameter-covariate correlations if predictions are restricted to interpolations. By contrast, biased results may be observed when predictions are aimed at extrapolations, i.e. the covariate distribution lies outside the range observed during model building. The use of meta-analysis, mechanistic models and other alternative methods in which prior or historical data are included for inferential purposes is therefore recommended for bridging and extrapolation of pharmacokinetic data across paediatric populations. In addition, parameterization of covariate effects based on the point estimate of the covariate distribution imposes the use of the same point estimate even when the population to be simulated differs from the original population.

These findings emphasize the need to discriminate between models for estimation (data-driven models based on small or unbalanced sample sizes aimed at describing pharmacokinetics in the same population, i.e. those patients included for parameter estimation) from models for simulation (mechanistic models whose predictive performance has been thoroughly validated or models based both on data and inferences that account for the correlation between parameters and covariates), which are required when performing bridging and extrapolations. Unfortunately, the discrepancies observed in the predicted distributions are not detectable with standard diagnostic tools currently used during model validation procedures.

Competing Interests

All authors have completed the Unified Competing Interest form at http://www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare CP had support from PENTA-LABNET (EC Seventh Framework contract 201057) for the submitted work, ODP is employed by GlaxoSmithKline, as indicated in the affiliations and MD declares no conflict of interest. There are no financial relationships with any organizations that might have an interest in the submitted work in the previous 3 years and no other relationships or activities that could appear to have influenced the submitted work.