Abstract
Following a brief tutorial on the application of factor analysis to hearing aid outcome measures, three studies of hearing aid outcome measures in elderly adults are presented and analyzed. Two of the studies were completed at Indiana University (IU-1 and IU-2), and one was a collaborative multisite study by the Veterans Administration and the National Institute of Deafness and other Communication Disorders (NIDCD/VA). IU-1 measured hearing aid outcome in 173 elderly wearers of single-channel, linear, in-the-ear hearing aids with output-limiting compression, whereas IU-2 obtained the same extensive set of outcome measures from 53 elderly wearers of two-channel, wide-dynamic-range compression, in-the-canal hearing aids. In the NIDCD/VA study, 333 to 338 participants wore three single-channel circuits in succession, with each circuit housed within an in-the-ear shell. The three circuits included in that study and in this analysis were: (1) linear with peak clipping, (2) linear with output-limiting compression, and (3) single-channel, wide-dynamic-range compression. Evaluation of the many outcome measures completed in each study using principal components factor analysis revealed that from three (both IU studies) to five (NIDCD/VA study) principal components captured the individual differences in hearing aid outcome. This was independent of hearing aid type (in-the-ear or in-the-canal) and circuitry. Subsequent multiple regression analyses of individual differences in performance along each dimension of hearing aid outcome revealed that these individual differences could be accounted for reasonably well by various prefit variables for some dimensions of outcome, but not others. In general, measures of speech recognition performance were well accounted for by prefit measures, with the best predictors being hearing loss, cognitive performance, and age. Measures of hearing aid usage were less well accounted for by prefit measures, with the most accurate predictor of current hearing aid use being prior hearing aid use. The outcome dimension accounted for most poorly was that associated with hearing aid satisfaction, with subjective measures of aided sound quality being the best predictor of performance along this dimension of hearing aid outcome. Additional multicenter, large-scale studies are needed to develop more complete models of hearing aid outcome and to identify the variables that influence various aspects of hearing aid outcome. It is only through this additional research that it will be possible to optimize outcome for hearing aid wearers.
Introduction
Much clinical and research interest in hearing aid outcome measures has been evidenced over the past decade (see Humes [2001] for a review). Basically, the central issue regarding hearing aid outcome is how one should document the benefits provided by the hearing aid to the wearer. This is of interest to clinicians, researchers, hearing aid manufacturers, third-party payers, and hearing aid wearers alike.
Although the general topic has been of interest to the research community over the past decade, most studies conducted have made use of small numbers of participants, typically 30 or fewer, and have focused on only a small subset of possible outcome measures. For example, very few studies have obtained measures of speech recognition, with and without the hearing aid, together with self-report measures of hearing aid performance, benefit, satisfaction, and usage.
As a result, one of the fundamental questions in this area has been impossible to answer. Specifically, what should be measured with regard to hearing aid outcome? Are measures of speech recognition performance together with self-report measures of hearing aid performance, benefit, satisfaction, and usage necessary? Perhaps some or all of these measures tap the same underlying construct and are unnecessarily redundant. Humes (1999) demonstrated how the application of principal components factor analysis can be used to address this issue of redundancy among outcome measures, although the studies available at the time of that evaluation were less than ideal in terms of the number of outcome measures and the number of participants. A somewhat related question regarding the number and nature of the outcome measures to be employed has to do with whether either varies with the style of hearing aid (eg, in-the-ear [ITE] versus in-the-canal [ITC]) or the type of circuitry (eg, single-channel linear circuit versus two-channel compression circuit). That is, does the answer to the question regarding what to measure interact with the style of hearing aid or the type of circuitry?
Since the previous application of principal components analyses to hearing aid outcome measures by Humes (1999), two large-scale studies of hearing aid outcome have been published (Larson et al., 2000; Humes et al., 2001). These studies used larger numbers of subjects than prior studies of hearing aid outcome and also included multiple measures of outcome, frequently obtaining multiple measures within a particular domain as well (ie, multiple measures of speech recognition or of hearing aid usage). In addition, numerous prefit variables were obtained from all subjects in each of these studies, such that regression analysis could potentially identify variables underlying individual differences in performance along a specific dimension of hearing aid outcome. In a follow-up to the Humes et al. (2001) study with linear ITE hearing aids, the author directed another study that used an identical study protocol, but instead used smaller-sized ITC hearing aids and incorporated different circuitry (two-channel, wide-dynamic-range compression). Although the sample size was only about one third the size of the published study (N = 53 versus 173), it was considered sufficiently large for further evaluation of hearing aid outcome measures.
The present paper evaluates the outcome measures from each of these three studies to determine the number and nature of the dimensions of hearing aid outcome. The results of this evaluation will provide the most complete answer to date with regard to what should be measured when the successful use of hearing aids in hearing-impaired adults is to be documented. In addition, a variety of prefit variables will be examined as possible predictors of individual differences in performance for each of the outcome dimensions identified. These analyses will provide a preliminary indication of those variables that underlie individual differences in hearing aid outcome, and in the process, might offer some insights into how various aspects of outcome can be maximized. Because two of the three studies have been described in detail in prior publications, and the third study used a protocol identical to that of one of the studies published previously (Humes et al., 2001), details regarding each study protocol are not presented here. Rather, the focus is on the use of principal-components factor analysis to analyze the results obtained in each study and the identification of variables that underlie individual differences along the outcome dimensions identified. The analyses for each study are presented in separate sections, followed by a general summary and a discussion of the entire series of analyses. Since a basic understanding of principal-components factor analysis is critical to the presentation of the data analyses in this paper, a brief review of the nature of this statistical tool is presented in the next section.
Principal Components Factor Analysis and Its Application to Hearing Aid Outcome Measures
Factor analysis has been the subject of several textbooks. Of these, Gorsuch (1983) has probably provided one of the most thorough and comprehensible treatments. Clearly, a comprehensive discussion of factor analysis is beyond the scope of this paper. Rather, a brief overview is provided for one type of factor analysis (perhaps the most common type), principal components analysis.
Factor analysis in general, and principal components analysis in particular, is a subset of a broader model in statistical analysis referred to as either the multivariate linear model or the general linear model. This same linear model underlies all regression analyses and all types of analysis of variance. Consider the measurement of dependent variable v in individual i. The multivariate linear model, describing individual i's performance on dependent variable v, would be represented as:
where Xiv is the response of individual i for dependent variable v, Fi represents individual i's score for the A to Gth factors, and wv represents the weight of dependent variable v on each of the A to Gth factors (Gorsuch, 1983).
In a sense, this particular representation is a simplified version that assumes that scores for the dependent variable are in terms of deviations from the mean, and the number of factors equals the number of variables (what Gorsuch [1983] refers to as the “full component model”). Typically, the final factor solution is a truncated version of the full component model (ie, number of factors < number of variables), with the truncated factors representing the inaccuracy of the model's fit (or error). Note that the factors (F) are tied to characteristics of the individual (i), whereas the weights (w) represent the weight of the dependent variable (v) on each factor.
According to this equation, the response or score of individual i for dependent variable v (ie, Xiv) can be represented as the linear sum of weighted factors. The crux of factor analysis is identifying the combination of subject-related factors (F) and variable-related weights (w) that will provide a good description of the responses of a large number of individuals for a set of dependent variables. In doing so, common constructs or factors that underlie performance for a variety of measures might be identified.
Principal components analysis is a variation of factor analysis in which the goal is to find those F and w values for the multivariate linear model that maximize the variance accounted for by the model. A hierarchical or stepwise approach is pursued in which the first factor accounts for the maximum amount of variance alone, then a second, uncorrelated factor is identified that accounts for the next largest increment in the explained variance, followed by a third factor that is uncorrelated with either of the first two factors, and so on. For a set of V dependent variables (v), this process is repeated until the Vth factor has been identified that will account for 100% of the variance in the data. However, usually a truncated set of principal components is used and the number of acceptable factors is such that each component included in the final solution accounts for at least 1/V of the total variance. For example, with a set of 20 dependent variables, only those principal components accounting for at least 1/20 (5%) of the total variance would be included in the final solution; however, this is not a hard and fast rule. The researcher is free to include additional factors or components, including those accounting for less than 1/V of the total variance, but some justification for doing so is typically expected. (This criterion, requiring a factor to account for at least 1/V proportion of variance in the solution, corresponds to what is also known as Kaiser's criterion, or the inclusion of only those factors having an eigenvalue > 1.0.)
Principal components analysis typically makes use of the correlation matrix for the set of dependent variables, v. One can think of principal components analysis as hunting for clusters of correlated dependent variables among the matrix and representing each such cluster as an underlying common factor or component. Using the multivariate linear model equation described previously, this would be akin to finding those dependent variables among the set that had similarly high weights (wv) for the same factor (F).
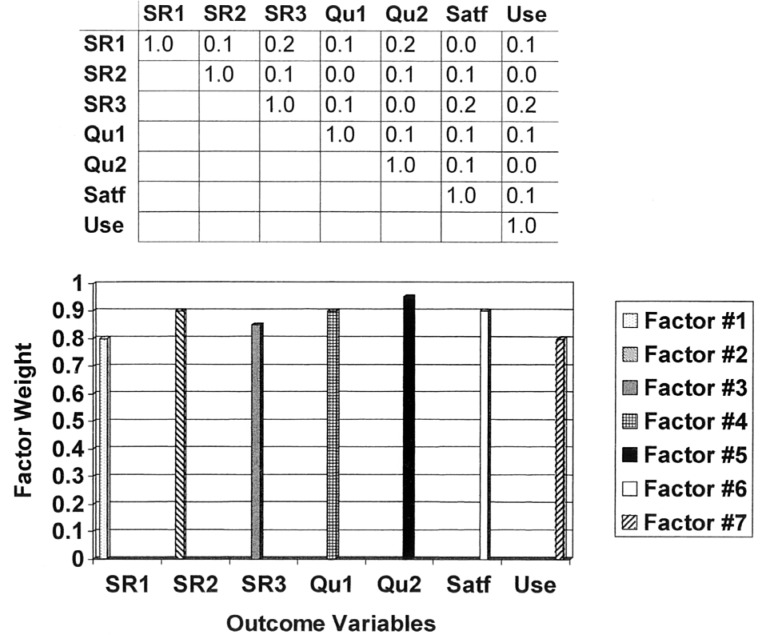
Before proceeding further in a general discussion of principal components analysis, let's look at a few examples of the possible results of such an analysis for a hypothetical set of seven hearing aid outcome measures. Consider, for example, a set of three aided measures of speech recognition (SR1, SR2, and SR3), two measures of sound quality (Qu1, Qu2), one measure of hearing aid satisfaction (Satf), and one measure of hearing aid usage (Use). These dependent variables would represent seven v values obtained from each individual hearing aid wearer under identical test conditions (same hearing aids, listening conditions, etc.). This set of variables is actually small for factor analysis, which will be discussed in more detail later, but will suffice for illustration purposes.
The top portion of Figure 1 reveals the 7 × 7 correlation matrix for the seven dependent variables or hearing aid outcome measures in this hypothetical illustration. Only the upper half of the matrix (that portion above the diagonal) is depicted, because the lower half is a mirror image of the upper half and provides no new information. Note that the correlation coefficients along the diagonal are assumed to be 1.0, as required in principal components analysis, and that the rest of the correlation coefficients in this example are all low. This indicates that none of the seven outcome measures is very closely associated with any of the other outcome measures. Thus, each variable appears to be measuring something that is unique and distinct from that measured by each of the other outcome measures.
Figure 1.
Illustration of a hypothetical correlation matrix (top) and resulting principal component factor solution (bottom) for a case in which there are no clusters of highly correlated dependent variables. Each of the three speech recognition measures (SR1, SR2, SR3), the two sound quality measures (Qu1, Qu2), the satisfaction measure (Satf) and the usage measure (Use) are weighted on a separate factor.
A plot of the hypothetical factor weights (wv) for each resulting factor (F) appears in the lower portion of Figure 1. Note that there is a one-to-one mapping of each outcome variable to a factor or principal component. That is, the principal components analysis of the set of seven hearing aid outcome measures resulted in seven components being identified, which reflects the lack of overlap or redundancy among the outcome measures. The factor weighting of the SR1 variable on Factor A is 0.8 (dotted vertical bar), but the weight for this variable on the other six factors is 0. Likewise, the factor weighting of the SR2 variable on Factor B is 0.9 (vertical bar with downward diagonal stripes) and 0.0 for the other six factors, and so on.
The results of the principal components analysis for the hypothetical situation depicted in Figure 1 represent one extreme regarding the possible factor solutions. In this case, nothing was gained via the factor analysis in that there do not appear to be any unifying constructs underlying the data that would reduce the set of seven variables to a smaller number of independent (uncorrelated) factors.
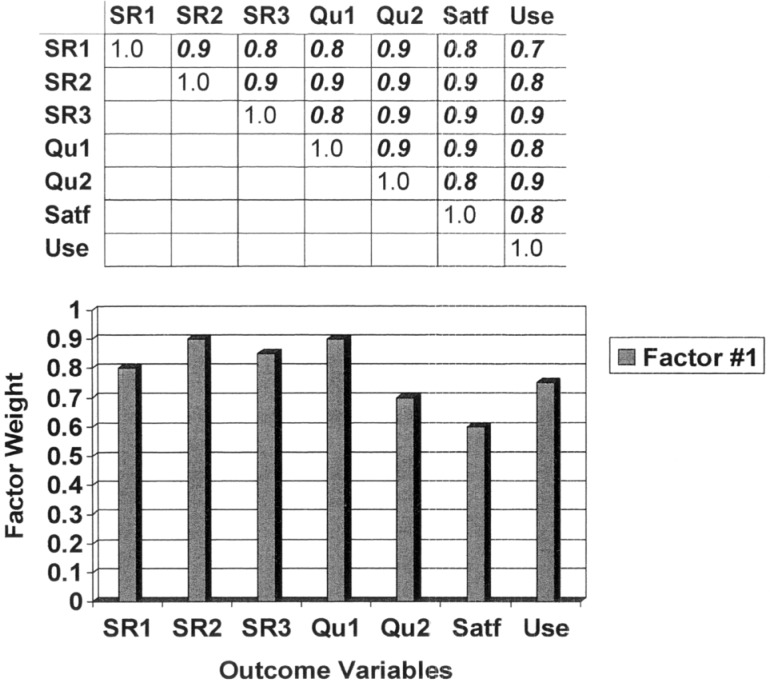
The other extreme for the possible principal component solutions is depicted in Figure 2. Note that the correlations in the matrix at the top of this figure are all very high (≥ 0.7). In this case, all seven hearing aid outcome measures are interrelated, such that an individual who scored high on the SR1 speech recognition measure also scored high on all of the other six outcome measures. Likewise, an individual who scored low on one of the sound quality measures (Qu1) also scored low on all of the other six outcome measures. Thus, a lot of overlap or redundancy exists among the set of seven outcome measures. Essentially, such a pattern would indicate that knowledge of an individual's performance on one outcome measure reveals that individual's relative performance on all other outcome measures. All seven dependent variables seem to be related to the same underlying construct or factor. The lower portion of Figure 2 reveals the factor weights (grey bars) of each variable for Factor A. Each outcome measure has a weight between 0.6 and 0.9 for Factor A, and no other factors are needed for the solution.
Figure 2.
Illustration of a hypothetical correlation matrix (top) and resulting principal component factor solution (bottom) for a case in which all dependent variables are highly correlated with one another. Each of the three speech recognition measures (SR1, SR2, SR3), the two sound quality measures (Qu1, Qu2), the satisfaction measure (Satf) and the usage measure (Use) are weighted on the same factor.
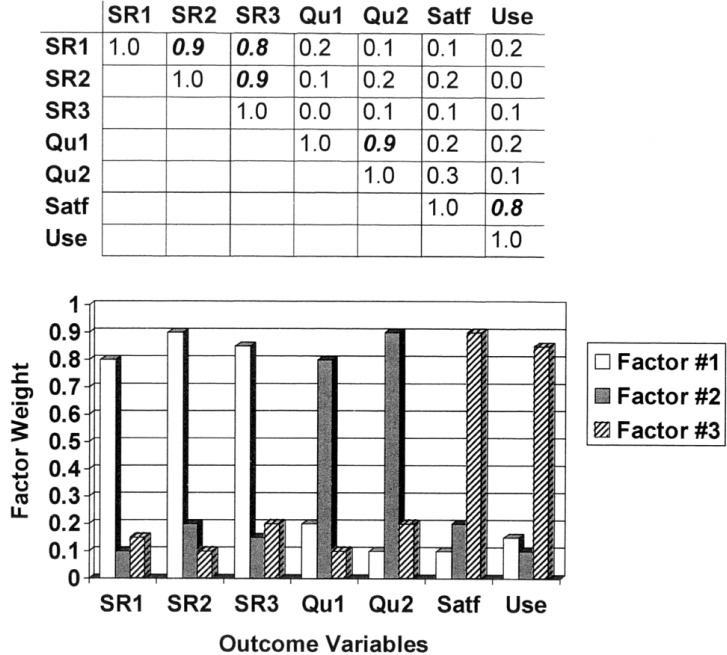
Having reviewed the two extreme factor solutions for our hypothetical example, Figure 3 presents a more typical outcome that lies between these two extremes. First, an examination of the correlation matrix in the top portion of the figure shows that there are three “clusters” of high correlations, indicated by correlation coefficients in a bold italicized font. The first cluster in the top left portion of the matrix indicates that all three measures of aided speech recognition are highly correlated with each other, but not with any of the other outcome variables. Next, the correlation coefficient of 0.9 in the middle of the matrix indicates that the two measures of aided sound quality are correlated with each other, but not with any other outcome measures. Finally, the correlation coefficient of 0.8 in the lower right portion of the correlation matrix indicates that the measures of hearing aid satisfaction and usage are correlated with one another, but not with any of the other outcome measures.
Figure 3.
Illustration of a hypothetical correlation matrix (top) and resulting principal component factor solution (bottom) for a more typical case in which there are several (three) clusters of highly correlated dependent variables. Each of the three speech recognition measures (SR1, SR2, SR3) are weighted heavily on only one factor (white bars), whereas the two sound quality measures (Qu1, Qu2) and the satisfaction (Satf) and usage measure (Use) are weighted on other factors (the grey and striped bars, respectively).
The pattern of factor weights that might be observed for such a correlation matrix is shown in the lower portion of Figure 3. Note that the weights for the three speech recognition measures are high for Factor A (white vertical bars), but the other four variables have very low weights for Factor A. Similarly, the two sound quality variables have high weights for Factor B (grey vertical bars), but all other outcome variables have low weights on this factor. Finally, hearing aid satisfaction and usage are weighted highly on Factor C (striped bars), and all other outcome measures have low weights on this factor. Thus, three general constructs or factors (FA, FB, FC) appear to underlie the seven hearing aid outcome measures in this hypothetical set of data.
In principle, only three outcome measures would need to be obtained in the future: one measure of aided speech recognition; one measure of aided sound quality; and a measure of either hearing aid satisfaction or usage, but not both. This, of course, assumes that each of the seven outcome measures is reliable. In addition, by an examination of the variables that load heavily on a particular factor, it is often possible for the researcher to label the factor appropriately. In the situation illustrated in Figure 3, for example, Factor A would be interpreted as a general aided speech-recognition factor that was apparently independent of the differences in materials or listening conditions involved in SR1, SR2, and SR3. Factor B, on the other hand, is clearly related to aided sound quality (again, independent of the differences in stimuli or listening conditions between Qu1 and Qu2), and Factor C is interpreted as a measure of hearing aid satisfaction and usage.
Recall that principal components analysis seeks to maximize the variance accounted for by the multivariate linear model. So, part of the evaluation of the quality of fit for a given factor solution is based on the total variance accounted for, with higher proportions of variance representing better fits. In addition, given the iterative nature of the solution, Factor A, the first identified, always accounts for the largest proportion of variance, with each successive factor accounting for a progressively lower proportion of variance. As noted previously, in general, only those factors accounting for a proportion of variance that exceeds 1/V (V = number of dependent variables) are likely to be robust and emerge in subsequent analyses. In the hypothetical example illustrated by Figure 3, Factor A (aided speech recognition) accounted for the greatest proportion of the total variance since it was the first component identified, but all three factors accounted for at least 14.3% of the variance (1/V = 1/7 = 0.143 = 14.3%).
In addition to examining the total variance accounted for by the factor solution, an important metric representing the goodness of fit is known as the communality. The communality is calculated for each variable included in the factor analysis and represents the proportion of each variable's variance that can be accounted for by the factors in the final solution (Gorsuch, 1983). Communality values can range from 0 to 1, but more appropriate lower and upper bounds are represented by the multiple correlation of the variable with all other dependent variables and the reliability coefficient of the variable, respectively. In general, low communality of a variable would be indicated by values ≤ 0.40 and reasonably high communality by values ≥ 0.70 (Gorsuch, 1983).
As noted, the examples illustrated in Figures 1 to 3 were only hypothetical and did not represent a typical set of variables common to most factor analyses. Moreover, the correlation coefficients were deliberately set to either be very high (≥ 0.7) or very low (≤ 0.3), which makes the “clustering” of correlated variables and the interpretation of the underlying factors straightforward. This is often not the case, however, and a statistical procedure such as factor analysis is needed to extract the common underlying factors, because they are not so readily apparent visually as the examples illustrated in these three figures. In addition, many more than seven dependent variables are typically being considered. For V dependent variables, the number of correlations to be examined above the diagonal is given by [V • (V-1)/2]. Thus, in our hypothetical examples, only 21 correlations needed to be scanned in each matrix to find clusters of correlated variables. In many applications, it is not unusual to have 20 to 25 dependent variables involved, which would lead to 190 to 300 correlations to be analyzed. Clearly, visual inspection of the correlation matrices is not appropriate in such cases.
Gorsuch (1983) indicates that there should be at least four dependent variables for the construct being assessed or represented in the factor analysis. Thus, in our hypothetical examples, assuming the same 4 domains of aided speech recognition, aided sound quality, hearing aid satisfaction, and hearing aid usage were to be represented, then a minimum of 16 dependent variables would be needed, 4 for each domain.
It is more difficult to define a precise rule or guideline for the number of individuals to be included in factor analysis studies. However, Gorsuch (1983) indicates that there should be at least 5 subjects per variable and seldom fewer than 100 subjects for such analyses. Continuing with our previous example, if one had a total of 16 outcome measures, 4 for each of 4 domains, then a subjects-to-variables ratio of 5 would mean that 80 subjects would be required in order to yield a robust factor solution. However, since 80 is less than the recommended minimum of 100, such a study would actually require 100 participants, each completing all 16 outcome measures.
Gorsuch's (1983) simple rules of thumb regarding minimum sample size and the subjects-to-variables ratio for factor analysis are oversimplifications (as Gorsuch also acknowledged). As noted by Guadagnoli and Velicer (1988) and MacCallum et al. (1999), for example, sample size, the subjects-to-variables ratio, the variables-to-factors ratio, and the communalities of the variables interact in a fairly complex manner. Basically, these studies demonstrate that if the communalities are generally greater than 0.6, then sample size can be small (50 to 60 subjects) and the number of variables per factor can also be small (eg, 3 variables per factor), with stable factor solutions still obtained.
These studies demonstrated that the communalities of the variables were of paramount importance to obtaining stable factor solutions. This was true, moreover, for either universally high communalities (eg, all values >0.6) or for a wide range of communalities in which values were roughly equally distributed from 0.2 to 0.8. It was only when the communalities were universally low (eg, all values ≤ 0.4), that the sample size needed to be increased to ≥ 400 subjects to yield stable factor solutions. Even in this case, however, if the subjects-to-factor ratio was increased to ≥ 6 while communalities remained low, a sample size as low as 100 proved to be acceptable (yielded stable factor solutions). As will be demonstrated later, communalities were never universally low (typically, quite high) for any of the factor analyses reported in this article. As such, relatively small sample sizes and variables-to-factors ratios are acceptable.
The foregoing discussion of factor analysis has been concerned with one type of factor analysis known as exploratory factor analysis. In this approach, there have not been many (or any) prior such analyses, and insufficient data exist to formulate well-articulated theories regarding the constructs or factors that might underlie performance. The primary purpose of exploratory factor analyses is to develop some initial theories or models regarding such constructs and then to guide subsequent research to further evaluate and develop the model and theory. That is, the result of exploratory factor analysis is seldom expected to result in a final model.
Confirmatory factor analysis, on the other hand, is based on prior exploratory analyses and refinement with additional research and theoretical work. Here, a specific model is constructed and factor analysis is used to test the model with new sets of data. Often, the new data result in modifications to and improvements in the model and underlying theory. For confirmatory factor analysis, it is often possible to get by with fewer dependent variables and fewer subjects. A few prior factor analyses of hearing aid outcome measures (eg, Humes, 1999; Humes et al., 2001) have been conducted, and the development of models and theories in this area is certainly in its infancy. Thus, in this paper, we are concerned only with exploratory factor analysis.
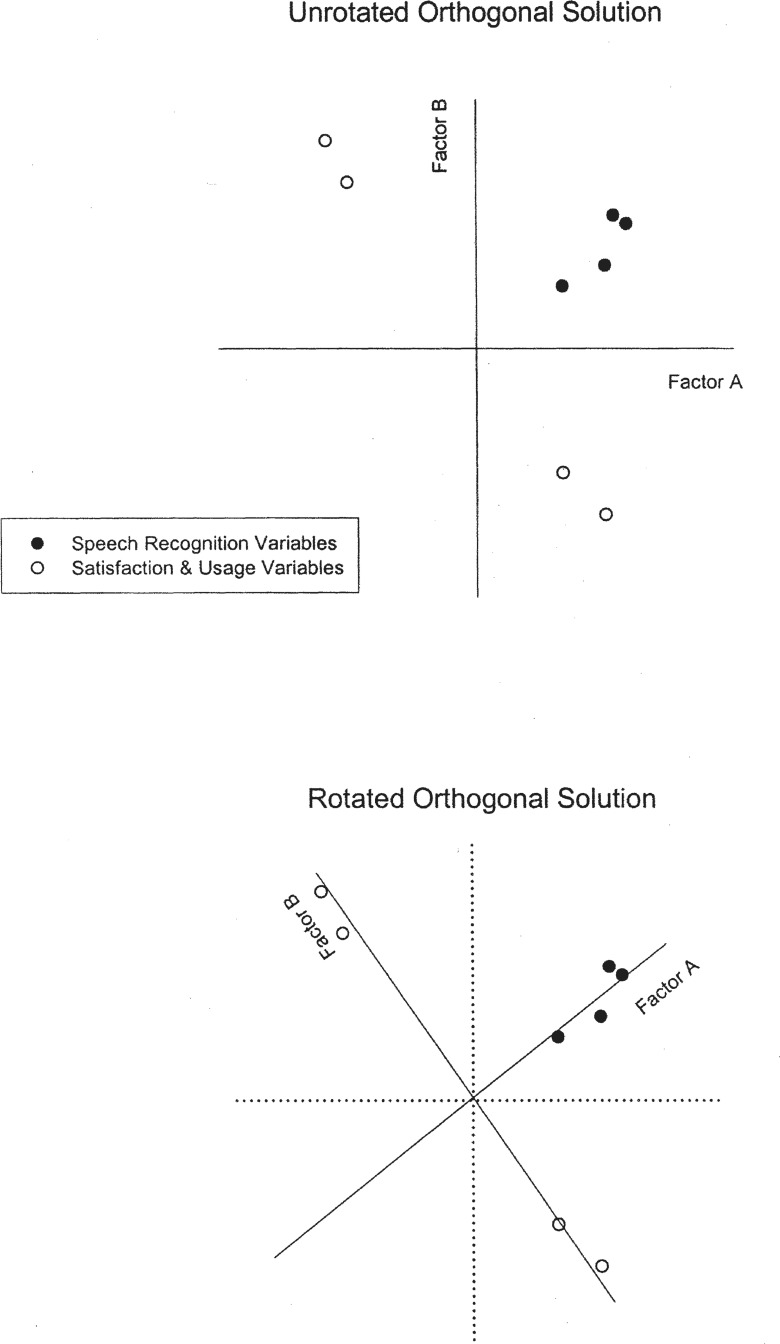
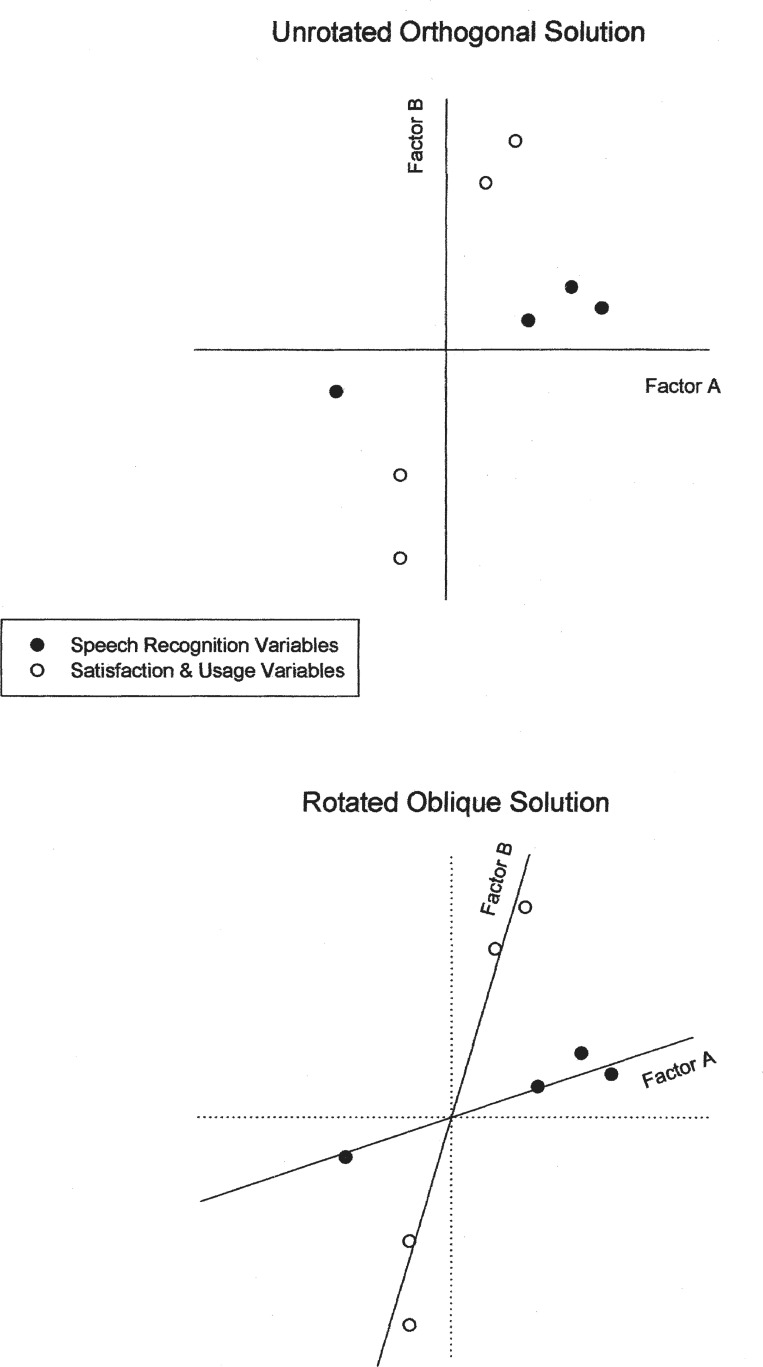
A final key concept central to factor analysis is something referred to as factor or component rotation. Consider the graphical presentation of the two-factor solution in the top panel of Figure 4. Two factors, A and B, were identified as principal components by factor analysis and are represented along the X and Y axes, respectively. Note that in this conventional representation of the x and y axes, the two axes are perpendicular to one another, which reflects their independence or lack of correlation. Factors A and B are uncorrelated or orthogonal components.
Figure 4.
Illustration of the concept of orthogonal rotation of factors for a hypothetical two-factor solution. Two sets of factor weights are shown, one for a set of speech recognition measures (filled circles) and one for a set of hearing aid satisfaction and usage measures (unfilled circles). The unrotated factor solution is shown in the top portion and the orthogonally rotated solution in the bottom portion of the figure. Note that the Factor A and Factor B axes are perpendicular (orthogonal) in both cases, but the axes have been rotated about 30 degrees counterclockwise in the bottom panel. Although the scatter of the data points in this two-dimensional plot remains the same in both illustrations (ie, the variance accounted for by the two-factor solution is the same), the interpretation of Factor A as a speech recognition factor and Factor B as a satisfaction and usage factor is much clearer for the rotated solution at the bottom.
Assuming that the origin has x, y coordinates of 0,0 and the extreme values on both axes are ±1, the two axes represent the factor weights (wv) of each variable on Factor A and Factor B. Note that the four speech recognition measures (filled circles) in this hypothetical illustration would be represented as moderate weights of about 0.2 to 0.6 on both Factor A and Factor B. Likewise, two of the four satisfaction and usage variables would have extreme weights for both factors (near −1 on Factor A and +1 on Factor B). This makes interpretation of the underlying factors difficult because there is not a clear mapping of variables to factors to assist in the interpretation. However, if one rotates the two axes, keeping the origin at 0,0 and the axes perpendicular, a rotated solution emerges, such as that depicted in the lower panel of Figure 4. Note that, in the case of the rotated axes, the speech recognition variables, and only these variables, have high weights for Factor A, whereas the satisfaction and usage measures, and only these measures, have high weights (either positive or negative) on Factor B.
Now, the interpretation of Factors A and B is much easier for the researcher. Clearly, Factor A is a speech recognition factor and Factor B is a hearing aid satisfaction and usage factor. These two factors, moreover, are independent of one another such that knowledge of an individual's speech recognition performance is entirely unrelated to the measured hearing aid satisfaction or usage. Thus, factor rotation is performed solely to enhance the interpretation of the factors derived. It does not have an impact on the number of factors identified or the amount of variance accounted for by the factors in the solution.
Various procedures have been established for optimal rotation of the factors (Gorsuch, 1983). Of those available, the varimax (Kaiser, 1958) procedure is the one most commonly used. This rotation criterion seeks to maximize the variance of the squared weights across a factor; hence the name, varimax.
As noted, principal component analysis assumes that each component in the factor solution is orthogonal or uncorrelated; that is, that the x and y axes in Figure 4 are perpendicular. Is this a valid assumption? For example, perhaps all measures of hearing aid outcome are correlated. Is this an unreasonable scenario? Probably not, at least during the initial development or exploration of models. To accommodate such a scenario, it is possible to allow for some correlation between factors in principal components solutions. In this case, the axes are no longer perpendicular, and as a result, the rotation of the factors is referred to as oblique rotation. Again, the reader should keep in mind that the rotation of factors, whether orthogonal or oblique, does not impact the number of factors or the variance accounted for in the solution. Rather, the purpose of factor rotation is to assist in the interpretation of the factors, including possible associations among factors.
Figure 5 illustrates another hypothetical factor solution for sets of speech recognition, satisfaction, and usage variables and is useful in illustrating the nature of oblique factor rotation. The top panel again depicts the unrotated orthogonal solution for this hypothetical set of data. Interpretation of the underlying factors from this solution is not easy, because many variables have moderate weights on both Factor A and Factor B. Maintaining perpendicular (orthogonal) axes and rotating them about 15° clockwise might facilitate interpretation of Factor B, but not Factor A. Likewise, orthogonal rotation of the axes about 15° counterclockwise might facilitate interpretation of Factor A, but not Factor B. However, as shown in the lower portion of Figure 5, if the requirement that the axes remain perpendicular is relaxed, an optimal rotation can be obtained for both factors. Such an oblique rotation makes it clear that Factor B is associated with hearing aid satisfaction and usage, and Factor A is associated with speech recognition performance. Thus, oblique rotation has facilitated the interpretation of the underlying factors or principal components.
Figure 5.
Illustration of the concept of oblique rotation of factors for a hypothetical two-factor solution. Two sets of factor weights are shown, one for a set of speech recognition measures (filled circles) and one for a set of hearing aid satisfaction and usage measures (unfilled circles). The unrotated factor solution is shown in the top portion and the obliquely rotated solution in the bottom portion of the figure. Note that the Factor A and Factor B axes are no longer perpendicular in the bottom illustration. Although the scatter of the data points in this two-dimensional plot remains the same in both illustrations (ie, the variance accounted for by the two-factor solution is the same), the interpretation of Factor A as a speech recognition factor and Factor B as a satisfaction and usage factor is much clearer for the rotated solution at the bottom. It is also clear that no matter how the perpendicular axes (dotted lines in bottom illustration) were rotated, a good alignment of the factor weights with the axes would not be possible. Thus, the oblique rotation is superior to the orthogonal rotation in this example (in terms of factor interpretation, not variance accounted for).
The improvement in factor interpretation, illustrated with oblique rotation in the lower portion of Figure 5, comes with an additional “cost.” Specifically, the resulting solution is now more complex than the simpler orthogonal solution. Recall that factor analysis operates on the correlation matrix for all dependent variables. If a set of factors emerge and the resulting factors are themselves correlated, resulting in another correlation matrix representing interfactor correlations, then an additional second-order factor analysis may need to be performed to determine a second set of higher-order factors.
It is not being suggested here that the added complexity is a negative aspect of the oblique rotation of factors, as this may in fact provide the most appropriate description of the phenomenon being studied by the researcher. On the other hand, parsimony would dictate that an orthogonal solution, with fewer levels of factors, would be preferred should such a solution provide a valid description of the data.
How does the researcher decide between an orthogonal or oblique rotation of the factors, especially for an exploratory factor analysis in which there is little prior work to guide hypotheses or to formulate theories regarding associations among factors? The most common approach to addressing this problem is to generate a correlation matrix among the principal components following oblique rotation.
Consider the simple case of two principal components, Factor A and Factor B, as illustrated previously in Figures 4 and 5. If the correlation between these two factors following oblique rotation is 0, then an orthogonal solution would be appropriate. At the other extreme, if the intercomponent correlation is 1.0, then the factor analysis would be redone with only one factor. So, oblique rotation is not needed for either of these extremes of very “low” or very “high” intercomponent correlations.
What exactly is meant by a “low” or “high” correlation? There are no hard and fast rules. In general, an oblique principal component solution with intercomponent correlations of less than 0.2 to 0.3 could probably be modeled appropriately with orthogonal components, whereas oblique solutions with intercomponent correlations greater than 0.7 to 0.8 would probably justify redoing the analysis with one less component. Gorsuch (1983) argues that the upper bound for intercomponent correlations cannot be expected to be greater than the correlations between the sets of variables weighted highly on each contributing factor. For example, consider the hypothetical oblique solution depicted previously in the lower panel of Figure 5. If the correlations between the two speech recognition variables weighted the highest on Factor A, and the two satisfaction or usage variables weighted the highest on Factor B ranged from 0.3 to 0.4, then this would represent the upper bound for the expected correlation between Factors A and B.
Why should one be concerned about the upper bound for the intercomponent correlations when evaluating the results from oblique rotations of the factors? Although many procedures are used in oblique rotation, the most common is known as promax (Hendrickson & White, 1964). A detailed description of this procedure is beyond the scope of this brief tutorial, but the name is derived from max imizing the solution using the mathematical Procrustes procedure; hence the name, promax.
Important to the present discussion, however, is that this oblique factor rotation method has a parameter, k, that is allowed to vary such that k is a positive integer. For k = 1, the orthogonal solution is obtained. So, for oblique rotation, k is typically greater than 1 and the most common initial value for k is 4 (Gorsuch, 1983). Importantly, the intercomponent correlations will increase proportionately with k. As a result, higher k values will always reveal higher intercomponent correlations. Thus, the criterion for the optimal k value and a valid representation of the intercomponent correlation cannot be based on the size of the correlation alone. Otherwise, the highest possible k value would always represent the best solution. If one takes this to the limit and k is allowed to increase continually, the intercomponent correlations will eventually become high enough to result in a model with fewer components. Thus, for the promax oblique factor rotation procedure, an upper bound for the intercomponent correlations must be set. As noted, Gorsuch (1983) recommends that this upper bound should correspond to the correlation between the sets of the most salient (highest weighted) dependent variables on each of the factors involved in the intercomponent correlations.
Whether the researcher uses oblique or orthogonal rotation of factors in factor analysis, the ultimate goal is to obtain the simplest possible structure that underlies the performance of a group of individuals on a set of dependent variables. Early in the development of factor analytic approaches, Thurstone (1947) identified several criteria for the evaluation of a solution's simplicity. These criteria are: (1) each variable should have at least one factor weighting of 0; (2) each factor should have several variables, unique to that factor, with factor weights of 0; (3) for every pair of factors, there should be several variables whose weights are 0 for one factor, but not for the other factor of the pair; (4) whenever four or more factors emerge, for every pair of factors, a large proportion of the variables should have factor weights of 0; and (5) for every pair of factors, only a small number of variables should have nonzero factor weights on both factors of the pair. These criteria represent general guidelines to the simplicity of the factor solution and are still appropriate to consider when alternative factor rotations are evaluated.
The foregoing paragraphs of this section have provided a brief overview of some of the principles and features of exploratory factor analysis in general, and principal components analysis in particular. It is hoped that one of the things that should have become apparent to the reader is that the researcher has a series of decisions to make regarding any factor analysis. For example, decisions must be made with regard to the number of components, their interpretation, and their correlation. Often, hard and fast rules are not available to guide the researcher, but only general guidelines. That an element of subjectivity exists in making each of these decisions can perhaps can be tolerated better when it is recalled that the purpose of exploratory factor analysis is seldom to obtain “the” solution or model for the problem being studied. Rather, it is an attempt to synthesize prior work and new data in the development of a preliminary model that will lead to subsequent research. Only with additional research and modeling will a “final” solution be obtained.
In the remaining sections of this article, principal components analysis is applied to three sets of data on hearing aid outcome measures. This tool is used to model the nature of the factors underlying the construct of hearing aid outcome. Once the number of dimensions and the intercomponent correlations were identified for hearing aid outcome, it was of interest to determine what variables obtained from the individuals in each might predict performance for a given dimension. This was accomplished by saving the factor scores (calculated via linear regression) from the final principal component solution for each data set and then conducting multiple regression analyses in an attempt to predict the factor scores (standardized factor scores were used in which the mean is always 0 and the standard deviation is 1).
Principal components analysis was again used prior to the multiple regression analyses to reduce the large set of potential predictor variables to a more manageable set. In this use of principal components analysis, no attempt was made to understand the factors underlying the collection of prefit variables, although the interpretation of the factor weights was straightforward in most cases. Instead, principal components analysis was just used as a statistical tool to reduce the redundancy in the set of predictor variables and, via orthogonal rotation, produce a set of uncorrelated predictors to avoid the problem of collinearity for the subsequent regression analyses.
Indiana University Study of Hearing Aid Outcome for Single-Channel, Linear ITE Hearing Aids (IU-1)
Study Overview
Details regarding the study sample, hearing aid fitting protocol, and outcome measures can be found in Humes et al. (2001). The details regarding most of the prefit predictor variables obtained from all participants in that study can be found in Humes (2002). As a result, only a general overview of this study will be presented here.
Table 1 summarizes the characteristics of the subject sample in the IU-1 study. As noted, 173 elderly individuals participated in the study, of whom about 68% were men, and 39.3% were prior hearing aid users. All participants were fit with the same full-concha ITE hearing aids, with the gain and output-limiting characteristics of the circuitry adjusted individually. The circuitry was a single-channel, linear amplifier with output-limiting compression. All hearing aids were fit binaurally.
Table 1.
Summary of Demographic Characteristics of each of the Three Hearing Aid Studies Evaluated
| Variable | IU-1 | Study IU-2 | NIDCD/VA |
|---|---|---|---|
| Number of Subjects (N) | 173 | 53 | 333–338* |
| Mean (SD) Age (years) | 73.1 (6.5) | 74.6 (6.9) | 67.2 (11.3) |
| Age Range (years) | 60–87 | 61–89 | 29–91 |
| Mean (SD) Pure-tone Average (dB HL)** | 39.3 (11.9) | 36.0 (10.5) | 39.0 (11.4) |
| Mean (SD) HF Pure-tone Average (dB HL) | 50.9 (11.4) | 48.2 (10.3) | 50.0 (10.4) |
| % of Study Sample, Male | 68 | 66 | 57 |
| % of Study Sample, Prior HA Users | 39.3 | 26.4 | 53.2 |
N varied with circuit type.
re: ANSI (1996).
IU, Indiana University; NIDCD/VA, National Institute of Deafness and other Communication Disorders/Veterans Administration.
Prior to being fit with the study hearing aids, each listener completed a series of audiological, auditory processing, cognitive, and psychological measures over a series of several test sessions. The psychological measures ranged from communication-related scales of attitudes, expectations, and handicap to more global measures of health-related locus of control and general healthcare attitudes. Again, details regarding most of these measures and the results obtained can be found in Humes (2002). However, most of the communication-related and health-related surveys obtained from the 173 study participants have not been described in detail previously and are described as follows:
Two communication-related surveys were administered. The first, completed during the prefit portion of the project, was a 12-item hearing aid expectations questionnaire developed by Bentler et al. (1993). Higher scores on this expectations scale reflect the subject's greater expectations regarding the potential benefit of the hearing aids. The second was the 25-item Hearing Handicap Inventory for the Elderly (HHIE) (Ventry and Weinstein, 1982). Overall HHIE scores, as well as scores for the social and emotional subscales, were recorded.
The 11-item Health Locus of Control (HLC) scale (Wallston et al., 1976) measures the extent to which one internalizes or externalizes the responsibility for one's health.
The 16-item Health Opinion Survey (HOS) (Krantz, Baum, and Wideman, 1980) produced composite scores and scores for 2 subscales recorded from each participant. This survey assesses preferences for different healthcare treatment approaches with one subscale measuring preferred sources for health-related information (self versus healthcare professional) and the other measuring preferred behavioral involvement in treatment (active self care versus passive reliance on healthcare professional).
The nine-hole peg test of finger dexterity (Mathiowetz et al., 1985) measures the time it takes for participants to place nine small pegs on a pegboard. Measures were repeated three times with each hand, with the first trial discarded as practice and the remaining two averaged. Scores were also obtained with the participant blindfolded to eliminate visual feedback. This measure was included since hearing aid wearers must often make adjustments to their devices without being able to see the devices or the controls on the devices. Four measures of finger dexterity were made: two for each hand, one with visual feedback and one without.
Twenty hearing aid outcome measures (multiple measures of hearing aid performance, benefit, satisfaction, and usage) were obtained from all 173 hearing aid wearers after 1 month of hearing aid use. The specific measures, organized by the general category of outcome measure, are summarized in Table 2. Ideally, as noted in the previous section, it is desirable to have three to four measures from each domain of interest, but only two measures of hearing aid satisfaction were available. Nonetheless, these measures were included in the ensuing principal components analysis.
Table 2.
Summary of the 20 Hearing Aid Outcome Measures in the IU-1 Study
| Outcome Category | Variable | Description |
|---|---|---|
| Hearing Aid Usage | HDABI-use | Mean frequency of hearing-aid usage, 14 situations |
| GHABP-use | Mean frequency of hearing-aid usage, 4 situations | |
| Daily use | Mean hours per day hearing-aid usage from daily diary | |
| Subjective Benefit | HAPI-spn | Mean score for speech-in-noise HAPI subscale |
| HAPI-spq | Mean score for speech-in-quiet HAPI subscale | |
| HAPI-red-cues | Mean score for HAPI subscale, speech with reduced cues | |
| HAPI-nonspeech | Mean score for HAPI subscale, non-speech sounds | |
| HDABI-ben | Mean helpfulness of hearing aids, 14 listening situations | |
| GHABP-ben | Mean helpfulness of hearing aids, 4 listening situations | |
| GHABP-perf | Mean aided performance rating of hearing aids, 4 situations | |
| Satisfaction | MarkeTrakIV* | Mean satisfaction rating on 28 items, 5-point scale |
| GHABP-sat | Mean satisfaction rating, 4 listening situations | |
| Speech Recognition | NST-unaided | Percentage correct on NST, 65 dB SPL, +8 dB SNR, unaided |
| NST-aided | Percentage correct on NST, 65 dB SPL, +8 dB SNR, aided | |
| CST50-unaided | Percentage correct on CST, 50 dB SPL, in quiet, unaided | |
| CST65-unaided | Percentage correct on CST, 65 dB SPL, +8 dB SNR, unaided | |
| CST80-unaided | Percentage correct on CST, 80 dB SPL, 0 dB SNR, unaided | |
| CST50-aided | Percentage correct on CST, 50 dB SPL, in quiet, aided | |
| CST65-aided | Percentage correct on CST, 65 dB SPL, +8 dB SNR, aided | |
| CST80-aided | Percentage correct on CST, 80 dB SPL, 0 dB SNR, aided |
Kochkin, 1997; HDABI, Hearing Disability and Benefit Inventory (Gatehouse, 1999); GHABP, Glasgow Hearing Aid Benefit Profile (Gatehouse, 1999); HAPI, Hearing Aid Performance Inventory (Walden et al., 1984); CST, Connected Speech Test (Cox et al., 1988); NST, Nonsense Syllable Test (Levitt and Resnick, 1978); IU, Indiana University.
In future research, however, the researcher should obtain additional measures of hearing aid satisfaction and, perhaps, hearing aid usage. At present, limited as it may be with regard to some potential domains of hearing aid outcome, this set of hearing aid outcome measures represents the most extensive set of such measures available from the same hearing aid wearers. In addition, the inclusion of both unaided and aided speech recognition scores as outcome measures, rather than aided measures together with the difference between aided and unaided scores as in Humes (1999) and Humes et al. (2001), followed from the Humes (2002) finding that a single speech recognition factor underlies both unaided and aided measures. This, in turn, afforded a more parsimonious account of factors underlying speech recognition performance in these listeners. (As will be seen in the next section, this also proved to be the case when the outcome measures that were associated with measured speech recognition performance were combined with several subjective or self-report measures of hearing aid outcome.)
Principal Component Factor Analyses
To examine the redundancy among the 20 outcome measures and to identify a more parsimonious underlying structure, principal component factor analyses (Gorsuch, 1983) were conducted. Factors were identified by the use of a selection criterion of eigenvalue >1.0, and missing data were replaced with mean values. In the worst case (aided speech recognition scores for the highest speech presentation level), 4% of the data were missing. Typically, less than 1% of the data for a given outcome measure were missing.
Three principal components, accounting for 66.5% of the total variance among the 20 hearing aid outcome measures, were identified. Table 3 presents the component weights of each of the 20 outcome variables for each of the resulting principal components following orthogonal rotation (the varimax procedure was used) of the three components. The communality value for each outcome variable is also provided in this table. For 8 of the 20 outcome variables, the communality was high (≥ 0.7), whereas it was at least of moderate strength for the remaining 12 outcome variables. That is, no variables were observed to have low communality (≤ 0.4) for this solution. Based on the observed pattern of principal component weights, the first factor, accounting for 26.5% of the total variance, was identified as hearing aid subjective benefit and satisfaction. The second factor, accounting for 25.2% of the variance, was labeled as a general speech recognition factor, based on the heavy loadings of both unaided and aided speech recognition scores on this factor. Finally, the third factor, accounting for 14.8% of the total variance, was identified as a hearing aid usage factor.
Table 3.
Principal Component Weights or Factor Loadings*
| Variable | PC-Subjective Benefit and Satisfaction (26.5%) | PC-Speech Recognition Performance (25.2%) | PC-Hearing Aid Usage (14.8%) |
|---|---|---|---|
| HDABI-use (0.81) | 0.35 | −0.80 | |
| GHABP-use (0.82) | −0.30 | 0.84 | |
| Daily use (0.68) | 0.82 | ||
| HAPI-spn (0.76) | 0.87 | ||
| HAPI-spq (0.70) | 0.75 | −0.34 | |
| HAPI-red-cues (0.69) | 0.79 | ||
| HAPI-nonspeech (0.76) | 0.79 | −0.35 | |
| HDABI-ben (0.53) | 0.67 | ||
| GHABP-ben (0.68) | −0.69 | 0.46 | |
| GHABP-perf (0.50) | 0.60 | 0.33 | |
| MarkeTrakIV (0.67) | −0.79 | ||
| GHABP-sat (0.72) | −0.76 | 0.37 | |
| NST-unaided (0.64) | 0.77 | ||
| NST-aided (0.54) | 0.72 | ||
| CST50-unaided (0.68) | 0.80 | ||
| CST65-unaided (0.78) | 0.86 | ||
| CST80-unaided (0.54) | 0.72 | ||
| CST50-aided (0.71) | 0.84 | ||
| CST65-aided (0.59) | 0.76 | ||
| CST80-aided (0.49) | 0.70 |
Loadings are given for each of the three orthogonal components identified in the analysis of the hearing-aid outcome measures from the Indiana University-1 (IU-1) study. The communality value for each variable has been provided in parentheses after the variable name. Weights less than 0.30 have been omitted from the table for clarity. The percentage of variance accounted for by each of the three principal components is indicated in parentheses following each component's label. PC, orthogonal principal component from factor analysis of prefit measures in the IU-1 study. See Table 2 for other abbreviations.
The orthogonal solution in Table 3, however, reveals that several outcome measures are loaded on more than one of the orthogonal components. For example, two of the top three measures in this table, all measures of hearing aid usage, are most heavily weighted on the third component, but still have some weight on the first component. This suggests that it may not be appropriate to model the three outcome dimensions as independent dimensions. Rather, the dimensions may be correlated with one another.
As noted in the previous section, one way within principal component analysis to examine this possibility is to make use of oblique, rather than orthogonal, rotation of the components. The promax rotation procedure, with the k parameter set to a value of 4, was used to examine oblique rotation. The oblique rotation of the three components yielded pattern and structure weights (which are similar to factor weights) consistent with the labeling of the three outcome dimensions from the orthogonal rotation that was previously described and indicated that the correlation between components was moderate in two of the three cases. Specifically, the correlation between the subjective benefit and satisfaction component and the speech recognition component was 0.01, whereas it was −0.42 between subjective benefit and satisfaction and the hearing aid usage component. The correlation between the speech recognition component and the hearing aid usage component was −0.32.
These intercomponent correlations are very similar to the expected upper bounds for the correlations, which as noted in the previous section, are based on the correlations observed among the variables corresponding to the most salient variables associated with each factor. Thus, the decision was made that it would be most appropriate to model the hearing aid outcome measures from this group of 173 elderly hearing aid wearers as three components, with two of the three moderately correlated with one another. This factor solution was used to generate factor scores for each of the three correlated (oblique) factors for all 173 participants.
Regression Analyses
Next, regression analyses were to be performed between the prefit variables and each of the three, correlated hearing aid outcome components identified above. Prior to performing such regression analyses, however, the redundancy among the large set of prefit predictor variables was examined and reduced. Principal components factor analysis was again used to accomplish this and resulted in 61 potential prefit variables being reduced to 16 orthogonal principal components accounting for 75.7% of the total variance. In addition, communality values for 45 of the 61 prefit variables were high, 16 were moderate, and 0 were low. Orthogonal rotation of principal components was used for the prefit measures to eliminate the potential for collinearity among the set of predictor variables in subsequent multiple regression analyses. The 16 principal components identified among the battery of prefit measures appear in the first 16 rows of Table 4.
Table 4.
Predictor Variables for the IU-1 Study
| Predictor Variable | Description |
|---|---|
| PC-Audibility | Average hearing loss, aided and unaided; hearing aid gain |
| PC-Verbal IQ | Raw scores on the verbal scales of the WAIS-R (Wechsler, 1981) |
| PC-LDL | Loudness discomfort levels (LDL) for pure tones, 1000–3000 Hz |
| PC-PBmax | Maximum monosyllabic word-recognition score under headphones |
| PC-DPOAE | Average DPOAE signal-to-noise ratio in dB, 2000–6300 Hz |
| PC-Nonverbal IQ | Raw scores on the nonverbal scales of the WAIS-R |
| PC-Dexterity | Scores on 9-hole peg test, with and without vision, right and left hands |
| PC-TempProc/Exp | Auditory temporal-processing measures and hearing-aid expectations |
| PC-As-worn Gain | Average as-worn hearing-aid gain, 1000–4000 Hz |
| PC-ABR | Wave-V latencies of the auditory brainstem response, both ears |
| PC-CPHI-adj | CPHI adjustment factor score and HHIE (negatively weighted) |
| PC-CPHI-import | CPHI communication-importance factor score |
| PC-DPOAE-lf | Average DPOAE signal-to-noise ratio in dB, 1000–1500 Hz |
| PC-CPHI-react | CPHI factor score representing reaction to communication problems |
| PC-HLC | Score on Health Locus of Control scale |
| PC-HOS | Score on Health Opinion Survey |
| JSQ-1 | PC, aided Judgements of Sound Quality scale (soft, full, spacious, total) |
| JSQ-2 | PC, aided Judgements of Sound Quality (bright, clear, near, loud) |
| Age | Chronological age in years (positively correlated with duration retired) |
| HA-exper | Hearing-aid experience categorized on a 0–5 scale, proportional to use |
| Dur-occup | Duration in primary occupation, in years |
| Other-prob | Problems with other prosthetic devices (eyeglasses, dentures) |
| Liv-arrange | Living arrangement (living alone independently, with spouse, children) |
| Activity-level | Number and frequency of outside interests and social activities |
| SES | Socioeconomic status based on self-reported annual income |
IU, Indiana University; DPOAE, distortion product otoacoustic emissions; CPHI, Communication Profile for the Hearing Impaired (Demorest and Erdman, 1987); PC, orthogonal principal component from factor analysis of prefit measures in the IU-1 study.
A set of 16 orthogonal factor scores representing these prefit measures was saved for each of the 173 participants. In addition to these 16 prefit factor scores (as noted in Table 4), 2 orthogonal principal components from an analysis of the aided sound-quality judgments (Humes et al., 2001; Narendran and Humes, in press) and 7 variables taken from the information each participant provided in the detailed case history (bottom seven rows of Table 4) were included.
The resulting 25 potential predictor variables for the 173 subjects served as the input to 3 stepwise multiple regression analyses, 1 regression analysis for each of the 3 hearing aid outcome factor scores. Table 5 summarizes the results of these multiple regression analyses. Significant linear regression fits were obtained in all three cases. However, only one predictor variable entered the regression equation when an attempt was made to predict factor scores associated with subjective benefit and satisfaction, and this variable accounted for only 7.1% of the total variance. The sole predictor variable in this equation was a factor score representing the perceived sound quality for amplified speech and music (JSQ-1). The standardized β coefficient in Table 5 for this predictor variable indicates that as the perceived sound quality of amplified speech and music increased, the subject's ratings of subjective benefit and satisfaction also tended to increase. As noted, however, this trend was a weak one and only accounted for a small percentage (about 7%) of the variance.
Table 5.
Summary of the Regression Analyses Performed from the IU-1 Study*
| Outcome PC | % Total Variance | Predictor Variable | β Coefficient | F (df) | P |
|---|---|---|---|---|---|
| PC-Subj Benefit/Satisfaction | 7.1 | JSQ-1 | 0.267 | 13.1 (1,171) | <.001 |
| ∑ = 7.1 | |||||
| PC-Speech Recognition Perf. | 44.9 | PC-Audibility | −0.514 | 18.6 (6, 166) | <.001 |
| 6.5 | PC-Verbal IQ | 0.274 | |||
| 5.6 | Age | −0.298 | |||
| 3.4 | HA-exper | −0.183 | |||
| 2.3 | PC-CPHI-adj | 0.161 | |||
| 2.1 | PC-LDL | −0.151 | |||
| ∑ = 64.8 | |||||
| PC-Hearing Aid Usage | 14.7 | HA-exper | 0.383 | 16.7 (3, 169) | <.001 |
| 5.0 | Dur-occup | 0.195 | |||
| 3.2 | PC-Verbal IQ | −0.182 | |||
| ∑ = 22.9 |
Analysis was for each of the three hearing aid outcome factor scores (oblique rotation). The β coefficients for each variable are in standardized form such that they range from −1 to 1. The F, degrees of freedom (df), and P values for each regression equation are also provided. PC, orthogonal principal component from factor analysis of prefit measures in the IU-1 study. Descriptions of predictor variables are provided in Table 4. IU, Indiana University.
The regression analysis was most effective for the prediction of individual differences in the factor associated with general speech recognition performance, both aided and unaided. As indicated in Table 5, the best-fitting regression equation for this outcome factor accounted for 64.8% of the total variance with six predictor variables. Examination of the variables, and the percentage of variance accounted for by each, indicates that nearly two thirds of the systematic variance was accounted for by one variable: hearing loss or audibility. As hearing loss increased, speech recognition performance decreased (whether measured in unaided or aided conditions). A review of the standardized β coefficients for the best-fitting regression equation in the lower portion of Table 5 indicates that speech recognition performance of the 173 elderly hearing aid wearers tended to increase as verbal IQ and adjustment to hearing loss (CPHI-adjust) increased, but decreased as age, prior hearing aid experience, and loudness discomfort levels (LDLs) increased.
It should be noted that the regression analysis for the outcome factor associated with speech recognition performance did not include the PB-max prefit measure as a predictor variable. It did not seem appropriate to include a prefit measure of speech recognition performance as a predictor of other measures of speech recognition performance. However, to examine the potential improvement in predictive accuracy by including PB-max as a predictor variable, a second regression analysis was completed for the factor score associated with speech recognition performance that included the PB-max measure as a predictor variable. As expected, the resulting regression analysis accounted for more of the total variance (72.1%) than that accounted for without the PB-max variable (64.8%), with the difference in variance accounted for associated almost entirely with the 8.9% of the total variance accounted for by the PB-max variable itself. That is, many of the other variables in the resulting regression equation were identical to those shown previously in Table 5, including the proportion of variance accounted for by each variable. For example, hearing loss and verbal IQ accounted for 44.9% and 6.5% of the total variance in both equations, whereas the percentage of variance accounted for by prior hearing aid experience decreased from 3.4% to 1.8%. In general, though, the variance accounted for by the regression equation with the full set of 25 predictor variables, including PB-max, was about 8% higher than that accounted for without it.
When the factor score associated with hearing aid usage was the dependent variable, the predictive accuracy of the regression equation was much better than for hearing aid satisfaction, but not as good as that for speech recognition performance, as shown in the bottom of Table 5. In this case, 22.9% of the total variance in hearing aid usage could be accounted for by three variables. As noted in Table 5, prior hearing aid experience was the best predictor of current hearing aid usage, with this variable alone accounting for about two thirds (14.7% of 22.9%) of the total systematic variance accounted for. Examination of the β coefficients for the best-fitting regression equation in Table 5 indicates that hearing aid usage increased as prior hearing aid experience and the number of years of employment increased, but decreased as verbal IQ increased.
Study Summary
The results from the IU-1 study suggest that three oblique (correlated) principal components captured the relevant aspects of hearing aid outcome: (1) subjective benefit and satisfaction; (2) aided and unaided speech recognition performance; and (3) hearing aid usage. The use of multiple regression analysis to identify the variables underlying individual differences in performance along each of these outcome dimensions was most successful for aided and unaided speech recognition performance and least successful for subjective benefit and satisfaction.
Indiana University-2 Study of Hearing Aid Outcome
Study Overview
The primary purpose of this smaller scale study (IU-2) of two-channel WDRC, ITC hearing aids was to determine whether the underlying dimensions of hearing aid outcome varied with the style of hearing aid and the type of electronic circuitry. The selection criteria for participation in this follow-up study were identical to those of the previously described study (IU-1) (Humes et al., 2001). Table 1 summarizes the basic demographics of this group of elderly hearing aid wearers.
The basic study protocol of the IU-2 study was identical to that of the IU-1 study, with the primary exception being the hearing aid-fitting protocol. Since the IU-2 study made use of nonlinear circuitry, the linear prescriptive procedure followed in the IU-1 study (NAL-RP; Byrne, Parkinson, and Newall, 1990) could not be used to set the targets for gain and output. Instead, the FIG6 prescriptive approach (Killion and Fikret-Pasa, 1993) was employed and the hearing aid was adjusted to match the level-dependent frequency-gain characteristics prescribed by this approach. The other primary difference between the IU-1 and IU-2 studies was that the circuitry was packaged in a full-concha ITE shell in the IU-1 study and in an ITC shell in the IU-2 study.
Identical hearing aid outcome measures were obtained in both the IU-1 and IU-2 studies, and these were summarized previously in Table 2. In addition to these 20 outcome measures, the prefit measures described for the IU-1 study were also obtained in the IU-2 study, but given the much smaller sample size of the IU-2 study, multiple regression analyses were not attempted. Rather, the focus was on the nature of the factor structure underlying the 20 hearing aid outcome measures obtained following use of a hearing aid that was different in type and circuitry from that of the IU-1 study. In addition, given the smaller sample size, a full exploratory factor analysis was not performed. Rather, the number of factors was fixed at three, and the solution was examined for both orthogonal and oblique rotation of the three factors.
Principal Component Factor Analyses
The rotated orthogonal principal components solution for the 20 outcome measures from the 53 elderly hearing aid wearers in the IU-2 study is presented in Table 6. The communality value of each outcome variable for the final solution is also provided in this table. The values were high for 12 of the 20 variables, moderate for 6 of the 20 dependent variables, and low for 2 of the 20 variables (GHABP-perf and HDABI-ben). The high communalities indicate that the factor solution is likely to be stable, even with a relatively small sample size (MacCallum et al., 1999). The three principal components that emerged from this analysis accounted for 67.7% of the total variance, similar to that accounted for in the IU-1 study with different subjects and hearing aids.
Table 6.
Principal Component Weights or Factor Loadings (IU-2 Study)*
| Variable | PC-Speech Recognition Performance (27.5%) | PC-Hearing Aid Usage (21.0%) | PC-Subjective Benefit and Satisfaction (19.2%) |
|---|---|---|---|
| HDABI-use (0.79) | −0.87 | ||
| GHABP-use (0.79) | 0.86 | ||
| Daily use (0.73) | 0.85 | ||
| HAPI-spn (0.72) | 0.83 | ||
| HAPI-spq (0.79) | −0.56 | 0.67 | |
| HAPI-red-cues (0.76) | 0.86 | ||
| HAPI-nonspeech (0.75) | −0.56 | 0.64 | |
| HDABI-ben (0.40) | 0.56 | ||
| GHABP-ben (0.68) | 0.71 | −0.40 | |
| GHABP-perf (0.31) | 0.48 | ||
| MarkeTrakIV (0.65) | 0.44 | −0.67 | |
| GHABP-sat (0.63) | 0.63 | −0.47 | |
| NST-unaided (0.74) | 0.85 | ||
| NST-aided (0.66) | 0.80 | ||
| CST50-unaided (0.72) | 0.85 | ||
| CST65-unaided (0.86) | 0.91 | ||
| CST80-unaided (0.44) | 0.66 | ||
| CST50-aided (0.81) | 0.88 | ||
| CST65-aided (0.77) | 0.88 | ||
| CST80-aided (0.54) | 0.62 | 0.30 |
These are for each of the three orthogonal components identified in the analysis of the hearing aid outcome measures from the IU-2 study. The communality value for each variable has been provided in parentheses after the variable name. Weights less than 0.30 have been omitted from the table for clarity. The percentage of variance accounted for by each of the three principal components is indicated in parentheses following each component's label. PC, orthogonal principal component from factor analysis; IU, Indiana University.
For the factor solution shown in Table 6, the first component was identified as aided and unaided speech recognition performance and accounted for 27.5% of the total variance. The second factor was interpreted as hearing aid usage and accounted for 21.0% of the total variance. Finally, the third factor was interpreted as hearing aid benefit and satisfaction and accounted for 19.2% of the total variance. Aside from the interpretation of the first factor, however, the assignment of labels to factors was more challenging for the factor loadings from the IU-2 study than for the previous IU-1 study. This was because much more overlap was apparent for the weighting of the second and third principal components. That is, many of the hearing aid outcome variables were weighted moderately high on both the second and third factors of this solution. This suggests, as with the IU-1 study, that the factors may be correlated and that an oblique rotation of the factors would be more appropriate.
To explore this further, oblique rotation of the three factors was accomplished by the use of the same method (promax procedure with k = 4) described previously in the analysis of the IU-1 study. The resulting component correlation matrix indicated that the speech recognition factor was not correlated strongly with either of the other two factors (r = −0.12 and 0.02), but that the subjective benefit and satisfaction factor was moderately correlated (r = −0.48) with the hearing aid usage factor.
Study Summary
The IU-1 and IU-2 study protocols were virtually identical, with the exception of the prescriptive procedures used to generate target gain and output values for the differing hearing aid circuitry and the associated procedures used to verify the match to the target values prescribed. The primary difference between studies was the style of hearing aid (full-concha ITE versus ITC) and the electronic circuitry (single-channel, linear circuit with output-limiting compression versus two-channel wide-dynamic-range-compression circuit). Despite these differences, very similar three-factor solutions were identified in both studies, with each accounting for about two thirds of the total variance in outcome measures. Moreover, the nature of the three underlying dimensions was similar in both IU studies, and moderate correlation between at least two of the three underlying components (subjective benefit and satisfaction, and hearing aid usage) was observed in both as well. Finally, despite the sample size being smaller than desired, the communality values and the percentage of total variance accounted for suggest that the resulting factor solution was a reasonable fit to this new set of data.
NIDCD/VA Study of Hearing Aid Outcome
Study Overview
Larson et al. (2000) presented the results from 360 hearing aid wearers participating in a large-scale crossover clinical trial in which each participant wore each of three hearing aid circuits packaged in an identical ITE shell. The three single-channel circuits worn by each listener in that study included: (1) a linear circuit with peak clipping; (2) a linear circuit with output-limiting compression; and (3) a circuit with wide-dynamic-range compression. Although 360 individuals were enrolled in this study, from 333 to 338 individuals actually completed all of the outcome measures for a given circuit.
Table 1 summarizes some of the demographic characteristics of the subjects comprising this study sample. Although the NIDCD/VA study did not specifically target elderly adults, 80% of the subjects in that study were at least 58 years of age. It is also clear from Table 1 that the subjects in all three studies analyzed here were very similar in terms of age, average hearing loss, and gender composition, although the three studies differed considerably in terms of the percentage of prior hearing aid users. In addition, the style of hearing aid, the circuitry for at least one of the circuits, and the prescriptive approach for the selection of frequency-gain characteristics for the NIDCD/VA study were identical to those of the IU-1 study. Further, in all three studies, hearing aids were fit to both ears.
The number and nature of the hearing aid outcome measures in the NIDCD/VA study, however, were only somewhat similar to those used in the two IU studies. The closest similarities were in the measures of unaided and aided speech recognition performance in which the Connected Speech Test (CST) (Cox et al., 1988) was the specific test used. In addition, all three studies analyzed here used at least three sets of speech levels and signal-to-noise ratios (SNRs). The NIDCD/VA study actually used nine combinations of speech level and SNR for the CST, plus an additional test in quiet, and the three conditions most like those from the two IU studies were selected for inclusion in these analyses.
All three studies included in this article also used measures of subjective benefit and satisfaction, and hearing aid usage. However, the NIDCD/VA study used a smaller number of measures than the two IU studies, and little or no overlap in instruments occurred across studies. For example, whereas the two IU studies used the HDABI (Gatehouse, 1999), GHABP (Gatehouse, 1999) and HAPI (Walden et al., 1984) as measures of subjective hearing aid benefit, the NIDCD/VA study used the PHAB (Cox and Gilmore, 1990).
In similar fashion, the NIDCD/VA study used measures of hearing aid usage and satisfaction that were less detailed and fewer in number than those used in the IU-1 and IU-2 studies. Nonetheless, some measures of subjective hearing aid satisfaction and usage were available from the NIDCD/VA study, which were combined with the six measures of aided and unaided speech recognition similar to those used in IU-1 and IU-2. This resulted in 16 outcome measures obtained from the approximately 320 participants, with complete data following the use of each of the 3 hearing aid circuits (N varied from 318 to 324 across the three circuits).
The outcome measures derived from the NIDCD/VA study are summarized by category in Table 7. As shown in the table, there were two self-report measures of hearing aid usage, five of subjective benefit, three of hearing aid satisfaction, and six measures of aided and unaided speech recognition performance. Regarding the measures of subjective benefit, only five of the seven scales of the PHAB were included. The aversiveness and distortion subscales of the PHAB were not included, as they were considered to be more akin to aided measures of perceived sound quality rather than of the helpfulness of the hearing aid. These two subscales, however, were used in the regression analyses, just as similar measures of sound quality had been used in the regression analyses for the IU-1 study. The 16 resulting outcome measures were then subjected to principal components factor analysis, as described in detail in the next section.
Table 7.
Summary of the 16 Hearing Aid Outcome Measures in the NIDCD/VA Study
| Outcome Category | Variable | Description |
|---|---|---|
| Hearing aid Usage | Daily use | Mean hours per day hearing aid usage from Form 8, Q #1 |
| Weighted Use | Daily use, weighted by number of aids worn and whether aids were worn everyday, Form 8, Q #2 & #3 | |
| Subjective Benefit | PHAB-ec | Mean, ease of communication PHAB subscale |
| PHAB-cft | Mean, communication with familiar talkers PHAB subscale | |
| PHAB-cbn | Mean, communication in background noise PHAB subscale | |
| PHAB-rv | Mean, communication in reverberation PHAB subscale | |
| PHAB-rc | Mean, communication with reduced cues PHAB subscale | |
| Satisfaction | HA-prob | Score from Form 8, Q #4; 14 items; no problems=100; problems with both hearing aids on all 14 items=0 |
| Weighted HA-prob | HA-prob, weighted by whether problems resulted in decreased use of hearing aids (Form 8, Q #5) | |
| Satisfaction-Rating | Scale of 1–10 (10=best); hearing aid rated (Form 8, Q #6) | |
| Speech Recognition | CST62n-unaided | Percent correct on CST, 62 dB SPL, +8 dB SNR*, unaided |
| CST74n-unaided | Percent correct on CST, 74 dB SPL, +2 dB SNR, unaided | |
| CST74q-unaided | Percent correct on CST, 74 dB SPL, quiet, unaided | |
| CST62n-aided | Percent correct on CST, 62 dB SPL, +8 dB SNR, aided | |
| CST74n-aided | Percent correct on CST, 74 dB SPL, +2 dB SNR, aided | |
| CST74q-aided | Percent correct on CST, 74 dB SPL, quiet, aided |
CST, Connected Speech Test; PHAB, Profile of Hearing Aid Benefit; SNR, signal-to-noise ratio (dB). NIDCD/VA, National Institute of Deafness and other Communication Disorders/Veterans Administration.
SNR values varied in the NIDCD/VA study from subject to subject. The median SNR value for the 62 dB SPL presentation condition was +5 dB. Other SNR values were 3 dB higher and lower than this middle value (ie, additional SNR values of +8 and +2 dB).
Principal Component Factor Analyses
The results of the principal components analyses for all three circuit types were virtually identical, with each solution identifying five identical factors and accounting for 76.3% to 77.3% of the total variance. The only differences among the three solutions were in the ordering of the final three components, but since each of the final three components accounted for 12% to 13% of the total variance, the ordering was not considered important. As a result, only the factor loadings for the variables in the orthogonal rotation of the components for the linear circuit with output-limiting compression are presented in detail here. This will afford a more direct comparison to the IU-1 study in which subjects wore similar hearing aids.
These factor loadings, or weights, appear as column headings in Table 8, with the percentage of total variance accounted for by each indicated in parentheses. The communality values of each outcome variable for the final solution are also provided in parentheses after each variable's name in the table. Of the 16 variables, 12 had high communality values and 4 had moderate communality values. Note in Table 8 that no variables were weighted greater than 0.3 on more than one factor. This implies that the orthogonal solution is most likely valid, and this was confirmed by exploring oblique rotation of the factors (promax procedure with k = 4). Most of the intercomponent correlations for the five-component oblique solutions for each of the three circuits were less than 0.25. However, the correlation between the two speech recognition components ranged from 0.36 to 0.38. Overall, the intercomponent correlations were considered not to be appreciably different from zero, and the orthogonal solution was adopted. Again, the same orthogonal, five-factor solutions were obtained for all three circuits, with the only differences being the order of the final three components. Sets of 5 orthogonal factor scores were saved for each of the 320 participants in the NIDCD/VA study, and these factor scores were used in the subsequent regression analyses described below.
Table 8.
Principal Component Weights or Factor Loadings (NIDCD/VA study)*
| Variable | PC-Subjective Benefit (23.6%) | PC-Speech in Noise (14.3%) | PC-Speech in Quiet (13.4%) | PC-Satisfaction (12.6%) | PC-Usage (12.6%) |
|---|---|---|---|---|---|
| Daily use (0.94) | 0.95 | ||||
| Weighted Use (0.94) | 0.95 | ||||
| PHAB-ec (0.77) | 0.85 | ||||
| PHAB-cft (0.65) | 0.73 | ||||
| PHAB-cbn (0.85) | 0.90 | ||||
| PHAB-rv (0.83) | 0.90 | ||||
| PHAB-rc (0.78) | 0.86 | ||||
| HA-prob (0.82) | 0.90 | ||||
| Weighted HA-prob (0.79) | 0.89 | ||||
| Satisfaction-Rating (0.46) | 0.61 | ||||
| CST62n-unaided (0.62) | 0.73 | ||||
| CST74n-unaided (0.78) | 0.87 | ||||
| CST74q-unaided (0.78) | 0.85 | ||||
| CST62n-aided (0.71) | 0.78 | ||||
| CST74n-aided (0.84) | 0.87 | ||||
| CST74q-aided (0.67) | 0.81 |
These are shown for each of the five orthogonal components identified in the analysis of the hearing-aid outcome measures. The communality value for each variable has been provided in parentheses after the variable name. Weights less than 0.30 have been omitted from the table for clarity. The percentage of variance accounted for by each of the five principal components is indicated in parentheses following each component's label. PC, orthogonal principal component from factor analysis; NIDCD/VA, National Institute of Deafness and other Communication Disorders/Veterans Administration.
Regression Analyses
The range of prefit predictor variables available from the NIDCD/VA study was not as extensive as that of the two IU studies, because prediction of outcome was not a goal of the former study. Nonetheless, the number of variables appeared large enough, and the nature of the variables diverse enough, to explore the prediction of individual differences for each of the five outcome factors. As with the IU-1 study, many of the potential prefit predictor variables were likely to be redundant. To eliminate this redundancy and minimize collinearity among the final set of predictor variables, the prefit measures available were subjected to principal components analysis and saved as orthogonal factor scores. Prefit measures included in this principal components analysis were: (1) 5 CPHI factor scores; (2) 10 air-conduction pure-tone thresholds from both ears for frequencies ranging from 250 through 8000 Hz; (3) ipsilateral and contralateral acoustic reflex thresholds for both ears for stimulus frequencies of 500 and 1000 Hz; and (4) LDLs from both ears for frequencies of 500, 1000, 2000, 3000, and 4000 Hz. This represented a total of 43 prefit variables, which were reduced to 9 orthogonal principal component factor scores for each of the participants. The nine principal components identified for these prefit variables are shown in the top nine rows of Table 9. The orthogonal solution accounted for 79.9% of the total variance among the 43 prefit variables, and the communalities were high for 38 of the 43 variables and never less than 0.52.
Table 9.
Predictor Variables for the NIDCD/VA Study
| Predictor Variable | Description |
|---|---|
| PC-Hearing Loss-lf | Pure-tone thresholds from 250 through 1000 Hz, both ears |
| PC-LDL | Loudness discomfort levels from 500 through 4000 Hz, both ears |
| PC-ART | Acoustic reflex thresholds, ipsilateral & contralateral, 500 & 1000 Hz, both ears |
| PC-Hearing Loss-hf | Pure-tone thresholds from 3000 through 6000 Hz, both ears |
| PC-Hearing Loss-mf | Pure-tone thresholds at 1500 and 2000 Hz, both ears |
| PC-LDL-slope | LDL at 500 Hz negatively weighted and LDL at 4000 Hz positively weighted |
| PC-CPHI-react | CPHI factor score representing reaction to communication problems |
| PC-CPHI-perf & imp | CPHI factor scores representing communication performance and importance |
| PC-CPHI-adj & inter | CPHI factor scores representing adjustment to hearing loss and interaction |
| Age | Chronological age in years |
| Age-Onset-R | Age of onset of hearing loss in right ear |
| Age-Onset-L | Age of onset of hearing loss in left ear |
| HA-exper | Previous hearing-aid use in years |
| Level-Educ | Highest formal educational level achieved |
| Marital-Status | 1=married, 0=not married (single, divorced, widow/widower, separated) |
| Others-household | Number of additional adults and children living with subject |
| QR-like | Mean aided quality rating, 6 conditions; how much liked the listening experience |
| QR-noisy-n | Mean aided quality rating, 3 noise conditions; rated noisiness of listening |
| QR-noisy-q | Mean aided quality rating, 3 quiet conditions; rated noisiness of listening |
| QR-loud-high | Mean aided quality rating, 4 higher SPL conditions; rated loudness |
| QR-loud-low | Mean aided quality rating, 2 lower SPL conditions; rated loudness |
| PHAB-distort | Mean score for the distortion subscale of the PHAB |
| PHAB-aversive | Mean score for the aversiveness subscale of the PHAB |
NIDCD/VA, National Institute of Deafness and other Communication Disorders/Veterans Administration; PC = orthogonal principal component from factor analysis of prefit measures in the NIDCD/VA study.
In addition to these nine prefit predictors, measures of aided sound quality and various measures from the case history were included in the set of predictor variables. With regard to the sound quality measures, Larson et al. (2000) asked the participants to rate the quality, noisiness, and loudness of amplified speech at various sound levels (from 52 to 74 dB SPL) in quiet and noisy backgrounds. Based on the author's evaluation of these data with principal components analysis, it appeared that five sound quality measures were needed to represent these data: one overall measure of how much they liked the quality of the aided sound; two measures of the noisiness of amplified sound, one obtained in background noise and one in quiet conditions; and two measures of the loudness of amplified sound, one for the higher presentation levels and one for the lowest presentation level. These five measures of the quality of amplified sound were combined with the two sound quality-related subscales of the PHAB (aversiveness and distortion) for a total of seven measures of sound quality. These aided sound quality measures are summarized in the bottom seven rows of Table 9.
In addition to measures of aided sound quality, six additional measures were taken from the case history or other data forms available from the study and appear in Table 9. Three of the variables (level of education, marital status, and total number of other persons living in the subject's household) were included to provide at least indirect estimates of cognitive abilities and opportunities for social interactions while the hearing aids were worn. In the IU-1 study, for example, both verbal IQ and level of education were available as measures, and these two variables were positively correlated (r = 0.34, P < .001), suggesting that level of education might provide at least an indirect measure of cognitive function for the participants in the NIDCD/VA study.
Twenty-three potential predictor variables were used in the multiple regression analysis for each of the five outcome factors. The final set of 23 predictor variables is summarized in Table 9.
Although regression analyses were conducted for all three circuit types included in the NIDCD/VA study, only the regression analysis for the linear circuit with output-limiting compression will be presented here. The results were nearly identical for all analyses, with differences among circuits confined primarily to the nature of the lower-order variables entered into each equation. That is, the number of variables required, the nature of those variables, and the total variance accounted for were all very similar across circuits. The results for the linear circuit with output-limiting compression were chosen for presentation here because this circuit is identical to that used in the IU-1 study, the other study in this article for which multiple regression analyses were completed.
Table 10 presents the results of the multiple regression analyses for each of the five hearing-aid outcome factors in the NIDCD/VA study. The predicted factor scores are presented in this table in the order of their identification. For factor scores associated with measures of subjective benefit (PHAB), seven predictor variables account for 21.2% of the total variance in factor scores. Of these seven predictor variables, about three fourths of the variance was accounted for by two variables, the communication performance and importance factor from the CPHI, and how much the subject liked the quality of amplified sound. The remaining systematic variance was accounted for by measures of hearing loss or audibility, age, and level of education. In general, the standardized β coefficients for the best-fitting regression equation indicated that self-reported hearing aid benefit was directly correlated with the perceived communication performance and importance, how much the subject liked the sound quality of amplified speech, the amount of hearing loss, and the level of education. Subjective benefit was found to be inversely related to age.
Table 10.
Summary of the Regression Analyses (NIDCD/VA Study)*
| Outcome PC | % Total Variance | Predictor Variable | β Coefficient | F (df) | P |
|---|---|---|---|---|---|
| PC-Subjective Benefit | 8.5 | PC-CPHI-perf & imp | 0.237 | 13.3 (7, 312) | <.001 |
| 7.0 | QR-like | 0.165 | |||
| 1.8 | PC-Hearing Loss-lf | 0.197 | |||
| 1.1 | PC-Hearing Loss-mf | 0.170 | |||
| 1.0 | PC-Hearing Loss-hf | 0.173 | |||
| 0.9 | Age | −0.235 | |||
| 0.9 | Level-Educ | 0.103 | |||
| ∑ = 21.2 | |||||
| PC-Speech in Noise | 6.7 | PC-Hearing Loss-mf | 0.264 | 23.6 (1, 316) | <.001 |
| ∑ = 6.7 | |||||
| PC-Speech in Quiet | 18.9 | PC-Hearing Loss-lf | −0.401 | 28.1 (8, 309) | <.001 |
| 5.4 | Level-Educ | 0.202 | |||
| 4.4 | QR-noisy-q | 0.206 | |||
| 3.7 | PC-Hearing Loss-hf | −0.160 | |||
| 2.7 | PC-Hearing Loss-mf | −0.182 | |||
| 2.8 | Age | −0.144 | |||
| 2.0 | PC-LDL | −0.148 | |||
| 0.7 | PC-CPHI-react | 0.101 | |||
| ∑ = 40.6 | |||||
| PC-Hearing-Aid Usage | 9.4 | HA-exper | 0.242 | 12.3 (5, 312) | <.001 |
| 2.0 | QR-loud-low | −0.131 | |||
| 1.5 | Marital-Status | 0.120 | |||
| 1.2 | PC-LDL | 0.122 | |||
| 1.0 | PHAB-distort | 0.114 | |||
| ∑ = 15.1 | |||||
| PC-Satisfaction | 2.8 | PHAB-aversive | 0.155 | 7.7 (3, 314) | <.001 |
| 2.0 | QR-noisy-n | 0.132 | |||
| 1.2 | PC-Hearing Loss-lf | −0.124 | |||
| ∑ = 6.0 |
Analyses were performed for each of the five orthogonal hearing aid outcome factor scores for the linear circuit with output-limiting compression. The β coefficients for each variable are in standardized form such that they range from −1 to 1. The F, degrees of freedom (df), and P values for each regression equation are also provided. Descriptions of predictor variables are provided in Table 9 and outcome dimensions in Table 8. NIDCD/VA, National Institute of Deafness and other Communication Disorders/Veterans Administration.
The regression analysis for the outcome factor score associated with speech recognition performance in noise, on the other hand, was considerably less successful (Table 10). One variable, mid-frequency (1500 and 2000 Hz) hearing loss, accounted for 6.7% of the total variance. As mid-frequency hearing loss increased, speech recognition in noise tended to increase as well.
The maximum amount of total variance accounted for (40.6%) with any of the five outcome factors from the NIDCD/VA study was observed for speech recognition in quiet. Eight predictor variables were identified, with one variable, low-frequency (250–1000 Hz) hearing thresholds, accounting for nearly half of the systematic variance. Two of the remaining seven predictor variables were also associated with hearing loss. Together, these three hearing loss measures represented 25.3% of the total variance, or about 62% of the systematic variance. In all three cases, as the degree of hearing loss increased, speech recognition performance in quiet decreased. Other variables making significant contributions to the regression equation included level of education, perceived noisiness for amplified speech in quiet listening conditions, age, LDL, and the reaction scale of the CPHI. Level of education, perceived noisiness for amplified speech in quiet, and scores for the reaction scale of the CPHI were directly related to the speech-in-quiet factor scores, whereas age and LDL were inversely related.
For hearing aid usage, five variables accounted for 15.1% of the total variance in outcome factor scores. The most significant contributor to this regression equation, accounting for 9.4% of the total variance alone, was the number of years of previous hearing aid usage. As prior usage increased, factor scores for the usage outcome dimension also increased. Additional measures making significant contributions to the regression equation included three that had to do with subjective or qualitative aspects of auditory perception: the perceived loudness of low-level sounds, LDL, and the distortion subscale of the PHAB. Those that rated the loudness of low-level sounds as less loud had higher LDLs, thought the hearing aid reduced distortion to a greater degree, and tended to have higher hearing aid usage factor scores. Marital status also played a role: married individuals tended to use their hearing aids more than single persons.
Finally, individual differences in factor scores associated with hearing aid satisfaction were least well accounted for in this study. Three variables accounted for 6.0% of the total variance in hearing aid satisfaction. Two were related to the perceived sound quality of aided speech, and one involved hearing loss. Generally, satisfaction increased if amplified speech was perceived to be less aversive and less noisy, but satisfaction decreased as the amount of low-frequency hearing loss increased.
Study Summary
This study identified five orthogonal hearing aid outcome components or dimensions: (1) subjective benefit, (2) speech recognition performance in noise, (3) speech recognition performance in quiet, (4) hearing aid usage, and (5) hearing aid satisfaction. The same orthogonal dimensions were observed in the analysis of outcome measures from all three circuit types, although the ordering of the final three components varied with circuit type. Regarding the identification of variables that underlie individual differences in each of the hearing aid outcome factor scores, the highest percentage of variance accounted for was observed for the outcome factor associated with speech recognition in quiet (40.6% of the total variance). The lowest percentage of variance accounted for was observed for both speech recognition in noise (6.7%) and hearing aid satisfaction (6.0%).
The results of the regression analyses lie between these two extremes for the outcome measures associated with subjective benefit (22.8%) and hearing aid usage (15.1%). The percentage of variance accounted for and the specific variables included in the regression equation for each dimension of hearing aid outcome were very similar for all three circuit types.
Summary and General Discussion
Number and Nature of Hearing Aid Outcome Dimensions
Similarities and differences existed between the two IU studies and the NIDCD/VA study in the number and nature of the dimensions of hearing aid outcome. Hearing aid usage was identified as a separate dimension of hearing aid outcome in all three studies. However, whereas subjective benefit and hearing aid satisfaction were represented jointly as one factor in the IU-1 and IU-2 studies, each was a separate factor in the NIDCD/VA study. Likewise, although the two IU studies found all speech recognition performance (aided and unaided, in quiet and in noise) to be represented by a single speech recognition performance component, two components, one for speech in quiet (aided and unaided) and one for speech in noise (aided and unaided) emerged from the NIDCD/VA study.
With regard to measures of speech recognition performance, moreover, the IU-1 and NIDCD/VA studies were very similar in terms of pertinent variables that could influence performance, including hearing aid circuitry (linear with output-limiting compression), prescriptive approach used to generate target frequency-gain characteristics (NAL-RP), test materials (CST), and listening conditions (a similar range of moderate sound pressure levels and combinations of background conditions). Thus, it is unclear why the two studies differ with regard to the need for one or two principal components to represent speech recognition performance, both aided and unaided.
A key difference existed between the IU studies and the NIDCD/VA study in terms of how the SNR values were established for the speech recognition measures. As noted previously, the IU studies simply fixed the speech levels and SNR values to cover a range of “typical” listening conditions, from soft speech in quiet to loud speech in noise, along the lines suggested previously by Walden (1997). Apparently, in an attempt to ensure that the noise was audible for the speech-in-noise conditions in the NIDCD/VA study, a different method was used to establish the specific SNR values employed with each subject. The speech levels of 52, 62, and 74 dB SPL were again selected to span a range from soft to loud speech, as in the IU study. Although the levels selected to represent loud speech differed considerably across the two studies (80 versus 74 dB SPL), there was good general agreement across studies in the presentation levels used.
To determine the so-called “nominal 0-dB SNR” value for the NIDCD/VA study, the CST materials were presented unaided at 62 dB SPL, and the background babble was adjusted to produce a speech recognition score of 50%. Once this SNR value was established for a given listener, two additional SNR values were employed, one that was 3 dB greater and one that was 3 dB lower than the nominal 0 dB condition, and these same three SNR values were employed at the other presentation levels. For the participants in the NIDCD/VA study, Larson et al. (2000) reported that the mean acoustical SNR value corresponding to the nominal 0-dB SNR was +7 dB. (The median SNR value, rather than mean, was +5 dB, and this was the value used in the foregoing analyses when trying to select roughly equivalent listening conditions across the IU and NIDCD/VA studies.) Thus, based on the mean acoustical SNR value of +7 dB, although the nominal SNR values were −3, 0, and +3 dB, the mean acoustical SNR values at each presentation level were +4, +7, and +10 dB.
To examine whether these procedural differences may have resulted in substantially different audibility across studies, two “equivalent” listening conditions from the NIDCD/VA and IU-1 study are compared in Figure 6. The filled and unfilled circles represent the rms speech and babble levels for the CST, respectively, for the 62 dB SPL, +7 dB SNR condition from the NIDCD/VA study in the top panel and the 65 dB SPL, +8 dB SNR condition from the IU-1 study in the bottom panel. The mean best-ear audiogram for each group of subjects is also shown as the heavy solid line in each panel. Clearly, the two conditions are nearly identical across studies. In both cases, the unamplified speech and noise stimuli are audible primarily below 1500 Hz and inaudible above 1500 Hz. Further, application of the same amount of amplification (NAL-RP) in both studies would result in similar aided audibility for both studies.
Figure 6.
Illustration of the similarity of the acoustical test conditions for one measure of speech recognition obtained in both the Indiana University-1 (IU-1) and the National Institute of Deafness and other Communication Disorders/Veterans Administration (NIDCD/VA) studies. In this case, unaided listening is illustrated for the Corrected Speech Test (CST) in a background of babble. For the NIDCD/VA study, the conditions were determined behaviorally using a criterion of 50% correct. The top panel illustrates the resulting audibility of the speech (filled circles) relative to the babble (unfilled circles) and mean better-ear hearing thresholds (heavy solid line). The babble is illustrated at the mean value of +7 dB reported by Larson et al. (2000). The lower panel illustrates the audibility of the speech signal for the comparison condition from the IU-1 study which fixed the speech and babble levels for all subjects. Clearly, the underlying acoustics of the listening conditions are very similar across studies, at least for the average listening conditions.
In summary, it remains unclear why two components were needed to account for the speech recognition data from the NIDCD/VA study, but only one was needed for the IU-1 data. It does not appear, however, that the use of a fixed SNR value in the IU-1 study and an individually determined SNR in the NIDCD/VA study resulted in substantially different speech audibility across studies on average.
It should be noted, however, that we have also observed previously that two components were needed to account for speech recognition performance in elderly hearing-impaired listeners, a general speech recognition factor and one more closely related to performance at high sound levels in noise (Humes et al., 1994).
Although further work may be needed to determine whether one or two principal components are needed to represent aspects of speech recognition performance associated with hearing aid outcome, either option would be more parsimonious than the three or more components suggested previously by Humes (1999, 2001) and Humes et al. (2001).
Perhaps across-study differences in the factor solutions might be attributable to the instability of one of the factor solutions. If so, replications of the same studies would yield somewhat different results in the analyses. The similarity of results across the IU-1 and IU-2 studies argues against an unstable factor solution, at least for the set of outcome measures common to those two studies.
Another way to examine the stability of a particular factor solution is to partition the original study sample into smaller groups and then redo the factor analysis (Gorsuch, 1983). This approach to evaluating the stability of the factor solution was pursued for both the NIDCD/VA study (linear circuit with output-limiting compression only) and the IU-1 study. For the analysis of the solution from the IU-1 study, 100 of the original 173 subjects were selected randomly on 10 separate occasions and the principal components analyses were repeated. In 9 of the 10 times, the factor solution was virtually identical to that described previously for this study with 3 principal components, and modest correlation occurred between 2 of the 3 components. On one of the 10 iterations, 4 components emerged with the speech recognition scores split into 2 factors; a solution not unlike that observed in the NIDCD/VA analyses. For the additional analyses of the data from the NIDCD/VA study, approximately 50% of the subjects were selected randomly in 10 iterations, and the subsequent 5-factor orthogonal solutions were essentially identical across all 10 iterations.
In addition, an examination of the oblique rotation for each iteration from the NIDCD/VA study failed to confirm the lone intercomponent correlation of 0.35 observed in the analysis reported previously in this article. All intercomponent correlations for the factor solutions from the NIDCD/VA data were less than 0.25, and about 95% were less than 0.20. In general, instability of the factor structures derived from each study does not appear to be a factor contributing to the differences in factor solutions across studies.
With regard to the issue of whether one or two components are needed to represent hearing aid satisfaction and benefit, the differences across studies could lie in the number and type of measures obtained within each domain. The two IU studies included multiple measures of subjective benefit (HAPI, HDABI, and GHABP) and hearing aid satisfaction (MarkeTrak IV and GHABP), whereas the NIDCD/VA study used one measure of subjective benefit (PHAB, although multiple scales from the PHAB) and one of satisfaction. The measure of satisfaction, moreover, was much less direct than those used in the two IU studies. Specifically, a scale of satisfaction was constructed around 14 queries about problems with various aspects of the hearing aids and a follow-up query as to whether these problems were serious enough to result in the subject discontinuing hearing aid use (and, if so, for how long). This indirect measure of hearing aid satisfaction had been proposed previously by Walden (1982) and was used as a measure of satisfaction in this analysis. There was also one direct measure among the surveys used in the NIDCD/VA study that asked the subject to rate overall satisfaction with the hearing on a scale of 1 to 10.
Data presented recently by Kochkin (2003) for 8,654 hearing aid purchasers suggest that measures of hearing aid satisfaction (MarkeTrak survey) and self-report measures of hearing aid benefit (abbreviated version of the PHAB) are, in fact, strongly and positively correlated. Although Kochkin (2003) does not report specific correlations for these two measures, it is apparent from a plot of both measures that the correlation is so strong that it is highly likely both measures would be loaded on the same factor had a factor analysis been performed. Thus, these data appear to be more in line with the factor solutions that emerged from the two IU studies.
Finally, the nature of the subjective benefit measures in the two IU studies differed from that in the NIDCD/VA study. Specifically, for all but one of the benefit measures from the GHABP, the subjects in the IU studies were asked to rate the “helpfulness” of their hearing aids in a variety of communication situations following 1 month of hearing-aid usage. For the PHAB instrument used in the NIDCD/VA study, on the other hand, subjects initially indicated the frequency with which they had difficulty in a particular listening situation for unaided listening; then, following a period of 3 months of hearing aid use, the same survey was completed, but referenced to each item based on aided listening over the prior 3-month period. By subtracting the two sets of scores, aided and unaided, a relative measure of improvement or benefit is obtained. Dillon, James, and Ginis (1997) have reviewed the assumptions underlying both approaches to estimating hearing aid benefit. It is not argued here that one approach is better than another, just that they may not be equivalent. This could also contribute to the differences between studies in the number of outcome factors needed to represent the dimensions of hearing aid satisfaction and subjective benefit.
It is not likely, however, that the observed differences in factor structure underlying the two IU studies and the NIDCD/VA study are attributable to the different postfit intervals at which the outcome measures were obtained. That is, for the two IU studies, the outcome measures analyzed were those obtained at the 1-month postfit interval, whereas the NIDCD/VA study used a 3-month postfit interval. In a series of studies and reports, however, it has been demonstrated that the outcome measures obtained in the IU-1 study, as well as the factor structure underlying those measures, were stable for at least 2 years following the hearing aid fit (Humes, 2001; Humes et al., 2002a, 2002b). Of course, as is always the case in comparing studies across different groups of subjects, the differences in underlying outcome measures simply could be due to differences between the groups of individuals comprising each study.
Although there are some differences in the number and nature of dimensions of hearing aid outcome identified in each study, including whether the dimensions are uncorrelated or correlated, within the two IU studies or within the NIDCD/VA study, the resulting outcome structure was not affected by the type of hearing aid or the circuit under evaluation. That is, the factor structure underlying the construct of “hearing aid outcome” is fairly robust with regard to hearing aid circuitry and hearing aid type, at least for the range of devices evaluated here. Additional research is required, however, to determine whether there are three or five relevant dimensions to hearing aid outcome and the specific nature of each of these dimensions.
Once this is more clearly established, clinicians and researchers alike will have a better idea as to the number and type of measurements required following the hearing aid fitting to determine the success of the intervention. If one assumes that tests exist or can be developed that are unbiased indicators of the underlying factors, then it appears that no more than five such measures would be required, one of each of the following: (1) hearing aid usage; (2) subjective hearing aid benefit; (3) hearing aid satisfaction; (4) aided speech recognition in quiet; and (5) aided speech recognition in noise. However, since performance on a given scale or test is likely to be determined through a combination of individual differences in subject traits underlying performance and the manner in which performance is measured (Flamme, 2001), further research will be needed to determine how performance for each of the three to five dimensions of outcome should be measured and whether one test per outcome dimension would suffice.
Variables Associated with Individual Differences in Outcome Dimensions
The results of the series of multiple regression analyses conducted for the IU-1 and NIDCD/VA studies in an effort to identify variables associated with individual differences in hearing aid outcome factors showed that once again, there were more similarities in the results of these analyses than differences. For example, in both the IU-1 and NIDCD/VA studies, the most accurate predictions were for outcome dimensions involving speech recognition performance (a global speech recognition factor in the IU-1 study and one specific to aided and unaided speech recognition performance in quiet in the NIDCD/VA study), and the least accurate predictions were observed for outcome dimensions involving hearing aid satisfaction. Across studies, variables associated with hearing loss, cognitive function, and age made the biggest contributions to the outcome dimension associated with speech recognition performance.
In addition, the number of years of prior hearing aid experience was the best predictor in both studies of individual differences in current hearing aid usage. Finally, although in both studies the variance accounted for in the outcome factor associated with hearing aid satisfaction was low, both studies identified aided measures of perceived sound quality as being among the best predictors for this outcome dimension.
It could be argued that perceived sound quality should itself be an outcome measure (Humes, 1999, 2001; Humes et al., 2001), rather than a predictor variable. Clearly, since the measures were of aided sound quality, rather than unaided, they were not typical “prefit” predictor variables. The author's conception of the aided sound quality measures from both the NIDCD/VA and IU-1 studies is that they represent an intermediate variable, obtainable only after the hearing aids have been fit, yet predictive of a broader outcome dimension that develops following hearing aid use: hearing aid satisfaction.
Aided sound quality, however, only accounts for small portions of the total variance and thus, doesn't account very well for individual differences in hearing aid satisfaction by itself. Perhaps this is because the aided sound quality measures provide only an indirect measure of other variables that underlie individual differences in hearing aid satisfaction, such as personality (Cox, Alexander, and Gray, 1999). This is highly speculative at this point and requires further study and subsequent validation. Ultimately, should sound quality emerge as yet another separate and possibly independent aspect of hearing aid outcome, the number of dimensions and corresponding outcome measures will need to be increased accordingly. At present, however, the field needs multiple measures of sound quality that have demonstrated reliability and validity for elderly hearing aid wearers (eg, Narendran and Humes, in press) for use in subsequent research on hearing aid outcome measures.
One of the differences between the regression analyses conducted for the speech recognition outcome factor in the IU-1 and NIDCD/VA studies was the percentage of variance that could be accounted for in each study. For instance, approximately 65% of the variance in speech recognition performance in the IU-1 study was accounted for, whereas only about 41% was accounted for in the NIDCD/VA study (for speech recognition performance in quiet only). This was true, moreover, despite the striking similarity in the predictor variables identified by the regression analyses in each study.
The biggest difference in the two resulting regression equations was not in the variables included in each, nor in the magnitude or sign of the β coefficients, but in the amount of variance attributable to individual differences in hearing loss between the two studies. Whereas 44.9% of the total variance was associated with a single predictor variable representing hearing loss in the IU-1 study, 25.3% of the total variance could be attributed to three hearing loss variables in the NIDCD/VA study. Given the similarity of the subject samples with regard to age, gender, and hearing loss (Table 1), as well as the similarity of the acoustical test conditions used in measuring speech recognition (Figure 6), the reasons for this difference between studies are unclear. It is perhaps not too surprising, however, that a study conducted at a single site by a smaller number of clinicians and with fewer subjects might result in more systematic variance and less error variance among the regression analyses than would be the case for a larger scale multisite investigation.
As noted previously in the brief tutorial on the application of factor analysis to hearing aid outcome measures, the purpose of initial exploratory analyses is never expected to result in a final answer regarding the phenomenon or construct under investigation. Rather, it is a statistical tool that enables the visualization of associations among large sets of variables which, when interpreted in light of existing theories or knowledge regarding the construct, can lead to more refined theories or models. Clearly, additional research that obtains multiple outcome measures from large numbers of individuals is needed to further refine our understanding of hearing aid outcome. Given the number of variables and participants required, it is most likely that further progress in this area will not be possible without continued support of multicenter collaborative projects such as the NIDCD/VA clinical trial.
More sophisticated statistical tools, such as structural equation models (eg, Bollen, 1989), provide an opportunity to further develop our understanding of hearing aid outcome and the variables that affect various aspects of outcome. Actually, both exploratory and confirmatory factor analysis can be viewed as special cases or subsets of broader structural equation models. A detailed discussion of structural equation models is beyond the scope of this article, but in the present context, one could envision it as simultaneously performing both the factor analysis to identify the factors underlying performance and the multiple regression analysis to predict the factor scores derived. It is also relatively easy to implement multiple layers of factors and causal connections among them in structural equation modeling.
The application of structural equation modeling (AMOS v4.0.1, Arbuckle and Wothke, 1999) to the data from the analyses of the IU-1 study resulted in the model depicted in Figure 7. In this diagram, the boxes on the left represent a subset of the prefit predictor variables identified in the multiple regression analyses summarized previously in Table 5, whereas the boxes on the right represent the factor scores for the oblique rotation of the three principal components derived from the IU-1 analyses. The arrows represent the associations among the various variables. The researcher predefines both the sets of variables and the links among them, and the structural equation model solves for the weights reflecting the direction and strength of the resulting associations. Standardized weights are shown in Figure 7 such that values range from −1 to +1. The ellipses in the model labeled e1, e2, and e3 represent error terms in this particular model, one error term for each outcome factor. Finally, the numbers above the top right corner of each box, representing the three dimensions of hearing aid outcome, show the proportion of variance accounted for by the predictor variables linked to that outcome factor.
Figure 7.
Illustration of the structural equation model (AMOS v4.0.1; Arbuckle & Wothke, 1999) fit to the data from the Indiana University-1 (IU-1) study. Boxes on the left represent various prefit variables and those on the right represent the three factor scores underlying hearing aid outcome. The arrows and the coefficients adjacent to them represent the direction and strength of various associations among the prefit and outcome measures. The ellipses labeled e1, e2, and e3 represent error terms needed when defining the model. Abbreviations: HA, hearing aid; JSQ, judgments of sound quality; LDL, loudness discomfort level; CPHI, Communication Profile for the Hearing Impaired (Demorest and Erdman, 1987).
There are numerous options to evaluate the fit of structural equation models, but one of the most universal is a fit index that compares the derived model to a default model that assumes no associations among any of the variables (the independence model). The comparative fit index (CFI) takes sample size into consideration and varies from 0.0 to 1.0, with higher values representing better fits (Bentler, 1990). CFI values above 0.90 reflect adequate fits to the data, whereas values above 0.95 reflect an excellent fit (Hu and Bentler, 1999). The CFI value for the structural equation model depicted in Figure 7 was 0.92, suggesting that it provides a reasonable fit.
The structural equation model in Figure 7 captures the salient features of the combination of principal components and multiple regression analyses for the data from the IU-1 study presented previously. The model was built from the knowledge gained from those earlier analyses and impacted decisions whether to link the outcome variables (assumed to be correlated on the basis of the results of prior oblique factor rotation) or the prefit variables (assumed to be independent since most were factor scores from prior orthogonal factor analysis of these variables). Structural equation modeling also can be applied to the raw data to derive the prefit factors and their associations in initial exploratory analyses. It is a potentially powerful statistical tool that can assist in the modeling of human behavior, including hearing aid outcome measures, but it typically requires even larger sample sizes given the larger degrees of freedom associated with the modeling.
The structural equation model depicted in Figure 7 was included solely for the purpose of illustration. Future development and evaluation of such models will require collaboration among several centers in the collection and analysis of large sets of data. It is only through such efforts, however, that our field will gain a good understanding of the various dimensions or aspects of hearing aid outcome and the ways in which outcome might be optimized for individual patients. Hopefully, this article has provided the reader with directions for future research in this area that will lead to significant advancements of our knowledge regarding hearing aid outcome.
Acknowledgments
This work was supported, in part, by a research grant from the National Institute on Aging (R01-AG08293). The author would also like to thank the Executive Committee of CSP Study #418 for access to the data from the NIDCD/VA study.
References
- American National Standards Institute Specifications for audiometers, ANSI S3.6–1996. New York, NY: American National Standards Institute, 1996
- Arbuckle JL, Wothke W. AMOS 4.0 User's Guide. Chicago: SmallWaters; Corporation, 1999 [Google Scholar]
- Bentler PM. Comparative fit indexes in structural models. Psych Bull 107: 238–246, 1990 [DOI] [PubMed] [Google Scholar]
- Bentler R, Niebuhr D, Getta J, Anderson C. Longitudinal study of hearing aid effectiveness. II: Subjective measures. J Speech Hear Res 36: 820–831, 1993 [DOI] [PubMed] [Google Scholar]
- Bollen KA. Structural equations with latent variables. New York: Wiley, 1989 [Google Scholar]
- Byrne D, Parkinson A, Newall P. Hearing aid gain and frequency response requirements for the severely/profoundly hearing impaired. Ear Hear 11: 40–49, 1990 [DOI] [PubMed] [Google Scholar]
- Cox RM, Alexander GC, Gilmore CG, Pusakulich KM. Use of the Connected Speech Test (CST) with hearing-impaired listeners. Ear Hear 9: 198–207, 1988 [DOI] [PubMed] [Google Scholar]
- Cox RM, Gilmore C. Development of the profile of hearing aid performance (PHAP). J Speech Hear Res 33: 343–357, 1990 [DOI] [PubMed] [Google Scholar]
- Cox RM, Alexander GC, Gray G. Personality and the subjective assessment of hearing aids. J Amer Acad Audiol 10: 1–13, 1999 [PubMed] [Google Scholar]
- Demorest M, Erdman S. Development of the Communication Profile for the Hearing Impaired. J Speech Hear Disord 52: 129–143, 1987 [DOI] [PubMed] [Google Scholar]
- Dillon H, James A, Ginis J. The Client Oriented Scale of Improvement (COSI) and its relationship to several other measures of benefit and satisfaction provided by hearing aids. J Amer Acad Audiol 8: 27–43, 1997 [PubMed] [Google Scholar]
- Flamme GA. Examination of the validity of auditory traits and tests. Trends Amplif 5: 111–138, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gatehouse S. Glasgow Hearing Aid Benefit Profile: Derivation and validation of a client-centered outcome measure for hearing aid services. J Amer Acad Audiol 10: 80–103, 1999 [Google Scholar]
- Gorsuch RL. Factor Analysis, 2nd edition. Hillsdale, NJ: Lawrence Erlbaum Associates, 1983 [Google Scholar]
- Guadagnoli E, Velicer WF. Relation of sample size to the stability of component patterns. Psychol Bull 103: 265–275, 1988 [DOI] [PubMed] [Google Scholar]
- Hendrickson AE, White PO. Promax: A quick method for rotation to oblique simple structure. Brit J Stat Psychol 17 (1): 65–70, 1964 [Google Scholar]
- Hu L-T, Bentler PM. Cutoff criteria for fit indexes in co-variance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling 6: 1–55, 1999 [Google Scholar]
- Humes LE. Dimensions of hearing aid outcome. J Amer Acad Audiol 10: 26–39, 1999 [PubMed] [Google Scholar]
- Humes LE. Issues in evaluating the effectiveness of hearing aids in the elderly: What to measure and when. Seminars in Hearing 22 (3): 303–314, 2001 [Google Scholar]
- Humes LE. Factors underlying the speech-recognition performance of elderly hearing-aid wearers. J Acoust Soc Amer 112: 1112–1132, 2002 [DOI] [PubMed] [Google Scholar]
- Humes LE, Garner CB, Wilson DL, Barlow NN. Hearing-aid outcome measures following one month of hearing aid use by elderly participants. J Speech Lang Hear Res 44: 469–486, 2001 [DOI] [PubMed] [Google Scholar]
- Humes LE, Watson BU, Christensen LA, Cokely CG, Halling DC, Lee L. Factors associated with individual differences in clinical measures of speech recognition among the elderly. J Speech Lang Hear Res 37: 465–474, 1994 [DOI] [PubMed] [Google Scholar]
- Humes LE, Wilson DL, Barlow NN, Garner CB. Measures of hearing-aid benefit following one or two years of hearing aid use by the elderly. J Speech Lang Hear Res 45: 772–782, 2002(a). [DOI] [PubMed] [Google Scholar]
- Humes LE, Wilson DL, Barlow NN, Garner CB, Amos N. Longitudinal changes in hearing-aid satisfaction and usage in the elderly over a period of one or two years following hearing aid delivery. Ear Hear 23: 428–438, 2002(b). [DOI] [PubMed] [Google Scholar]
- Kaiser HF. The varimax criterion for analytic rotation in factor analysis. Psychometrika 23 (3): 187–200, 1958 [Google Scholar]
- Killion MC, Fikret-Pasa S. The 3 types of sensorineural hearing loss: Loudness and intelligibility considerations. The Hear J 46 (11): 31–36, 1993 [Google Scholar]
- Kochkin S. Subjective measures of satisfaction and benefit: Establishing norms. Seminars in Hearing 18 (1): 37–48, 1997 [Google Scholar]
- Kochkin S. On the issue of value: Hearing aid benefit, price, satisfaction and brand repurchase rates. Hearing Rev 10 (2): 12–26, 2003 [Google Scholar]
- Krantz DS, Baum A, Wideman MV. Assessment of preferences for self-treatment and information in health care. J Personality Soc Psychol 39: 977–990, 1980 [DOI] [PubMed] [Google Scholar]
- Larson VD, Williams DW, Henderson WG, Luethke LE, Beck LD, et al. Efficacy of 3 commonly used hearing aid circuits: A crossover trial. JAMA 284: 1806–1813, 2000 [DOI] [PubMed] [Google Scholar]
- Levitt H, Resnick SB. Speech reception by the hearing impaired: Methods of testing and development of materials. Scand Audiol Suppl 6: 107–129, 1978 [PubMed] [Google Scholar]
- MacCallum RC, Widaman KF, Zhang S, Hong S. Sample size in factor analysis. Psychol Meth 4: 84–99, 1999 [Google Scholar]
- Mathiowetz V, Weber K, Kashman N, Volland G. Adult norms for the Nine Hole Peg Test of finger dexterity. Occup Ther J Res 5 (1): 24–38, 1985 [DOI] [PubMed] [Google Scholar]
- Narendran MM, Humes LE. Evaluations of judgements of sound quality in elderly hearing-aid wearers: Reliability and validity of measurements. Ear Hear (in press). [DOI] [PubMed]
- Thurstone LL. Multiple factor analysis. Chicago: University of Chicago Press, 1947 [Google Scholar]
- Ventry I, Weinstein B. The hearing handicap inventory for the elderly: A new tool. Ear Hear 3: 128–134, 1982 [DOI] [PubMed] [Google Scholar]
- Walden BE. Validating measures of hearing aid success. In Studebaker GA, Bess FA, eds: The Vanderbilt Hearing Aid Report. Upper Darby, Pennsylvania: Monographs in Contemporary Audiology, pp. 188–192, 1982 [Google Scholar]
- Walden BE. Toward a model clinical-trials protocol for substantiating hearing aid user-benefit claims. Amer J Audiol 6: 13–24, 1997 [Google Scholar]
- Walden BE, Demorest ME, Hepler EL. Self-report approach to assessing benefit derived from amplification. J Speech Hear Res 27: 49–56, 1984 [DOI] [PubMed] [Google Scholar]
- Wallston BS, Wallston KA, Kaplan GO, Maides SA. Development and validation of the health locus of control (HLC) scale. J Cons Clin Psychol 44: 580–585, 1976 [DOI] [PubMed] [Google Scholar]
- Wechsler D. The Wechsler Adult Intelligence Scale-Revised. New York: The Psychological Corporation, 1981 [Google Scholar]