Wavelet Analysis for Detection of Phasic Electromyographic Activity in Sleep: Influence of Mother Wavelet and Dimensionality Reduction

Abstract

Phasic electromyographic (EMG) activity during sleep is characterized by brief muscle twitches (duration 100–500 msec, amplitude four times background activity). High rates of such activity may have clinical relevance. This paper presents wavelet (WT) analyses to detect phasic EMG, examining both Symlet and Daubechies approaches. Feature extraction included 1 sec epoch processing with 24 WT-based features and dimensionality reduction involved comparing two techniques: principal component analysis and a feature/variable selection algorithm. Classification was conducted using a linear classifier. Valid automated detection was obtained in comparison to expert human judgment with high (>90%) classification performance for 11/12 datasets.

1. Introduction

Labor-intensive, visual analysis of surface electromyographic (EMG) activity during human sleep studies (i.e., polysomnography, PSG) has provided a quantitative, physiologic research metric to potentially track development of some neurodegenerative conditions [1]. High rates of EMG activity during rapid eye movement (REM) sleep occur in patients with idiopathic REM behaviour disorder (RBD), a dramatic condition in which patients act out their dreams and engage in potentially disruptive, injurious and even dangerous behaviors (e.g., walking through glass doors) while asleep [2]. RBD appears, in some cases, to be the earliest sign of impending Parkinson’s Disease (PD), which may occur decades later [3]. The elevated phasic muscle activity is subtle but can be a potentially stable and objective physiological marker of disease process [4] even on nights without dream enactment. This makes it a potentially attractive metric as a diagnostic tool for widespread use in sleep medicine. However, visual analyses of such activity are extremely labor intensive (approximately 6 to 8 hours of visual scoring time per sleep recording [1]) and hinder immediate application in the clinical setting of overnight diagnostic PSG. The work that we present here expedites detection of phasic muscle activity by introducing a computerized identification scheme. This work builds upon our previous investigation of unsupervised, feature-based phasic EMG activity identification [5] by evaluating the performance of a supervised phasic EMG activity detector, based on the discrete wavelet (WT) transform [6]. We describe use of WT analysis to decompose the EMG signal to discriminate between phasic and non-phasic EMG activity. In this work we use the WT transform to improve such discrimination, which contrasts to the approach shown in [5], which considered time and frequency components of the EMG signal separately. We excluded several features used previously [5] because of redundancy.

Few computerized methods for quantification of surface EMG signals recorded during human sleep to track neurodegenerative disease have been attempted to date [7, 8]. Apart from a small range of features analyzed, such prior attempts all relied prematurely on case identification to derive estimates of case sensitivity and case specificity, a strategy which ultimately confounds the two separate issues of signal identification performance and patient (case) versus control identification [5]. Such confusion can greatly exaggerate performance estimates of a computerized system by essentially “stacking the deck,” against the presence or absence of time-based signals that occur stochastically in both patients and controls over seconds to minutes during the course of a night of sleep. Before evaluating the performance of any case-based identifying computerized system in a clinical or epidemiologic setting, its accuracy regarding signal identification and validity must be demonstrated in real time.

Materials and methods

a. Polysomnographic (PSG) Data Collection

We analyzed twelve overnight de-identified PSG data sets (each consisting of separate left and right leg recordings from six individuals) derived from the sleep laboratory at Emory University School of Medicine in Atlanta, Georgia under an Institutional Review Board approved protocol. Sleep durations for selected epochs of PSG data for the six individuals are shown in Table 1. Extraction of real time leg muscle activity was obtained from bipolar (i.e., two active sites on each leg) surface electrodes with impedances below 10,000 ohms placed above the right and left anterior tibialis. Data acquisition was accomplished using the Embla (MedCare, Bloomfield, CO) sleep monitoring model N-7000 digital PSG system, with the software program Somnologica ® 2.0 at sampling rates of at least 200Hz, which ensures sufficient sampling to capture phasic EMG activity occurring within the 0.1 second range specified within classical visual scoring guidelines. EMG data was converted from Somnologica Embla format to .edf format, using the MATLAB (version 7.8 R2009a) toolbox BioSig (Schloegl A-Graz University of Technology, Graz, Austria). WT analysis and classification routines were run using MATLAB (MathWorks®; Natick, MA) software programs.

Table 1.

Sleep duration and relative distribution of sleep stages (% sleep in min) for epochs selected for EMG analysis.

Subject	Duration of Sleep (min)	NREM (% of sleep[duration])	REM (% of sleep[duration])
001	134	64.08	35.92
002	191	74.61	25.39
003	184	64.34	35.66
004	187	67.03	32.97
005	197	74.96	25.04
006	196	76.67	23.34

b. Visual labeling of phasic EMG activity

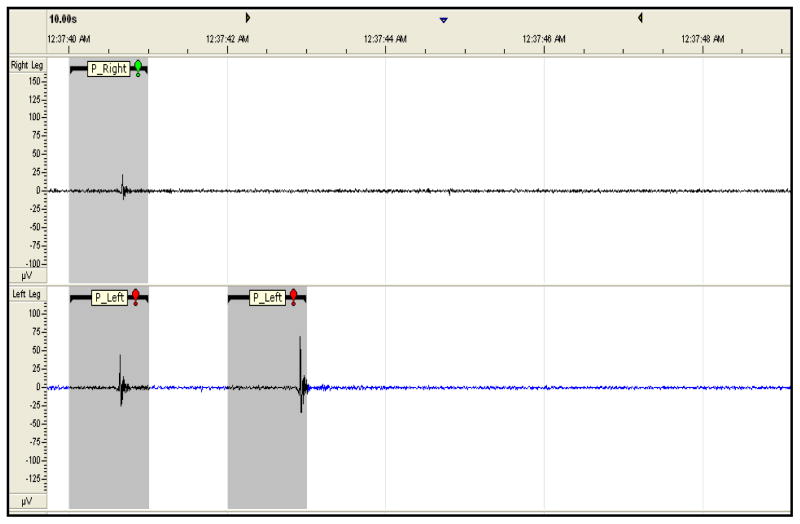
Performance of the automated scheme was evaluated with respect to guidelines for manual assessment of phasic muscle activity found in our previous work [1]. The twelve overnight PSGs were first visually labeled for phasic and non-phasic muscle activity by the same trained visual scorer. Individual one second epochs containing visually identifiable artifacts were excluded. The left and right leg EMG recordings were separately marked at one second intervals (epochs) as either non-phasic (0), or phasic muscle activity (1). Data epochs that contained signal amplitudes of four times the surrounding background activity, visually estimated for that epoch, with duration ranges of 100 to 500 msec were marked as phasic muscle activity [1, 5]. Epochs that did not meet the criteria for phasic muscle activity (e.g. activity > 500 msec) were marked as non-phasic muscle activity. Scoring was conducted within the Somnologica software platform with a screen resolution display of 10 seconds per viewing window and a screen size of 15″ (see Figure 1). Table 2 contains a summary of the frequency of these visual scoring binary classifications for each data set. EMG epochs with artifacts that included gross movements, ballistocardiographic interference and other spurious information were manually removed prior to formulation of the final data sets and are not included in Table 2.

Figure 1.

Plot of electromyogram (EMG) labeling, 9.5 second duration of EMG activity-from the S001 data set, in stage REM sleep, P_Right indicates right leg phasic EMG activity (top panel, shaded gray region) and bottom panel indicates left leg phasic EMG activity (P_LEFT, gray regions).

Table 2.

Distribution of phasic and non-phasic seconds for selected analyzed epochs^*.

Subject	Phasic EMG Epochs (sec)	Non-Phasic EMG Epochs (sec)
001	L = 698; R = 880	L= 7,384; R= 7,199
002	L = 80; R = 1,452	L = 11,432 ; R = 10,066
003	L = 286; R = 736	L = 10,798; R = 10,352
004	L = 3,340; R = 2,956	L = 7,933; R = 8,318
005	L = 1,774; R = 2,042	L = 10,095; R = 9,800
006	L = 2,672; R = 3,154	L = 9,145; R = 8,646

^*L = left leg; R = right leg; Numbers refer to number of 1 sec epochs labeled as phasic or non-phasic activity; some 1 sec epochs not included due to gross signal artifact

c. Computerized detection algorithm

i. General Approach

In order to discriminate between phasic and non-phasic EMG data segments, we implemented a pattern classification approach (see Figure 2), which involved data collection, feature extraction (WT decomposition), dimensionality reduction (feature/variable selection [FVS] and principal components analysis [PCA]), and linear classification. We consider feature extraction to be the most essential component of classification system development, because the selection of a “good” set of features are required to fully characterize EMG data for successful automated phasic and non-phasic EMG activity discrimination. To compensate for potentially redundant or irrelevant features, the feature extraction stage was followed by a dimensionality reduction stage which further condensed relevant information in order to reduce classifier training time and increase generalizability of the classifier. Generalizability would be expected to be important if the classification approach was to be readily exported to PSG recordings not included in this initial validation.

Figure 2.

Schematic of the phasic EMG activity classification system.

We tested both: (a) a linear transformation technique, PCA and (b) a FVS algorithm represented by Forward Floating Search (FFS) using a filter approach [9, 10]. Lastly, for automated phasic and non-phasic EMG activity discrimination we employed a linear classifier since it has been cited to provide comparable results to more advanced non-linear classifiers when applied to real data sets [11], resembling the time and frequency components of human muscle activity recorded with surface EMG.

ii. Feature Extraction

Classical approaches in signal processing typically have incorporated short-time Fourier transform (STFT) analysis, however, WT analysis has advantages for non-stationary time series, which typically characterize biopotentials [12]. WT analysis differs from traditional STFT by its approach to information in time and frequency domains. More specifically, WTs trade one type of resolution (time vs. frequency) for the other, making them robust for the analysis of non-stationary signals [6]. WTs decompose a signal into scales, each representing a particular “coarseness” of the signal. Data sets containing a mixture of features residing at different time and frequency resolutions are well-suited for WT analysis relative to STFT [13]. The presumed benefits of WT (vs. STFT) to track phasic EMG activity, which appears in varying high frequency bands (see Figure 1), was a major factor underlying our testing in order to determine whether WT analysis offered unique EMG signal analysis advantages, as was the conventionality of this technique. Other advantages included the lower computational cost of the WT approach.

A WT ψ(t) is a localized waveform (a short-term duration wave), which characterizes waveforms by vanishing moments (VMs) of varying complexity [13]. Two basic manipulations can be performed on the WT, stretching or squeezing (dilation) and moving (translation). Dilation is governed by the scale parameter a, whereas translation is governed by the parameter b. Smaller scales correspond to higher frequency components and higher scales correspond to lower frequency components. Dilated and translated versions of the original mother WT comprise a family of WTs defined by (with the original mother WT defined by parameters values a=1 and b=0):

$${\psi }_{a,b}(t)=\frac{1}{\sqrt{a}}\psi \left(\frac{t-b}{a}\right)$$ (1)

In our analysis we employed the discrete time WT transform (DTWT), also known as the pyramid algorithm, which is defined as [14]:

$$T_{m,n}=2^{-m/2}\sum _{k}x[k]\psi \left[2^{-m}k-n\right]$$ (2)

such that x[k] is the discrete EMG signal and the mother WT is considered real valued and m, n ∈ 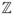. If the discrete dyadic grid WTs are chosen to be orthogonal, the information stored in a WT coefficient T_m,n is not repeated elsewhere. Therefore, the information represented at a certain scale m is disjoint and independent from the information at all other scales. Although various mother WTs have been proposed and methods exist for the development of customized WTs [15], results produced by the use of these customized WTs are usually insignificant compared to the application of existing WTs [16].

Given this background, our work used traditional Daubechies and Symlet families with different values of VMs because the literature has shown that the selection of VMs is dependent on the application [17]. The Daubechies and Symlet WT families provide compact support such that the WT transform can be computed efficiently with finite impulse response conjugate mirror filters using a fast filter bank algorithm [13]. Daubechies WTs have a compact support of minimum size for any given number p of VMs. Symlets are also WTs of minimum compact support, for any given number p of VMs, but they are more symmetric compared to Daubechies WTs. The minimum support is a desired property in this application since phasic muscle activity usually last a few msec. Daubechies and Symlet WTs are described in greater detail elsewhere [13, 15].

Preliminary results, not shown here, revealed that relevant information for phasic EMG activity discrimination was concentrated at low levels of WT decomposition. (Examinations at higher levels using area under curve [AUC] as criterion consistently showed AUC values approaching 1.0 at levels of m < 5 or lower.) Therefore, WT decomposition was performed at m values of 1, 2, 3 and 4) and WT coefficients (extracted by Equation 2) were used to compute the set of features illustrated in equations (3) to (8) below. In each equation below, N is represented by N_m as the number of wavelet coefficients at level m (with N_m ≈ 2N_m+1 due to the decimation by 2 between consecutive levels in the pyramid algorithm). Features were selected based upon consultation with sleep practitioners and a review of previous quantitative metrics used in biological signal processing [18]:

• Standard deviation,

  $${\mathit{std}}_m={\left(\frac{1}{N-1}\sum _n{\left(T_{m,n}-\frac{1}{N}\sum _n{T}_{m,n}\right)}^2\right)}^{1/2}$$ (3)
• Shannon’s entropy (inputs included the normalized squared detailed WT coefficients).

  $$S_m=-\sum _n\frac{{\left(T_{m,n}\right)}^2}{{\displaystyle \sum _n}{\left(T_{m,n}\right)}^2}log\frac{{\left(T_{m,n}\right)}^2}{{\displaystyle \sum _n}{\left(T_{m,n}\right)}^2}$$ (4)
• Mean absolute deviation,

  $${\mathit{mad}}_m=\frac{1}{N}\sum _n\left|T_{m,n}-\frac{1}{N}\sum _n{T}_{m,n}\right|$$ (5)
• Mean curve length,

  $${\mathit{mcl}}_m=\frac{1}{N}{\displaystyle \sum _n}\left|T_{m,n+1}-T_{m,n}\right|$$ (6)
• Skewness

  $${\mathit{skew}}_m=\frac{\frac{1}{N}{\displaystyle \sum _n}{\left(T_{m,n}-\frac{1}{N}{\displaystyle \sum _n}{T}_{m,n}\right)}^3}{{\left(\frac{1}{N}{\displaystyle \sum _n}{\left(T_{m,n}-\frac{1}{N}{\displaystyle \sum _n}{T}_{m,n}\right)}^2\right)}^{3/2}}$$ (7)
• Kurtosis,

  $${\mathit{kurt}}_m=\frac{\frac{1}{N}{\displaystyle \sum _n}{\left(T_{m,n}-\frac{1}{N}{\displaystyle \sum _n}{T}_{m,n}\right)}^4}{{\left(\frac{1}{N}{\displaystyle \sum _n}{\left(T_{m,n}-\frac{1}{N}{\displaystyle \sum _n}{T}_{m,n}\right)}^2\right)}^2}-3.$$ (8)

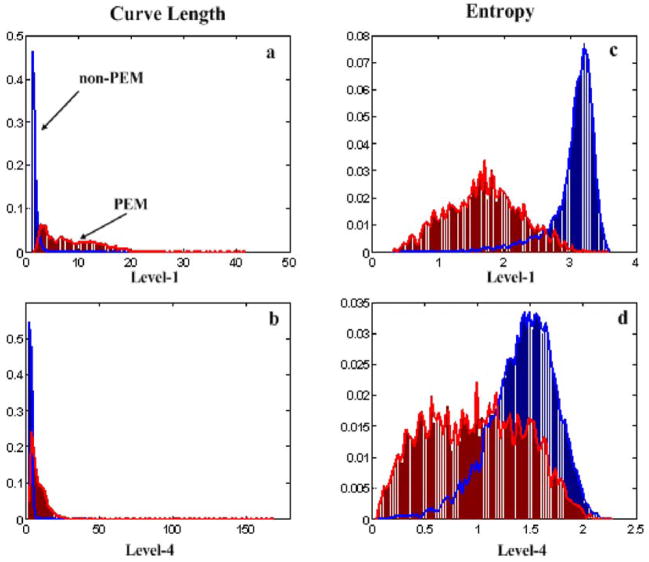
A total of 24 features were calculated for each EMG epoch {std_m, S_m, mad_m, mcl_m, skew_m, kurt_m} and WT level m (m=1, 2, 3 and 4). Figure 3 depicts examples of histograms (empirical approximation of the underlying probability density functions of the mean curve length and Shannon’s entropy features, using the WT coefficients produced from the WT transform with a Symlet mother WT consisting of four VMs, at WT levels m=1 and m=4, for a single leg data set from one individual. Figure 3 indicates that the two classes, phasic and non-phasic EMG activity, are characterized by distinct ranges of feature values. Higher decomposition levels characterize lower frequency ranges and usually manifest greater amount of overlapping, hence less distinct discrimination between phasic and non-phasic EMG activity segments, as can be seen in Figure 3 (panels b and d). Also, different levels of overlapping are observed depending on the decomposition level. Lower decomposition levels characterizing higher frequency ranges indicate less overlap, hence, more distinct discrimination between phasic and non-phasic EMG activity segments occur, as can be seen in Figure 3 (panels a and c).

Figure 3.

“Empirical” probability density functions (pdfs) of the curve length and Shannon’s entropy features of the wavelet coefficients (using Symlet with four vanishing moments) at level 1 and 4 (where non-phasic EMG activity is labelled Non-PEM (blue) and phasic EMG activity is labelled PEM (red)): a) curve length feature at wavelet decomposition level 1 b) Curve length feature at wavelet decomposition level 4 c) Shannon’s entropy feature at wavelet decomposition level 1 d) Shannon’s entropy feature at wavelet decomposition level 4, with feature values indicated on the x-axis and probability density values displayed on the y-axis.

iii. Dimensionality Reduction using PCA

PCA (Karhunen-Loeve Transformation) linearly transforms the original feature space [19] [20] by projecting the d-dimensional data onto l eigenvectors (l ≤ d) from the covariance matrix of the zero mean original feature matrix corresponding to the l largest eigenvalues. Even if the latter entails that the entire set of eigenvectors is retained (resulting in a lack of dimensionality reduction), this may still lead to an improvement of classification performance due to the uncorrelated nature of the new set of features

ii. Dimensionality Reduction with FVS using FFS

FVS determines a subset of l features from a given set of d measurements/features, such that the selected subset retains the greatest ability to discriminate between classes. The “goodness” of a particular feature subset is evaluated by using an objective function, J(Y_k), where Y_k is a feature subset of size k.

In this work we employed an approach that included an objective function based on scatter matrices, namely inter/intra distance calculations [19, 21]:

$$J=\mathit{trace}\left(S_w^{-1}{S}_b\right)$$ (9)

with S_w the within scatter matrix describing the average scattering within classes (the scatter of samples around their respective class mean vectors)

$$S_w=\frac{1}{N}\sum _{i=1}^K\sum _{n=1}^{N_i}\left({\mathbf{x}}_{i,n}-{\mathbf{\mu }}_i\right){\left({\mathbf{x}}_{i,n}-{\mathbf{\mu }}_i\right)}^T$$ (10)

and S_b the between scatter matrix describing the scattering of the classes dependent means with respect to the overall mean,

$$S_b=\frac{1}{N}\sum _{i=1}^K{N}_i\left({\mathbf{\mu }}_i-\mathbf{\mu }\right){\left({\mathbf{\mu }}_i-\mathbf{\mu }\right)}^T$$ (11)

where μ_i is the mean value of class i, μ is the overall mean (for all classes), x_i,n is the n^th data point belonging to class i, K is the number of classes (K=2 in our case phasic EMG and non-phasic EMG), N is the total number of data and N_i is the number of examples belonging in class i (i=1,2, …, K).

The inter/intra distance criterion was combined with Pudil’s FFS method in order to form the subset of features to be fed into the classification stage [19, 22]. The FFS method allows the addition and removal of a non-predefined number of features; assuming that Y_k = {x₁, x₂, …, x_k} is the best subset of features according to a criterion J and Y_{d − k} is the set of the remaining d−k features. In the latter, all the subsets with lower cardinality (number of features in the set): Y₁, Y₂, …, Y_k−1 are also kept. The next stage proceeds as follows:

• Step 1: Select the feature x_j from Y_{d − k} that yields the maximum value for J

• Step 2: Find the feature x_r in the set Y_k+1 that reduces the value of J the least. If this feature is the same as x_j then retain the current subset, set k=k+1 and return to step 1; otherwise remove x_r to form $Y_k^{\prime }=Y_{k+1}-x_r$

• Step 3: Continue removing features from the set $Y_k^{\prime }$, to form $Y_{k-1}^{\prime }$ while $J\left(Y_{k-1}^{\prime }\right)>J\left(Y_{k-1}\right)(k=k-1)$ or k=2; then return to step 2.

The algorithm is initialized using the sequential forward FVS algorithm [19] to form Y₂ (the feature with the highest value of J is kept and feature pairs/subsets are created that contain the feature selected from the first stage and any features retained in subsequent stages such that the final feature subset has the maximum value for J) and is terminated when the required l features are obtained.

v. Classification

In this study, we discriminated between phasic EMG and non-phasic EMG segments. Many classification methods have been proposed in the field of pattern recognition. However, for real world data sets, conventional classifiers tend to perform adequately when compared to more complex classifiers [11]. Therefore, a simple minimum Mahalanobis distance classifier (using decision boundaries between compartments in the feature space that are linear [hyper] planes) [19, 20] was used to detect phasic EMG and non-phasic EMG segments. This follows Hand’s observation [11] that for many real world data sets, a linear approach works surprisingly well. In the Mahalanobis classifier, each feature vector x is assigned to class i (phasic EMG or non-phasic EMG) such that the value of the corresponding discriminant function is maximized:

$$i=\underset{i}{argmax}\left\{2lnP\left({\omega }_i\right)-{\left(\mathbf{x}-{\mathbf{\mu }}_i\right)}^T{\mathbf{C}}^{-1}\left(\mathbf{x}-{\mathbf{\mu }}_i\right)\right\}$$ (12)

where μ_i is the mean of class i, P(ω_i) is the prior probability of class i, and C is the estimated covariance matrix, which is assumed constant across all classes.

vi. Evaluation Performance

Eight sets of experiments were conducted on each of the six individuals’ data sets separately, testing (a) recordings from the left and the right leg (b) Daubechies and Symlet family WTs analysis and (c) linear transformation of the input features via PCA and FVS. For each set of experiments we varied the number of VMs from 1 to 15 and the number of components of the reduced input vector from 1 to 24 for PCA and the number of features from 1 to 15 for the FVS approach, these parameters were selected due to our desire to test a classification scheme that would be computationally feasible and translational within clinical settings.

To ensure minimum bias we tested the aforementioned approach using an “inner” and an “outer” loop validation scheme. The outer loop tracked the phasic EMG and non-phasic EMG detection performance while the inner loop refined the classification scheme parameters (number of retained principal components (PCs) or number of retained features and the selection of the number of VMs. EMG data in the outer loop was divided into two sets: training and testing (80% for training and 20% for testing) followed by a random reshuffle of the phasic EMG and non-phasic EMG data segments. Next, the training set was further sub-divided into another training and testing data set (75% for training and 25% for testing) using a similar randomized reshuffle scheme, as mentioned previously. Classical approaches in data mining suggest that two-thirds of the data are allocated to the training set, and the remaining one-third is allocated to the testing set. Therefore in our work we used training-set to testing-set ratios approximating these [23]. Eight inner loop iterations were used and the optimal model configuration (number of PCs and VMs), in terms of average classification performance was selected. Lastly, retraining of the model was conducted using both the training and testing sets of the inner loop and final model validation was obtained using the testing set of the outer loop (using 30 iterations). This validation scheme decoupled the parameter selection stage from the estimation of the classification performance [24, 25], which avoided obtaining overly optimistic conclusions (over-fitting).

b. Statistical Analyses

For each individual and leg, we performed a separate Kruskal-Wallis analysis of variance and six Mann-Whitney U-tests with Bonferroni correction as post-hoc tests for dimensionality reduction and WT family technique configurations. Non-parametric statistical procedures were favored because of the relatively small sample size. Values of p lower than 0.05 were considered statistically significant. We defined the statistical significance threshold for the multiple comparisons as p< 0.0083 (i.e., 0.0500/6 via Bonferroni correction). The null hypothesis for each inferential statistical test separately presumed equal median True Positive % (TP) and True Negative % (TN) values across dimensionality reduction and WT family configurations.

These were defined as:

$$TP\mathit{rate}=\left(\text{number}\text{of}\text{correct}\text{phasic}\text{EMG}\text{detections}\right)/\left(\text{number}\text{of}\text{correct}\text{phasic}\text{EMG}\text{detections}+\text{number}\text{incorrect}\text{nonphasic}\text{EMG}\text{detections}\right)$$

$$TN\mathit{rate}=\left(\text{number}\text{of}\text{correct}\text{nonphasic}\text{EMG}\text{detections}\right)/\left(\text{number}\text{of}\text{correct}\text{nonphasic}\text{EMG}\text{detections}+\text{number}\text{of}\text{incorrect}\text{phasic}\text{EMG}\text{detections}\right)$$

2. Results

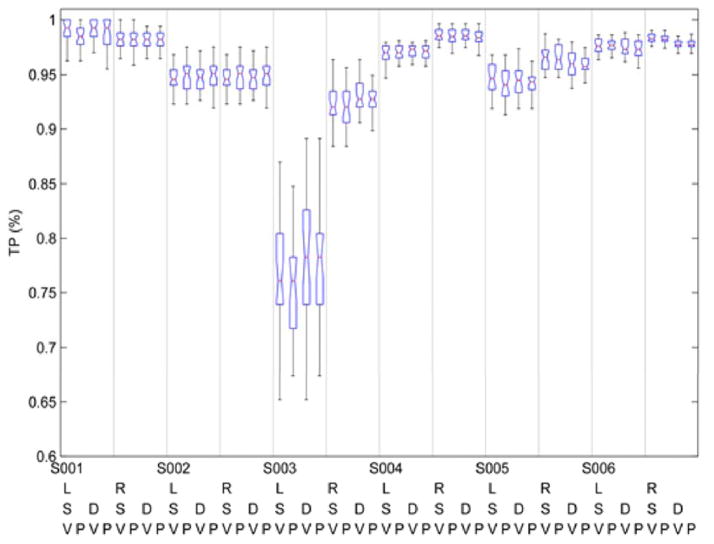
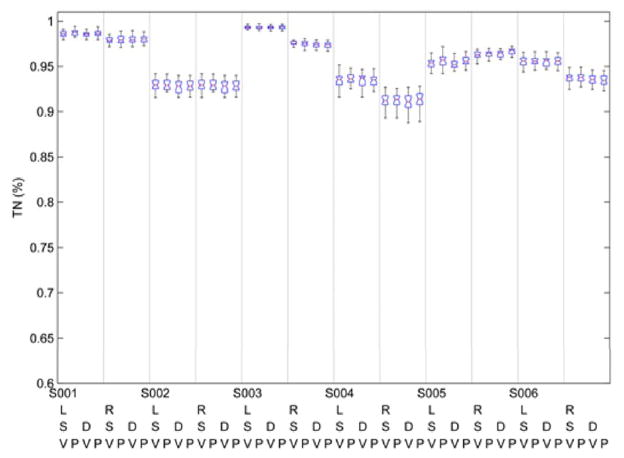
Figure 4 includes the respective TP% for each of the eight aforementioned configurations for each of the six individuals. TP %’s exceed 90% for all recordings, the sole exception being a single leg recording (left) from one individual. Apart from this effect, there is some suggestion of individual differences (e.g., S001 versus S005) but this occurs at very absolute levels of accuracy (range of 90–100%). Figure 5 indicates uniformly rates of TN % above 90%, without differences by individual or leg.

Figure 4.

True Positive (TP) % for each subject with respect to the classification scheme parameters: L = left leg; R = right leg; S = Symlet Mother Wavelet, D = Daubchies Mother Wavelet, V = Feature/Variable Selection Algorithm, P = Principal Component Analysis. Each box and whiskers plot represents the median (horizontal line), the 25^th and 75^th percentiles (edge of box) and the 95% confidence intervals (whiskers).

Figure 5.

True Negative (TN) % for each subject with respect to the classification scheme parameters: L = left leg; R = right leg; S = Symlet Mother Wavelet, D = Daubchies Mother Wavelet, V = Feature/Variable Selection Algorithm, P = Principal Component Analysis. Each box and whiskers plot represents the median (horizontal line), the 25^th and 75^th percentiles (edge of box) and the 95% confidence intervals (whiskers).

3. Discussion

We intentionally selected signals for these analyses that represented de-identified data from individuals without the disorders in question, because we were attempting to achieve accurate computer-derived classification apart from more difficult and complex clinically related issues related to case identification. To that end, we selected over 131,000 seconds of surface EMG signals from 6 different individuals (x 2 legs) that were free from apparent artifacts or otherwise spurious signals, at least as detectable using the gold standard of expert visual analysis. Although we did not specifically select patients with neurodegenerative diseases for this analyses, the range of ratios of phasic seconds to total (phasic + non-phasic) seconds of signal varied widely across individuals, thus providing us with a broad overview of likelihood of such signals occurring during human sleep. It is of interest that the left leg of individual 003 was relatively low in frequency of phasic activity relative to the occurrence non-phasic activity. However, the ratio was not the lowest (c.f., left leg of individual 002) thus suggesting that low TP% of individual 003 was not simply related to the differences in the ratio of base rate. These data instead raise the possibility that some subtle introduction of noise components may occur for some recording of surface EMGs, that fact perhaps being a function of the bipolar recording derivation used in that signal (e.g., left leg recording of individual 003), rather than a person-related factor per se. Electrode application on humans is not an exact science, and although there are guidelines for technologists to guide such procedures, small differences in person-based electrode impedance may impact signals from which WT-based feature analysis and dimensionality reduction strategies ultimately derive accuracy. Our future work will examine more carefully how unequivocal artifacts can impact classification accuracy. In the interim, our suggestion is that minimizing impedance through proper electrode application techniques will minimize the possibility of potentially spurious results. Development of a library of artifacts and their impact upon WT-based features may ultimately inform us as to the robustness of these techniques for the routine clinical practice of sleep medicine.

Somewhat surprising to us was the relative equivalence of Symlet and Daubechies WT analysis results seen in these data (excluding S003-the noise sensitive case, which displayed a TP% approaching 90% only for the Daubechies and not the Symlet WT). Although these two approaches contain slightly different geometric properties for each mother WT (Symlet, an essentially symmetric waveform vs. Daubechies, a non-symmetrical waveform), this geometric distinction did not impact performance evaluation, which suggests robustness in usage of either WT family in analyzing human EMG activity recordings. In this study, we did not elect to examine customized WTs, because the diversity of waveforms covered by the Symlet/Daubechies approaches was very broad. Future work might consider examining WTs different from the two examined here. Regarding dimensionality reduction approaches, we found no evidence that the complex FVS algorithm was superior to PCA. Therefore, for clinical application we suggest implementation of the PCA due to its faster execution time. Prospective examination of the utility of such an approach in clinical populations would still be required (see final paragraph below).

A final limitation of our WT-based approach is that we have made a somewhat arbitrary selection of features for incorporation here. For example, in our previous work [5], we employed some features that were not included here (e.g., zero crossings, squared signal amplitude) but in the interest of simplicity we elected to investigate whether a smaller set of features could provide efficient results when applying WT decomposition. Additionally, our prior efforts extracted features limited to the time or frequency domain, whereas WT analysis uses both, which represents a more complementary and comprehensive approach for processing human muscle potentials. However, in future work we will include features overlooked in this study, as the possibility remains that some may prove to be valuable as we establish automated pre-processing methods to detect and compensate for artifacts that were manually excluded at this point.

The primary goal of this investigation was the establishment of an automated scheme that uses surface EMG activity to detect phasic data which, we propose, requires the development of a resilient quantitative model. We have, in this study, established that Symlet or Daubechies and FVS or PCA represent viable feature extraction and dimensionality reduction methods, respectively, to be utilized in the desired model. Also, we found that the application of either supervised or unsupervised classification methods (investigated in our previous work [5]) both provided efficient performance in detecting phasic activity (maximum unsupervised TP% ~97% and maximum supervised TP% ~99%, for S001). Having determined that supervised and unsupervised classification provides efficient phasic detection, we will apply the method that fits best within computational constraints that will be explored in our continued studies. We also suggest that applications of phasic EMG quantification extend beyond the 1-, 2-, or 3-second processing window boundary used by ourselves [1] and others [3, 7, 8]. Such fixed segmentation may significantly contribute to lack of concordance, since in some situations the majority of disagreement mostly involves seconds crossing segmentation boundaries. In future work, we will focus on these borderline situations by considering more flexible, continuous interval approaches. Generally, we found that the investigated supervised, WT-based approach provides efficient benchmarking parameters to be included within the development of a robust quantitative model to process surface EMG signals derived from overnight polysomnography.

This study intentionally avoided patients with disease in examining the utility of WTs in phasic EMG identification. We did this because the prevalence of PD and RBD in the general population approximates 1–2%, whereas prior attempts to validate digitized processing of the EMG signals during sleep select patients at a rate approximating 50% [7, 8], thus grossly exaggerating the accuracy of their models. The approach that we have taken here is less biased, since it focuses on the occurrence of EMG signals at rates encountered in the general population. As such, WTs would be expected to at least be equivalent to or possibly exceed accuracy of other digitized approaches in future disease/non-disease comparisons. It also remains to be seen whether the current findings are limited to specific features selected for analysis here, the dimensionality reduction approaches and/or the linear classifier function employed.

4. Summary

Phasic (< 100 msec duration) muscle activity recorded during human sleep is relevant for the study of certain neurodegenerative diseases, however, visual quantification of such activity is time-intensive. We developed a computer-based, digitized system for quantifying such activity using wavelet (WT) approaches. We considered both Symlet and Daubechies functions and applied these to various features extracted from the overnight recordings encompassing over 131,000 individual artifact-free seconds of surface-recorded muscle activity in human sleep. This was followed by dimensionality reduction, employing both principal components analysis (PCA) and a feature/variable selection (FVS) algorithm. A linear classifier was used to distinguish each individual second of recording as phasic activity present or phasic activity absent. Performance evaluation of the classifier was determined by calculating the True Positive and True Negative percentages relative to human visual classification, which represented the gold standard. Results indicated generally high levels of classification performance that was independent from specifics of WT function (Symlet or Daubechies) or dimensionality reduction technique (PCA or FVS). These findings may present an optimistic pathway for future development of phasic muscle quantification of the human polysomnogram.