Regional Probabilistic Fertility Forecasting by Modeling Between-Country Correlations

Abstract

BACKGROUND

The United Nations (UN) Population Division produces probabilistic projections for the total fertility rate (TFR) using the Bayesian hierarchical model of Alkema et al. (2011), which produces predictive distributions of the TFR for individual countries. The UN is interested in publishing probabilistic projections for aggregates of countries, such as regions and trading blocs. This requires joint probabilistic projections of future country-specific TFRs, taking account of the correlations between them.

OBJECTIVE

We propose an extension of the Bayesian hierarchical model that allows for probabilistic projection of aggregate TFR for any set of countries.

METHODS

We model the correlation between country forecast errors as a linear function of time invariant covariates, namely whether the countries are contiguous, whether they had a common colonizer after 1945, and whether they are in the same UN region. The resulting correlation model is incorporated into the Bayesian hierarchical model’s error distribution.

RESULTS

We produce predictive distributions of TFR for 1990–2010 for each of the UN’s primary regions. We find that the proportions of the observed values that fall within the prediction intervals from our method are closer to their nominal levels than those produced by the current model.

CONCLUSIONS

Our results suggest that a substantial proportion of the correlation between forecast errors for TFR in different countries is due to countries’ geographic proximity to one another, and that if this correlation is accounted for, the quality of probabilitistic projections of TFR for regions and other aggregates is improved.

1 Introduction

The United Nations (UN) Population Division produces population estimates and projections every two years for all countries and publishes them in the biennial World Population Prospects (WPP). These projections are used by UN agencies and governments for planning, monitoring development goals and as inputs to climate change and other models. They are also widely used by social and health science researchers and the private sector. The UN produces these population forecasts by projecting countries’ age- and sex-specific fertility, mortality, and migration rates, and combining them to obtain age- and sex-specific population sizes using the standard cohort component method.

In this paper, we focus on the fertility component. Country fertility in a given time period is summarized by the period total fertility rate (TFR), which is the average number of children a woman would bear if she lived past the end of the reproductive age span and at each age experienced the age-specific fertility rate of the given country and time period. Projections of future TFR are decomposed using forecasted age schedules to obtain projections of age-specific fertility rates.

The WPP reports three projection variants (low, medium, and high) for the population and vital rates based on expert opinion and models of historical patterns. The low and high variants correspond to TFR half a child below and above the medium value, respectively. A drawback of these projections is that the range given by the low and high variants has no probabilistic interpretation and hence does not reflect the uncertainty in the forecasts.

For the 2010 WPP (United Nations, Department of Economic and Social Affairs, Population Division, 2011), the UN used as its medium projection the predictive median of TFR from a Bayesian hierarchical model developed by Alkema et al. (2011). We refer to this model as the “current model”. This model produces predictive probability distributions of each country’s TFR, although the distributions were not used in the 2010 WPP. The model is based on the demographic transition, where countries move from high birth and death rates to low birth and death rates, and is composed of three phases: before, during and after the fertility transition. Predictions from this model are typically summarized by the median country TFR prediction and the 80% or 95% prediction interval.

In addition to producing population estimates at the country level, the UN also provides projections for country aggregates such as geographic regions and trading blocs. The country TFR projections from the current Bayesian hierarchical model of Alkema et al. (2011) can be combined to obtain regional probabilistic TFR projections, provided the current model takes account of the dependence between countries’ fertility rates. However, if dependence exists between country TFRs that is not accounted for in the Bayesian hierarchical model, treating the country-specific projections as independent may underestimate the uncertainty about the future TFRs and populations of aggregates.

Figure 1 shows the UN’s 22 primary regions of the world and Table 1 summarizes the coverage probability of the out-of-sample TFR prediction intervals for these regions based on the current model. The coverage probabilities of the region-specific predictive intervals are smaller than the nominal levels, even though the country-specific coverages have been found to be approximately correct (Alkema et al., 2011). This suggests that the assumption of independent forecast errors may not be appropriate.

Figure 1.

Primary regions of the world as identified by the UN.

Table 1.

Proportion of observed regional TFRs that fall within the specified out-of-sample prediction intervals obtained from the current Bayesian hierarchical model of Alkema et al. (2011).

Time Period	80% CI	90% CI	95% CI
1990–1995	0.73	0.86	0.95
1995–2000	0.68	0.73	0.86
2000–2005	0.59	0.73	0.82
2005–2010	0.73	0.82	0.91
All	0.68	0.78	0.89

The importance of modeling between country correlations in stochastic projections is well recognized and others have proposed methods for addressing it. Lutz et al. (1997) combined stochastic projections, where the within and/or between region country correlation was zero or one, to incorporate forecast uncertainty due to between country correlation. This procedure was formalized by Alho and Spencer (2005) based on the use of random seeds and it was used to generate regional TFR forecasts in Statistics Netherlands (2005) (see also Alho et al. (2006)). Although this method is able to produce forecast errors with any desired marginal correlation, the individual forecasts come from a mixture distribution of two extreme scenarios neither of which is realistic, and confidence intervals for aggregate values based on the empirical quantiles of the forecast simulations are invalid. Lutz et al. (2001) generated correlated fertility forecast deviations assuming a between region correlation of 0.7, but provided no empirical justification for this value.

Keilman and Pham (2004) and Alho (2008) estimated correlations between TFR forecast errors for a set of European countries for which long and high quality time series data are available, and for which the TFRs have been low for a long time in most cases. Similarly, Wilson and Bell (2007) developed probabilistic population projections for Queensland and the rest of Australia using an empirical correlation between TFR errors. These studies represent best case scenarios, for which empirical estimates of the correlations are reasonably accurate and further modeling is probably unnecessary. This is not the case for our problem here: the number of empirical forecast errors is extremely limited for many countries, leading to undefined or unreliable empirical estimates.

In this article, we propose an extension to the Bayesian hierarchical model that produces TFR estimates for any aggregate of countries by modeling the residual correlation between country TFRs. Our extension adds a correlation structure to the error distribution in the hierarchical model, where the correlation between a pair of countries is modeled as a linear function of time invariant covariates. Three covariates are chosen: whether two countries are contiguous, whether they had a common colonizer after 1945, and whether they are in the same UN region. This model provides estimates of the correlation between any pair of countries, even when empirical estimates are not available.

This paper is organized as follows. In the next section we review the current model and introduce the correlation model extension. We also describe the exploratory analyses that led to the choice of model extension. An estimation procedure based on a pseudo-likelihood function is described, and model validation results are then presented for the prediction of the TFR in each of the UN’s regions. We show theoretically which regional prediction intervals are most affected by the correlation model and compare the pairwise country correlation values from our model and those obtained in previous studies. We conclude with a discussion of previous work.

2 Methodology

2.1 Current Model

The Bayesian hierarchical model of Alkema et al. (2011) divides the evolution of TFR in a country into three phases: before, during and after the fertility transition. During the fertility transition, the TFR for country c in time period t, f_c,t, is modeled as following a systematic decline curve with normally distributed random errors. After the fertility transition is complete, the TFR is modeled as a first order autoregressive process that ultimately fluctuates about 2.1, which is considered replacement level fertility (see Section 5 for extensions that relax this assumption). If f_t = (f_1,t, …., f_C,t) is the TFR for all countries at time t, the model can be written as follows:

$${\mathit{f}}_{\mathit{t}}={\mathit{m}}_{\mathit{t}}+{\mathit{\epsilon }}_{\mathit{t}},{\mathit{\epsilon }}_{\mathit{t}}~\mathrm{N}(0,{\mathrm{\Sigma }}_t={\tilde{\mathit{\sigma }}}_{\mathit{t}}^{\mathit{T}}{\tilde{\mathit{\sigma }}}_{\mathit{t}})$$ (1)

Fertility transition phase:	Post-transition phase:
mc,t = fc,t−1 − d(θc, fc,t−1),	mc,t = 2.1 + 0.9(fc,t−1 − 2.1),
σ̃c,t = σc,t(θc, fc,t−1).	σ̃c,t = s = 0.2.

In (1), the quantities in bold font are vectors whose elements correspond to different countries, d(θ_c, f_c,t−1) is a double logistic function controlling the rate of the fertility decline, and θ_c is a vector of country-specific parameters specifying country c’s unique decline pattern. The elements of θ_c determine various aspects of the decline, such as the starting fertility level, the overall pace of the transition, and the timing and acceleration of the decline (see Alkema et al. (2011) for more details). The expected TFR in the next time period, m_c,t, and the variances of the random errors, ${\tilde{\sigma }}_{c,t}^2$, differ in the transition and post-transition phases. Since a country’s TFR is not modeled before the fertility decline, the vector f_t for any time point t contains only those countries that have started or completed their fertility transition.

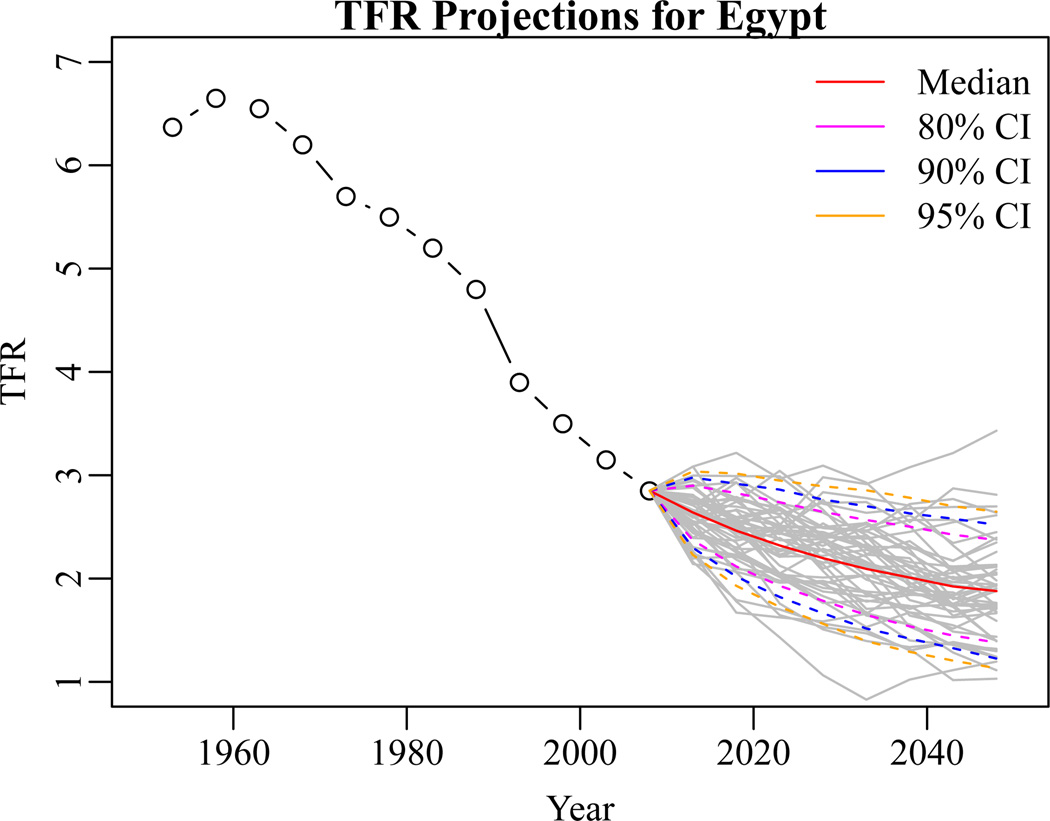
The data used to estimate the country parameters θ_c in the current model are the five-year time period TFR estimates from 1950 to 2010 in the 2010 WPP. A posterior distribution of the parameters is produced which indicates the probable values of the parameters given the data. In addition, a predictive distribution of TFR values for each country can be obtained by forecasting future values using the relations in (1). Figure 2 shows the predictive distribution of TFR for Egypt from 2010 to 2050. This distribution is summarized by the median prediction and the 80%, 90%, and 95% prediction intervals.

Figure 2.

The plot shows TFR projections (grey) and probabilistic prediction intervals for Egypt from 2010 to 2050 from the Bayesian hierarchical model.

2.2 Correlation Model

As discussed above, the regional TFR prediction intervals from the current model tend to be too narrow (see Table 1). This suggests there is excess correlation between countries’ TFRs that is not accounted for in the current model. To capture this excess correlation, we propose modifying the error structure in (1) to allow for correlation between countries as follows:

$${\mathit{\epsilon }}_{\mathit{t}}~\mathrm{N}(0,{\mathrm{\Sigma }}_t={\tilde{\mathit{\sigma }}}_{\mathit{t}}^{\mathit{T}}{R}_t{\tilde{\mathit{\sigma }}}_{\mathit{t}}).$$ (2)

The (i, j) element of the matrix R_t is the correlation between the TFR forecast errors (i.e. the deviations from the mean predicted values m_c,t) for country i and country j in time period t.

Our exploratory analyses, described below, indicated that the correlations had a different pattern when both countries had low fertility than otherwise, and our model allows for this. We sought to model the correlations using temporally stable characteristics of the country pairs, so that they could reasonably be used for projection. Thus, the elements of the correlation matrix are modeled as follows:

$$R_t[i,j]=\{\begin{array}{cc}1\hfill & \text{if}i=j,\hfill \\ {\rho }_{i,j}^{(1)}\hfill & \text{if}{f}_{i,t-1}<\kappa \text{and}{f}_{j,t-1}<\kappa ,\hfill \\ {\rho }_{i,j}^{(2)}\hfill & \text{if}{f}_{i,t-1}\ge \kappa \text{or}{f}_{j,t-1}\ge \kappa ,\hfill \end{array}$$ (3)

$${\rho }_{i,j}^{(k)}={\beta }_0^{(k)}+{\beta }_1^{(k)}{\text{contig}}_{i,j}+{\beta }_2^{(k)}{\text{comcol}}_{i,j}+{\beta }_3^{(k)}{\text{sameRegion}}_{i,j}\text{for}k\in \{1,2\},i\ne j,$$

where contig_i,j = 1 if countries i and j are contiguous and 0 if not, comcol_i,j = 1 if they had a common colonizer after 1945, and sameRegion_i,j = 1 if they are in the same UN region. As mentioned above, a key feature of this model is that all covariates are time invariant, eliminating the need for a model that forecasts the covariates. If, for example, we modeled the correlation between two countries as a function of the ratio of their GDPs in the previous year, a model that predicted countries’ future GDP would be necessary.

The correlation model in (3) states that when countries i and j both have TFR below κ, the correlation of their errors in the next time period is ${\rho }_{i,j}^{(1)}$, and when at least one of them has a TFR greater than κ, the correlation is ${\rho }_{i,j}^{(2)}$. In both cases, the correlation between two countries is modeled as a linear combination of the three pairwise country covariates. The parameters to be estimated therefore include the threshold κ, $\{{\beta }_0^{(1)},{\beta }_1^{(1)},{\beta }_2^{(1)},{\beta }_3^{(1)}\}$ for the correlation when both countries have TFR less than κ, and $\{{\beta }_0^{(2)},{\beta }_1^{(2)},{\beta }_2^{(2)},{\beta }_3^{(2)}\}$ for the correlation when at least one of the two TFRs is greater than κ.

Since the diagonal elements of R_t are equal to one, the joint predictive distribution of all country TFRs will have the same country marginal predictive distributions as those from the current model. Thus expanding the model to allow for correlation will not change the marginal country-specific predictive distributions, which is desirable given the good performance of the current model for individual countries.

2.3 Exploratory Analysis

Exploratory analysis of one-time-period-ahead forecast errors from the model of Alkema et al. (2011) and WPP data from 1950 to 2010 guided specification of the correlation model structure. For each time period and country, the forecast error is the difference between the observed TFR and the average predicted value given TFR in the previous time period. Estimating the correlations between these forecast errors is difficult because the estimates are based on a number of data points (at most 11 five-year periods), and because the country-specific predictive means and variances are given by the Bayesian hierarchical model. To obtain empirical estimates of the correlation between the forecast errors for two countries, conditional on their predictive variances, we used the posterior mean with an arc-sine prior. This estimator was proposed by Fosdick and Raftery (2012), who showed it to have good small sample performance compared to other frequentist and Bayesian estimators.

Table 2 shows the number of overlapping five-year time periods from 1955 to 2010 for each country pair after both had started their fertility decline. These counts represent the number of forecast errors available to compute each correlation estimate. Since a number of countries have only recently started their fertility decline, many pairwise correlation estimates were based on only a few observations or, in the case of only two overlapping time periods, were not computed at all. We therefore chose to model the correlation structure rather than directly use the noisy empirical estimates from the raw data.

Table 2.

Numbers of unique country pairs with each number of overlapping five-year time periods since the start of each country's fertility decline.

No. time periods	2	3	4	5	6	7	8	9	10	11
No. country pairs	389	385	1,131	3,009	1,635	2,550	2,508	2,750	1,978	2,775

Since the representation of TFR in the Bayesian hierarchical model differs when it is high (during the transition) compared to when it is low (post-transition), there was concern that country correlations might vary with TFR level as well. To investigate this, separate posterior mean correlation estimates were computed based on the forecast errors when both countries had TFR above three and when both countries have TFR below three. Table 3 shows the results from significance tests on these correlation estimates which test whether each estimate is non-zero (see Fosdick and Raftery (2012) for more details on these tests). Results are shown for only the correlation estimates that are based on at least five overlapping time periods. Based on 0.05-level tests, over 17% of the correlation estimates for country pairs with low TFRs were deemed significantly non-zero. This is much larger than the 5% we would expect if there was no correlation in forecast errors. The percentage significant when countries have low TFR was 3.3, close to that expected in the absence of correlation. The stark difference in the percentage of non-zero correlations when both countries have low TFR compared to when they both have high TFR led us to specify one model for the correlation when the TFRs of both countries are below a threshold κ, and a different model when at least one country has TFR above κ, where κ is to be estimated from the data.

Table 3.

Results from level-0.05 significance tests on the correlation estimates testing whether each estimate is non-zero. Only the correlation estimates that were based on at least five overlapping time periods were considered here.

	Number of country pairs	Number significant	Percent significant
Both country TFRs above 3	1857	60	3.3
Both country TFRs below 3	1356	235	17.3

The average estimated correlation between countries in the same UN-defined region when both have TFR below 3 was 0.37, and for countries in different regions was 0.09, using only correlation estimates based on at least eight time periods. This suggests that the correlation between forecast errors at low TFR levels may be related to geographical proximity, and motivates modeling the correlation as a function of geographical predictors.

Since our aim is to make long-term projections, we consider only predictors that are essentially time invariant. A database of country pairwise covariates is available from the Centre d’Études Prospectives et d’Informations Internationales (CEPII) (Mayer and Zignago, 2006). In order to select which covariates to include in the correlation model, we used a Bayesian model averaging approach as implemented in the BMA package in the statistical program R (Raftery, 1995; Raftery et al., 2005, 2013c). This method considers all regression models corresponding to subsets of the covariates and based on the evidence in the data in favor of each model, computes the posterior probability of each covariate being in the model (i.e. the probability the variable’s regression coefficient β is non-zero).

Table 4 shows the results for all variables in the CEPII database, as well as two additional indicator variables that signify whether pairs of countries are in the same UN area and same UN region. Note here we are only considering correlation estimates based on errors when both countries had TFR less than 3 and share at least five overlapping time periods. We chose to focus on estimates when TFR is low since these were determined to contain the most excess correlation and this correlation will have the most impact on long-term forecasts. The posterior inclusion probabilities for the covariates related to whether countries are contiguous (config), share a common colonizer after 1945 (comcol), and are in the same UN region (sameRegion) are equal to one. This suggests there is strong evidence in the data for each of these covariates as predictors of country correlation. Barbieri and Berger (2004) showed that the single regression model with the predictors whose posterior inclusion probabilities are above 50% is predictively optimal, and so following them we choose the model with these three covariates.

Table 4.

Output from the BMA package in R. The second column contains the posterior probability of each variable being in the regression model, while the third and forth columns contains the regression coefficient posterior mean estimates and posterior standard deviations, weighted and averaged over all possible models containing subsets of the covariates.

	P(β ≠ 0)	Estimate (β)	Std Deviation
intercept	100.0	.062	.001
contiguous (contig)	100.0	.211	.034
common colonizer after 1945 (comcol)	100.0	.270	.039
same UN region indicator (sameRegion)	100.0	.117	.020
colonial relationship after 1945	41.8	.056	.072
colonial link	19.5	.018	.039
were/are the same country	14.5	−.014	.039
distance weighted by city pop: harmonic mean	9.5	0	0
distance weighted by city pop: arithmetic mean	9.1	0	0
share a language spoken by at least 9%	2.5	0	.001
common official language	2.2	.001	.001
currently in a colonial relationship	0.0	0	0
geodesic distance by most important cities	0.0	0	0
geodesic distance by capital cities	0.0	0	0
same UN area indicator	0.0	0	0

3 Parameter Estimation

Our method for estimating the parameters of the correlation model in (3) relies on the one-time-period-ahead standardized forecast errors. The Bayesian hierarchical model of Alkema et al. (2011) was fit to the 2010 WPP TFR estimates from 1950 to 2010, and posterior distributions of θ_c given the data were obtained for each country. Using these parameter estimates and the TFR in a given time period, a predictive distribution of the expected TFR m_c,t for the next time period was computed. The value of m_c,t for a parameter vector θ_c is

$${\widehat{m}}_{c,t}|f_{c,t-1}^{WPP},{\mathit{\theta }}_{\mathit{c}}=\{\begin{array}{cc}{f}_{c,t-1}^{WPP}-d({\mathit{\theta }}_{\mathit{c}},f_{c,t-1}^{WPP}),\hfill & \text{during the fertility transition},\hfill \\ 2.1+\rho (f_{c,t-1}^{WPP}-2.1),\hfill & \text{after the fertility transition},\hfill \end{array}$$

where $f_{c,t-1}^{WPP}$ is the 2010 WPP TFR estimate for country c at time period t − 1. For each sample ${\mathit{\theta }}_{\mathit{c}}^{\mathbf{(}\mathit{k}\mathbf{)}}$ from the posterior distribution, there is a corresponding expected TFR value at time t.

We define the parameter-specific standardized forecast error e_c,t(θ_c) for country c, time period t, and parameter vector θ_c as

$$e_{c,t}({\mathit{\theta }}_{\mathit{c}})=\frac{f_{c,t}-E[f_{c,t}|f_{c,t-1},{\mathit{\theta }}_{\mathit{c}}]}{SD[f_{c,t}|f_{c,t-1},{\mathit{\theta }}_{\mathit{c}}]}=\frac{f_{c,t}^{WPP}-{\widehat{m}}_{c,t}|f_{c,t-1}^{WPP},{\mathit{\theta }}_{\mathit{c}}}{{\tilde{\sigma }}_{c,t}}.$$

We define the standardized one-time-period-ahead forecast error e̅_c,t as the average over the posterior samples of the parameter-specific forecast errors, namely

$${\overline{e}}_{c,t}=\frac{1}{K}\sum _{k=1}^K{e}_{c,t}({{\mathit{\theta }}_{\mathit{c}}}^{(k)}),$$

where K is the number of parameter samples from the posterior distribution.

The standardized errors can be viewed as samples from a multivariate normal model with correlation matrix R_t, e̅_t(θ) ~ N(0,R_t) for t = 1955, …, 2010. Ideally we would estimate the correlation model parameters $\{\kappa ,{\beta }_0^{(1)},{\beta }_1^{(1)},{\beta }_2^{(1)},{\beta }_3^{(1)},{\beta }_0^{(2)},{\beta }_1^{(2)},{\beta }_2^{(2)},{\beta }_3^{(2)}\}$ via maximum likelihood estimation based on the multivariate normal model. However, this is made challenging by the fact that for any time period t, the vector e̅_t contains standardized errors for only those countries that have started their fertility decline by time t, and that for many parameter values the estimated correlation matrix is not positive definite, making the likelihood undefined.

Instead, we took a pseudo-likelihood approach that approximates the multivariate normal likelihood by a product of bivariate normal likelihoods (Besag, 1975). We call this the Aggregation Pseudo-Likelihood (APL) and define it as

$${\mathrm{L}}_{\mathrm{A}\mathrm{P}\mathrm{L}}(\kappa ,{\mathit{\rho }}^{\mathbf{(}\mathbf{1}\mathbf{)}},{\mathit{\rho }}^{\mathbf{(}\mathbf{2}\mathbf{)}}|\overline{\mathit{e}})=\prod _{t=1}^T\prod _{i<j}[{\mathrm{L}}_1({\rho }_{i,j}^{(1)}|{\overline{e}}_{i,t},{\overline{e}}_{j,t})·\mathrm{I}[(f_{i,t-1}<\kappa )\text{and}(f_{j,t-1}<\kappa )]+{\mathrm{L}}_2({\rho }_{i,j}^{(2)}|{\overline{e}}_{i,t},{\overline{e}}_{j,t})·\mathrm{I}[(f_{i,t-1}\ge \kappa )\text{or}(f_{j,t-1}\ge \kappa )]],$$ (4)

where T is the number of observed time periods and I(A) is a indicator function that equals 1 if the condition A is true and 0 otherwise. L₁ and L₂ are bivariate normal likelihoods with zero means, variances equal to one, and correlations ${\rho }_{i,j}^{(1)}\text{and}{\rho }_{i,j}^{(2)}$, respectively.

The APL can be maximized separately over $\{{\beta }_0^{(1)},{\beta }_1^{(1)},{\beta }_2^{(1)},{\beta }_3^{(1)}\}\text{and}\{{\beta }_0^{(2)},{\beta }_1^{(2)},{\beta }_2^{(2)},{\beta }_3^{(2)}\}$ for a fixed value of κ. For each value of the threshold κ from 0.5 to 9 children at intervals of 0.1, we estimated the model parameters by maximizing the APL in (4) numerically using a Nelder-Mead method subject to the constraint that the correlations ${\rho }_{i,j}^{(1)}\text{and}{\rho }_{i,j}^{(2)}$, defined by the β’s, lie in the interval [−1, 1] for all i and j.

The APL was maximized at κ = 5 children, and the corresponding regression coefficients are shown in Table 5. These estimates mirror the exploratory analysis result that correlations are larger on average when both countries have lower TFR. At TFR values below κ, the correlation between two countries that are contiguous and in the same region but do not share a common colonizer is 0.46. The correlation between countries that are not in the same region but are contiguous is 0.37. The corresponding values when at least one TFR is above κ are 0.13 and 0.11, respectively. Country pairs with no colonial or geographic relationship have a correlation of 0.11 when both TFRs are below κ, and 0.05 otherwise. This illustrates that the correlation between two countries is associated with their geographic and colonial relationship.

Table 5.

Parameter estimates for the correlation model (3). The estimate of the threshold κ is 5.

	intercept (β0)	contig (β1)	comcol (β2)	sameRegion (β3)
Both country TFRs below κ	0.11	0.26	0.05	0.09
At least one country TFR greater than κ	0.05	0.06	0.00	0.02

For many time periods, the APL estimates of the parameters result in estimated correlation matrices R_t that are symmetric but not positive semidefinite. However, the correlation matrix must be positive semidefinite to use it for simulation of forecast errors. The symmetric positive semidefinite matrix closest in Frobenius norm to a given symmetric matrix is obtained by zeroing out all negative eigenvalues of the original matrix (Driessel, 2007) and then reconstructing the matrix. Thus, at each time point t for which R_t is not positive semidefinite, we perform the following procedure:

1. Compute the eigenvalue decomposition of R_t to express it as R_t = UDU^T, where U is an orthogonal matrix of eigenvectors and D is a diagonal matrix of eigenvalues.

2. Replace all the negative eigenvalues by zero. The matrix D is thereby changed to D̃.

3. Compute the reconstructed matrix R̃_t = U D̃U^T.

4. The diagonal elements of R̃_t will not equal one unless the original matrix was positive semidefinite. Therefore, treat R̃_t as a covariance matrix and rescale it to obtain a reconstructed and rescaled correlation matrix R̂_t to use in the projections.

The rescaling of the correlation matrix in step 4 ensures that the predictive distribution of TFR for any individual country remains the same as from the current Bayesian hierarchical model of Alkema et al. (2011). Thus, only joint predictive distributions of the TFRs in more than one country are affected. Note that the matrix approximation R̂_t that results from this procedure is singular unless the original matrix R_t is positive definite, but the predictive distributions remain well defined.

4 Results

4.1 Model Validation

We assessed the model by estimating the current hierarchical model parameters from the data for 1950 to 1990, projecting regional TFR for the UN’s 22 primary regions from 1990 to 2010 using the error correlation structure, and comparing the probabilistic projections with the actual observations for the four held-out five-year periods. We approximated regional TFR by a weighted average of country-specific TFRs, with weights proportional to the current female populations of each country. A similar approximation was used for regional life expectancy by Raftery et al (2013b).

Posterior distributions of the Bayesian hierarchical model parameters were obtained based on data from 1950 to 1990. The parameter values in Table 5 were used in the correlation model and not re-estimated based on the restricted data set, since these estimates are already based on very limited data. Projections of TFR were obtained for the four five-year time periods from 1990 to 2010 under the current model assuming independent errors and using our proposed error correlation structure. The predictive distributions of the weighted average TFR for each of the 22 regions were compared to the observed weighted average values.

Table 6 shows the proportion of observed weighted averages that fell within the 80%, 90%, and 95% prediction intervals from both approaches. In each case the observed proportion was closer or as close to the theoretical value under the correlation model than under the independence model.

Table 6.

Proportion of observed regional weighted average TFRs that fall within the specified prediction intervals.

Time Period	Model	80% CI	90% CI	95% CI
1990–1995	Independence	0.73	0.86	0.95
	Correlation	0.86	0.91	0.95
1995–2000	Independence	0.68	0.73	0.86
	Correlation	0.73	0.86	0.95
2000–2005	Independence	0.59	0.73	0.82
	Correlation	0.64	0.73	0.95
2005–2010	Independence	0.73	0.82	0.91
	Correlation	0.77	0.86	0.91
All	Independence	0.68	0.78	0.89
	Correlation	0.75	0.84	0.94

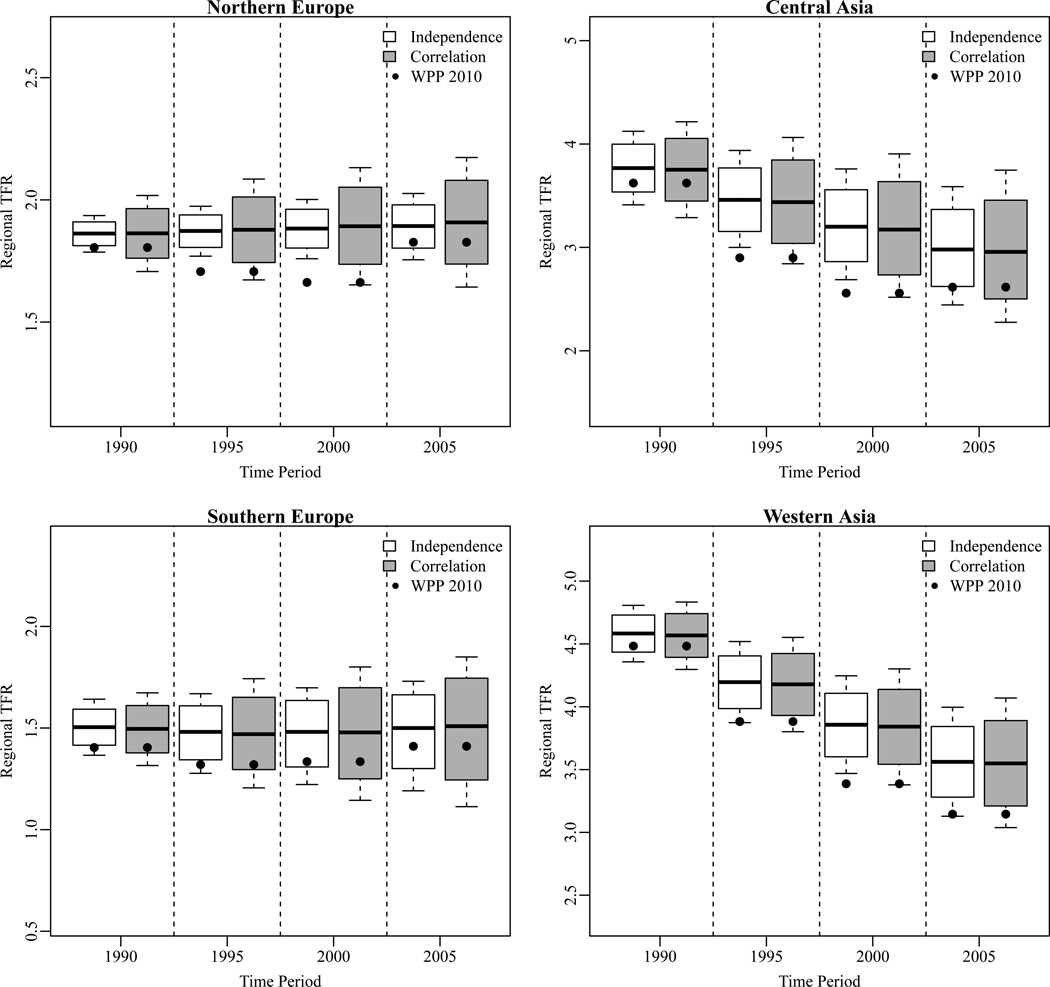
Figure 3 shows the posterior distribution of regional TFR for four regions, along with the observed regional value. The box associated with a given period and projection method represents the 80% interval and the ends of the whiskers correspond to the 95% interval. For Northern Europe the current model prediction intervals do not cover the observed value in 1995 and 2000, but the correlation model prediction intervals do. Similar patterns are seen in the other regions: the prediction intervals based on the correlation model are wider, reflecting greater uncertainty, and contain more of the observed regional TFR values than the current model assuming independent errors.

Figure 3.

Boxplots showing the 80% and 95% prediction intervals for the regional weighted average TFR for the current model assuming independent errors and that with the correlation error structure. The box of each boxplot represents the 80% prediction interval and the ends of the whiskers mark the 95% prediction interval. The corresponding observed average TFR based on the 2010 WPP is also shown.

Since the estimated correlations are larger when both countries have low TFR values, bigger differences between the current model and the correlation model prediction intervals are seen for regions like Northern Europe and Central Asia, for which the majority of the countries have completed most of the fertility decline. Regions that have few countries with TFR less than 5, such as Eastern and Western Africa, showed little change between the prediction intervals from the current model and the correlation model, as expected.

4.2 Effect of Taking Account of Correlation

For a given parameter vector θ and time period t, the effect of taking account of correlation on the variance of the regional TFR can be quantified analytically. We denote by p_i the proportion of the region’s female population that resides in country i, by f_i the TFR in country i in time period t, and by N the number of countries in the region. The regional weighted average TFR is then ∑_i p_if_i where the sum is over all countries in the region.

If the forecast errors are assumed to be independent as in the current model, the predictive variance of the regional TFR in time period t is $\text{Var}[{\sum }_i{p}_i{f}_i]={\sum }_i{p}_i^2\text{Var}[f_i],\text{where Var}[f_i]={\tilde{\sigma }}_{i,t}^2$. As we project TFR into the future, eventually all countries will be in the last phase of the model, having completed their fertility transition, where Var[f_i] = s². When all countries in the region are in the post-transition phase,

$$\text{Var}\left[\sum _i{p}_i{f}_i\right]=s^2\sum _i{p}_i^2$$ (5)

under the current model.

We will refer to $\sum _i{p}_i^2$ as the independence factor (IF) since it represents the ratio of the regional variance to the country-specific variance assuming independence in the post-transition phase. It indicates the effect of the distribution of the population across countries in the region and shows that the more evenly the regional female population is spread amongst the countries within the region, the greater the variability in the regional estimate. This comes from the fact that the IF is maximized when each $p_i=\frac{1}{N}$ for all countries in the region.

The variance of a region’s TFR under the correlation model is

$$\text{Var}\left[\sum _i{p}_i{f}_i\right]=(\sum _i{p}_i^2\text{Var}[f_i]+2\sum _{i<j}{p}_i{p}_j\sqrt{\text{Var}[f_i]\text{Var}[f_i]}{R}_t[i,j]).$$

When all countries have completed the fertility transition, this becomes

$$\text{Var}\left[\sum _i{p}_i{f}_i\right]=s^2(\sum _i{p}_i^2+2\sum _{i<j}{p}_i{p}_j{R}_t[i,j]).$$ (6)

We will refer to $({\sum }_i{p}_i^2+2{\sum }_{i<j}{p}_i{p}_j{R}_t[i,j])$ as the dependence factor (DF) since it is the multiplicative factor in the variance under the correlation model. Equation (6) shows that the larger the country correlations, especially between those countries with a relatively high proportion of the regional female population, the larger the variance of the regional TFR.

The ratios of the dependence factor to the independence factor for the 22 UN regions are shown in Table 7. The regions with the largest ratios are those whose predictive distributions are most impacted by between-country correlations. For example, Western Africa and Eastern Asia’s ratios are both greater than 2.5, indicating that the variance of the regional TFR predictive distributions is more than 2.5 times greater for the model with the correlation structure than that from the current model. Those regions with ratios close to 1, such as Northern America and Australia/New Zealand, have similar predictive distributions from the two models.

Table 7.

The effect of the correlation model on the variance of the regional weighted average TFRs. The ratio of the dependence factor to the independence factor (DF/IF) indicates the multiplicative increase in the variance of the regional TFR when using the correlation model compared to the current model where forecast errors are assumed independent. The “max proportion” column shows the largest proportion of the current region female population that is attributed to a single country and N is the number of countries in the region.

Region	DF/IF	Max Proportion	N
Eastern Africa	3.03	0.22	15
Western Asia	2.57	0.33	18
Central Asia	2.11	0.45	5
Middle Africa	1.98	0.48	6
South America	1.95	0.50	13
Caribbean	1.94	0.27	16
Northern Africa	1.92	0.39	7
Western Europe	1.91	0.43	7
Eastern Europe	1.88	0.49	10
South-Eastern Asia	1.76	0.40	10
Southern Europe	1.65	0.39	12
Western Africa	1.43	0.59	13
Northern Europe	1.34	0.63	11
Southern Asia	1.34	0.73	8
Polynesia	1.33	0.48	3
Central America	1.25	0.73	8
Micronesia	1.22	0.62	2
Southern Africa	1.14	0.87	5
Melanesia	1.12	0.78	5
Northern America	1.10	0.90	2
Eastern Asia	1.09	0.85	8
Australia/New Zealand	1.08	0.83	2

Both the between-country correlations and the proportion of the regional female population within each country influence the effect of the correlations. The number of countries in the region and the proportion of the regional female population that live in the largest country are also shown in Table 7. If a high proportion of the female population lives in a single country, correlations will not have a large effect on the prediction intervals for the region. Examples of this include Northern America and Eastern Asia which have low DF/IF ratios and high proportions of the female population in a single country. Overall, the regions whose predictive intervals in the future will be most highly affected by between-country correlations include Middle, Eastern and Northern Africa, Western and Central Asia, Eastern and Western Europe, South America, and the Caribbean.

4.3 Comparison to Previous Results

Others have investigated the correlation between country forecast errors and obtained similar results to those reflected by the correlation model here. Keilman and Pham (2004) modeled TFR in 18 countries in the European Economic Area (EEA) with an autoregressive conditional heteroscedastic model and calculated the average correlation between country TFR errors to be 0.33. Although not all countries in the EEA are within the same UN region, in our model two countries with low TFR that are in the same region and not contiguous have a correlation of 0.20 and those not in the same region but are contiguous have a value of 0.37.

When Alho (2008) further studied the correlation matrix obtained by Keilman and Pham (2004) (see also Statistics Netherlands (2005)), he found a stark contrast between the correlations between the Mediterranean countries (Portugal, Spain, Italy, and Greece) and all others. His estimate of the average correlation between forecast errors in Mediterranean and non-Mediterranean countries was 0.12 and the correlation within each of these groups was 0.3. Recall that in our model, the correlation between countries that have low TFR and have no geographic or colonial relation is 0.11.

Wilson and Bell (2007) modeled TFR using a random walk with drift and found the correlation between errors for Queensland and the rest of Australia to be 0.40. According to our correlation model, when TFR is less than 5, as it has been in Australia for many decades, the correlation between Australia and a hypothetical country contiguous to it would be 0.46. This is comparable to the result of Wilson and Bell (2007).

5 Discussion

When producing probabilistic population projections for country aggregates, it is vital to take account of between-country correlations in forecast errors of vital rates (Lutz, 1996; Lee, 1998; Bongaarts and Bulatao, 2000). In this paper we have proposed a method for estimating between-country correlations in forecast errors of the TFR for all countries and using them to produce probabilistic TFR forecasts for aggregates of countries such as regions. For many country pairs there are few relevant data available, and so we estimate the correlations by modeling them as a function of three time-invariant predictors.

The resulting method yields the same probabilistic projections of TFR for individual countries as the Bayesian hierarchical model of Alkema et al. (2011), which was used by the UN for its (deterministic) medium population projections for all countries in the 2010 WPP (United Nations, Department of Economic and Social Affairs, Population Division, 2011). In an out-of-sample validation experiment, our correlation extension yielded better coverage of predictive intervals than the current model of Alkema et al. (2011) that does not explicitly take account of between-country correlations. The posterior samples produced by our method can be incorporated into probabilistic population projections in the same way as those produced by the current method Raftery et al. (2012).

The assumption in (1) that in the long-term (post-transition phase) every country TFR will fluctuate around 2.1 can be relaxed. Raftery et al (2013a) proposed an extension that allows each country to have its own long-term mean TFR. This extension has been incorporated into the bayesTFR package in R, along with the TFR correlation model presented here (Ševčíkoá et al., 2011).

While we have discussed procedures for aggregating country-specific TFR projections, the methods proposed here could be adapted to address excess correlation between any set of stochastic forecasts, such as mortality rates, migration rates, etc. The key task would be obtaining a set of time-invariant covariates that explain the between country correlation. The existence of excess correlation is a function of the mean model specification and may not always be present. For example, Raftery et al (2013b) found no evidence for cross country correlation in life expectancy forecasts. Nonetheless depending on the complexity and mean model fit, excess correlation may exist and adapting the methods presented here may provide better uncertainty estimates for aggregate quantities.