Abstract
Increases over birth cohorts in psychometric abilities may impact effects of aging. Data from 2 cohorts of the Long Beach Longitudinal Study, matched on age but tested 16 years apart, were modeled over ages 55–87 to test the hypothesis that the more fluid abilities of reasoning, list and text recall, and space would show larger cohort differences than vocabulary. This hypothesis was confirmed. At age 74, average performance estimates for people from the more recently born cohort were equivalent to those of people from the older cohort when they were up to 15 years younger. This finding suggests that older adults may perform like much younger ones from the previous generation on fluid measures, indicating higher levels of abilities than expected. This result could have major implications for the expected productivity of an aging workforce as well as for the quality of life of future generations. However, cohort improvements did not mitigate age declines.
Keywords: cohort aging, longitudinal, cognition, intelligence
Over the last 50 years, there have been systematic increases in fluid intelligence measures across birth cohorts in many developed countries (e.g., Flynn, 1987). Despite this finding, the vast majority of studies in cognitive aging (e.g., Salthouse, 2004) have compared people of different ages and generations to estimate aging effects. Their conclusions therefore rest on the assumption that cohort does not bias results. In this paper, we test hypotheses about the role of cohort on age changes on five different cognitive psychometric tests. Cohort-sequential panel data from the Long Beach Longitudinal Study were analyzed over age using latent growth modeling, with cohort effects tested as differences between two panels of participants from the same age ranges but initially tested 16 years apart. Findings of cohort differences in psychometric aging would not only have implications for theories of cognitive decline, but may translate into the lengthening of the productive life span, as well as to reduced prevalence of cognitive impairment in late old age.
Cohort Change in Intelligence
Flynn (1987) reported increases of up to 1.5 standard deviations in reasoning scores between 19-year-olds tested in 1950 and those in 1980. Those tested in 1950 were born during the Great Depression and those in 1980 after World War II. Today, those Depression-era adults would be in their late 70s and postwar adults would be in their late 40s. The mean differences between individuals aged 48 and 78 on reasoning in a cross-sectional study conducted in 2008 would theoretically include that 1.5 standard deviation difference documented at age 19. This would inflate estimates of the 30-year age difference. Such biasing effects could have profound consequences for conclusions about cognitive aging because reasoning, which is considered representative of fluid intelligence, shows earlier and more substantial age declines than tasks that are more representative of crystallized intelligence. (e.g., McArdle, Ferrer-Caja, Hamagami, & Woodcock, 2002). Inflated age estimates could also arise in single-panel longitudinal studies, as they generally include a wide range of ages over a relatively short retest interval and are often analyzed over age rather than measurement occasion (e.g., McArdle et al., 2002).
Cohort differences in abilities have been consistently observed in comparisons of different birth groups in multicohort studies such as the Seattle Longitudinal Study (Schaie, 1996). Estimates suggest average increases in reasoning performance for people born in 1910 compared to those born in 1896 (e.g., Schaie, 1996) suggesting that such cohort trends have been a phenomenon of at least the past century. The dramatic rise in fluid reasoning observed by Flynn (1987) is likely to be based on continuous increments that happened to be sampled at a wide time interval (see also Flynn, 2003; Raven, 2000).
Despite substantial generational increases in fluid abilities, changes in normative data in children and young adults for more crystallized abilities have been mixed. For example, minimal cohort differences have been reported for the Mill Hill Vocabulary tests (e.g., Raven, 2000) and also for the arithmetic subtest of the Wechsler Intelligence Scale for Children—Revised (Flynn, 2003). Alwin (1991; Alwin & McCammon, 2001) suggested that once effects of education are removed, there is a reversal of the Flynn effect in a population sample, with more recent cohorts poorer in vocabulary ability than earlier born ones. However, this finding may be related to a confound between sampling of particular ages and cohorts in that study; a recent study extending cohort-sequential modeling to the sample and vocabulary test evaluated by Alwin indicated cohort increases (Bowles, Grimm, & McArdle, 2005; see also Wilson & Gove, 1999).
Although some theorists disagree whether the Flynn effect is based on actual changes in ability levels or to a lack of psychometric invariance (e.g., Rodgers, 1999)—that is, that differences across cohorts in intelligence exist because the scores do not have the same measurement properties such as equal factor loadings, uniquenesses, and factor intercepts—invariance or at least partial invariance has been established for some indices of fluid abilities across cohorts of children and young adults in developed countries (Wicherts et al., 2004). Despite disagreements about the broad explanations proposed by Flynn and colleagues (e.g., Dickens & Flynn, 2001) to explain the eponymous effect (Loehlin, 2002; Rowe & Rodgers, 2002), and some recent studies suggesting that the Flynn effect may have recently plateaued or reversed for military conscripts in the 1990s in two Scandinavian countries (e.g., Sundet, Barlaug, & Torjussen, 2004; Teasdale & Owen, 2005), it is likely that the skills underlying fluid ability performance increased during young adulthood for cohorts that are now aging.
The most widely cited explanations for the Flynn effect are those of cultural changes, including improvements in nutrition and hygiene, population movement from rural to urban areas, increased access to schooling in the first half of the 20th century, increased educational levels of parents, smaller families, parental engagement in practices that encourage cognitive development (e.g., Williams, 1998), and changes in processing from more characteristically verbal to more iconic representations due to the rise of visually oriented modalities in film, television, computer games, and other media (for descriptions see Greenfield, 1998). Blair, Gamson, Thorne, and Baker (2005) suggested that recent fluid ability increases additionally reflect a shift in the content of mathematical curricula in primary and secondary schools toward fluid-like tasks that involve working memory and improve frontal functioning.
The less consistent findings of cohort-related increases for some types of crystallized abilities have also been interpreted as due to historical changes in reinforcement. Instructional time spent imparting traditional school related knowledge has been reduced (see Williams, 1998), and people are more likely to watch movies and television than to read. The visual environment of movies and television promotes basic vocabulary and use of contextualized grammatical structures rather than the more advanced vocabulary and complex, decontextualized grammatical forms of written literature, leading to stable vocabulary scores on intelligence tests yet simultaneously declining verbal SAT scores (e.g., Greenfield, 1998). Consistent with this explanation, Bowles et al. (2005) reported that a cohort-sequential analysis over age showed greater improvement in more recently born cohorts for basic vocabulary items than for advanced ones.
In summary, it has been suggested that culture affects the cognitive environment so that cognitive abilities adapt to it (e.g., Barber, 2005). This leads to the hypothesis that discrepancies in cohort effects in older populations will vary to the extent that larger cohort increases will be observed for the fluid-like cognitive skills that have been more emphasized in recent decades than previously, whereas crystallized skills that have been consistently emphasized over the past century would show less cohort change. The fluid/crystallized theory (e.g., Horn & Cattell, 1967) also predicts age effects that parallel the cohort effects, that is, that age declines are larger for fluid than crystallized abilities. However, it is important to vary age and cohort systematically to determine whether the declines attributed to age are confounded with cohort.
Cohort and Aging
Although it has been suggested that cohort differences may be responsible for much of the observed age decline in fluid abilities (Raven, 2000), it is not likely that they explain all apparent age-related effects, as there are substantial and reliable declines for a wide range of cognitive abilities with age, including the crystallized-like abilities (e.g., Salthouse, 2004). The finding of consistent age differences across abilities suggests that, if tracked over age, different cohorts would show parallel age declines. However, it is conceivable that cohort would interact with age due to selective attrition.
People who drop out from longitudinal studies perform more poorly and tend to be older than those who remain (e.g., Cooney, Schaie, & Willis, 1988; Kennison & Zelinski, 2005). There are also age differences in initial selection into a sample. Simply being willing to participate in cognitive testing signals greater selectivity in older adults because advanced age is associated with higher rates of refusal to complete cognitive tests in a population survey (e.g., Zelinski, Burnight, & Lane, 2001) and in normative studies of intelligence (e.g., Raven, 2000). Even if later-born cohorts are intellectually advantaged, elderly individuals from earlier cohorts may be more select than younger ones just because they have survived to the age at which they are tested (see Rabbitt et al., 2002; Verhaeghen, 2003). Because there are likely to be stronger survival effects in earlier cohorts, more recent cohorts may be less likely to show those benefits because they are relatively less select (e.g., Singer, Verhaeghen, Ghisletta, Lindenberger, & Baltes, 2003). Thus cohort could conceivably have no biasing effect in cross-sectional studies because the cohort advantage may wash out.
Age Declines
Cohort effects may be implicated in the rate of average decline with age, which is not likely to be constant across the entire span of late adulthood. Neugarten (1975) coined the terms “young-old” (below age 75) and “old-old” (above 75) to differentiate age groups in the elderly population. There are clear age differences between the young-old and the old-old, with worse performance on cognitive tasks in old-old people, even when differences in education and health have been accounted for (e.g., Zelinski, Crimmins, Reynolds, & Seeman, 1998). Longitudinal studies generally report an acceleration of estimated declines in the old-old (e.g., Rabbitt et al., 2002; Singer et al., 2003; Sliwinski, Hofer, Hall, Buschke, & Lipton, 2003). Hypotheses based on the fluid-crystallized distinction suggest greater acceleration of declines in the old-old for more fluid than crystallized ones (Horn & Cattell, 1967), which has been supported longitudinally (e.g., Singer et al., 2003). Thus it is important to evaluate change across a wide range of ages in late adulthood.
Interval Scaling
Tests of the generality of the Flynn effect require direct comparisons across cognitive measures. However, with raw scores, it is impossible to determine whether an age or cohort difference of, say, 5 points on a memory task is equivalent to a difference of 5 points on a reasoning test. Another problem with raw scores is that across individuals, differences between scores on the same test may not be equivalent at different points of the scale (Wright & Stone, 1979). For example, the 2-point difference between scores of 20 and 18 on a 20-item recall task may not be interpreted as reflecting the same amount of difference in performance as the difference between scores of 14 and 12, or 2 and 0, even though the relative ordering of individuals’ scores is clear. This is a problem for testing interactions, where assumptions of statistical tests require that scores are equivalent across their full range (Embretson, 1996). Mathematical transformations of raw scores, such as z scores or proportion correct, do not redistribute them so that differences between points on the scale are equal (Wright & Stone, 1979). However, Rasch scaling can be applied to data to assure equivalence of scores across tests and persons by using an algorithm that treats item difficulty and person ability separately. It ensures that the differences between scores at every point of the scale are the same and that these differences can be directly compared across variables through logistic transformation (see, e.g., Zelinski & Gilewski, 2003). Thus, whether age declines accelerate differentially across psychometric tests has only been directly evaluated by McArdle et al. (2002), who used the Rasch scaled Woodcock-Johnson test battery. They found smaller declines that occur later in the life span for crystallized abilities than for more fluid ones for people under age 75.
In the present study, Rasch scaled scores were used for five measures that are likely to show differential cohort and age patterns. We evaluated decline patterns in people ages 55–87 and tested the hypothesis that average decline accelerates with age. We estimated changes with age and cohort independently with cohort-sequential analyses (Schaie, 1965). Two longitudinal panels, which were treated as different cohorts studied over the same range of ages but born 16 years apart, were examined to determine whether patterns of decline are similar, even if there are cohort differences in performance at the intercept.
Schaie’s (1996) longitudinal estimates, as well as cross-sectional estimates in standard score scaling for similar tasks by Salthouse (2004), suggest that slopes of age declines should be comparable for reasoning and space. Using the same items and time restrictions for the vocabulary test as Schaie, we expected that the age effect for vocabulary would be similar to those of the other psychometric tests largely because that test has a strong speed component (Hertzog, 1989; Zelinski & Lewis, 2003). Yet only small cohort effects were anticipated because the vocabulary subtest of the Schaie–Thurstone Adult Mental Abilities Test (STAMAT; Schaie, 1985) is of a crystallized-like ability. Extrapolating from Schaie’s and Salthouse’s estimates, we expected accelerating age changes for vocabulary, space, and reasoning. Both Schaie’s and Salthouse’s estimates suggest minimal acceleration of decline in late old age for recall tasks.
Method
The Long Beach Longitudinal Study design, participants, and measures are described in detail elsewhere (Zelinski & Burnight, 1997; Zelinski & Lewis, 2003). Participants are volunteers residing in the communities of Long Beach and Orange County, California. The convenience sample shows performance characteristics similar to a representative sample of older Americans who have at least a high school education (e.g., Zelinski, Burnight, & Lane, 2001). This suggests that the sample represents the upper levels of older adult performance.
Participants
The data of two cohorts of participants varying in age from 55–87 were used for the analyses. Cohort 1 participants (baseline n = 456) were born between 1893 and 1923 and were tested on as many as five test occasions in 1978, 1981, 1994, 1997, and 2000 (see top panel of Table 1). Cohort 2 participants (baseline n = 482) were born between 1908 and 1940 and were tested up to four times in 1994, 1997, 2000, and 2003. It is important to note that the overlap in the birth years of the two cohorts does not confound comparisons because the age matching held the 16-year cohort difference constant. However, Cohort 1 participants could have an advantage because they had been in the study longer than Cohort 2. To determine whether there might be retest effects for Cohort 1 participants in 1994, when Cohort 2 was initially tested, participants aged 71–87 were compared on their 1994 scores. There were 76 individuals from Cohort 1 and 294 from Cohort 2 in the analyses of variance. There were no differences on four of the tasks with Fs(1, 368) ranging from 0.0 to 2.7; however, Cohort 1 participants had significantly better 1994 scores on reasoning, F(1, 368) = 5.8, p < .05, suggesting minimal retest bias.
Table 1.
Baseline Demographic Characteristics of the Sample by Wave of Testing and Cohort
| Measure | Wave 1 | Wave 2 | Wave 3 | Wave 4 | Wave 5 |
|---|---|---|---|---|---|
| Years from baseline | |||||
| Cohort 1 | 0 | 3 | 16 | 19 | 22 |
| Cohort 2 | 0 | 3 | 6 | 9 | |
| Age | |||||
| Cohort 1 | |||||
| M | 69.8 | 68.7 | 64.0 | 62.3 | 60.6 |
| SD | 7.2 | 7.5 | 6.5 | 6.4 | 4.9 |
| Cohort 2 | |||||
| M | 72.2 | 70.8 | 68.2 | 67.9 | |
| SD | 8.5 | 8.2 | 7.4 | 7.4 | |
| Education | |||||
| Cohort 1 | |||||
| M | 12.5 | 12.9 | 13.7 | 13.5 | 14.4 |
| SD | 2.8 | 2.8 | 2.8 | 2.4 | 2.0 |
| Cohort 2 | |||||
| M | 13.7 | 13.9 | 14.1 | 14.1 | |
| SD | 2.9 | 2.9 | 2.8 | 2.7 | |
| Female (%) | |||||
| Cohort 1 | 53.3 | 52.2 | 53.7 | 48.4 | 54.5 |
| Cohort 2 | 47.8 | 50.5 | 48.8 | 49.5 | |
| N | |||||
| Cohort 1 | 456 | 232 | 82 | 31 | 11 |
| Cohort 2 | 482 | 282 | 138 | 106 | |
The mean baseline age for Cohort 1 (M = 69.81, SD = 7.17) was reliably younger than for Cohort 2 (M = 72.15, SD = 8.46), F(1, 935) = 20.81, MSE = 61.74. Members of Cohort 1 (M = 12.54, SD = 2.76) reported fewer years of formal education than Cohort 2 (M = 13.69, SD = 2.94), F(1, 935) = 36.42, MSE = 8.12. Cohort 1 consisted of 53.3% women and Cohort 2 consisted of 47.8% women; there were no differences in gender representation across cohorts, χ2(1, N = 937) = 0.08.
Test intervals were approximately 3 years apart with the exception of a 13-year interval between the second (1981) and third (1994) testings of Cohort 1. The irregularity of this interval is assumed to have no undue influence on data modeling because the data were analyzed over age rather than time. In addition, Zelinski and Burnight (1997) reported no differences in 1978 scores for Cohort 1 participants who returned in 1994, regardless of whether they were tested in 1981 or not. All had better initial scores than permanent dropouts. This suggests general selection effects for Cohort 1 participants returning in 1994 rather than practice effects.
Psychometric Tests
Five measures of cognitive performance were examined. Three of them were from the STAMAT: Recognition Vocabulary, reasoning (Letter and Word Series), and space (Figure and Object Rotation). Recognition Vocabulary required selection of definitions for 50 target words from an array of four choices in 4 min. Reasoning was a composite score of the STAMAT Letter and Word Series tests. Letter Series required selection of the next item in 30 series, such as a b c c b a d e f f e, in 6 min, and Word Series was a parallel version with items using days of the week and months. Space was a composite score of the STAMAT Figure and Object Rotation tests. In these tasks, participants had 6 min to select up to three rotations of a target from an array of six choices. The items for Figure Rotation were abstract line figures, whereas those for Object Rotation were line drawings of common household items such as a bleach bottle. There were 20 items in this test. List recall was immediate written recall of a list of 20 concrete high-frequency nouns. The words were presented on a sheet of paper and participants were given 3.5 minutes to study the list. The test was not timed. Text recall involved immediate written recall of a 227-word passage containing 104 idea units. The passage was read by participants while they also listened to an audio reading of it presented at a rate of approximately 155 words per minute. The proportion of idea units correctly recalled according to the parsing model of Turner and Greene (1977) was the dependent measure of text recall.
Rasch Scaling
Interval measurement scaling is based on the following equation (Rasch, 1966):
| (1) |
where fni1 is the person n’s probability of scoring 1 rather than 0 on item i, bn is the ability of person n, and di1 is the difficulty of the item. Rasch scaling assumes that the construct being measured is unidimensional; difficulty of items on a cognitive test is consistent with ability such that correct scores on more difficult items reflect greater ability and more difficult items always have a lower probability of being correctly answered than less difficult ones, independent of person ability. It also assumes that individuals with greater levels of ability will be more likely to score correct on more items. They always have a higher probability of correctly answering any item, independent of item difficulty, than those with low ability (Wright & Stone, 1979).
In Rasch scaling, person parameters are conditioned out of the model when item difficulties are being calibrated, and item parameters are conditioned out of the model when person parameters are being calibrated by repetitive inversion of the items and persons data matrix. Items are ordered by difficulty and persons by ability, with maximum-likelihood modeling used to identify items that best discriminate responses and people from one another. The most discriminating items are those that have an equal likelihood of obtaining a correct or incorrect response at a given level of ability. The logarithmic transformations of the item and person data shown in Equation 1 convert the ordinal data into interval data. The size of the intervals is determined by the item and person performance probabilities. Rasch scaled person scores are log odds units or logit scores representing the 50% probability of responding correctly to items at the level of ability, 75% probability of being able to respond correctly to items 1 logit below the ability level, and 25% probability of being able to respond correctly to items 1 logit above the ability level (Bond & Fox, 2001). When data are rescaled, the logit properties remain but vary with the scaling factors used to create the desired score properties. For example, rescaling list recall in the present study from a logistic score with a mean of 0 to a 0–100 range involved rescaling the logit units from 1 to 11.15. Thus, if a participant declined 11.15 points, that would indicate a 25% probability of responding to items that previously would have been associated with a 50% probability. An increase of 11.15 points on the recall task would indicate a 75% probability of responding correctly to items associated with a 50% probability previously.
Fit indexes for Rasch analyses are computed separately for persons and items. They use mean squares to show the amount of distortion in the data relative to the Rasch model. The expected value of the mean squares is 1.0. Values substantially less than 1.0 indicate underfit, with possible unmodeled noise in the data; values substantially greater than 1.0 indicate overfit. Values between 0.5 and 1.5 are productive for measurement, and those between 1.5 and 2.0 are unproductive but suggest that the measurement is not degraded; values over 2.0 are problematic (Linacre, 2006).
The infit mean square is a fit statistic sensitive to unexpected patterns of observations made by persons on items at their approximate ability level and by items on persons at the item’s approximate difficulty level. The outfit mean square is a fit statistic sensitive to unexpected observations made by persons on items that are expected to be either very easy or very difficult or by items on persons of very low or high ability. The overall root-mean-square error (RMSE) for the model is the square root of the average error variance computed over persons or items. It indicates the upper limit to the reliability of measures based on the items and persons sampled (Linacre, 2006). Reliabilities are computed separately across persons and items, in contrast to reliabilities such as Cronbach’s alpha, which is computed for persons only. However, the values of the person and item reliabilities are interpreted as is alpha, with values close to 1 indicating high reliability.
The WINSTEPS Rasch measurement program Version 3.61.1 (Linacre, 2006) was used for the interval scaling. Individual items for all tasks were the units of analysis, that is, a 1 (correct) or 0 (incorrect) for each item on each test. For the recall tasks, each word or proposition in the study materials served as an item. Item scores within each test were calibrated with the data stacked over occasions and cohorts so that each observation for a particular subject was treated as independent, as would be done in the computation of z scores over occasions. Scores were initially scaled so that at the item level they had a mean of zero. The relative range of mean age performance could be identified from the person ability scores. Table 2 provides fit information for the Rasch calibration of each of the five tests. All results were good fitting and discriminating based on their infit and outfit mean squares, low RMSEs, and high reliability for individuals and for items. Examples of interval item scores converted from raw total scores for list recall and a mental status test are found in Zelinski and Gilewski (2003).
Table 2.
Summary Statistics for Rasch Scaling
| Parameter | Personsa
|
Items
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonextreme observations (n)b |
Measurec | Infit | Oufit | Model RMSE |
Model reliability |
Nonextreme observations (n) |
Measure | Infit | Outfit | Model RMSE |
Model reliability |
|
| Reasoning | 2,261 | .46 | .96 | 60 | .09 | 1.00 | ||||||
| M | −1.13 | 0.98 | 1.22 | 0 | 0.97 | 1.83 | ||||||
| SD | 2.14 | 0.35 | 1.79 | 2.79 | 0.16 | 1.88 | ||||||
| List recall | 2,170 | .56 | .76 | 20 | .05 | 1.00 | ||||||
| M | 0.40 | 1.00 | 1.04 | 0 | 1.00 | 1.04 | ||||||
| SD | 1.14 | 0.16 | 0.47 | 0.81 | 0.04 | 0.13 | ||||||
| Text recall | 2,213 | .28 | .91 | 104 | .06 | 1.00 | ||||||
| M | −1.32 | 1.00 | 1.01 | 0 | 1.00 | 1.01 | ||||||
| SD | 0.94 | 0.15 | 0.38 | 1.07 | 0.08 | 0.21 | ||||||
| Space | 2,281 | .19 | .95 | 40 | .03 | 1.00 | ||||||
| M | 1.92 | 0.95 | 0.94 | 0 | 0.91 | 0.94 | ||||||
| SD | 0.87 | 0.44 | 0.76 | 1.01 | 0.20 | 0.32 | ||||||
| Vocabulary | 2,128 | .62 | .92 | 50 | .10 | 1.00 | ||||||
| M | 2.62 | 0.98 | 1.76 | 0 | 0.97 | 2.44 | ||||||
| SD | 2.15 | 0.33 | 2.47 | 2.11 | 0.37 | 2.41 | ||||||
Note. RMSE = root-mean-square error.
Person measures are calculated over persons, as is done with traditional raw score scaling; item measures are calculated over items, that is, with the traditional person-item matrix transposed.
Nonextreme observations are observations with neither perfect scores nor zero scores; extreme observations are perfectly predicted by the Rasch model and are therefore not informative.
Measure is the logistic score based on the Rasch model for the test being calibrated. It is set to a mean of zero for the items analysis and can vary by persons, by sample, and by measurement occasion. These scores were then scaled to a range of 0–100 for the longitudinal analyses. This scaling does not affect fit indices.
For the analyses, we rescaled the Rasch item scores from the logistic scores to a 0–100 range to increase interpretability. The rescaled means (and standard deviations) of the person scores were, for reasoning, M = 39.66 (13.07); list recall, M = 54.78 (12.67); text recall, M = 40.29 (7.30); space, M = 63.72 (5.83); and vocabulary, M = 68.25 (15.18). The scaling factors for the logits were 6.12, 11.15, 7.80, 6.72, and 7.4, respectively.
Longitudinal Analysis
We used growth modeling (McArdle & Bell, 2000) with the Mplus program (Version 4.2; Muthén & Muthén, 1998–2007) to test hypotheses about age and cohort differences in longitudinal performance on the Rasch-scaled measures. The models were fit to data configured over 3-year age “buckets” to increase the number of observations for the ages studied (e.g., Bowles et al., 2005). The 3-year age ranges at which people were tested were treated as manifest variables, and those age ranges at which they were not tested as latent variables. The ranges were 55–57, 58–60, 61–63, 64–66, 67–69, 70–72, 73–75, 76–78, 79–81, 82–84, and 85–87. For simplicity, we refer to these age buckets by the middle value for a given bucket. For example, the 73–75 bucket will be referred to as age 74.
Growth models that utilize maximum likelihood methods provide accurate parameter estimates even with missing data, provided that the missing at random assumption is met (e.g., McArdle & Hamagami, 1991; Schafer, 1997). This assumption requires that missingness can be estimated from the data included in the analyses. Logistic regression analyses predicting dropout from the study by the fourth testing were conducted to aid in the selection of appropriate covariates to increase the accuracy of estimates (see Kennison & Zelinski, 2005). Age, cohort membership, gender, and education were included in these analyses as possible predictors, resulting in a statistically reliable fit to the data, χ2(4) = 103. However, the only significant predictors of dropout were cohort, Wald (1) = 51.6, and baseline age, Wald (1) = 43.8, with Cohort 1 members and older individuals more likely to drop out; thus no additional covariates were included in the analyses reported here.
As shown in Table 3, five different growth models were evaluated to determine the best representation of longitudinal change for the five psychometric tests. Initial analyses were of age basis coefficients reflecting annualized change intervals. However, because of convergence problems in the analyses of several of the psychometric scores, coefficients representing the different age buckets were rescaled so that they represented 6-year effects. This rescaling resolved convergence issues and permitted consistent application of the basis coefficients across all analyses. This scaling reflects the suggestion made by Zelinski and Burnight (1997) that age declines are not generally observed over less than 5 years.
Table 3.
Fit for Alternative Longitudinal Models for Each of the Psychometric Tests
| Psychometric test | Fit indexes
|
|||||
|---|---|---|---|---|---|---|
| −2LL | Free parameters (n) | Δ −2LL | Δ df | AIC | RMSEA | |
| Reasoning | ||||||
| Level only | 15,020 | 3 | 15,025 | .088 | ||
| Linear | 14,582 | 6 | 438* | 3 | 14,593 | .040 |
| Quadratic | 14,530 | 10 | 52* | 4 | 14,549 | .031 |
| Two pieces | 14,542 | 10 | 40* | 4 | 14,561 | .034 |
| Three pieces | 14,538 | 15 | 4 | 5 | 14,568 | .036 |
|
| ||||||
| List recall | ||||||
| Level only | 16,564 | 3 | 16,570 | .071 | ||
| Linear | 16,360 | 6 | 204* | 3 | 16,373 | .048 |
| Quadratic | 16,326 | 10 | 34* | 4 | 16,345 | .044 |
| Two pieces | 16,318 | 10 | 42* | 4 | 16,339 | .043 |
| Three pieces | 16,318 | 15 | 0 | 5 | 16,347 | .043 |
|
| ||||||
| Text recall | ||||||
| Level only | 13,868 | 3 | 13,875 | .065 | ||
| Linear | 13,632 | 6 | 236* | 3 | 13,644 | .032 |
| Quadratic | 13,622 | 10 | 10* | 4 | 13,641 | .032 |
| Two pieces | 13,622 | 10 | 10* | 4 | 13,641 | .031 |
| Three pieces | 13,608 | 15 | 14* | 5 | 13,638 | .031 |
|
| ||||||
| Space | ||||||
| Level only | 11,918 | 3 | 11,923 | .086 | ||
| Linear | 11,622 | 6 | 296* | 3 | 11,633 | .058 |
| Quadratic | 11,590 | 10 | 30* | 4 | 11,615 | .057 |
| Two pieces | 11,598 | 10 | 32* | 4 | 11,619 | .057 |
| Three pieces | 11,592 | 15 | 6 | 5 | 11,610 | .057 |
|
| ||||||
| Vocabulary | ||||||
| Level only | 17,098 | 3 | 17,104 | .058 | ||
| Linear | 16,942 | 6 | 156* | 3 | 16,954 | .036 |
| Quadratic | 16,928 | 10 | 14* | 4 | 16,948 | .036 |
| Two pieces | 16,928 | 10 | 14* | 4 | 16,947 | .035 |
| Three pieces | 16,916 | 15 | 12* | 5 | 16,947 | .035 |
Note. LL = log likelihood; AIC = Akaike’s information criterion; RMSEA = root-mean-square error of approximation.
p < .05.
The models to evaluate the age basis were a level-only (no change) model, level plus linear change, a second-order polynomial model with level, linear and quadratic parameters, a piecewise model consisting of level and two linear pieces—one from ages 56 to 71 and the other from 77 to 86, following the young-old/old-old distinction (Neugarten, 1975)—and a three-piece model, representing spans from ages 56 to 66, 67 to 78, and 79 to 87, to evaluate age effects separately for early, middle, and late old age (the authors thank an anonymous reviewer for this suggestion). For all models the intercept was set at age 74. Fit indexes reported are the −2 log likelihood (−2LL), Akaike’s Information Criteria (Akaike, 1987)—an index based on −2LL that penalizes for the number of parameters tested, with lower values indicating better fit—and the root-mean-square error of approximation, with values less than .05 representing good fit, and .08 indicating adequate fit (Browne & Cudeck, 1993). The Δχ2/Δdf for differences in −2LL was used to evaluate change in fit.
Table 3 indicates that more complex models provided better fits than linear models. Across psychometric tests, the two-piece and quadratic models most consistently provided the greatest improvement in fits. Although quadratic models did not generally differ in fit from the two-piece models, the main purpose of the study was to make direct comparisons of young-old and old-old age changes and of cohort effects across psychometric tests, and so the two-piece model is reported for all variables.
The two-piece latent growth model tested evaluated the effects of cohort on the level and two age pieces using the equations:
| (2) |
| (3) |
| (4) |
| (5) |
Equation 2 is the Level 1 equation representing an individual subject’s scores at a given age. The a1ti term represents ages below the “knot” point of 74, and a2ti represents ages above 74. Age 74 has a zero value and represents the intercept. The term eti represents residual error. The second-level equations represent the level π0 (3); the 56–71 age piece, π1i (4); and the 75–86 age piece, π2i (5). Cohort membership (cohorti) was coded as 0 for Cohort 1 and 1 for Cohort 2. The v00, v10, and v20 parameters are the intercepts; and v01, v11, and v21, respectively, are the slopes of the second-level equations. Their variance components are r0i for level, and r1i and r2i for the two age slopes.
Results
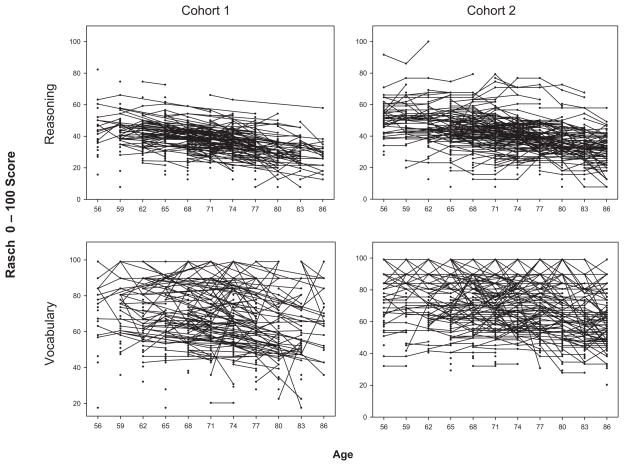
Individual data plots of reasoning and vocabulary scores for the participants of each cohort appear in Figure 1. These plots illustrate individual change and differences in variability among scores. They include all of the data that were included in the reported age models. Both sets of plots suggest declines, but variability appears to be greater for vocabulary.
Figure 1.
Data plots for individuals on reasoning (top) and vocabulary (bottom) by cohort. Plots include all data from Cohorts 1 and 2 for ages 55 to 87.
The parameter values of the models for the five psychometric tests appear in Table 4 for the unconditional models. At age 74, reasoning was the most difficult test, with the lowest growth intercept parameter, followed by text recall, then list recall, space, and vocabulary. The 6-year unconditional effect sizes in standard deviation units (Cohen’s d) for the estimated parameters of the young-old and old-old age pieces were .45 and .71 for reasoning, .43 and .38 for list recall, .50 and .41 for text recall, .50 and .65 for space, and .25 and .51 for vocabulary.
Table 4.
Unconditional Analysis Parameters for the Five Psychometric Measures
| Parameter | Psychometric tests
|
||||
|---|---|---|---|---|---|
| Reasoning | List | Text | Space | Vocabulary | |
| Growth parameters | |||||
| Level | 36.87*** | 53.16*** | 39.34*** | 62.64*** | 69.28*** |
| Age 56–71 | −1.80*** | −2.80*** | −1.53*** | −0.97*** | −1.47*** |
| Age 77–86 | −3.67*** | −2.80*** | −1.96*** | −1.44*** | −4.12*** |
|
| |||||
| Growth parameter SEs | |||||
| Level | 0.42 | 0.57 | 0.29 | 0.19 | 0.62 |
| Age 56–71 | 0.25 | 0.40 | 0.19 | 0.12 | 0.36 |
| Age 77–86 | 0.32 | 0.45 | 0.29 | 0.14 | 0.50 |
|
| |||||
| Variance components | |||||
| Level | 111.92*** | 137.44*** | 24.58*** | 19.25*** | 232.26*** |
| Age 56–71 | 5.45*** | 23.11*** | 0.88 | 1.23** | 8.25* |
| Age 77–86 | 10.77*** | 14.43* | 6.92* | 0.13 | 12.00 |
| Error | 10.96*** | 50.12*** | 20.77*** | 4.28*** | 39.03*** |
|
| |||||
| Variance component SEs | |||||
| Level | 7.55 | 11.94 | 3.11 | 1.45 | 16.46 |
| Age 56–71 | 1.51 | 4.92 | 1.26 | 0.48 | 4.18 |
| Age 77–86 | 3.29 | 6.56 | 3.10 | 0.53 | 6.66 |
| Error | 0.64 | 2.54 | 1.03 | 0.23 | 2.13 |
p < .05.
p < .01.
p < .001.
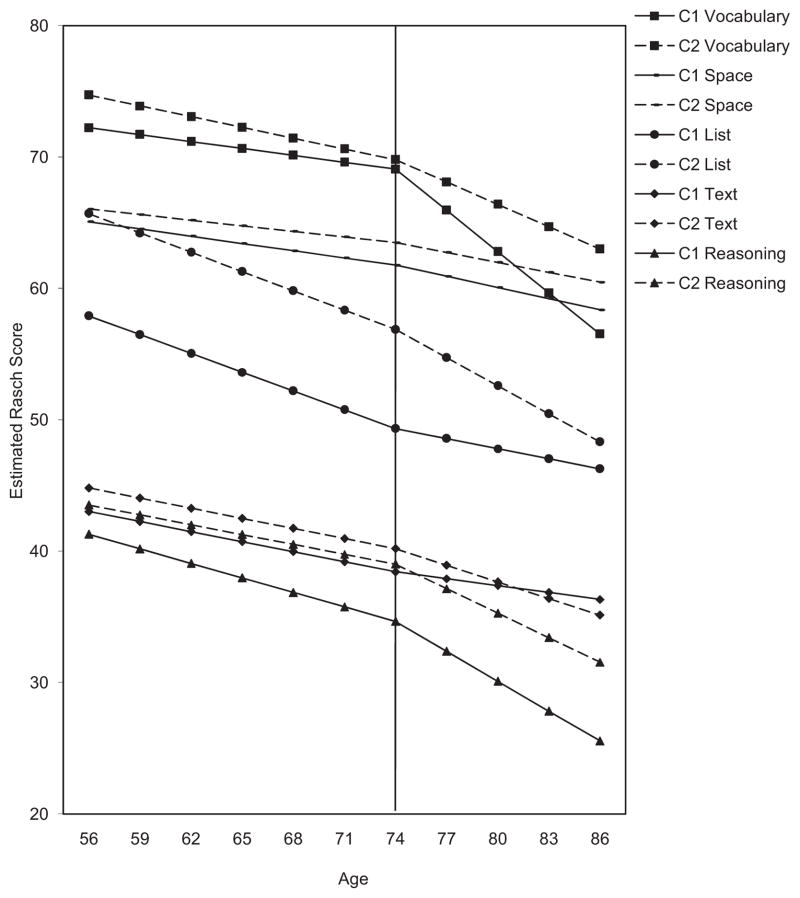
Table 5 shows effects for the conditional models, which included cohort as a predictor of the level, young-old, and old-old age pieces and are illustrated in Figure 2. Parameters included in Table 5 are the fixed effect estimates for the intercept (level) at age 74, and the young-old (56–71) and old-old (77–86) age pieces. Also included are the estimated regression coefficients of cohort on the two growth estimates. The random variance estimates for the intercept (level) at age 74, and the two age pieces appear at the bottom of the table. The model results indicate that declines were generally observed and that they steepened in the old-old age piece compared to the young-old age piece for reasoning, space, and vocabulary. For list and text recall, declines were more modest for the old-old age piece compared to the young-old age piece.
Table 5.
Conditional Analysis Piecewise Growth Model Coefficients for the Five Psychometric Tests
| Parameter | Psychometric tests
|
||||
|---|---|---|---|---|---|
| Reasoning | List | Text | Space | Vocabulary | |
| Growth intercept parameters | |||||
| Level (v00) | 34.65*** | 49.33*** | 38.43*** | 61.77*** | 69.08*** |
| Age 56–71 (v10) | −2.21*** | −2.86*** | −1.53*** | −1.10*** | −1.05 |
| Age 77–86 (v20) | −4.55*** | −1.53 | −1.05 | −1.70*** | −6.28*** |
|
| |||||
| Growth intercept SEs | |||||
| Level (v00) | 0.61 | 0.82 | 0.42 | 0.28 | 0.93 |
| Age 56–71 (v10) | 0.37 | 0.59 | 0.28 | 0.18 | 0.56 |
| Age 77–86 (v20) | 0.58 | 0.83 | 0.55 | 0.25 | 0.93 |
|
| |||||
| Cohort effect parameters | |||||
| Level (v01) | 4.37*** | 7.54*** | 1.76*** | 1.72*** | 0.71 |
| Age 56–71 (v11) | 0.71 | −0.08 | −0.01 | 0.25 | −0.59 |
| Age 77–86 (v21) | 0.82 | −2.75* | −1.48* | 0.19 | 2.88* |
|
| |||||
| Cohort effect SEs | |||||
| Level (v01) | 0.82 | 1.10 | 0.56 | 0.37 | 1.24 |
| Age 56–71 (v11) | 0.46 | 0.77 | 0.37 | 0.23 | 0.72 |
| Age 77–86 (v21) | 0.69 | 0.99 | 0.65 | 0.29 | 1.10 |
|
| |||||
| Variance components | |||||
| Level (r0) | 105.85*** | 122.61*** | 23.44*** | 18.33*** | 228.28*** |
| Age 56–71 (r1) | 5.32** | 22.52*** | 0.71 | 1.18* | 7.81 |
| Age 77–86 (r2) | 11.08** | 12.10 | 5.79 | 0.18 | 7.77 |
| Error (SE e) | 10.90*** | 50.23*** | 20.77*** | 4.28*** | 39.50*** |
|
| |||||
| Variance component SEs | |||||
| Level (r0) | 7.24 | 11.04 | 3.02 | 1.40 | 16.16 |
| Age 56–71 (r1) | 1.48 | 4.73 | 1.24 | 0.47 | 4.12 |
| Age 77–86 (r2) | 3.37 | 6.36 | 3.02 | 0.53 | 6.27 |
| Error (e) | 0.63 | 2.53 | 1.02 | 0.23 | 2.15 |
p < .05.
p < .01.
p < .001.
Figure 2.
Estimated longitudinal changes for vocabulary, space, list recall, text recall, and reasoning for Cohort 1 (C1) and Cohort 2 (C2) between ages 55 and 87 for the two-piece models. The line at age 74 represents the intercept of the models.
Age Changes
We tested hypotheses of different slopes for the two age pieces across psychometric tests (see McArdle et al., 2002) by evaluating models of the equality of age parameters for each of the pieces in the conditional models. Fit indices for models with pairs of slopes allowed to be free were compared to models with the two slopes constrained to be identical. The Δχ2 test was used to determine whether fit declined for the constrained model compared to the free model, using a nested comparison. Worse fits for the constrained model compared to the free model would indicate that one slope is steeper than the other. Conversely, if model fit was not affected by constraining the slopes to be equal, then the rate of age change is best characterized as similar across the tests.
Results are presented in Table 6. For the young-old, the coefficients for longitudinal declines were greater for reasoning than space, and for list compared to text, space, and vocabulary. For the old-old, reasoning and vocabulary declines did not differ, but declines for both tests were greater than for list or text recall, or space, which did not differ from each other. The vocabulary decline for the older age ranges is steep and similar to that reported by Schaie (1996); however, it is likely that the decline observed here occurred not only because of losses of vocabulary ability, but also due to age-related declines in speed, a major component of performance on this particular test (see Hertzog, 1989).
Table 6.
Changes in Fit Statistics (Δχ2) for Comparisons of Free Versus Equal Parameter Models Across Psychometric Tests
| Parameter | Both age pieces free vs. ages 55–74 equal | Both age pieces free vs. ages 74–86 equal | Cohorts free vs. equal | ||
|---|---|---|---|---|---|
| Compared with reasoning | |||||
| List recall | 0 | 7* | 5* | ||
| Text recall | 2 | 18* | 6* | ||
| Space | 6* | 22* | 9* | ||
| Vocabulary | 3 | 1 | 4* | ||
|
| |||||
| Compared with list recall | |||||
| Text recall | 4* | 1 | 21* | ||
| Space | 8* | 0 | 25* | ||
| Vocabulary | 5* | 15* | 17* | ||
|
| |||||
| Compared with text recall | |||||
| Space | 2 | 2 | 0 | ||
| Vocabulary | 1 | 22* | 1 | ||
|
| |||||
| Compared with space | |||||
| Vocabulary | 0 | 21* | 0 | ||
Note. Tests of all differences involve one parameter. Significant values indicate that parameters differ between psychometric tests.
p < .05.
Cohort Differences
Positive 16-year cohort effects were expected for reasoning, list recall, text recall, and space, but not for vocabulary. As shown in Table 5, the coefficient for cohort as a predictor of level was 4.37 (d = .33) for reasoning, 7.54 (d = .42) for list recall, 1.76 (d = .19) for text recall, 1.72 (d = .29) for space, and 0.71 (d = .03) for vocabulary. Thus, at the intercept of age 74, the two cohorts differed on their rescaled scores by these parameter values. The 16-year d values reported here, except for vocabulary, compared favorably with the effect sizes estimated for 14-year cohort improvements for the same birth cohorts observed by Schaie (1996).
Pairwise comparisons showed that coefficients for the cohort effect varied significantly. Table 6 indicates that the cohort effect was significantly larger for list recall than for any of the other tasks. The cohort effect for reasoning was also greater than for text, space, and vocabulary, which did not differ from one another.
It has been suggested that cohort may account for cross-sectional age changes (Raven, 2000). Although there were reductions in the effect sizes for age, age declines remained. The d values from the analyses with cohort as a covariate (conditional models) for the young-old age piece were .37, .30, .34, .38, and .12 for reasoning, list recall, text recall, space, and vocabulary. In Table 4, we found no interactions between cohort and the young-old age piece for any of the psychometric tests as seen in the coefficients. Reductions in age effects also occurred for the old-old age piece with the inclusion of cohort, with ds of .49, .11, .12, .42, and .43 for reasoning, list recall, text recall, space, and vocabulary, respectively. There were interactions between cohort and the old-old age piece for list and text recall, and for vocabulary. The cohort effect on the 6-year age slopes for the two recall measures was negative (d = −0.17 and −0.14) indicating increasing convergence for the slopes of decline across cohort for those age pieces, as seen in Figure 2. The cohort effect on the slope for vocabulary was positive (d = .16), indicating that the older cohort had steeper declines and greater divergence of slopes from that of Cohort 2. That these interactions had small effect sizes and were significant, despite low power (Hertzog, Lindenberger, Ghisletta, & von Oertzen, 2006) and paradoxical direction, makes interpretation difficult.
Discussion
The two-piece models tested slopes of change in old age with a knot point of age 74. The d values for age declines in the unconditional models, that is, without the cohort effect, ranged from .25 to .71, slightly larger than those estimated from studies using standard scores, which were extrapolated to range from .2 to .6 over 6 years, suggesting that estimated longitudinal declines in our sample may be greater with interval scaling than with uncalibrated scaling. Our finding that the size of age changes differs across tasks— up to age 75—reinforces the observation by McArdle et al. (2002), who also used Rasch scaled test scores. Schaie’s (1996) data also suggested that age declines accelerate for reasoning, space, and vocabulary. In contrast, Salthouse (2004) compared cross-sectional decline estimates from z scores of a wide range of tasks and concluded that there were similar slopes of decline across speed, reasoning, and memory.
This is the first study in which direct comparisons of cohort effects on age decline were made possible with interval scaling. Average 16-year cohort-sequential effects at age 74 indicated that effect sizes varied by task: They were moderate for list recall, reasoning, and space; small for text recall; and almost nil for vocabulary. These results are the first to quantify relative cohort differences in tasks in older adults that parallel the conclusions obtained with children and young adults (e.g., Flynn, 2003). Extrapolating the ds from the observed 16-year effect to a 32-year effect, the cohort-related increase in performance standard deviation was about .84 for list recall, .66 for reasoning, .57 for space, about .38 for text recall, and .07 for vocabulary.
Implications for Gf-Gc Theory
The correspondence between fluid abilities, aging, and cohort effects may be more complex than Gf-Gc theory suggests. The theory suggests that the size of age declines should reflect fluid ability involvement in tasks; yet large cohort effects have also been observed for fluid abilities (e.g., Flynn, 1987). The age/cohort phenomenon was not consistent in this study for fluid-like abilities. The amount of age decline in recall, controlling for cohort, was not significant for the old-old, even though the age declines were substantial for reasoning. Similar age decline rates for list and for text recall in the old-old, which were small, were accompanied by larger cohort effects for list than for text recall. Despite increasing declines from age 74 on, the cohort effect for vocabulary did not differ from zero. Taken together, the findings suggest that the fluid-crystallized distinction may be more closely predictive of cohort effects than of the size of age declines in the present study.
Interestingly, this conclusion suggests what has been implied in the intelligence literature: The fluid/crystallized distinction does not arise because fluid abilities are culture-independent and more biological in nature and that crystallized ones are culture-specific, as suggested by Horn and Cattell (1967). Instead, both types of abilities are culture-specific as they are selectively modified by the cultural reinforcement of relevant skills (see also McArdle, Hamagami, Meredith, & Bradway, 2000). Following this suggestion, we suggest that reasoning and recall performance are likely to involve overlapping skills that involve both retention and the ability to use strategies. We have previously observed that decline in reasoning is related to decline in recall in Cohort 1 (Zelinski & Stewart, 1998). The present study does not inform whether either decline in reasoning or in recall, or of some underlying process such as executive functioning components (e.g., Miyake, Friedman, Emerson, Witzki, & Howerter, 2000), is the leading indicator of change in the other variable. However, because increases in text recall were smaller than for list recall in the younger cohort, it may suggest that the underlying skills for text recall are not as similar to those of reasoning. Similarly, although visuospatial processing is thought to be reinforced by mathematical training approaches in elementary schools, especially since the 1970s (Blair et al., 2005), the cohorts studied would have completed high school before many of these approaches were implemented, explaining relatively smaller cohort effects for space compared to reasoning.
The findings suggest that if the model of cultural reinforcement is correct, differential patterns in cohort effects may be the rule. Thus, cohort effects could change or vary if educational and other social institutions emphasize certain abilities over others and depending on when changes are introduced (Blair et al., 2005; Greenfield, 1998). It is therefore also possible that cohort effects can asymptote as practice changes or as performance reaches a maximal level. This may explain the apparent plateau or decline of fluid abilities in more recent military conscripts in Norway (Sundet et al., 2004) and Denmark (Teasdale & Owen, 2005).
Age and Cohort
Although cohort was a significant covariate for those tests traditionally showing large age differences, it impacted the magnitude of parameters for only 3 of 10 tested age effects in Table 5 (2 age pieces × 5 psychometric tests). This suggests that cohort effects do not completely confound cross-sectional age declines in the abilities studied. That is, mechanisms related to increasingly poorer performance are not only related to cohort-specific experiences. Small interactions of cohort with age, for the old-old age piece for list and text recall, indicated that Cohort 2 experienced steeper recall declines than Cohort 1. Although one explanation is that there was greater memory decline in the younger cohort, it is more likely that there was increased selectivity for people over age 74 in the older cohort. For example, over testing waves, the difference in mean education level between cohorts became increasingly smaller. Selectivity in the old-old age range may be an important factor in reducing the apparent acceleration of cognitive decline, with survival effects in late old age masking apparent decline for the two recall tasks (see also Zelinski et al., 1998). However, it is then a mystery why Cohort 1, if it represented greater selection, declined more in vocabulary than Cohort 2 over the old-old age range.
Cohort did affect cross-sectional age change estimates in the context of the estimated average performance of subjects at specific ages. In the present study, cohort had an impact on the predicted means at various ages. Figure 2 shows that the estimated mean for Cohort 2 on reasoning at age 74 was approximately the same as the mean for age 62 from Cohort 1. The Cohort 2 mean at age 74 was approximately the same as that of Cohort 1 at age 59 for list recall. The age 74 means for Cohort 2 were about the same as the Cohort 1 age 65 means for space and for text recall. Thus, 74-year-olds from Cohort 2 were estimated to be psychometrically up to 15 years “younger” than same-aged people born about 16 years earlier. Examining performance for the late old age piece of the models, we see that the cohort effects were slightly less beneficial. On reasoning and space, the mean for Cohort 1 at age 74 was about the same as the mean for age 80 in Cohort 2. For list recall, the mean for Cohort 1 at age 74 was about the same as the mean at age 83 in Cohort 2. Finally, for text recall, the age 74 mean was similar to that of age 77 in Cohort 2. Thus, in the context of the model, Cohort 2 participants in late old age experienced psychometric aging “delays” of up to 9 years.
These findings imply that average cross-sectional age declines as estimated by widely used tasks such as recall and reasoning are likely to be inflated. By including participants from widely differing cohorts and ages, even short-term longitudinal studies may violate the convergence assumption (McArdle & Bell, 2000), that is, a strong correspondence between cross-sectional and longitudinal results (Hertzog & Nesselroade, 2003). Explicit cohort-sequential evaluations are necessary to separate age from cohort effects in order to confirm cross-sectional age decline estimates, as demonstrated here (see also Rönnlund, Nyberg, Bäckman, & Nilsson, 2005).
If we are to assume that cohort-related increases affect mean level performance, the implication is that even with increasing age, people from more recently born cohorts will perform better on abilities like reasoning or list recall at specific ages than those born earlier. The cumulative effects of cohort differences in reasoning and list recall showed that people at age 74 from Cohort 2 were on average as cognitively capable as those in their 60s born as recently as 16 years earlier. This suggests that for occupations requiring strong reasoning and memory abilities, more recently born cohorts of older adults should have the functional ability to remain productively employed into their 70s.
These results are important for theories of cognitive aging, which have generally focused on declines estimated between college students and young-old adults. Our study did not have adequate data on a younger sample to make generalizations about these comparisons, which is an important limitation. However, it is likely that cohort differences are large between individuals born in the 1980s and those in the 1940s, as there have been larger increments in fluid abilities after the 1970s in the United States (see Flynn, 1998). Even if there are measurable age declines in abilities from very early into middle adulthood, it is likely that these declines are smaller than those we have documented in our study for people aged 55–87. It would not be surprising if a larger portion of the differences between means in many current cross-sectional aging studies is due to cohort differences, as we demonstrated for list recall, which has relatively small age declines compared to reasoning. At the very least, the findings clearly suggest that for some abilities, age norms collected in the past are not directly applicable to contemporary older adults (see also Raven, 2000).
Limitations
To provide some context to our findings, we note that this is the first analysis of cohort and age effects at the upper end of the life span, and the psychometric tests evaluated do not represent the full range of cognitive tasks. Although we found that cohort could affect selected age estimates, it did not account for age declines in cognition across all variables and ages. Slope parameters are associated with the intercept in the growth models, and may not be equally affected by cohort at all possible intercepts.
The sample represents older adults who already have a high school education or better, indicating that the participants studied here are in the range of the higher end of performance. We do not know whether individuals with less education would show larger cohort effects; some studies have suggested that the Flynn effect may partially represent increases in those who have traditionally had the lowest scores (see Sundet et al., 2004). We also do not know from the present sample what specific health conditions or other lifestyle variables might differentiate the cohorts. Clearly, this study is only the beginning of the work that must be done to fully understand cohort increases in ability.
The first baby boomers turn 65 in 2011. As the largest segment of the population in the United States and other countries, this cohort’s experience of cognitive aging may be even more positive than that of people from Cohort 2 in our study, who were largely from the pre-World War II generation. It has been suggested that high cognitive functioning in younger adulthood will be associated with high cognitive performance and possibly survival in later life because of behaviors that maintain health and cognition (Gottfredson & Deary, 2001). It is not currently clear whether the longitudinal data for people of recent or upcoming birth cohorts will bear this out. Paradoxically, the hardiness thought to produce survival in people born in previous cohorts may wash out cohort differences. In the present study, the very small effect sizes for the trend towards convergence for the younger cohort for recall tasks remind us that the benefits of cohort may be limited to specific segments of old age. It will be increasingly important to examine whether age effects combined with survival into very old age eliminate the cohort-related improvements seen with younger cohorts (e.g., Singer et al., 2003), or whether the positive cohort effects we observed will predominate. This could have major implications for future cohorts as public policymakers develop predictions of disability and low quality of life due to poor cognitive function in older adults (e.g., Freedman, Akyan, & Martin, 2001; Langa et al., 2001).
Acknowledgments
This research was supported by National Institute on Aging Grants R01 AG10569 and T32 AG00037.
Contributor Information
Elizabeth M. Zelinski, University of Southern California
Robert F. Kennison, California State University, Los Angeles
References
- Akaike H. Factor analysis and AIC. Psychometrika. 1987;52:317–332. [Google Scholar]
- Alwin DF. Family of origin and cohort differences in verbal ability. American Sociological Review. 1991;56:625–638. [Google Scholar]
- Alwin DF, McCammon RJ. Aging, cohorts, and verbal ability. Journals of Gerontology, Series B: Psychological Sciences and Social Sciences. 2001;56:S151–S161. doi: 10.1093/geronb/56.3.s151. [DOI] [PubMed] [Google Scholar]
- Barber N. Educational and ecological correlates of IQ: A cross-national investigation. Intelligence. 2005;33:273–284. [Google Scholar]
- Blair C, Gamson D, Thorne S, Baker D. Rising mean IQ: Cognitive demand of mathematics education for young children, population exposure to formal schooling, and the neurobiology of the pre-frontal cortex. Intelligence. 2005;33:93–106. [Google Scholar]
- Bond TG, Fox CM. Applying the Rasch model. Mahwah, NJ: Erlbaum; 2001. [Google Scholar]
- Bowles RP, Grimm KJ, McArdle JJ. A structural factor analysis of vocabulary knowledge and relations to age. Journals of Gerontology, Series B: Psychological Sciences and Social Sciences. 2005;60:234–241. doi: 10.1093/geronb/60.5.p234. [DOI] [PubMed] [Google Scholar]
- Browne MW, Cudeck R. Alternative ways of assessing model fit. In: Bollen KA, Long JS, editors. Testing structural equation models. Newbury Park, CA: Sage; 1993. pp. 136–162. [Google Scholar]
- Cooney TM, Schaie KW, Willis SL. The relationship between prior functioning on cognitive and personality dimensions and subject attrition in longitudinal research. Journals of Gerontology, Series B: Psychological Sciences and Social Sciences. 1988;43:12–17. doi: 10.1093/geronj/43.1.p12. [DOI] [PubMed] [Google Scholar]
- Dickens WT, Flynn JR. Heritability estimates versus large environmental effects: The IQ paradox resolved. Psychological Review. 2001;108:346–369. doi: 10.1037/0033-295x.108.2.346. [DOI] [PubMed] [Google Scholar]
- Embretson SE. Item response theory models and spurious interaction effects in factorial ANOVA designs. Applied Psychological Assessment. 1996;20:201–212. [Google Scholar]
- Flynn JR. Massive IQ gains in 14 nations: What IQ tests really measure. Psychological Bulletin. 1987;101:171–191. [Google Scholar]
- Flynn JR. IQ gains over time: Toward finding the causes. In: Neisser U, editor. The rising curve: Long-term gains in IQ and related measures. Washington, DC: American Psychological Association; 1998. pp. 25–66. [Google Scholar]
- Flynn JR. Movies about intelligence: The limitations of g. Psychological Science. 2003;12:95–99. [Google Scholar]
- Freedman VA, Aykan H, Martin LG. Aggregate changes in cognitive impairment among older Americans: 1993 and 1998. Journals of Gerontology, Series B: Psychological Sciences and Social Sciences. 2001;56:S100–S111. doi: 10.1093/geronb/56.2.s100. [DOI] [PubMed] [Google Scholar]
- Gottfredson LS, Deary IJ. Intelligence predicts health and longevity, but why? Current Directions in Psychological Science. 2001;13:1–4. [Google Scholar]
- Greenfield PM. The cultural evolution of IQ. In: Neisser U, editor. The rising curve: Long-term gains in IQ and related measures. Washington, DC: American Psychological Association; 1998. pp. 81–123. [Google Scholar]
- Hertzog C. Influences of cognitive slowing on age differences in intelligence. Developmental Psychology. 1989;25:636–651. [Google Scholar]
- Hertzog C, Lindenberger U, Ghisletta P, von Oertzen T. On the power of multivariate latent growth curve models to detect individual differences in change. Psychological Methods. 2006;11:244–252. doi: 10.1037/1082-989X.11.3.244. [DOI] [PubMed] [Google Scholar]
- Hertzog C, Nesselroade JR. Assessing psychological changes in adulthood: An overview of methodological issues. Psychology and Aging. 2003;18:639–657. doi: 10.1037/0882-7974.18.4.639. [DOI] [PubMed] [Google Scholar]
- Horn JL, Cattell RB. Age differences in fluid and crystallized intelligence. Acta Psychologica. 1967;26:107–129. doi: 10.1016/0001-6918(67)90011-x. [DOI] [PubMed] [Google Scholar]
- Kennison RF, Zelinski EM. Estimating age change in 7-year list recall in AHEAD: The roles of independent predictors of missing-ness and dropout. Psychology and Aging. 2005;20:460–475. doi: 10.1037/0882-7974.20.3.460. [DOI] [PubMed] [Google Scholar]
- Langa KM, Chermew ME, Kabeto MW, Herzog AR, Ofstedal MB, Willis RJ, et al. National estimates of the quantity and cost of informal caregiving for the elderly with dementia. Journal of General Internal Medicine. 2001;16:770–777. doi: 10.1111/j.1525-1497.2001.10123.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linacre JM. A user’s guide to WINSTEPS MINISTEP Rasch-model computer programs [Computer software and manual] Chicago: Winsteps; 2006. [Google Scholar]
- Loehlin JC. The IQ Paradox: Resolved? Still an open question. Psychological Review. 2002;109:754–758. doi: 10.1037/0033-295x.109.4.754. [DOI] [PubMed] [Google Scholar]
- McArdle JJ, Bell RQ. An introduction to latent growth models for developmental data analysis. In: Little TD, Schnabel KU, Baumert J, editors. Modeling longitudinal and multilevel data: Practical issues, applied approaches, and specific examples. Mahwah, NJ: Erlbaum; 2000. pp. 69–107. [Google Scholar]
- McArdle JJ, Ferrer-Caja E, Hamagami F, Woodcock RW. Comparative longitudinal structural analyses of the growth and decline of multiple intellectual abilities over the life span. Developmental Psychology. 2002;38:115–142. [PubMed] [Google Scholar]
- McArdle JJ, Hamagami F. Modeling incomplete longitudinal and cross-sectional data using latent growth structural models. Experimental Aging Research. 1991;18:145–166. doi: 10.1080/03610739208253917. [DOI] [PubMed] [Google Scholar]
- McArdle JJ, Hamagami F, Meredith W, Bradway KP. Modeling the dynamic hypotheses of Gf-Gc theory using longitudinal life-span data. Learning and Individual Differences. 2000;12:53–79. [Google Scholar]
- Miyake A, Friedman NP, Emerson MJ, Witzki AH, Howerter A. The unity and diversity of executive functions and their contributions to complex “frontal lobe” tasks: A latent variable analysis. Cognitive Psychology. 2000;41:49–100. doi: 10.1006/cogp.1999.0734. [DOI] [PubMed] [Google Scholar]
- Muthén LK, Muthén BO. Software manual. 4. Los Angeles: Author; 1998–2007. Mplus user’s guide. [Google Scholar]
- Neugarten BL. The future and the young-old. Gerontologist. 1975;15:4–9. doi: 10.1093/geront/15.1_part_2.4. [DOI] [PubMed] [Google Scholar]
- Rabbitt PMA, Watson P, Donlan C, McInnes L, Horan M, Pendleton N, Clague J. Effects of death within 11 years on cognitive performance in old age. Psychology and Aging. 2002;17:468–481. doi: 10.1037//0882-7974.17.3.468. [DOI] [PubMed] [Google Scholar]
- Rasch G. An item analysis which takes individual differences into account. British Journal of Mathematical and Statistical Psychology. 1966;19:49–57. doi: 10.1111/j.2044-8317.1966.tb00354.x. [DOI] [PubMed] [Google Scholar]
- Raven J. The Raven’s Progressive Matrices: Change and stability over culture and time. Cognitive Psychology. 2000;41:1–48. doi: 10.1006/cogp.1999.0735. [DOI] [PubMed] [Google Scholar]
- Rodgers JL. A critique of the Flynn effect: Massive IQ gains, methodological artifacts, or both? Intelligence. 1999;26:337–356. [Google Scholar]
- Rönnlund M, Nyberg L, Bäckman L, Nilsson LG. Stability, growth, and decline in adult life span development of declarative memory: Cross-sectional and longitudinal data from a population-based study. Psychology and Aging. 2005;20:3–18. doi: 10.1037/0882-7974.20.1.3. [DOI] [PubMed] [Google Scholar]
- Rowe DC, Rodgers JL. Expanding variance and the case of historical changes in IQ means: A critique of Dickens and Flynn (2001) Psychological Review. 2002;109:759–763. doi: 10.1037/0033-295x.109.4.759. [DOI] [PubMed] [Google Scholar]
- Salthouse TA. What and when of cognitive aging. Current Directions in Psychological Science. 2004;13:140–144. doi: 10.1177/0963721414535212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schafer J. Analysis of incomplete multivariate data. London: Chapman & Hall; 1997. [Google Scholar]
- Schaie KW. A general model for the study of developmental problems. Psychological Bulletin. 1965;64:92–107. doi: 10.1037/h0022371. [DOI] [PubMed] [Google Scholar]
- Schaie KW. Schaie–Thurstone Adult Mental Abilities Test. Palo Alto, CA: Consulting Psychologists Press; 1985. [Google Scholar]
- Schaie KW. Intellectual development in adulthood. Cambridge, England: Cambridge University Press; 1996. [Google Scholar]
- Singer T, Verhaeghen P, Ghisletta P, Lindenberger U, Baltes PB. The fate of cognition in very old age: Six-year longitudinal findings in the Berlin Aging Study (BASE) Psychology and Aging. 2003;18:318–331. doi: 10.1037/0882-7974.18.2.318. [DOI] [PubMed] [Google Scholar]
- Sliwinski MJ, Hofer SM, Hall C, Buschke H, Lipton RB. Modeling memory decline in older adults: The importance of preclinical dementia, attrition, and chronological age. Psychology and Aging. 2003;18:658–671. doi: 10.1037/0882-7974.18.4.658. [DOI] [PubMed] [Google Scholar]
- Sundet JM, Barlaug DG, Torjussen TM. The end of the Flynn effect? A study of secular trends in mean intelligence test scores of Norwegian conscripts during half a century. Intelligence. 2004;32:349–362. [Google Scholar]
- Teasdale TW, Owen DR. A long-term rise and recent decline in intelligence test performance: The Flynn Effect in reverse. Personality and Individual Differences. 2005;39:837–843. [Google Scholar]
- Turner A, Greene E. Tech Rep No 63. Boulder: Department of Psychology, University of Colorado; 1977. The construction and use of a propositional text base. [Google Scholar]
- Verhaeghen P. Aging and vocabulary score: A meta-analysis. Psychology and Aging. 2003;18:332–339. doi: 10.1037/0882-7974.18.2.332. [DOI] [PubMed] [Google Scholar]
- Wicherts JM, Dolan CV, Hessen DJ, Oosterveld P, Van Baal G, Caroline M, et al. Are intelligence tests measurement invariant over time? Investigating the nature of the Flynn effect. Intelligence. 2004;32:509–537. [Google Scholar]
- Williams WM. Are we raising smarter children today? School-and home-related influences on IQ. In: Neisser U, editor. The rising curve: Long-term gains in IQ and related measures. Washington, DC: American Psychological Association; 1998. pp. 125–154. [Google Scholar]
- Wilson JA, Gove WR. The intercohort decline in verbal ability: Does it exist? American Sociological Review. 1999;64:253–266. [Google Scholar]
- Wright BD, Stone MH. Best test design: Rasch measurement. Chicago: MESA Press; 1979. [Google Scholar]
- Zelinski EM, Burnight KP. Sixteen-year longitudinal and time lag changes in memory and cognition in older adults. Psychology and Aging. 1997;12:503–513. doi: 10.1037//0882-7974.12.3.503. [DOI] [PubMed] [Google Scholar]
- Zelinski EM, Burnight KP, Lane CJ. The relationship between subjective and objective memory in the oldest-old: Comparisons of findings from a representative and a convenience sample. Journal of Aging and Health. 2001;13:248–266. doi: 10.1177/089826430101300205. [DOI] [PubMed] [Google Scholar]
- Zelinski EM, Crimmins E, Reynolds S, Seeman T. Do medical conditions affect cognition in older adults? Health Psychology. 1998;17:504–512. doi: 10.1037//0278-6133.17.6.504. [DOI] [PubMed] [Google Scholar]
- Zelinski EM, Gilewski MJ. Effects of demographic and health variables on Rasch scaled cognitive scores. Journal of Aging and Health. 2003;15:435–464. doi: 10.1177/0898264303253499. [DOI] [PubMed] [Google Scholar]
- Zelinski EM, Lewis KL. Adult age differences in multiple cognitive functions: Differentiation, dedifferentiation, or process-specific change? Psychology and Aging. 2003;18:727–745. doi: 10.1037/0882-7974.18.4.727. [DOI] [PubMed] [Google Scholar]
- Zelinski EM, Stewart S. Individual differences in 16-year memory changes. Psychology and Aging. 1998;13:622–630. doi: 10.1037//0882-7974.13.4.622. [DOI] [PubMed] [Google Scholar]