Accurate measurement of force and displacement with optical tweezers using DNA molecules as metrology standards

Abstract

Optical tweezers facilitate measurement of piconewton-level forces and nanometer-level displacements and have broad applications in biophysics and soft matter physics research. We have shown previously that DNA molecules can be used as metrology standards to define such measurements. Force-extension measurements on two DNA molecules of different lengths can be used to determine four necessary measurement parameters. Here, we show that the accuracy of determining these parameters can be improved by more than 7-fold by incorporating measurements of the DNA overstretching transition and using a multi-step data analysis procedure. This method results in very robust and precise fitting of DNA force-extension measurements to the worm-like chain model. We verify the accuracy through independent measurements of DNA stretching, DNA unzipping, and microsphere contact forces.

In the method referred to as optical tweezers, micron-sized dielectric particles are trapped in aqueous solution by focused laser beams and can be used as transducers for measuring small forces and displacements acting on the microscopic scale.^1–3 This method has found wide applications in both biophysics and soft-matter physics research.^4–11

Most optical tweezers configurations require calibration to measure forces and displacements in physical units.^2,3,12–14 We previously introduced a method by which double-stranded DNA molecules could be used as standards to determine all of the necessary measurement parameters.¹³ We have used this approach in a number of biophysical studies involving DNA manipulation.^15–18 More broadly, the use of standards to ensure accurate measurements is a concern of the field known as metrology.¹⁹ With growing interest in the study of nanoscale structures in the physical and biological sciences and engineering comes an increasing need for readily accessible standards to ensure the accuracy of measurements across different laboratories. The advantage of DNA as a nanoscale standard is that a given molecule has well defined physical properties. For example, the length of DNA can be controlled in increments of a single base pair (∼0.34 nm) and exact copies of the molecule can be produced using standard techniques in molecular biology.

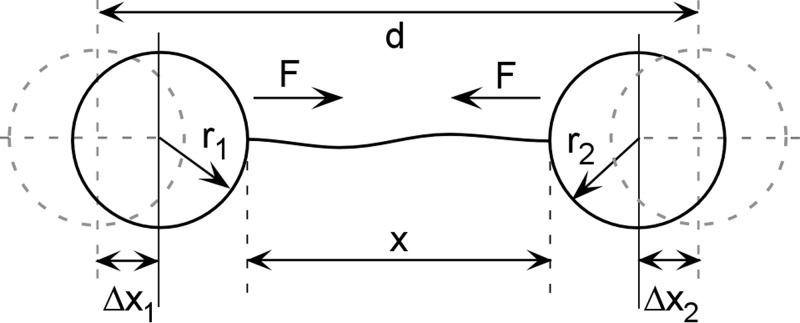
The DNA-based metrology method is based on the fact that DNA has a well-defined force-extension relationship that can be measured by stretching DNA molecules with optical tweezers (Fig. 1). We consider here DNA stretched between two trapped microspheres, but the approach is adaptable to other common configurations, such as when a single optical trap or atomic force microscope cantilever is used to stretch a DNA molecule tethered to a surface. The method allows four measurement parameters to be determined: trap compliance, force scale factor, displacement scale factor, and displacement offset.¹³ A trapped microsphere subject to an external force F is displaced from its equilibrium position by a distance Δx = γF, where γ is the trap compliance. This induces deflection of the trapping laser beam, which is measured by a position-sensing photodetector (PSD), such that F = αV_PSD, where V_PSD is the measured PSD signal and α is the force scale factor. The separation between the two traps is controlled by optics that steer one of the trapping beams; specifically, by a control voltage V that tilts a piezo-actuated mirror. The separation d between the two traps is given by d = β(V − V₀) + r₁ + r₂, where β is the length scale factor, V₀ is the displacement offset factor, and r₁ and r₂ are the radii of the microspheres. V₀ is the control voltage when the microspheres first come into contact, where the distance between the traps is d = r₁ + r₂.

FIG. 1.

Experimental geometry for DNA force-extension measurement in a dual optical trap system. The distance between the traps is d, the end-to-end extension of the DNA is x, the radii of the microspheres are r₁ and r₂, the force on the microspheres is F, and their displacements from the trap centers are Δx₁ and Δx₂.

To determine these measurement parameters, we take advantage of the fact that the elasticity of DNA is well described by the worm-like chain (WLC) model.^20,21 For sufficiently large molecules (≳3 kbp) and stretching forces (>1 pN), the force-extension relationship is accurately described by the model function

$$x/L=1-\sqrt{kT/4FP}+ F/S,$$ (1)

where x is the end-to-end extension of the molecule, L is the molecular contour length, P is the persistence length, S is the stretch modulus, and kT is the thermal energy (∼4.1 pN-nm at room temperature).^15,20–22 As described previously, measurements of force-extension curves for two DNA molecules of different lengths provide sufficient information to determine all four parameters by fitting the model to the data.¹³

After testing this procedure with several different optical tweezers systems, however, we found that certain measurement parameters were not always as accurately determined as desired. As an example, a set of measurements of DNA molecules of lengths 10 051 bp and 13 747 bp, prepared as described previously,¹⁵ were recorded with a newly built dual-trap optical tweezers system. The DNA was tethered between 2.2 μm diameter polystyrene microspheres. This system is similar to that described previously¹³ except a piezo-actuated mirror is used for beam steering instead of an acousto-optic deflector. The system was calibrated using the procedure described previously, but an independent check revealed a discrepancy. Specifically, it led to a 33% underestimate of the force at which the well-known overstretch transition of DNA occurs.^21,23–27

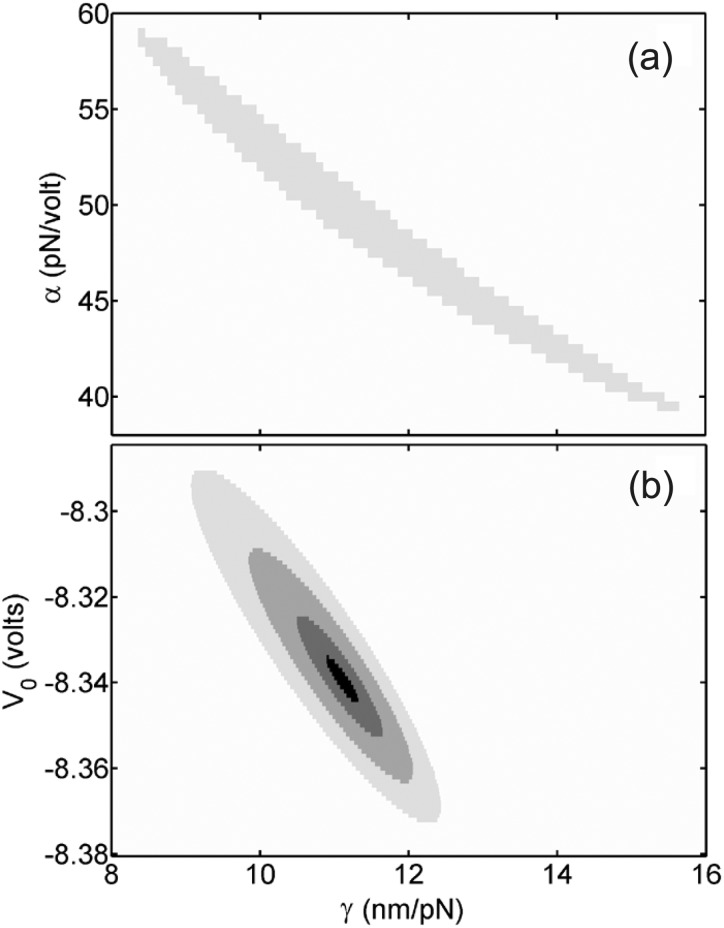
To investigate the source of this discrepancy, we systematically examined how the quality of the fits of the WLC model to the data varied as a function of the measurement parameters. We found that nearly equally good fits could be obtained for a fairly wide range of α and γ values, in which higher α values could be compensated for by lower γ values, or vice-versa. This is illustrated in Fig. 2(a), in which we calculate the average coefficient of determination,²⁸ ⟨$R^2$⟩, to characterize the quality of fits to the 10 051 bp and 13 747 bp data sets. Values of α and γ varying over a wide range from 40 to 58 pN/V and 8.5 to 15.5 nm/pN, respectively, yielded reasonable fits (⟨$R^2$⟩ = 0.95 to 0.975 out of a maximum value of 1). This analysis indicates that the previous fitting procedure¹³ is limited in its ability to accurately constrain both α and γ.

FIG. 2.

Dependence on measurement parameters of the quality of fits of the WLC model to averaged force-extension measurements with 10.1 and 13.7kbp DNA molecules. Greyscale shades indicate regions where the average coefficient of determination, ⟨$R^2$⟩, is <0.95 (white), 0.95–0.975 (light gray), 0.975–0.99 (medium gray), 0.99–0.995 (dark gray), and >0.995 (black), out of a maximum of 1. (a) Dependence on trap compliance, γ, and force scale factor, α, using the prior method.¹³ (b) Dependence on trap compliance, γ, and displacement offset factor, V₀, using the new method (inwhich α is determined independently).

The above analysis suggested that the accuracy could be improved if α or γ could be constrained with additional experimental information. In this Letter, we present an improved approach in which we determine α independently through measurements of the DNA overstretch transition and subsequently determine the other three measurement parameters through a multi-step analysis. We describe the method in detail and present independent measurements confirming that it results in greatly improved accuracy.

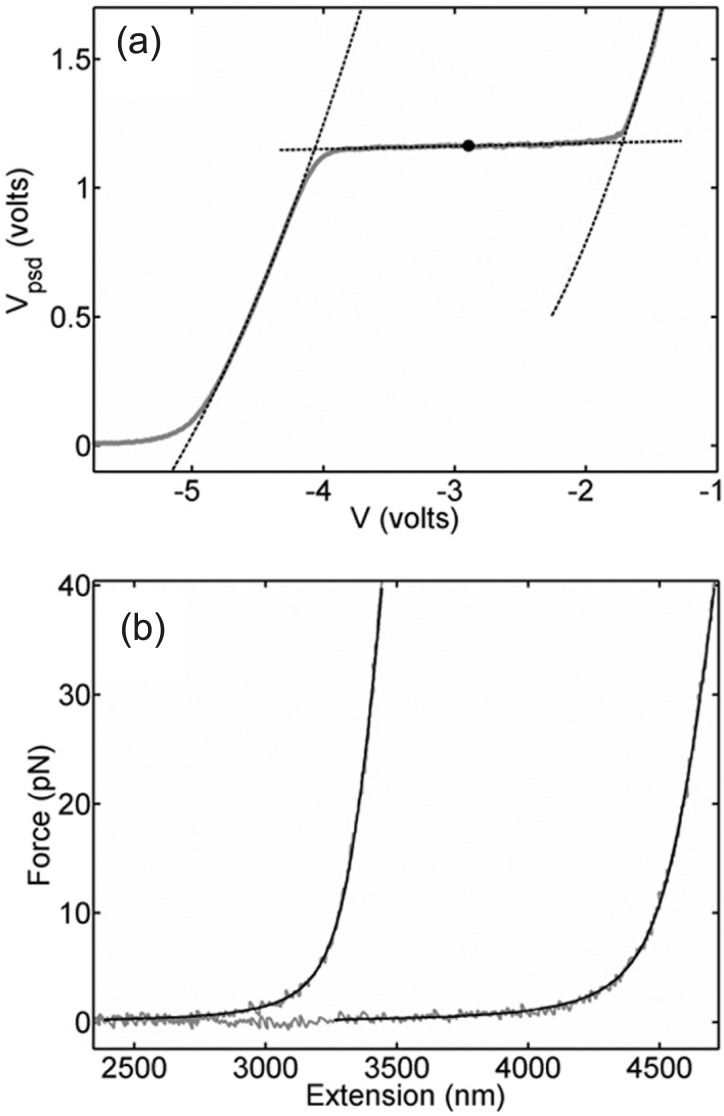
Systematic studies have shown that the overstretch transition occurs at a characteristic force that depends on solution conditions (ionic strength and pH) and this feature has been used in some studies to confirm force measurements.^29,30 The overstretch plateau is clearly seen in our measurements (Fig. 3(a)) and can be analyzed to determine the characteristic overstretch force F_os, defined as the half-way point through the plateau.²⁷ To determine F_os, we fit second-order polynomials to the two portions of the raw PSD voltage data before and after the overstretch plateau and fit a line to the plateau region (Fig. 3(a)). We determine the PSD voltage V_os corresponding to F_os as the point on this line half-way between the two points where the line intercepts the polynomials. We then calculate the force scale factor as α = F_os/V_os, where we use F_os = 63.6 pN based on measurements reported in the literature²⁷ for conditions similar to ours (10 mM Tris-HCl, pH 7.5, 150 mM NaCl). We obtain α = 54.2 ± 0.2 pN/V (average over measurements on 34 molecules).

FIG. 3.

(a) Averaged force-extension measurements in instrument units for the 10.1 kbp DNA (grey points) and fits (dashed lines) to identify the mid-point of the overstretching transition (black point). (b) Fits of the WLC model (black lines) to a typical pair of force vs. extension measurements on the 10.1 kb and 13.7 kb DNA molecules (grey points).

Next, to determine the length scale factor, β, we use the fact that, according to the WLC model (Eq. (1)), the extension (x) of DNA is equal to its contour length (L) at a particular force, which is 33.4 pN for values of the persistence length (P = 45 nm) and stretch modulus (S = 1275 pN) appropriate to our solution conditions.²⁷ After converting PSD voltage to force using α determined above, we determine the displacement control voltages V₁ and V₂ that yield F = 33.4 pN for each of the two DNA molecules. We then calculate β = (L₂ − L₁)/(V₂ − V₁), where L₁ and L₂ are the contour lengths of the two molecules. This method has the advantage of determining β in a manner that does not involve curve fitting and does not depend on the values of γ and V₀, which we determine in a subsequent analysis step. We obtain β = 979 ± 7 nm/V (average over 34 measurements of 10.1 kbp molecules and 33 measurements of 13.7 kbp molecules).

Finally, to determine the series compliance of the traps, γ, and displacement offset factor, V₀, we perform two-parameter fits for γ and V₀ of the WLC model to each force-extension data set for both DNA lengths (Fig. 3(b)) where α and β are fixed to the values already determined above. To quantify the quality of the fit between the predicted WLC model (x, F) values (Eq. (1)) and observed (x, F) values, we calculate the coefficient of determination R², where the observed values are evaluated by the equations¹³ x = β(V − V₀) − γF and F = αV_PSD and a particular set of α, β, γ, and V₀. Then, with α and β fixed to the values determined above we iterate over γ and V₀ values to find the set that yield the greatest R² (i.e., the global best fit) and thus the best determination of γ and V₀ for our system. Fitting was done over the range from 4 to 40 pN to minimize effects of instrumental noise at low force and the onset of the overstretch transition at high force,¹³ yielding excellent fits with ⟨$R^2$⟩ = 0.994, and the values V₀ = −8.330 ± 0.003 and γ = 11.0 ± 0.1 nm/pN (average over 34 measurements of 10.1 kbp molecules and 33 measurements of 13.7 kbp molecules).

This approach results in a dramatic improvement in the robustness of the determination of the measurement parameters. Whereas the prior method determined all four parameters through fits to the WLC model, the present method reduces the number of fit parameters to only two (V₀ and γ). The quality-of-fit analysis of the prior method (Fig. 2(a)) showed that α and γ were not tightly constrained. In contrast, the improved method determines α independently, and a similar quality-of-fit analysis (Fig. 2(b)) shows that these remaining two parameters are tightly constrained (0.02 V range in V₀, and 0.1 nm/pN range in γ).

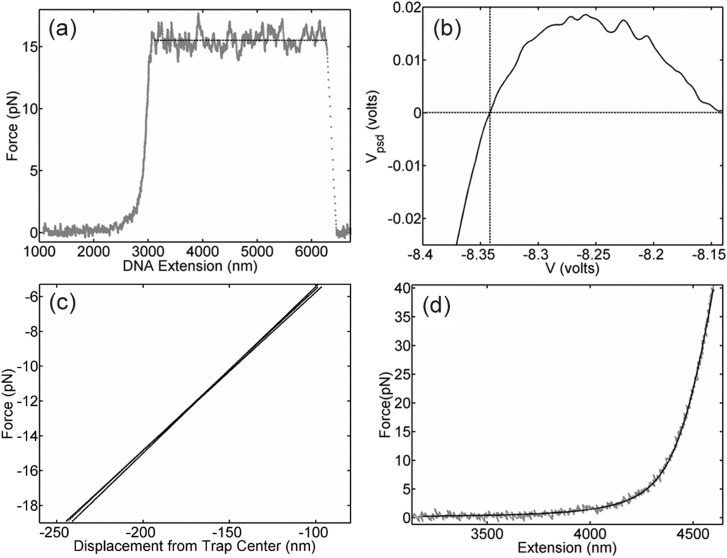
To independently check the accuracy of the determined force scale factor, α, we conducted measurements of another characteristic DNA property different than the overstretch transition: the force required to unzip double-stranded DNA, which has been previously reported in the literature.^31–33 Here, we unzip a section of λ phage DNA ranging from base 8015 to 4392 (Fig. 4(a)) and measure an average PSD voltage of 0.286 V during unzipping (average over measurements on 44 molecules). The known unzipping force from the literature, accounting for our solution conditions and DNA sequence, is 16 pN which implies α = 16/0.286 = 55.9 pN/V, which agrees to within 3% with the value of 54.2 we determined above. We note that the agreement of both the overstretch transition and unzipping transition with literature values also validates that force is a linear function of PSD voltage (F = αV_PSD) for our system.

FIG. 4.

(a) Measurement of DNA unzipping with the λ DNA construct (grey points). The dashed line indicates the average unzipping force. (b) Measurement in instrument units of contact force between two microspheres vs. separation between the two traps (average of 64 measurements), used to check the displacement offset factor, V₀. Dashed lines mark the V_PSD = 0 crossing point. The small increase to V_PSD > 0 is due to cross-interaction when the two optical traps are very close (i.e., trap #1 exerts force on the microsphere in trap #2). (c) Measurements of contact force vs. trap separation in the linear portion of the F < 0 regime (grey points; three individual measurements shown) and linear fits to each dataset (solid lines). (d) Typical force-extension measurement with the 13.4 kbp molecule (grey points) and comparison with the WLC model prediction (solid line).

To independently check the accuracy of the displacement offset factor, V₀, we conducted measurements of the contact forces between the two trapped microspheres in the absence of DNA. When the traps are moved together and the microspheres come into contact, V₀ is the control voltage at which the force transitions from near-zero to negative values (Fig. 4(b)). This measurement yields V₀ = −8.341 ± 0.006 V, in excellent agreement with the value of −8.330 determined above. The difference between these values corresponds to a deviation of βΔV₀ = 11 nm.

Microsphere contact measurements also provide a way to confirm the compliance, γ. After the microspheres touch, when the traps are moved closer by a distance d, the microspheres are pushed a net distance d = γF_c from their trap centers, where F_c is the contact force (Fig. 4(c)). We only include contact events in which there is no slipping of the microspheres in a direction perpendicular to d. By measuring the slope of the linear portions of the F_c vs. d plot, we obtain γ = 10.46 ± 0.03 nm/pN (standard deviation in the mean, average for 92 pairs of microspheres), which agrees to within 5% with the value of 11.0 nm/pN determined above.

To confirm the accuracy of the displacement scale factor, β, we conducted force-extension measurements with a third DNA molecule having a different length (L = 13 424 bp) than the other two used for metrology (Fig. 4(d)). These data are used to derive a check as follows. Recall that DNA extension is given by x = β( V − V₀) − γF (Fig. 1) and x = L at F = 33.4 pN. Thus, β = (L + γF)/(V^* − V₀), where V^* is the observed displacement control voltage for which F = 33.4 pN. Fixing α, γ, and V₀ to the values determined by our procedure above, we find β = 980 ± 1 nm/V (average from measurements on 59 molecules), which agrees to within 0.1% with the value of 979 determined above. We note that these measurements also agree well with the prediction of the WLC model, which further supports this method as a way of determining accurate measurement parameters.

In summary, multiple confirmations via independent measurements show that the proposed method is much more accurate than the prior method. The greatest absolute improvements are in the determination of α and γ. The relative improvements in accuracy over the prior method¹³ can be characterized by the difference in present vs. prior values divided by the difference in present vs. confirmed values, indicating improvements of 10-fold in α, 19-fold in β, 8-fold in γ, and 7-fold in V₀.