Ionic strength independence of charge distributions in solvation of biomolecules

Abstract

Electrostatic forces enormously impact the structure, interactions, and function of biomolecules. We perform all-atom molecular dynamics simulations for 5 proteins and 5 RNAs to determine the dependence on ionic strength of the ion and water charge distributions surrounding the biomolecules, as well as the contributions of ions to the electrostatic free energy of interaction between the biomolecule and the surrounding salt solution (for a total of 40 different biomolecule/solvent combinations). Although water provides the dominant contribution to the charge density distribution and to the electrostatic potential even in 1M NaCl solutions, the contributions of water molecules and of ions to the total electrostatic interaction free energy with the solvated biomolecule are comparable. The electrostatic biomolecule/solvent interaction energies and the total charge distribution exhibit a remarkable insensitivity to salt concentrations over a huge range of salt concentrations (20 mM to 1M NaCl). The electrostatic potentials near the biomolecule's surface obtained from the MD simulations differ markedly, as expected, from the potentials predicted by continuum dielectric models, even though the total electrostatic interaction free energies are within 11% of each other.

I. INTRODUCTION

A favorable electrostatic free energy of hydration promotes protein and nucleic acid binding, molecular recognition,¹ folding,^1,2 enzymatic activity,³ and more. Electrostatics plays an essential role in descriptions of solvation free energies, catalysis, redox potentials, and acid-base equilibria.⁴ These complex phenomena are often analyzed⁵ with continuum models^4,6 or atomistic integral equation methods^7–10 that must be validated, in part, by comparisons with all-atom simulations¹¹ whose analysis often provides important insights enabling improvement of the approximate descriptions. For example, Roux et al. use MD simulations and a continuum model to study liquid-vacuum interfaces,¹² and McCammon et al. apply MD simulations to calculate the electrostatic potential around a protein and to compare the results with Poisson-Boltzmann calculations.^13–15 In addition to determining the charge density and potential around the 20 amino acid types, Roux et al. determine optimized Born radii from free energy perturbation MD simulations.¹⁶

Pettitt et al. have introduced the concept of proximal radial charge distribution functions (pRCDFs) as a means of predicting the charge distributions surrounding deca-alanine and the electrostatic free energy of hydration.¹⁷ Proximal radial charge distribution functions are analogs of the previously analyzed proximal radial density distributions (pRDFs) and likewise emerge here as being universal for all globular proteins.^18–20 Here we calculate separate pRCDFs for water and for the sodium and chloride ions from all-atom MD simulations of 5 proteins and 5 RNA molecules for four very different ionic concentrations (for a total of 40 different combinations). Water provides the dominant contribution to the charge density distribution, even for the highest ionic concentration (1M NaCl). By artificially separating the TIP3P partial charges of the water molecules into separate contributions to total positive and negative charge densities, quite remarkably, the total charge density distribution is found to be insensitive to the concentration of salt. The electrostatic interaction free energies between the biomolecule and the ions or water individually exhibit the expected strong dependence on salt concentration, yet their sum is virtually independent of ionic concentration. Finally, electrostatic potential energy maps constructed from the MD simulations are compared to those obtained from solving the Poisson-Boltzmann equation. The pRDFs, pRCDFs, and potential maps demonstrate several characteristic features originating from the discrete nature of water molecules that are well known to be absent in electrostatic potential maps produced by the Poisson-Boltzmann equation. Nevertheless, continuum calculations for the ten biomolecules also display the surprisingly small dependence of the total electrostatic free energies on ionic strength. The total free energies calculated from the explicit solvent and continuum approaches are similar when expressed in relative terms (1%–17%), although the MD-determined free energies are larger by 14–1433 kcal mol⁻¹ in absolute terms. Pettitt et al. have compared calculated charge density distributions around DNA using integral equations and MD simulations with results from the Poisson-Boltzmann equation.¹⁰

II. METHODS

A. MD simulations

MD simulations employing NAMD,²¹ with the AMBER99²² force field and the TIP3P model for water, are performed separately for the five RNAs and five proteins chosen for convenience from five protein/RNA complexes found in the Protein Data Bank (PDB), namely, 1A1T,²³ 1G70,²⁴ 1HJI,²⁵ 1S03,²⁶ and 2A9X.²⁷ Four different sets of simulations for each molecule cover the wide range of ion concentrations, 20 mM NaCl, 145 mM NaCl, 145 mM NaCl plus 10 mM MgCl₂, and 1M NaCl. Using the Visual Molecular Dynamics (VMD) plugin autoionize, all of the macromolecules are first neutralized, and then ions are added to reach the target concentration. Table I summarizes the number of ions and water molecules in each simulation. All solute atoms are held immobile throughout the course of the subsequent MD simulation to keep the structure of the biomolecule from deviating from that of the crystal structure and to prevent the solvent charge density from being blurred by protein motions, especially of the side groups. The simulations enforce NVT (constant number of atoms, volume, and temperature) conditions, because NPT (constant number of atoms, pressure, and temperature) simulations do not work well when a large number of atoms remain immobile. Electrostatic interactions are computed with particle mesh Ewald summations. Protonation is set by assuming standard states for pH = 7. All simulations have box sizes whose dimensions extend 15 Å beyond the solute molecule on all sides. The density of the bulk solvent is determined in each case from all water molecules situated at distances exceeding 10 Å from the solute. The electrons are approximated as being located at the nuclei, and if the computed electron density of the bulk water is either less than 0.333 e⁻ Å⁻³ or greater than 0.335 e⁻ Å⁻³, the simulation box size is adjusted to produce the correct bulk density. The dimensions of the simulation boxes are presented in Table II, along with the simulation box volume and the Debye length. The Debye length slightly exceeds the 15 Å padding between the biomolecule and the edge of the simulation in two examples. The padding for all simulations with 20 mM ionic concentration is less than twice the Debye length. Section III E shows that the simulation box can be truncated without significantly affecting the solute/solvent electrostatic free energy.

Table I.

The number of Na⁺ ions, Cl⁻ ions, and H₂O molecules in each simulation.

		RNA			Protein
Solute	Target concentration	Na+	Cl−	H2O	Na+	Cl−	H2O
1A1T	20 mM NaCl	21	2	18 258	3	14	22 323
	145 mM NaCl	36	17	18 168	20	31	22 221
	145 mM NaCl, 10 mM MgCl2	36	19	18 159	30	33	22 212
	1M NaCl	133	114	17 586	139	150	21 507
1G70	20 mM NaCl	34	3	22 836	1	6	10 809
	145 mM NaCl	52	21	22 728	10	17	10 755
	145 mM NaCl, 10 mM MgCl2	52	23	22 719	10	15	10 746
	1M NaCl	174	143	21 996	68	73	10 407
1HJI	20 mM NaCl	16	2	15 141	2	8	15 243
	145 mM NaCl	28	14	15 060	14	20	15 171
	145 mM NaCl, 10 mM MgCl2	28	16	15 060	14	22	15 162
	1M NaCl	109	95	14 583	95	101	14 685
1S03	20 mM NaCl	51	5	36 855	4	9	32 073
	145 mM NaCl	79	29	36 687	29	34	31 923
	145 mM NaCl, 10 mM MgCl2	79	37	36 669	29	38	31 905
	1M NaCl	277	205	35 499	200	205	30 897
2A9X	20 mM NaCl	30	3	21 708	1	8	10 539
	145 mM NaCl	47	20	21 606	10	17	10 485
	145 mM NaCl, 10 mM MgCl2	47	22	21 597	10	19	10 476
	1M NaCl	163	136	20 910	66	73	10 149

Table II.

The dimensions of the simulation boxes, the volumes, and the Debye lengths assuming a dielectric constant of 82.

		RNA					Protein
Solute	Target concentration	X (Å)	Y (Å)	Z (Å)	V (Å3)	λD (Å)	X (Å)	Y (Å)	Z (Å)	V (Å3)	λD (Å)
1A1T	20 mM NaCl	51.748	73.882	48.993	187 300	11.2	53.033	71.016	61.088	230 100	17.1
	145 mM NaCl	51.782	73.931	49.026	187 700	6.5	53.072	71.068	61.133	230 600	7.4
	145 mM NaCl, 10 mM MgCl2	51.790	73.942	49.033	187 800	6.0	53.087	71.088	61.151	230 800	6.9
	1M NaCl	51.953	74.175	49.187	189 500	3.0	53.295	71.367	61.390	233 500	3.0
1G70	20 mM NaCl	56.393	74.860	56.048	236 600	11.0	50.019	48.894	44.934	109 900	13.3
	145 mM NaCl	56.412	74.886	56.067	236 900	6.9	50.065	48.940	44.976	110 200	6.7
	145 mM NaCl, 10 mM MgCl2	56.431	74.910	56.085	237 100	6.0	50.054	48.929	44.966	110 100	6.6
	1M NaCl	56.625	75.169	56.279	239 500	3.0	50.245	49.115	45.137	111 400	3.0
1HJI	20 mM NaCl	48.844	56.782	55.843	154 900	13.4	50.439	69.081	44.726	155 800	13.3
	145 mM NaCl	48.881	56.825	55.885	155 200	7.0	50.476	69.132	44.759	156 200	12.1
	145 mM NaCl, 10 mM MgCl2	48.876	56.819	55.880	155 200	6.7	50.477	69.133	44.759	156 200	6.5
	1M NaCl	49.062	57.036	56.093	157 000	3.0	50.665	69.390	44.927	157 900	3.0
1S03	20 mM NaCl	64.202	63.716	92.969	380 300	12.5	68.769	65.551	74.776	337 100	17.2
	145 mM NaCl	64.242	63.756	93.027	381 000	6.9	68.801	65.582	74.811	337 600	7.9
	145 mM NaCl, 10 mM MgCl2	64.227	63.741	93.005	380 800	6.9	68.802	65.583	74.812	337 600	7.1
	1M NaCl	64.511	64.022	93.416	385 800	3.0	69.068	65.835	75.100	341 500	3.1
2A9X	20 mM NaCl	50.962	73.910	59.282	223 300	12.0	42.755	53.013	47.322	107 300	13.6
	145 mM NaCl	50.992	73.953	59.317	223 700	6.8	42.778	53.042	47.348	107 400	6.9
	145 mM NaCl, 10 mM MgCl2	51.001	73.966	59.328	223 800	6.5	42.778	53.042	47.348	107 400	6.9
	1M NaCl	51.239	74.312	59.604	227 000	2.8	42.943	53.246	47.530	108 700	3.0

Energy minimization and equilibration proceed in several stages. The solvent is first energy minimized for 200 000 steps; then, with all atoms in the nucleic acids immobilized, the temperature is initially set at 10 K and then is raised by 10 K every 100 ps until reaching the final temperature of 277 K. The systems are equilibrated for another 4 ns. A 1 fs time step is used, and snapshots are saved every 1 ps.

B. Electrostatics calculations

According to linear response theory, the protein or RNA/solvent electrostatic interaction free energy is approximated by Coulomb's law as¹⁷

$$G_{elec}=\frac{1}{2}\sum _i^N\sum _j^M\frac{q_i{q}_j}{4\pi {\varepsilon }_o{r}_{ij}},$$ (1)

where q_i and q_j are the charges on solute and solvent atoms i and j, respectively, r_ij is their separation, N and M are the number of solute and solvent atoms, respectively, and ɛ_o is the vacuum permittivity. The electrostatic interaction free energy for every frame is averaged across the MD trajectory.

C. Charge density maps and proximal radial charge density distribution functions

The analysis of the water and ion distributions surrounding the proteins and the RNAs proceeds by decomposing the simulation space into cubes with volumes (0.4 Å)³. The average charge density due to each type of ion and to water's hydrogen and oxygen atoms is calculated for each cube. The sums of the individual distributions provide the total charge density maps.

The pRCDFs describe the charge density distributions proximal to the biomolecule's surface, and their evaluation proceeds as follows: Partial charges on the solute atoms are taken from the protein structure file. The MD simulation box is partitioned into (0.4 Å)³ cubes, and each cube within the solvent is assigned to the closest solute atom, where “closest” is defined as the shortest distance between the center of the cube and a sphere surrounding the solute atom, with the radius of the sphere equal to 0.53 times the van der Waals radius. The average net charge densities within each cube as a function of the separation between each type of solute and solvent atoms define the entire pRCDF for each combination of solute and solvent atom types. This procedure separately treats the highly correlated charge distributions from the positive and negative partial charges on the TIP3P water molecules, a seemingly artificial separation that enables uncovering interesting new insights into the electrostatics of biomolecular solvation.

D. Nonlinear Poisson-Boltzmann calculations

The nonlinear Poisson-Boltzmann equation is solved for each of the proteins and nucleic acids using DelPhi,^14,28 with E_{solute/solvent} evaluated using the energy (ion,s,c,g) option, and the free energies reported are given by the “Energy arising from solvent and boundary pol” in the DelPhi log files that include nonlinear ion terms.^29,30 The dielectric constant of the solvent is set to 82, which accords with Simonson finding that the dielectric constant of the TIP3P water model is 82 ± 5.³¹ Since the solute atoms remain immobile during the MD simulations, the motions of the solute atoms do not contribute to the dielectric constant. The absence of polarizabilities in the force field implies that polarizabilities likewise do not contribute to the dielectric constant of the solute, which is thus set to 1. The same van der Waals radii and charges on the solute atoms are used in DelPhi and the MD simulations. The boundary potentials are approximated by the Debye-Hückel potential. The grid size is set to 0.5 Å, and there are 211 grid points per side.

E. Bulk solvent ionic concentrations

The ionic concentrations noted in Sec. II are only the target concentrations that omit the counterions. In addition, the biomolecules attract and repel ions, increasing or decreasing the number ions in the bulk regions of the solvent, and thereby changing the bulk ion concentration. Table III summarizes the actual bulk ion concentrations at distances exceeding 10 Å from the biomolecules. The presence of counterions increases the bulk solvent ionic concentrations. The effect is greater at weak ionic conditions and is larger for RNA molecules since they need more counterions. Consequently, in going from the target concentration of 20 mM NaCl to the target concentration of 1M NaCl condition, the actual bulk ionic concentrations increase by a factor of 17–31 for the protein solutions, while for the RNAs, the ionic concentrations only grow by a factor of 8–11. Large differences appear in some cases for the sodium and chloride ion concentrations in the bulk solvent. The fact that the bulk ionic concentrations differ implies that the counterions are not all concentrated near the biomolecule. However, the net charge within 10 Å of the surface of the biomolecules nearly vanishes as a result of the orientation of the water molecules. For example, the net charge on the RNA portion of 1A1T is −19 in the 20 mM NaCl solution, whereas the average net charge of all solvent atoms within 10 Å of the biomolecule is 18.95, the average net charge of sodium ions within 10 Å of the biomolecule is 11.67, and the average net charge of chloride ions is only −0.32. The average net charge of all water oxygen atoms is −1258.17 (from an average of 1508.6 water oxygen atoms), and the average net charge of all water hydrogen atoms is 1265.72 (from an average of 3035.3 water hydrogen atoms) in the region which is within 10 Å of the biomolecule. The ions contribute a net charge of 11.38, and the atoms of water contribute a net charge of 7.55 to the region which is within 10 Å of the biomolecule. Hence, the counterions within 10 Å of the biomolecules by themselves fail to neutralize the biomolecule, but the counterions and the orientated water molecules conspire together to neutralize the biomolecule. Because water molecules are neutral, water cannot neutralize the charges in the water box of the MD simulation. Rather, the water molecules become polarized by the charges and thereby screen the charges within the simulation box. In order to study the electrostatics of the ion distributions and the screening of charges by water, it proves convenient to separate the positive and negative charges on the TIP3P water molecules into separate water “positive and negative charge distributions,” recognizing that these two distributions are highly correlated. The use of this artificial separation, however, facilitates uncovering interesting invariances in the electrostatics of the solvating environment of the proteins and RNAs. Since not all the sodium counterions participate in neutralizing the region within 10 Å of the biomolecule, the sodium ion concentration in the more distant region exceeds that of the chloride ion concentration. The target concentration and not the actual bulk ionic concentrations are specified unless otherwise stated.

Table III.

The actual ionic concentration more than 10 Å away from the biomolecule. [NaCl] is set to the average of [Na⁺] and [Cl⁻].

		RNA bulk			Protein bulk
Solute	Target concentration	[Na+]	[Cl−]	[NaCl]	[Na+]	[Cl−]	[NaC]
1A1T	20 mM NaCl	139 mM	15 mM	77 mM	18 mM	48 mM	32 mM
	145 mM NaCl	251 mM	203 mM	227 mM	153 mM	200 mM	177 mM
	145 mM NaCl, 10 mM MgCl2	281 mM	218 mM	249 mM	157 mM	214 mM	186 mM
	1M NaCl	1.05M	1.03M	1.04M	1.09M	1.06M	1.08M
1G70	20 mM NaCl	126 mM	33 mM	80 mM	22 mM	87 mM	55 mM
	145 mM NaCl	237 mM	164 mM	200 mM	206 mM	230 mM	218 mM
	145 mM NaCl, 10 mM MgCl2	279 mM	216 mM	247 mM	182 mM	227 mM	205 mM
	1M NaCl	1.07 mM	1.06 mM	1.07	1.06M	1.09M	1.08M
1HJI	20 mM NaCl	24 mM	84 mM	54 mM	30 mM	80 mM	55 mM
	145 mM NaCl	237 mM	163 mM	200 mM	43 mM	90 mM	67 mM
	145 mM NaCl, 10 mM MgCl2	193 mM	192 mM	193 mM	178 mM	239 mM	209 mM
	1M NaCl	1.05M	1.10M	1.07M	1.04M	1.09M	1.07M
1S03	20 mM NaCl	89 mM	34 mM	62 mM	24 mM	41 mM	33 mM
	145 mM NaCl	223 mM	178 mM	201 mM	147 mM	163 mM	155 mM
	145 mM NaCl, 10 mM MgCl2	197 mM	167 mM	182 mM	153 mM	189 mM	171 mM
	1M NaCl	1.13M	1.09M	1.11M	1.02M	1.04M	1.03M
2A9X	20 mM NaCl	106 mM	30 mM	68 mM	20 mM	84 mM	52 mM
	145 mM NaCl	222 mM	193 mM	208 mM	162 mM	241 mM	202 mM
	145 mM NaCl, 10 mM MgCl2	242 mM	181 mM	211 mM	150 mM	212 mM	181 mM
	1M NaCl	1.20M	1.23M	1.21M	1.06M	1.07M	1.07M

III. RESULTS AND DISCUSSION

A. Charge density maps

In order to gain insight into the electrostatic contributions to the solvation of biomolecules, we perform a series of all-atom explicit solvent MD simulations for five proteins and five RNAs in four target ionic conditions, 20 mM NaCl, 145 mM NaCl, 145 mM NaCl/10 mM MgCl₂, and 1M NaCl. Focus on the solvation is facilitated by maintaining the biomolecules immobile throughout the simulations to remove the added complications from protein or RNA dynamics, as previously implemented in our calculations of protein hydration.^19,32 An analysis of the dependence on ionic strength of the three-dimensional charge distributions of the positive and negative partial charges of the water molecules and of the ions surrounding the biomolecules for each of these 40 different combinations enables decomposing the electrostatic free energy of hydration from the simulations into individual contributions from the water and the ions.

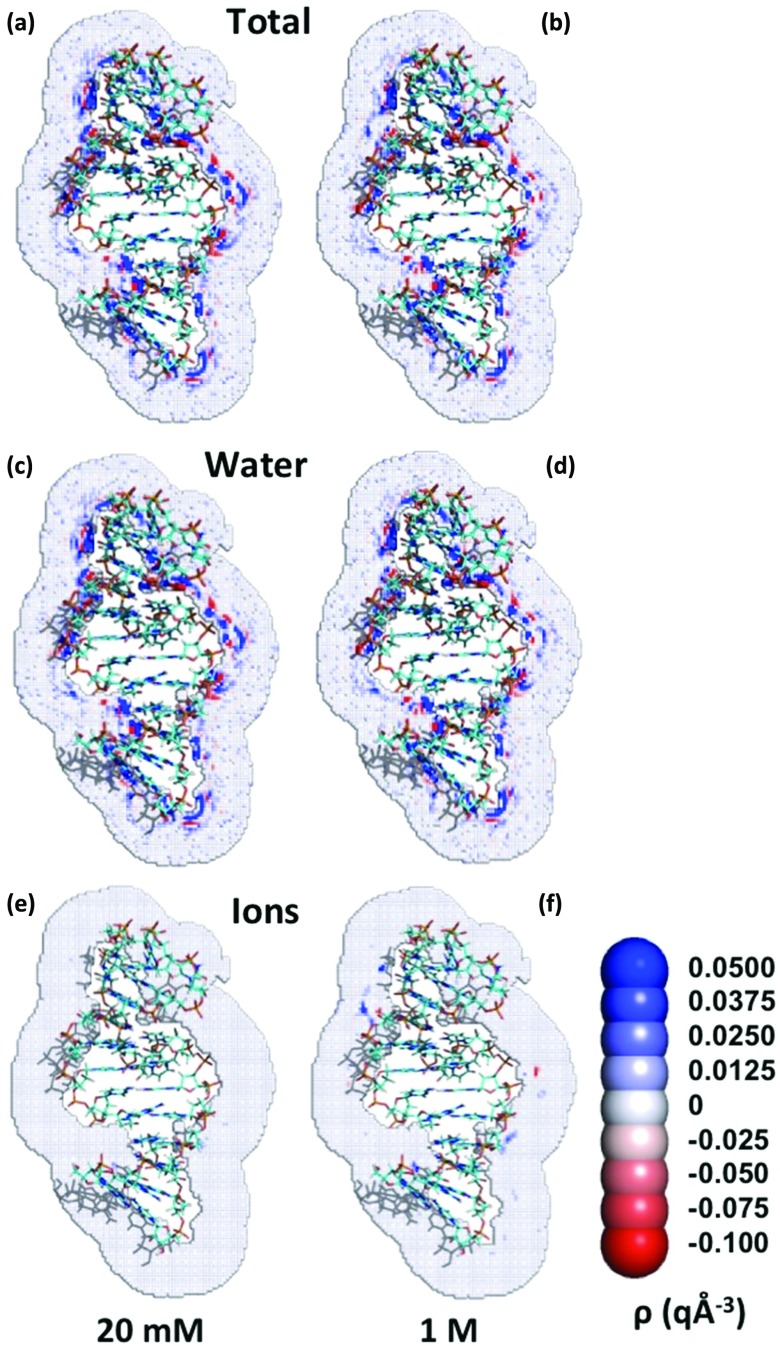
Regions of alternating high positive and negative charge densities around the TAR RNA (2A9X.pdb) appear as expected, in part, because of the alignment of water dipoles, with the length scale set by the 2.8 Å diameter of water (Fig. 1). Surprisingly, nearly all the spatial variation of the net charge around the biomolecules arises due to the distribution of water molecules, even for very high ionic strength 1M NaCl solutions (Fig. 1(b)). Many regions of high positive density are formed by oriented water molecules whose hydrogen atoms point towards the negative charges, especially near the phosphates on the RNA backbone and the carbonyl oxygen atoms on proteins. Similarly, the oxygen atoms of water preferentially lie near the positively charged hydrogen atoms of the solute. Although the water distributions behave as anticipated, the total charge density maps surrounding the biomolecules, quite unexpectedly, are nearly identical for the four ionic conditions (Fig. 2). Regions of high positive or negative ion charge density are absent in 20 mM NaCl solutions, and only four regions of high ion charge density are noticeably visible for 1M NaCl (Fig. 1(c)).

FIG. 1.

Depiction of two-dimensional slices through the charge density maps for TAR RNA (2A9X) in solutions with 20 mM and 1M NaCl.

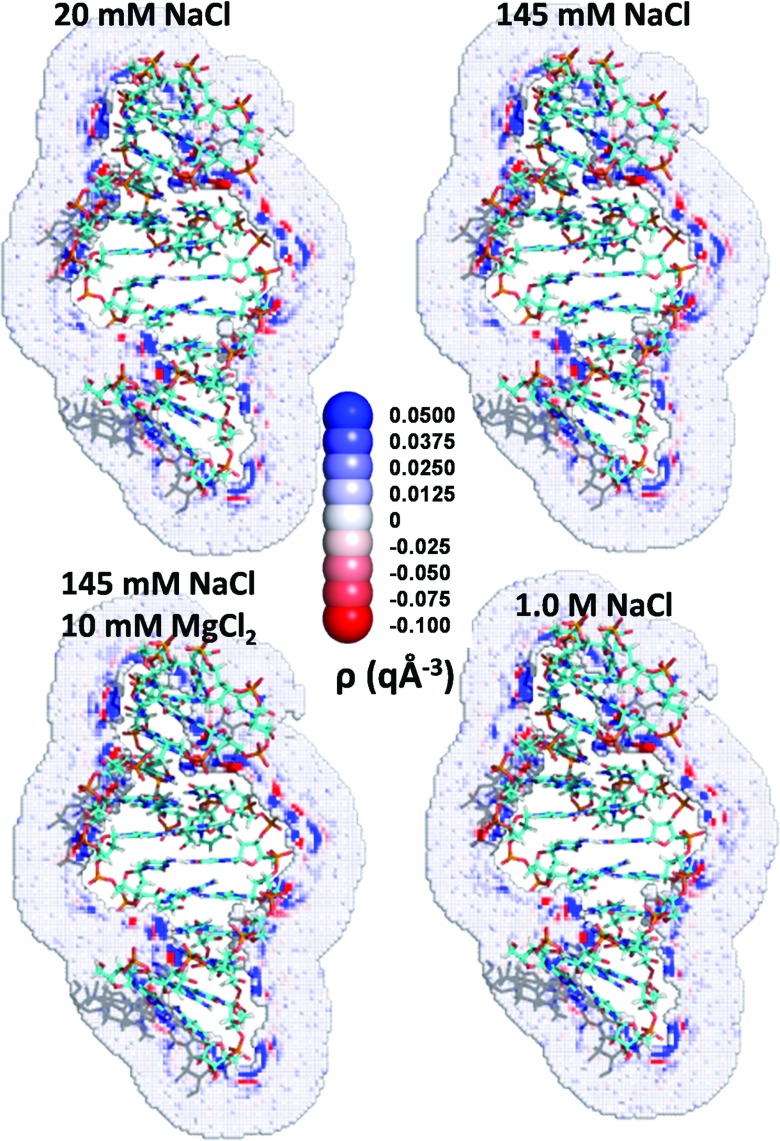
FIG. 2.

Influence of ionic conditions on the charge density distribution around RNA. A cross section of the charge density distribution of the RNA portion of 2A9X for four different ionic conditions.

Many regions of high positive density (blue) appear near the RNA due to oriented water molecules, whose hydrogen atoms lie near the negative charges of the RNA, and to the presence of sodium ions. Similarly, oxygen atoms of water preferentially reside near positively charged hydrogen atoms. Regions of high positive charge density are followed at larger distances by regions of high negative charge density (red), a pattern largely imposed because of the alignment of multiple water dipoles. The total charge density drops to approximately zero (white) within a few angstroms from the surface of the RNA molecule. Very similar cross sections again appear in the charge density map for 20 mM and 1M NaCl solutions (Figs. 1(a) and 1(b)), as well as in the contribution of water to the charge density maps for 20 mM and 1M NaCl solutions (Figs. 1(c) and 1(d)). High density regions are absent from the cross sections of the contribution of ions to the charge density for the 20 mM NaCl solution, and only 4 regions of high charge density appear for the 1M solution, implying that the water molecules provide the dominant contribution to the cross sections for the charge density distribution as displayed in Figs. 1(a) and 1(b).

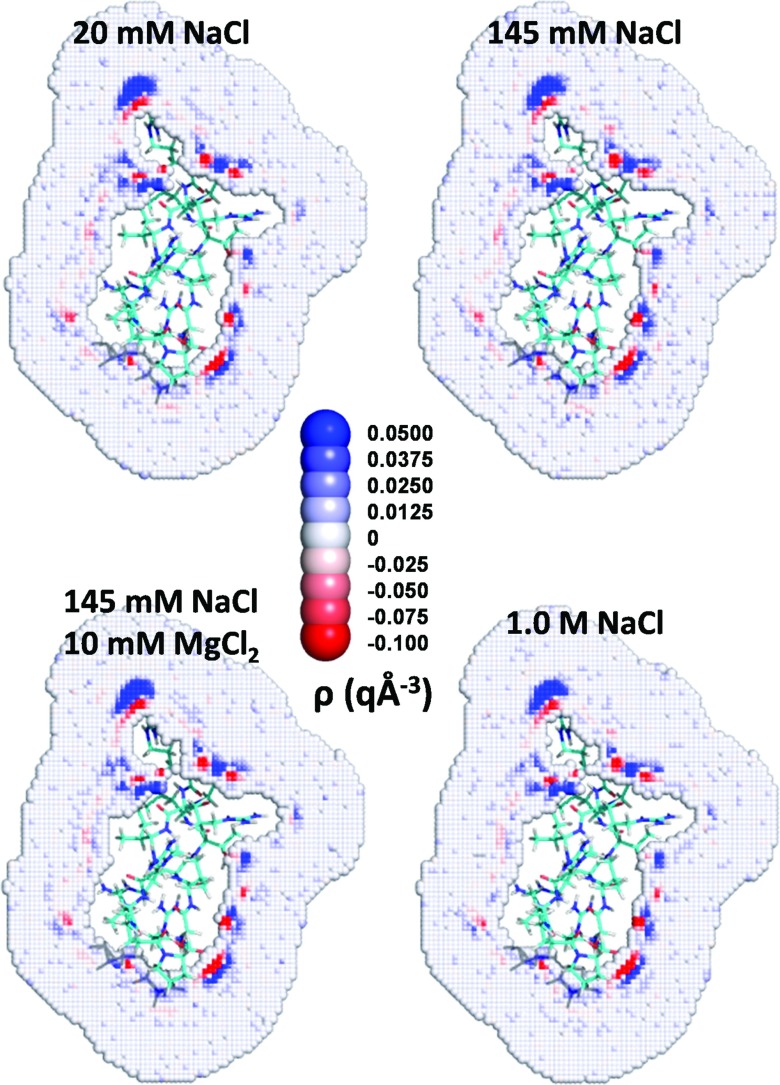
Figure 2 highlights the similarity of the charge density cross sections of the TAR RNA for the four different ionic conditions. A similar behavior emerges for the protein in 2A9X, although the cross sections exhibit far fewer regions of high charge density (Fig. 3). This difference appears because of disparities in the net charges, 7 q on the protein and −27 q on the RNA. The presence of positive charge on the surface induces the formation of regions of high negative charge density close to the protein because of the proximal oxygen atoms of water and of the chloride ions. The regions of high negative charge density are followed at larger distances by regions of high positive charge density, again since the negatively charged oxygen atoms prefer to reside next to positively charged hydrogen atoms.

FIG. 3.

Influence of ionic condition on charge density distribution around proteins. A cross section of the charge density distribution for the protein portion of 2A9X for four different ionic conditions.

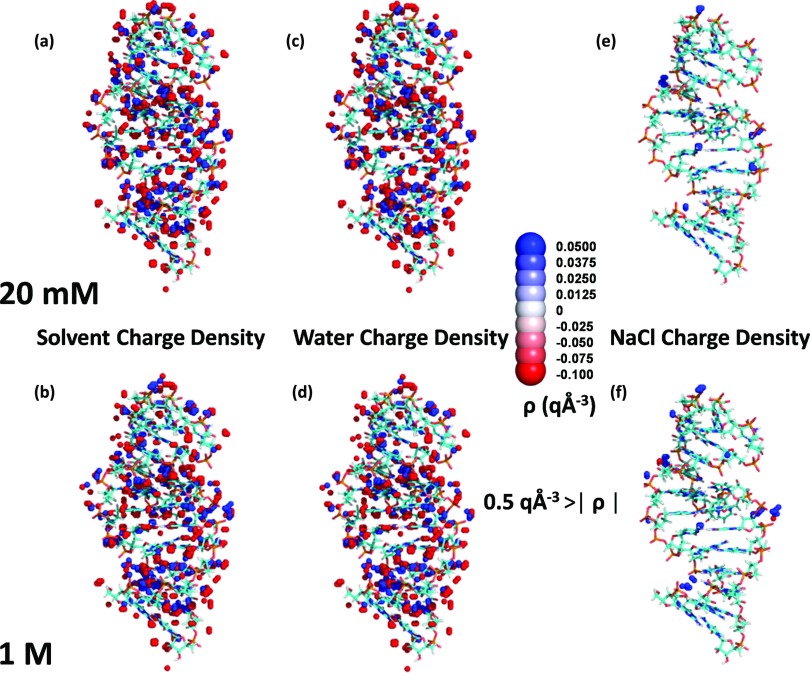
The sodium ions remain more localized than the water molecules and produce a few small regions of high charge density. The sodium ions nevertheless contribute significantly to the electrostatic interaction free energy E_RNA/solvent. Figure 4(e) displays the regions in which the absolute value of the charge density contributed by the sodium and chloride ions exceeds 0.5 q Å⁻³ in the simulation of the TAR RNA at 20 mM. Figure 4(f) contains two unexpected regions of high negative charge density for 1M NaCl solutions. Chloride ions are clustered near both the negatively charged phosphate backbone and regions of high positive charge density from sodium ions and hydrogen atoms of water. The sodium ions produce similar regions but of high positive charge density for the 20 mM NaCl solution, with one exception, indicating that the distributions of the sodium ions in the 20 mM NaCl simulation have converged. The charge density distribution at 1M NaCl only contains a few regions of high positive charge density, produced by sodium ions. These regions are absent for 20 mM NaCl, indicating that the influence of ions already approaches a plateau at the lowest ionic concentration investigated.

FIG. 4.

Three dimensional distribution of regions with high positive and negative charge densities, from MD simulations of the RNA portion of 2A9X. Only regions for which the absolute value of the charge density is greater than 0.5 q Å⁻³ are displayed. Results from the 20 mM NaCl MD simulation are displayed on top, and those from the 1M NaCl MD simulation are presented on the bottom. (a) and (b) High charge density regions. (c) and (d) High charge density regions due to water. (e) and (f) High charge density regions due to sodium and chloride ions.

The cross sections displayed in Fig. 1 might lead to the belief that ions do not contribute significantly to the electrostatic free energy of hydration for RNA molecules. However, as discussed in Sec. III E, ions provide the major contribution to the electrostatic free energy of hydration for RNA molecules because the small separation of charges in the dipole moment of water implies that the contributions from the hydrogen and the oxygen atoms of water largely offset each other. Whenever the hydrogen atoms of water produce a region of high positive charge density near the solute, the oxygen atoms of water counter with a region of high negative charge density further away. The pattern of alternate regions of high positive and negative charge density is absent from the charge density distribution of the ions. Instead, isolated regions of high positive charge from the sodium ions are evident at 20 mM NaCl but are mostly unaccompanied by regions of high negative charge density from chloride ions. The separately mobile sodium and chloride ions do not locally counteract each other, while water's highly correlated oxygen and hydrogen atoms do counterbalance each other. Thus, the contribution of the ions to electrostatic interaction free energy E_RNA/solvent exceeds that of water, even though most of the local field variations appear by virtue of the water molecules.

B. pRCDFs

The solvent is discretized into (0.4 Å)³ cubes. Every cube is assigned to the scaled van der Waals surface closest solute atom, where the scaled van der Waals surface is defined as a sphere of radius 0.53 times the van der Waals radius surrounding the solute atom. The pRCDF is the average charge density of a solvent species (e.g., O or H atoms of water or Na⁺) in cubes as a function of the distance to the nearest solute atom for each solute atom type.

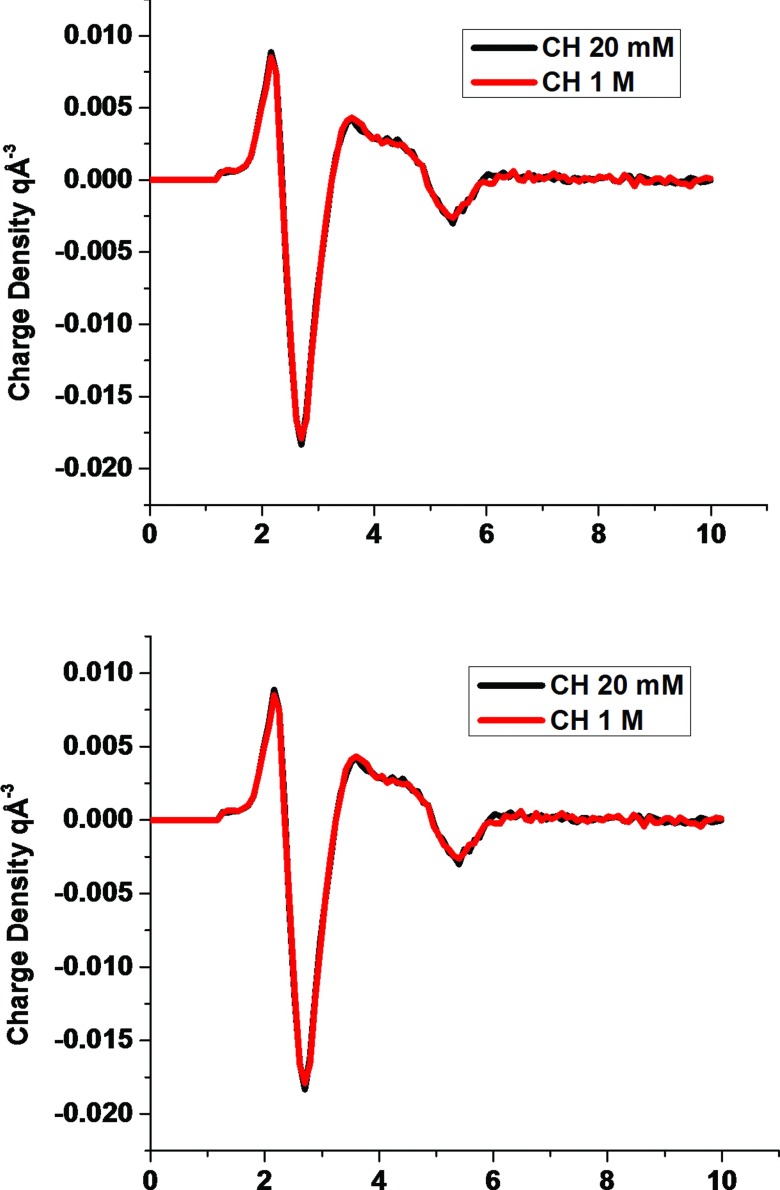
Figure 5 displays the pRCDFs deduced from the MD simulations for the CH and O atom types of the solute. The pRCDFs are very similar to those obtained for individual amino acids¹⁶ and are virtually independent of ionic concentration. Since hydrogen atoms bonded to carbon atoms are not highly charged, they only weakly attract ions or align the dipoles of water. Thus, only small net charge densities appear around hydrogen atoms bonded to carbon. Although hydrogen atoms carry slightly positive partial charges, the charge density right next to this class of hydrogen atoms is slightly positive and is a consequence of their smaller van der Waals radius, relative to oxygen's, which enables them to approach the solute atoms closer than do the oxygen atoms of water.

FIG. 5.

Charge density pRCDFs for the CH and O atom types in 20 mM and 1M NaCl solutions.

Adjacent to the region closest to biomolecule's CH atoms, which possess slightly positive densities, the pRCDF of CH becomes relatively large and negative because of the localization of the oxygen atoms of water. The negatively charge region is followed at larger distances by three additional layers of alternating positive and negative regions arising from the ordering of water molecules in the second and third water layers around the biomolecules. The pRCDF for the O atom type is highly positive at short distances because of the attraction of the hydrogen atoms of water and of the positively charged ions to the negatively charged solute oxygen atoms. A region of high negative charge density emerges from oxygen atoms of water that reside in contact with the hydrogen atoms proximal to the solute oxygen atoms. Beyond the region of negative charge density, a second more diffuse region of positive charge density forms due to the second hydrogen atoms of water, hydrogen atoms of other water molecules, and sodium ions.

C. Dependence of pRCDFs on ionic conditions

The charge density maps are nearly independent of ionic conditions. The pRCDFs for atom types CH and O in 20 mM and 1M NaCl solutions (Fig. 5) are very similar to each other. When the target NaCl concentration increases from 20 mM to 1M, the separate changes in the contributions of water and the ions to the pRCDF for the O atom type are constructive for some distances and destructive for some others (Fig. 6). The alteration of the contribution from water with increasing ion concentration resembles the variation in the contribution of NaCl to the charge density distribution, except that the change in water's contribution causes to the pRCDF to shift to larger distances and to yield an initial negative charge density peak followed by two additional negative charge density peaks. In contrast, the change in the contribution of NaCl to the pRCDF lacks negative peaks. The absolute value of the greatest peak in the change to the contribution of the charge density is about 0.004 q Å⁻³, which is small compared to the 0.09 q Å⁻³ peak in the pRCDF of the O atom type.

FIG. 6.

The difference between the pRCDF for the O atom type at 20 mM and at 1M NaCl. The blue curve is the total change in the pRCDF, the black curve is the change due to ions, and the red curve is the change due to water.

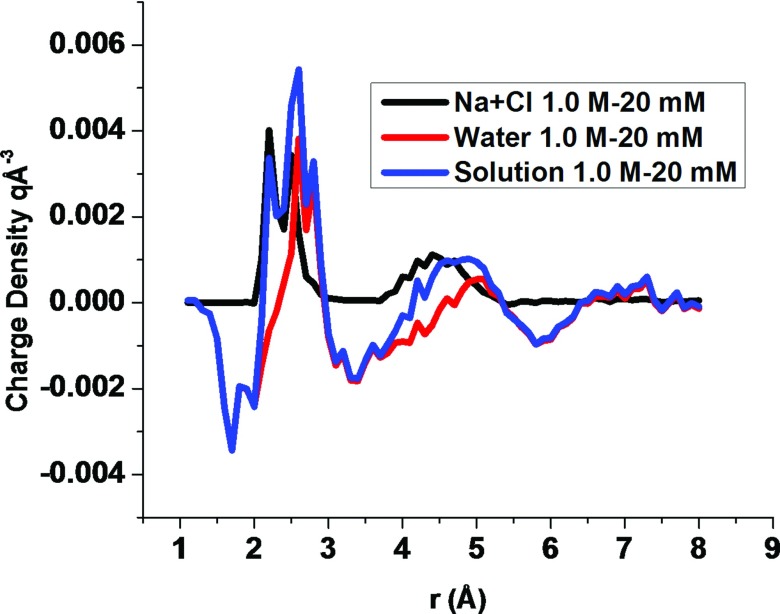
Figure 7 illustrates a pRDF evaluated from the MD simulations for the distributions of Na⁺ and Cl⁻ near oxygen atoms and CH groups of RNAs for the 0.145 and 1M NaCl solutions. The peak in the sodium ion pRDF of the CH atom type is 1.2M and 2.6M, respectively, for the 145 mM and 1M NaCl solutions. Thus, a ∼7 fold increase in sodium ion concentration only elevates the peak by about a factor of 2 because the first few ions near a group of solute atoms screen the charges on the solute. The sodium ions near solute oxygen atoms are even closer to saturation. The maximum concentration of Na⁺ near oxygen atoms of RNA is 8.4M, when the bulk concentration is 1M, which is consistent with Manning counterion condensation theory.³³ The maximum concentration of sodium ions near RNA oxygen atoms is 5.4M when the bulk NaCl concentration is 0.145M. Thus, even for the 0.145M NaCl solution, the sodium ion concentration near the oxygen atoms of RNA is nearly saturated, and a nearly 7 fold increase in the bulk sodium ion concentration only induces a 56% growth in the maximum sodium ion concentration near RNA oxygen atoms. The chloride ion pRDF of the O atom type vanishes for distances less than 4 Å, even when the NaCl concentration is 1M, because of the strong repulsion of chloride ions by the oxygen atoms of RNA. The peak in the sodium ion pRDF of the CH atom type appears at 4 Å where the chloride ion pRDF has a value of 0.1M when the NaCl concentration is 145 mM, and the peak grows to 0.6M when the NaCl concentration is increased to 1M. The maximum chloride ion concentration at the peak increases 6 fold, while the sodium ion concentration only doubles because the elevated concentration of sodium ions attracts chloride ions.

FIG. 7.

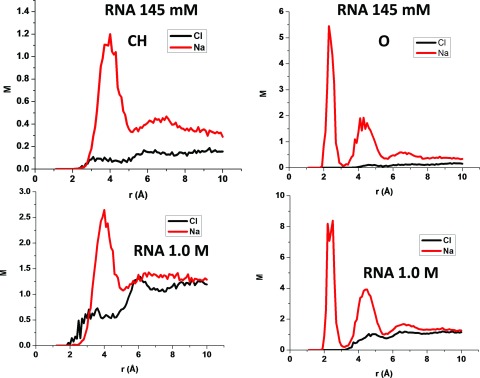
The sodium and chloride ion pRDFs for the CH and O atom types from the 145 mM and 1M NaCl MD simulations.

D. Comparison between protein and RNA ion pRDFs

Figure 8 illustrates the pRDFs (in M) of sodium and chloride ions for the CH and O atom types of RNAs and proteins. Obviously, because of the signs of the charges on the molecules, the concentration of sodium ions always exceed the concentration of the chloride ions in the solvent surrounding RNA molecules, while the opposite applies for the positively charged (RNA binding) proteins studied. Thus, the concentration of chloride ions near the CH atom type for proteins exceeds the concentration of sodium ions, while the opposite naturally appears for RNA molecules because the CH atoms only weakly influence the distribution of ions, whereas their neighbors strongly affect the distribution of ions. The sodium ion pRDFs of the O atom type display very large peaks that are induced by the attraction of the sodium ions to the negatively charged oxygen atoms.

FIG. 8.

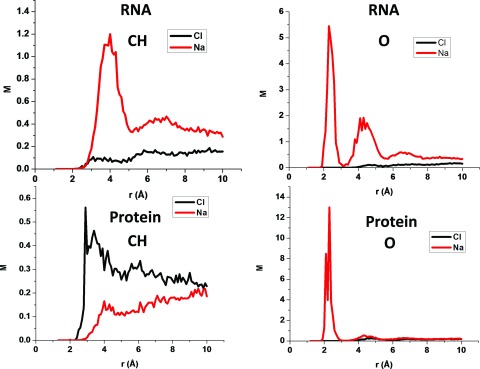
The sodium and chloride ion pRDFs for the CH and O atom types for RNA and proteins.

E. Electrostatic free energies

The solute-solvent electrostatic interaction free energy is approximated as one half of the energy given by Coulomb's law. Although water generates nearly the whole charge distribution and the variation in the local electrostatic potential, water's net contribution to the total electrostatic free energy is comparable to that of the ions (Table IV). This apparent contradiction arises from the largely counterbalancing contributions of the highly correlated positive and negative partial charges on the oxygen and hydrogen atoms of water molecules. In contrast, the individually mobile ions do not locally counterbalance each other, and their contribution to the electrostatic free energy exceeds that of water, even when the ions’ charge distribution is much less pronounced.

Table IV.

Electrostatic interaction free energies.

		ERNA/water	ERNA/ions	ERNA/solvent	EProt/water	EProt/ions	EProt/solvent
Solute	Ionic condition	(kcal mol−1)	(kcal mol−1)	(kcal mol−1)	(kcal mol−1)	(kcal mol−1)	(kcal mol−1)
1A1T	20 mM NaCl	−2631 ± 2	−3237 ± 3	−5869 ± 1	−1750 ± 4	−1033 ± 3	−2783 ± 2
	145 mM NaCl	−2203 ± 2	−3674 ± 2	−5876 ± 1	−1633 ± 3	−1158 ± 3	−2791 ± 1
	145 mM NaCl, 10 mM MgCl2	−2231 ± 2	−3644 ± 2	−5874 ± 1	−1586 ± 3	−1209 ± 3	−2794 ± 1
	1M NaCl	−1782 ± 2	−4105 ± 2	−5886 ± 1	−1309 ± 4	−1496 ± 4	−2805 ± 2
1G70	20 mM NaCl	−4018 ± 4	−7691 ± 4	−11 709 ± 1	−653 ± 2	−232 ± 1	−885 ± 1
	145 mM NaCl	−3689 ± 4	−8021 ± 4	−11 710 ± 1	−590 ± 2	−294 ± 2	−884 ± 1
	145 mM NaCl, 10 mM MgCl2	−3532 ± 5	−8184 ± 5	−11 716 ± 1	−550 ± 3	−335 ± 2	−886 ± 1
	1M NaCl	−2713 ± 4	−9021 ± 4	−11 734 ± 1	−465 ± 2	−421 ± 2	−886 ± 1
1HJI	20 mM NaCl	−1814 ± 1	−1885 ± 1	−3650 ± 1	−999 ± 3	−365 ± 3	−1363 ± 1
	145 mM NaCl	−1589 ± 1	−2066 ± 1	−3654 ± 1	−940 ± 3	−422 ± 2	−1362 ± 1
	145 mM NaCl, 10 mM MgCl2	−1550 ± 2	−2108 ± 2	−3658 ± 1	−902 ± 3	−462 ± 2	−1364 ± 1
	1M NaCl	−1313 ± 1	−2343 ± 1	−3657 ± 1	−716 ± 3	−648 ± 3	−1364 ± 1
1S03	20 mM NaCl	−6694 ± 19	−15 631 ± 20	−22 325 ± 3	−2145 ± 3	−236 ± 2	−2382 ± 2
	145 mM NaCl	−5879 ± 17	−16 497 ± 18	−22 376 ± 3	−2001 ± 3	−375 ± 2	−2376 ± 2
	145 mM NaCl, 10 mM MgCl2	−5917 ± 17	−16 465 ± 18	−22 382 ± 3	−1965 ± 3	−418 ± 3	−2383 ± 2
	1M NaCl	−4519 ± 10	−17 874 ± 10	−22 394 ± 3	−1688 ± 4	−710 ± 3	−2397 ± 2
2A9X	20 mM NaCl	−3852 ± 5	−5733 ± 5	−9585 ± 1	−611 ± 2	−460 ± 2	−1071 ± 1
	145 mM NaCl	−3342 ± 4	−6251 ± 4	−9593 ± 1	−584 ± 3	−487 ± 3	−1071 ± 1
	145 mM NaCl, 10 mM MgCl2	−3299 ± 4	−6296 ± 3	−9595 ± 1	−545 ± 2	−527 ± 2	−1072 ± 1
	1M NaCl	−2542 ± 4	−7064 ± 4	−9606 ± 1	−425 ± 2	−646 ± 2	−1071 ± 1

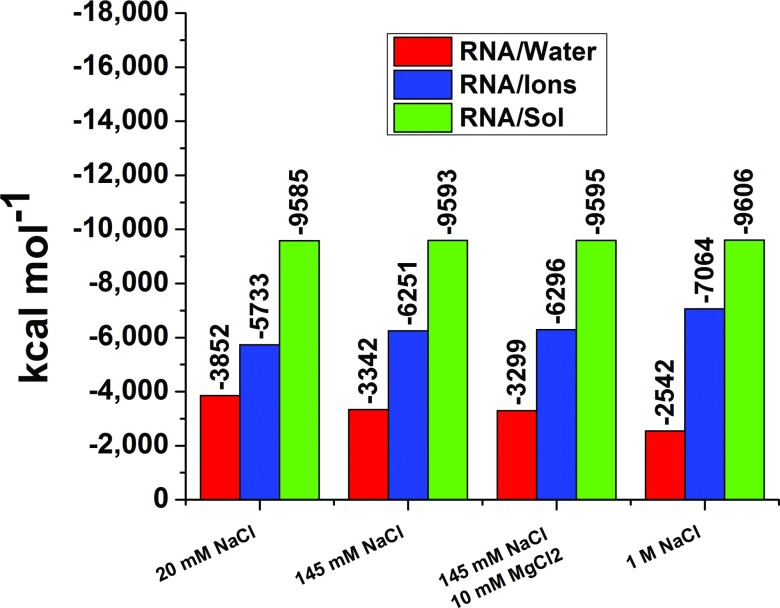
Quite remarkably, the total electrostatic interaction free energy between a biomolecule and the solvating solution emerges is nearly independent of ionic strength from solutions of 0.02–1M NaCl for all ten biomolecules (Table IV). For example, a miniscule 0.22% change in interaction free energy appears over this range in ion concentrations between the TAR RNA (2A9X) and the solution. A visual demonstration of this invariance is provided in Fig. 9. When the ionic concentration increases from 0.02M to 1.0M, the interaction free energy grows by only 0%–0.79% for the ten biomolecules (Table IV). The errors listed for the E_RNA/solvent in Table IV are smaller than the errors for either E_RNA/water or E_RNA/ions because E_RNA/water and E_RNA/ions are anti-correlated from frame to frame in the MD simulations. Thus, the standard deviation of the sum of E_RNA/water and E_RNA/ions is less than the standard deviations of either the E_RNA/water or E_RNA/ions.

FIG. 9.

Separate contributions from water and ions to the electrostatic free energy of hydration of the RNA portion of 2A9X for four different ionic concentrations. Although the contributions from water and ions change drastically, the total remains unchanged.

The biomolecule-water and the biomolecule-ion electrostatic interaction free energies are comparable at low ionic strengths. The balance naturally shifts towards the biomolecule-ion interaction at increasing salt concentration, with a near-exact compensating decrease in the biomolecule-water electrostatic free energy. Even in 20 mM NaCl solutions, the lowest concentration of NaCl for which MD simulations are performed, E_RNA/ions exceeds the E_RNA/water for all RNA molecules simulated here. For example, when the concentration of NaCl is increased from 20 mM to 1M for solutions containing 1A1T, E_RNA/ions decreases from −3237 to −4105 kcal mol⁻¹, a change of 868 kcal mol⁻¹, while the favorability of E_RNA/water increases from −2631 kcal mol⁻¹ to −1782 kcal mol⁻¹, an increase of 849 kcal mol⁻¹. Thus, the total change of E_RNA/solvent is 17 kcal mol⁻¹ (only 0.29%) which, however, is large compared to thermal energies.

Tables V and VI illustrate the influence of truncating the simulation box on the calculated electrostatic free energies. In addition to calculating the electrostatic free energies from the full MD simulation boxes, the electrostatic free energies are calculated using only atoms that are located within a sphere that extends 10 Å from the biomolecule. The solute/solvent electrostatic free energies are very similar; however, considerable differences in solute/water and solute/ion electrostatic energies appear at low ionic concentrations, whereas for most cases of 1M NaCl concentrations, the truncation does not impact solute/water and solute/ion electrostatic free energies significantly. The solute/water electrostatic free energies tend to be lower and change more with ionic concentration when the MD simulation box is truncated. The truncation fails to impact the overall solute/solvent electrostatic free energy but does affect the contributions of the ions and water to the electrostatic free energy because every spherical shell further than 10 Å from the biomolecules is approximately neutral, but the net charge of ions is nonzero and the net charge of the water hydrogen and oxygen atoms is nonzero.

Table V.

Electrostatic interaction free energies of RNA calculated using the full MD simulation box and only atoms within a sphere extending 10 Å beyond the biomolecule.

		ERNA/water	ERNA/water	ERNA/ions	ERNA/ions	ERNA/solvent	ERNA/solvent
Solute	Ionic condition	Full	Sphere	Full	Sphere	Full	Sphere
1A1T	20 mM NaCl	−2631 ± 2	−2741 ± 14	−3237 ± 3	−3136 ± 6	−5869 ± 1	−5858 ± 13
	145 mM NaCl	−2203 ± 2	−2329 ± 16	−3674 ± 2	−3558 ± 7	−5876 ± 1	−5887 ± 14
	145 mM NaCl, 10 mM MgCl2	−2231 ± 2	−2317 ± 15	−3644 ± 2	−3567 ± 6	−5874 ± 1	−5884 ± 13
	1M NaCl	−1782 ± 2	−1760 ± 18	−4105 ± 2	−4128 ± 11	−5886 ± 1	−5888 ± 15
1G70	20 mM NaCl	−4018 ± 4	−4289 ± 32	−7691 ± 4	−7468 ± 13	−11 709 ± 1	−11 756 ± 30
	145 mM NaCl	−3689 ± 4	−3791 ± 27	−8021 ± 4	−7943 ± 13	−11 710 ± 1	−11 734 ± 25
	145 mM NaCl, 10 mM MgCl2	−3532 ± 5	−3572 ± 29	−8184 ± 5	−8172 ± 14	−11 716 ± 1	−11 744 ± 26
	1M NaCl	−2713 ± 4	−2629 ± 29	−9021 ± 4	−9090 ± 16	−11 734 ± 1	−11 719 ± 26
1HJI	20 mM NaCl	−1814 ± 1	−1998 ± 16	−1885 ± 1	−1653 ± 6	−3650 ± 1	−3651 ± 15
	145 mM NaCl	−1589 ± 1	−1698 ± 16	−2066 ± 1	−1986 ± 7	−3654 ± 1	−3684 ± 15
	145 mM NaCl, 10 mM MgCl2	−1550 ± 2	−1613 ± 16	−2108 ± 2	−2044 ± 8	−3658 ± 1	−3657 ± 14
	1M NaCl	−1313 ± 1	−1292 ± 16	−2343 ± 1	−2366 ± 10	−3657 ± 1	−3659 ± 15
1S03	20 mM NaCl	−6694 ± 19	−6259 ± 39	−15 631 ± 20	−16 130 ± 18	−22 325 ± 3	−22 389 ± 35
	145 mM NaCl	−5879 ± 17	−5575 ± 52	−16 497 ± 18	−16 863 ± 26	−22 376 ± 3	−22 438 ± 47
	145 mM NaCl, 10 mM MgCl2	−5917 ± 17	−5361 ± 38	−16 465 ± 18	−17 086 ± 17	−22 382 ± 3	−22 447 ± 35
	1M NaCl	−4519 ± 10	−4188 ± 43	−17 874 ± 10	−18 216 ± 25	−22 394 ± 3	−22 404 ± 37
2A9X	20 mM NaCl	−3852 ± 5	−4061 ± 28	−5733 ± 5	−5552 ± 12	−9585 ± 1	−9612 ± 26
	145 mM NaCl	−3342 ± 4	−3287 ± 24	−6251 ± 4	−6316 ± 12	−9593 ± 1	−9603 ± 21
	145 mM NaCl, 10 mM MgCl2	−3299 ± 4	−3282 ± 22	−6296 ± 3	−6350 ± 10	−9595 ± 1	−9633 ± 21
	1M NaCl	−2542 ± 4	−2466 ± 29	−7064 ± 4	−7179 ± 17	−9606 ± 1	−9645 ± 25

Table VI.

Electrostatic interaction free energies of protein calculated using the full MD simulation box and only atoms within a sphere extending 10 Å beyond the biomolecule.

		EProt/water	EProt/water	EProt/ions	EProt/ions	EProt/solvent	EProt/solvent
Solute	Ionic condition	Full	Sphere	Full	Sphere	Full	Sphere
1A1T	20 mM NaCl	−1750 ± 4	−1818 ± 14	−1033 ± 3	−948 ± 5	−2783 ± 2	−2766 ± 13
	145 mM NaCl	−1633 ± 3	−1678 ± 4	−1158 ± 3	−1111 ± 4	−2791 ± 1	−2789 ± 9
	145 mM NaCl, 10 mM MgCl2	−1586 ± 3	−1628 ± 10	−1209 ± 3	−1165 ± 5	−2794 ± 1	−2793 ± 9
	1M NaCl	−1309 ± 4	−1302 ± 11	−1496 ± 4	−1507 ± 7	−2805 ± 2	−2809 ± 10
1G70	20 mM NaCl	−653 ± 2	−687 ± 6	−232 ± 1	−184 ± 2	−885 ± 1	−871 ± 5
	145 mM NaCl	−590 ± 2	−617 ± 7	−294 ± 2	−270 ± 3	−884 ± 1	−886 ± 6
	145 mM NaCl, 10 mM MgCl2	−550 ± 3	−581 ± 7	−335 ± 2	−270 ± 3	−886 ± 1	−886 ± 6
	1M NaCl	−465 ± 2	−475 ± 6	−421 ± 2	−413 ± 4	−886 ± 1	−888 ± 6
1HJI	20 mM NaCl	−999 ± 3	−1019 ± 5	−365 ± 3	−341 ± 3	−1363 ± 1	−1360 ± 5
	145 mM NaCl	−940 ± 3	−949 ± 5	−422 ± 2	−412 ± 3	−1362 ± 1	−1361 ± 5
	145 mM NaCl, 10 mM MgCl2	−902 ± 3	−919 ± 5	−462 ± 2	−453 ± 3	−1364 ± 1	−1372 ± 5
	1M NaCl	−716 ± 3	−718 ± 5	−648 ± 3	−640 ± 4	−1364 ± 1	−1358 ± 5
1S03	20 mM NaCl	−2145 ± 3	−2170 ± 6	−236 ± 2	−213 ± 8	−2382 ± 2	−2383 ± 6
	145 mM NaCl	−2001 ± 3	−2011 ± 7	−375 ± 2	−354 ± 3	−2376 ± 2	−2365 ± 6
	145 mM NaCl, 10 mM MgCl2	−1965 ± 3	−1984 ± 6	−418 ± 3	−404 ± 3	−2383 ± 2	−2389 ± 6
	1M NaCl	−1688 ± 4	−1686 ± 7	−710 ± 3	−713 ± 4	−2397 ± 2	−2399 ± 6
2A9X	20 mM NaCl	−611 ± 2	−682 ± 7	−460 ± 2	−395 ± 2	−1071 ± 1	−1077 ± 7
	145 mM NaCl	−584 ± 3	−633 ± 9	−487 ± 3	−439 ± 4	−1071 ± 1	−1072 ± 8
	145 mM NaCl, 10 mM MgCl2	−545 ± 2	−589 ± 8	−527 ± 2	−490 ± 4	−1072 ± 1	−1079 ± 7
	1M NaCl	−425 ± 2	−412 ± 8	−646 ± 2	−650 ± 5	−1071 ± 1	−1062 ± 7

The influence of ionic concentration on the properties of a solute molecule, such as binding to a ligand, is governed by the double difference ΔΔG of the free energies. For example, to determine the binding affinity of the RNA 1A1T to a protein as a function of ionic concentration, E_RNA/solvent and several other energies associated with the 1A1T-ligand complex must be known as a function of ionic concentration. Thus, the change ΔG of 17 kcal mol⁻¹, from above, in electrostatic free energy of hydration must be considered in the context of the ΔΔG of interest. Nevertheless, the ΔG = 17 kcal mol⁻¹ shift in E_RNA/solvent provides an order of magnitude estimate for the electrostatic influence of the ions.

The minimal variation in the total electrostatic free energy E_RNA/solvent with salt concentration exemplifies the remarkable ability of water to reorient and thereby counteract the influences of the charges on a solute molecule. While this insensitivity may at first appear surprising, it is a consequence of the high dielectric constant of water. Two ions in water do not feel each other's presence as greatly as two ions in vacuum because of the reorientation of the water molecules. Similarly, the polarization by water screens the interaction between the ions and the charged atoms in the solutes. Ions situated near energetically favorable locations of the biomolecule displace water molecules, which would otherwise interact favorably with the biomolecule.

When the NaCl concentration increases 50 fold from 20 mM to 1M, the change in E_RNA/ions remains below 27% for the RNA molecules studied. Thus, E_RNA/ions already is approaching a plateau at 20 mM NaCl because the few cations in the simulation box readily find favorable positions proximal to the negatively charged groups of the biomolecule. Once these ions neutralize the biomolecule, the remaining cations are free to roam throughout the simulation box.

The computed E_RNA/solvent are independent of ionic concentration to a much greater degree than E_RNA/ions for three reasons. First, the change in E_RNA/water with concentration largely balances the change in the E_RNA/ions. Second, the first few ions in the solution screen the charges on the RNA molecule. Finally, the water molecules also participate in screening the charges on the RNA molecule.

When the NaCl concentration is elevated from 20 mM to 1M, the E_prot/ions increases by 41%–201%, depending on the protein. This change is much larger than the change in E_RNA/ions and indicates that the ionic neutralization has not reached a plateau for the protein-ion interaction. A 17–31 fold increase in bulk NaCl concentration occurs at 1M NaCl for the proteins, as compared to 8–11 fold increase for the RNAs. This suggests that the change in E_prot/ions may exceed that in E_RNA/ions, because the change in concentration of ions is larger for the proteins than for the RNA molecules (Table IV).

Our illustration of water's dielectric power reflects the general phenomenon that the orientation and finite size of the water dipoles by the field of the biomolecule produces a pattern of alternating positive and negative regions emanating from the biomolecule's surface. The charge distribution from this pattern dwarfs the ionic contribution to the charge distributions, even for a highly charged RNA or protein molecule in 1M NaCl.

The E_prot/solvent exhibited in Table IV depend even less on ionic conditions than the E_RNA/solvent, with the exception of the protein portions of complexes 1A1T and 1S03. Three of the E_prot/solvent values for the 20 mM and 1M NaCl solutions are equal within the mutual error bars. The E_prot/solvent are smaller than the E_RNA/solvent because the protein atoms on average have less partial charge than the RNA atoms (Table VII). The E_prot/ions is less favorable than the E_prot/water for 20 mM NaCl solutions, whereas the opposite is true for the RNAs due to their higher charges. Hence, ions are less concentrated near the protein than near the RNA molecule. Moreover, since the water density is close to its maximum near both RNA molecules and proteins, the difference between E_prot/water and E_RNA/water is less than the difference between E_prot/ions and E_RNA/ions. The tendency of E_prot/solvent to be far less favorable than E_RNA/solvent occurs as a consequence of the greater charges on the RNA molecules.

Table VII.

The charges on the protein and RNA molecules used in the simulations.

	Solute	Charge (e-)
	1A1T RNA	−19
	1G70 RNA	−31
	1HJI RNA	−14
	1S03 RNA	−46
	2A9X RNA	−27
	1A1T protein	11
	1G70 protein	5
	1HJI protein	6
	1S03 protein	5
	2A9X protein	7

F. Comparison to DelPhi

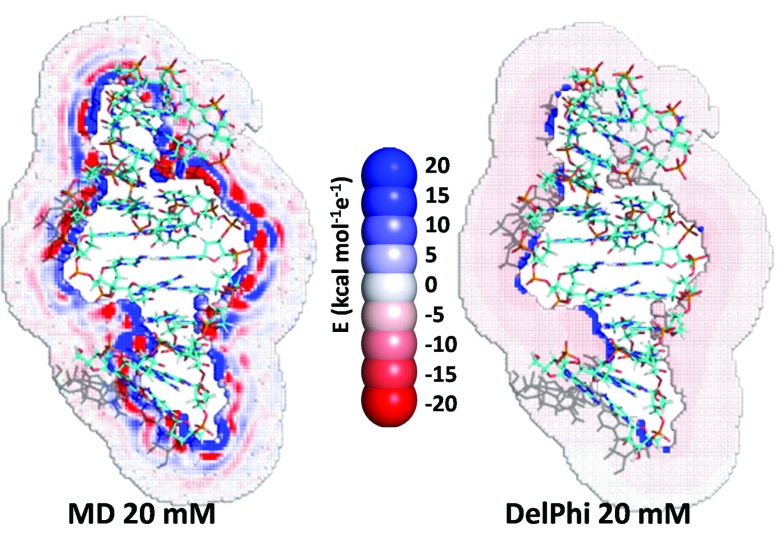
The electrostatic potential energy maps calculated from the charge density distributions display similar structure as found in the charge density distributions but are absent in continuum dielectric models,³⁴ such as the Poisson-Boltzmann model (Fig. 10). Consequently, as is well known, continuum models, such as the Poison-Boltzmann model, fail to replicate molecular details of the solvent response near the surface of the biomolecule. Despite these deficiencies of the Poison-Boltzmann model, the electrostatic free energies of hydration produced by this model generally are similar to those obtained from MD (Table VIII).

FIG. 10.

Electrostatic potential maps of the RNA portion of 2A9X, calculated from a MD simulation and from the Poisson-Boltzmann routines in DelPhi.

Table VIII.

Electrostatic free energies calculated from MD simulations and Poisson–Boltzmann equation.

		RNA MD simulation	RNA DelPhi	Protein MD simulation	Protein DelPhi
Solute	Ionic condition	(kcal mol−1)	(kcal mol−1)	(kcal mol−1)	(kcal mol−1)
1A1T	20 mM NaCl	−5869 ± 1	−5324	−2783 ± 2	−2741
	145 mM NaCl	−5876 ± 1	−5328	−2791 ± 1	−2743
	145 mM NaCl, 10 mM MgCl2	−5874 ± 1	−5328	−2794 ± 1	−2743
	1M NaCl	−5886 ± 1	−5330	−2805 ± 2	−2744
1G70	20 mM NaCl	−11 709 ± 1	−10 888	−885 ± 1	−905
	145 mM NaCl	−11 710 ± 1	−10 895	−884 ± 1	−905
	145 mM NaCl, 10 mM MgCl2	−11 716 ± 1	−10 896	−886 ± 1	−905
	1M NaCl	−11 734 ± 1	−10 899	−886 ± 1	−905
1HJI	20 mM NaCl	−3650 ± 1	−3286	−1363 ± 1	−1374
	145 mM NaCl	−3654 ± 1	−3288	−1362 ± 1	−1374
	145 mM NaCl, 10 mM MgCl2	−3658 ± 1	−3288	−1364 ± 1	−1374
	1M NaCl	−3657 ± 1	−3289	−1364 ± 1	−1375
1S03	20 mM NaCl	−22 325 ± 3	−21 121	−2382 ± 2	−2115
	145 mM NaCl	−22 376 ± 3	−21 138	−2376 ± 2	−2116
	145 mM NaCl, 10 mM MgCl2	−22 382 ± 3	Failed to converge	−2383 ± 2	−2116
	1M NaCl	−22 394 ± 3	−21 150	−2397 ± 2	−2117
2A9X	20 mM NaCl	−9585 ± 1	−8866	−1071 ± 1	−1124
	145 mM NaCl	−9593 ± 1	−8872	−1071 ± 1	−1124
	145 mM NaCl, 10 mM MgCl2	−9595 ± 1	−8872	−1072 ± 1	−1124
	1M NaCl	−9606 ± 1	−8874	−1071 ± 1	−1124

The DelPhi calculations for E_{solute/solvent} agree with our MD-based calculations for most of the proteins. The discrepancies for the 20 mM NaCl solutions of the proteins in 1A1T, 1G70, and 1HJI are 1.5%, 2.2%, and 0.08%, respectively, while the errors incurred by DelPhi increase to 4.9% and 11.2% for 2A9X and 1S03, respectively. The DelPhi calculations for the more highly charged RNA molecules are poorer than for the proteins and consistently underestimate the MD simulation by between 5.4% and 10.0% (7.8% average), probably due to the higher charge on the RNA. DelPhi calculations of the change in E_RNA/solvent with ionic condition deviate from MD by between 4 kcal mol⁻¹ and 40 kcal mol⁻¹

The agreement between DelPhi and the MD simulations might be improved by adjusting the parameters used in the DelPhi calculations. The dielectric constant of the solvent in the DelPhi calculations should be the same as the dielectric constant of the water in the MD simulations. We use a dielectric constant of 82 for water for the DelPhi calculations, rather than the experimental value of 78, to properly compare to the MD simulations since the dielectric constant of the TIP3P water model is 82. In addition, solute/solvent electrostatic free energies calculated using DelPhi are only moderately insensitive to the dielectric constant of the solvent. For example, E_RNAsolvent for 1A1T at 20 mM NaCl concentration is −5324 kcal mol⁻¹ when the dielectric constant of water is 82 and is −5235 kcal mol⁻¹ when the dielectric constant of water is 40. The finite size of the MD simulation box is a source of error. For example, the concentrations of Na⁺ and Cl⁻ ions are unequal at the boundary of the simulation box, due to the finite size of the simulation box. Simulation box sizes sufficiently large to have equal concentrations of cations and anions at the simulation box boundary would have been computationally infeasible. However, Tables V and VI indicate that the box sizes are sufficient to provide accurate solute/solvent electrostatic free energies. An issue with the comparison between the MD and DelPhi calculations appears because the NaCl concentration is not well defined for the MD simulations, since the Na⁺ and Cl⁻ ion concentrations are unequal at the simulation box boundary. The boundary conditions also partly explain the differences between the two methods. The MD simulations use periodic boundary conditions, while the DelPhi calculations use Debye-Hückel theory. Near the boundary edges, the ions and water molecules feel the biomolecule images as much as the biomolecule itself. The DelPhi calculations are unaffected. Another source of disagreement could arise because the electrostatic free energy from the MD simulations is approximated using linear response theory. The finite DelPhi grid spacing also impacts on the calculated electrostatic free energy.

IV. CONCLUSION

The dielectric solvating power of water is illuminated by MD-based calculations of the charge density around proteins and RNAs for a wide range of ionic concentrations. The orientation of water dipoles is responsible for generating nearly the whole charge distribution. However, because water molecules are net neutral, their net electrostatic energetic contribution to the interaction with the biomolecules is smaller than that of the ions. The contribution of the ions to the electrostatic free energy is large and increases markedly with ion concentration. However, the increase is nearly exactly canceled by a decrease in the contribution from water. Consequently, only a minimal change in total electrostatic free energy ensues from 20 mM to 1M NaCl. The electrostatic potential maps and pRCDFs likewise emerge as insensitive to ionic concentration, further exemplifying the remarkable ability of water to reorient and counteract the influence of the charges. The charge density and electrostatic potential exhibit alternating regions of positive and negative density due to the finite size of water. DelPhi, a continuum method, cannot reproduce this fine structure, and values of the electrostatic free energy differ by 10–1244 kcal mol⁻¹ (1%–11%). However, the DelPhi electrostatic free energy still exhibits the independence on ionic strength for the total electrostatic free energy, suggesting that this method is most accurate when estimating differences of bulk properties.