Sample size considerations in the design of cluster randomized trials of combination HIV prevention

Abstract

Background

Cluster randomized trials have been utilized to evaluate the effectiveness of human immunodeficiency virus (HIV) prevention strategies on reducing incidence. Design of such studies must take into account possible correlation of outcomes within randomized units.

Purpose

To discuss power and sample size considerations for cluster randomized trials of combination HIV prevention, using an HIV prevention study in Botswana as an illustration.

Methods

We introduce a new agent-based model to simulate the community-level impact of a combination prevention strategy and investigate how correlation structure within a community affects the coefficient of variation–an essential parameter in designing a cluster randomized trial.

Results

We construct collections of sexual networks and then propagate HIV on them to simulate the disease epidemic. Increasing level of sexual mixing between intervention and standard of care communities reduces the difference in cumulative incidence in the two sets of communities. Fifteen clusters per arm and 500 incidence cohort members per community provides 95% power to detect the projected difference in cumulative HIV incidence between standard of care and intervention communities (3.93% and 2.34%) at the end of the third study year, using a coefficient of variation 0.25. Although available formulas for calculating sample size for cluster randomized trials can be derived by assuming an exchangeable correlation structure within clusters, we show that deviations from this assumption do not generally affect the validity of such formulas.

Limitations

We construct sexual networks based on data from Likoma Island, Malawi and base disease progression on longitudinal estimates from an incidence cohort in Botswana and in Durban as well as a household survey in Mochudi, Botswana. Network data from Botswana and larger sample sizes to estimate rates of disease progression would be useful in assessing the robustness of our model results.

Conclusions

Epidemic modeling plays a critical role in planning and evaluating interventions for prevention. Simulation studies allow us to take into consideration available information on sexual network characteristics, such as mixing within and between communities as well as coverage levels for different prevention modalities in the combination prevention package.

Background

Individual-level HIV prevention approaches, including antiretroviral treatment as prevention, male circumcision, pre-exposure prophylaxis (in some populations) and preventing mother-to-child transmission, have shown efficacy. Efforts are underway to investigate whether combining them can achieve community-level control of HIV infection [1].

HIV incidence depends on subject-level factors, like risk behavior, and community-level factors, like sexual network characteristics. To reduce the need for treatment, a modified treatment as prevention approach that targets only high viral load carriers is part of a combination prevention strategy that is under study in a cluster randomized trial in Botswana. About 25% of new HIV-1 subtype C infections in southern Africa (where C is most prevalent) maintain high viral load levels for at least 1–2 years and have faster cluster of differentiation 4 (CD4) cell count decline [2,3]. Identifying and treating this subset can both delay onset of acquired immunodeficiency syndrome (AIDS) and reduce HIV transmissions [4].

Cluster randomized trials investigate both direct and indirect effects of prevention interventions on infectious diseases [5,6]; design and sample size calculation must take into account possible correlation of outcomes within randomized units. Sample size formula make use of either intraclass correlation (ρ) or coefficient of variation (k) for this purpose [7,8,9]. Simulation studies to estimate power have made use of a generalized linear mixed model framework as the data generating model [10].

To address the well-known difficulties inherent in estimating k and ρ [8,11,12], Hayes and Bennett [7] recommend examining a range of plausible values of k. Spiegelhalter [13] proposes a Bayesian method to incorporate the use of prior opinion. Shih [14] suggests an internal pilot study when feasible. Campbell et al. [15] review methods for dealing with the uncertainty of ρ [16,17] in the planning stage.

In HIV prevention studies, sample size depends on the magnitude of intervention effect as well as the HIV incidence in the control group, inaccurate estimates of which threaten power. The Mema Kwa Vijana trial of HIV prevention in Tanzania [18] provides an example of a negative study with lower than anticipated power. An additional threat arises from the attenuating effect of sexual relations formed between individuals who reside in communities randomized to different conditions. Hayes et al. [5] discuss a strategy to minimize such contamination by using large, geographically defined clusters as randomization units and individuals centrally located within each cluster as evaluation cohorts.

This paper describes sample size considerations for cluster randomized trials of combination HIV prevention, motivated by the design of a study in Botswana. We introduce a new agent-based simulation model to simulate the impact of combination prevention strategy and the coefficient of variation, taking into account different levels of the contamination effect. We also investigate how correlation structure within a community affects k. The sample size formula we use can be derived from random effects models in which cluster-level effects are assumed to be independent across clusters, as are individual outcomes within clusters. We discuss the impact of deviations from the exchangeable-correlation assumption, which is likely to be violated for the outcome of HIV infection; correlation between partners would be expected to be higher than that between people who are distant in a sexual network but reside within a community.

Methods

Study design overview

The Botswana study investigates whether implementation of a combination of prevention interventions reduces HIV incidence. Villages in Botswana will be randomized into one of the two arms:

1. “standard of care” with antiretroviral therapy for HIV-infected individuals with CD4<350 cells/mm³ or AIDS;

2. antiretroviral therapy for the subjects above and for those with high viral load (>10,000 copies/ml), enhanced HIV testing and counseling, prevention of mother to child transmission, enhanced linkage of testing to care, and male circumcision.

HIV incidence will be estimated from a cohort identified through a random sample of 20% of households in each community that includes consenting eligible HIV-negative household members who are citizens (or their spouses) between ages 16 to 64 and are able to provide informed consent. Incidence cohort subjects are tested annually for HIV. Ease of logistics is the reason for sampling of households rather than individuals. The choice of a 20% sample represents a trade-off between adequacy of power and restriction of the attenuating effect of home-based testing in standard of care communities. To improve efficiency, the Botswana Study is qualitatively matched on population size, nature of health facilities, age structure, and geographic location; there is no available information matching on predicted incidence, which might be ideal.

Sample size determination

Sample size was calculated from a formula developed for matched cluster randomized trials [19]:

$$c=2+{(z_{\alpha /2}+z_{\beta })}^2\frac{{\pi }_0(1-{\pi }_0)/m+{\pi }_1(1-{\pi }_1)/m+k_m^2({\pi }_0^2+{\pi }_1^2)}{{({\pi }_0-{\pi }_1)}^2},$$

where c is the number of clusters per treatment arm, π₀ and π₁ are the true proportions of individuals who reach endpoint in the two arms; m is the number of sampled individuals within each cluster, and z_α/2 and z_β are the usual upper tail normal probabilities. k_m is the coefficient of variation in true proportions between clusters within matched pairs in the absence of intervention, and is defined as the standard deviation of the two proportions of clusters within matched pairs divided by their mean.

To predict cumulative incidence over the study period in communities, we used an agent-based epidemic model - a simulation of the actions and interactions of autonomous agents to assess their effects on an entire system - to simulate the HIV spread on collections of generated sexual networks. Parameter values in the model (see Table 1) were set based on published results as well as information from three sources: (1) the Mochudi study, a pilot study to evaluate the uptake of an HIV prevention program for the northeast sector of Mochudi, a village in Botswana with a population of around 45,000 [20]; (2) the Botswana/Durban cohort, a cohort of newly infected individuals combined from two southern African cohorts: the HIV pathogenesis Programme Acute Infection Study in Durban, KwaZulu-Natal, South Africa [21] and the Tshedimoso Study in Gaborone, Botswana [3,22,23]; and (3) the Likoma Island sexual network, a cross-sectional sociocentric survey of sexual partnerships aiming to investigate the population-level structure of sexual networks connecting the young adult population of several villages on Likoma Island, Malawi [24].

Table 1.

Model input parameters to estimate impact of combination prevention package scale-up in intervention communities versus standard of care communities over 3 years

Parameters common to both communities:
Parameter	Value
Duration of Partnerships	See Figure 2
Degree Distribution	Negative Binomial (r = 5, p = .7, cutoff = 7)
Probability of Transmission per 100 person-years
Viral Load < 400 copies/ml	1
Viral Load 400 – 3499 copies/ml	4.8
Viral Load 3500 – 9999 copies/ml	12
Viral Load 10, 000 – 49, 999 copies/ml	14
Viral Load 50000+ copies/ml	23
HIV prevalence	24.8%
Percent on treatment at time 0 among those eligible (CD4 < 350 cells/mm3)	60.9%
Reduction in transmission risk from knowledge of serostatus	30%
Duration of high viral load after infection	Estimates from the Botswana/Durban cohort
Rate of CD4 decline	Estimates from the Botswana/Durban cohort
Reduction in acquisition risk from circumcision	60%
Reduction in trans. risk for condoms	85%
Percent of individuals using condoms	40%

Parameters differ by treatment arm:
	Standard of Care Arm			Intervention Arm
	HTC1	MC2	Linkage to Care	HTC1	MC2	Linkage to Care
Baseline	37%3	12.7%3	80%	37%	12.7%3	80%
End of Year1	37%	31.4%4	80%	81%	46.4%	90%
End of Year2	45%	50.0%4	80%	90%5	80%6	90%
End of Year3	52%	60.0%4	80%	90%5	80%6	90%

¹HIV testing and counseling.

²Male circumcision.

³The Botswana HIV/AIDS impact survey III results, 2008.

⁴Male circumcision campaigns in standard of care communities will be ongoing, and may reach 60% coverage by the end of year 3 post randomization, if Ministry of Health targets are met.

⁵Assume that the project aims to increase HIV testing and counseling coverage to ≥90% in intervention communities by the end of the second study year and maintain this thereafter.

⁶Assume that the project aims to reach 80% male circumcision coverage in intervention communities by the end of the second study year and maintain this thereafter.

Generation of sexual networks

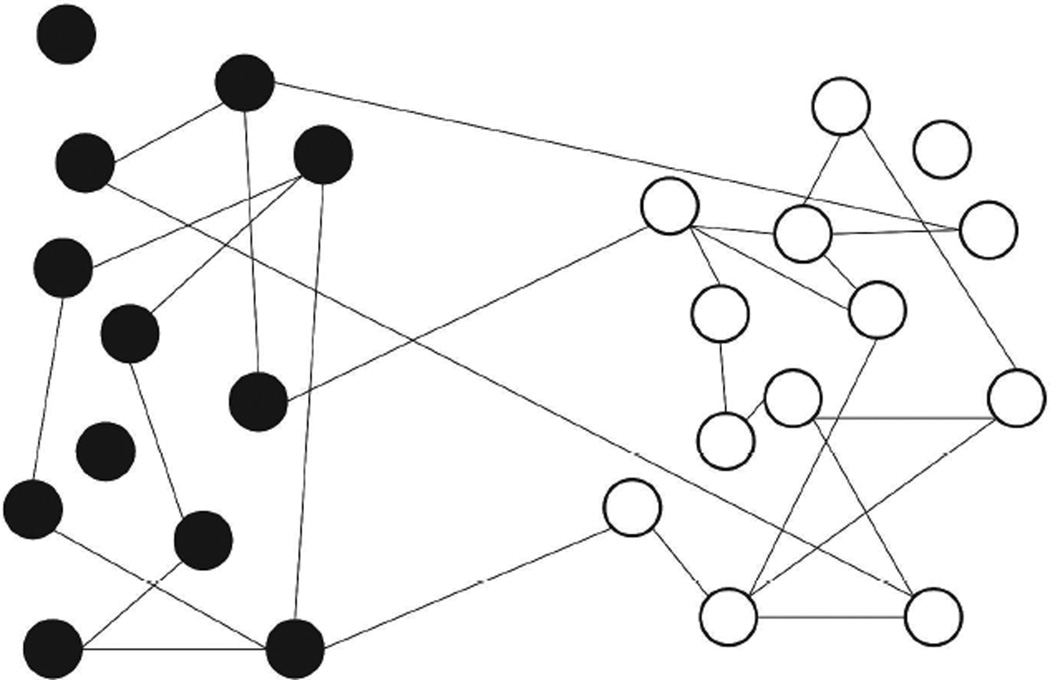
In our models, the evolution of sexual relationships are represented as a dynamic network, in which each node represents an individual (male or female), and each edge represents a sexual relationship between nodes. The networks are bipartite and only represent relation-ships between opposite genders, reflecting the fact that in Botswana heterosexual contact is believed to be the principle mode of transmission [25] and homosexual contact is hard to document. Each network represents all of the sexual relationships that occur in sets of matched pairs of communities during the study. A schematic illustration of a static network of 2 communities is provided in Figure 1.

Figure 1.

A schematic illustration of a static network of 2 communities. Solid circles and open circles represent individuals in different communities. Within each community, the location of circles does not represent their geographical locations.

In a sexual contact network, the number of edges adjacent to a particular node is called its degree, and the degree distribution can be obtained by the collection of nodal degrees [26]. We construct degree distributions using a negative binomial distribution [27,28] based on parameters (r=5, p=0.7, cutoff=7) estimated from the reported number of sexual partners in four years from Likoma Island using a likehood approach.

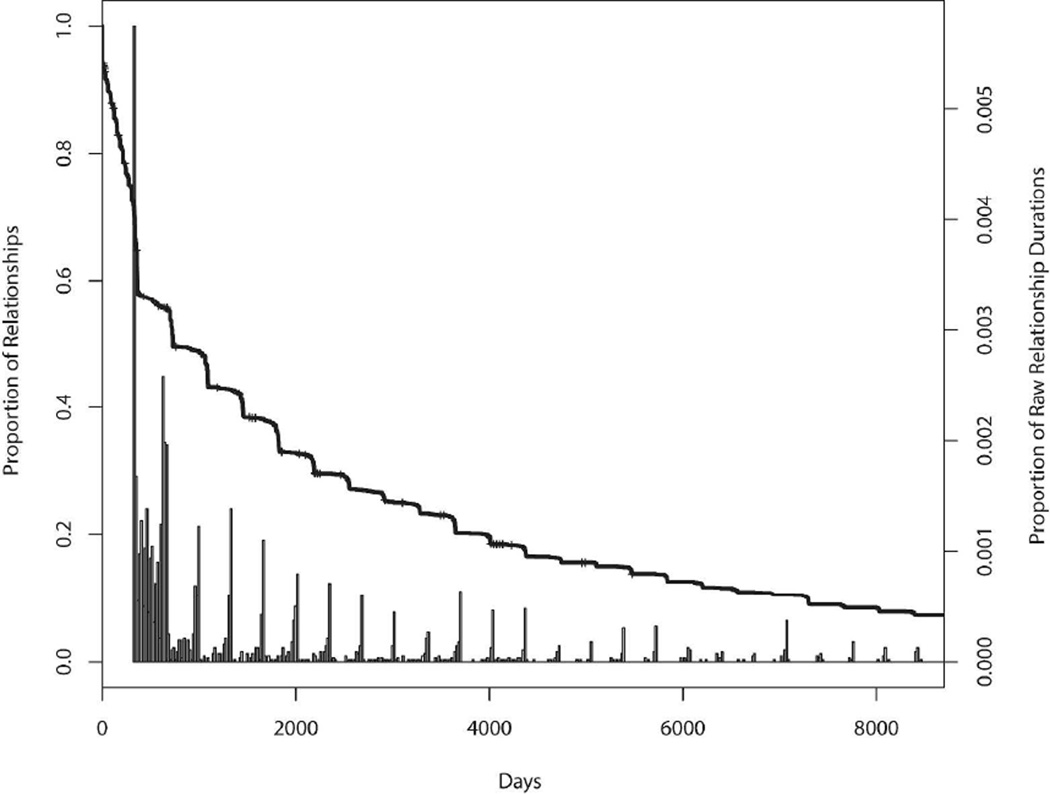
Using the methods proposed in Goyal et al. [29] that permit incorporation of user-specified uncertainty associated with particular network properties, we generate networks that are consistent with both a prescribed degree sequence and the target distribution for mixing between a pair of communities. A Metropolis-Hastings algorithm provides the basis for generating a collection of networks that satisfy the probability distribution assigned to the proportion of mixing across communities. The procedure constrains the degree distribution by proposing only networks with the prescribed degree distribution and the accept-reject probability ensures that the proportion of mixing across communities is consistent with the target probability distribution specified by the investigator. The networks are generated assuming that the probability of forming a partnership does not depend on the total number of partnerships of the two individuals or other personal characteristics. Relationship durations, d, are drawn from a survival distribution estimated from self-reported relationship start and end dates from the Mochudi study. A start date is drawn from a uniform distribution on the interval from start of study minus d to end of study; this ensures that the relationship is present during the study period and avoids time trends in the number of relationships. A histogram of the partnership durations and its corresponding Kaplan-Meier estimates are given in Figure 2.

Figure 2.

Histogram of relationship durations and the corresponding Kaplan-Meier estimates in Mochudi.

Simulation of the disease epidemic

In addition to data from the Mochudi study and the Botswana/Durban cohort, our model takes into account community characteristics including population size, varying coverage levels for different prevention modalities, as well as individual characteristics including transmission risk, disease progression, condom use, linkage to care, and circumcision status.

At time 0, the start of the simulation, we set the initial condition for each community. Each eligible individual is assigned an initial HIV infection status based on the current prevalence in Botswana, estimated to be 24.8%, and independently of partnership characteristics or position in the network. Each infected individual is assigned to a viral load category (<400, 400–3,499, 3,500–9,999, 10,000–49,999, or 50,000+ copies/ml) as well as an initial CD4 count based on estimates of their distributions from the household survey in Mochudi. For CD4 counts below threshold for treatment, subjects are modeled as receiving antiretroviral therapy according to estimates from Mochudi. Background antiretroviral therapy coverage for CD4<350 cells/mm³ is set at 60.9% at the start based on a recent survey of the Mochudi district in 2011. The percentage of condom use is set as 40% and male circumcision rate at the start, at 12.7%, the estimated rate for Botswana [30]. The probability of transmitting to a partner is based on the infected individual’s viral load category, awareness of infection status, circumcision status, and treatment status, each of which is subject to change over time. For example, as disease progresses, a subject’s CD4 count may decrease to levels below threshold for treatment guidelines and therefore make the subject eligible for treatment. Disease progression is assumed to follow estimates based on the Botswana/Durban cohort and HIV is only transmitted to partners when their partnership is active. Impact of viral load category on transmission risk is based on results reported in Quinn et al. [31]; sensitivity analyses are performed using rates reported in Attia et al. [32] and Lingappa et al. [33]. Reductions in transmission risks associated with knowing infection status and with condom use are set as 30% and 85% and assumed to be independent. Reduction in HIV acquisition risks for circumcision is set at 60%. We randomly pick 20% of the population in each community to form the incidence cohort. Subjects in the incidence cohort are tested annually for HIV infection, and subjects outside of this cohort are tested with probabilities set to be the specified coverage levels for testing. The rates for male circumcision, HIV testing and counseling and linkage to care (Table 1) are chosen to be the targeted levels for the intervention communities and the current and anticipated levels for the standard of care communities over the study period. These coverage levels are allowed to vary over time. Therefore, the model allows assessment of the impact of a slower-than-expected intervention roll-out. In the standard of care communities, subjects become eligible for treatment based on national treatment guidelines; in the intervention communities subjects identified as high viral load carriers (>10,000 copies/ml) are also eligible for treatment.

Effect of within-cluster correlation structure on coefficient of variation

Although the sample size formula we used can be derived from models assuming an exchangeable correlation structure within clusters, we find that deviations from this assumption do not affect the validity of the sample size formula. When this assumption is violated, the intraclass correlation ρ does not represent correlation between any two subjects in the same cluster, but instead represents the average correlation of observations from the same cluster. Even with arbitrary variance-covariance structure within cluster, the increase in variance resulting from cluster sampling, commonly measured by the design effect [34], can be expressed by a function of ρ and the number of subjects within cluster. The parameter k, which provides equivalent information regarding variance inflation as the intraclass correlation, captures the heterogeneity in outcomes across clusters resulting from the correlations among subjects from the same cluster. To illustrate (see supplementary materials), we consider the setting where we have c clusters and sample m subjects within each cluster. The variance-covariance matrix for the m individuals within each cluster conditional on cluster-level summary is arbitrary. We derive the formulas for ρ, k and the design effect and show that to estimate these quantities, it is sufficient to use summary measures from each cluster.

When departure from exchangeable correlation structure is expected, it is important that the studies used to estimate k employ the same sampling strategy as will the proposed study. Consider the case where outcomes of individuals within the same households are more correlated than those of individuals from different households within the same community. Assume that the sampling strategy is such that within each of the c clusters, we randomly sample a households and b_ij subjects within each household. We assume that $b_{ij}^{\prime }s$ are the same across different clusters and suppress i in the subsequent development.

The data generating process for a continuous outcome Y_ijk can be expressed as:

$$Y_{ijk}=\mu +{\alpha }_i+{\gamma }_j+{\epsilon }_{ijk},$$

where i = 1, …, c represents clusters, j = 1, …, a represents households, and k = 1, …, b_j represents subjects. We assume that ${\alpha }_i~N(0,{\sigma }_{BC}^2),{\gamma }_j~N(0,{\sigma }_{BH}^2),{\epsilon }_{ijk}~N(0,{\sigma }_{WH}^2)$. Although the subsequent development focuses on a continuous outcome, the results are applicable to binary outcomes by considering the corresponding model: Let the probability of successes in the ith cluster be μ_i, and ${\mu }_i~N(\mu ,{\sigma }_{BC}^2)$; let the probability of successes in the jth households be γ_ij, and ${\gamma }_{ij}|{\mu }_i~N({\mu }_i,{\sigma }_{BH}^2)$. Within the ith cluster and jth house-hold, Y_ij1, …, Y_ijbj are independently and identically distributed according to Bernoulli (γ_ij).

Under this model,

$$\mathit{\text{var}}(Y_{ijk})={\sigma }_{BC}^2+{\sigma }_{BH}^2+{\sigma }_{WH}^2,\mathit{\text{cov}}(Y_{ijk},Y_{ijk\prime })={\sigma }_{BC}^2+{\sigma }_{BH}^2,\mathit{\text{cov}}(Y_{ijk},Y_{ij\prime k\prime })={\sigma }_{BC}^2.$$

The between-cluster variance is

$${\sigma }_B^2={\sigma }_{BC}^2+\frac{{\sum }_{j=1}^a{b}_j(b_j-1)}{{\sum }_j{b}_j({\sum }_j{b}_j-1)}{\sigma }_{BH}^2.$$

If we sample one person per household, b_j = 1 for j = 1, …, a, the coefficient of variation $k_1=\frac{{\sigma }_{BC}}{\mu }$; when we sample all eligible members in each household, b_j ≥ 1,

$$k_2=\frac{\sqrt{{\sigma }_{BC}^2+{\sum }_{j=1}^a{b}_j(b_j-1){\{{\sum }_j{b}_j({\sum }_j{b}_j-1)\}}^{-1}{\sigma }_{BH}^2}}{\mu }.$$

k₁ < k₂ if any of the b_j ’s > 1. The k estimated from sampling one person per household would underestimate the k applicable to a study sampling entire households and could therefore result in insufficient power.

Results

Effect of sexual mixing between communities

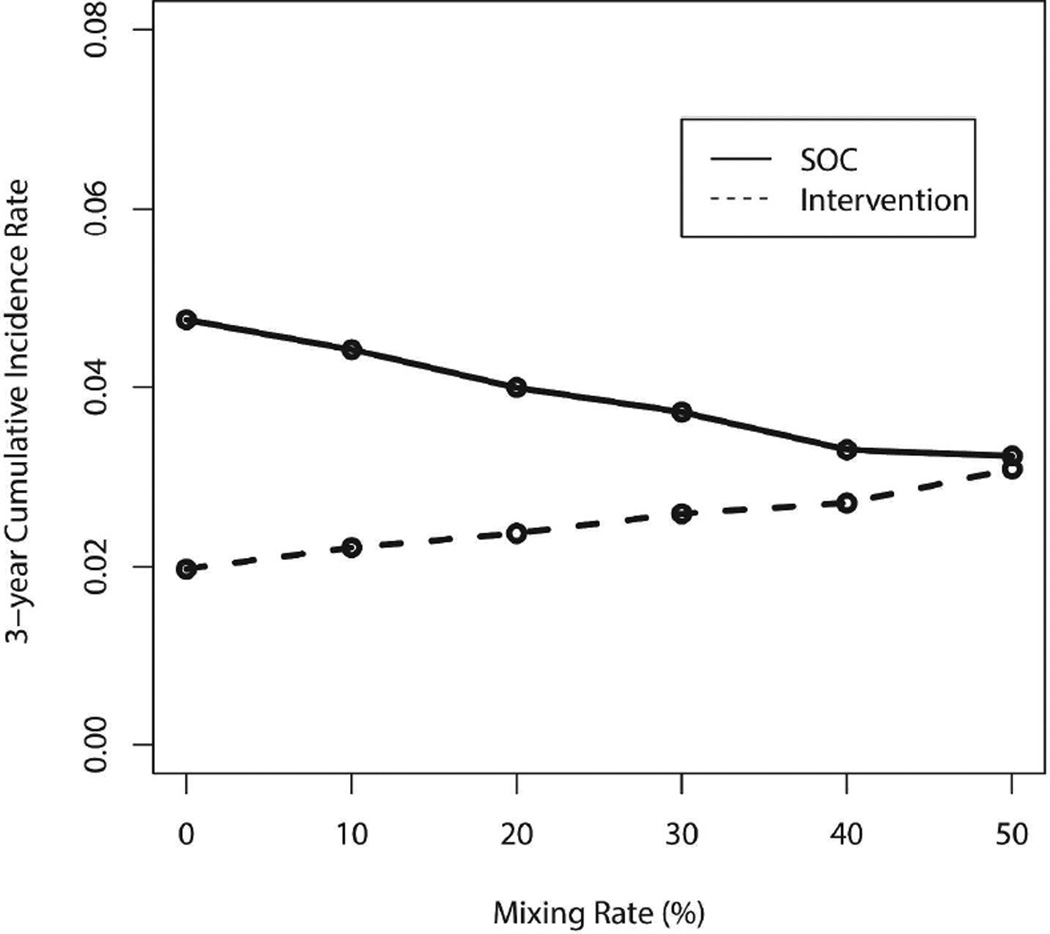
Sexual mixing between intervention and standard of care communities will tend to increase incidence in intervention and decrease it in standard of care communities. Figure 3 illustrates the impact of increasing levels of mixing while holding other conditions fixed, the effect of which is to make the cumulative incidences in two sets of communities more similar. When the mixing level reaches 50%, implying that subjects are equally likely to have partners within and outside of their community, the expected cumulative incidence rates become similar.

Figure 3.

Cumulative incidence of intervention and standard of care (SOC) communities over the 3-year period with varying levels of mixing, based on input parameters listed in Table 1 and results from 1000 pairs of communities.

Projected cumulative HIV incidence in standard of care versus intervention communities

Simulation of the impact of the combination prevention is based on input parameters listed in Table 1. Self-reported data from the Mochudi study suggest that approximately 30% of partnerships were formed outside of that community. Mixing between communities randomized to the same intervention or between standard of care communities and those not in the study does not attenuate intervention effects. Furthermore, many Mochudi residents work in the nearby capital city Gaborone, the residence of a considerable number of outside partners. By contrast most villages in the Botswana study are relatively far from major urban centers. Therefore for our setting, we choose a lower level of mixing, 20%, with standard error 2.5%. These choices imply that about 95% of sampled values will be between 15% to 25%. Table 2 below presents the projected cumulative HIV incidences in standard of care and intervention communities over 3 years of follow-up.

Table 2.

Projected cumulative HIV incidence in standard of care versus intervention communities over 3 years of study follow-up, based on results from 1500 pairs of communities.

	Standard of Care	Intervention
	Cumulative Incidence	Cumulative Incidence	% Reduction
End of Year1	1.74%	1.42%	18.4%
End of Year2	2.98%	1.99%	33.2%
End of Year3	3.93%	2.34%	40.5%

Projected coefficient of variation and study power

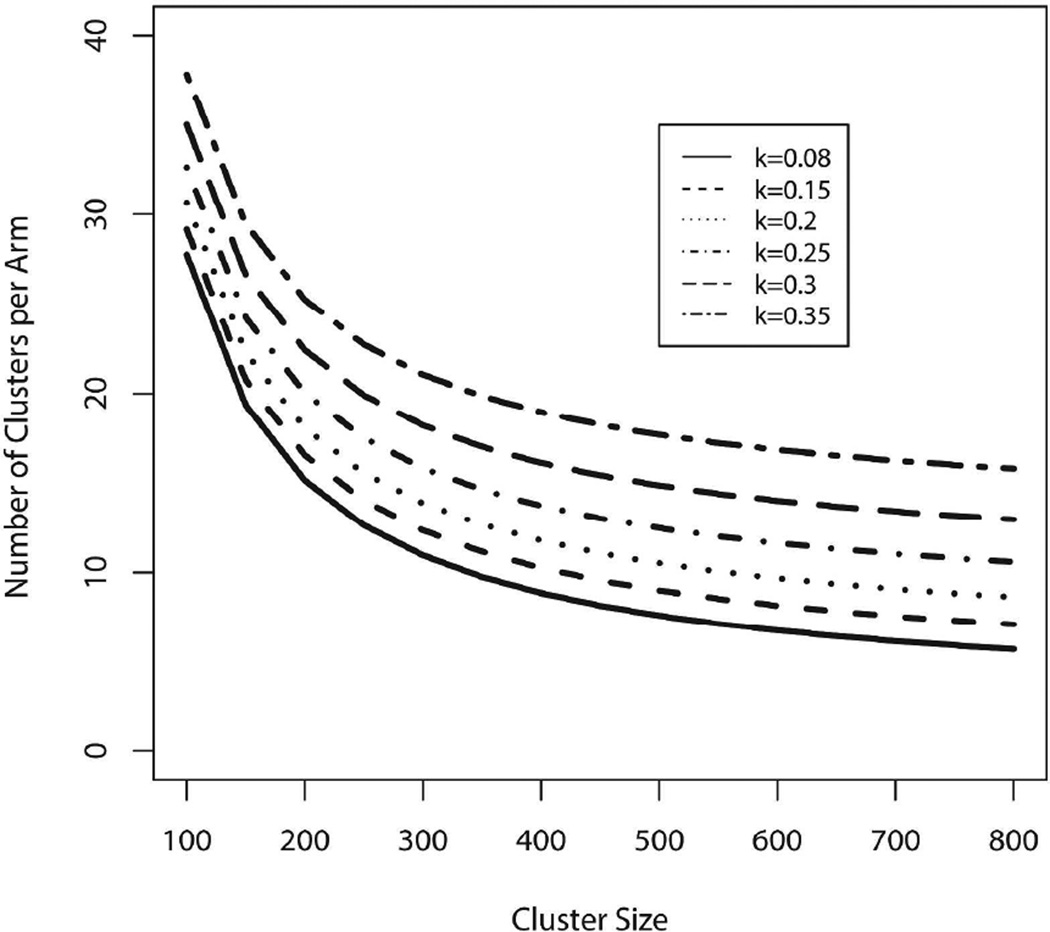
To obtain a simulated value of k relevant for a matched-pair design, we assign both communities to standard of care, calculate a coefficient of variation for each pair, and then take the average across many pairs, in our case across 1500 pairs, yielding a value of 0.08. All clusters are assumed to have the same population sizes, initial conditions, and rates of disease progression for infected subjects. These actually vary over communities, and although matched pairs are intended to be quite similar in conditions, 0.08 serves as a lower bound. To reflect possible heterogeneity in matched communities, we consider a range of values of k from 0.08 to 0.35. Figure 4 displays the number of clusters and cluster sizes needed to achieve >90% power to detect the projected difference in 3-year cumulative incidences in standard of care and intervention communities. Note that mixing does not affect simulated values of k because both communities within a pair are assigned to standard of care.

Figure 4.

Number of clusters per arm versus cluster size needed to ensure >90% power to detect anticipated differences in 3-year cumulative HIV incidence between standard of care (3.93%) and intervention arms (2.34%), for varying coefficient of variation k.

Fifteen clusters per arm and 500 incidence cohort members per community yields 99% power to detect the anticipated difference in model-projected cumulative HIV incidence between standard of care and intervention communities (3.93% vs. 2.34%; see Table 2) by the end of the third study year, for k = 0.08 and 84% power for k = 0.35.

Sensitivity analyses

We perform sensitivity analyses for scenarios associated with varying model input parameters that differ between standard of care and intervention communities, such as rates of male circumcision, HIV testing and counseling, and/or linkage to care. Table 3 presents model input parameters, resulting projected incidence rates and corresponding power for selected settings. Settings 1–3 correspond to settings where only one set of these three parameters is changed and setting 4 corresponds to the setting where all three are changed to the values listed in this table. These settings are chosen to be lower than the values in Table 1 to reflect the possibility that the targeted coverage levels may not be reached. The difference in these values between standard of care and intervention communities is in general smaller to assess the associated power loss. As the coverage levels for male circumcision, HIV testing and counseling, and/or linkage to care decrease, the incidence rates increase as expected. Nevertheless, the planned sample size still achieves >80% power for all the settings considered here for a k as large as 0.3.

Table 3.

Model input parameters, projected 3-year cumulative incidences and power associated with selected settings of sensitivity analyses, based on results from 1500 pairs of communities.

	Setting 1		Setting 2		Setting 3		Setting 4
	MC1		HTC2		Linkage to Care		Varying all three
	SOC3	Intervention	SOC3	Intervention	SOC3	Intervention	SOC3	Intervention
Baseline	12.7%	12.7%	37%	37%	60%	70%	MC1, HTC2, and Linkage to Care set to values listed in settings 1–3
End of Year1	31.4%	46.4%	37%	70%	60%	70%
End of Year2	31.4%	46.4%	37%	70%	60%	70%
End of Year3	31.4%	46.4%	37%	70%	60%	70%
3-Year
Cumulative Incidence	4.07%	2.42%	4.06%	2.59%	3.89%	2.34%	4.28%	2.65%
Power
k=0.3	91%		82%		89%		87%

¹Male circumcision.

²HIV testing and counseling.

³Standard of Care.

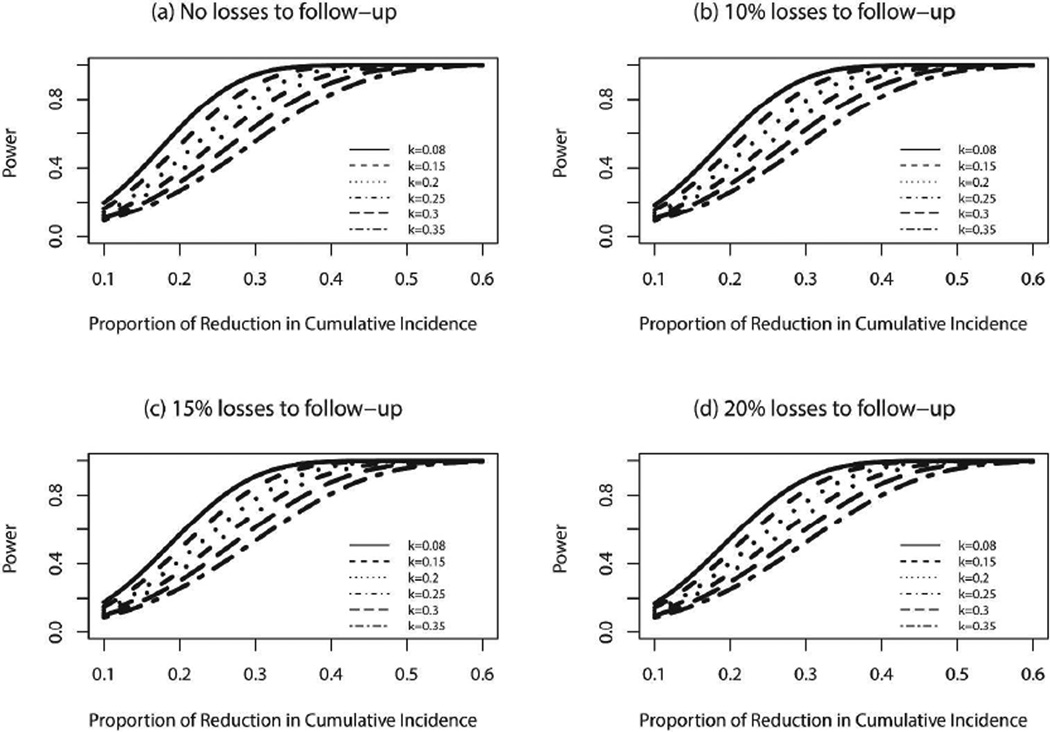
Additional sensitivity analyses for scenarios associated with lower than projected treatment effects and varying rates of losses to follow-up (see Figure 5) show that for the planned sample size and k of 0.25 the study has >80% power to detect a reduction of 34% in the cumulative incidence even with 20% loss to follow-up.

Figure 5.

Power to detect varying potential reductions of intervention effect in 3-year cumulative HIV incidence with varying rates of losses to follow-up.

Discussion

Mathematical modeling plays a critical role in planning and evaluating treatment for prevention [35] but requires investigation of underlying assumptions and impact of different choices of input parameters and limitations [36]. We construct our sexual network based on data from Likoma Island (no such data exist in Botswana), and base disease progression for incident cases and prevalent cases on longitudinal estimates from the fairly limited Botswana/Durban incidence cohort (n=77) and the Mochudi study. The similarity of our model estimates for the annual and cumulative incidence rates of the standard of care communities to the projected estimates from the Joint United Nations Programme on HIV/AIDS Spectrum model (http://www.unaids.org/en/dataanalysis/datatools/spectrumepp2013/) provides reassurance about our results. Extensive analyses of sensitivity to lower-than-projected treatment effects and varying rates of losses to follow-up (Figure 5) demonstrate that, for the planned sample size and a k of 0.25, with a 20% losses to follow-up rate, the study has >80% power to detect a reduction of 34% in the cumulative incidence in the intervention arm compared to the standard of care arm (3.93%).

The data on relationship duration exhibit “heaping”, i.e., grouping around certain values (e.g. integers) because subjects may round their responses. We know of no systematic tendency to round up or down responses, but even if it exists, we expect no substantial effect of heaping because the transmission probability per day is small. Patterns of sexual behavior and networking vary across populations. Because sexual network structure information for the communities under study are not available, we allow for considerably greater than observed variation in network structures by sampling degree distribution from a negative binomial distribution whose parameters were estimated from Likoma Island network data.

Our model did not incorporate different types of sexual relationships, e.g., regular and casual, with different frequencies of sex and probability of condom usage; the assumption that variation in these factors does not greatly impact on outcomes reflects limited available information. The impact of the intervention could be affected by differential rates of treatment uptake for people engaged in various types of relationships. The model also does not specifically target concurrency metrics, about which little relevant data are available. Some mathematical models imply an important role for concurrency, but correlation of concurrency and incidence was not observed in rural South Africa [37].

Although our simulation study assigns initial infection status randomly among the population, correlation may exist between HIV status and network properties. Further work is necessary to properly account for this potential correlation. Data currently available from Botswana are ego-centric, obviating the possibility of estimating the correlation. Using only partnerships residing within the same household may produce biased estimates as multiple partnerships are common in Botswana and many partners are not co-habiting. Ego-centric data also limit our ability to estimate parameters associated with mixing by activity level. Our model also assumes independence of knowledge of HIV infection status and sexual practice due to lack of available information.

Our simulation model randomly samples individuals, but the Botswana study will enroll all eligible members of randomly selected households. We expect the difference between the two sampling strategies to be small because in Botswana, many sexual partners do not live together, implying that correlation in HIV infection rates within household members may not be higher than that between households. If this does not hold, the treatment effect estimate from our model would not be affected, but the k associated with household samples would likely be greater than that for samples of individuals. The potential power loss can be assessed using the formula in the Methods section.

All HIV incident cases are modeled to arise from within the simulated pair of communities. In the Botswana study, communities outside of the trial will receive standard of care. As it is possible that there will be a greater uptake of services in the control arm compared to the communities outside of the trial, sexual contacts with communities outside of the trial may modestly increase incidence in the control arm. For the intervention communities, the effect of mixing with outside communities should be mostly captured through our model of mixing with the control communities, though the effect of this mixing could be slightly greater if incidence is higher in the outside than in the control communities. We would expect only modest effects of mixing with outside communities above and beyond the mixing across study communities randomized to different conditions. Any increase in HIV incidence in control communities will result in a larger treatment effect and greater power than projected.

The Botswana study is one of the two large HIV prevention trials commissioned by the Presidents Emergency Plan For AIDS Relief that are currently underway. The other is HPTN 071 [38], which investigates a combination of interventions including universal testing, counseling and antiretroviral therapy in Zambia and South Africa. A special feature of the Botswana study is its focus on identifying high viral carriers and treating them with antiretroviral therapy. Both studies rely on mathematical modeling to investigate the plausibility of different intervention effect sizes. These models make use of information from a wide variety of sources regarding biology and behavior information that will be updated during the course of the studies and at their completion.