Automated Assessment of the Quality of Diffusion Tensor Imaging Data Using Color Cast of Color-Encoded Fractional Anisotropy Images

Abstract

Diffusion Tensor Imaging (DTI) data often suffer from artifacts caused by motion. These artifacts are especially severe in DTI data from infants, and implementing tight quality controls is therefore imperative for DTI studies of infants. Currently, routine procedures for quality assurance of DTI data involve the slice-wise visual inspection of color-encoded, fractional anisotropy (CFA) images. Such procedures often yield inconsistent results across different datasets, across the different operators who are examining those datasets, and sometimes even across time when the same operator inspects the same dataset on two different occasions. We propose a more consistent, reliable, and effective method to evaluate the quality of CFA images automatically using their color cast, which is calculated on the distribution statistics of the 2D histogram in the color space as defined by the International Commission on Illumination (CIE) on lightness and a and b (LAB) for the color-opponent dimensions (also known as the CIELAB color space) of the images. Experimental results using DTI data acquired from neonates verified that this proposed method is rapid and accurate. The method thus provides a new tool for real-time quality assurance for DTI data.

Introduction

Diffusion Tensor Imaging (DTI) has become a useful tool for noninvasive study of tissue organization in the brain. It provides insights on various aspects of tissue organization based on the property of local anisotropic diffusion of water molecules in the living tissue. Diffusion anisotropy is modeled by estimating a diffusion tensor at each spatial location in the brain from a series of measures from Diffusion Weighted Images (DWIs). The DWIs are acquired by applying diffusion gradients along many non-collinear orientations in 3D space. Signal differences across DWIs acquired under differing diffusion gradients are assumed to derive from the diffusion of water. By fitting a diffusion tensor to the observed measurements using a linear least squares method, the principal direction of the tensor is expected to reflect the direction of local diffusion of these water molecules. Various useful diffusion anisotropy indices (DAIs), such as fractional anisotropy (FA) (Basser and Pierpaoli 1996), ellipsoidal area ratio (EAR) (Xu, Cui et al. 2009), and mean diffusivity (MD), each characterizing a different aspect of tissue organization, can subsequently be derived from the calculated tensor.

However, DWI data often suffer from artifacts. Some are caused by "physiological noise", such as cardiac pulsation, some are from "system-related artifacts", such as thermal radio frequency noise and distortions induced by eddy currents (Jones 2011), and some are from head movements. Erroneous DWI measures resulting from these artifacts introduce errors into the estimation of diffusion tensors and the indices calculated from them, thereby undermining the validity of inferences about tissue organization. Sometimes artifacts are not visually perceptible but will propagate nevertheless throughout the entire data analytic stream. Therefore, detecting and removing corrupted images and outliers are important steps in maintaining the quality of the imaging data, the validity of the findings, and the physiological inferences based on them.

Various methods have been proposed to prevent corruption of DTI data during acquisition. The use of parallel imaging to support a full k-space acquisition of data can reduce vibration artifacts (Gallichan, Scholz et al. 2010). The navigator technique is also used to detect and correct motion in DTI data (Atkinson, Porter et al. 2000, Miller and Pauly 2003, Kober, Gruetter et al. 2012). External devices have also been developed to track and correct head motion (Rohde, Barnett et al. 2004; Zaitsev, Dold et al. 2006; Qin, van Gelderen et al. 2009; Forman, Aksoy et al. 2010). These techniques may provide very precise motion information down to the micrometer scale. Landmarks, typically markers attached to the skin or bite bars, are also used to track bulk head motion, but that requires complicated setup and additional computational time. Consequently, these methods are not always practical to implement, and they do not obviate the need for quality control of the DTI data once acquired.

Post-processing techniques can help to improve data quality retrospectively, by detecting and then removing or correcting outliers in the imaging data. Ding et al (Ding, Gore et al. 2005) developed a technique of anisotropic smoothing for reducing noise in DTI data. This extended the traditional method for filtering anisotropic diffusion images by allowing isotropic smoothing within homogeneous regions and anisotropic smoothing along structure boundaries. Hasan (Hasan 2007) proposed a theoretical framework for quality control and parameter optimization in DTI. This approach is based on the analytical error propagation of the MD obtained directly from the DWI data acquired using rotationally invariant and uniformly distributed icosahedral encoding schemes. Moreover, error propagation of the cylindrical tensor model has been further extrapolated to spherical tensor cases (diffusion anisotropy close to 0) in order to analytically relate the precision error in FA to the mean diffusion-to-noise ratio. Mangin et al. (Mangin, Poupon et al. 2002) presented a method to correct distortion and robustly estimate diffusion tensors. The distortion correction relies on maximizing mutual information to estimate the three parameters of a geometric distortion model based on the basic physics of DTI data acquisition. In order to reduce outlier-related artifacts, Mangin et al. used the Geman-McLure M-estimator instead of the standard least squares method for tensor estimation. Chang et al. (Chang, Jones et al. 2005) proposed an approach for robust tensor estimation by rejecting outliers. This regression-based method iteratively reweights least-squares to identify potential outliers and subsequently excludes them during tensor estimation. Liu et al. (Liu Z. 2010) presented a full DWI preprocessing framework for automatic DWI quality control. They used the normalized correlation between successive slices and across all the diffusion gradients to screen for artifacts. Dubois et al. (Dubois, Poupon et al. 2006) proposed a method to generate a schema of diffusion gradient orientations that allow the diffusion tensor to be reconstructed from partial clinical DTI datasets. A general energy-minimization electrostatic model was also developed in which the interactions between orientations are weighted according to their temporal order during acquisition. Jiang et al. (Jiang 2009) proposed an outlier detection method for DTI by testing the consistency in the apparent diffusion coefficient (ADC). The detection criterion uses the smoothness of the fitted surface of the peanut-shaped ADC directional profile. Error-maps are then created based on this criterion and a cluster analysis is performed on the error maps. The potential outliers are excluded from subsequent tensor fitting process. Zhou et al. (Zhou, Liu et al. 2011) proposed an automated approach to artifact detection and removal for improved tensor estimation in motion-corrupted DTI datasets using a combination of local binary patterns and 2D partial least squares. Rohde et al. (Rohde, Barnett et al. 2004) proposed a comprehensive approach for correction of motion and distortion in DTI. This approach uses a mutual information-based registration technique and a spatial transformation model which contains parameters that correct for eddy current-induced image distortion as well as rigid body motion in three dimensions. Liu et al. (Liu et al. 2012) also proposed an improvement over the iterative cross-correlation algorithm (Haselgrove and Moore, 1996) for correcting eddy-current induced distortion in DWI data by pre-excluding cerebrospinal fluid (CSF) from the DWI data to maximize mutual-information between DWI and baseline imaging data. Lauzon et al. (Lauzon et al., 2012, 2013) proposed a parallel processing pipeline for quantitative quality control of MRI data using DTI as an experimental test case. Assessment of variance and bias in DTI contrasts was implemented by modern statistical methods (wild bootstrap and SIMEX). The final quality of DTI data was assessed by FA power calculation.

Despite the progress in detecting DTI data outliers or artifacts, most of these approaches emphasize only on outlier detection and robust tensor estimation, while they fail to provide a definite and quantitative measure for the quality of DTI data. For example, some of these approaches have shown that the percentage of definiteness of the tensors increased with implementation of the post-processing algorithm, but whether the tensors thus estimated were correct or not remained unclear. Therefore, the questions of how to evaluate the effectiveness of these post-processing algorithms and how to assess the quality of the estimated tensor remain open issues.. In this paper we propose an efficient and automated method for assessing the quality of DTI data. We focus primarily on the efficacy of assessing the quality of DTI data using color-encoded fractional anisotropy (CFA) images. Which we believe will form the basis for a supplemental tool to automatically evaluate the quality of DTI data in real time, during data acquisition.

Methods

Motivation

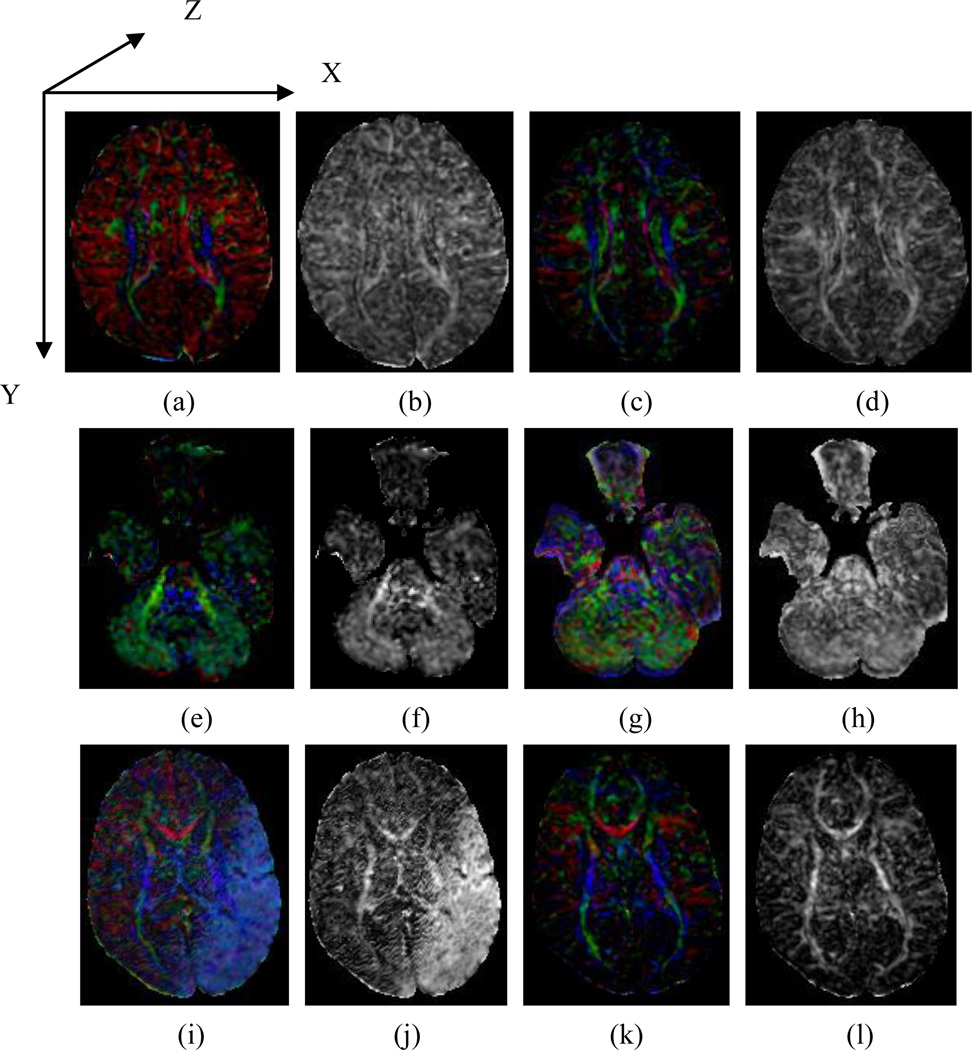
FA images provide information only on the magnitude, and not the direction, of diffusion anisotropy at each location in the brain. Without this directional information, motion-corrupted data can generate FA maps that appear nearly normal (e.g., Fig. 1b). Maps of color-encoded direction (e.g., CFA), however, retain directional information because they are constructed explicitly to encode, with color, the spatial direction of each tensor’s primary eigenvector. Our lab uses red to encode diffusion along x-axis, green along the y-axis, and blue along the z-axis, following the coordinate-system in an image volume (Fig.1a). Diffusion along a particular direction is thus shown as a mixture of the three color elements corresponding to the x, y, and z components. Therefore, assessing the color scheme in a CFA image can provide information regarding possible subject motion, because, in general, their motion produces a signal change in the relevant DWI volume along the given measuring direction of diffusion gradient (if they are not perpendicular to each other), as the signal directly reflects the diffusion of the water molecules in the tissue, which is also motion and contributes to the estimation of the tensor’s spatial orientation. The presence of a tint affecting the entire image is termed a color cast. For example, a red cast in Fig.1(a), green in Fig.1(e), and blue in Fig.1.(i) suggest the possible presence of motion. Difference in CFA images for motion-corrupted and motion-free DTI data -- i.e., a color cast -- can serve as a metric for assessing the quality of DTI data.

Fig. 1.

A comparison of motion-corrupted and normal DTI data. (a)(e)(i) are color-encoded fractional anisotropy (CFA) images of a typical, motion-corrupted DTI dataset. (b)(f)(j) are the fractional anisotropy (FA) images corresponding to (a)(e)(i), respectively. (c)(g)(k) are the CFA images of a motion-free DTI dataset from the same participant. (d), (h) and (l) are the corresponding FA images corresponding to (c), (g), and (k), respectively. The difference in the CFA images between the motion-corrupted and motion-free DTI data is a color cast, whereas the FA images of motion-corrupted and motion-free diffusion-weighted images can appear similar (Fig. 1b and d). In the figures, we mapped X-component of a direction to red, Y to green and Z to blue.

In practice, the quality of DTI data is often assessed after tensor estimation by inspecting the CFA image visually on a slice-wise basis (Liu Z. 2010) (Zhou, Liu et al. 2011), which is inherently subjective, time-consuming, and unreliable across different datasets and observers. Assuring the quality of DTI data in real time using an objective and automated approach is therefore important to prevent errors from propagating to subsequent steps of processing and data analysis. This is especially important for imaging data from populations that tend to move frequently, such as infants and neuropsychiatric patients with tics.

Detecting Color Cast in CFA images

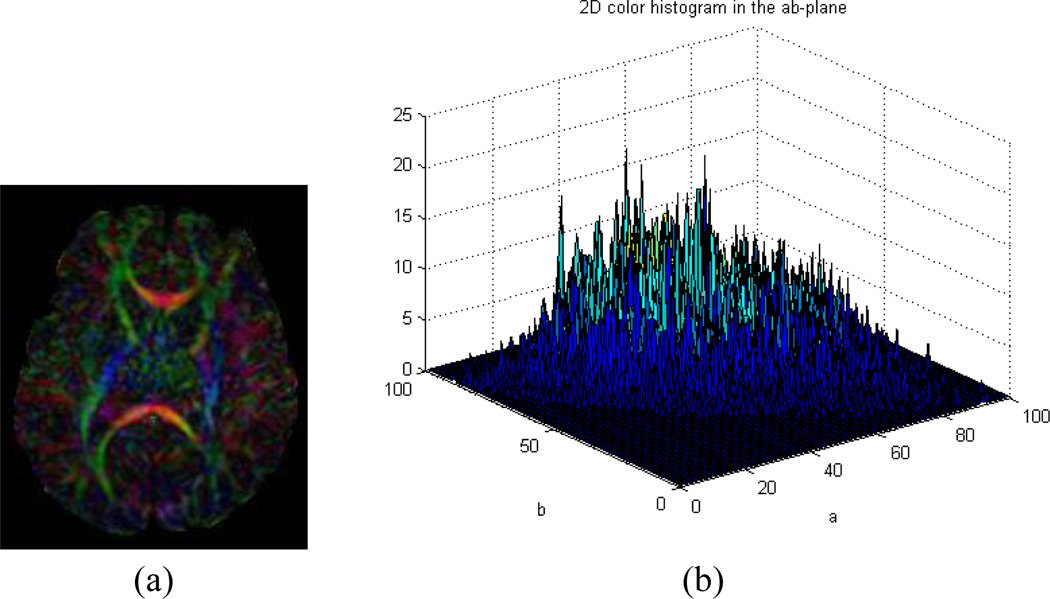
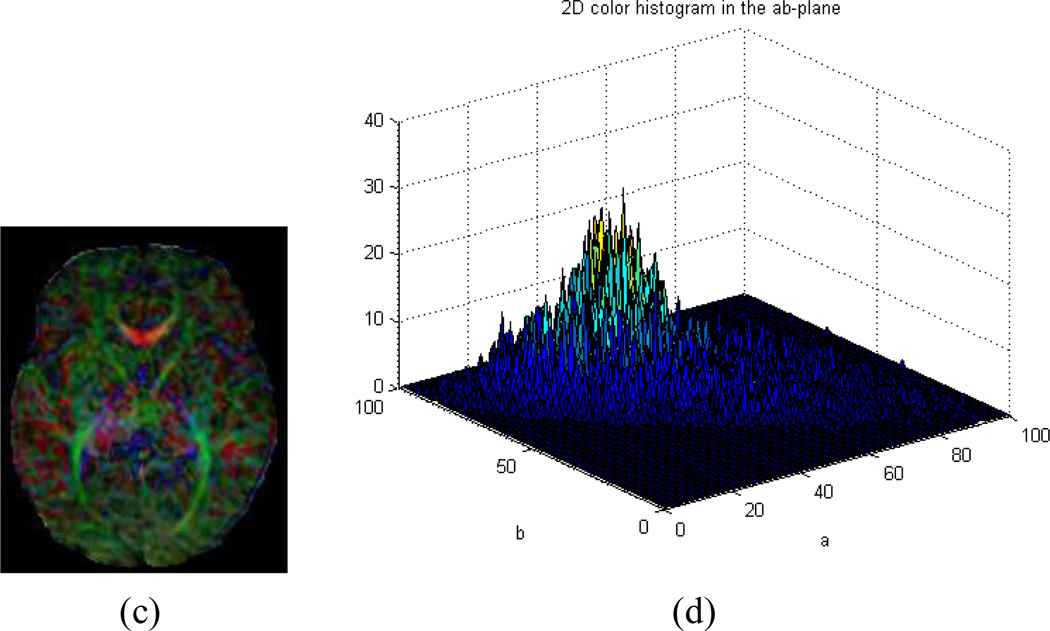
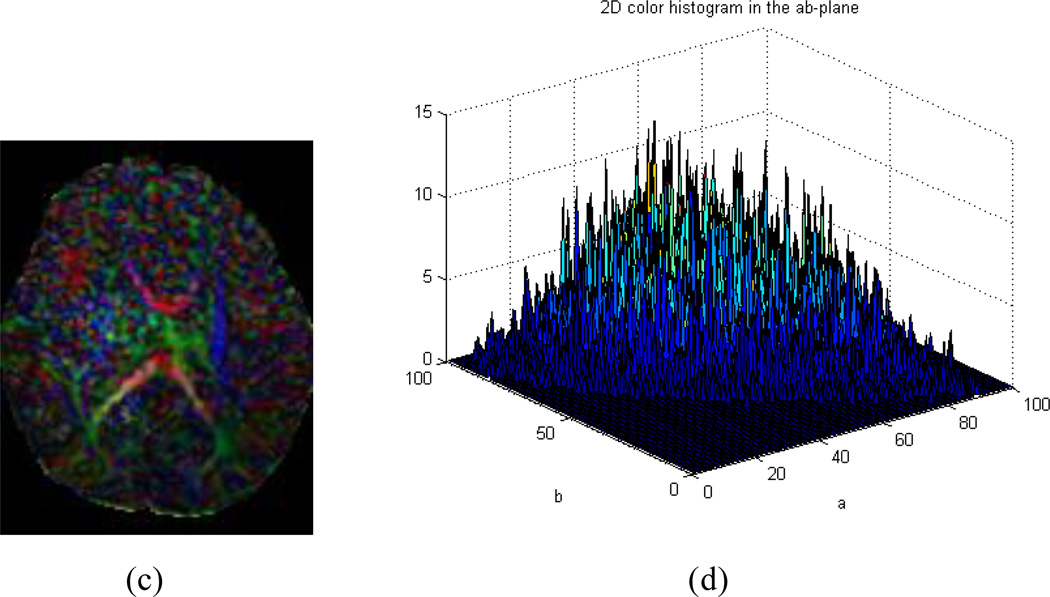
We hypothesize that if tensor estimation suffers from motion artifact in the DWI data, CFA images calculated from the estimated tensors will be color-cast. We know that the color space, as defined by the International Commission on Illumination (CIE) on lightness and a and b (LAB) for the color-opponent dimensions (also known as CIELAB color space) (Hunt 1987), is perceptually uniform and can effectively quantify color differences as seen by human eyes. We thus map the RGB values of a CFA image into CIELAB space (Finlayson 1997; Cooper 2000) and then examines a 2-D histogram formed by considering only the a and b color aspects of the image to assess image quality (Gasparini and Schettini 2004). For a motion-free CFA image, its 2D histogram generally contains clustered peaks distributed throughout the ab-plane (Fig. 2a and b), whereas the histogram for a color-cast CFA image generally contains a single narrow peak in a limited spatial region on that plane (Fig. 2c and d). The more concentrated the peaks in the 2D histogram and the farther they are from the neutral axis (the center of the ab-plane), the more intense the color cast. The motion-corrupted CFA image can therefore easily and automatically be distinguished from motion-free ones by measuring the distribution of the 2D histogram in the ab-plane.

Fig. 2.

(a)~(b) A color-encoded fractional anisotropy (CFA) image containing no color cast contains several peaks distributed throughout the 2D histogram in the ab-plane of CIELAB color space. (a) A motion-free CFA image. (b) 2D histogram of (a) in the ab-plane of CIELAB color space; (c)~(d) A motion-corrupted CFA image with a color cast showing a 2D histogram with a localized peak far from center in the ab-plane. (c) A CFA image with color cast. (d) 2D histogram of (c) in the ab-plane of CIELAB color space.

The procedures we propose for the quality assessment of CFA images are as follows. First we map the RGB space of the CFA image to CIELAB space (CIE1931):

$$\left[\begin{array}{c}\hfill X\hfill \\ \hfill Y\hfill \\ \hfill Z\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill 0.4124\hfill & \hfill 0.3576\hfill & \hfill 0.1805\hfill \\ \hfill 0.2126\hfill & \hfill 0.7152\hfill & \hfill 0.0722\hfill \\ \hfill 0.0193\hfill & \hfill 0.1192\hfill & \hfill 0.9505\hfill \end{array}\right]\left[\begin{array}{c}\hfill R\hfill \\ \hfill G\hfill \\ \hfill B\hfill \end{array}\right]$$ (1)

where Y is luminance, Z is quasi-equal to blue stimulation, and X is a mix (a linear combination) of cone response curves chosen to be non-negative. In CIE XYZ color space, the tri-stimulus values are regarded as 'derived' parameters from the long-, medium-, and short-wavelength cones for human color vision.

We then map the tri-stimulus values in CIELAB color space using the following equations (Hunt 1987), in which the CIE Standard Illuminant D65 (in short, D65) is a commonly-used standard illuminant defined by the International Commission on Illumination (CIE):

$$\left[\begin{array}{c}L\hfill \\ a\hfill \\ b\hfill \end{array}\right]=\left[\begin{array}{c}{L}^{*}\hfill \\ 500\times (f_X^{*}-f_Y^{*})\hfill \\ 200\times (f_Y^{*}-f_Z^{*})\hfill \end{array}\right]$$ (2)

where L-a-b color space is a color-opponent space with dimension L for lightness and a and b representing the color-opponent dimensions, based on nonlinearly compressed CIE XYZ color space coordinates. The other variables are calculated as follows:

$$f_X=\frac{X}{0.9505},f_Y=Y,f_Z=\frac{Z}{1.0888}{L}^{*}=\left\{\begin{array}{cc}116\times \sqrt[3]{f_Y}-16\hfill & \mathit{\text{for}}{f}_Y>0.008856\hfill \\ 903.3\times f_Y\hfill & \mathit{\text{for}}{f}_Y\le 0.008856\hfill \end{array}\right\}{f}_i^{*}=\left\{\begin{array}{cc}\sqrt[3]{f_i}\hfill & \mathit{\text{for}}{f}_i>0.008856\hfill \\ 7.787\times f_i+0.1379\hfill & \mathit{\text{for}}{f}_i\le 0.008856\hfill \end{array}\right\},i=X,Y,Z$$

Second, we calculate the distribution statistics of the 2D histogram in the ab-plane. The color distribution is modeled using the following statistical measures (Gasparini and Schettini 2004):

$${\mu }_i=\frac{\sum _{j=1}^{N_i}j\times P_i(a,b)}{\sum _{j=1}^{N_i}{P}_i(a,b)}$$ (3)

$${\sigma }_i=\sqrt{\frac{\sum _{j=1}^{N_i}{(j-{\mu }_i)}^2\times P_i(a,b)}{\sum _{j=1}^{N_i}{P}_i(a,b)}}$$ (4)

where, µ_i and σ_i are the mean values and variances of the histogram projections along the two chromatic axes a and b respectively, N_i is the length of the projection with i = a, b, and P_i (a b is the 2D histogram projection along the chromatic axes a and b.

We then use µ and ratio ω to characterize the distribution statistics of the 2D histogram, where $\mu =\sqrt{{\mu }_a^2+{\mu }_b^2},\sigma =\sqrt{{\sigma }_a^2+{\sigma }_b^2},\omega =\frac{\mu }{\sigma }$. Because µ profiles the distance from center of the 2D histogram to the neutral axis and σ characterizes the variance of the 2D histogram, the ratio of µ and σ allows us to quantify the strength of the color cast. Third, if the value of µ is greater than a specified threshold T_µ or the ratio ω is greater than the threshold T_ω - where thresholds are determined using training samples of motion-free DTI from a reference group, we will designate the CFA image as having a color cast.

Data acquisition

We scanned 20 newborn infants (average post-menstrual age (PMA) = 42.5 weeks, and standard deviation = 2 weeks at the time of scan) with written, informed consent from their parents, as part of a study on the effects of exposure to drugs of abuse on brain development. The study protocol was approved by the Institutional Review Board of the New York State Psychiatric Institute.

DTI data were acquired on a GE 3.0 Tesla MR scanner (Milwaukee, WI). We used a single-shot spin echo, echo planar imaging sequence for DWI acquisitions, with diffusion gradients applied along 11 non-collinear spatial directions at b=600 s/mm² and three baseline images at b=0 s/mm² for each infant. The thickness of each slice was 2.0 mm without gap, and the in-plane resolution was 0.74 mm. Other imaging parameters of the DWI/DTI sequence were: a minimal echo time at approximately 70 ms; repetition time = 13925 ms; field of view =19 cm × 19 cm and acquisition matrix =132×128 (machine-interpolated to 256×256 for post processing). Scan time for each excitation was 3 minutes 43 seconds and the number of excitations was 2. We visually assessed data quality to ensure that each infant had at least one motion-free series. We collected 47 series in total for the 20 infants. Our visual examination identified 27 motion-free and 20 motion-corrupted datasets out of the 47.

Preprocessing and Tensor estimation

We used the software library developed by the Oxford Centre for Functional MRI of the Brain (FMRIB, also known as FMRIB's Software Library (FSL)) (Jenkinson et al. 2012) for data-processing, including correction of eddy current distortion and removal of the scalp. We then reconstructed the diffusion tensor image using least squares fitting based on the DWI data along all gradient directions and then calculated the CFA images. We used red for encoding the X-component of the orientations (which is along left-right hemispheres in our data), green for Y (anterior-posterior), and blue for Z (inferior-superior).

Experimental Design

We randomly split each of the two types of datasets (27 motion-free and 20 motion-corrupted datasets) into two halves, one for training and the other for testing. The training set was used to obtain the two thresholds (T_µ and T_ω). For the selected motion-free series in the training set, we calculated their distances from the center of the 2D histogram (projection along the chromatic axes a and b) to the neutral axis (µ) and their ratios of the distance to the standard deviation (ω). The maximum µ and ω were set as thresholds T_µ and T_ω respectively. We thus simply used these threshold values to automatically assess the quality of CFA images in order to determine whether or not any slice in the imaging dataset contained a color cast. If µ or ω of the tested CFA image was greater than T_µ or T_ω, respectively, then the CFA image was classified as having a color cast. If at least one slice had a color cast in the assessed series, the series was tagged as motion-corrupted. We then compared this automated assessment with our gold-standard visual classification and recorded the accuracy of the automated classification. We repeated this procedure (i.e., random splits of training and test datasets) 20 times and obtained the average accuracy of our automated detection of motion-corrupted DTI datasets.

Results

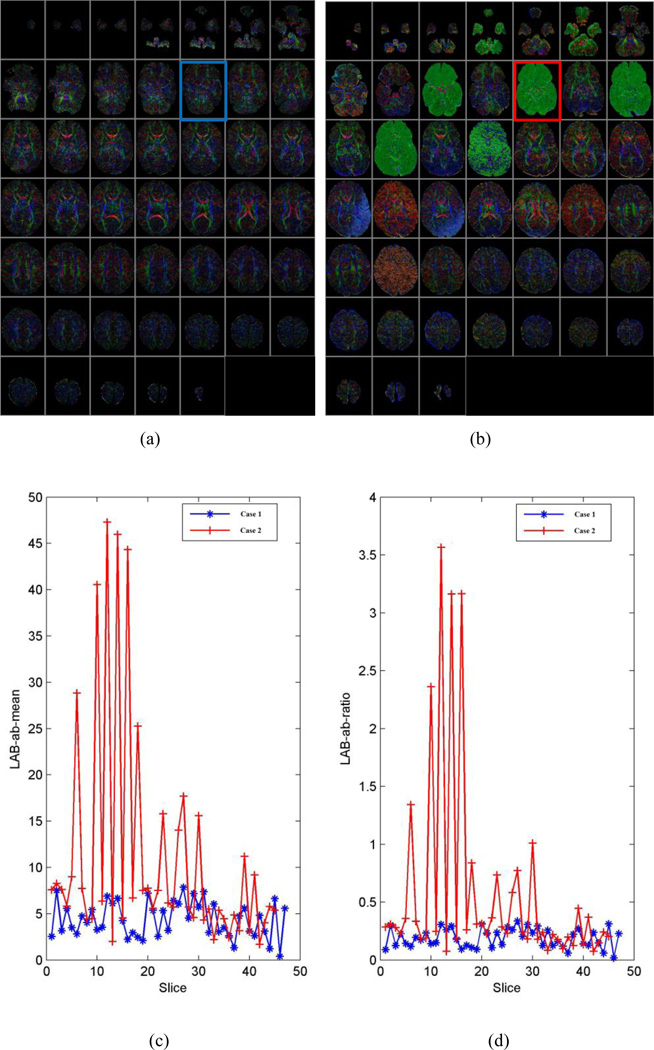
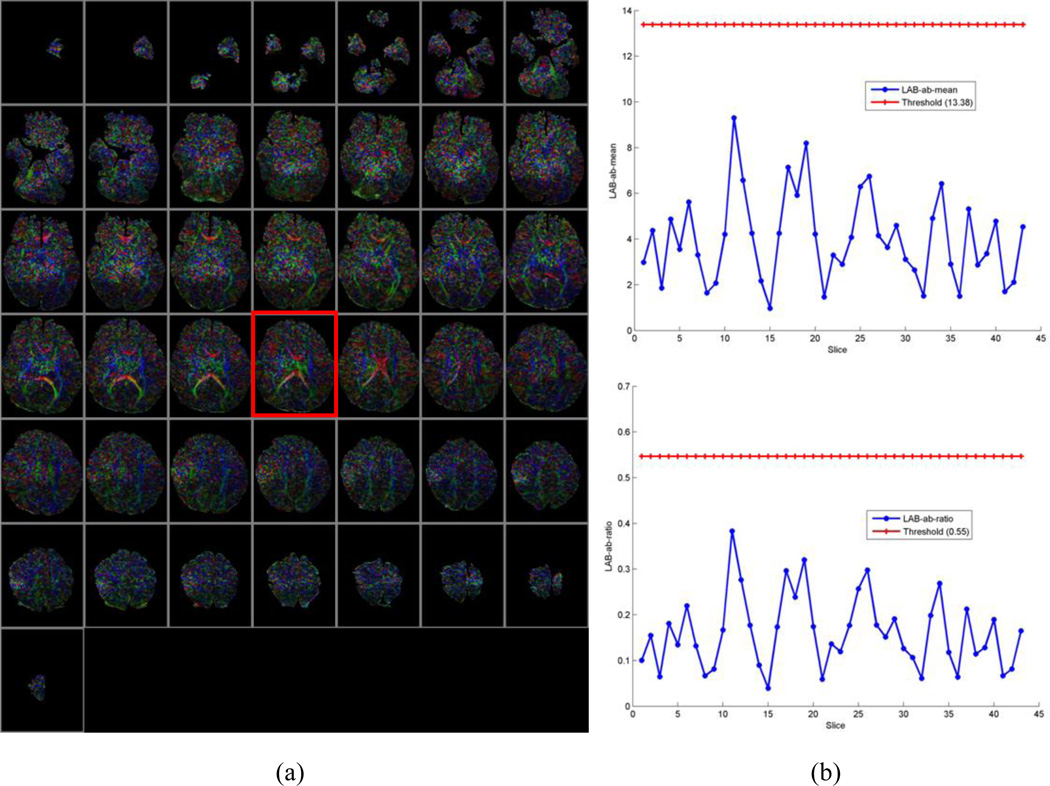
The distance from the center of the 2D histogram to the neutral axis (µ) and ratio of the distance to the standard deviation of distances (ω) were effective descriptive statistics for the 2D histogram that discriminated motion-free and motion-corrupted CFA images (Fig. 3). The higher the values of µ and ω, the worse the quality of the corresponding CFA image. Therefore, we screened CFA images with high values for µ and ω and tagged them as outliers (e.g. slice#12 in Fig. 3).

Fig. 3.

Typical DTI datasets used for training and their LAB ab-means and ratios. (a) Color-encoded fractional anisotropy (CFA) image of a motion-free series (case 1). (b) CFA image of a motion-corrupted series (case 2). (c) Distribution of distance from the center of the 2D histogram to the neutral axis (µ) for two DTI series (cases 1 and 2). (d) Distribution of the ratio (ω) of the distance to the standard deviation for the two DTI series. The higher the values of µ and ω, the worse the quality of the corresponding CFA image, such as the image highlighted in blue and red rectangles (i.e., slice#12) in figure (a) and (b).

For a typical set of training images, the distributions of µ and ω for motion-free series (Fig.4a and b) are more concentrated than those of motion-corrupted series (Fig.4.c and d). Therefore, the maximum values of µ and ω in the motion-free series are statistically smaller than those in the motion-corrupted series, and their threshold values can be determined (Fig.4. a and b). Consequently, most of the motion-corrupted series selected randomly in the training set must contain certain slices for which µ or ω are greater than the thresholds T_µ or T_ω (marked as dashed red line in Fig. 4 c and d). For the test series, many slices bear µ or ω values greater than the thresholds T_µ or T_ω -- i.e., they are motion-corrupted (Fig.5).

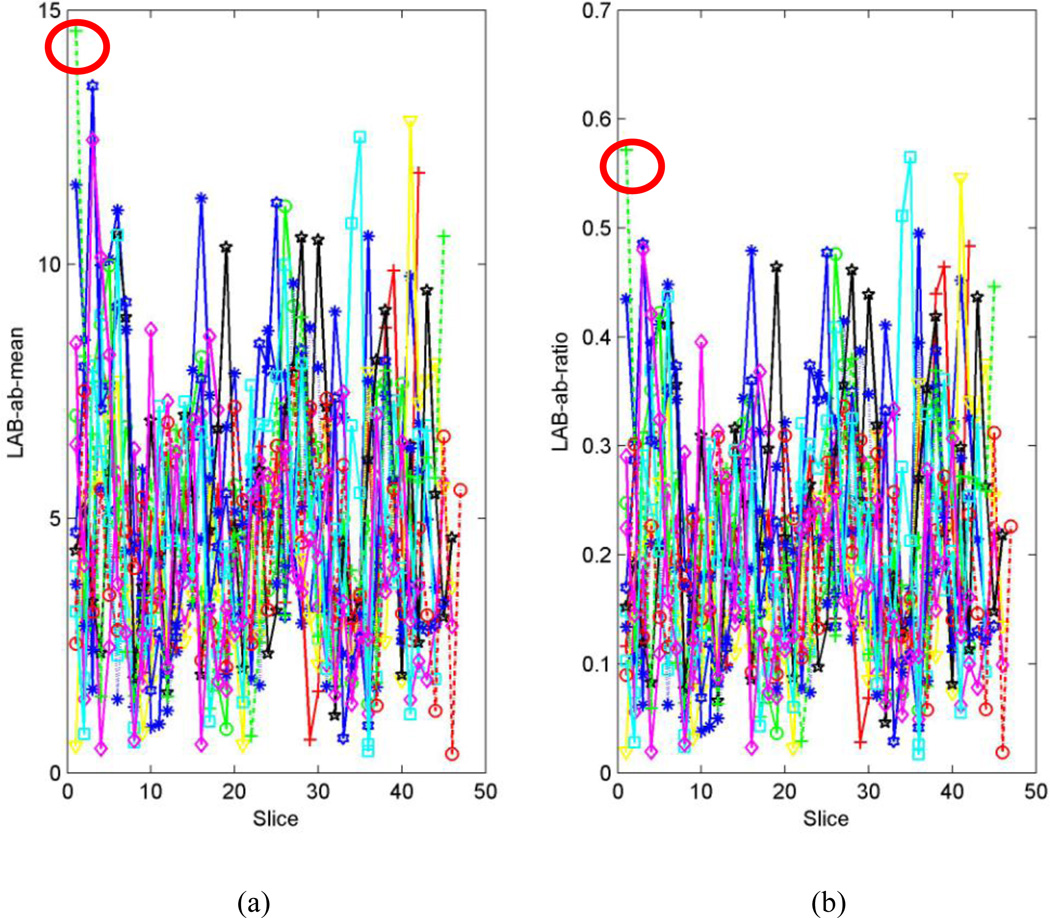
Fig. 4.

Randomly-selected series from a DTI dataset used for training. Each line represents one series. (a). Distribution of distance from the center of the 2D histogram to the neutral axis (µ) for the motion-free series in the training set. The maximum µ is 14.6 in this case (marked with a red circle). (b). Distribution of the ratio (ω) of the distance to the standard deviation for motion-free series in the training set. The maximum ω is 0.6 (marked with a red circle). (c). Distribution of distances to the neutral axis for the motion-corrupted series in the training set. The threshold value for the distance (i.e., µ =14.9) is denoted by the dashed red line. (d). Distribution of the ratio of distance to the standard deviation for the distance in the motion-corrupted series of the training set. The threshold value for the ratio (i.e., ω =0.6) is denoted by the dashed red line.

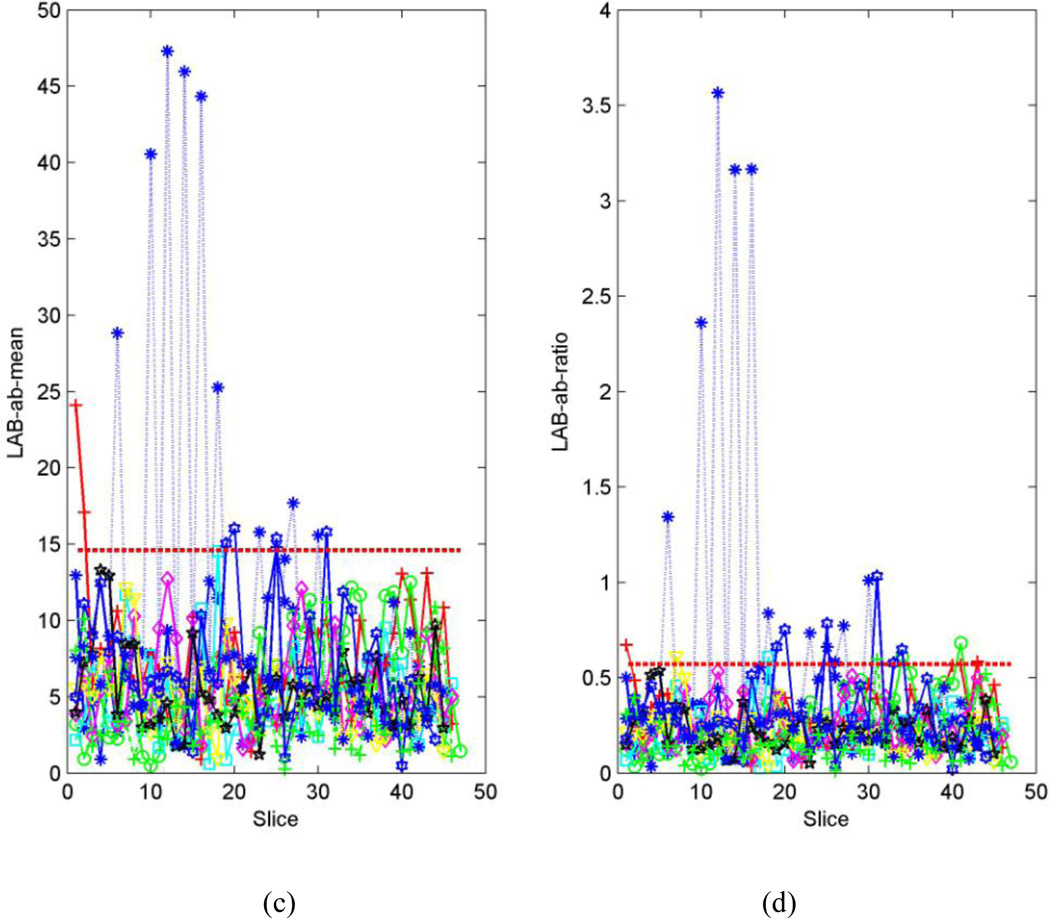
Fig. 5.

Randomly-selected series from the DTI dataset for testing. Each line represents one series. (a). Distribution of distance from center of the 2D histogram to the neutral axis (µ) to the neutral axis for the all series in the testing set. (b). Distribution of ratio (ω) of the distance to the standard deviation for the all series in the testing set. If the µ of the assessed CFA image is greater than T_µ (dashed red line) or if the ratio ω of the assessed CFA image is greater than T_ω (dashed red line), then the CFA image is classified as having a color cast.

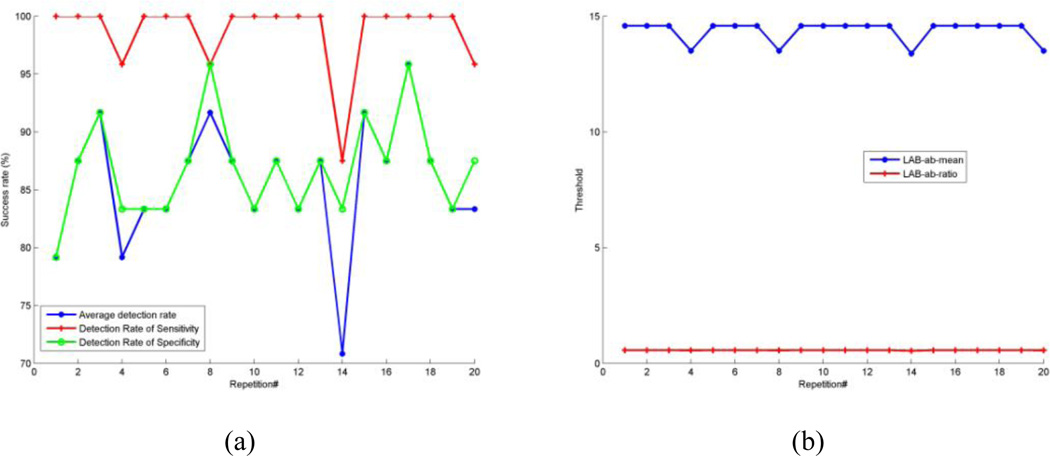
Based on the 20 repetitions of random splits of the training and test sets, the overall average accuracy of detecting motion-corrupted series was 85.63%. In addition to overall accuracy, we also calculated both sensitivity and specificity so that we knew how well it performed in detecting artifacts that actually present (sensitivity) and how well it performed in determining that artifact were in fact absent (specificity). Mean sensitivity was 98.75%. Mean specificity was 86.88% (Fig.6). The computation time required for a volume with size of 256×256×57 voxels was approximately 100ms per slice using MATLAB Version 7.7.0.471 (R2008b) on a 2.4G Intel Processor with 3G RAM.

Fig. 6.

Detection result for the testing dataset for all 20 repetitions. (a). Detection result for overall average detection rate, sensitivity rate, and specificity rate, respectively. (b). Threshold of distance from center of the 2D histogram to the neutral axis (µ) and threshold of ratio (ω) of the distance to the standard deviation.

Discussion

DWI/DTI measures thermal motion of water molecules in living tissue. Therefore, any motion of the subject will alter the molecular motion that is supposed to be measured by the MRI scanner, thereby causing changes in DWI signal. While a DWI volume is associated with a particular spatial orientation along which a diffusion gradient is applied, subject motion during acquisition of a particular DWI volume will inevitably modify the signal in this DWI volume and therefore change the signal along this particular direction. Consequently, color cast is a way to uniquely mark this possible motion.

We have proposed an automated assessment of image quality for DTI data using the color cast of CFA images. This algorithm first requires training using sample datasets that optimize the selection of threshold values that then be applied to new DTI data in order to identify datasets that contain motion artifacts. The algorithm is entirely automated. In a cohort of 47 infant DTI dataset, it identified motion-corrupted images with a sensitivity of 99% and a specificity of 87% and an overall accuracy of 86%. Sensitivity and specificity depend on the selection of the thresholds T_µ and T_ω, and these parameters can be adjusted to emphasize sensitivity over specificity, and vice versa. Therefore, the size of an ideal training set for obtaining the thresholds T_µ and T_ω should be large enough to cover all possible cases including marginal conditions.

We used the judgment of human inspectors as the “gold-standard” on the 47 datasets because no agreed upon standard is available for these real world datasets. As some datasets may contain artifacts imperceptible by human eyes, we suggest setting stricter threshold values to favor automated detection so that datasets containing invisible outliers (to the human eyes) can be identified. But even with the current setting, the experiments achieved sensitivity and specificity above 85% indicating that our algorithm performs as reliably as a human inspector.

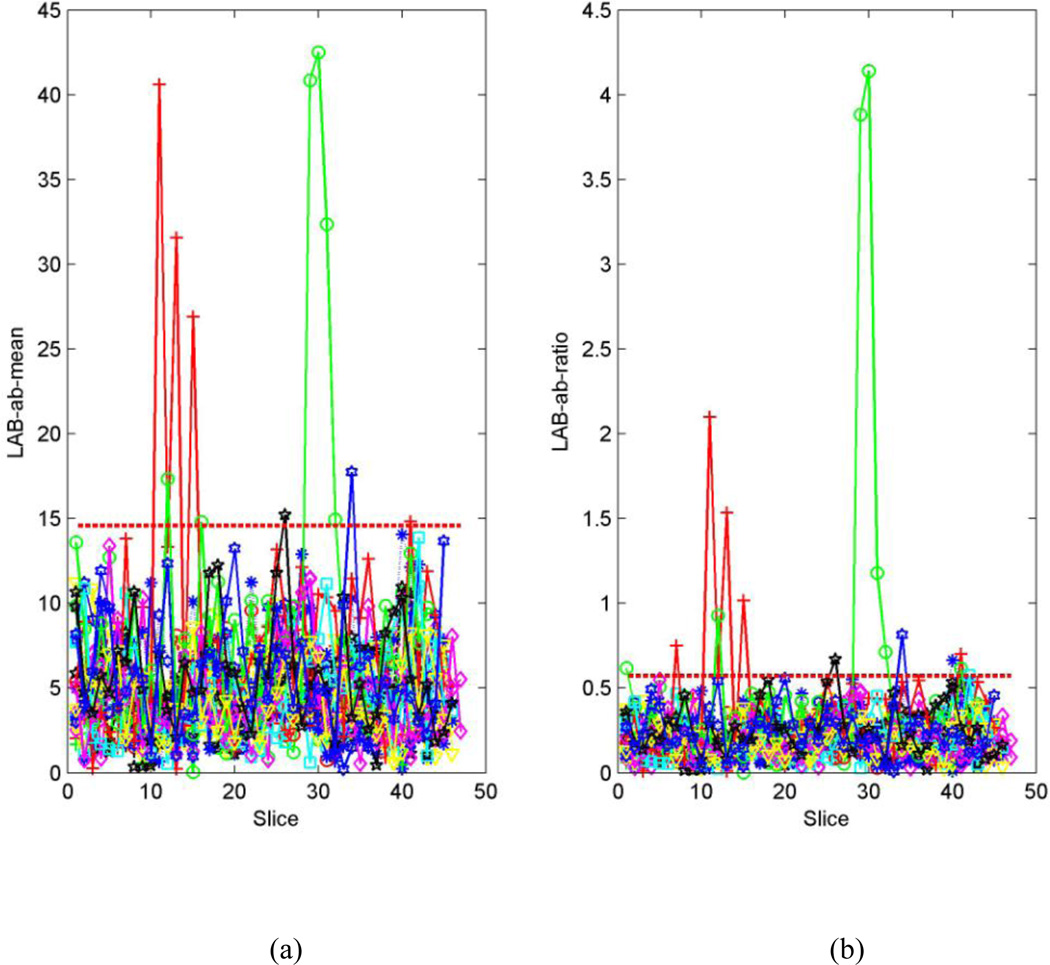
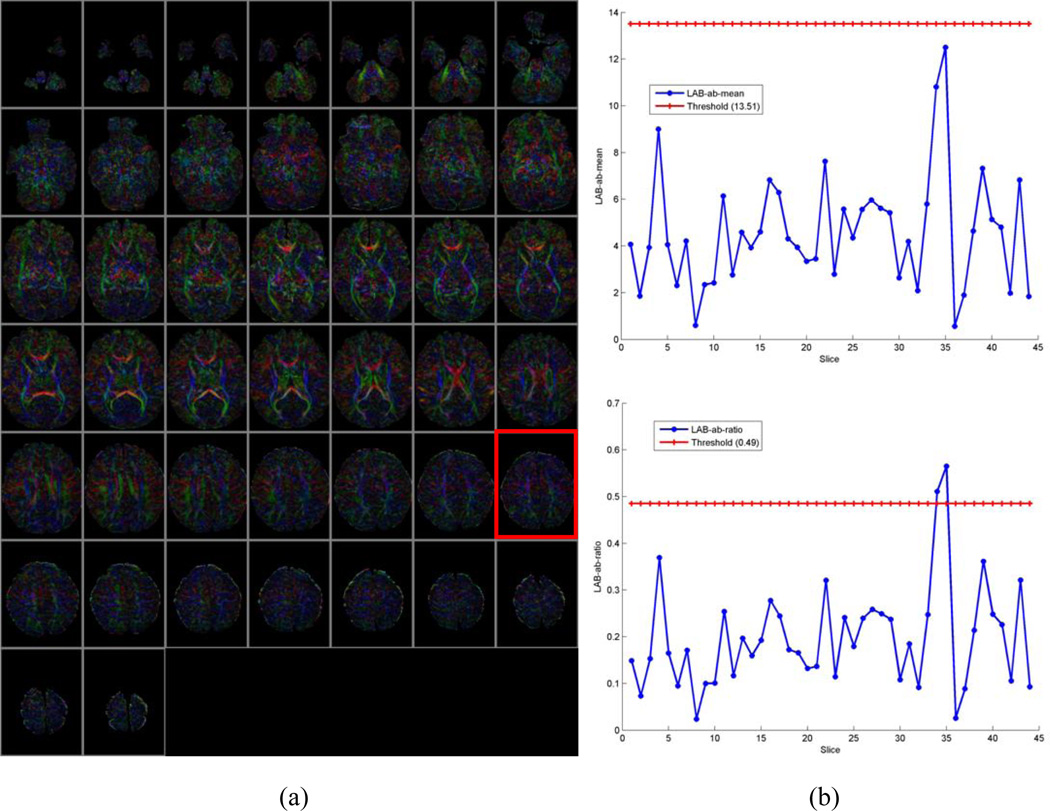
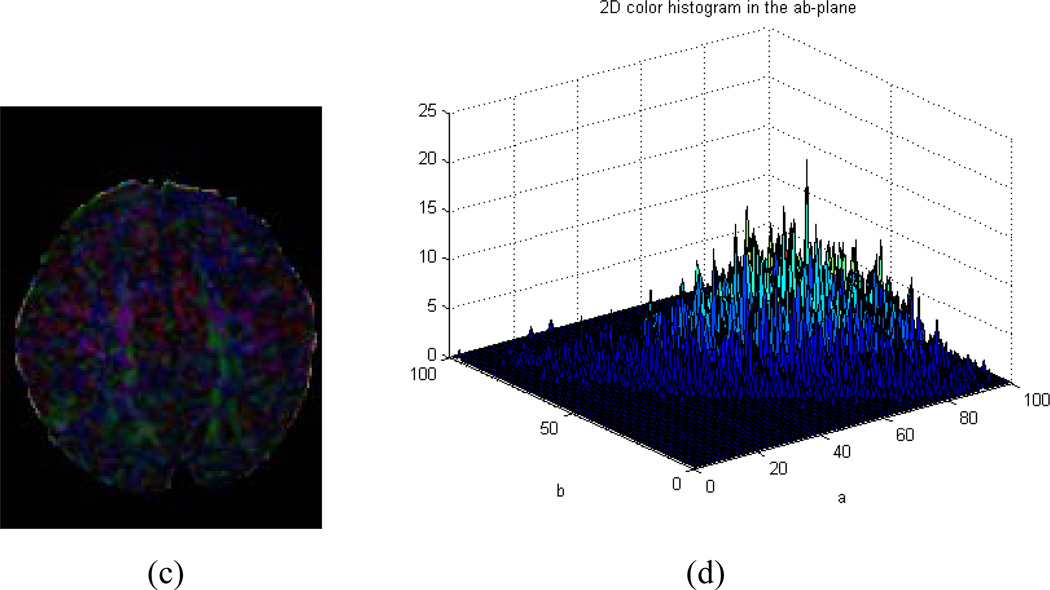
Our algorithm can fail to identify motion-corrupted datasets correctly in two general circumstances: (1) If a CFA image contains significant noise but does not show color cast (Fig.7. c and d), or (2) A DTI dataset derives a CFA image that does in fact contain a color cast but that cast does not originate from motion (Fig.8. c and d). In the first case, it will result in a false positive that we have decided to consider a bad series in the ground-truth. This particular case is a result of excessive noise contained in the corresponding CFA image, as illustrated (Fig. 7a), although no color cast can be detected, as the values of µ and ω were below the thresholds T_µ and T_ω (Fig. 7 b). This case could happen when tensors are estimated using only 6 gradient directions instead of 11 in our Babies DTI datasets. The rate of misidentification can be reduced by combining current method with other detection methods during the tensor reconstruction. For example, by using the robust estimation of tensors by outlier rejection (Chang, Jones et al. 2005), so that only an optimal subset of DWI data are used for the estimation; or referring to a white matter atlas so that only images with reasonable agreement of the white matter structures and Lab-color balance can pass quality assurance. Because we focus on the quality of the reconstructed tensor data rather than the process of the reconstruction, we opt not to consider this situation in this paper. In the second case, it will result in false negative because we will classify the data as good. Nevertheless, the values of µ and ω are larger than the thresholds T_µ or T_ω (Fig.8. a and b, slice#35 marked in a red rectangle).The key is to discriminate color cast and the predominant color (Fig. 2c and d versus Fig. 8c and d). While color cast refers to a tint covering the entire image universally, a predominant color only occurs in a portion of the image or some of the slices such as those near cerebral cortex, albeit a relatively large percentage of the image. In other words, a color cast will identify the color component in every voxel of the slice, but a predominant color will not. Our future work will incorporate this judgment for more precise detection.

Fig. 7.

Example of false positive. (a) CFA images of all slices. (b). Upper : distribution of distance from the center of the 2D histogram to the neutral axis (µ); Bottom: distribution of the ratio (ω) of the distance to the standard deviation. (c). CFA image of Slice#25 marked with red rectangle in (a). (d). 2D histogram of (c) in the ab-plane of CIELAB color space. This is an example of a CFA image with no color cast but with random noises around the corpus callosum.

Fig. 8.

Example of false negative. (a) CFA images of all slices. (b). Upper: distribution of distance from the center of the 2D histogram to the neutral axis (µ); Bottom: distribution of the ratio (ω) of the distance to the standard deviation. (c). CFA image of Slice#35 marked with red rectangle in (a). (d). 2D histogram of (c) in the ab-plane of CIELAB color space. This is an example of a CFA image with no color cast but with predominant color closing the cerebral cortex.

Although our method was inspired and subsequently developed for detecting motion artifacts, it could potentially be used to detect other outlier, because any artifacts in DWI data will result in biased estimation of tenors. The wrong tensors will, in turn, very likely lead to biases in tensor orientations, resulting in color deviation in the CFA maps. Certain adaptions may be needed to customize to particular type artifacts and outliers.

Conclusion

We have proposed an automatic quality assessment for CFA images. Color cast is detected using efficient statistics of 2D histogram distribution in the ab-plane of CIELAB color space which describes all the colors visible to the human eye. The proposed method eliminates the need for detecting motion corrupted images by visual inspection and also automatically spatially localizes outliers that would be easily missed by visual inspection. This method can be implemented quickly and used for the real time quality evaluation of DTI scans especially in infant scans. Moreover, the proposed method is also promising as criteria for evaluating the quality of tensor estimation offline. We believe that this approach would be particularly useful for routine processing of clinical DT-MRI data by providing an objective and operator-independent quality assessment for CFA images.