Stochastic variability in HIV affects viral eradication

When combination antiretroviral therapy (ART) was first administered to HIV-infected individuals in the 1990s, patient viral loads declined so rapidly that it seemed a cure could be achieved within 2–3 y of therapy (1). However, the presence of a long-lived reservoir of latently infected CD4⁺ memory T cells (2) diminished these hopes. When ART was interrupted in patients, even after many years, viremia rapidly rebounded from the latent reservoir and the estimates indicated that it would take many decades of suppressive therapy for the reservoir to dissipate. To achieve an HIV cure, the latent reservoir would need to be actively emptied while the resulting virus was destroyed using antiretroviral drugs. The strategy became known as “activate-and-kill” (Fig. 1A), and a vigorous research campaign ensued to identify agents capable of reactivating latent HIV. Candidate latency-reversing agents (LRAs) were—and continue to be—identified in cell-culture models, with some having been tested in patients to determine their efficacy in depleting the reservoir (3). In PNAS, Hill et al. (4) calculate the level of reservoir depletion that would be required to prevent viremia rebound after interrupting ART. In so doing, the authors set a quantitatively defined goal for the activate-and-kill approach.

Fig. 1.

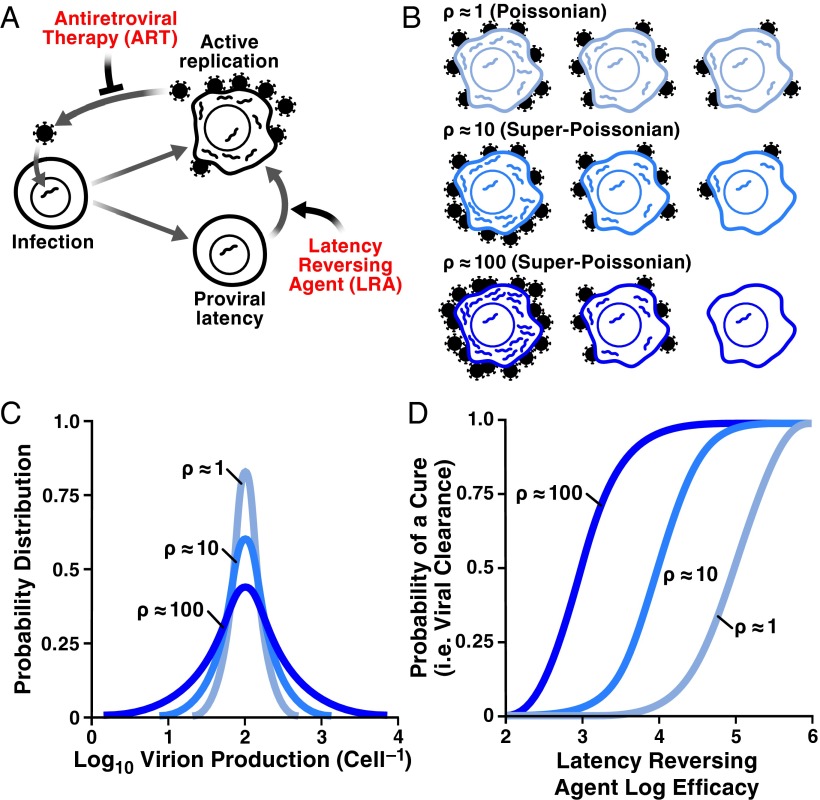
The influence of stochastic HIV burst size on viral eradication. (A) The HIV infection cycle showing the activate-and-kill HIV-cure strategy. (B) Schematics depicting potential variability in HIV burst size from Poissonian variability ρ = 1 (lightest blue) to super-Poissonian variability ρ = 10 (blue) and ρ = 100 (darkest blue). (C) Histograms quantifying variability in HIV burst size (corresponding to B): Poissonian variability ρ = 1 (lightest blue) to super-Poissonian variability ρ = 10 (blue) and ρ = 100 (darkest blue). (D) Effects of Poissonian and super-Poissonian HIV burst-size variability on eradication. Super-Poissonian would require less depletion for activate-and-kill to be effective (in 50% of patients).

Hill et al. (4) begin by developing a mathematic model of latent reactivation. Because viral reactivation begins from activation of a single latent provirus, it is essentially stochastic, requiring the use of a sophisticated branching-processes technique, which the authors then cross-validate numerically. After estimating model parameters from various sources and conducting sensitivity tests, Hill et al. predict that a 10,000-fold depletion in the latent reservoir would be required to avert viral rebound in 50% of patients. Current LRAs are quite far from achieving this level of depletion in patients (5).

A critically important prediction is that it may not be necessary to eliminate all latent cells to prevent viral rebound (in 50% of patients). Intuitively, the reasoning underlying this prediction is that high variability in the viral “burst” size (the number of viral progeny generated from actively infected cells) increases the likelihood that the progeny of an activated provirus will go extinct because of stochastic diffusion. Mathematically, as long as the variability in HIV's burst size is greater than standard Poisson variability (i.e. is super-Poissonian) (Fig. 1B) there is a likelihood that one could prevent viral rebound with <10,000-fold depletion of the reservoir. The super-Poisson effect can be conveniently characterized by the Fano factor (ρ = variance/mean). For pure Poisson statistics, ρ is equal to 1, whereas for super-Poisson cases, ρ > 1 (Fig. 1C). For example, for ρ = 10, which Hill et al. (4) choose as their central estimate of ρ, a 10,000-fold depletion of the latent reservoir is required to prevent the rebound in 50% of patients (ρ = 100 and ρ = 1 require depletions of ∼1,000-fold and 100,000-fold, respectively) (Fig. 1D). Although several physiological mechanisms could contribute to such super-Poissonian variability (e.g., the immune response might destroy a cell before virions are produced), the role and strength of these mechanisms are unclear.

There is a process intrinsic to virus replication itself that could generate super-Poissonian variability. HIV transcription is an inherently stochastic (i.e., noisy) process and generates strong fluctuations in HIV gene products (6–8). This stochastic noise produces large super-Poissonian variability in HIV gene expression between individual cells and likely leads to the stochastic reactivation recently seen in patient cells (9). Measurements of noise in HIV transcription provide one method to calculate ρ.

Hill et al. (4) in fact use three different methods to estimate the value of ρ. First, an upper bound of ρ ∼10³ is found from the low estimates of the “effective” HIV population size, N_eff ∼10⁵ cells, and HIV census size, ∼10⁸ (10, 11). Using another indirect method, the authors obtain ρ ∼10 from the exit rate of the reservoir, assumed to be five cells per day. Finally, an estimate of ρ is deduced from single-cell data on transcriptional fluctuations from the HIV promoter (6, 8). These data imply that ρ can vary from 1 to 20 for different HIV-integration sites; in fact, single-molecule counting of HIV mRNAs in individual cells has measured ρ ∼80 for some integration sites (12). Importantly, estimates of ρ from HIV transcriptional noise assume that variations in transcription rate and virion yield are linearly proportional. Although it is possible that downstream viral processes, such as Rev-negative autoregulation, buffer promoter fluctuations (driving ρ lower), HIV’s Tat positive-feedback circuitry substantially amplifies promoter fluctuations (13) and the virion-formation process is known to generate large heterogeneities in other viruses (14).

Overall, the different methods place ρ anywhere between 1 and 1,000 (and it could vary substantially between different viral integration sites), which translates to a broad variation for the required reservoir depletion, 10²–10⁵ (Fig. 1D). To make a more specific prediction, systematic measurements of viral production across individual cells within a population will be required. Nevertheless, the estimates from stochastic fluctuations in HIV transcription could prove to be lower bounds on ρ, indicating an upper edge for the range of depletion that

Hill et al. calculate the level of reservoir depletion that would be required to prevent viremia rebound after interrupting ART.

will be required for eradication (Fig. 1D). Along these lines, it may be most intriguing to examine the effects of novel LRAs that enhance HIV noise (15). Such noise enhancers could increase ρ upon reactivation, thereby lowering the level of reservoir depletion required for efficient eradication.

A major clinical implication of this study is that—given the stochastic nature of HIV activation (9)—suboptimal depletions of the reservoir will merely generate variable delays in viremia rebound (e.g., a ∼1,000-fold instead of 10,000-fold reduction in the reservoir would generate, on average, a 1-y delay in rebound). This prediction is unfortunately supported by recent reports of viremia rebound in the “Mississippi baby” (16) and the “Boston” patients (17), HIV-infected patients who were originally thought to be cured. Other examples of cured patients, such as the “Berlin” patient (18) and the VISCONTI cohort (19) have not exhibited viremia rebound for years. It could be that the requisite reservoir reduction was achieved in these patients, but it is also possible that these patients are within the predicted delay period before viremia rebound.

This possibility, coupled with the recent finding that latency is established in the first 3 d after infection (20), raises the specter that purging the latent reservoir will be exceptionally challenging. It may therefore be worthwhile for the field to consider, in parallel, alternates to the activate-and-kill HIV-cure strategy. One such approach could be a latency stabilization approach where latent cells are permanently kept latent and reactivation is prevented. This approach could represent an alternate functional cure and there is recent evidence indicating that such latency-stabilizing agents can be identified through screening (15). Although latency stabilization would represent a management strategy and a radical departure from current HIV-cure initiatives, it may also be the practical alternative.