Mixtures of opposing phosphorylations within hexamers precisely time feedback in the cyanobacterial circadian clock

Significance

Many organisms possess biological clocks that schedule their behavior throughout the day. To function properly, these clocks must maintain a period near 24 hours despite fluctuations in conditions. In a simple three-protein oscillator from cyanobacteria, timing information is stored in KaiC, a phosphorylated protein which forms hexameric rings. We show that the feedback loop that allows oscillation depends cooperatively on phosphorylation throughout the KaiC hexamer. Two phosphorylation sites with different kinetics have opposing effects, and this creates a sharp transition between the day and night states of the ring. This mechanism, based on opposing modifications, generates circadian rhythms across the relevant range of protein stochiometries and may be used generally in biochemical networks for precise timing.

Abstract

Circadian oscillations are generated by the purified cyanobacterial clock proteins, KaiA, KaiB, and KaiC, through rhythmic interactions that depend on multisite phosphorylation of KaiC. However, the mechanisms that allow these phosphorylation reactions to robustly control the timing of oscillations over a range of protein stoichiometries are not clear. We show that when KaiC hexamers consist of a mixture of differentially phosphorylated subunits, the two phosphorylation sites have opposing effects on the ability of each hexamer to bind to the negative regulator KaiB. We likewise show that the ability of the positive regulator KaiA to act on KaiC depends on the phosphorylation state of the hexamer and that KaiA and KaiB recognize alternative allosteric states of the KaiC ring. Using mathematical models with kinetic parameters taken from experimental data, we find that antagonism of the two KaiC phosphorylation sites generates an ultrasensitive switch in negative feedback strength necessary for stable circadian oscillations over a range of component concentrations. Similar strategies based on opposing modifications may be used to support robustness in other timing systems and in cellular signaling more generally.

Circadian clocks are biological timing systems that allow organisms to anticipate and prepare for daily changes in the environment. A hallmark of a circadian oscillator is its ability to drive self-sustained rhythms in gene expression and behavior with a period close to 24 h, even in the absence of environmental cues (1). A general challenge for the biochemical machinery that generates rhythms is to precisely define the duration of the day in the face of perturbations, including fluctuations in the cellular abundance of the molecular components. The importance of maintaining precise circadian timing is underscored by experiments showing that mismatch between the clock period and the rhythms in the external environment results in health problems and fitness defects (2, 3).

Although circadian clocks are found across all kingdoms of life, the Kai oscillator from cyanobacteria presents a uniquely powerful model system to study the design principles inherent in the molecular interactions that generate rhythms. A mixture of the purified proteins KaiA, KaiB, and KaiC results in stable oscillations in the phosphorylation state of KaiC in vitro that persist for many days and share many of the properties of circadian clocks in vivo (4–6). In particular, the oscillator can successfully generate near–24-h rhythms over a range of concentrations of the clock proteins both in vivo and in vitro (7–9), so fine-tuning of gene expression is not needed to support a functional clock. Much has been learned about the behavior of the isolated Kai proteins, including the determination of high-resolution crystal structures of all three components (10–12). A critical challenge that remains is to understand how the properties of the Kai proteins are integrated together in the full system to generate precisely timed rhythms.

KaiC appears to be the central hub of timing information in the oscillator. Each KaiC molecule consists of two AAA+ family ATPase domains that consume the free energy of ATP hydrolysis to drive oscillations. Like many other members of this family, KaiC forms hexamers, and the enzymatic active sites are formed at the subunit interfaces where nucleotides are bound. The C-terminal, or CII, domain of KaiC has additional phosphotransferase activities that are unusual for the AAA+ family: it can phosphorylate and dephosphorylate two residues near the subunit interface, Ser431 and Thr432 (13). KaiC autokinase and autophosphatase activities occur at the same active site (14, 15). In isolation, KaiC has high phosphatase activity, but the enzyme is pushed toward kinase activity by the activator protein KaiA, which interacts directly with the KaiC C-terminal tail (16, 17). Roughly speaking, kinase activity predominates during the day, and phosphatase activity predominates during the night (18). Thus, understanding the feedback mechanisms that generate a precise time delay between these modes is crucial to understanding timing in the oscillator (19).

Inactivation of KaiA and a transition from kinase to phosphatase mode occur when KaiB•KaiC complexes form, closing a negative feedback loop by sequestering KaiA in a ternary complex and leaving it unable to act on other KaiC molecules (20, 21). By temporarily removing KaiA molecules from their activating role, this molecular titration mechanism may act to synchronize the activity of all KaiC hexamers in the reaction (20, 22, 23). Phosphorylation and dephosphorylation proceed in a strongly ordered fashion so that in response to a change in KaiA activity, Thr432 is (de)phosphorylated first, followed later by Ser431 (18, 20, 21). It is known that phosphorylated Ser431 is important for allowing the formation of KaiB•KaiC complexes. However, recent work has made it clear that the binding of KaiB involves both KaiC domains—in particular, the slow ATPase activity of the N-terminal CI domain, which is not phosphorylated, is required for KaiB interaction (24, 25).

Because of the importance of precisely timing negative feedback via KaiB•KaiC complex formation for generating appropriate rhythms (22), we wanted to understand the role of phosphorylation of the KaiC hexamer in controlling this process. The involvement of both KaiC domains suggests that information about phosphorylation in CII is communicated allosterically through changes in hexamer structure to the CI domain, potentially through ring–ring stacking interactions (24, 26). We therefore hypothesized that the KaiC phosphorylation sites on each subunit might act as allosteric regulators in the context of a hexameric ring so that phosphorylation of one subunit would alter the ability of all other subunits in the ring to engage with KaiA and KaiB, providing a cooperative mechanism to control the timing of these interactions.

We conducted a series of biochemical experiments and perturbations to study the effect of altering the status of each phosphorylation site on the KaiC hexamer. To interpret these results, we then developed a mathematical model analogous to classical models of allosteric transitions in multimeric proteins. We constrain the kinetic parameters in this model using experimental measurements of rate constants, allowing us to compare the predictions of the model directly with data. We conclude that maintenance of circadian timing over a range of protein concentrations requires an effectively ultrasensitive switch in each KaiC hexamer from an exclusively KaiA-binding state to a state that can bind to KaiB as phosphorylation proceeds. This effect requires that KaiC hexamers consist of mixtures of differentially phosphorylated subunits, as would be produced by stochastic autophosphorylation of a hexamer. Ultrasensitivity results from opposing effects of phosphorylation on Thr432 and Ser431 in controlling a concerted transition within a given KaiC hexamer. Including this mechanism in the model is necessary to explain the experimentally observed tolerance of the system to altered protein concentrations.

Results

KaiC Hexamers Are Composed of Subunits in Different Phosphorylation States.

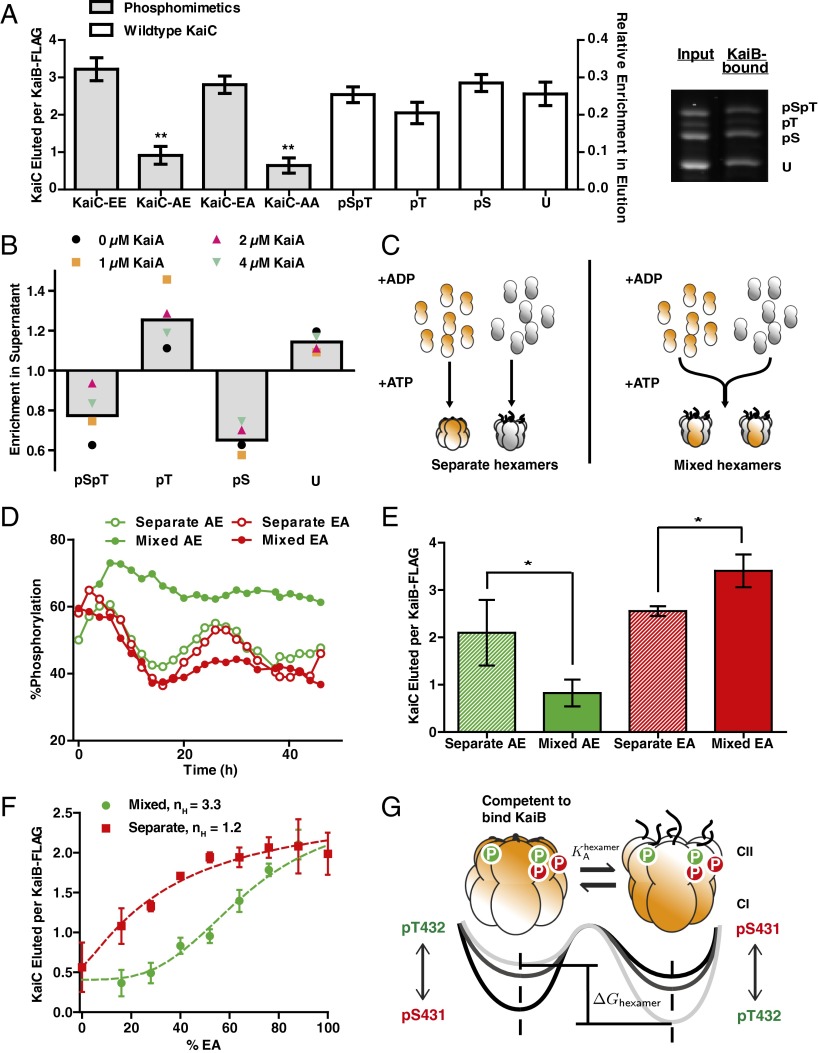
To experimentally interrogate the role of phosphorylation in regulating interaction with KaiB, we coimmunoprecipitated (co-IPed) KaiC bound to KaiB during oscillating reactions (Fig. S1), then analyzed the phosphorylation state of KaiC using electrophoresis conditions that resolve the modification status of Ser431 and Thr432 (Fig. 1A). This allowed us to sample a wide range of phosphoform abundances as both KaiC phosphorylation and the formation of KaiB•KaiC complexes oscillate over time (18, 20). As standards, we prepared mutants of KaiC whereby a phosphorylation site was mutated either to Ala to prevent phosphorylation or to Glu to mimic phosphorylation. When prepared as homogeneous hexamers, these mutants interact very strongly with KaiB if Ser431 is phosphomimetic, but weakly if not (6, 18, 20, 22). In contrast, in the case of wild-type KaiC hexamers, all forms of the KaiC subunits may be found bound to KaiB, including unphosphorylated KaiC and KaiC phosphorylated only on Thr432 (Fig. 1A).

Fig. 1.

KaiB–KaiC interaction favors KaiC hexamers with appropriate mixtures of phosphorylated subunits. (A, Left) Phosphorylation site mutants in homogeneous hexamers co-IPed by KaiB-FLAG (gray bars, right axis). Error bars represent SE of three replicates after 24-h incubation. Average amount (n = 4) of each KaiC phosphoform co-IPed by KaiB-FLAG starting from a highly phosphorylated state (white bars, left axis). Error bars represent SD over a 4-h time course. Values were determined by gel densitometry as the ratio of the KaiC band intensity to the KaiB-FLAG band. (Right) Representative SDS/PAGE gel image of the input and elution phosphoform compositions of KaiC co-IPed by KaiB-FLAG. **t tests vs. KaiC-EA and KaiC-EE both gave P < 0.01 (Fig. S1). (B) Enrichment of each KaiC phosphoform in the supernatant relative to the material bound to KaiB-FLAG in clock reactions. Colored symbols show an average from seven to nine time points taken over 24 or 34 h. Gray bars indicate averages over all KaiA concentrations and time points. (C) Schematic for preparation of mixed and separate hexamers. KaiC phosphomimetics (orange) and His₆-tagged wild-type KaiC (His₆–KaiC, gray) are monomerized by the replacement of ATP with ADP, and mixed in a 1:1 ratio before (“mixed”) or after (“separate”) rehexamerization with ATP. (D) Phosphorylation dynamics of wild-type KaiC in clock reactions in the presence of phosphomimetics either as mixed or separate hexamers. (E) Amounts of total KaiC co-IPed by KaiB-FLAG during the dephosphorylation phase (6–12 h) in clock reactions with KaiC-AE and wild-type KaiC (green bars) or during the phosphorylation phase (22–28 h) in clock reactions with KaiC-EA and wild-type KaiC (red bars). Bar heights show averages of three to four time points. Error bars indicate SD. *P < 0.05 by Student t test. (F) Total amount of KaiC co-IPed by KaiB-FLAG as a function of the percentage of KaiC-EA combined with KaiC-AE in either mixed or separate hexamer preparations. Points show the averages of three measurements, and the error bars indicate SD. Dotted lines show fits to Hill functions $y=y_{max}\frac{1}{1+{\left(\frac{K}{\%EA}\right)}^{{\text{n}}_{\text{H}}}}$, where n_H is the Hill coefficient. (G) An allosteric framework for modeling the KaiC hexamer. The phosphorylation state of each subunit contributes to the free energy difference between two conformational states of the hexamer: one that is competent to bind KaiB and one that is not. Tails extending from the CII domain suggest changes in A-loop conformation associated with each conformational state. Arrowheads indicate proposed influence of the phosphorylation sites on the stability of the two hexameric states.

We interpret these data to indicate that KaiC subunits that do not favor KaiB interaction are often co-IPed in the context of a hexameric ring that nevertheless is bound to KaiB. This suggests that wild-type KaiC hexamers consist of mixtures of subunits in various phosphorylation states. However, because the phosphorylation site mutations indicate that Ser431 phosphorylation is required for KaiB interaction, we hypothesized that although wild-type KaiC hexamers may contain subunits in all possible states, the relative abundance of each phosphorylation state within a hexamer should bias the probability of that hexamer binding to KaiB.

We therefore asked whether there are systematic trends in the enrichment of the various possible phosphorylation states of the KaiC bound to KaiB. To detect trends across many KaiC phosphorylation conditions, we sampled several reactions with different concentrations of KaiA at various time points throughout the oscillator cycle (Fig. S1). As expected, KaiC phosphorylated only on Ser431 was strongly enriched in the material bound to KaiB relative to the unbound material. However, KaiC phosphorylated only on Thr432 was preferentially excluded from the KaiB–KaiC interaction and enriched in the unbound material (Fig. 1B and Fig. S1). These results suggest a working hypothesis in which the ability of KaiC to interact with KaiB indeed depends on the relative abundance of each phosphorylation state within a given KaiC hexamer.

Two KaiC Phosphorylation Sites Have Opposing Effects on the Ability of Mixed Hexamers to Interact with KaiB.

According to this hypothesis, the phosphorylation state of one subunit will alter the ability of the entire hexamer to interact with KaiB through allosteric communication within the KaiC ring. Therefore, experimentally forming mixed hexamers that contain both wild-type KaiC and phosphomimetic mutants should alter the ability of the wild-type KaiC to interact with KaiB and disrupt the function of the oscillator. In contrast, if each subunit acts independently of its hexameric context, producing mixed rings would result in no greater effect than leaving the mutant and wild-type segregated into separate hexamers. To distinguish between these alternatives, we used an ATP depletion protocol to prepare pools of largely monomeric KaiC S431A;T432E (KaiC-AE, a mimic of pT432-only), KaiC S431E;T432A (KaiC-EA, a mimic of pS431-only), and His₆-tagged wild-type protein (15). To create mixtures of KaiC mutants and wild-type monomers within the same hexamers, we combined pools of monomers and reintroduced ATP to hexamerize the mixture. As a control, we reversed the order of this procedure so that the proteins were rehexamerized without mixing before being combined (Fig. 1C). This monomerization and rehexamerization procedure does not compromise the ability of the wild-type protein to oscillate (Fig. S2). We used the His₆ tag on wild-type KaiC to verify that our procedure succeeded in creating forced mixtures of mutant and wild-type in which a large majority of hexamers are composite. When we rehexamerized the pools of mutant and wild-type protein separately, they remained largely segregated for at least 48 h. In contrast, our forced mixing procedure succeeded in creating a population of hexamers that was largely composite (Fig. S2).

To test the oscillator function of these mixed hexamers, we then added KaiA and KaiB to initiate clock reactions. Consistent with our hypothesis, oscillations fail when KaiC-AE is forced to mix into wild-type hexamers, resulting in highly phosphorylated KaiC, the expected phenotype if KaiB cannot act. Mixing KaiC-EA into wild-type hexamers causes oscillations to fail with the opposite phenotype—weakly phosphorylated KaiC. However, in both cases, circadian oscillations are maintained when the mutants are present but segregated into separate hexamers (Fig. 1D). These failure modes of the oscillator correspond to disrupted interaction with KaiB induced by the mixing of KaiC-AE (or KaiC-AA) into wild-type KaiC hexamers, or enhanced interaction with KaiB induced by the mixing of KaiC-EA into wild-type hexamers (Fig. 1E and Fig. S2). These results also are consistent with a recently published report from Kitayama et al. (27) showing that the activity of KaiC hexamers depends on their subunit composition.

To quantitatively assess how hexameric mixtures of Ser431- and Thr432-phosphorylated subunits regulate binding to KaiB, we prepared hexamers using various percentages of KaiC-AE and KaiC-EA phosphomimetics. We found that a preparation of hexamers containing a mixture of KaiC-AE with KaiC-EA subunits suppressed the total amount of KaiB–KaiC interaction relative to a control in which the same proteins were present, but segregated into separate hexamers (Fig. 1F and Fig. S2). This indicates that the presence of pThr432 subunits within the same hexamer can prevent the interaction of pSer431 subunits with KaiB, consistent with the correlations we observed in the wild-type oscillator.

Crucially, hexameric mixtures of pSer431 and pThr432 mimics show a sigmoidal dependence of KaiB interaction strength on the fraction of pSer431 mimic present in the mixture (effective Hill coefficient ∼3.3), an effect that was absent (effective Hill coefficient ∼1.2) when the two phosphomimetics were kept in separate hexamers (Fig. 1F). Because of the kinetic ordering of phosphorylation reactions in KaiC, oscillations are characterized by periods in which either pThr432 or pSer431 alternately dominates in relative abundance (18, 20). Considering the switch-like transition in KaiB–KaiC interaction we observed as the balance within hexamers is shifted to favor pSer431 over pThr432, we hypothesized that dynamic changes in the mixture of phosphorylation states in a hexamer might be key to understanding the timing of the transition between the phosphorylation and dephosphorylation phases of the circadian rhythm.

To mathematically model these effects, in which the binding affinity of a KaiC hexamer for KaiB depends on the mixture of posttranslational modifications on all the KaiC subunits, we introduce a simple allosteric framework. In classical models of allostery in oligomeric proteins, such as the Monod–Wyman–Changeux treatment of hemoglobin, it is assumed that each subunit can adopt different conformational states but that, because breaking the symmetry of the molecule is disfavored, all the subunits in a given oligomer must always be in the same conformational state. The role of ligand binding is then to bias the free energies of the possible subunit conformations, resulting in a cooperative switch in the conformation of the oligomers as ligand concentration increases (28).

We extend this treatment to describe allosteric effects in KaiC, by hypothesizing that KaiC hexamers may exist in two conformational states: one that allows interaction with KaiB and one that does not. These two conformational states likely are related to changes in the stacking interactions between the CII and CI rings and the exposure or burial of the hydrogen-bonded network of KaiA-binding activation loops recently identified by structural studies (19, 24, 26, 29). Consistent with this picture of allostery, recent structural work identified changes in solvent accessibility across both domains of KaiC when it is bound to KaiB (26).

As in Monod–Wyman–Changeux, we assume that the dynamic interconversion between these states is rapid and must be all-or-none within a given hexamer. We take phosphorylation of KaiC to play a role similar to that of ligand binding in hemoglobin so that the free energy difference between the subunit conformations, and thus the probability of each state occurring at equilibrium, is biased by the combination of phosphorylations in a given KaiC hexamer (Fig. 1G). To describe this effect mathematically, we introduce an energetic cost for the conformational interconversion of each subunit that depends on its phosphorylation state. Because each subunit has two phosphorylation sites (Ser431 and Thr432), it may exist as four possible phosphoforms. This introduces four unknown thermodynamic parameters to our model: $\mathrm{\Delta }{G}_U,\mathrm{\Delta }{G}_{pS},\mathrm{\Delta }{G}_{pT},\mathrm{\Delta }{G}_{pSpT}$. Under these assumptions, the total free energy difference between the two allosteric states of a hexamer is a linear combination $\mathrm{\Delta }{G}_{hexamer}={\displaystyle {\sum }_{i=1}^6\mathrm{\Delta }{G}_i}$. In this model, the ultrasensitivity in KaiB interaction (Fig. 1F) arises from the exponential (Boltzmann) dependence of the equilibrium occupancy of each allosteric state on hexamer phosphorylation. We now proceed to test the validity of this allosteric framework, and we place constraints on the free energies associated with the phosphorylation state of a KaiC subunit.

Binding to KaiB Is Allosterically Incompatible with Stimulation by KaiA.

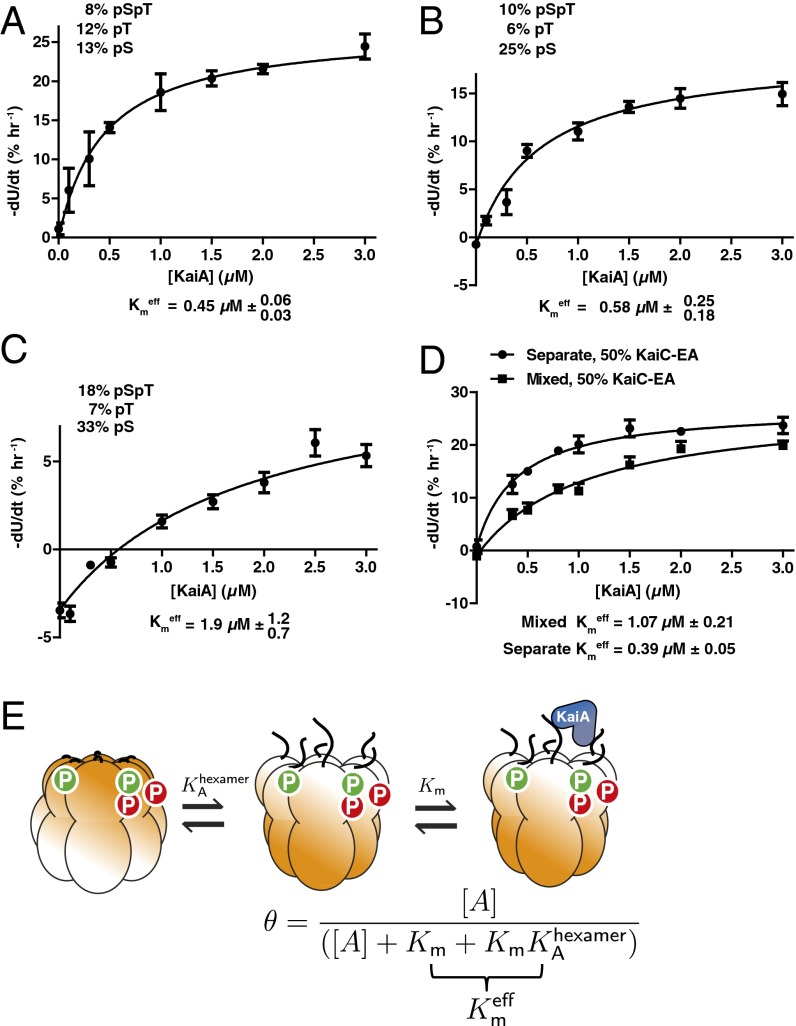
Given our data showing that mixtures of KaiC phosphorylation states regulate the ability of a KaiC hexamer to interact with KaiB, we speculated that the ability of KaiA to stimulate KaiC also might depend on the composite phosphorylation state of an entire hexamer. To examine the influence of phosphorylation on the sensitivity of KaiC to KaiA, we prepared wild-type KaiC in different initial phosphorylation states, then added various concentrations of KaiA and measured initial rates of phosphorylation for the unphosphorylated KaiC molecules (Fig. 2 A–C and Fig. S3). In all cases, the effective Michaelis constant for KaiA-stimulated autophosphorylation increased with increasing phosphorylation on Ser431, and is more than a factor of 4 higher when KaiC is heavily phosphorylated on Ser431 (Fig. 2D and Fig. S3).

Fig. 2.

KaiC hexamers with increased Ser431 phosphorylation are less sensitive to KaiA. (A–C) Rates of KaiA-stimulated KaiC autokinase activity as a function of [KaiA] for various initial phosphorylation states. Fits are to a modified Michaelis–Menten equation with baseline, V_i = V_max [KaiA]/([KaiA] + K_m^eff) + V_dephos, to account for KaiA-independent dephosphorylation. (D) Same as in (A–C) with 1:1 KaiC-EA and dephosphorylated wild-type KaiC (total, 3.5 μM), either as mixed hexamers or separate hexamers. (E) Cartoon of KaiC kinase activation by KaiA in the allosteric framework: KaiA selectively binds and activates KaiC hexamers in the non-KaiB binding state. Changes in the phosphorylation state of a hexamer changes K_A, the allosteric equilibrium constant and, hence, also K_m^eff = K_m (1 + K_A).

To isolate the allosteric effect of pSer431 on the function of a KaiC hexamer, we then measured the ability of KaiA to drive phosphorylation of unphosphorylated wild-type KaiC in the presence of varying amounts of the pSer431 phosphomimetic mutant. We observed a dose-dependent increase in the effective Michaelis constant for KaiA acting on KaiC, similar in magnitude to the effects we observed with differentially phosphorylated wild-type protein. Importantly, these effects are present only when the pSer431 mimic is mixed into the wild-type hexamers and not when it is present as separate hexamers (Fig. 2E and Figs. S4 and S5). This mixing-dependent effect indicates that phosphorylation on Ser431 acts allosterically in the KaiC hexamer to lower the sensitivity of the other subunits to KaiA. These results are consistent with recent observations that high concentrations of KaiA are needed to sustain KaiC phosphorylation (30) and that phosphomimetic mutation at Ser431 makes the KaiA-binding “A loops” inaccessible to proteolytic cleavage (31).

Because phosphorylation on Ser431 promotes an allosteric transition toward KaiB binding, the increase in K_m^eff associated with higher Ser431 phosphorylation levels suggests that KaiA selectively binds and activates KaiC in an allosteric state that KaiB cannot bind. In other words, activation by KaiA is incompatible with the state of KaiC that triggers KaiB binding. We can describe this effect mathematically using a quasi-steady state approximation valid in the limit that both interconversion between the allosteric states of KaiC and interaction with KaiA occur much faster than changes in phosphorylation. Then, the probability of a hexamer being activated for autophosphorylation by KaiA is $\frac{\left[KaiA\right]}{\left[KaiA\right]+K_{\text{m}}(1+K_{\text{A}}\left(pS,pT,pSpT\right))}$, where K_A is a phosphorylation-dependent allostery constant (see SI Appendix for derivation). Consistent with the data, this describes a Michaelis–Menten-like dependence of the autokinase rate on [KaiA] starting from a given phosphorylation state, and the higher effective Michaelis constant K_m(1 + K_A) results from higher Ser431 phosphorylation, which increases K_A (Fig. 2F).

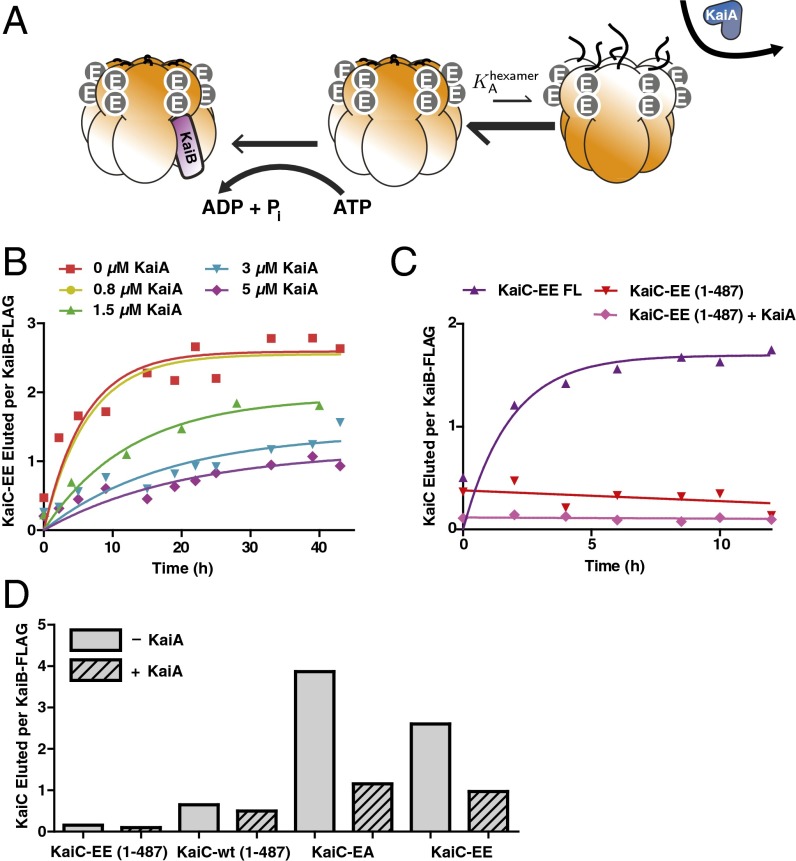
This model further predicts that because KaiA is stabilizing the kinase-active state, sufficient stimulation by KaiA should shift the allosteric equilibrium away from the state that can bind KaiB, even when the phosphorylation state is held fixed, causing KaiC to resist interaction with KaiB (Fig. 3A). To test this prediction, we used a mimic of the doubly phosphorylated form, KaiC S431E;T432E (KaiC-EE), and measured kinetics of the formation of KaiB•KaiC complexes in the presence of various amounts of KaiA. Despite the fact that kinase activation by KaiA cannot alter the phosphorylation state of these mutant residues, we found that high concentrations of KaiA could disrupt the interaction with KaiB, consistent with a model in which KaiA is stabilizing an allosteric state of KaiC incompatible with KaiB binding (Fig. 3B). The very slow (longer than a day) kinetics of binding that result from the antagonistic effect of KaiA on this mutant likely are related to the long period transcriptional oscillations that have been reported in the KaiC-EE mutant strain (9). Similar results held for the KaiC-EA mutant (Fig. S6).

Fig. 3.

KaiA allosterically stabilizes a KaiC state that KaiB cannot bind. (A) Cartoon of allosteric state selection by KaiA and KaiB. Stimulation of the kinase active mode by KaiA shifts the allosteric equilibrium away from KaiB binding. (B) Time course of KaiC-EE co-IPed by KaiB-FLAG in the presence of various concentrations of KaiA. Normalized co-IP amounts were calculated as the ratio of gel densitometry measurements of KaiC-EE to KaiB-FLAG in the eluate. Fits (solid lines) are to a first-order exponential. (C) Time course of KaiB interaction assessed by co-IP with KaiB-FLAG for either full-length KaiC-EE (KaiC-EE FL) or a mutant (KaiC-EE 1–487) that mimics the KaiA-activated state, in the presence or absence of 1.5 μM KaiA. (D) Normalized amounts of KaiC co-IPed by KaiB-FLAG at 24 h for various KaiC mutants, with or without KaiA. The concentration of KaiA is 5 μM for the KaiC-EE case and 1.5 μM for all other reactions.

To investigate the structural basis of this effect, we deleted the C-terminal tail of KaiC, a manipulation that mimics hyperactivation by KaiA and permanently locks the enzyme into the kinase mode (19). As predicted, this mutation causes severe defects in KaiB interaction (Fig. 3 C and D). The extent to which KaiB binding is disrupted is correlated with KaiA’s ability to stimulate KaiC kinase activity: a CII domain catalytically impaired mutant (E318Q) mutation allows KaiC-EE to bind to KaiB, even in the presence of KaiA, and an N-terminal deletion produces hyperactive KaiA that can inhibit the KaiB–KaiC interaction at a lower dosage than wild-type KaiA (Fig. S6).

The mutations made here and the known KaiA binding site on KaiC are distant from proposed KaiB–KaiC interaction sites (24, 32). Manipulating KaiC kinase activity either mutationally or by increasing the KaiA concentration, affects the strength of KaiB–KaiC interaction. We thus interpret our results as indicating an allosteric conflict between the action of KaiA and KaiB on KaiC. However, our data cannot exclude the possibility of an unknown mode of interaction in which KaiA might physically occlude a KaiB binding site.

Allosteric Models Constrained by Experimental Data Can Reproduce Circadian Rhythms That Adapt to Altered Protein Concentrations.

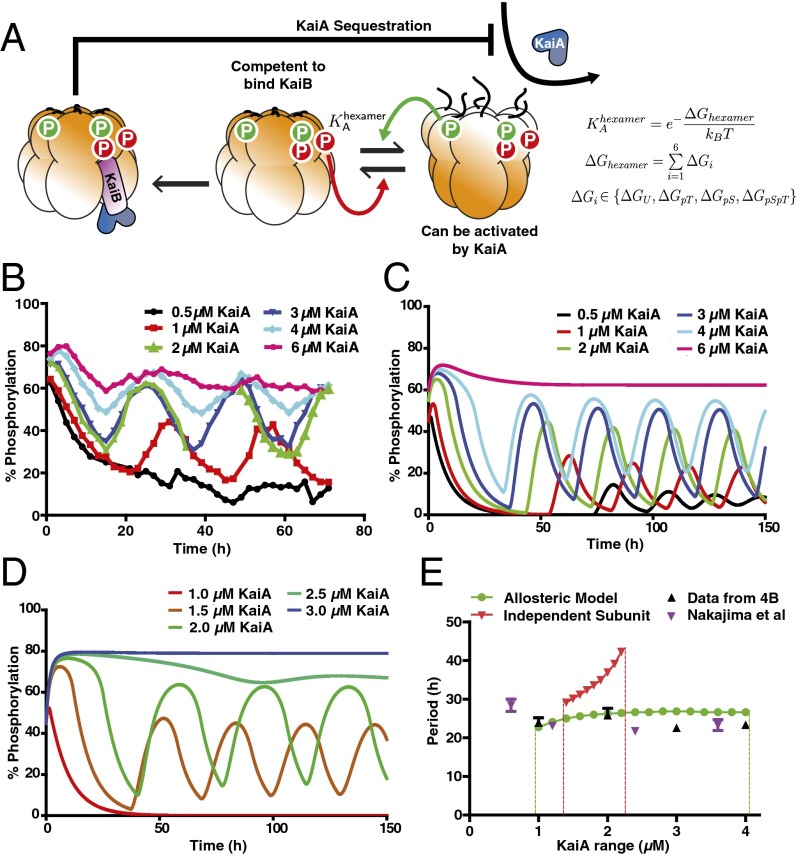
Taken together, our experimental data indicate that a role of the KaiC phosphorylation sites is to regulate an allosteric transition in the KaiC hexamer that permits KaiB binding. A simpler alternative scenario is that the phosphorylation sites on each KaiC subunit independently present a binding surface for KaiB, as in some previously studied mathematical models (20). To analyze the consequences of these two possible scenarios and gain insight into the role of each phosphorylation site, we constructed two mathematical models: an allosteric model in which the ability of KaiC to interact with KaiB and KaiA is determined by an allostery constant set by the phosphorylation state of a given hexamer (Fig. 4A), and an “independent subunits” model in which each KaiC subunit can interact independently with KaiB with a binding affinity that depends on its phosphorylation state.

Fig. 4.

The allosteric model predicts the experimentally observed robustness of the oscillator period to changes in component concentrations. (A) Allosteric multisite phosphorylation clock model: KaiC hexamers switch in a concerted fashion between a state competent for KaiB binding and a state that can be activated by KaiA. The probability of a given hexamer occupying either state is determined by the thermodynamic equilibrium set by a linear combination of phosphorylation-dependent subunit free energies. Phosphorylation on Thr432 (green) and Ser431 (red) have opposing effects on the allosteric transition. Kinase activation by KaiA allosterically stabilizes the non-KaiB binding state. Both allosteric transitions and interaction with KaiA are at quasi-steady state relative to the slow phosphorylation changes and CI ATPase-mediated KaiB binding reactions. KaiB•KaiC complexes sequester KaiA to drive a global negative feedback loop on KaiA-dependent phosphorylation. (B) Experimental time course of KaiC phosphorylation in purified clock reactions with various concentrations of KaiA. (C) Simulated reactions in the optimized allosteric model at various concentrations of KaiA. (D) Simulated reactions in an optimized model in which KaiC subunits interact with KaiB independently, at various concentrations of KaiA. (E) Experimental oscillator period estimated from data from this study (black ▲) or data from Nakajima et al. (7) (purple ▼) compared with the optimized allosteric multisite phosphorylation model (green curve) and the optimized independent subunits model (red curve). Dashed lines estimate the boundaries at which stable oscillations fail. Error bars on the experimental period indicate fitting error from least-squares regression to a sinusoid.

In both models, KaiA stimulates KaiC phosphorylation, which occurs in an uncoordinated fashion once a hexamer is activated. KaiA subsequently is inhibited globally by sequestration into KaiA•KaiB•KaiC complexes at a stoichiometry of one KaiA dimer to one KaiC subunit, consistent with recent structural work (32). The rate constants for phosphorylation and dephosphorylation on each site and for the slow, CI ATPase-mediated assembly of KaiB•KaiC are constrained by experimental kinetic studies (20, 25). Thus, our allosteric oscillator model shares features with previous treatments of allostery in the KaiABC system (23), but now explicitly includes distinct roles for the two KaiC phosphorylation sites and uses experimentally derived kinetic parameters to allow us to make direct comparisons with experimental data.

Because we do not have direct measurements of the influence of each KaiC subunit’s phosphorylation state on KaiB binding, we initially left the models agnostic about the influence of phosphorylation on protein–protein interaction. In the allosteric model, this is represented by unknown free energy contributions, $\mathrm{\Delta }{G}_U,\mathrm{\Delta }{G}_{pS},\mathrm{\Delta }{G}_{pT},\mathrm{\Delta }{G}_{pSpT}$, to the allostery constant. In the independent subunits model, these are replaced by phosphorylation-dependent binding constants for KaiB binding to each subunit.

To compare the two models, we randomly sampled parameter space for these unknown parameters and attempted to optimize each model for its ability to simulate oscillations measured in the experimental system with a period near 24 h over a wide range of KaiA concentrations, a feature of the system that has been difficult for models to describe correctly (7) (Fig. 4B). With appropriate thermodynamic parameters, the allosteric model qualitatively recapitulates the tolerance of the system to varying protein concentrations, including the increase in the abundance of specific phosphoforms as [KaiA] increases (Fig. 4C and Fig. S7).

Remarkably, the range of protein concentrations over which this model can generate circadian rhythms is nearly the same as the experimental system (Fig. 4D). The role of KaiA in stabilizing the allosteric state that cannot bind KaiB helps enhance the robustness of the period in this model (Fig. S8). In contrast, the independent subunits model can generate oscillations only over a narrow range of conditions, and the period of that model is much more sensitive to KaiA concentration than the experimental system (Fig. 4E). These conclusions still hold when the rate constants in the two models are randomly varied near the best-fit values, indicating that the improved robustness of the allosteric model is a property of the fundamentally different role for the phosphorylation sites in that model, rather than a consequence of a particular choice of kinetic parameters (Fig. S9). We conclude that models that describe subunit phosphorylation as mediating a concerted allosteric transition in the KaiC hexamer are much more successful at recapitulating experimentally observed circadian rhythms than models without these mechanisms.

Robust Timing Requires That the Two Phosphorylation Sites Have Opposing Effects, Creating an Ultrasensitive Switch in KaiC Activity.

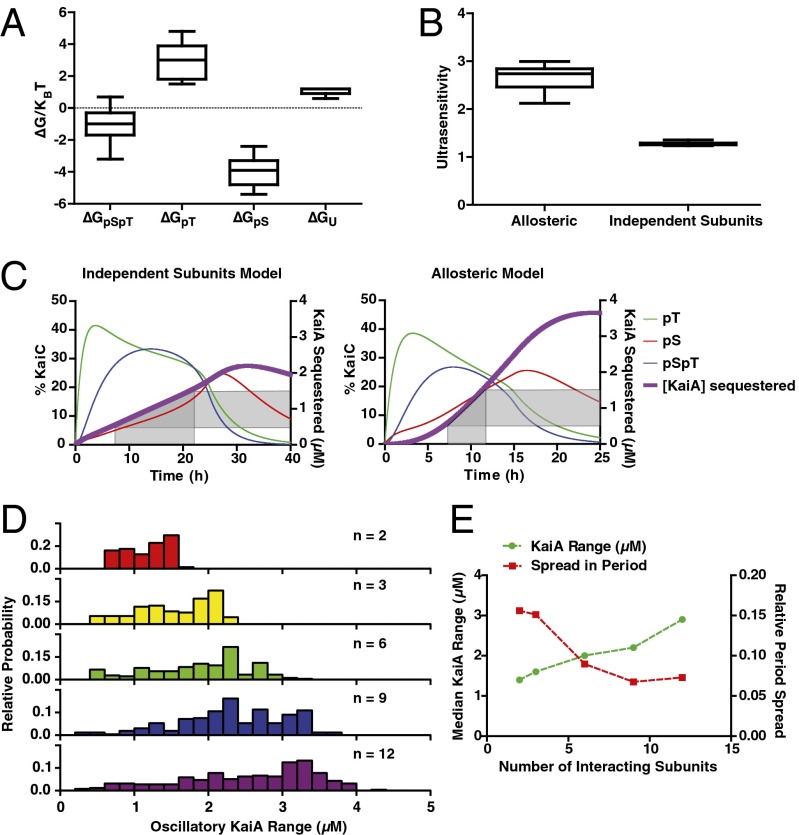
We then asked whether there were common features of the parameter sets in the allosteric model that successfully generated circadian oscillations over the range of protein concentrations observed experimentally. First, we analyzed the values of the free energy parameters from our search, which produced stable oscillations with a relative SD in the resulting oscillator period of <10% over an ∼3-μM range of KaiA concentrations, as seen in the experimental system. Strikingly, these results predict that for robust oscillations, pSer431 must always favor KaiB interaction $\left(\mathrm{\Delta }{G}_{pS}<0\right)$ and pThr432 must always oppose it $\left(\mathrm{\Delta }{G}_{pT}>0\right)$. Although opposite in sign, these two energetic parameters have the largest magnitudes; hence, changes in the balance of pSer431-only and pThr432-only subunits, as occurs when the oscillator shifts from the phosphorylation phase to the dephosphorylation phase, most critically determine the KaiB-binding capacity of the system (Fig. 5A). These findings parallel the enrichment and depletion for pSer431 and pThr432, respectively, that we observed experimentally for KaiC hexamers interacting with KaiB (compare Fig. 1B). Further, the median free energy parameters for pThr432 and pSer431 that allow the model to meet these criteria have a magnitude on the order of k_BT, the energy scale of thermal fluctuations, implying that changing a single subunit’s phosphorylation state has a large but not overwhelming effect on the allosteric state of the KaiC hexamer.

Fig. 5.

Opposing effects of pSer431 and pThr432 on the allosteric equilibrium produce an ultrasensitive switch in negative feedback necessary for a robust period. (A) Box-and-whisker plot of the free energy (∆G) distribution associated with each subunit phosphorylation state for parameter sets that produce oscillations over the experimental range of KaiA concentrations with <10% SD in period and a circadian period (22–29 h) at 1.5 μM KaiA. (B) Distribution of the effective Hill coefficient (measure of ultrasensitivity) describing the sigmoidal increase in KaiB•KaiC complexes over time in simulated clock reactions in either the allosteric multisite model or the independent subunits model. Criteria are the same as described in A, except the requirement on the SD of the period was relaxed for the independent subunits model. (C) Representative time courses of simulated KaiC phosphorylation and the amount of KaiA sequestered in the allosteric multisite model (Right) and the independent subunits model (Left). Shaded regions show the spread in time delays required to achieve inactivation of a threefold range of KaiA concentrations in both models. (D) Distribution of the range of KaiA concentrations that produce stable oscillations from 10,000 randomly sampled free energy parameters for allosteric clock models with varying numbers (n) of allosterically linked subunits. (E) Dependence of the median SD of the oscillator period (red ■) and the median range of KaiA concentrations that support stable oscillations (green ●) on the number of allosterically linked subunits.

Why do these parameter sets allow the model to work well? We reasoned that the ordered phosphorylation of Ser431 and Thr432 and their opposing effects on KaiC conformation could cause an effectively ultrasensitive switch from a KaiA-activated state to a KaiB-binding competent state as the degree of the phosphorylation within a hexamer is increased (compare Fig. 1B). The threshold in this switch is crossed after a specific time because of kinetic ordering of phosphorylation in KaiC: because Thr432 phosphorylation occurs first, KaiB interaction initially is inhibited, and this inhibition is overcome only at late times when Ser431 phosphorylation has risen enough to cancel out the effect of pThr432. To quantify this effect, we determined how the amount of KaiB•KaiC complexes changes in the models as KaiC phosphorylation increases over time by fitting a simulated time course of KaiB•KaiC complex formation to a Hill function: $1/(1+{\left(\frac{K}{t}\right)}^{{\text{n}}_{\text{H}}})$, where n_H is a Hill coefficient that quantifies the sigmoidal, switch-like character to the kinetics, and n_H > 1 indicates ultrasensitivity. The parameter sets that allow circadian rhythms over a wide range of KaiA concentrations all show a Hill coefficient of at least 2 (Fig. 5B).

We then sought to understand in qualitative terms why an ultrasensitive dependence of the KaiB interaction on phosphorylation state can allow the oscillator to function properly over a wide range of conditions. We compared the optimally tuned allosteric model and the independent subunits model by simulating a time course of phosphorylation when an oscillator reaction is first initiated from the unphosphorylated state. On these plots we overlaid the capacity of the pool of hexamers to inhibit various amounts of KaiA by forming KaiB•KaiC complexes (Fig. 5C). In the allosteric model, ultrasensitivity from opposition between the phosphorylation sites allows the inhibitory strength of negative feedback against KaiA to rise sharply after an initial lag. The result is that for different amounts of KaiA, the onset of inhibition happens at a similar time and the timing of the oscillation is therefore similar (Fig. S10). For the independent subunits model, the reaction requires substantially different delays to inhibit different amounts of KaiA, resulting in a period of oscillation that changes markedly as [KaiA] increases, and complete failure of rhythms outside of a narrow range of conditions.

The success of the allosteric model comes from a cooperative mechanism whereby the phosphorylation states of the six subunits in a hexamer are weighed together to compute a single functional output, manifested as the KaiB-binding state of the entire ring. Because of the importance of having all six interacting subunits linked as a concerted allosteric unit, we asked how the model would perform if the number of subunits that could interact allosterically were altered. We found that the range of KaiA concentrations over which the system shows oscillations grows rapidly as the number of subunits participating in the allosteric switch increases (Fig. 5D and Fig. S10), whereas the spread in oscillator period seen over this KaiA range decreases (Fig. 5E and Fig. S10). Both these effects are correlated with increased ultrasensitivity of KaiB–KaiC complex formation (Fig. S10). Once hexameric interactions are included, the model has the potential to reach the full oscillatory range seen in the experimental data, with minimal spread in period. The oscillator can function over an even wider range of KaiA concentrations if even higher-order (unrealistic) oligomeric interactions are present in the model, underscoring the importance of allosteric coupling between many oligomeric subunits for this mechanism (Fig. 5 D and E and Fig. S10).

Discussion

The simplicity of the purified KaiABC oscillator makes it a remarkably powerful model system to investigate the mechanistic origins of circadian rhythms and to study the robustness of biochemical circuits generally. We wanted to understand which biochemical features of the proteins are crucial for generating oscillations with a precisely defined period, with the goal of producing a mechanistic mathematical model that can account for the behavior of the purified components.

The key negative feedback process that allows sustained oscillation in this system is the sequestration of the activator KaiA into inactive KaiB-dependent complexes. This kind of molecular titration is used widely throughout biology, including in the control of morphogens in development (33), regulation of transcription through sigma/anti-sigma interactions (34), and microRNA–mRNA buffering (35). The dynamics of stochiometric titration mechanisms typically are quite sensitive to the relative concentrations of the components involved, which is why it has been argued that when they are used in timing systems, tight controls must be placed on gene expression (36).

Our modeling-based analysis of the KaiABC system shows that one way to make the dynamics of such a negative feedback loop less dependent on component concentration is to make the ability of molecules that can participate in sequestering the activator an ultrasensitive function of their activation state. In other words, if the system abruptly switches from very little sequestration to its full capacity, timing can be maintained precisely even if the activator concentration is not tightly controlled, extending the range of conditions over which a biochemical circuit can function.

We found that this ultrasensitivity can be realized in the hexameric architecture of KaiC only when the two phosphorylation sites, Ser431 and Thr432, oppose each other’s influence. Effectively, each KaiC hexamer acts as a comparator, switching its state when modification on Ser431 outweighs modification on Thr432. This helps explain the role of Thr432 in the clock; because Thr432 is phosphorylated quickly after a hexamer is stimulated by KaiA and then favors an allosteric state of KaiC that can be activated further, it effectively forms a fast positive feedback loop on KaiA activity. Subsequent Ser431 phosphorylation then acts as a dominant slow negative feedback loop. This fast positive–slow negative network motif is a common means of generating oscillations (37).

KaiC is related to the AAA+ ATPases, many of which exhibit strong long-range allosteric communication effects, both within a ring when subunits change, e.g., their nucleotide-bound state, and through ring–ring stacking interactions (38). We propose that KaiC has evolved to make use of these communication mechanisms to ensure precise timing: antagonism between differentially phosphorylated subunits within the CII ring to precisely define timing and then ring–ring stacking interactions to transduce this signal to the CI ring to allow KaiB-dependent feedback. The result is that although the strength of negative feedback can adapt dynamically to accommodate changes in protein concentration, the timing of the response is precise.

Because of the ease of using opposed posttranslational modifications to drive an allosteric switch, we suspect that other biological timing circuits may have analogous mechanisms to achieve precise timing. In eukaryotic clock systems, the analysis is complicated by the presence of many phosphorylation sites. However, it appears that the Frequency protein in Neurospora crassa has distinct clusters of phosphorylation sites that have opposing effects on the clock period when mutated (39). Allosteric response of protein structure to multisite posttranslational modification may allow clock proteins to cooperatively communicate the opposing effects of phosphorylation sites throughout the protein, effecting an ultrasensitive switch in activity, a key mechanism for precise timing that the cyanobacteria have implemented via the KaiC hexameric ring structure.

Materials and Methods

Protein Purification and in Vitro Protein Reactions.

All proteins were recombinantly expressed and purified from Escherichia coli, and protein reactions were prepared as previously described (25). Unless otherwise specified, all reactions were performed by using 3.5 μM KaiB and 3.5 μM KaiC at 30 °C in a reaction buffer containing 10% (vol/vol) glycerol, 150 mM NaCl, 20 mM Tris⋅HCl (pH 8.0), 5 mM MgCl₂, 50 μM EDTA, and 5 mM ATP. For full details, see SI Appendix.

Measuring KaiB–KaiC Interaction.

Clock reactions at varying KaiA concentrations (1–4 μM), 3.5 μM KaiC, and 3.5 μM KaiB-FLAG were first preincubated for 16 h to allow the initial transient behavior to decay. Samples then were taken every 4 h over a 24-h cycle by flash freezing in liquid nitrogen. For the no-KaiA condition, KaiC was first hyperphosphorylated by using HA-tagged KaiA, which was removed by immunoprecipitation before addition of KaiB-FLAG (20). The input, supernatant, and eluate samples from the immunoprecipitation were analyzed by SDS/PAGE electrophoresis to resolve each of the four KaiC phosphoforms. Percentages of each subunit phosphorylation state relative to the total KaiC loaded per lane were extracted by densitometry of the scanned SDS/PAGE gels. We propagated an estimated 2% absolute error in our gel densitometry measurements through the calculation of these enrichment ratios and then excluded points from the final average with a relative error >1.0. For full details, see SI Appendix.

Reactions with Artificially Mixed KaiC Hexamers.

Monomerization of KaiC was carried out following Nishiwaki et al. (15). Briefly, KaiC was buffer exchanged into a buffer with 0.5 mM ADP and incubated at 4 °C to disrupt hexamer structure. To prepare “mixed” hexamers, monomerized KaiC mutants or wild type were mixed 1:1 before rehexamerization via the addition of ATP, as detailed in SI Appendix. To prepare “separate” hexamers, KaiC mutants or wild type were first rehexamerized separately and then combined.

Standard clock reactions were prepared with 3.5 μM total of the phosphomimetic and wild-type KaiC preparations. Identical reactions with KaiB-FLAG in place of KaiB were sampled every 2–6 h to assay KaiB•KaiC interaction by anti-FLAG immunoprecipitation. To assess the extent of mixing in these experiments, one of the KaiC mutants or wild-type KaiC carried an N-terminal His₆ tag. Mixing was determined as the extent to which untagged KaiC could be coprecipitated with tagged KaiC. Detailed protocols for His-tag pulldowns and anti-FLAG immunoprecipitation may be found in SI Appendix.

Michaelis Constant (K_m) Determination for KaiA Acting on KaiC.

KaiC with various levels of phosphorylation was produced by dephosphorylation of hyperphosphorylated KaiC for 33, 9.5, or 4 h at 30 °C (Fig. 2 A–C, respectively). Various concentrations of KaiA then were reintroduced to a 3.5-μM solution of these partially dephosphorylated KaiC samples. Subsequent KaiC phosphorylation was analyzed by SDS/PAGE. Initial rates of change of unphosphorylated KaiC were determined by linear regression to the early portions of the time course (Fig. S3). Initial rates were plotted with respect to KaiA concentration and fit to a Michaelis–Menten function with baseline $(V_i=V_{dephos}+V_{max}[KaiA]/(\left[KaiA\right]+K_{\text{m}}^{eff})$ to determine the effective Michaelis constant, or $K_{\text{m}}^{eff}$. Upper and lower error bounds on $K_{\text{m}}^{eff}$ were determined by the distribution of fits using bootstrapped datasets.

To determine the effective K_m for KaiC mixed with KaiC-EA, wild-type His₆–KaiC was first fully dephosphorylated by incubation at 30 °C for 36 h, and then prepared as “separate” or “mixed” hexamers with KaiC-EA at various molar ratios. The preparations then were diluted to 3.5 μM, mixed with various concentrations of KaiA, and assayed as described above. We assayed degree of mixing by His₆-tag copreciptation. Complete details are in SI Appendix.

Mathematical Modeling of the KaiABC Oscillator.

A detailed derivation and analysis of the allosteric model and the independent subunits model may be found in SI Appendix. Differential equations governing the rate of change for each possible KaiC hexamer phosphorylation state were numerically integrated over time by using the ode45 algorithm in MATLAB. Kinetics rates for KaiB binding and KaiC phosphorylation and dephosphorylation were constrained by fits to experimental kinetics as previously reported (20, 25). Each KaiC subunit state (U, pT, pS, pTpS) was assigned a free energy parameter defining its influence on the equilibrium between the two allosteric hexamer states. Negative $\mathrm{\Delta }G$ favors the KaiB-binding competent state.