Highly sensitive detection of nanoparticles with a self-referenced and self-heterodyned whispering-gallery Raman microlaser

Significance

To date, loss compensation in optical microresonators has been done using rare-earth ions, which requires additional processing steps and costs and raises biocompatibility concerns. An alternative to integrating rare-earth ions for loss compensation is the use of intrinsic gain mechanisms such as Raman and parametric gain present in the materials from which resonators are fabricated. Here, we report the first implementation to our knowledge of Raman gain-induced loss compensation in silica whispering-gallery-mode (WGM) resonators for improved detection and the first demonstration to our knowledge of mode splitting in a WGM Raman microlaser for detecting and counting single nanoparticles down to 10 nm. This intrinsically self-referenced, self-heterodyned, and biocompatible scheme has enabled achieving record-high polarizability sensitivity (down to 3.82 × 10⁻⁶ μm³) without using plasmonic effects, passive or active stabilization, or frequency locking.

Abstract

Optical whispering-gallery-mode resonators (WGMRs) have emerged as promising platforms for label-free detection of nano-objects. The ultimate sensitivity of WGMRs is determined by the strength of the light–matter interaction quantified by quality factor/mode volume, Q/V, and the resolution is determined by Q. To date, to improve sensitivity and precision of detection either WGMRs have been doped with rare-earth ions to compensate losses and increase Q or plasmonic resonances have been exploited for their superior field confinement and lower V. Here, we demonstrate, for the first time to our knowledge, enhanced detection of single-nanoparticle-induced mode splitting in a silica WGMR via Raman gain-assisted loss compensation and WGM Raman microlaser. In particular, the use of the Raman microlaser provides a dopant-free, self-referenced, and self-heterodyned scheme with a detection limit ultimately determined by the thermorefractive noise. Notably, we detected and counted individual nanoparticles with polarizabilities down to 3.82 × 10⁻⁶ μm³ by monitoring a heterodyne beatnote signal. This level of sensitivity is achieved without exploiting plasmonic effects, external references, or active stabilization and frequency locking. Single nanoparticles are detected one at a time; however, their characterization by size or polarizability requires ensemble measurements and statistical averaging. This dopant-free scheme retains the inherited biocompatibility of silica and could find widespread use for sensing in biological media. The Raman laser and operation band of the sensor can be tailored for the specific sensing environment and the properties of the targeted materials by changing the pump laser wavelength. This scheme also opens the possibility of using intrinsic Raman or parametric gain for loss compensation in other systems where dissipation hinders progress and limits applications.

There is an increasing demand for new technologies to detect small molecules, nanoparticles, and airborne species (1–4). In the past decade we have witnessed a boost in the number of label-free detection techniques with varying levels of sensitivities. Techniques relying on electrical conductance (5), light scattering and interferometry (6–8), surface and localized plasmon resonance (9, 10), nanomechanical resonators (11, 12), and optical resonances (13–17) have been demonstrated.

Whispering-gallery-mode (WGM) microresonators with their high quality factor, Q, and small mode volume, V, are known to enhance light–matter interactions and have extraordinary sensitivities to changes and perturbations in their structure or proximity (18, 19). They have been of great interest for sensing biomarkers, DNA, and medium-size proteins at low concentrations, as well as for detecting viruses and nanoparticles at single-particle resolution (19–31). A particle or molecule entering the mode volume of a resonator or binding onto its surface induces a net change in the polarizability of the resonator-surrounding system and perturbs its optical properties (19). This manifests itself as a shift of the resonance frequency, broadening of the resonance linewidth, or formation of a doublet via mode splitting depending on the interaction strength and the scattering and absorption properties of the binding particle or the molecule (14, 15, 17, 32, 33).

In WGM sensors, the fundamental limit of sensitivity is determined by Q/V, which quantifies the strength of the interaction between the particle and the cavity field. Thus, it can be improved by decreasing V or increasing Q. One can increase Q by compensating the losses and decrease V by shrinking the size of the WGM resonator (WGMR). However, decreasing the resonator size below a critical value inevitably increases bending losses and eventually decreases Q. Instead, hybrid systems combining high-Q WGMs with highly confined (small-V) localized plasmons have been demonstrated (21, 22, 24, 27, 34), achieving detection of single proteins and very small viruses. Q enhancement of WGM resonances by compensating losses via optical gain has also been demonstrated (15, 35, 36) in silica microtoroids doped with rare-earth ions such as erbium (Er³⁺) and ytterbium (Yb³⁺). Resonators with optical gain are referred to as active resonators (36–38). When such a WGMR is optically pumped above lasing threshold, the resultant laser has a narrower linewidth than the cold cavity and thereby improves the detection limit and sensitivity beyond what can be achieved by the passive (no optical gain-providing mechanism) or by the active resonator below lasing threshold (15, 35, 38). However, fabricating WGM–plasmon hybrids and active WGMRs with dopants introduces additional processing steps and costs. For example, WGM–plasmon hybrids require preparation and adsorption of plasmonic nanostructures onto the resonator surface, and active resonators suffer from the fact that most rare-earth ions are not biocompatible and that for each different wavelength band of operation a different rare-earth ion and a different pump laser should be used.

Results and Discussion

In this work we take a fundamentally different physical process to increase Q/V and thereby the fundamental sensitivity limit, as well as the detection limit. Instead of embedding rare-earth ions as the gain medium in a silica microtoroid resonator, we use the intrinsic Raman gain (38, 39) in silica to achieve loss compensation and highly sensitive nanoparticle detection. This does not require any dopant or additional fabrication complexities. We demonstrate Raman gain-induced Q enhancement (linewidth narrowing via loss compensation), Raman gain-enhanced detection of mode splitting in the transmission spectra, and splitting in Raman lasing for single-nanoparticle detection and counting. We have detected NaCl nanoparticles of radii 10 nm that have smaller polarizabilities than polystyrene and gold nanoparticles of the same size. This level of sensitivity is achieved without using plasmonic enhancement or any laser stabilization and noise cancelation schemes. Integrating plasmonics and stabilization techniques into our scheme will further enable significant improvement in the sensitivity and detection limit.

Our approach of replacing rare-earth ion-doped WGM microresonator/microlaser by WGM silica Raman microresonator/microlaser for mode splitting-based nanoparticle detection brings six fundamental improvements: (i) an intrinsically self-referenced (i.e., no need for an external reference to eliminate or suppress thermal drifts and laser noise) and self-heterodyned sensor (i.e., nanoparticle-induced splitting of a Raman lasing line creates a doublet that when detected by a photodetector generates a beatnote signal whose frequency corresponds to the amount of mode splitting); (ii) higher sensitivity and lower detection limit at single-particle resolution using WGMRs pumped below lasing threshold (i.e., active resonators have much narrower linewidth and better sensitivity than a passive resonator) or above lasing threshold (i.e., microlaser); (iii) a dopant-free low-threshold WGM microresonator/microlaser for sensing applications, which retains the inherent biocompatibility of silica; (iv) faster detection owing to the elimination of the need for scanning the wavelength of a tunable laser around a resonance to obtain the amount of splitting; (v) a WGM sensor with significantly lower cost because it eliminates the need for narrow linewidth tunable lasers and does not require dopants or plasmonic structures [In silica microtoroids, Raman lasing with a fundamental linewidth as narrow as 4 Hz has been reported (40). This is much narrower than the commercially available tunable lasers.]; and (vi) the ability to use the same WGMR as a microlaser with emission in different spectral bands just by changing the wavelength of the pump laser or by using a broadband pump. In WGM microlasers with rare-earth-ion dopants, one should not only change the dopant but also the pump to obtain emission in different spectral windows. Exploiting the Raman gain enables one to operate the same WGMR at different wavelengths and loosens the requirement of specific wavelength for pump lasers. WGM sensors can benefit from this in various ways, as will be explained in the discussions of experimental results.

Stimulated Raman scattering is a nonlinear optical process that provides optical gain in a broad variety of materials. The Raman process generates photons at a frequency that is up- or down-shifted (anti-Stokes or Stokes) from the frequency of the incident photons by an amount equivalent to the frequency of an internal oscillation of the material system, such as vibration, rotation, stretching, or translation (39). Raman gain has found many applications in biology, material science, sensing, environmental monitoring, optical communication, laser science, and spectroscopy (41–45). However, in most of the materials, such as silica, silicon, and CaF₂, Raman gain is very small (of the order of 10⁻¹³ m/W), requiring high-intensity pump lasers to drive the system above its lasing threshold. This is overcome by field confinement and resonant enhancement in waveguides and resonators. Raman lasing has been observed in silicon waveguide cavities (46), silicon waveguides within fiber ring cavities (47), silicon photonic crystal cavities (48), and WGMRs such as silicon microring (49), silica microspheres (50), silica microtoroids (40, 51), glycerol–water droplets (52), and CaF₂ disks (53). However, to date Raman gain or Raman lasing has not been used for loss compensation to enhance optical detection capabilities at single-particle resolution.

WGM microtoroidal silica resonators are ideally suited for Raman laser applications because they can be mass-fabricated on a silicon chip such that different spectral bands can be covered on a single chip. They have high Q and microscale V, which make it easier to achieve high intracavity powers to enhance nonlinear effects and obtain low threshold lasing (P_threshold ∼ V/Q²). Finally, they are compatible with optical fibers and can be readily integrated into existing optical fiber networks. The Raman gain spectra for silica is given in Fig. 1C, Inset, which depicts that Raman gain takes place within a band of 5–30 THz with the highest gain at about 10–15 THz away from the pump frequency. This translates to 15–23 nm for a pump in 660-nm band, 33–51 nm for a pump in 980-nm band, 74–113 nm for a pump in 1,450-nm band, and 85–130 nm for a pump in the 1,550-nm band, suggesting that the spectral band where Raman gain contributes is pump wavelength-dependent. This broad spectrum of Raman gain is due to the rapid dephasing of phonons. In addition to the spectral band to which it contributes, the Raman gain itself is wavelength-dependent and varies inversely with wavelength (54). For a pump with wavelength 1.55 μm, the peak Raman gain g_R ∼ 10⁻¹³ m/W of silica occurs for a shift of 13.2 THz (54), whereas for a pump of 526 nm the peak Raman gain of silica is reported as 1.49 × 10⁻¹³ m/W at a shift of 10.1 THz (55).

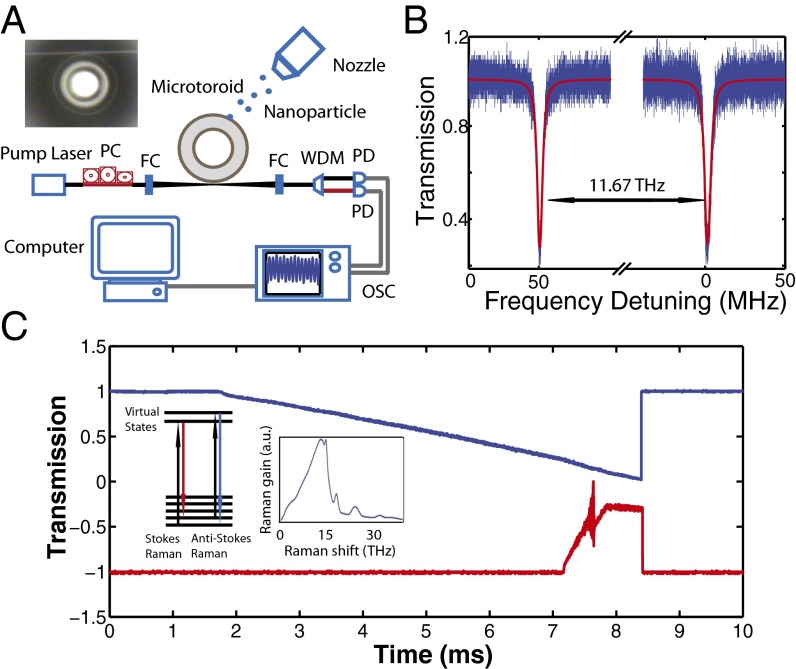
Fig. 1.

Experimental setup and measurement method. (A) Schematic illustration of the experimental setup used in the study of Raman gain-enhanced detection of single nanoparticles using mode splitting. A differential mobility analyzer with a nozzle is used to deposit nanoparticles into the mode volume of the resonator one by one. Light from a pump laser is coupled to the WGM of a microtoroid resonator by a fiber-taper coupler. The residual pump, Stokes photons, and the Raman laser were out-coupled from the resonator with the same fiber taper. The silicon chip with the silica microtoroids was placed on a 3D nanopositioning stage to precisely tune the distance between the fiber taper and the microtoroid. A fiber polarization controller (PC) was used to change the polarization state of the pump laser to maximize the coupling efficiency. The pump light and the Raman laser light (probe light in case of below lasing threshold operation) are separated from each other using a wavelength division multiplexer (WDM) and detected with photodetectors (PD) connected to an oscilloscope (OSC). (Inset) The top view of a fiber-taper-coupled silica microtoroid resonator taken by an optical microscope. FC, fiber connector. (B) Transmission spectra of the silica microtoroid obtained in the 1,450-nm and 1,550-nm bands at low optical power. The resonances in these bands are separated from each other by 11.67 THz, which lies within the Raman gain spectra given in C, Insets. (C) Typical transmission spectra obtained in the experiments for the pump in the 1,450-nm band and Raman gain and the laser in the 1,550-nm band when the wavelength of the pump laser (blue) is scanned in time. The sawtooth-like waveform is due to the thermal broadening of the resonance line. As we move along this sawtooth-like form in time, more pump light is coupled into the resonator, and cavity power build-up sufficient to produce Raman gain and lasing is achieved as seen in the increased signal in the transmission obtained in the 1,550-nm band (red). (Insets) The Raman process and the Raman gain spectra for silica, which implies that Raman gain is provided within a band of 5–30 THz away from the pump light.

Experimental Setup and Characterization

A schematic of the experimental setup is shown in Fig. 1A. The microtoroids used in this study were 40 μm in major diameter and 8 μm in minor diameter. An optical microscope image of a typical resonator used in our experiments is shown in Fig. 1A, Inset. External cavity lasers with emission in the 660-, 980-, 1,450-, and 1,550-nm band were used as pump lasers. Optical spectra of the pump and the resulting Raman laser were measured by an optical spectrum analyzer with 0.1-nm resolution. To obtain the transmission spectra of the resonators in different bands, lasers were scanned repeatedly through a frequency range of 30 GHz around a single WGM and the transmitted power was measured. Fig. 1B shows typical resonance spectra obtained for a silica microtoroid in the 1,450-nm pump band and 1,550-nm Raman gain band. The quality factors of these resonance modes are 4 × 10⁷ and 3.5 × 10⁷, respectively.

We used a differential mobility analyzer (DMA) accompanied by a nozzle to deposit nanoparticles onto the WGMR. Nanoparticles were carried out from their colloidal solution using a collison atomizer (17). After the evaporation of the solvent in polydisperse droplets, the solid particles were neutralized to maintain a well-defined charge distribution. Then they were sent to the DMA, which classified them according to their electrical mobility. The output slit of the DMA allows only the particles within a narrow range of sizes to exit and land on the WGMR via the nozzle. The flow rate and the concentration of the colloidal solution were set low to ensure deposition of particles one by one.

Typical transmission spectra obtained for the pump in the 1,450-nm band and the Raman signal in the 1,550-nm band as the pump wavelength was scanned are given in Fig. 1C. As a result of the high Q and strong pump power, the cavity power build-up in the pump mode becomes so high that a strong thermal broadening is clearly seen in the 1,450-nm band as the wavelength of the pump laser was up-scanned from shorter to longer wavelengths. This thermal broadening helped the pump light to stay on resonance long enough to achieve Raman gain and Raman lasing in the 1,550-nm band.

Raman Gain Enhanced Detection of Mode Splitting in the Transmission Spectra.

Here, for the first time to our knowledge, we show that Raman gain in silica can be used to compensate for a portion of the optical losses in a microtoroid and thereby improve the sensitivity of the mode-splitting technique.

It is known that WGMRs support two counterpropagating modes (clockwise, CW and counterclockwise, CCW) at the same resonance frequency ω, and that a scattering center (e.g., a nanoparticle, a virus, or a molecule) can lift this degeneracy, leading to the splitting of the single resonance mode into two modes, by mediating a scattering-induced coupling between the CW and CCW modes (17, 29, 56). Mode splitting can then be resolved in the transmission spectra of the WGMR if the amount of splitting 2g = −αf²ω/V is larger than the total loss of the system, quantified by the strict condition |2g| > Γ + ω/Q for well-resolved mode-splitting (57). Here f is the field distribution of the WGM, $\alpha =4\pi R^3\left(n_p^2-1\right)/\left(n_p^2+2\right)$ is the polarizability of the particle of radius R and refractive index n_p with the surrounding medium as air, Γ = (8/3)gπ²α/λ³ is the additional loss induced by the scatterer, and ω/Q is the linewidth of the resonance (quantifying loss before the scatterer is introduced). For very small particles we have Γ ≪ ω/Q, thus the strict condition reduces to 2g > ω/Q. In practice, satisfying this strict condition is in general difficult, and the split modes overlap with each other. Although in principle we can resolve splittings as small as ω/NQ, where N is a number in the range 10−50 depending on the experimental system and signal processing capabilities, there is a detection limit beyond which the mode splitting cannot be resolved. The dependence of 2g on f² and α implies that if the overlap between the mode field and the scatterer is not high enough or if the particle is too small the induced mode splitting may be so small that it cannot be resolved within the background noise. In such cases, providing optical gain to increase the Q and hence to reduce the linewidth of the resonance will help to resolve the mode splitting (15, 35).

We conducted two sets of experiments to verify the Raman gain-assisted Q enhancement via loss compensation and hence improved detection of mode splitting. In the first experiment, we intentionally induced a small mode splitting using a fiber tip such that mode splitting could not be resolved by a low-Q resonance in the 1,550-nm band. By pumping the silica microtoroid using a laser in the 1,450-nm band, we monitored the transmission spectrum in the 1,550-nm band by a probe laser whose power was set so low that no thermal broadening was observed in the transmission spectra. As the pump power was increased, generated Stokes photons compensated for the losses, leading to narrowing of the linewidth of the resonance (Fig. 2) in the probe band. As a result, initially unobservable mode splitting became clear (Fig. 2A).

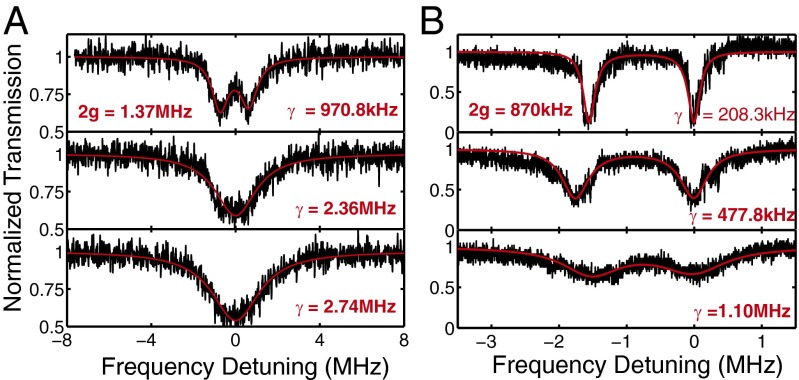
Fig. 2.

Raman gain-enhanced detection of scatterer-induced mode splitting. The experiments were performed by a pump-and-probe method. A pump laser in the 1,450-nm band was used to provide Raman gain in the probe band of 1,550 nm. As the pump power was increased, provided Raman gain increased from bottom to top in A and B where the spectra in the bottom panels were obtained when the pump was turned off (no gain). Because the power of the probe laser was set 1.2 μW and 2.0 μW in A and B, respectively, we do not see thermal broadening for the probe mode in the 1,550-nm band. (A) Initially unseen mode splitting in the transmission spectra (Bottom, pump was off) became visible (Top, pump power was 151 μW) owing to the narrowing of resonance linewidth as the pump power was increased. (Middle) The pump power was 87 μW, which was enough to induce linewidth narrowing for the probe mode but not sufficiently high to help resolve the splitting. Note that at these high pump powers there is thermal broadening in the 1,450-nm band. (B) Initially barely seen mode splitting (Bottom, pump was off) became much clearer and well-resolved (Middle and Top, pump power was set as 69 μW and 97 μW, respectively) as the pump power was increased. Moreover, the split resonances become deeper, implying that the provided Raman gain, which compensates intrinsic losses of the resonator, moves the taper-resonator systems from the undercoupling regime to closer to the critical coupling. Note that the distance between the resonator and the taper was kept fixed, thus there is no change in the coupling loss. In A and B, experimentally obtained transmission spectra are given in black, and the the best theoretical fit to the experimental data are given in red. γ denotes the linewidth of resonance modes and is obtained from the red fitting curve.

In the second experiment, we adjusted the position of the fiber tip in the mode volume such that it introduced a very small amount of mode splitting. Then we set the taper-resonator system to undercoupling regime so that the features of the mode splitting were barely seen when there was no pump. When the pump laser was turned on and its power was increased, a clear mode splitting of 1.5 MHz was observed in the transmission spectrum. This is an indication of the enhancement of the Q of the probe mode in the 1,550-nm band. We also observed that the gain shifted the taper-resonator system from undercoupling regime to close-to-critical coupling. This can be understood as follows. In the undercoupling regime coupling losses quantified by κ_ext is much smaller than the intrinsic losses κ_o (i.e., κ_o ≫ κ_ext). Because during the experiment the distance between the fiber taper and the resonator was kept fixed, κ_ext stayed the same. The induced gain reduced κ_o and brought it closer to κ_ext, and thus shifted the system from undercoupling regime to critical coupling where κ_o = κ_ext. This is reflected in the transmission spectra as a transition from a close-to-unity transmission to close-to-zero transmission at resonance and better resolution in detecting the splitting (Fig. 2B). We should note here that one can move from one coupling regime to another in two different ways: (i) by keeping κ_o fixed and varying κ_ext via tuning the distance between the resonator and the fiber-taper or (ii) by keeping κ_ext constant (i.e., taper-resonator distance is fixed) and varying κ_o, which can be done either by introducing extra losses or by compensating the losses. Here, we, for the first time to our knowledge, demonstrate this second approach.

Raman Lasing in the Same WGMR at Different Bands.

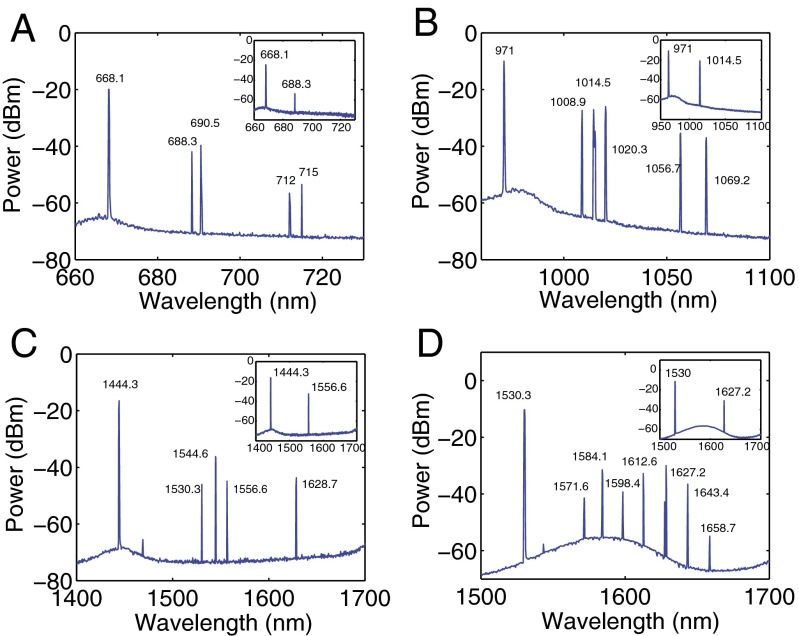
Once the pump power exceeds a threshold value, lasing was observed at frequencies red-shifted relative to the pump frequency. By fine tuning the pump power and the taper-resonator coupling strength, we obtained single and multimode lasing in the same microtoroid. This suggests that a single WGMR can be used to generate lasing at different colors covering a large range of the spectrum and hence can be used for optical detection and sensing in all these bands (Fig. 3). The lowest lasing thresholds in our experiments were 147.2 μW for the 1,550-nm pump, 169.5 μW for the 1,450-nm pump, 92.1 μW for the 980-nm pump, and 79.3 μW for the 660-nm pump. At much higher pump powers we observed that the spectra evolved from single mode (Fig. 3, Insets) to a spectrum with multiple Raman lasing peaks separated by the free spectral range, as well as cascaded Raman lasing lines separated by the Raman shift. The first-order Raman lasing in the resonator serves as the pump for the second-order Raman lasing, so we observed multiple second-order Raman lasing lines for the pumps in the bands of 660 nm, 980 nm, and 1,450 nm. Our optical spectrum analyzer only goes to 1,700 nm, so we could not observe the second-order Raman lasing lines for the pump in the 1,550-nm band.

Fig. 3.

Emission spectra of Raman lasing obtained in the same silica microtoroid resonator at different bands of the spectrum covering visible to near-IR. The pump lasers are in (A) 660-nm, (B) 980-nm, (C) 1,450-nm, and (D) 1,550-nm bands. Higher-order cascaded Raman Stokes lasing is clearly seen in all of the spectra. (Insets) The single-mode operation of the Raman lasers obtained by tuning the pump power and the coupling condition.

The ability to operate the same WGM sensor in different spectral bands is important in different ways. First, optical losses associated with the operating medium (i.e., aqueous solution, serum, air, etc.) are wavelength-dependent. Light sources and WGM resonances in the near-IR and IR bands are not preferable for operation in water owing to strong absorption. Shifting the operating wavelength to the visible band minimizes losses, leading to higher Q and easy excitation of WGM lasing. Owing to the pump wavelength dependence of the Raman gain, the same dopant-free resonator can be used in many different media for lasing and sensing applications by choosing the proper pump wavelength and WGM. Second, loss induced by a binding particle scales as R⁶/λ⁴, where R is the radius of the particle and λ is the wavelength of the light. Thus, operating the sensors in longer wavelengths will help to minimize particle-induced losses and enable detecting and characterizing larger particles. The same Raman WGM sensor can still be operated at shorter wavelengths for detecting smaller particles whose detection is limited mostly by the resonance linewidth. Thus, WGM sensors using Raman gain will have larger operating range. Third, different resonances and lasing modes in the same resonator have different spatial field distributions. Therefore, their responses to a binding particle/molecule/protein are different. A nanoparticle inducing splitting or frequency shift in one lasing mode may not be able to induce a resolvable splitting in a different lasing mode in the same WGM microlaser. Therefore, the ability to have multiple-wavelength lasing, in principle, can avoid missing a binding nanoparticle/molecule or decrease the probability of a binding particle’s going undetected. Thus, having lasing in the same resonator at multiple wavelengths will help to improve detection efficiency and decrease the number of binding events gone undetected. Raman gain allows multiwavelength lasing in different bands and is suitable for the purpose listed here. Fourth, the Raman process allows one to generate lasing at many different spectral bands for which there is no commercially available laser. For situations in which there exists no laser covering the bands where a particle has its maximum absorption or scattering cross-section, a Raman microlaser will be very useful to detect and discriminate particles by monitoring their responses (absorption, scattering, etc.) to light at different wavelengths. Similarly, in situations where high absorption of a binding particle at a specific wavelength band significantly degrades Q, interfering with lasing conditions or even preventing lasing, Raman gain can be useful because one can tune the operation wavelength far from the absorption band of the particles. Thus, the ability to work at different spectral bands with the same WGM sensor using Raman gain may help one choose the proper operating band according to the properties of the particle/molecule/analyte and the surrounding, as well as to use specific wavelength-dependent responses of the particles/molecules and the medium for improving the operating range, detection efficiency, and sensitivity.

Scatterer-Induced Splitting of WGM Raman Lasing Lines.

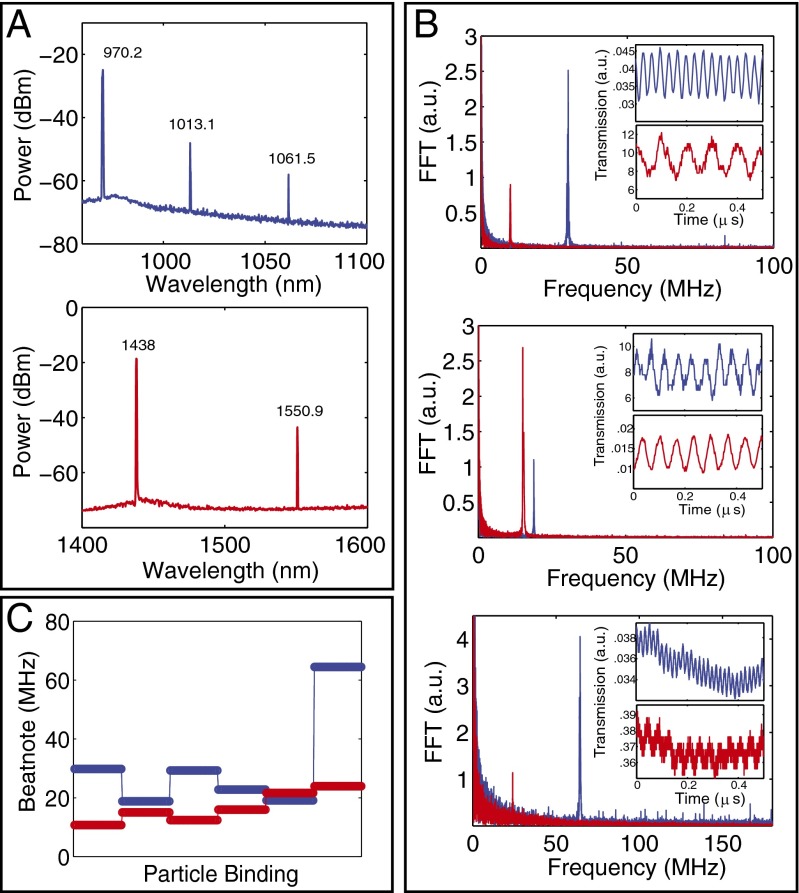
We confirmed the generation of a beatnote signal due to scatterer-induced mode splitting by introducing a nanofiber tip into the mode volume of a Raman WGM microlaser and monitored the self-heterodyne beatnote signal in response to its position (Fig. 4). Performing similar experiments using different lasing lines in the same resonator revealed that the beatnote signal and its frequency are not only affected by the size of the nanofiber within the mode volume but also by its spatial overlap with the fields of the lasing lines. At a fixed location of the nanofiber, the amount of splitting experienced by Raman lasers at different spectral bands is different (Fig. 4): Splitting may increase or decrease for all lasing modes in different bands or may decrease for some lasing modes but increase for the others. The amount of change in the splitting is different for different lasing modes. This is attributed to the facts that the spatial overlap between the nanofiber and the fields of different lasing modes are different and that mode splitting scales inversely with the wavelength. These imply that measurements at multiple wavelengths or spectral bands enable detecting scattering centers (e.g., nanofiber) that could have gone undetected if only a single lasing mode were used.

Fig. 4.

Detection of scatterer-induced mode splitting using WGM Raman lasing in two different bands in the same silica microtoroid. A nanofiber tip introduced into the mode volume of the resonator was used to simulate scatterers within the mode volume. The color codes blue and red correspond to the experiments performed with pump laser in the 980-nm (blue) and 1,450-nm (red) bands. (A) Optical spectra of Raman lasers with pumps at 980-nm (Upper) and 1,450-nm (Lower) bands. (B) Change in the beatnote signal (Inset) and its frequency obtained using fast Fourier transform (FFT) when the nanofiber tip was within the mode volume. (C) Changes in the beatnote frequency as the fiber tip repeatedly enters and exits the mode volume, each time at a different position and with different effective tip size in the mode volume. The response of the lasing modes at different bands are different. Splitting of the lasing modes (beatnote frequency) may increase or decrease depending on how the scatterers are distributed within the mode volume of each mode: Splitting may increase or decrease for both lasing modes in different bands or may decrease for one lasing mode and increase for the other lasing mode.

Detecting and Counting Single Nanoparticles with Mode Splitting in a Raman WGM Microlaser.

We evaluated the performance of the WGM Raman microlaser and the mode-splitting method to detect nanoparticles with single-particle resolution.

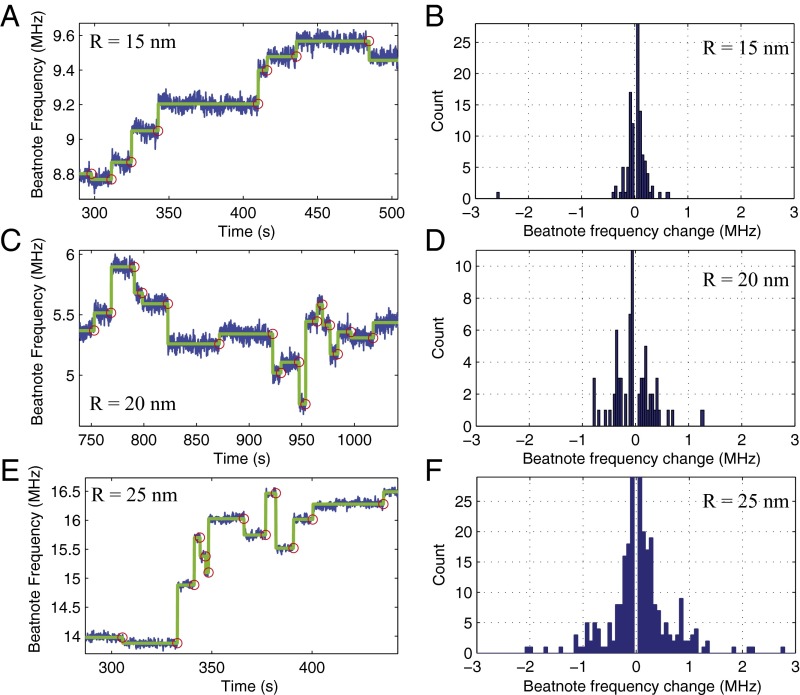
We tested our system using Au, polystyrene (PS), and NaCl nanoparticles. As discussed in the previous section, particle binding to the WGM microlaser led to the splitting of a lasing line into two, which eventually gave a self-heterodyne beatnote signal when mixed at a photodetector. The beatnote frequency corresponds to the amount of splitting. Each consecutive nanoparticle binding event led to a discrete change in the beatnote frequency. The frequency may increase or decrease depending on the location of each particle with respect to the field distribution of the lasing modes and the position of the particle with respect to previously deposited particles in the mode volume (15, 17, 28, 29, 35, 56). In Fig. 5, we give the change in beat frequency and hence the splitting of the lasing mode as NaCl nanoparticles of size R = 15 nm (Fig. 5A), 20 nm (Fig. 5C), and 25 nm (Fig. 5E) were continuously deposited onto the WGM Raman laser. With each particle binding event we observe a discrete up or down jump in the beat frequency. The histograms shown in Fig. 5 B, D, and F reveal that the larger the particles, the wider the distribution of the changes in the beatnote frequency.

Fig. 5.

Detection of NaCl nanoparticles using the scatterer-induced splitting of WGM Raman laser. Each discrete upward or downward jump in the beatnote frequency spectra corresponds to a binding event of one nanoparticle with radius (A) R = 15 nm, (C) R = 20 nm, and (E) R = 25 nm. Histograms of the beat frequency changes for each nanoparticle binding event for NaCl nanoparticles of size (B) R = 15 nm, (D) R = 20 nm, and (F) R = 25 nm imply a correlation between the size of the particle and the width (SD or rms) of the distribution.

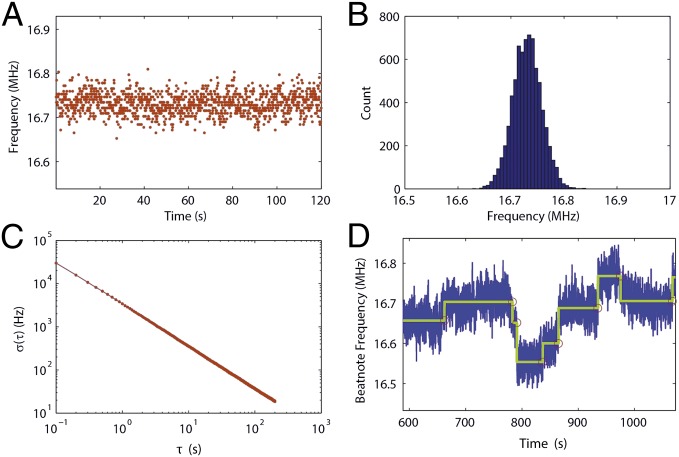
To estimate the reproducibility of the measured beatnote frequency, we stopped nanoparticle deposition at some point and continuously measured beat frequency for extended durations of time. Fig. 6 A and B depict the beat frequency as a function of time and the histogram of measured frequencies, respectively. The measured frequencies stayed within 100 kHz of the mean frequency. We also calculated the Allan deviation, which is a commonly used technique to estimate the frequency stability. The Allan deviation for the beat frequency was obtained using segments (integration time) from 0.1 to 200 s. The result is shown in Fig. 6C. In Fig. 6D we present the measurement results for NaCl nanoparticles of R = 10 nm. It is seen that whereas some of the particle-binding events led to resolvable changes in the beat frequency the changes in some others were not very clear and were obstructed by the noise level in our system.

Fig. 6.

Noise analysis. (A) Change in the measured beatnote frequency as a function of time. (B) Histogram of the measured beatnote frequency. (C) Allan deviation of measured frequency as a function of time. (D) Beatnote frequency measured for NaCl nanoparticles of size R = 10 nm.

Considering that we can resolve the binding events even at the present noise level without any active or passive stabilization procedure, we can safely say that the detection limit of the WGM Raman microlaser is 10 nm for NaCl particles. This corresponds to a polarizability of 3.82 × 10⁻⁶ μm³, which is 100-fold smaller than that of the gold nanorods detected with a silica microtoroid stabilized using the Pound–Drever–Hall technique (30). We should note that WGM-type sensors respond to the changes in the effective polarizability; therefore, they measure the polarizability of a particle/molecule entering the mode volume. Size or volume measurement is possible when the refractive index of the nanoparticle is known. Two particles in the same environment having the same volume (size) will have different polarizability if their refractive indexes are different; the one with higher refractive index has higher polarizability. Metallic nanoparticles (e.g., Au, Ag, etc.) with or without plasmonic enhancement have higher refractive index than dielectric particles (e.g., PS, NaCl, KCl, or silica). Thus, with the same sensor and under the same measurement conditions the size of the smallest detectable nanoparticles by plasmonic enhancement is always smaller than the size of the smallest detectable dielectric nanoparticle where plasmonic effects are not valid. Therefore, detecting particles with smaller volume does not necessarily mean better sensitivity.

Noise Analysis.

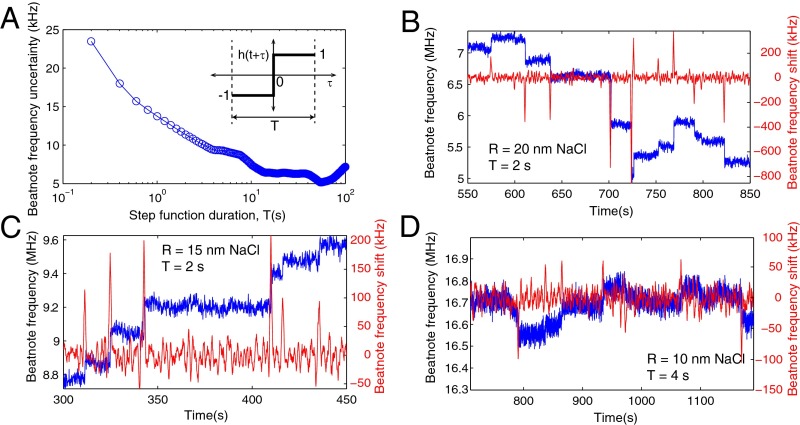
In our experiments, the raw noise and hence the sensitivity was at a level of 100 kHz (Fig. 6A), which translates into an SD of 26.4 kHz. To estimate the frequency noise floor (i.e., the uncertainty in the beat frequency) and hence the sensitivity limit in our measurements, we performed cross-correlation $\delta \nu \left(t\right)=\left(2/T\right){\displaystyle {\int }_{-T/2}^{T/2}\nu \left(t\right)h\left(t+\tau \right)d\tau }$ between the raw beat-frequency data ν(t) and a step function h(t) of duration T (Fig. 7A, Inset) (33). To determine the noise floor, we stopped the particle deposition after the first particle-binding event and monitored beat frequency over the time window during which the particle flow was stopped. As seen in Fig. 7A, the uncertainty in the the beat-frequency change decreases as the duration of the step function increases (i.e., more data are included). We observed that uncertainty in the measured beat frequency dropped from ∼23.5 kHz for T = 0.2 s to ∼16 kHz for T = 0.5 s, reaching a noise floor of 14 kHz for T = 1 s. For step functions longer than 4 s the noise floor is mainly determined by the fluctuations of the coupling conditions. In the case that a binding event takes place within the duration of the step function, the noise floor increases significantly. For cases similar to our experiments in which binding events take place at random time instants and the arrival times of the particles cannot be controlled, the duration T of the step function should be chosen carefully, taking into account the low-frequency noises (33). Fig. 7 B–D depict the results of the cross-correlation method together with the raw beat-frequency data. Clearly, when the duration of the step function is properly chosen, the cross-correlation method captures the binding events that lead to beat-frequency changes.

Fig. 7.

Noise analysis. (A) Uncertainty in the beatnote frequency as a function of the duration of the step function (Inset) used in the cross-correlation. (B–D) Beatnote frequency as a function of time for NaCl particles of radius (B) R = 20 nm, (C) R = 15 nm, and (D) R = 10 nm. Blue curves are raw data of beatnote frequency obtained in the experiments. Red curves denote the beat-frequency changes captured by the cross-correlation method using step functions of duration (B) T = 2 s, (C) T = 2 s, and (D) T = 4 s.

In Fig. 7 C and D, an increase is seen in the raw noise as well as the noise floor at time intervals 343−410 s and 791−837 s, respectively, These correspond to time intervals between consecutive binding events that are clearly resolved by the cross-correlation method. The measured noise levels of ∼13.2 kHz and ∼9.7 kHz, respectively, for T = 2 s and T = 4 s during these time intervals are clearly higher than the noise floors ∼11.4 kHz and ∼9.4 kHz estimated from Fig. 7A. We think that the increase in the noise in these intervals is due to hidden and unresolved binding events that take place between two consecutive resolved detection events, within the duration of the step functions used in the cross-correlation method. We should note that the cross-correlation method indeed results in some peaks or dips that are higher or deeper than the surrounding points; however, we cannot assign detection events for those points within these intervals with high confidence.

Estimating the Size of Nanoparticles.

Although each discrete change in the beatnote frequency corresponds to a nanoparticle binding and detection event, we cannot extract the size or polarizability of each detected nanoparticle directly from these changes, because the amount of the changes is determined not only by the polarizability of the detected particle but also by its location within the mode volume as well as by its location with respect to previously deposited nanoparticles (15, 17, 58). Therefore, statistical analysis is needed to assign an average polarizability or size to a particle ensemble.

As shown in Fig. 5, each discrete change of the beatnote frequency signals a nanoparticle landing in the mode volume. Different heights for the same particle size are due to different amounts of overlaps between the WGM and the detected particles. The distribution of these discrete jumps contains information on the particle size (15, 58): The larger the particles, the wider is the distribution for beatnote frequency jumps (Fig. 5 B, D, and F). Because we used the same particle delivery system that has a nozzle of inner diameter 80 μm and an output air cone covering a much larger area than the microtoroid resonator, its effect on distribution of the particles on the microtoroid is negligible. Thus, we can safely say that the distributions of particle positions in the resonator mode volume and the shape of the distribution function for the beatnote frequency jumps are the same for different particle sizes. However, they cannot be directly compared by calculating the SD of the detected jumps because the jump events below noise level cannot be resolved.

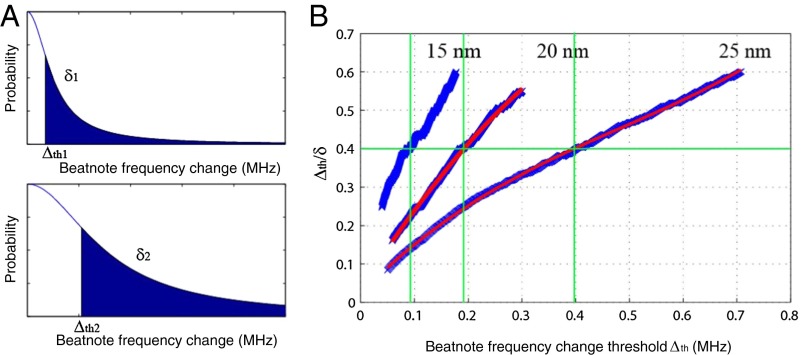
To extract the size information, we calculated the rms (denoted as δ here) of the beatnote frequency changes that are above a threshold value Δ_th. For different particle sizes, the distributions of the beat-frequency changes follow the same statistical model, and thus the ratio Δ_th/δ should be equal when Δ_th is at the same position with respect to each distribution (Fig. 8A). Therefore, by plotting Δ_th/δ for different Δ_th values, one can estimate the effective width of the respective jump distributions. Fig. 8B shows the curves of Δ_th/δ versus Δ_th for three different sizes of NaCl particles. By comparing the scaling of the horizontal axis for all three cases, we can extract the ratio of the widths of the distributions. This suggests that by using measurement results from an ensemble of particles with known sizes one can use a referencing scheme to assign an average size to a given ensemble of particles: For the reference ensemble and the ensemble of the particle of interest, one first obtains Δ_th1/δ₁ and Δ_th2/δ₂, respectively, as a function of δ₁ and δ₂ from the measured data, and then finds Δ_th1 and Δ_th2, which satisfy Δ_th1/δ₁ = Δ_th2/δ₂. In Fig. 8, we used Δ_th1/δ₁ = Δ_th2/δ₂ = 0.4. Because the discrete jump heights are related to particle polarizability, which is proportional to R³, one can estimate the size ratio between the reference ensemble and the ensemble of the particles of interest using Δ_th1/Δ_th2 = (R₁/R₂)³. Using this method, we estimated the size ratios among the three different ensembles of NaCl particles to be 30.6: 39.3: 50.0, which represents less than 3% error compared with nominal values.

Fig. 8.

Measurement of an ensemble of nanoparticles using scatterer-induced beatnote frequency changes of a WGM Raman microlaser. (A) The distribution of the discrete changes in Raman laser beatnote frequency. Larger particles induce larger changes with wider distribution. However, the shapes of beatnote frequency-change distributions are the same. (B) The relations between Δ_th/δ and Δ_th for detected NaCl particles of radii 15, 20, and 25 nm (from left to right). At the same Δ_th/δ ratio, the corresponding Δ_th value gives the estimated width of the distribution of beatnote frequency changes.

Conclusions

In conclusion, we have demonstrated that Raman gain in silica WGMRs can be used to compensate losses, to enhance Q, and to enable gain-enhanced detection and characterization of nanoparticles at single nanoparticle resolution using the mode-splitting method. When the Raman gain in the WGMR is below lasing threshold, loss compensation increases Q and hence enables detection of smaller splitting (35, 36). When the WGMR is pumped above lasing threshold, split lasing modes induced by a binding particle leads to a beatnote frequency that changes abruptly with each binding event. By monitoring the changes in the beatnote frequency one can count the number of particles binding to the sensor but cannot extract the polarizability of each detected particle. Instead, multiple measurements and histograms are used to assign an average polarizability to the ensemble of detected particles. In both of the cases, mode splitting provides a self-referencing scheme immune to laser frequency noise and thermal drift of resonances (59, 60). This is an intrinsic property of our scheme, in contrast to other schemes where external reference interferometers were used to subtract the probe laser noise by offline signal processing or noise was minimized by frequency stabilization techniques.

We should note that when the particles are deposited onto the resonator they may or may not fall onto a location that overlaps with the spatial mode of the WGM. Particles that do not land on the mode volume will certainly go undetected. For a particle landing on a location within the mode volume, particle polarizability (or size) and the intensity of the WGM field at the location of the particle are the parameters determining the amount of change in mode splitting: A large particle overlapping with a weak field may cause smaller splitting than a smaller particle overlapping with a stronger field (17). A particle in the mode volume may even go undetected if the interaction is not strong enough to induce resolvable change in the splitting.

Our experiments presented here have been performed in a dry environment. However, recent demonstrations of particle-induced mode splitting (31, 61, 62) and WGM Raman lasing (63) in a liquid environment imply that the techniques developed here can be extended to loss compensation of these devices in a liquid environment and biosensing in biological fluids. Moreover, similar to what we have demonstrated here for a silica microtoroid (Raman gain in silica for loss compensation and for improving the detection limit of WGM resonators), Raman gain in materials that are used to fabricate photonic crystals, plasmonic and metamaterial structures, and as well as other types of WGMRs can also be used to compensate for losses and enhance their performance by eliminating the drawbacks associated with dopants. For example, Raman gain in silicon can be used for loss compensation in silicon microrings and silicon photonic crystal structures. The ideas developed here can be extended to parametric gain in silica and other materials for loss compensation. We believe that this dopant-free loss compensation technique will find applications in other photonic devices and can be effectively used to improve their performance and enhance the sensitivity and the detection limits of sensors based on resonance effects. Achieving the detection of nanoparticles down to 10 nm in size and counting them one by one are encouraging for us to continue the research to push the detection limit to single-molecule resolution using the proposed loss-compensation technique. It should be noted that plasmonic effects (21, 22, 27, 30), laser frequency stabilization, and noise suppression techniques (28, 30, 33) can be integrated into our schemes to further enhance the sensitivity and lower detection limit.