Abstract
Nanoparticles are potentially powerful therapeutic tools that have the capacity to target drug payloads and imaging agents. However, some nanoparticles can activate complement, a branch of the innate immune system, and cause adverse side-effects. Recently, we employed an in vitro hemolysis assay to measure the serum complement activity of perfluorocarbon nanoparticles that differed by size, surface charge, and surface chemistry, quantifying the nanoparticle-dependent complement activity using a metric called Residual Hemolytic Activity (RHA). In the present work, we have used a decision tree learning algorithm to derive the rules for estimating nanoparticle-dependent complement response based on the data generated from the hemolytic assay studies. Our results indicate that physicochemical properties of nanoparticles, namely, size, polydispersity index, zeta potential, and mole percentage of the active surface ligand of a nanoparticle, can serve as good descriptors for prediction of nanoparticle-dependent complement activation in the decision tree modeling framework.
Introduction
Nanoparticles are potentially powerful therapeutic tools that have the capacity to target drug payloads and imaging agents and could assist in the diagnosis and treatment of a variety of human disease conditions1. One problem encountered by this relatively new approach occurs when nanoparticles encounter the scrutiny of the resident immune system. Complement is a part of innate immunity and serves as a first line of defense of the intravascular space2. Complement proteins react to potential targets within minutes, directing their rapid clearance and initiating powerful inflammatory pathways. Nanoparticles that activate complement can produce adverse side-effects3–5. Thus, the complement system represents a major obstacle to the safe use of nanomaterials. Therefore, it is important to assess the complement activating characteristics of nanoparticles in pre-clinical nanoparticle characterization studies.
Recently, we employed an in vitro hemolytic assay to measure the complement activity of perfluorocarbon nanoparticles of differing size, charge and surface chemistry6. The protocol we developed consists of two steps: First, pooled human serum is pre-incubated with nanoparticles, permitting NP-dependent activity to occur. Next, the residual capacity of each reaction mixture to lyse antibody-sensitized sheep erythrocyte cells is evaluated by titration. Each titration series is represented graphically as a curve with the volume of reaction mixture in each titration point on the x-axis and the fraction of cells lysed on the y-axis. Incubation with negative control NPs shows little or no detectable complement activation and the resulting titration curve overlaps with the serum control curve. Incubation with complement-activating NPs will deplete complement activity in the serum, which will result in a titration curve below that of serum control curve6. To quantify the change in the hemolytic activity of serum due to NP-treatment, we defined a metric called Residual Hemolytic Activity (RHA), which is the ratio of the area under the nanoparticle–treated serum curve to that of the untreated serum curve. The RHA ratio ranges from 1.0 (no detectable nanoparticle-dependent hemolytic activity) to 0 (robust nanoparticle-dependent hemolytic activity). We validated this protocol using untreated positive control nanoparticles, negative control nanoparticles, and standard complement activators and we calibrated its sensitivity to be consistent with animal model results. Details of the protocol, its validation and application to the assessment of NP-dependent complement activation, are reported in reference6.
It would be time-consuming and expensive to experimentally measure the nanoparticle-dependent (NP) complement response of every new type of nanoparticle that can be formulated for biomedical applications such as drug delivery, imaging, and disease detection. Since these nanoparticles are often multi-component systems formulated with small molecules, they can be inherently diverse in their physicochemical properties; their chemical composition, size, geometry, morphology and surface chemistry will all influence the extent of NP complement activation. One way to reduce the time and cost associated with large number of experiments is by developing computational models for predicting the NP complement response from the physicochemical properties of nanoparticles. Since there are no models that relate the physicochemical properties of nanoparticles to complement activation, one has to rely on experiments to evaluate the complement activating characteristics of every nanoparticle formulation. Modeling the relationship between complement activation and nanoparticle physicochemical properties can be useful for the rational design of nanoparticles that have minimal effect on complement activation without losing the desired functionality. Quantitative structure-activity relationship (QSAR) models can be used for assessing the potential risk of new or modified nanoparticles and prioritizing them for further assessments using experiments7. Descriptors that quantify the nanomaterial surface properties under biological conditions have already been determined for developing QSAR models of carbon-based nanomaterials (carbon nanotubes, fullerenes) and a few metal oxide nanoparticles, using the biological surface adsorption index (BSAI) approach8, 9.
In this work, we follow a machine-learning approach to model the relationship between NP-dependent complement activation and NP physicochemical properties by analyzing a diverse data set of nanoparticle formulations that vary in their size, surface charge, and surface chemistry. Machine learning approaches based on classification and multivariate regression techniques have been successfully applied to develop quantitative structure-activity relationship (QSAR) models for predicting the cytotoxicity and in vivo toxicity of metal oxide nanoparticles10–13, and the cellular uptake and apoptosis induced by nanoparticles with metallic core and organic coating14–17. The current work uses a model tree18, which is a decision tree with a linear model at each leaf node. Construction of model trees involves learning the nonlinear relationships between target attribute (continuous endpoint values) and predictor attributes (descriptors) of the samples from a data set, and expressing those relationships as a collection of linear models with the support of a decision tree. The linear model at each leaf node of the model tree is a linear regression function with parameters fitted using the data instances that end up in that leaf node. In this paper, we present such a model tree that was trained and validated using the RHA values and physicochemical property values of the sixty nanoparticle formulations listed in Table S1. These formulations include lipid-encapsulated perfluorocarbon (perfluoro-octyl bromide; PFOB) nanoemulsions, a polymeric nanoparticle and some liposome-based nanoparticles.
It is noted that the robustness and predictive power of the model tree will depend on the quality of the training dataset, the number of data instances available for training the model, the predictive power of the descriptors (the physicochemical properties), and the distribution of data points in the RHA/descriptor space. A good model is one that when trained on one data set can predict the endpoint values of new data instances at an acceptable level of accuracy. Typically, the model can be expected to perform well on new data points that fall within the model’s domain of applicability†19 if the data quality is good, the number of training data instances is very large, the descriptors have good predictive power, and the data points are uniformly distributed in the RHA/descriptor space.
Methods and data sets
Calculation of Residual Hemolytic Activity
Residual Hemolytic Activity (RHA) is a measure of nanoparticle-dependent complement activity, which is derived by comparing the residual hemolytic activity of nanoparticle-treated serum to that of untreated control serum6. RHA is defined as the area under the nanoparticle-treated serum titration curve divided by area under the untreated serum titration curve. The areas were computed by the trapezoidal integration method. Outliers in the set of RHA values obtained from repeated experiments on the same nanoparticle formulation were identified using boxplots. These outliers were removed before calculating the average RHA value for each nanoparticle formulation (Supplementary Table S1).6
Data set
The data set used for training the model tree is shown in Table S2. Data on the PFOB nanoparticles were taken from reference6 (supplementary information). There are 584 data instances listed in Table S2, where each instance is represented as a vector of five nanoparticle attribute values, namely, size, polydispersity index (PDI)‡, zeta potential, mole percentage of the active surface ligand, and RHA of a nanoparticle sample. There are sixty nanoparticle formulations listed in Table S1. Most of the nanoparticle formulations were assayed on different days; altogether over 600 samples were assayed. Therefore, the data set initially consisted of over 600 data instances but the number was reduced to 584 after excluding the data instances of those samples that were outliers (with respect to RHA values) among other samples of the same nanoparticle formulation. RHA values were considered as outliers if they were larger than q3 + w(q3 − q1) or smaller than q1 − w(q3 − q1), where q1 and q3 are the 25th and 75th percentiles, respectively, and w is 1.5.20
We considered the attributes of size, PDI, zeta potential, and ligand mole % as potential descriptors in the RHA model for the following reasons. First, values for size, PDI, and zeta potential were readily available from our dynamic light scattering measurements. Second, the biological activities of nanoparticles can be strongly influenced by their size, shape, and surface properties. Since all the nanoparticles in the dataset were assumed to have spherical shapes, we only considered those features related to size and surface characteristics of the nanoparticles as potential predictors of RHA. The ‘size’ attribute values in the data set are the average diameters of the nanoparticles as determined by dynamic light scattering. The ‘PDI’ attribute characterizes the size distribution of the nanoparticles and the ‘zeta potential’ attribute characterizes the surface charge on the nanoparticles. Since the effect of the active surface ligand will depend on its amount present on the surface of the nanoparticles, we used the mole % of the ligand as another RHA predictor. The values of size, PDI, and zeta potential were measured immediately after the nanoparticles were synthesized as described in reference6. The minimum and maximum values of each predictor attribute, as found in the training data set, are listed in Table 1. Six out of sixty formulations have PDI values missing in the data set. In order to include the six formulations in the decision tree analysis, the missing PDI values were set (imputed) to zero. The decision tree results remain the same, whether or not the imputed PDI values are zero or any value less than or equal to the maximum PDI value found in the dataset (i.e., 0.261). For sake of convenience, the missing PDI values were set to zero.
Table 1.
The minimum and maximum values of nanoparticle attributes used as predictors of RHA.
| Predictor attribute | Minimum value | Maximum value |
|---|---|---|
| Size (nm) | 79.1 | 308 |
| Polydispersity index or PDI | 0 | 0.261 |
| Zeta potential (mV) | −70.74 | 62.71 |
| Ligand mole percentage (%) | 0 | 50 |
The scatter plots for pairs of different attributes are shown in Figure S1. The plots indicate that no two attributes have a strong linear relationship to each other across the entire range of their values in the data set. The Pearson correlation coefficient calculation (shown in Table S3) also indicates that the strength of the linear correlation is very poor for all the pairs of dissimilar attributes, while ligand mole % and RHA having the highest (negative) correlation at value −0.77.
Model tree algorithm
To construct the model tree, we used the Weka (v. 3.6.8)21 implementation of the M5P algorithm. The algorithm is a slightly modified version of the M5 algorithm22 with some features added from CART algorithm23. Details of the M5P algorithm can be found in reference18; here, we provide a brief overview of how the algorithm constructs a model tree. Starting from a single node consisting of all the data instances, the M5P algorithm constructs the model tree in three stages. In the first stage, the tree is grown by splitting the instances at every node over a chosen attribute. The attribute selected for splitting the instances at a node is that which gives the largest reduction in the standard deviation of the target attribute values (the actual/experimental RHA values). Specifically, the standard deviation of the target attribute values that reach a node is calculated as a measure of error for that node. Before selecting the splitting attribute for a node (S), the expected reduction in error (also known as the standard deviation reduction (SDR)) is calculated by evaluating each attribute at that node using the formula,
| (1) |
In equation (1), sd(S) is the standard deviation of the target attribute values in node S, sd(Si) is the standard deviation of the target attribute values in node Si resulting due to the split, n(S) is the count of instances in node S, n(Si) is the count of instances in node Si. The attribute that maximizes SDR is then selected for splitting the instances at node S. The splitting stops at a node when there is only slight variation in the target attribute values of all instances reaching that node, or when the number of instances reaching that node is equal to some very low number. In our application of the algorithm, the minimum number of instances in a node was set at 4, which is the default value used in Weka.
The second stage of the model tree construction is the pruning stage where the initial tree is pruned by removing the sub-trees below some nodes of the tree. Pruning simplifies the model tree, reduces the over-fitting of the data, and improves the predictive accuracy of the model. For pruning the tree, a multivariate linear model based on standard regression is first constructed at each interior (non-leaf) node of the un-pruned tree using the attributes that were tested in the subtree below that node. The linear model is used to predict the target attribute value for each instance at the node from the predictor attributes. The algorithm computes the absolute error between the predicted value and the actual value of the target attribute for all instances at the node, and then the errors are averaged. In general, the average error can underestimate the expected error due to unseen instances, so the algorithm estimates the expected error by multiplying the average training error by a factor (m + p)/(m−p), where m is the number of training instances at the node and p is the number of parameters in the linear model18, 22. The estimated expected error at the node is then minimized by (greedily) eliminating the terms, reducing p, one-by-one from the linear model, which reduces the multiplicative factor. Eliminating terms from the linear model generally causes the average error to increase, but it also reduces the multiplicative factor; therefore, the estimated expected error can decrease upon elimination of terms. In some cases, the model will end up having only the constant term, having all the variable (attribute) terms removed. The eliminated terms are typically those that contribute little to the predictive power of the model. As a result, a simplified linear model is constructed at each interior node. If the estimated error based on the linear model at an interior node (starting from the bottom of the tree) is lower than that of the model subtree below the node, then the model is chosen and the node is turned into a leaf-node by pruning the node’s subtree22. In essence, the tree is pruned back from its leaf nodes, so long as the estimated error decreases18.
The third stage of the model tree construction is smoothing the sharp discontinuities that can occur between the adjacent linear models at the leaves of the pruned tree18, 22. Since sharp discontinuities usually occur for models that are trained from a small number of training instances, the smoothing process is effective in improving the predictive accuracy of such models18. In the M5 smoothing process, the value predicted by a model at a leaf-node is adjusted to reflect the predicted values at nodes along the path from the root to that leaf. Specifically, if Si is a branch of subtree S, ni is the number of training instances in Si, PV(Si) is the predicted value at Si, and M(Si) is the value given by the model at S, then the predicted value backed up to S, PV(S), is calculated using the formula,
| (2) |
where K is a smoothing constant (set to the default value of 15).
Model tree validation
The robustness and predictive power of a QSAR model can be tested by external validation and internal validation methods. In external validation, the data set is divided into two sets of instances – training set and test set. The model is trained using the training data set and then applied to predict the endpoint values of instances in the test data set. Appropriate measures, such as, coefficient of determination and root mean square error (RMSE) measures are typically used to quantify the fitting, robustness, and predictability of the trained model19.
Internal validation, also called ‘cross-validation’, is especially useful when the number of instances in the data set is so small that splitting the instances into a training set and a test set will result in inadequate number of training instances for obtaining a robust and predictive model. In a cross-validation scheme, the entire data set is randomly partitioned into several non-overlapping splits or folds. One type of cross-validation is called k-fold cross-validation, in which a data set with ‘N’ number of instances is divided into ‘k’ equally-sized non-overlapping groups (folds). For every fold, a model is trained on the instances from the other k−1 folds and then applied to predict the endpoint values of the instances in that fold. Thus, the cross-validation process is repeated k times. The predicted values from all the k iterations are then used to compute determination coefficient measures and root mean square error (RMSE) of the cross-validation. The cross-validation is called leave-one-out cross-validation (LOOCV) when exactly one instance is left out from the training set, which corresponds to the case when the number of folds is equal to the number of instances (k = N); i.e., the endpoint value of each instance is predicted using a model that is trained on the other (N−1) instances.
At every iteration of a cross-validation process (total k iterations), a different model tree is trained and tested. Thus, the cross-validation process is not actually a test on the performance of the model tree that is trained on the whole data set (containing n instances); instead, it can be interpreted as a test on the performance of the M5P algorithm and on the adequateness of the whole data set for generating a robust, stable, and a reliable model.
In this work, we use LOOCV rather than external validation because of insufficient number in the variety of formulations available for training the model tree. We perform two types of LOOCV: sample-based LOOCV and formulation-based (group-based) LOOCV. Since each instance in the data set is that of a sample, the basic LOOCV described earlier is referred to (in this work) as the sample-based LOOCV. In the formulation-based LOOCV, all data instances of a formulation are considered as part of the test set while the instances of all the other formulations are considered as part of the training set. Since there are sixty formulations in the data set, the formulation-based LOOCV will be repeated sixty times (once for each formulation).
In addition to the LOOCV, we also perform another type of cross-validation where we carry out 10,000 iterations such that, in every iteration 90% of the data instances are randomly selected as part of the training set while the remaining 10% instances form the test set.
For all the three validation schemes – sample-based LOOCV, formulation-based LOOCV, and the 90%-10% split CV – we evaluate the goodness-of-fit, robustness, and predictability of the models using the statistical measures, such as, Pearson product-moment correlation coefficient (r), determination coefficient in the training set (R2)19, LOOCV determination coefficient ( )19, root mean square error of calibration (RMSEC)19, and root mean square error of cross-validation (RMSECV)19.
The Pearson product-moment correlation coefficient (r) measures how closely two variables (e.g., the actual and predicted endpoint values) are linearly related to each other and can take values from +1 to −1. A positive or negative value means that the two variables are linearly related to each other with a positive or negative slope, respectively. A value of zero means that they are not linearly related to each other. The determination coefficient in the training set (R2) is a goodness-of-fit measure that determines how closely the model fits the training data set. The LOOCV determination coefficient ( ) measures the robustness and predictability of the model based on the values predicted based on LOOCV. The root mean square error of calibration (RMSEC) measures the root mean square errors between the actual endpoint values and the values predicted by the model of the training set. The root mean square error of cross-validation (RMSECV) measures the root mean errors between the actual endpoint values and the values predicted by the models trained during LOOCV.
A good model is characterized by high values for r, R2, and (close to 1) and very low values (close to zero) for the errors (RMSEC and RMSECV).
Results and discussion
M5P model tree
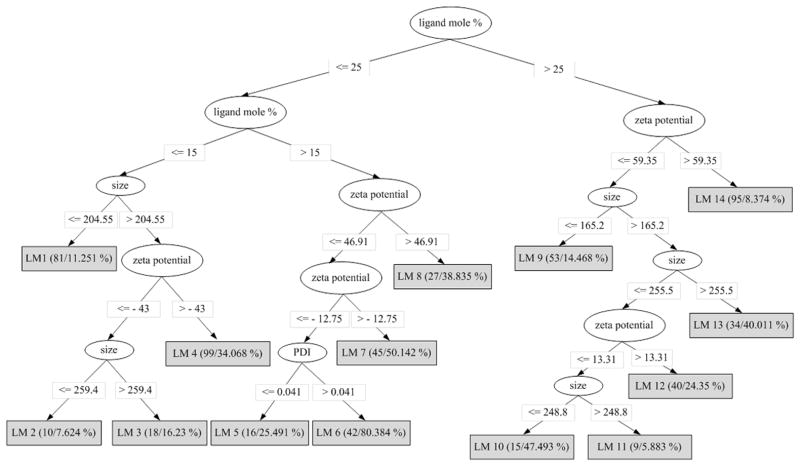
Figure 1 shows the pruned M5P model tree that was trained using the 584 instances of the data set provided in Table S2. The tree describes the splitting rules used by the M5P algorithm to separate the 584 nanoparticles samples into 14 groups (leaf nodes of the model tree) based on the data. It can be seen that ligand mole percentage is the most informative of all the four predictor attributes that get selected as part of the splitting rules. The data at each leaf node is fitted to a multivariate linear regression equation of the form,
Figure 1.
Pruned M5P model tree trained using the data set provided in Table S2.
| (3) |
where ai (i =1, 2, 3, 4, 5) is a constant, and α, β, γ, and η are variables representing the predictor attributes of the nanoparticles, namely, size, PDI, zeta potential, and ligand mole percentage, respectively. The values of ai in each leaf node equation are listed in Table S4. Shown in parentheses at each leaf node, are the number of instances reaching the node and the percentage of incorrectly classified instances as a result of the sample-based leave-one-out cross-validation. The leaf with the lowest number of instances in the model has nine instances (LM11); which is greater than the value (four) used to set the minimum number of instances at a node. However, when the minimum value is increased to values greater than nine, the performance of the model tree begins to decrease.
The linear model estimates the RHA value of a nanoparticle formulation and not of its individual samples, since the model does not contain descriptor values that distinguish the samples of a formulation. Therefore, the present model can be used only to estimate the RHA value of a nanoparticle formulation and compare that value to the average experimental RHA value of the nanoparticle formulation, computed from the RHA values of all its samples. As shown in Figure 2, the predicted RHA values compare very well to the average RHA values (r = 0.9405, R2 = 0.8598, RMSEC = 0.1288). Note that a model tree that was trained using the average RHA values of a nanoparticle formulation, instead of the samples’ RHA values, had only one node and did not fit the data well (r = 0.7235, R2 = 0.5868, RMSEC = 0.2402).
Figure 2.
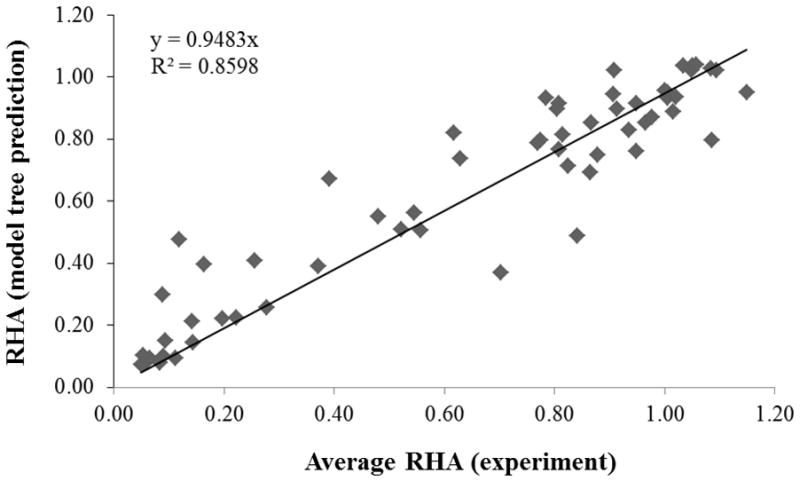
RHA values predicted by the linear models versus the average RHA values (experiment) for each nanoparticle formulation. The line represents the best-fit between the predicted (y) and experimental (x) values.
To know which formulations are present at a leaf node, we constructed a table (Table S5) that provides a count of all the samples of a formulation in each leaf node. From this table, we can identify which formulations are similar to each other, as all their samples will be grouped together in the same leaf node. The formulations in each leaf node are listed in Table 2. For example, the six formulations grouped in node LM9 are those that have an active surface ligand mole percentage of 50; the ligand could be phosphatidylserine, DOTAP (with 5 mole % PEG350 PE), dipalmitoylphosphatidylserine, glutamate-cholesterol, or EPC (without PEG or with 5 mole % PEG350 PE).
Table 2.
List of nanoparticle formulations in each leaf node of the M5P model tree.
| Leaf node | Name | Description |
|---|---|---|
| LM1 | ASP7-130 | 2/0/20 PFOB (reprep RWF8-162) |
| RWF8-171 | 2/0/20 PFOB, 2mol% Phosphatidylserine | |
| GH12-49 | 2/0/20 PFOB control fibrinopeptide Rhodamine | |
| ASP8-142 | Liposome, No PEG | |
| ASP8-144 | Liposome, 5mol% PEG350 PE | |
| ASP8-146 | Liposome, 5mol% PEG3000 PE | |
| LM2 | RWF8-153 | 2/0/20 PFOB, 10mol% Sulfatide Lipid, NO DOTAP |
| LM3 | RWF8-159 | 2/0/20 PFOB, 10mol% Ganglioside Lipid, NO DOTAP |
| RWF8-179 | 2/0/20 PFOB, 5mol% PEG3000 PE, NO DOTAP | |
| RWF8-180 | 2/0/20 PFOB, 5mol% PEG3000 PE, 2mol% DOTAP | |
| LM4 | RWF8-162 | 2/0/20 PFOB, NO Ganglioside Lipid, NO DOTAP (Negative Control) |
| ASP8-30 | 2/0/20 PFOB | |
| ASP6-38 | 2/0/20 PFOB, 2mol% DOTAP, NO PEG | |
| ASP6-36 | 2/0/20 PFOB, 2mol% DOTAP, 5mol% PEG350 PE | |
| RWF9-48 | 2/0/20 PFOB, 2mol% 16:0 EPC | |
| RWF9-49 | 2/0/20 PFOB, 10mol% 16:0 EPC | |
| ASP6-46 | 2/0/20 PFOB, 2mol% Glutamate-Cholesterol, NO PEG | |
| ASP6-44 | 2/0/20 PFOB, 2mol% Glutamate-Cholesterol, 5mol% PEG350 PE | |
| ASP6-54 | 2/0/20 PFOB, 2mol% Glutamate-Cholesterol-DOTA, NO PEG | |
| ASP6-52 | 2/0/20 PFOB, 2mol% Glutamate-Cholesterol-DOTA, 5mol% PEG350 PE | |
| ASP6-132 | 2/0/20 PFOB, 2mol% Gd-DOTA-PEG-Cholesterol, NO PEG PE | |
| ASP6-130 | 2/0/20 PFOB, 2mol% Gd-DOTA-PEG-Cholesterol, 5mol% PEG350 PE | |
| bkim98 | polymeric BRIJ72/PS-b-PAA (13mg/ml) | |
| GH11-105 | 2/0/20 PFOB icam1-c11 peptide | |
| GH11-103 | 2/0/20 PFOB icam1-c16 peptide | |
| LM5 | ASP7-002 | 2/0/20 PFOB, 20mol% Gd DOTA PE |
| LM6 | RWF8-172 | 2/0/20 PFOB, 20mol% Phosphatidylserine |
| ASP6-50 | 2/0/20 PFOB, 20mol% Glutamate-Cholesterol, NO PEG | |
| ASP6-48 | 2/0/20 PFOB, 20mol% Glutamate-Cholesterol, 5mol% PEG350 PE | |
| ASP8-26 | 2/0/20 PFOB, 20mol% dipalmitoylphosphatidylserine | |
| ASP6-134 | 2/0/20 PFOB, 20mol% Gd-DOTA-PEG-Cholesterol, 5mol% PEG350 PE | |
| LM7 | RWF9-50 | 2/0/20 PFOB, 20mol% 16:0 EPC |
| ASP6-40 | 2/0/20 PFOB, 20mol% DOTAP, 5mol% PEG350 PE | |
| ASP8-22 | 2/0/20 PFOB, 20mol% DOTAP | |
| RWF8-154 | 2/0/20 PFOB, 10mol% Sulfatide Lipid, 20mol% DOTAP | |
| RWF8-181 | 2/0/20 PFOB, 5mol% PEG3000 PE, 20mol% DOTAP | |
| ASP6-136 | 2/0/20 PFOB, 20mol% Gd-DOTA-PEG-Cholesterol, NO PEG PE | |
| RWF8-160 | 2/0/20 PFOB, 10mol% Ganglioside Lipid, 20mol% DOTAP | |
| LM8 | ASP6-42 | 2/0/20 PFOB, 20mol% DOTAP, NO PEG |
| LM9 | RWF8-173 | 2/0/20 PFOB, 50mol% Phosphatidylserine |
| ASP8-16 | 2/0/20 PFOB, 50mol% DOTAP, 5mol% PEG350 PE | |
| ASP8-28 | 2/0/20 PFOB, 50mol% dipalmitoylphosphatidylserine | |
| RWF8-167 | 2/0/20 PFOB, 10mol% Ganglioside Lipid, 50mol% Glutamate-Cholesterol | |
| ASP8-46 | 2/0/20 PFOB, 50mol% EPC, No PEG | |
| ASP8-48 | 2/0/20 PFOB, 50mol% EPC, 5mol% PEG350 PE | |
| LM10 | ASP8-52 | 2/0/20 PFOB, 50mol% Phosphatidic Acid |
| ASP6-126 | 2/0/20 PFOB, 50mol% Glutamate-Cholesterol, 5mol% PEG350 PE | |
| ASP7-012 | 2/0/20 PFOB, 1mol% carboxy-PEG-DSPE, 30mol% Gd-DTPA-BOA | |
| LM11 | ELK5-183 | 2/0/20 PFOB, 30mol% Gd DOTA PE |
| LM12 | RWF9-51 | 2/0/20 PFOB, 50mol% 16:0 EPC |
| ASP8-50 | 2/0/20 PFOB, 50mol% EPC, 5mol% PEG3000 PE | |
| RWF8-155 | 2/0/20 PFOB, 10mol% Sulfatide Lipid, 50mol% DOTAP | |
| ASP6-90 | 2/0/20 PFOB, 50mol% DOTAP, 5mol% PEG350 PE | |
| ASP8-18 | 2/0/20 PFOB, 50mol% DOTAP, 5mol% PEG3000 PE | |
| LM13 | RWF8-161 | 2/0/20 PFOB, 10mol% Ganglioside Lipid, 50mol% DOTAP |
| ASP6-128 | 2/0/20 PFOB, 50mol% Glutamate-Cholesterol, NO PEG | |
| RWF8-182 | 2/0/20 PFOB, 5mol% PEG3000 PE, 50mol% DOTAP | |
| LM14 | ASP8-14 | 2/0/20 PFOB, 50mol% DOTAP, No PEG |
| RWF9-47 | 2/0/20 PFOB, 50mol% DOTAP, NO PEG (RePrep of ASP6-92) | |
| ASP8-24 | 2/0/20 PFOB, 50mol% DOTAP |
Model tree cross-validation results
Since we used the whole data set to train the model tree, there is no separate (validation) data set for testing the goodness-of-fit, robustness and predictability of the model. Therefore, we have performed three types of internal validation on the model using the same training data set, which are 1) sample-based leave-one-out cross-validation (LOOCV), 2) formulation-based LOOCV, and 3) 90%-10% split CV.
Sample-based leave-one-out cross validation
The Pearson correlation coefficient (r) for the sample-based LOOCV is 0.9014, the determination coefficient ( ), is 0.8104, and the root-mean-square error (RMSECV) is 0.1779. These values for the r, , and RMSECV of the sample-based LOOCV indicate that the model tree fits the data well and the physicochemical descriptors (size, PDI, zeta potential, and ligand mole %) can serve as good predictors of RHA. Also, its correlation coefficient is only slightly below 0.9405 – the r value between the actual RHA values and those predicted by the model tree (shown in Figure 1) trained on all the 584 instances. It can be expected that the M5P algorithm is choosing and learning a model that is very close to the one shown in Figure 1 at every iteration of the sample-based LOOCV. In the data set, multiple samples of the same formulation vary with respect to the actual RHA values but their physicochemical descriptor values are the same. Hence, the model used for test one of the samples belonging to a formulation, has already been trained with the other samples of the same formulation. As a result, we can expect the linear models of the model tree trained at every iteration of the sample-based LOOCV to interpolate/extrapolate the RHA value of the tested sample very well, if the actual RHA value of the tested sample falls within or close to the RHA values of other samples of the same formulation.
90%–10% split cross-validation results
Results from the 10,000 iterations of the 90%-10% split CV indicate that the M5P models perform very well: average r = 0.9023 (s.d. = 0.0314), average (s.d. = 0.0390), and average RMSECV = 0.1922 (s.d. = 0.0167).
Formulation-based leave-one-out cross-validation
The values of r, , and RMSECV measures for the formulation-based LOOCV are 0.6040, 0.2420, and 0.3247. The difference (error) between the predicted RHA and actual RHA values, calculated from the formulation-based LOOCV, are listed in Table S6. Ten out of the sixty formulations have the magnitude of their error values higher than 0.5. These are ASP6-126, ASP6-134, ASP6-50, ASP7-002, ASP7-012, ASP8-26, RWF8-153, RWF8-155, RWF8-179, and RWF8-182.
If a test formulation falls out of the domain of applicability of the model, the performance of the M5 algorithm can diminish. Therefore, in the formulation-based LOOCV, one can expect to see a decrease in the performance of the M5P models because the model trained in each iteration (total 60 iterations) was not trained on any of the samples of the test formulation. In this regard, the formulation-based LOOCV can be thought of as a stringent test of the M5P model’s reliability compared to the sample-based LOOCV and can be considered closer to an external validation scheme. Increasing the uniformity and number of data points in the RHA/descriptor space, by testing on a larger variety of nanoparticles, is likely to improve the model’s performance.
Classification
Figure 3 shows the box-plots that summarize the distribution of (experimental) RHA values of all the samples at each leaf node of the model tree (Figure 1). As seen from the plots, some of the leaf nodes, especially, LM2, LM5, LM9, LM11, LM12, and LM14, are characterized by nanoparticle formulations that highly activate complement. The average RHA (experimental) values of all the formulations in these leaf nodes are less than 0.4; this value could be thought of as a threshold RHA value for grouping the sixty nanoparticle formulations into complement activating (class CY) and non-activating (class CN) groups. In such a case, the rules provided by the model tree could be used to classify the formulations into the two groups given the values for the size, PDI, zeta potential, and ligand mole % of each nanoparticle formulation.
Figure 3.
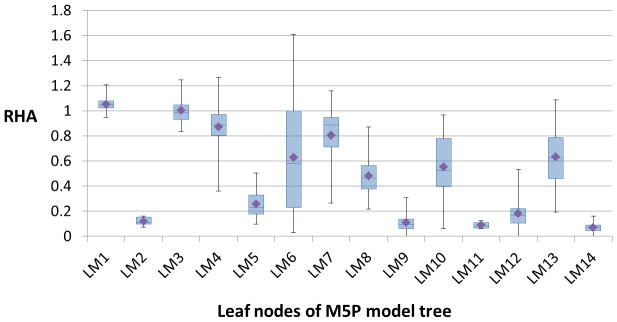
Box-plots summarizing the distribution of experimental RHA values of samples at each leaf node of the M5P model tree. The diamond symbol in each box-plot corresponds to the average RHA value calculated based on the RHA values of all samples in the respective leaf node.
Although there is no universally accepted RHA threshold value for grouping the nanoparticle formulations into the two classes (activating and non-activating), it is possible to analyze the training data set using different classification algorithms by assuming different RHA threshold values for the binary classification of the sixty nanoparticle formulations. In particular, we apply several classification algorithms, such as classification trees23, 24, Support Vector Machine (SVM)/Sequential Minimal Optimization (SMO)25–27, logistic regression28, and random forests29 to classify the sixty nanoparticle formulations based on their physicochemical descriptors. For a given RHA threshold value (<= 0.5), we label a nanoparticle formulation as belonging to class CY or CN: if the average RHA value is less than or equal to the threshold value, it is assigned the class CY; otherwise the class CN. Then using each classifier, we calculate the ROC area for the classification with 10-fold and leave-one-out cross validation. The threshold value that gives the highest ROC area is then selected as the best threshold value for the classification. The results of the classification studies are summarized in Table S7. As seen from the table, any value from 0.35 to 0.45 can be considered as the best threshold RHA value for classifying the sixty nanoparticle formulations into complement activating and non-activating groups.
Conclusion
We applied the M5P model tree algorithm to model the relationship between the in vitro complement activity and physicochemical properties of nanoparticles that we had used to develop a hemolytic assay protocol for assessing the complement response to nanoparticles. Most of the nanoparticles were lipid-encapsulated perfluorocarbon (perfluoro-octyl bromide (PFOB)) nanoemulsions, while the others included three liposome-based nanoparticles and one polymeric nanoparticle. The complement response to a nanoparticle was quantified with our hemolytic assay protocol using a metric called Residual Hemolytic Activity (RHA). The M5P model tree was trained and internally validated using a data set that contained 584 nanoparticle samples representing sixty nanoparticle formulations. The physicochemical descriptors used in the model were size, polydispersity index (PDI), zeta potential, and mole percentage of the active surface ligand, with RHA as the endpoint of prediction.
The M5P modeling approach provides a framework for predicting the RHA values of nanoparticle formulations from their physicochemical properties. The M5P model trained on the whole data set was found to fit the RHA/descriptor data very well, indicating that the physicochemical descriptors, such as size, PDI, zeta potential, and ligand mole % can serve as good predictors for assessing the complement activity of nanoparticles within the M5P modeling framework. The formulation-based leave-one-out cross-validation results indicate that the M5P models can perform poorly in predicting the RHA values of an unseen test formulation. The magnitude of the difference between the predicted and actual RHA values was found to be greater than 0.5 for ten out of the sixty formulations in the formulation-based LOOCV analysis. However, the robustness and predictability of the M5P model can be improved by training the model with more number of data points that are uniformly distributed in the RHA/descriptor space. Overall, the present analysis has served as a framework for: 1) identifying the relationship patterns between RHA values of nanoparticles and their physicochemical properties; 2) identifying the groups of chemically dissimilar nanoparticles that exhibit similar complement activating properties; and, 3) testing the applicability of model trees as a modeling tool for evaluating the complement activating characteristics of nanoparticles.
The present analysis shows that physicochemical parameters play a significant role in complement activation but it does not address the underlying mechanisms. We have previously demonstrated that certain highly reactive nanoparticles, specifically PFOB nanoparticles incorporating 30 mol% Gd-DOTA30 or 50 mol% DOTAP6, are recognized by antibodies, which in turn activate the complement classical pathway. Moreover, in the case of 30 mol% Gd-DOTA, IgM has been identified as the predominant antibody species30. Of note, IgM has been shown to be particularly effective at binding nanoparticles near 250 nm in diameter, well within the typical PFOB size range31; this is likely due to the differential effects of particle size (curvature) on (antibody) binding strength.
Supplementary Material
Figure S1. Matrix scatter plots of the nanoparticle attribute values found in the training data set, generated with R [http://www.r-project.org]).
Table S1. Nanoparticle formulations characterized using the hemolytic assay protocol along with their physicochemical properties and RHA values (experiment and model tree predictions).
Table S2. Data set used for training the M5P model tree.
Table S3. Pearson correlation coefficients (p value ~ 0) obtained using the rcorr function in R.
Table S4. Coefficients of the linear models of the M5P model tree.
Table S5. Sample counts in each leaf node of the M5P model tree.
Table S6. RHA values predicted for each nanoparticle formulation in the formulation-based LOOCV.
Table S7. Classification results using different RHA threshold values and classifiers.
Acknowledgments
We gratefully acknowledge the National Institutes of Health (NIH) and the Food and Drug Administration (FDA) for funding this work through Grant No. U01NS073457. This work was also partly supported by the Signature Discovery Initiative at Pacific Northwest National Laboratory. It was conducted under the Laboratory Directed Research and Development Program at PNNL, a multi-program national laboratory operated by Battelle for the U.S. Department of Energy.
Footnotes
The model’s applicability domain is the theoretical region of the chemical space defined by the descriptor values and the endpoint (RHA) values of the samples (the RHA/descriptor space), where, the model’s predictions are reliable.
Polydispersity index is a dimensionless number ranging from 0 to 1, and is calculated from particle size and count measurements. It is a measure of the particle size distribution in a sample. A value close to 1 indicates that the sample has a broad size distribution (http://nano.indiana.edu/Zetasizer_faq.html).
The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH or the FDA.
References
- 1.Petros RA, DeSimone JM. Strategies in the design of nanoparticles for therapeutic applications. Nat Rev Drug Discov. 2010;9:615–627. doi: 10.1038/nrd2591. [DOI] [PubMed] [Google Scholar]
- 2.Ricklin D, Hajishengallis G, Yang K, Lambris JD. Complement: a key system for immune surveillance and homeostasis. Nat Immunol. 2010;11:785–797. doi: 10.1038/ni.1923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chanan-Khan A, Szebeni J, Savay S, Liebes L, Rafique NM, Alving CR, Muggia FM. Complement activation following first exposure to pegylated liposomal doxorubicin (Doxil): possible role in hypersensitivity reactions. Ann Oncol. 2003;14:1430–1437. doi: 10.1093/annonc/mdg374. [DOI] [PubMed] [Google Scholar]
- 4.Szebeni J. Complement activation-related pseudoallergy: A new class of drug-induced acute immune toxicity. Toxicology. 2005;216:106–121. doi: 10.1016/j.tox.2005.07.023. [DOI] [PubMed] [Google Scholar]
- 5.Szebeni J, Muggia F, Gabizon A, Barenholz Y. Activation of complement by therapeutic liposomes and other lipid excipient-based therapeutic products: Prediction and prevention. Adv Drug Deliver Rev. 2011;63:1020–1030. doi: 10.1016/j.addr.2011.06.017. [DOI] [PubMed] [Google Scholar]
- 6.Pham CNT, Thomas DG, Beiser J, Mitchell LM, Huang JL, Senpan A, Hu G, Gordon M, Baker NA, Pan D, Lanza GM, Hourcade DE. Application of a hemolysis assay for analysis of complement activation by perfluorocarbon nanoparticles. Nanomedicine: Nanotechnology, Biology, and Medicine. 2013 doi: 10.1016/j.nano.2013.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gajewicz A, Rasulev B, Dinadayalane TC, Urbaszek P, Puzyn T, Leszczynska D, Leszczynski J. Advancing risk assessment of engineered nanomaterials: Application of computational approaches. Adv Drug Deliver Rev. 2012;64:1663–1693. doi: 10.1016/j.addr.2012.05.014. [DOI] [PubMed] [Google Scholar]
- 8.Xia XR, Monteiro-Riviere NA, Riviere JE. An index for characterization of nanomaterials in biological systems. Nat Nanotechnol. 2010;5:671–675. doi: 10.1038/nnano.2010.164. [DOI] [PubMed] [Google Scholar]
- 9.Xia XR, Monteiro-Riviere NA, Mathur S, Song XF, Xiao LS, Oldenberg SJ, Fadeel B, Riviere JE. Mapping the Surface Adsorption Forces of Nanomaterials in Biological Systems. Acs Nano. 2011;5:9074–9081. doi: 10.1021/nn203303c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Liu R, Rallo R, George S, Ji ZX, Nair S, Nel AE, Cohen Y. Classification NanoSAR Development for Cytotoxicity of Metal Oxide Nanoparticles. Small. 2011;7:1118–1126. doi: 10.1002/smll.201002366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Liu R, Rallo R, Weissleder R, Tassa C, Shaw S, Cohen Y. Nano-SAR Development for Bioactivity of Nanoparticles with Considerations of Decision Boundaries. Small. 2013;9:1842–1852. doi: 10.1002/smll.201201903. [DOI] [PubMed] [Google Scholar]
- 12.Puzyn T, Rasulev B, Gajewicz A, Hu XK, Dasari TP, Michalkova A, Hwang HM, Toropov A, Leszczynska D, Leszczynski J. Using nano-QSAR to predict the cytotoxicity of metal oxide nanoparticles. Nat Nanotechnol. 2011;6:175–178. doi: 10.1038/nnano.2011.10. [DOI] [PubMed] [Google Scholar]
- 13.Zhang HY, Ji ZX, Xia T, Meng H, Low-Kam C, Liu R, Pokhrel S, Lin SJ, Wang X, Liao YP, Wang MY, Li LJ, Rallo R, Damoiseaux R, Telesca D, Madler L, Cohen Y, Zink JI, Nel AE. Use of Metal Oxide Nanoparticle Band Gap To Develop a Predictive Paradigm for Oxidative Stress and Acute Pulmonary Inflammation. Acs Nano. 2012;6:4349–4368. doi: 10.1021/nn3010087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fourches D, Pu DQY, Tassa C, Weissleder R, Shaw SY, Mumper RJ, Tropsha A. Quantitative Nanostructure-Activity Relationship Modeling. Acs Nano. 2010;4:5703–5712. doi: 10.1021/nn1013484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fourches D, Pu DQY, Tropsha A. Exploring Quantitative Nanostructure-Activity Relationships (QNAR) Modeling as a Tool for Predicting Biological Effects of Manufactured Nanoparticles. Comb Chem High T Scr. 2011;14:217–225. doi: 10.2174/138620711794728743. [DOI] [PubMed] [Google Scholar]
- 16.Epa VC, Burden FR, Tassa C, Weissleder R, Shaw S, Winkler DA. Modeling Biological Activities of Nanoparticles. Nano Lett. 2012;12:5808–5812. doi: 10.1021/nl303144k. [DOI] [PubMed] [Google Scholar]
- 17.Winkler DA, Mombelli E, Pietroiusti A, Tran L, Worth A, Fadeel B, McCall MJ. Applying quantitative structure-activity relationship approaches to nanotoxicology: Current status and future potential. Toxicology. 2013;313:15–23. doi: 10.1016/j.tox.2012.11.005. [DOI] [PubMed] [Google Scholar]
- 18.Wang Y, Witten IH. Inducing model trees for continuous classes. Proceedings of the 9th European Conference on Machine Learning. 1997;1997:128–137. [Google Scholar]
- 19.Puzyn T, Leszczynska D, Leszczynski J. Toward the Development of “Nano-QSARs”: Advances and Challenges. Small. 2009;5:2494–2509. doi: 10.1002/smll.200900179. [DOI] [PubMed] [Google Scholar]
- 20.Mcgill R, Tukey JW, Larsen WA. Variations of Box Plots. Am Stat. 1978;32:12–16. [Google Scholar]
- 21.Hall M, Frank E, Holmes G, Pfahringer B, Reutemann P, Witten IH. The WEKA data mining software: an update. SIGKDD Explorations Newsletter. 2009;11:10–18. [Google Scholar]
- 22.Quinlan JR. Learning with continuous classes 1992. World Scientific; 1992. pp. 343–348. [Google Scholar]
- 23.Breiman L, Friedman JH, Olshen RA, Stone CJ. Classification and regression trees (CART) Chapman & Hall/CRC; 1984. [Google Scholar]
- 24.Quinlan JR. C4.5: Programs for machine learning. Morgan Kaufmann Publishers; 1993. [Google Scholar]
- 25.Platt JC. Advances in kernel methods. MIT Press; 1999. Fast training of support vector machines using sequential minimal optimization; pp. 185–208. [Google Scholar]
- 26.Keerthi SS, Shevade SK, Bhattacharyya C, Murthy KRK. Improvements to Platt’s SMO algorithm for SVM classifier design. Neural Comput. 2001;13:637–649. [Google Scholar]
- 27.Hastie T, Tibshirani R. Classification by pairwise coupling. Adv Neur In. 1998;10:507–513. [Google Scholar]
- 28.Lecessie S, Vanhouwelingen JC. Ridge Estimators in Logistic-Regression. Appl Stat-J Roy St C. 1992;41:191–201. [Google Scholar]
- 29.Breiman L. Random forests. Mach Learn. 2001;45:5–32. [Google Scholar]
- 30.Pham CT, Mitchell LM, Huang JL, Lubniewski CM, Schall OF, Killgore JK, Pan D, Wickline SA, Lanza GM, Hourcade DE. Variable antibody-dependent activation of complement by functionalized phospholipid nanoparticle surfaces. The Journal of biological chemistry. 2011;286:123–30. doi: 10.1074/jbc.M110.180760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Pedersen MB, Zhou X, Larsen EK, Sorensen US, Kjems J, Nygaard JV, Nyengaard JR, Meyer RL, Boesen T, Vorup-Jensen T. Curvature of synthetic and natural surfaces is an important target feature in classical pathway complement activation. Journal of immunology. 2010;184:1931–45. doi: 10.4049/jimmunol.0902214. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1. Matrix scatter plots of the nanoparticle attribute values found in the training data set, generated with R [http://www.r-project.org]).
Table S1. Nanoparticle formulations characterized using the hemolytic assay protocol along with their physicochemical properties and RHA values (experiment and model tree predictions).
Table S2. Data set used for training the M5P model tree.
Table S3. Pearson correlation coefficients (p value ~ 0) obtained using the rcorr function in R.
Table S4. Coefficients of the linear models of the M5P model tree.
Table S5. Sample counts in each leaf node of the M5P model tree.
Table S6. RHA values predicted for each nanoparticle formulation in the formulation-based LOOCV.
Table S7. Classification results using different RHA threshold values and classifiers.