Feature Screening via Distance Correlation Learning

Abstract

This paper is concerned with screening features in ultrahigh dimensional data analysis, which has become increasingly important in diverse scientific fields. We develop a sure independence screening procedure based on the distance correlation (DC-SIS, for short). The DC-SIS can be implemented as easily as the sure independence screening procedure based on the Pearson correlation (SIS, for short) proposed by Fan and Lv (2008). However, the DC-SIS can significantly improve the SIS. Fan and Lv (2008) established the sure screening property for the SIS based on linear models, but the sure screening property is valid for the DC-SIS under more general settings including linear models. Furthermore, the implementation of the DC-SIS does not require model specification (e.g., linear model or generalized linear model) for responses or predictors. This is a very appealing property in ultrahigh dimensional data analysis. Moreover, the DC-SIS can be used directly to screen grouped predictor variables and for multivariate response variables. We establish the sure screening property for the DC-SIS, and conduct simulations to examine its finite sample performance. Numerical comparison indicates that the DC-SIS performs much better than the SIS in various models. We also illustrate the DC-SIS through a real data example.

1. INTRODUCTION

Various regularization methods have been proposed for feature selection in high dimensional data analysis, which has become increasingly frequent and important in various research fields. These methods include, but are not limited to, the LASSO (Tibshirani, 1996), the SCAD (Fan and Li, 2001; Kim, Choi and Oh, 2008; Zou and Li, 2008), the LARS algorithm (Efron, Hastie, Johnstone and Tibshirani, 2004), the elastic net (Zou and Hastie, 2005; Zou and Zhang, 2009), the adaptive LASSO (Zou, 2006) and the Dantzig selector (Candes and Tao, 2007). All these methods allow the number of predictors to be greater than the sample size, and perform quite well for high dimensional data.

With the advent of modern technology for data collection, researchers are able to collect ultrahigh dimensional data at relatively low cost in diverse fields of scientific research. The aforementioned regularization methods may not perform well for ultrahigh dimensional data due to the simultaneous challenges of computational expediency, statistical accuracy and algorithmic stability (Fan, Samworth and Wu, 2009). These challenges call for new statistical modeling techniques for ultrahigh dimensional data. Fan and Lv (2008) proposed the SIS and showed that the Pearson correlation ranking procedure possesses a sure screening property for linear regressions with Gaussian predictors and responses. That is, all truly important predictors can be selected with probability approaching one as the sample size diverges to ∞. Hall and Miller (2009) extended Pearson correlation learning by considering polynomial transformations of predictors. To rank the importance of each predictor, they suggested a bootstrap procedure. Fan, Samworth and Wu (2009) and Fan and Song (2010) proposed a more general version of independent learning which ranks the maximum marginal likelihood estimators or the maximum marginal likelihood for generalized linear models. Fan, Feng and Song (2011) considered nonparametric independence screening in sparse ultrahigh dimensional additive models. They suggested estimating the nonparametric components marginally with spline approximation, and ranking the importance of predictors using the magnitude of nonparametric components. They also demonstrated that this procedure possesses the sure screening property with vanishing false selection rate. Zhu, Li, Li and Zhu (2011) proposed a sure independent ranking and screening (SIRS) procedure to screen significant predictors in multi-index models. They further show that under linearity condition assumption on the predictor vector, the SIRS enjoys the ranking consistency property (i.e, the SIRS can rank the important predictors in the top asymptotically). Ji and Jin (2012) proposed the two-stage method: screening by Univariate thresholding and cleaning by Penalized least squares for Selecting variables, namely UPS. They further theoretically demonstrated that under certain settings, the UPS can outperform the LASSO and subset selection, both of which are one-stage approaches. This motivates us to develop more effective screening procedures using two-stage approaches.

In this paper, we propose a new feature screening procedure for ultrahigh dimensional data based on distance correlation. Szekely, Rizzo and Bakirov (2007) and Szekely and Rizzo (2009) showed that the distance correlation of two random vectors equals to zero if and only if these two random vectors are independent. Furthermore, the distance correlation of two univariate normal random variables is a strictly increasing function of the absolute value of the Pearson correlation of these two normal random variables. These two remarkable properties motivate us to use the distance correlation for feature screening in ultrahigh dimensional data. We refer to our Sure Independence Screening procedure based on the Distance Correlation as the DC-SIS. The DC-SIS can be implemented as easily as the SIS. It is equivalent to the SIS when both the response and predictor variables are normally distributed. However, the DC-SIS has appealing features that existing screening procedures including SIS do not possess. For instance, none of the aforementioned screening procedures can handle grouped predictors or multivariate responses. The proposed DC-SIS can be directly employed for screening grouped variables, and it can be directly utilized for ultrahigh dimensional data with multivariate responses. Feature screening for multivariate responses and/or grouped predictors is of great interest in pathway analyses. As in Chen, et al. (2011), pathway here means sets of proteins that are relevant to specific biological functions without regard to the state of knowledge concerning the interplay among such protein. Since proteins may work interactively to perform various biological functions, pathway analyses complement the marginal association analyses for individual protein, and aim to detect a priori defined set of proteins that are associated with phenotypes of interest. There is a surged interest in pathway analyses in the recent literature (Ashburner, et al., 2000; Mootha, et al., 2003; Subramanian, et al., 2005; Tian, et al., 2005; Bild, et al., 2006; Efron and Tibsirani, 2007; Jones, et al., 2008). Thus, it is of importance to develop feature screening procedures for multivariate responses and/or grouped predictors.

We systematically study the theoretic properties of the DC-SIS, and prove that the DC-SIS possesses the sure screening property in the terminology of Fan and Lv (2008) under very general model settings including linear regression models, for which Fan and Lv (2008) established the sure screening property of the SIS. The sure screening property is a desirable property for feature screening in ultrahigh dimensional data. Even importantly, the DC-SIS can be used for screening features without specifying a regression model between the response and the predictors. Compared with the model-based screening procedures (Fan and Lv, 2008; Fan, Samworth and Wu, 2009; Wang, 2009; Fan and Song, 2010; Fan, Feng and Song, 2011), the DC-SIS is a model-free screening procedure. This virtue makes the proposed procedure robust to model misspecification. This is a very appealing feature of the proposed procedure in that it may be very difficult in specifying an appropriate regression model for the response and the predictors with little information about the actual model in ultrahigh dimensional data.

We conduct Monte Carlo simulation studies to numerically compare the DC-SIS with the SIS and SIRS. Our simulation results indicate that the DC-SIS can significantly outperform the SIS and the SIRS under many model settings. We also assess the performance of the DC-SIS as a grouped variable screener, and the simulation results show that the DC-SIS performs very well. We further examine the performance of the DC-SIS for feature screening in ultrahigh dimensional data with multivariate responses; simulation results demonstrate that screening features for multiple responses jointly may have dramatic advantage over screening features with each response separately.

The rest of this paper is organized as follows. In Section 2, we develop the DC-SIS for feature screening and establish its sure screening property. In Section 3, we examine the finite sample performance of the DC-SIS via Monte Carlo simulations. We also illustrate the proposed methodology through a real data example. This paper concludes with a brief discussion in Section 4. All technical proofs are given in the Appendix.

2. INDEPENDENCE SCREENING USING DISTANCE CORRELATION

2.1. Some Preliminaries

Szekely, Rizzo and Bakirov (2007) advocated using the distance correlation for measuring dependence between two random vectors. To be precise, let φ_u(t) and φ_v(s) be the respective characteristic functions of the random vectors u and v, and φ_u,v(t, s) be the joint characteristic function of u and v. They defined the distance covariance between u and v with finite first moments to be the nonnegative number dcov(u, v) given by

$$d{cov}^2(\mathbf{u},\mathbf{v})={\int }_{R^{d_u+d_v}}{\left|\right|{\phi }_{\mathbf{u},\mathbf{v}}(\mathbf{t},\mathbf{s})-{\phi }_{\mathbf{u}}(\mathbf{t}){\phi }_{\mathbf{v}}(\mathbf{s})\left|\right|}^{2}w(\mathbf{t},\mathbf{s})d\mathbf{t}d\mathbf{s},$$ (2.1)

where d_u and d_v are the dimensions of u and v, respectively, and

$$w(\mathbf{t},\mathbf{s})={\left\{c_{d_u}{c}_{d_v}{\left|\right|\mathbf{t}\left|\right|}_{d_u}^{1+d_u}{\left|\right|\mathbf{s}\left|\right|}_{d_v}^{1+d_v}\right\}}^{-1}$$

with c_d = π^(1+d)/2/Γ{(1+d)/2}. Throughout this paper, ||a||_d stands for the Euclidean norm of a ∈ ℝ^d, and ||φ||² = φφ̄ for a complex-valued function φ with φ̄ being the conjugate of φ. The distance correlation (DC) between u and v with finite first moments is defined as

$$\text{dcorr}(\mathbf{u},\mathbf{v})=\frac{\text{dcov}(\mathbf{u},\mathbf{v})}{\sqrt{\text{dcov}(\mathbf{u},\mathbf{u})\text{dcov}(\mathbf{v},\mathbf{v})}}.$$ (2.2)

Szekely, Rizzo and Bakirov (2007) systematically studied the theoretic properties of the DC.

Two remarkable properties of the DC motivate us to utilize it in a feature screening procedure. The first one is the relationship between the DC and the Pearson correlation coefficient. For two univariate normal random variables U and V with the Pearson correlation coefficient ρ, Szekely, Rizzo and Bakirov (2007) and Szekely and Rizzo (2009) showed that

$$\text{dcorr}(U,V)={\left\{\frac{\rho arcsin(\rho )+\sqrt{1-{\rho }^2}-\rho arcsin(\rho /2)-\sqrt{4-{\rho }^2}+1}{1+\pi /3-\sqrt{3}}\right\}}^{1/2},$$ (2.3)

which is strictly increasing in |ρ|. This property implies that the DC-based feature screening procedure is equivalent to the marginal Pearson correlation learning for linear regression with normally distributed predictors and random error. In such a situation, Fan and Lv (2008) showed that the Pearson correlation learning has the sure screening property.

The second remarkable property of the DC is dcorr(u, v) = 0 if and only if u and v are independent (Szekely, Rizzo and Bakirov, 2007). We note that two univariate random variables U and V are independent if and only if U and T(V), a strictly monotone transformation of V, are independent. This implies that a DC-based feature screening procedure can be more effective than the marginal Pearson correlation learning in the presence of nonlinear relationship between U and V. We will demonstrate in the next section that a DC-based screening procedure is a model-free procedure in that one does not need to specify a model structure between the predictors and the response.

Szekely, Rizzo and Bakirov (2007, Remark 3) stated that

$${\text{dcov}}^2(\mathbf{u},\mathbf{v})=S_1+S_2-2S_3,$$

where S_j, j = 1, 2 and 3, are defined below:

$$\begin{array}{l}{S}_1=E\{{\left|\right|\mathbf{u}-\stackrel{\sim }{\mathbf{u}}\left|\right|}_{d_u}{\left|\right|\mathbf{v}-\stackrel{\sim }{\mathbf{v}}\left|\right|}_{d_v}\},\\ S_2=E\{{\left|\right|\mathbf{u}-\stackrel{\sim }{\mathbf{u}}\left|\right|}_{d_u}\}E\{{\left|\right|\mathbf{v}-\stackrel{\sim }{\mathbf{v}}\left|\right|}_{d_v}\},\\ S_3=E\{E({\left|\right|\mathbf{u}-\stackrel{\sim }{\mathbf{u}}\left|\right|}_{d_u}\mid \mathbf{u})E({\left|\right|\mathbf{v}-\stackrel{\sim }{\mathbf{v}}\left|\right|}_{d_v}\mid \mathbf{v})\},\end{array}$$ (2.4)

where (ũ, ṽ) is an independent copy of (u, v).

Suppose that {(u_i, v_i), i = 1, ···, n} is a random sample from the population (u, v). Szekely, Rizzo and Bakirov (2007) proposed to estimate S₁, S₂ and S₃ through the usual moment estimation. To be precise,

$$\begin{array}{l}{\widehat{S}}_1=\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n{\left|\right|{\mathbf{u}}_i-{\mathbf{u}}_j\left|\right|}_{d_u}{\left|\right|{\mathbf{v}}_i-{\mathbf{v}}_j\left|\right|}_{d_v}\\ {\widehat{S}}_2=\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n{\left|\right|{\mathbf{u}}_i-{\mathbf{u}}_j\left|\right|}_{d_u}\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n{\left|\right|{\mathbf{v}}_i-{\mathbf{v}}_j\left|\right|}_{d_v},\text{and}\\ {\widehat{S}}_3=\frac{1}{n^3}\sum _{i=1}^n\sum _{j=1}^n\sum _{l=1}^n{\left|\right|{\mathbf{u}}_i-{\mathbf{u}}_l\left|\right|}_{d_u}{\left|\right|{\mathbf{v}}_j-{\mathbf{v}}_l\left|\right|}_{d_v}.\end{array}$$

Thus, a natural estimator of dcov²(u, v) is given by

$${\widehat{\text{dcov}}}^2(\mathbf{u},\mathbf{v})={\widehat{S}}_1+{\widehat{S}}_2-2{\widehat{S}}_3.$$

Similarly, we can define the sample distance covariances $\widehat{\text{dcov}}(\mathbf{u},\mathbf{u})$ and $\widehat{\mathrm{dcov}}(\mathbf{v},\mathbf{v})$. Accordingly, the sample distance correlation between u and v can be defined by

$$\widehat{\text{dcorr}}(\mathbf{u},\mathbf{v})=\frac{\widehat{\text{dcov}}(\mathbf{u},\mathbf{v})}{\sqrt{\widehat{\text{dcov}}(\mathbf{u},\mathbf{u})\widehat{\text{dcov}}(\mathbf{v},\mathbf{v})}}.$$

2.2. An Independence Ranking and Screening Procedure

In this section we propose an independence screening procedure built upon the DC. Let y = (Y₁, ···, Y_q)^T be the response vector with support Ψ_y, and x = (X₁, …, X_p)^T be the predictor vector. We regard q as a fixed number in this context. In an ultrahigh-dimensional setting the dimensionality p greatly exceeds the sample size n. It is thus natural to assume that only a small number of predictors are relevant to y. Denote by F(y | x) the conditional distribution function of y given x. Without specifying a regression model, we define the index set of the active and inactive predictors by

$$\begin{array}{l}\mathcal{D}=\{k:F(\mathbf{y}\mid \mathbf{x})\text{functionally}\text{depends}\text{on}{X}_k\text{for}\text{some}\mathbf{y}\in {\mathrm{\Psi }}_y\},\\ \mathcal{I}=\{k:F(\mathbf{y}\mid \mathbf{x})\text{does}\text{not}\text{functionally}\text{depends}\text{on}{X}_k\text{for}\text{any}\mathbf{y}\in {\mathrm{\Psi }}_y\}.\end{array}$$ (2.5)

We further write x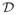 = {X_k : k ∈ 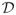} and x = {X_k : k ∈ 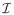}, and refer to x 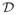as an active predictor vector and its complement x as an inactive predictor vector. The index subset 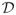of all active predictors or, equivalently, the index subset 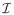of all inactive predictors, is the objective of our primary interest. Definition (2.5) implies that y ⫫ x | x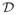, where ⫫ denotes statistical independence. That is, given x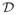, the remaining predictors x are independent of y. Thus the inactive predictors x are redundant when the active predictors x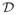 are known.

For ease of presentation, we write

$${\omega }_k={\text{dcorr}}^2(X_k,\mathbf{y}),\text{and}{\widehat{\omega }}_k={\widehat{\text{dcorr}}}^2(X_k,\mathbf{y}),\text{for}k=1,\cdots ,p$$

based on a random sample {x_i, y_i}, i = 1, …, n. We consider using ω_k as a marginal utility to rank the importance of X_k at the population level. We utilize the DC because it allows for arbitrary regression relationship of y onto x, regardless of whether it is linear or nonlinear. The DC also permits univariate and multivariate response, regardless of whether it is continuous, discrete or categorical. In addition, it allows for groupwise predictors. Thus, this DC based screening procedure is completely model-free. We select a set of important predictors with large ω̂_k. That is, we define

$${\widehat{\mathcal{D}}}^{\ast }=\{k:{\widehat{\omega }}_k\ge {cn}^{-\kappa },\text{for}1\le k\le p\},$$

where c and κ are pre-specified threshold values which will be defined in condition (C2) in the subsequent section.

2.3. Theoretical Properties

Next we study the theoretical properties of the proposed independence screening procedure built upon the DC. The following conditions are imposed to facilitate the technical proofs, although they may not be the weakest ones.

• (C1) Both x and y satisfy the sub-exponential tail probability uniformly in p. That is, there exists a positive constant s₀ such that for all 0 < s = ≤ 2s₀,

  $$\underset{p}{sup}\underset{1\le k\le p}{max}E\{exp(s{\left|\right|X_k\left|\right|}_1^2)\}<\infty ,\text{and}E\{exp(s{\left|\right|\mathbf{y}\left|\right|}_q^2)\}<\infty .$$

• (C2) The minimum distance correlation of active predictors satisfies

  $$\underset{k\in \mathcal{D}}{min}{\omega }_k\ge 2{cn}^{-\kappa },\text{for}\text{some}\text{constants}c>0\text{and}0\le \kappa \le 1/2.$$

Condition (C1) follows immediately when x and y are bounded uniformly, or when they have multivariate normal distribution. The normality assumption has been widely used in the area of ultrahigh dimensional data analysis to facilitate the technical derivations. See, for example, Fan and Lv (2008) and Wang (2009).

Next we explore condition (C2). When x and y have multivariate normal distribution, (2.3) gives an explicit relationship between the DC and the squared Pearson correlation. For simplicity, we write dcorr(X_k, y) = T₀ (|ρ(X_k, y)|) where T₀(·) is strictly increasing given in (2.3). In this situation, condition (C2) requires essentially that $\underset{k\in \mathcal{D}}{min}\mid \rho (X_k,\mathbf{y})\mid \ge T_{\mathit{inv}}(2{cn}^{-\kappa })$, where T_inv(·) is the inverse function of T₀(·). This is parallel to condition 3 of Fan and Lv (2008) where it is assumed that $\underset{k\in \mathcal{D}}{min}\mid \rho (X_k,\mathbf{y})\mid \ge 2{cn}^{-\kappa }$. This intuitive illustration implies that condition (C2) requires that the marginal DC of active predictors cannot be too small, which is similar to condition 3 of Fan and Lv (2008). We remark here that, although we illustrate the intuition by assuming that x and y are multivariate normal, we do not require this assumption explicitly in our context. The following theorem establishes the sure screening property for the DC-SIS procedure.

Theorem 1

Under condition (C1), for any 0 < γ < 1/2 − κ, there exist positive constants c₁ > 0 and c₂ > 0 such that

$$Pr\left(\underset{1\le k\le p}{max}\mid {\widehat{\omega }}_k-{\omega }_k\mid \ge {cn}^{-\kappa }\right)\le O(p[exp\{-c_1{n}^{1-2(\kappa +\gamma )}\}+nexp(-c_2{n}^{\gamma })]).$$ (2.6)

Under conditions (C1) and (C2), we have that

$$Pr\left(\mathcal{D}\le {\widehat{\mathcal{D}}}^{★}\right)\ge 1-O(s_n[exp\{-c_1{n}^{1-2(\kappa +\gamma )}\}+nexp(-c_2{n}^{\gamma })]),$$ (2.7)

where s_n is the cardinality of .

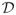The sure screening property holds for the DC-SIS under milder conditions than those for the SIS (Fan and Lv, 2008) in that we do not require the regression function of y onto x to be linear. Thus, the DC-SIS provides a unified alternative to existing model-based sure screening procedures. Compared with the SIRS, the DC-SIS can effectively handle grouped predictors and multivariate responses.

To balance the two terms in the right hand side of (2.6), we choose the optimal order γ = (1 − 2κ)/3, then the first part of Theorem 1 becomes

$$Pr\left(\underset{1\le k\le p}{max}\mid {\widehat{\omega }}_k-{\omega }_k\mid \ge {cn}^{-\kappa }\right)\le O(p[exp\{-c_1{n}^{(1-2\kappa )/3}\}]),$$

for some constant c₁ > 0, indicating that we can handle the NP-dimensionality of order log p = o(n^(1−2κ)/3. If we further assume that X_k and y are bounded uniformly in p, then we can obtain without much difficulty that

$$Pr\left(\underset{1\le k\le p}{max}\mid {\widehat{\omega }}_k-{\omega }_k\mid \ge {cn}^{-\kappa }\right)\le O(p[exp\{-c_1{n}^{1-2\kappa }\}]).$$

In this case, we can handle the NP-dimensionality log p = o (n^1−2κ).

3. NUMERICAL STUDIES

In this section we assess the performance of the DC-SIS by Monte Carlo simulation. Our simulation studies were conducted using R code. We further illustrate the proposed screening procedure with an empirical analysis of a real data example.

In Examples 1, 2 and 3, we generate x = (X₁, X₂, ···, X_p)^T from normal distribution with zero mean and covariance matrix Σ = (σ_ij)_p×p, and the error term ε from standard normal distribution 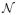(0, 1). We consider two covariance matrices to assess the performance of the DC-SIS and to compare with existing methods: (i) σ_ij = 0.8^|i−j| and (ii) σ_ij = 0.5^|i−j|. We fix the sample size n to be 200 and vary the dimension p from 2,000 to 5,000. We repeat each experiment 500 times, and evaluate the performance through the following three criteria.

1. : the minimum model size to include all active predictors. We report the 5%, 25%, 50%, 75% and 95% quantiles of out of 500 replications.

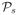2. : the proportion that an individual active predictor is selected for a given model size d in the 500 replications.

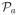3. : the proportion that all active predictors are selected for a given model size d in the 500 replications.

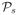The is used to measure the model complexity of the resulting model of an underlying screening procedure. The closer to the minimum model size the is, the better the screening procedure is. The sure screening property ensures that and 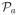are both close to one when the estimated model size d is sufficiently large. We choose d to be d₁ = [n/log n], d₂ = 2[n/log n] and d₃ = 3[n/log n] throughout our simulations to empirically examine the effect of the cutooff, where [a] denotes the integer part of a.

Example 1

This example is designed to compare the finite sample performance of the DC-SIS with the SIS (Fan and Lv, 2008) and SIRS (Zhu, Li, Li and Zhu, 2011). In this example, we generate the response from the following four models:

$$Y=c_1{\beta }_1{X}_1+c_2{\beta }_2{X}_2+c_3{\beta }_3\mathbf{1}(X_{12}<0)+c_4{\beta }_4{X}_{22}+\epsilon ,$$ (1.a)

$$Y=c_1{\beta }_1{X}_1{X}_2+c_2{\beta }_2\mathbf{1}(X_{12}<0)+c_4{\beta }_3{X}_{22}+\epsilon ,$$ (1.b)

$$Y=c_1{\beta }_1{X}_1{X}_2+c_3{\beta }_2\mathbf{1}(X_{12}<0)X_{22}+\epsilon ,$$ (1.c)

$$Y=c_1{\beta }_1{X}_1+c_2{\beta }_2{X}_2+c_3{\beta }_3\mathbf{1}(X_{12}<0)+exp(c_4\mid X_{22}\mid )\epsilon ,$$ (1.d)

where 1(X₁₂ < 0) is an indicator function. The regression functions E(Y | x) in models (1.a)–(1.d) are all nonlinear in X₁₂. In addition, models (1.b) and (1.c) contain an interaction term X₁X₂, and model (1.d) is heteroscedastic. Following Fan and Lv (2008), we choose β_j = (−1)^U(a + |Z|) for j = 1, 2, 3 and 4, where $a=4logn/\sqrt{n}$, U ~ Bernoulli(0.4) and Z ~ 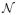(0, 1). We set (c₁, c₂, c₃, c₄) = (2, 0.5, 3, 2) in this example to challenge the feature screening procedures under consideration. For each independence screening procedure, we compute the associated marginal utility between each predictor X_k and the response Y. That is, we regard x = (X₁, …, X_p)^T ∈ ℝ^p as the predictor vector in this example.

Tables 1 and 2 depict the simulation results for , 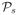and 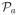. The performances of the DC-SIS, SIS and SIRS are quite similar in model (1.a), indicating that the SIS has a robust performance if the working linear model does not deviate far from the underlying true model. The DC-SIS outperforms the SIS and SIRS significantly in models (1.b), (1.c) and (1.d). Both the SIS and SIRS have little chance to identify the important predictors X₁ and X₂ in models (1.b) and (1.c), and X₂₂ in model (1.d).

Table 1.

The 5%, 25%, 50%, 75% and 95% quantiles of the minimum model size out of 500 replications in Example 1.

	SIS					SIRS					DC-SIS
Model	5%	25%	50%	75%	95%	5%	25%	50%	75%	95%	5%	25%	50%	75%	95%
case 1: p = 2000 and σij = 0.5|i−j|
(1.a)	4.0	4.0	5.0	7.0	21.2	4.0	4.0	5.0	7.0	45.1	4.0	4.0	4.0	6.0	18.0
(1.b)	68.0	578.5	1180.5	1634.5	1938.0	232.9	871.5	1386.0	1725.2	1942.4	5.0	9.0	24.5	73.0	345.1
(1.c)	395.9	1037.2	1438.0	1745.0	1945.1	238.5	805.0	1320.0	1697.0	1946.0	6.0	10.0	22.0	59.0	324.1
(1.d)	130.5	611.2	1166.0	1637.0	1936.5	42.0	304.2	797.0	1432.2	1846.1	4.0	5.0	9.0	41.0	336.2
case 2: p = 2000 and σij= 0.8|i−j|
(1.a)	5.0	9.0	16.0	97.0	729.4	5.0	9.0	18.0	112.8	957.1	4.0	7.0	11.0	31.2	507.2
(1.b)	26.0	283.2	852.0	1541.2	1919.0	103.9	603.0	1174.0	1699.2	1968.0	5.0	8.0	11.0	17.0	98.0
(1.c)	224.5	775.2	1249.5	1670.0	1951.1	118.6	573.2	1201.5	1685.2	1955.0	7.0	10.0	15.0	38.0	198.3
(1.d)	79.0	583.8	1107.5	1626.2	1930.0	50.9	300.5	728.0	1368.2	1900.1	4.0	7.0	17.0	73.2	653.1
case 3: p = 5000 and σij = 0.5|i−j|
(1.a)	4.0	4.0	5.0	6.0	59.0	4.0	4.0	5.0	7.0	88.4	4.0	4.0	4.0	6.0	34.1
(1.b)	165.1	1112.5	2729.0	3997.2	4851.5	560.8	1913.0	3249.0	4329.0	4869.1	5.0	11.8	45.0	168.8	956.7
(1.c)	1183.7	2712.0	3604.5	4380.2	4885.0	440.4	1949.0	3205.5	4242.8	4883.1	7.0	17.0	53.0	179.5	732.0
(1.d)	259.9	1338.5	2808.5	3990.8	4764.9	118.7	823.2	1833.5	3314.5	4706.1	4.0	5.0	15.0	77.2	848.2
case 4: p = 5000 and σij = 0.8|i−j|
(1.a)	5.0	10.0	26.5	251.5	2522.7	5.0	10.0	28.0	324.8	3246.4	5.0	8.0	14.0	69.0	1455.1
(1.b)	40.7	639.8	2072.0	3803.8	4801.7	215.7	1677.8	3010.0	4352.2	4934.1	5.0	8.0	11.0	21.0	162.0
(1.c)	479.2	1884.8	3347.5	4298.5	4875.2	297.7	1359.2	2738.5	4072.5	4877.6	8.0	12.0	22.0	83.0	657.9
(1.d)	307.0	1544.0	2832.5	4026.2	4785.2	148.2	672.0	1874.0	3330.0	4665.2	4.0	7.0	21.0	165.2	1330.0

Table 2.

The proportions of 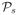and 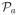in Example 1. The user-specified model sizes d₁ = [n/log n], d₂ = 2[n/log n] and d₃ = 3[n/log n].

		SIS					SIRS					DC-SIS
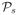
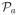
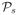
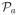
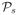
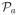
model	size	X1	X2	X12	X22	ALL	X1	X2	X12	X22	ALL	X1	X2	X12	X22	ALL
case 1: p = 2000 and σij = 0.5|i−j|
(1.a)	d1	1.00	1.00	0.96	1.00	0.96	1.00	1.00	0.95	1.00	0.94	1.00	1.00	0.97	1.00	0.96
	d2	1.00	1.00	0.98	1.00	0.97	1.00	1.00	0.96	1.00	0.96	1.00	1.00	0.98	1.00	0.98
	d3	1.00	1.00	0.98	1.00	0.98	1.00	1.00	0.97	1.00	0.97	1.00	1.00	0.99	1.00	0.98
(1.b)	d1	0.08	0.07	0.97	1.00	0.03	0.02	0.03	0.98	1.00	0.00	0.72	0.70	0.99	1.00	0.58
	d2	0.12	0.13	0.98	1.00	0.06	0.05	0.05	0.99	1.00	0.01	0.85	0.84	1.00	1.00	0.76
	d3	0.15	0.17	0.99	1.00	0.07	0.06	0.06	0.99	1.00	0.01	0.89	0.88	1.00	1.00	0.82
(1.c)	d1	0.12	0.13	0.01	0.99	0.00	0.04	0.03	0.51	1.00	0.01	0.93	0.93	0.77	1.00	0.65
	d2	0.17	0.18	0.03	0.99	0.00	0.07	0.05	0.67	1.00	0.01	0.97	0.96	0.84	1.00	0.79
	d3	0.21	0.21	0.05	0.99	0.00	0.09	0.08	0.75	1.00	0.02	0.98	0.97	0.89	1.00	0.84
(1.d)	d1	0.42	0.22	0.14	0.42	0.02	1.00	0.98	0.87	0.05	0.04	1.00	0.91	0.81	0.99	0.73
	d2	0.48	0.29	0.22	0.50	0.03	1.00	0.99	0.91	0.10	0.09	1.00	0.94	0.87	1.00	0.82
	d3	0.56	0.32	0.26	0.54	0.04	1.00	0.99	0.93	0.12	0.11	1.00	0.96	0.92	1.00	0.88
case 2: p = 2000 and σij = 0.8|i−j|
(1.a)	d1	1.00	1.00	0.63	1.00	0.63	1.00	1.00	0.62	1.00	0.62	1.00	1.00	0.78	1.00	0.77
	d2	1.00	1.00	0.71	1.00	0.72	1.00	1.00	0.70	1.00	0.69	1.00	1.00	0.84	1.00	0.84
	d3	1.00	1.00	0.77	1.00	0.78	1.00	1.00	0.75	1.00	0.75	1.00	1.00	0.86	1.00	0.86
(1.b)	d1	0.12	0.13	0.81	1.00	0.06	0.04	0.04	0.88	1.00	0.02	0.97	0.98	0.92	1.00	0.88
	d2	0.19	0.19	0.86	1.00	0.12	0.07	0.07	0.91	1.00	0.03	0.99	0.99	0.95	1.00	0.94
	d3	0.22	0.23	0.88	1.00	0.15	0.09	0.11	0.93	1.00	0.06	1.00	0.99	0.96	1.00	0.96
(1.c)	d1	0.17	0.16	0.03	0.99	0.00	0.04	0.04	0.53	1.00	0.02	1.00	1.00	0.75	1.00	0.75
	d2	0.22	0.22	0.06	1.00	0.01	0.08	0.08	0.71	1.00	0.03	1.00	1.00	0.85	1.00	0.86
	d3	0.27	0.27	0.10	1.00	0.03	0.10	0.10	0.81	1.00	0.05	1.00	1.00	0.90	1.00	0.90
(1.d)	d1	0.44	0.38	0.11	0.45	0.03	1.00	1.00	0.73	0.05	0.04	0.99	0.98	0.68	1.00	0.67
	d2	0.51	0.46	0.18	0.53	0.05	1.00	1.00	0.81	0.09	0.08	1.00	0.98	0.76	1.00	0.75
	d3	0.55	0.49	0.22	0.57	0.06	1.00	1.00	0.84	0.14	0.11	1.00	0.99	0.80	1.00	0.80
case 3: p = 5000 and σij = 0.5|i−j|
(1.a)	d1	1.00	1.00	0.94	1.00	0.94	1.00	0.99	0.92	1.00	0.92	1.00	0.99	0.96	1.00	0.95
	d2	1.00	1.00	0.95	1.00	0.95	1.00	1.00	0.95	1.00	0.95	1.00	1.00	0.97	1.00	0.97
	d3	1.00	1.00	0.96	1.00	0.96	1.00	1.00	0.96	1.00	0.96	1.00	1.00	0.98	1.00	0.98
(1.b)	d1	0.06	0.06	0.94	1.00	0.02	0.02	0.02	0.96	1.00	0.00	0.59	0.60	0.98	1.00	0.46
	d2	0.09	0.09	0.96	1.00	0.03	0.03	0.03	0.97	1.00	0.01	0.72	0.72	0.99	1.00	0.61
	d3	0.12	0.10	0.97	1.00	0.04	0.05	0.04	0.98	1.00	0.01	0.79	0.78	0.99	1.00	0.68
(1.c)	d1	0.06	0.06	0.01	0.99	0.00	0.03	0.02	0.30	1.00	0.00	0.86	0.87	0.61	1.00	0.41
	d2	0.10	0.10	0.02	1.00	0.00	0.04	0.03	0.45	1.00	0.00	0.92	0.93	0.69	1.00	0.57
	d3	0.12	0.12	0.02	1.00	0.00	0.05	0.05	0.53	1.00	0.00	0.94	0.95	0.73	1.00	0.64
(1.d)	d1	0.39	0.21	0.11	0.40	0.01	1.00	0.97	0.82	0.02	0.02	0.99	0.87	0.74	0.99	0.65
	d2	0.44	0.24	0.14	0.45	0.01	1.00	0.98	0.88	0.04	0.03	0.99	0.90	0.81	0.99	0.75
	d3	0.48	0.28	0.17	0.47	0.02	1.00	0.99	0.90	0.06	0.05	0.99	0.92	0.85	1.00	0.79
case 4: p = 5000 and σij = 0.8|i−j|
(1.a)	d1	1.00	1.00	0.55	1.00	0.55	1.00	1.00	0.55	1.00	0.55	1.00	1.00	0.70	1.00	0.69
	d2	1.00	1.00	0.61	1.00	0.62	1.00	1.00	0.61	1.00	0.61	1.00	1.00	0.76	1.00	0.76
	d3	1.00	1.00	0.67	1.00	0.67	1.00	1.00	0.64	1.00	0.64	1.00	1.00	0.80	1.00	0.80
(1.b)	d1	0.10	0.09	0.74	1.00	0.05	0.02	0.02	0.83	1.00	0.00	0.94	0.94	0.90	1.00	0.82
	d2	0.12	0.13	0.81	1.00	0.07	0.03	0.04	0.87	1.00	0.01	0.97	0.97	0.93	1.00	0.89
	d3	0.15	0.16	0.84	1.00	0.10	0.05	0.06	0.90	1.00	0.02	0.98	0.98	0.95	1.00	0.92
(1.c)	d1	0.10	0.10	0.02	0.98	0.00	0.02	0.03	0.34	1.00	0.00	1.00	1.00	0.64	1.00	0.63
	d2	0.13	0.14	0.04	0.99	0.01	0.04	0.04	0.50	1.00	0.01	1.00	1.00	0.74	1.00	0.74
	d3	0.16	0.18	0.05	0.99	0.01	0.05	0.05	0.61	1.00	0.02	1.00	1.00	0.79	1.00	0.79
(1.d)	d1	0.42	0.32	0.09	0.40	0.01	1.00	1.00	0.66	0.02	0.01	0.99	0.97	0.63	0.98	0.59
	d2	0.48	0.39	0.12	0.44	0.02	1.00	1.00	0.74	0.04	0.03	0.99	0.97	0.70	1.00	0.68
	d3	0.51	0.42	0.15	0.46	0.02	1.00	1.00	0.78	0.05	0.04	0.99	0.98	0.73	1.00	0.71

Example 2

We illustrate that the DC-SIS can be directly used for screening grouped predictors. In many regression problems, some predictors can be naturally grouped. The most common example which contains group variables is the multi-factor ANOVA problem, in which each factor may have several levels and can be expressed through a group of dummy variables. The goal of ANOVA is to select important main effects and interactions for accurate predictions, which amounts to the selection of groups of dummy variables. To demonstrate the practicability of the DC-SIS, we adopt the following model:

$$Y=c_1{\beta }_1{X}_1+c_2{\beta }_2{X}_2+c_3{\beta }_3\{\mathbf{1}(X_{12}<q_1)+1.5\times \mathbf{1}(q_1\le X_{12}<q_2)+2\times \mathbf{1}(q_2\le X_{12}<q_3)\}+c_4{\beta }_4{X}_{22}+\epsilon ,$$

where q₁, q₂ and q₃ are the 25%, 50% and 75% quantiles of X₁₂, respectively. The variables X with the coefficients c_i’s and β_i’s are the same as those in Example 1. We write

$${\stackrel{\sim }{\mathbf{x}}}_{12}={\{\mathbf{1}(X_{12}<q_1),\mathbf{1}(q_1\le X_{12}<q_2),\mathbf{1}(q_2\le X_{12}<q_3))\}}^{\text{T}}.$$

These four correlated variables naturally become a group. The predictor vector in this example becomes x = (X₁, …, X₁₁, x̃₁₂, X₁₃, …, X_p)^T ∈ ℝ^p+2. We remark here that the marginal utility of the grouped variable x̃₁₂ is defined by

$${\widehat{\omega }}_{12}={\widehat{\text{dcorr}}}^2({\stackrel{\sim }{\mathbf{x}}}_{12},Y).$$

The 5%, 25%, 50%, 75% and 95% percentiles of the minimum model size are summarized in Table 3. These percentiles indicate that with very high probability, the minimum model size to ensure the inclusion of all active predictors is small. Note that [n/log(n)] = 37. Thus, almost all and 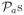of the DC-SIS equal 100%. All active predictors including the grouped variable x̃₁₂ can perfectly be selected into the resulting model across all three different model sizes. Hence, the DC-SIS is efficient to select the grouped predictors.

Table 3.

The 5%, 25%, 50%, 75% and 95% quantiles of the minimum model size out of 500 replications in Example 2.

	p = 2000					p = 5000
	5%	25%	50%	75%	95%	5%	25%	50%	75%	95%
σij = 0.5|i−j|	4.0	4.0	4.0	5.0	12.0	4.0	4.0	4.0	6.0	16.1
σi j= 0.8|i−j|	4.0	5.0	7.0	9.0	15.2	4.0	5.0	7.0	9.0	21.0

Example 3

In this example, we investigate the performance of the DC-SIS with multivariate responses. The SIS proposed in Fan and Lv (2008) cannot be directly applied for such settings. In contrast, the DC-SIS is ready for screening the active predictors by the nature of DC. In this example, we generate y = (Y₁, Y₂)^T from normal distribution with mean zero and covariance matrix Σ_y|x = (σ_x,ij)_2×2, where σ_x,₁₁ = σ_x,₂₂ = 1 and σ_x,₁₂ = σ_x,₂₁ = σ(x). We consider two scenarios for the correlation function σ(x):

• (3.a): $\sigma (\mathbf{x})=sin({\mathit{\beta }}_1^{\text{T}}\mathbf{x})$, where β₁ = (0.8, 0.6, 0, …, 0)^T.

• (3.b): $\sigma (\mathbf{x})=\{exp({\mathit{\beta }}_2^{\text{T}}\mathbf{x})-1\}/\{exp({\mathit{\beta }}_2^{\text{T}}\mathbf{x})+1\}$, where β₂ = (2 − U₁, 2 − U₂, 2 − U₃, 2 − U₄, 0, …, 0)^T with U_i’s being independent and identically distributed according to unisform distribution Uniform[0, 1].

Tables 4 and 5 depict the simulation results. Table 4 implies that the DC-SIS performs reasonably well for both models (3.a) and (3.b) in terms of model complexity. Table 5 indicates that the proportions that the active predictors are selected into the model are close to one, which supports the assertion that the DC-SIS processes the sure screening property. It implies that the DC-SIS can identify the active predictors contained in correlations between multivariate responses. This may be potentially useful in gene co-expression analysis.

Table 4.

The 5%, 25%, 50%, 75% and 95% quantiles of the minimum model size out of 500 replications in Example 3.

		p = 2000					p = 5000
	Model	5%	25%	50%	75%	95%	5%	25%	50%	75%	95%
σij = 0.5|i−j|	(3.a)	4.0	9.0	18.0	39.3	112.3	6.0	22.0	48.0	95.3	296.4
	(3.b)	6.0	19.0	43.0	92.0	253.1	14.0	45.0	92.5	198.8	571.6
σij = 0.8|i−j|	(3.a)	2.0	3.0	6.0	12.0	40.0	2.0	6.0	14.0	32.0	98.0
	(3.b)	4.0	4.0	4.0	6.0	10.0	4.0	4.0	5.0	8.0	18.1

Table 5.

The proportions of 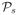and in Example 3. The user-specified model sizes d₁ = [n/log n], d₂ = 2[n/log n] and d₃ = 3[n/log n].

		p = 2000								p = 5000
		(3.a)			(3.b)					(3.a)			(3.b)
	size	X1	X2	ALL	X1	X2	X3	X4	ALL	X1	X2	ALL	X1	X2	X3	X4	ALL
σij = 0.5|i−j|	d1	0.95	0.76	0.74	0.71	0.98	0.98	0.72	0.47	0.79	0.49	0.42	0.48	0.91	0.90	0.53	0.20
	d2	0.98	0.90	0.90	0.85	0.99	0.99	0.85	0.71	0.93	0.70	0.67	0.67	0.97	0.97	0.71	0.45
	d3	1.00	0.95	0.95	0.91	0.99	1.00	0.90	0.81	0.97	0.81	0.80	0.75	0.98	0.99	0.78	0.55
σij = 0.8|i−j|	d1	0.98	0.95	0.94	1.00	1.00	1.00	1.00	1.00	0.92	0.84	0.81	1.00	1.00	1.00	0.99	0.99
	d2	1.00	0.98	0.99	1.00	1.00	1.00	1.00	1.00	0.98	0.95	0.93	1.00	1.00	1.00	1.00	1.00
	d3	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.99	0.96	0.96	1.00	1.00	1.00	1.00	1.00

Example 4

The Cardiomyopathy microarray dataset was once analyzed by Segal, Dahlquist and Conklin (2003) and Hall and Miller (2009). The goal is to identify the most influential genes for overexpression of a G protein-coupled receptor (Ro1) in mice. The response Y is the Ro1 expression level, and the predictors X_k’s are other gene expression levels. Compared with the sample size n = 30 in this dataset, the dimension p = 6319 is very large.

The DC-SIS procedure ranks two genes, labeled Msa.2134.0 and Msa.2877.0, at the top. The scatter plots of Y versus these two gene expression levels with cubic spline fit curves in Figure 1 indicate clearly the existence of nonlinear patterns. Yet, our finding is different from Hall and Miller (2009) in that they ranked Msa.2877.0 and Msa.1166.0 at the top with their proposed generalized correlation ranking. A natural question arises: which screening procedure performs better in terms of ranking? To compare the performance of these two procedures, we fit an additive model as follows:

$$Y={\ell }_{k1}(X_{k1})+{\ell }_{k2}(X_{k2})+{\epsilon }_k,\text{for}k=1,2.$$

Figure 1.

The scatter plot of Y versus two genes expression levels identified by the DC-SIS.

The DC-SIS, corresponding to k = 1, regards Msa.2134.0 and Msa.2877.0 as the two predictors, while the generalized correlation ranking proposed by Hall and Miller (2009), corresponding to k = 2, regards Msa.2877.0 and Msa.1166.0 as predictors in the above model. We fit the unknown link functions ℓ_ki using the R mgcv package. The DC-SIS method clearly achieves better performance with the adjusted R² of 96.8% and the deviance explained of 98.3%, in contrast to the adjusted R² of 84.5% and the deviance explained of 86.6% for the generalized correlation ranking method. We remark here that deviance explained means the proportion of the null deviance explained by the proposed model, with a larger value indicating better performance. Because both the adjusted R² values and the explained deviance are very large, it seems unnecessary to extract any additional genes.

4. DISCUSSION

In this paper we proposed a sure independence screening procedure using distance correlation. We established the sure screening property for this procedure when the number of predictors diverges with an exponential rate of the sample size. We examined the finite-sample performance of the proposed procedure via Monte Carlo studies and illustrated the proposed methodology through a real data example. We followed Fan and Lv (2008) to set the cutoff d in this paper and examine the effect of different values of d. As pointed out by a referee, the choice of d is very important in the screening stage. Zhao and Li (2012) proposed an approach to selecting d for Cox models based on controlling false positive rate. Their approach is merely for model-based feature screening methods. Zhu, Li, Li and Zhu (2011) proposed an alternative method to determine d for the SIRS. One may adopt their procedure for the DC-SIS. We opt not to pursue this further. Certainly, the selection of d is similar to selection of the tuning parameter in regularization methods, and plays an important role in practical implementation. This is a good topic for future research.

Similar to the SIS, the DC-SIS may fail to identify some important predictors which are marginally independent of the response. Thus, it is of interest to develop an iterative procedure to fix such an issue. In the earlier version of this paper, we proposed an iterative version of DC-SIS. Our empirical studies including Monte Carlo simulation and real data analysis imply that the proposed iterative DC-SIS may be used to fix the problem in a similar spirit of ISIS (Fan and Lv, 2008). Theoretical analysis of the iterative DC-SIS needs further study. New methods to deal with identification of important predictors which are marginally independent of the response is an important topic for future research.

Biographies

Runze Li is Professor, Department of Statistics and The Methodology Center, The Pennsylvania State University, University Park, PA 16802-2111.rli@stat.psu.edu. His research was supported by National Institute on Drug Abuse (NIDA) grant P50-DA10075 and National Natural Science Foundation of China (NNSFC) grant 11028103.

Wei Zhong is the corresponding author and Assistant Professor of Wang Yanan Institute for Studies in Economics, Department of Statistics and Fujian Key Laboratory of Statistical Science, Xiamen University, China. wxz123@psu.edu. His research was supported by a NIDA grant P50-DA10075 as a graduate research assistant during his graduate study, and by the NNSFC grant 71131008 (Key Project).

Liping Zhu is Associate Professor of School of Statistics and Management, Shanghai University of Finance and Economics, China. zhu.liping@mail.shufe.edu.cn. His research was supported by a NNSFC grant 11071077 and a NIDA grant R21-DA024260.

APPENDIX

Appendix A: Some Lemmas

Lemmas 1 and 2 will be used repeatedly in the proof of Theorem 1. These two lemmas provide us two exponential inequalities, and are extracted from Lemma 5.6.1.A and Theorem 5.6.1.A of Serfling (1980, page 200–201).

Lemma 1

Let μ = E(Y). If Pr(a ≤ Y ≤ b) = 1, then

$$E[exp\{s(Y-\mu )\}]\le exp\{s^2{(b-a)}^2/8\},\mathit{for}\mathit{any}s>0.$$

Lemma 2

Let h(Y₁, ···, Y_m) be a kernel of the U-statistic U_n, and θ = E {h(Y₁, ···, Y_m)}.

If a ≤ h(Y₁, ···, Y_m) ≤ b, then, for any t > 0 and n ≥ m,

$$Pr(U_n-\theta \ge t)\le exp\{-2[n/m]t^2/{(b-a)}^2\},$$

where [n/m] denotes the integer part of n/m.

Due to the symmetry of U-statistic, Lemma 2 entails that

$$Pr(\mid U_n-\theta \mid \ge t)\le 2\text{exp}\{-2[n/m]t^2/{(b-a)}^2\}.$$

Let us introduce some notations before giving the proof of Theorem 1. Let {X̃_k, ỹ} be an independent copy of {X_k, y}, and define S_k1 = E||X_k − X̃_k||₁||y − ỹ||q, S_k2 = E||X_k − X̃_k||₁E||y − ỹ||_q, and S_k3 = E{E(||X_k − X̃_k||₁|X_k)E(||y − ỹ||_q|y)}, and their sample counterparts

$$\begin{array}{l}{\widehat{S}}_{k1}=\frac{1}{n^2}\sum _{i,j=1}^n{\left|\right|X_{ik}-X_{jk}\left|\right|}_1{\left|\right|{\mathbf{y}}_i-{\mathbf{y}}_j\left|\right|}_q,\\ {\widehat{S}}_{k2}=\frac{1}{n^2}\sum _{i,j=1}^n{\left|\right|X_{ik}-X_{jk}\left|\right|}_1\frac{1}{n^2}\sum _{i,j=1}^n{\left|\right|{\mathbf{y}}_i-{\mathbf{y}}_j\left|\right|}_q,\\ {\widehat{S}}_{k3}=\frac{1}{n^3}\sum _{i,j=1}^n{\left|\right|X_{ik}-X_{lk}\left|\right|}_1{\left|\right|{\mathbf{y}}_j-{\mathbf{y}}_l\left|\right|}_q.\end{array}$$

By definitions of distance covariance and sample distance covariance, it follows that

$${\text{dcov}}^2(X_k,\mathbf{y})=S_{k1}+S_{k2}-2S_{k3}\text{and}{\widehat{\text{dcov}}}^2(X_k,\mathbf{y})={\widehat{S}}_{k1}+{\widehat{S}}_{k2}-2{\widehat{S}}_{k3}.$$

Appendix B: Proof of Theorem 1

We aim to show the uniform consistency of the denominator and the numerator of ω̂_k under regularity conditions respectively. Because the denominator of ω̂_k has a similar form as the numerator, we deal with its numerator only below. Throughout proof, the notations C and c are generic constants which may take different values at each appearance.

We first deal with Ŝ_k1. Define ${\widehat{S}}_{k1}^{\ast }={\{n(n-1)\}}^{-1}{\displaystyle \sum _{i\ne j}}{\left|\right|X_{ik}-X_{jk}\left|\right|}_1{\left|\right|({\mathbf{y}}_i-{\mathbf{y}}_j)\left|\right|}_q$, which is a usual U-statistic. We shall establish the uniform consistency of ${\widehat{S}}_{k1}^{\ast }$ by using the theory of U-statistics (Serfling, 1980, Section 5). By using the Cauchy-Schwartz inequality,

$$\begin{array}{l}{S}_{k1}=E({\left|\right|X_{ik}-X_{jk}\left|\right|}_1{\left|\right|{\mathbf{y}}_i-{\mathbf{y}}_j\left|\right|}_q)\le {\{E({\left|\right|X_{ik}-X_{jk}\left|\right|}_1^2)E({\left|\right|{\mathbf{y}}_i-{\mathbf{y}}_j\left|\right|}_q^2)\}}^{1/2}\\ \le 4{\{E(X_k^2)E{\left|\right|\mathbf{y}\left|\right|}_q^2\}}^{1/2}.\end{array}$$

This together with condition (C1) implies that S_k1 is uniformly bounded in p, that is, $\underset{p}{sup}\underset{1\le k\le p}{max}{S}_{k1}<\infty$. For any given ε > 0, take n large enough such that S_k1/n < ε. Then it can be easily shown that

$$\begin{array}{l}Pr(\mid {\widehat{S}}_{k1}-S_{k1}\mid \ge 2\epsilon )=Pr\{\mid {\widehat{S}}_{k1}^{\ast }(n-1)/n-S_{k1}(n-1)/n-S_{k1}/n\mid \ge 2\epsilon \}\\ \le Pr\{\mid {\widehat{S}}_{k1}^{\ast }-S_{k1}\mid (n-1)/n\ge 2\epsilon -S_{k1}/n\}\\ \le Pr(\mid {\widehat{S}}_{k1}^{\ast }-S_{k1}\mid \ge \epsilon ).\end{array}$$ (B.1)

To establish the uniform consistency of Ŝ_k1, it thus suffices to show the uniform consistency of ${\widehat{S}}_{k1}^{\ast }$. Let h₁(X_ik, y_i; X_jk, y_j) = ||X_ik − X_jk||₁||y_i − y_j||_q be the kernel of the U -statistic ${\widehat{S}}_{k1}^{\ast }$. We decompose the kernel function h₁ into two parts: h₁ = h₁1(h₁ > M) + h₁1(h₁ ≤ M) where M will be specified later. The U-statistic can now be written as follows,

$$\begin{array}{l}{\widehat{S}}_{k1}^{\ast }={\{n(n-1)\}}^{-1}\sum _{i\ne j}{h}_1(X_{ik},{\mathbf{y}}_i;X_{jk},{\mathbf{y}}_j)\mathbf{1}\{h_1(X_{ik},{\mathbf{y}}_i;X_{jk},{\mathbf{y}}_j)\le M\}+{\{n(n-1)\}}^{-1}\sum _{i\ne j}{h}_1(X_{ik},{\mathbf{y}}_i;X_{jk},{\mathbf{y}}_j)\mathbf{1}\{h_1(X_{ik},{\mathbf{y}}_i;X_{jk},{\mathbf{y}}_j)>M\}\\ ={\widehat{S}}_{k1,1}^{\ast }+{\widehat{S}}_{k1,2}^{\ast }.\end{array}$$

Accordingly, we decompose S_k1 into two parts:

$$\begin{array}{l}{S}_{k1}=E[h_1(X_{ik},{\mathbf{y}}_i;X_{jk},{\mathbf{y}}_j)\mathbf{1}\{h_1(X_{ik},{\mathbf{y}}_i;X_{jk},{\mathbf{y}}_j)\le M\}]+E[h_1(X_{ik},{\mathbf{y}}_i;X_{jk},{\mathbf{y}}_j)\mathbf{1}\{h_1(X_{ik},{\mathbf{y}}_i;X_{jk},{\mathbf{y}}_j)>M\}]\\ =S_{k1,1}+S_{k1,2}.\end{array}$$

Clearly, ${\widehat{S}}_{k1,1}^{\ast }$ and ${\widehat{S}}_{k1,2}^{\ast }$ are unbiased estimators of S_k1,1 and S_k1,2, respectively.

We deal with the consistency of ${\widehat{S}}_{k1,1}^{\ast }$ first. With the Markov’s inequality, for any t > 0, we can obtain that

$$Pr({\widehat{S}}_{k1,1}^{\ast }-S_{k1,1}\ge \epsilon )\le exp(-t\epsilon )exp(-{tS}_{k1,1})E\{exp(t{\widehat{S}}_{k1,1}^{\ast })\}.$$

Serfling (1980, Section 5.1.6) showed that any U-statistic can be represented as an average of averages of independent and identically distributed (i.i.d) random variables. That is, ${\widehat{S}}_{k1,1}^{\ast }={(n!)}^{-1}{\displaystyle \sum _{n!}}{\mathrm{\Omega }}_1(X_{1k},{\mathbf{y}}_1;\cdots ;X_{nk},{\mathbf{y}}_n)$, where ${\displaystyle \sum _{n!}}$ denotes the summation over all possible permutations of (1, …, n), and each Ω₁(X_1k, y₁; ···; X_nk, y_n) is an average of m = [n/2] i.i.d random variables (i.e., ${\mathrm{\Omega }}_1=m^{-1}{\displaystyle \sum _r}{h}_1^{(r)}\mathbf{1}\{h_1^{(r)}\le M\}$). Since the exponential function is convex, it follows from Jensen’s inequality that, for 0 < t ≤ 2s₀,

$$\begin{array}{l}E\{exp(t{\widehat{S}}_{k1,1}^{\ast })\}=E[exp\{t{(n!)}^{-1}\sum _{n!}{\mathrm{\Omega }}_1(X_{1k},{\mathbf{y}}_1;\cdots ;X_{nk},{\mathbf{y}}_n)\}]\\ \le {(n!)}^{-1}\sum _{n!}E[exp\{t{\mathrm{\Omega }}_1(X_{1k},{\mathbf{y}}_1;\cdots ;X_{nk},{\mathbf{y}}_n)\}]\\ =E^m\{exp(m^{-1}{th}_1^{(r)}\mathbf{1}\{h_1^{(r)}\le M\})\},\end{array}$$

which together with Lemma 1 entails immediately that

$$\begin{array}{l}Pr({\widehat{S}}_{k1,1}^{\ast }-S_{k1,1}\ge \epsilon )\le exp(-t\epsilon )E^m\{exp(m^{-1}t[h_1^{(r)}\mathbf{1}\{h_1^{(r)}\le M\}-S_{k1,1}])\}\\ \le exp\{-t\epsilon +M^2{t}^2/(8m)\}.\end{array}$$

By choosing t = 4εm/M², we have $Pr({\widehat{S}}_{k1,1}^{\ast }-S_{k1,1}\ge \epsilon )\le exp(-2{\epsilon }^{2}m/M^2)$. Therefore, by the symmetry of U-statistic, we can obtain easily that

$$Pr(\mid {\widehat{S}}_{k1,1}^{\ast }-S_{k1,1}\mid \ge \epsilon )\le 2exp(-2{\epsilon }^{2}m/M^2).$$ (B.2)

Next we show the consistency of ${\widehat{S}}_{k1,2}^{\ast }$. With Cauchy-Schwartz and Markov’s inequality,

$$\begin{array}{l}{S}_{k1,2}^2\le E\{h_1^2(X_{ik},{\mathbf{y}}_i;X_{jk},{\mathbf{y}}_j)\}Pr\{h_1(X_{ik},{\mathbf{y}}_i;X_{jk},{\mathbf{y}}_j)>M\}\\ \le E\{h_1^2(X_{ik},{\mathbf{y}}_i;X_{jk},{\mathbf{y}}_j)\}E[exp\{s^{\prime }{h}_1(X_{ik},{\mathbf{y}}_i;X_{jk},{\mathbf{y}}_j)\}]/exp(s^{\prime }M),\end{array}$$

for any s′ > 0. Using the fact (a² + b²)/2 ≥ (a + b)²/4 ≥ |ab|, we have

$$\begin{array}{l}{h}_1(X_{ik},{\mathbf{y}}_i;X_{jk},{\mathbf{y}}_j)={\{{(X_{ik}-X_{jk})}^2{({\mathbf{y}}_i-{\mathbf{y}}_j)}^{\text{T}}({\mathbf{y}}_i-{\mathbf{y}}_j)\}}^{1/2}\le 2{\{(X_{ik}^2+X_{jk}^2)({\left|\right|{\mathbf{y}}_i\left|\right|}_q^2+{\left|\right|{\mathbf{y}}_j\left|\right|}_q^2)\}}^{1/2}\le {\{{(X_{ik}^2+X_{jk}^2+{\left|\right|{\mathbf{y}}_i\left|\right|}_q^2+{\left|\right|{\mathbf{y}}_j\left|\right|}_q^2)}^2\}}^{1/2}\\ =X_{ik}^2+X_{jk}^2+{\left|\right|{\mathbf{y}}_i\left|\right|}_q^2+{\left|\right|{\mathbf{y}}_j\left|\right|}_q^2,\end{array}$$

which yields that

$$\begin{array}{l}E[exp\{s^{\prime }{h}_1(X_{ik},{\mathbf{y}}_i;X_{jk},{\mathbf{y}}_j)\}]\le E[exp\{s^{\prime }(X_{ik}^2+X_{jk}^2+{\left|\right|{\mathbf{y}}_i\left|\right|}_q^2+{\left|\right|{\mathbf{y}}_j\left|\right|}_q^2)\}]\\ \le E\{exp(2s^{\prime }{X}_{ik}^2)\}E\{exp(2s^{\prime }{\left|\right|{\mathbf{y}}_i\left|\right|}_q^2)\}.\end{array}$$

The last inequality follows from the Cauchy-Schwartz inequality. If we choose M = cn^γ for 0 < γ < 1/2 − κ, then S_k1,₂ ≤ ε/2 when n is sufficiently large. Consequently,

$$Pr(\mid {\widehat{S}}_{k1,2}^{\ast }-S_{k1,2}\mid >\epsilon )\le Pr(\mid {\widehat{S}}_{k1,2}^{\ast }\mid >\epsilon /2).$$ (B.3)

It remains to bound the probability $Pr(\mid {\widehat{S}}_{k1,2}^{\ast }\mid >\epsilon /2)$. We observe that the events satisfy

$$\{\mid {\widehat{S}}_{k1,2}^{\ast }\mid >\epsilon /2\}\subseteq \{X_{ik}^2+{\left|\right|{\mathbf{y}}_i\left|\right|}_q^2>M/2,\text{for}\text{some}1\le i\le p\}.$$ (B.4)

To see this, we assume that $X_{ik}^2+{\left|\right|{\mathbf{y}}_i\left|\right|}_q^2\le M/2$ for all 1 ≤ i ≤ p. This assumption will lead to a contradiction. To be precise, under this assumption, $h_1(X_{ik},{\mathbf{y}}_i;X_{jk},{\mathbf{y}}_j)\le X_{ik}^2+X_{jk}^2+{\left|\right|{\mathbf{y}}_i\left|\right|}_q^2+{\left|\right|{\mathbf{y}}_j\left|\right|}_q^2\le M$. Consequently, $\mid {\widehat{S}}_{k1,2}^{\ast }\mid =0$, which is a contrary to the event $\mid {\widehat{S}}_{k1,2}^{\ast }\mid >\epsilon /2$. This verifies the relation (B.4) is true.

By invoking condition (C1), there must exist a constant C such that

$$Pr({\left|\right|X_k\left|\right|}_1^2+{\left|\right|\mathbf{y}\left|\right|}_q^2\ge M/2)\le Pr({\left|\right|X_k\left|\right|}_1\ge \sqrt{M}/2)+Pr({\left|\right|\mathbf{y}\left|\right|}_q\ge \sqrt{M}/2)\le 2Cexp(-sM/4).$$

The last inequality follows from Markov’s inequality for s > 0. Consequently,

$$\begin{array}{l}\underset{1\le k\le p}{max}Pr(\mid {\widehat{S}}_{k1,2}^{\ast }\mid >\epsilon /2)\le n\underset{1\le k\le p}{max}Pr({\left|\right|X_k\left|\right|}_1^2+{\left|\right|\mathbf{y}\left|\right|}_q^2\ge M/2)\\ \le 2\mathit{nC}exp(-sM/4).\end{array}$$ (B.5)

Recall that M = cn^γ. Combining the results (B.2), (B.3) and (B.5), we have

$$Pr(\mid {\widehat{S}}_{k1}-S_{k1}\mid \ge 4\epsilon )\le 2exp(-{\epsilon }^2{n}^{1-2\gamma })+2\mathit{nC}exp(-{sn}^{\gamma }/4).$$ (B.6)

In the sequel we turn to Ŝ_k2. We write Ŝ_k2 = Ŝ_k2,₁Ŝ_k2,₂, where ${\widehat{S}}_{k2,1}=n^{-2}{\displaystyle \sum _{i\ne j}}{\left|\right|X_{ik}-X_{jk}\left|\right|}_1$, and ${\widehat{S}}_{k2,2}=n^{-2}{\displaystyle \sum _{i\ne j}}{\left|\right|{\mathbf{y}}_i-{\mathbf{y}}_j\left|\right|}_q$. Similarly, we write S_k2 = S_k2,₁S_k2,₂, where S_k2,₁ = E{||X_ik − X_jk||₁} and S_k2,₂ = E{||y_i − y_j||_q}. Following arguments for proving (B.6) we can show that

$$\begin{array}{l}Pr(\mid {\widehat{S}}_{k2,1}-S_{k2,1}\mid \ge 4\epsilon )\le 2exp(-{\epsilon }^2{n}^{1-2\gamma })+2\mathit{nC}exp(-{sn}^{2\gamma }/4),\text{and}\\ Pr(\mid {\widehat{S}}_{k2,2}-S_{k2,2}\mid \ge 4\epsilon )\le 2exp(-{\epsilon }^2{n}^{1-2\gamma })+2\mathit{nC}exp(-{sn}^{2\gamma }/4).\end{array}$$ (B.7)

Condition (C1) ensures that $S_{k2,1}\le {\{E({\left|\right|X_{ik}-X_{jk}\left|\right|}_1^2)\}}^{1/2}\le {\{4E(X_k^2)\}}^{1/2}$ and $S_{k2,2}\le {\{E({\left|\right|{\mathbf{y}}_i-{\mathbf{y}}_j\left|\right|}_q^2)\}}^{1/2}\le {\{4E({\left|\right|\mathbf{y}\left|\right|}_q^2)\}}^{1/2}$ are uniformly bounded. That is,

$$max\{\underset{1\le k\le p}{max}{S}_{k2,1},S_{k2,2}\}\le C,$$

for some constant C. Using (B.7) repetitively, we can easily prove that

$$\begin{array}{l}Pr\{\mid ({\widehat{S}}_{k2,1}-S_{k2,1})S_{k2,2}\mid \ge \epsilon \}\le Pr(\mid {\widehat{S}}_{k2,1}-S_{k2,1}\mid \ge \epsilon /C)\\ \le 2exp\{-{\epsilon }^2{n}^{1-2\gamma }/(16C^2)\}+2\mathit{nC}exp(-{sn}^{2\gamma }/4),\\ Pr(\mid S_{k2,1}({\widehat{S}}_{k2,2}-S_{k2,2})\mid \ge \epsilon )\le Pr(\mid {\widehat{S}}_{k2,2}-S_{k2,2}\mid \ge \epsilon /C)\\ \le 2exp\{-{\epsilon }^2{n}^{1-2\gamma }/(16C^2)\}+2\mathit{nC}exp(-{sn}^{2\gamma }/4),\end{array}$$ (B.8)

and

$$\begin{array}{l}Pr\{\mid ({\widehat{S}}_{k2,1}-S_{k2,1})({\widehat{S}}_{k2,2}-S_{k2,2})\mid \ge \epsilon \}\le Pr(\mid {\widehat{S}}_{k2,1}-S_{k2,1}\mid \ge \sqrt{\epsilon })+Pr(\mid {\widehat{S}}_{k2,2}-S_{k2,2}\mid \ge \sqrt{\epsilon })\\ \le 4exp(-\epsilon n^{1-2\gamma }/16)+4\mathit{nC}exp(-{sn}^{2\gamma }/4).\end{array}$$ (B.9)

It follows from Bonferroni’s inequality, inequalities (B.8) and (B.9) that,

$$\begin{array}{l}Pr\left(\left|{\widehat{S}}_{k2}-S_{k2}\right|\ge 3\epsilon \right)=Pr\left(\left|{\widehat{S}}_{k2,1}{\widehat{S}}_{k2,2}-S_{k2,1}{S}_{k2,2}\right|\ge 3\epsilon \right)\\ \le Pr\left\{\left|({\widehat{S}}_{k2,1}-S_{k2,1})S_{k2,2}\right|\ge \epsilon \right\}+Pr\left\{\left|S_{k2,1}({\widehat{S}}_{k2,2}-S_{k2,2})\right|\ge \epsilon \right\}\\ +Pr\left\{\left|({\widehat{S}}_{k2,1}-S_{k2,1})({\widehat{S}}_{k2,2}-S_{k2,2})\right|\ge \epsilon \right\}\\ \le 8exp\{-{\epsilon }^2{n}^{1-2\gamma }/(16C^2)\}+8\mathit{nC}exp(-{sn}^{2\gamma }/4),\end{array}$$ (B.10)

where the last inequality holds when ε is sufficiently small and C is sufficiently large.

It remains to the uniform consistency of Ŝ_k3. We first study the following U -statistic:

$$\begin{array}{l}{\widehat{S}}_{k3}^{\ast }=\frac{1}{n(n-1)(n-2)}\sum _{i<j<l}\{{\left|\right|X_{ik}-X_{jk}{\left|\right|}_1\left|\right|{\mathbf{y}}_j-{\mathbf{y}}_l\left|\right|}_q+{\left|\right|X_{ik}-X_{lk}\left|\right|}_1{\left|\right|{\mathbf{y}}_j-{\mathbf{y}}_l\left|\right|}_q+\\ {\left|\right|X_{ik}-X_{jk}\left|\right|}_1{\left|\right|{\mathbf{y}}_i-{\mathbf{y}}_l\left|\right|}_q+{\left|\right|X_{lk}-X_{jk}\left|\right|}_1{\left|\right|{\mathbf{y}}_i-{\mathbf{y}}_l\left|\right|}_q+\\ {\left|\right|X_{lk}-X_{jk}\left|\right|}_1{\left|\right|{\mathbf{y}}_i-{\mathbf{y}}_j\left|\right|}_q+{\left|\right|X_{lk}-X_{ik}\left|\right|}_1{\left|\right|{\mathbf{y}}_i-{\mathbf{y}}_j\left|\right|}_q\}\\ =:\frac{6}{n(n-1)(n-2)}\sum _{i<j<l}{h}_3(X_{ik},{\mathbf{y}}_i;X_{jk},{\mathbf{y}}_j;X_{lk},{\mathbf{y}}_l).\end{array}$$ (B.11)

Here, h₃(X_ik, y_i; X_jk, y_j; X_lk, y_l) is the kernel of U -statistic ${\widehat{S}}_{k3}^{\ast }$. Following the arguments to deal with ${\widehat{S}}_{k1}^{\ast }$, we decompose h₃ into two parts: h₃ = h₃1(h₃ > M) + h₃1(h₃ ≤ M). Accordingly

$$\begin{array}{l}{\widehat{S}}_{k3}^{\ast }=\frac{6}{n(n-1)(n-2)}\sum _{i<j<l}{h}_3\mathbf{1}(h_3\le M)+\frac{6}{n(n-1)(n-2)}\sum _{i<j<l}{h}_3\mathbf{1}(h_3>M)\\ ={\widehat{S}}_{k3,1}^{\ast }+{\widehat{S}}_{k3,2}^{\ast },\\ S_{k3}=E\{h_3\mathbf{1}(h_3\le M)\}+E\{h_3\mathbf{1}(h_3>M)\}=S_{k3,1}+S_{k3,2}.\end{array}$$

Following similar arguments for proving (B.2), we can show that

$$Pr(\mid {\widehat{S}}_{k3,1}^{\ast }-S_{k3,1}\mid \ge \epsilon )\le 2exp(-2{\epsilon }^2{m}^{\prime }/M^2),$$ (B.12)

where m′ = [n/3] because ${\widehat{S}}_{k3,1}^{\ast }$ is a third-order U -statistic.

Then we deal with ${\widehat{S}}_{k3,2}^{\ast }$. We observe that $h_3(X_{ik},{\mathbf{y}}_i;X_{jk},{\mathbf{y}}_j;X_{lk},{\mathbf{y}}_l)\le 4(X_{ik}^2+X_{jk}^2+X_{lk}^2+{\left|\right|{\mathbf{y}}_i\left|\right|}_q^2+{\left|\right|{\mathbf{y}}_j\left|\right|}_q^2+{\left|\right|{\mathbf{y}}_l\left|\right|}_q^2)/6$, which will be smaller than M if $X_{ik}^2+{\left|\right|{\mathbf{y}}_i\left|\right|}_q^2\le M/2$for all 1 ≤ i ≤ p. Thus, for any ε > 0, the events satisfy

$$\{\mid {\widehat{S}}_{k3,2}^{\ast }\mid >\epsilon /2\}\subseteq \{X_{ik}^2+{\left|\right|{\mathbf{y}}_i\left|\right|}_q^2>M/2,\text{for}\text{some}1\le i\le p\}.$$

By using the similar arguments to prove (B.5), it follows that

$$Pr(\mid {\widehat{S}}_{k3,2}^{\ast }-S_{k3,2}\mid >\epsilon )\le Pr(\mid {\widehat{S}}_{k3,2}^{\ast }\mid >\epsilon /2)\le 2\mathit{nC}exp(-sM/4).$$ (B.13)

Then, we combine the results (B.12) and (B.13) with M = cn^γ for some 0 < γ < 1/2 − κ to obtain that

$$Pr\left(\left|{\widehat{S}}_{k3}^{\ast }-S_{k3}\right|\ge 2\epsilon \right)\le 2exp(-2{\epsilon }^2{n}^{1-2\gamma }/3)+2\mathit{nC}exp(-{sn}^{\gamma }/4).$$ (B.14)

By the definition of Ŝ_k3,

$${\widehat{S}}_{k3}=\frac{(n-1)(n-2)}{n^2}\left\{{\widehat{S}}_{k3}^{\ast }+\frac{1}{(n-2)}{\widehat{S}}_{k1}^{\ast }\right\}.$$

Thus, using similar techniques to deal with Ŝ_k1, we can obtain that

$$Pr\left(\left|{\widehat{S}}_{k3}-S_{k3}\right|\ge 4\epsilon \right)=Pr\left\{\left|\frac{(n-1)(n-2)}{n^2}\left({\widehat{S}}_{k3}^{\ast }-S_{k3}\right)-\frac{3n-2}{n^2}{S}_{k3}+\frac{n-1}{n^2}\left({\widehat{S}}_{k1}^{\ast }-S_{k1}\right)+\frac{n-1}{n^2}{S}_{k1}\right|\ge 4\epsilon \right\}.$$

Using similar arguments for dealing with S_k1, we can show that S_k3 is uniformly bounded in p. Taking n large enough such that {(3n − 2)/n²}S_k3 ≤ ε and {(n − 1)/n²}S_k1 ≤ ε, then

$$\begin{array}{l}Pr(\mid {\widehat{S}}_{k3}-S_{k3}\mid \ge 4\epsilon )\le Pr(\mid {\widehat{S}}_{k3}^{\ast }-S_{k3}\mid \ge \epsilon )+Pr\{\mid {\widehat{S}}_{k1}^{\ast }-S_{k1}\mid \ge \epsilon \}\\ \le 4exp(-{\epsilon }^2{n}^{1-2\gamma }/6)+4\mathit{nC}exp(-{sn}^{\gamma }/4).\end{array}$$ (B.15)

The last inequality follows from (B.6) and (B.14). This, together with (B.6), (B.10) and the Bonferroni’s inequality, implies

$$\begin{array}{l}Pr\{\mid ({\widehat{S}}_{k1}+{\widehat{S}}_{k2}-2{\widehat{S}}_{k3})-(S_{k1}+S_{k2}-2S_{k3})\mid \ge \epsilon \}\le Pr(\mid {\widehat{S}}_{k1}-S_{k1}\mid \ge \epsilon /4)+Pr(\mid {\widehat{S}}_{k2}-S_{k2}\mid \ge \epsilon /4)+Pr(\mid {\widehat{S}}_{k3}-S_{k3}\mid \ge \epsilon /4)\\ =O\{exp(-c_1{\epsilon }^2{n}^{1-2\gamma })+nexp(-c_2{n}^{\gamma })\},\end{array}$$ (B.16)

for some positive constants c₁ and c₂. The convergence rate of the numerator of ω̂_k is now achieved. Following similar arguments, we can obtain the convergence rate of the denominator. In effect the convergence rate of ω̂_k has the same form of (B.16). We omit the details here. Let ε = cn^−κ, where κ satisfies 0 < κ + γ < 1/2. We thus have

$$\begin{array}{l}Pr\{\underset{1\le k\le p}{max}\mid {\widehat{\omega }}_k-{\omega }_k\mid \ge {cn}^{-\kappa }\}\le p\underset{1\le k\le p}{max}Pr\{\mid {\widehat{\omega }}_k-{\omega }_k\mid \ge {cn}^{-\kappa }\}\\ \le O(p[exp\{-c_1{n}^{1-2(\kappa +\gamma )}\}+nexp(-c_2{n}^{\gamma })]).\end{array}$$

The first part of Theorem 1 is proven.

Now we deal with the second part of Theorem 1. If 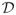⊈ , then there must exist some k ∈ 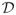such that ω̂_k < cn^−κ. It follows from condition (C2) that |ω̂_k − ω_k| > cn^−κ for some k ∈ 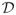, indicating that the events satisfy { ⊈ } ⊆ {|ω̂_k − ω_k| > cn^−κ, for some k ∈ }, and hence ${\mathcal{E}}_n=\{\underset{k\in \mathcal{D}}{max}\mid {\widehat{\omega }}_k-{\omega }_k\mid \le {cn}^{-\kappa }\}\subseteq \{\mathcal{D}\subseteq {\widehat{\mathcal{D}}}^{★}\}$. Consequently,

$$\begin{array}{l}Pr(\mathcal{D}\subseteq {\widehat{\mathcal{D}}}^{★})\ge Pr({\mathcal{E}}_n)=1-Pr({\mathcal{E}}_n^c)=1-Pr(\underset{k\in \mathcal{D}}{min}\mid {\widehat{\omega }}_k-{\omega }_k\mid \ge {cn}^{-\kappa })\\ =1-s_{n}Pr\{\mid {\widehat{\omega }}_k-{\omega }_k\mid \ge {cn}^{-\kappa }\}\\ \ge 1-O(s_n[exp\{-c_1{n}^{1-2(\kappa +\gamma )}\}+nexp(-c_2{n}^{\gamma })]),\end{array}$$

where s_n is the cardinality of . This completes the proof of the second part.