Parental Education and Child Health: Evidence from a Natural Experiment in Taiwan

Abstract

In 1968, the Taiwanese government extended compulsory education from six to nine years and opened over 150 new junior high schools at a differential rate among regions. Within each region, we exploit variations across cohorts in new junior high school openings to construct an instrument for schooling and employ it to estimate the causal effects of mother’s or father’s schooling on infant birth outcomes in the years 1978–1999. Parents’ schooling does indeed cause favorable infant health outcomes. The increase in schooling associated with the reform saved almost 1 infant life in 1,000 live births.

“The one social factor that researchers agree is consistently linked to longer lives in every country where it has been studied is education. It is more important than race; it obliterates any effects of income.” Gina Kolata, “A Surprising Secret to Long Life: Stay in School,”

New York Times, January 3, 2007, p. 1.

This paper is a contribution to the literature on the relationship between years of formal schooling completed and good health. In particular we investigate whether the positive relationship between these two variables implies causality from the former to the latter. As the quotation from Kolata indicates, there is a large literature, reviewed in detail by Michael Grossman and Robert Kaestner (1997) and Grossman (2000, 2006), that shows that an individual’s own schooling is the most important correlate of his or her health and that parents’ schooling, especially mother’s schooling, is the most important correlate of child health. This finding emerges whether health levels are measured by mortality rates, morbidity rates, self-evaluation of health status, or physiological indicators of health, and whether the units of observation are individuals or groups.

Improvements in child health are widely accepted public policy goals in developing and developed countries. The positive correlation between mother’s schooling and child health in numerous studies was one factor behind the World Bank’s campaign in the 1990s to encourage increases in maternal education in developing countries (World Bank 1993). In a 2002 issue of Health Affairs devoted primarily to the nonmedical determinants of health, Angus Deaton (2002) argues that policies to increase education in the U.S. and to increase income in developing countries are very likely to have larger payoffs in terms of health than those that focus on health care, even if inequalities in health rise. The same proposition with regard to the U.S. can be found in a much earlier study by Richard Auster, Irving Leveson, and Deborah Sarachek (1969). Since more education typically leads to higher income, policies to increase the former appear to have large returns for more than one generation throughout the world.

Efforts to improve the health of an individual by increasing the amount of formal schooling that he or she acquires or that try to improve child health by raising maternal schooling assume that the schooling effects reported in the literature are causal. A number of investigators have argued, however, that reverse causality from health to schooling or omitted “third variables” may cause schooling and health to vary in the same direction. Governments can employ a variety of policies to raise the educational levels of their citizens. These include compulsory schooling laws, new school construction, and targeted subsidies to parents and students. If proponents of the third-variable hypothesis are correct or if health causes schooling, evaluations of these policies should not be based on studies that relate adult health or child health to actual measures of schooling because these measures may be correlated with unmeasured determinants of the outcomes at issue.

In this paper we propose to use techniques that correct for biases due to the endogeneity of schooling to evaluate the effects of a policy initiative that radically altered the school system in Taiwan and led to an increase in the amount of formal schooling acquired by the citizens of that country during a period of very rapid economic growth. In 1968 Taiwan extended compulsory schooling from six years to nine years. In the period from that year through 1973, many new junior high schools were opened at a differential rate among regions of the country. We form treatment and control groups of women or men who were age 12 or under on the one hand and between the ages of 13 and 20 or 25 on the other hand in 1968. Within each region, we exploit variations across cohorts in new junior high school openings to construct an instrument for schooling. We employ this instrument to estimate the causal effects of mother’s or father’s schooling on the incidence of low birthweight and mortality of infants born to women in the treatment and control groups or the wives of men in these groups in the period from 1978 through 1999.

The paper proceeds as follows. Section I outlines a conceptual framework, followed by a review of the related literature. Section II provides some background on education reform in 1968 in Taiwan. Section III indicates how we exploit aspects of the reform to construct instruments for parents’ schooling, presents estimates of the effects of the instrument on schooling, and discusses the specification of infant health outcome equations. Section IV contains reduced form and structural estimates of these equations, and Section V concludes.

I. Analytical Framework and Review of Literature

Models that generate two-way causality between schooling and good health and that introduce third-variables that cause both outcomes to vary in the same direction are discussed in detail by Grossman (2006). Consequently, they will be outlined briefly here. Causality from own schooling to own health or from parents’ schooling to child health results when the more educated are more efficient producers of these outcomes or when education changes tastes in favor of health. The efficiency effect can take two forms. Productive efficiency pertains to a situation in which the more educated obtain a larger health output from given amounts of endogenous (choice) inputs. Allocative efficiency pertains to a situation in which schooling increases information about the true effects of the inputs on health. For example, the more educated may have more knowledge about the harmful effects of cigarette smoking or about what constitutes an appropriate diet.

Endogenous taste models also generate causality from schooling to health. For example, Gary S. Becker and Casey B. Mulligan (1997) show that the more educated have greater incentives to make investments that make them or their children more future oriented. The resulting reduction in the rate of time preference for the present raises optimal investment in health.

Now consider causality from health to schooling. In the case of these outcomes for the same person, healthier individuals have longer life expectancies and hence greater payoffs to schooling investments since the number of periods over which returns accrue is larger. Moreover, students in poor health are almost certain to miss more days of school due to illness than their healthy peers and may also learn less while in school. Both factors suggest negative effects of poor health in childhood on school achievement and ultimately on years of formal schooling completed. In the case of child health, parents who demand higher levels of this outcome may obtain more schooling because it is a mechanism to achieve this goal.

Since health and schooling are both endogenous, unobserved third variables may cause both of these outcomes to vary in the same direction. The third-variable hypothesis has received the most amount of attention in the literature because it is related to the hypothesis that the positive effect of schooling on earnings, explored in detail by Jacob Mincer (1974) and in hundreds of studies since his seminal work (see David Card 1999, 2001 for reviews of these studies), is biased upward by the omission of ability. For example, Victor R. Fuchs (1982) identifies time preference as the third variable. He argues that persons who are more future oriented (who have a high degree of time preference for the future or discount it at a modest rate) attend school for longer periods of time and make larger investments in their own health and in the health of their children. Thus, the effects of schooling on these outcomes are biased if one fails to control for time preference.

The forces just discussed can be summarized in the following two-equation structural model:

$$\mathrm{S}=\mathrm{S}({\mathrm{P}}_{\mathrm{S}},\mathrm{H},\mathrm{U})$$ (1)

$$\mathrm{H}=\mathrm{H}({\mathrm{P}}_{\mathrm{H}},\mathrm{S},\mathrm{U}).$$ (2)

Here S and H are positive correlates of completed schooling and health, P_S is the price of schooling (or the prices of a vector of schooling inputs), P_H is the price of health (or the prices of a vector of health inputs), and U is an unobserved third variable. The prices are uncorrelated with U. Solving equations (1) and (2) simultaneously, one obtains the reduced form schooling equation and health equations:

$$\mathrm{S}=\mathrm{S}({\mathrm{P}}_{\mathrm{S}},{\mathrm{P}}_{\mathrm{H}},\mathrm{U}).$$ (3)

$$\mathrm{H}=\mathrm{H}({\mathrm{P}}_{\mathrm{S}},{\mathrm{P}}_{\mathrm{H}},\mathrm{U}).$$ (4)

Our aim is to estimate equations (2), (3), and (4). We have no direct measures of the prices of health inputs and assume either that they are not correlated with P_S or that they are captured by county and year indicators (see Section III for more details). The application of ordinary least squares to equation (2) produces inconsistent coefficient estimates if S and U are correlated. Hence, we employ the program intensity variable described in Sections II and III (a measure of P_S) as an instrument for schooling in a two-stage least squares estimation of equation (2).¹

Our research strategy is related to that in a growing literature that employs instrumental variables techniques (IV) to estimate the causal impact of schooling on health. The earliest studies to employ these techniques are by Mark C. Berger and J. Paul Leigh (1989), William Sander (1995a, 1995b), and Leigh and Rachna Dhir (1997). All four studies employ U.S. data and pertain to adults. In almost all cases the IV coefficients are at least as large in absolute value as the ordinary least squares coefficients. These findings point to causal impacts of schooling on health. This conclusion should be interpreted with caution because some of the instruments employed (parents’ schooling, parents’ income, and cognitive test scores) may be correlated with omitted third variables.

Very recent work by Adriana Lleras-Muney (2005), Scott J. Adams (2002), Jacob N. Arendt (2005, 2008), Jasmina Spasojevic (2003), Philip Oreopoulos (2006), Damien de Walque (2007), Franque Grimard and Daniel Parent (2007), Piero Cipollone, Debora Radicchia, and Alfonso Rosolia (2007), Jeremy Arkes (2004), Donald Kenkel, Dean Lillard, and Alan Mathios (2006), Mary A. Silles (2009), Valerie Albouy and Laurent Lequien (2009), and Hans van Kippersluis, Owen O’Donnell, and Eddy van Doorslaer (2009) address the schooling-health relationship by using compulsory education laws, exemption from military service, unemployment rates during a person’s teenage years, and requirements for high school completion and for the receipt of a General Educational Development High School Equivalency Diploma (GED) to obtain consistent estimates of the effect of schooling on adult health or on cigarette smoking--a key determinant of many adverse health outcomes. These variables, some of which result from quasi-natural experiments, are assumed to be correlated with schooling but uncorrelated with time preference and other third variables. Hence, they serve as instruments for schooling in the estimation of health equations by two-stage least squares and its variants. These fourteen second-generation studies improve on the four first-generation ones by employing instruments that are more likely to be uncorrelated with omitted third variables. Like the earlier studies, however, they conclude that the IV effects of schooling on health are at least as large as the OLS effects.²

The IV studies just reviewed examine the effects of the amount of schooling an individual has completed on his or her health as an adult. There are only five corresponding IV studies that consider the effects of parents’ schooling on child health or on the complementary outcome of fertility. Janet Currie and Enrico Moretti (2003) examine the relationship between maternal education and birthweight among U.S. white women with data from individual birth certificates from the Vital Statistics Natality files for 1970 to 2000. They use information on college openings between 1940 and 1990 to construct an availability measure of college in a woman’s 17th year as an instrument for schooling. They find that the negative effect of maternal schooling on the incidence of low birthweight increases in absolute value when it is estimated by instrumental variables. They also find that the negative IV coefficient of maternal schooling in an equation for the probability of smoking during pregnancy exceeds the corresponding OLS coefficient in absolute value. Since it is well known that prenatal smoking is the most important modifiable risk factor for poor pregnancy outcomes in the United States, they identify a very plausible mechanism via which more schooling causes better birth outcomes. Their results suggest that the increase in maternal education between the 1950s and the 1980s accounts for 12 percent of the 6 percentage point decline in the incidence of low birthweight in that period.

Lucia Breierova and Esther Duflo (2004) capitalize on a primary school construction program in Indonesia between 1973–1974 and 1978–1979. In that period 61,000 primary schools were constructed. Program intensity, measured by the total number of new schools constructed as of 1978–1979 per primary-school age child in 1971, varied considerably across the country’s 281 districts. In a study of the effects of schooling on earnings, Duflo (2000, 2001) shows that average educational attainment rose more rapidly in districts where program intensity was greater. She also argues that the program had a bigger effect for children who entered school later in the 1970s and no effect for children who entered school before 1974. Therefore, she uses the interaction between year of birth and program intensity as an instrument for schooling in male wage functions in the 1995 intercensal survey of Indonesia. These functions are restricted to men who were between the ages of 2 and 24 in 1974. The instrument in question turns out to be an excellent predictor of schooling.

Breierova and Duflo (2004) use the instrument just described to estimate the effects of mother’s and father’s education on child mortality in the same survey employed by Duflo. They employ fertility and infant mortality histories of approximately 120,000 women between the ages of 23 and 50 in 1995. They find that mother’s and father’s schooling have about the same negative effects on infant mortality. Some, but not all, of the IV coefficients exceed the corresponding OLS coefficients. The authors treat their results as very preliminary.

Justin McCrary and Heather Royer (2006) use age-at-school entry policies to identify the effect of mother’s schooling on the probability of a low-birthweight birth and the probability of an infant death for all births in Texas in the years 1989–2001 and on the probability of a low-birthweight birth for all births in California in 1989–2002. When combined with the effects of compulsory schooling laws on education, school entry age laws suggest that some children born one day after the school entry cutoff will obtain less schooling than comparable children born one day earlier. McCrary and Royer observe this effect for maternal education. They find little evidence, however, that the laws affect infant health outcomes, either in the reduced form or in TSLS with the law combined with the mother’s exact date of birth used to form an instrument for schooling. They caution that their results may be heavily influenced by the experience of women from low socioeconomic backgrounds, since other researchers have shown that the parents of these women are more likely to comply with school entry policies.

Maarten Lindeboom, Ana Llena-Nozal, and Bas van der Klaauw (2009) use compulsory school reform in 1947 in the United Kingdom, which raised the minimum school leaving age from 14 to 15, to assess the causal impact of parents’ schooling on child health in the National Child Development Study. This is a panel of 17,000 babies born in Great Britain in the first week of March 1958. The authors consider a variety of health measures at birth and at ages 7, 11, and 16 and include both mother’s and father’s schooling in most models. Like McCrary and Royer, they find little evidence that schooling has beneficial effects on child health in the instrumental variable estimates, even when mother’s schooling or father’s schooling is omitted as a regressor.

Una O. Osili and Bridget T. Long (2008) examine the effects of female schooling on fertility in Nigeria. In 1976 that country introduced a nationwide program that provided tuition-free primary education and increased the number of primary school classrooms at a differential rate among the 19 states of Nigeria. Following Duflo (2001) and Breierova and Duflo (2004), Osili and Long employ the interaction between year of birth and program intensity, measured by the per capita amount of federal funds given to each state for classroom construction, as an instrument for mother’s schooling in an equation in which the number of births before age 25 in the 1999 Nigerian Demographic Health Survey is the dependent variable. Their TSLS estimate of the effect of mother’s schooling on this outcome is negative and four times larger in absolute value than the OLS estimate. This is relevant to child health because the quantity-quality substitution model developed by Becker and H. Gregg Lewis (1973) predicts that the reduction in family size should be accompanied by an increase in health.

In summary, the majority of the studies reviewed conclude that schooling causes health and that the IV effects are at least as large as the TSLS effects. Only five of these studies, however, deal with children’s health, and only the ones by Breierova and Duflo (2004) and Osili and Long (2008) deal with developing countries. Of course, there is a large literature summarized by John Strauss and Duncan Thomas (1995), Grossman and Kaestner (1997), and Grossman (2006) that reports positive relationships between parents’ schooling and child health in developing countries. The study by Yuyu Chen and Hongbin Li (2009), which considers the effect of mother’s schooling on the health of adopted children in China, is a very recent example of this literature. Using height-for-age as the measure of health, they find that the positive effect of mother’s schooling on this outcome in the adoptee sample is similar to that in the own birth sample, suggesting that it is not due to genetic factors. Like all previous studies in this literature with the exception of the two mentioned above, Chen and Li do not employ instrumental variable techniques. Hence, they are careful to conclude that the evidence that the schooling effect is causal is tentative, especially since the sample of adoptees is relatively small.

II. 1968 Education Reform in Taiwan

In 1968, the Taiwan government extended compulsory education from six to nine years, which required all school-age children (between 6 and 15) to attend elementary school for six years and junior high school for three years. To accommodate the expected increase in enrollment in junior high schools, the government opened 150 new junior high schools, an increase of almost 50 percent, at the beginning of the school year 1968–69 (September 1, 1968). This education reform created the largest expansion in junior high school construction and student enrollment in Taiwan’s history (Diana E. Clark and Chang-Tai Hsieh 2000; Chris A. Spohr 2000, 2003; When-Jyuan Tsai 2007a, 2007b; and the sources listed in Table 1).

Table 1.

Cumulative Number of New Junior High School Openings per Thousand Children Ages 12–14, by School Year and County, 1968–1973

County	1968	1969	1970	1971	1972	1973
Taipei City	0.188	0.222	0.223	0.217	0.211	0.214
Taichung City	0.124	0.150	0.234	0.227	0.218	0.210
Keelung City	0.162	0.156	0.153	0.152	0.150	0.150
Tainan City	0.086	0.111	0.136	0.134	0.133	0.132
Kaohsiung City	0.018	0.052	0.081	0.078	0.075	0.101
Taipei County	0.135	0.186	0.189	0.254	0.214	0.204
Ilan County	0.062	0.153	0.211	0.240	0.265	0.266
Taoyuan County	0.100	0.134	0.130	0.144	0.191	0.182
Chaiyi County	0.070	0.125	0.167	0.168	0.183	0.200
Hsinchu County	0.045	0.133	0.154	0.174	0.193	0.190
Miaoli County	0.119	0.164	0.185	0.184	0.182	0.181
Taichung County	0.220	0.219	0.234	0.251	0.249	0.245
Nantou County	0.166	0.164	0.258	0.330	0.401	0.402
Changhua County	0.024	0.035	0.047	0.059	0.071	0.071
Yunlin County	0.106	0.106	0.152	0.169	0.200	0.200
Tainan County	0.229	0.228	0.228	0.228	0.255	0.257
Kaohsiung County	0.016	0.046	0.061	0.075	0.133	0.130
Pingtung County	0.195	0.193	0.222	0.221	0.220	0.219
Hualien County	0.385	0.410	0.408	0.408	0.408	0.408
Taitung County	0.424	0.540	0.578	0.579	0.578	0.578
Penghu County	0.529	0.516	0.708	0.803	0.904	0.911
Country as a whole	0.136	0.164	0.188	0.201	0.212	0.212

Note: Denominator pertains to children ages 12–14 in a given year. The figure for the country as a whole is a weighted average of the figures for each county where the set of weights is the county-specific number of children 12–14. Sources: Ministry of Education, Fourth Education Yearbook of the Republic of China, 1974 and web sites of selected schools for the number of new junior high schools, 1968–1972; the web site of each individual school for 1973; and Directorate-General of Budgets, Accounts, and Statistics, Executive Yuan, Statistical Abstract of the Republic of China, 1983 for the population ages 12–14 in 1968–1973.

Primary school education in Taiwan was nearly universal by the mid-1960s, but approximately one-half of primary school graduates did not obtain additional education because enrollment in public junior high school was restricted by a competitive national examination and by the limited number of junior high schools, especially in rural areas. The national examination was so difficult that parents had to enroll their primary school children in costly after-school tutoring classes if they wanted their children to be admitted to a nominally free public junior high school (Spohr 2003). There were a very small number of private junior high schools, but their tuition amounted to approximately one percent of per capita gross national product (Spohr 2003). The 1968 reform abolished the junior high school entrance examination and made it possible for all primary school graduates to continue their education. Children who had previously ended their education after primary school also were allowed to continue their education as long as they were under the age of 15 in 1968 but were unlikely to do so as shown in the next section.

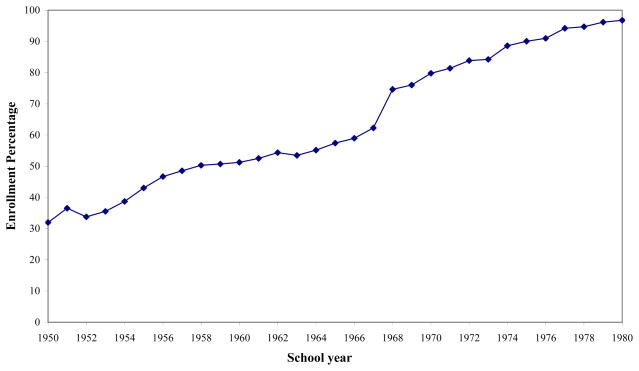
The sizable new junior high school openings in 1968 increased the number of these schools from 0.3 schools per thousand children ages 12 through 14 in the school year 1967–1968 to 0.4 schools per thousand children in that age range in the school year 1968–1969 (see Table 1 for sources).³ The immediate impact was to increase the percentage of primary school graduates who entered junior high school from 62 percent in 1967 to 75 percent in 1968 (see Figure 1). Spohr (2003) reports that there were no comparable jumps in enrollments for senior high school or senior vocational school relative to underlying trends. He concludes that the large increase in junior high school enrollment in 1968 was due to the legislation rather than to other factors.

Figure 1. Percentage of Primary School Graduates Entering Junior High School.

Note: Percentage of primary school graduates in June of school year t-1 who entered junior high school in September of school year t. Source: Directorate-General of Budgets, Accounts, and Statistics, Executive Yuan, Statistical Abstract of the Republic of China, 1983.

By 1973, an additional 104 public junior high schools had opened, increasing the total number of these schools from 311 in 1967 to 565 in 1973 (0.5 per thousand children ages 12–14). The junior high school entry percentage rose to 84 percent in the same year. Hence, the number of junior high schools almost doubled in a six-year period, the number per thousand children ages 12 through 14 rose by almost 70 percent, and the junior high school entry percentage grew by 35 percent. After 1973, the government’s six-year plan to implement the 1968 legislation ended. The growth in junior high schools slowed, with additional openings resulting mainly from population growth.

A notable aspect of the school construction program was that its intensity varied across regions of Taiwan. Table 1 contains the number of new junior high schools that opened in 1968 per thousand children between the ages of 12 and 14 in that year in each of the 21 cities or counties of Taiwan.⁴ The table also contains the cumulative number of new junior high schools in each of the years 1969 through 1973 per thousand children between the ages of 12 and 14 in that year. In 1968, program intensity varied from 0.02 in Kaohsiung City and Kaohsiung County to 0.53 in Penghu County. By 1973, intensity varied from 0.07 in Changhua County to 0.91 in Penghu County.

Hence, the nine-year compulsory schooling legislation provides a “natural experiment” to evaluate the impacts of parents’ schooling on the health of their children. In particular, those over the age of 12 on September 1, 1968 when the school year began were not affected by school reform and constitute a control group. On the other hand, those 12 years of age and under on September 1, 1968 were very likely to have been affected by school reform and constitute a treatment group.⁵ Moreover, the effects of school reform on the number of years of formal schooling completed in the treatment group should be larger the larger is the program intensity measure in city or county of birth. (Hereafter the term county refers to city or county of birth.) We employ the products of cohort indicators and the program intensity measure in Table 1 as instruments for schooling. Greater intensity among younger cohorts should lead to more schooling but should be uncorrelated with unmeasured determinants of the well-being of the offspring of these cohorts. We employ this instrument to estimate the causal effects of mother’s or father’s schooling on the incidence of low birthweight and mortality of infants born to women in the treatment and control groups or the wives of men in these groups in the period from 1978 through 1999.

We describe the instrument in more detail in the next section. Here we want to point out that our methodology follows the one developed by Duflo (2001) to obtain an instrument for schooling in male wage earnings functions in Indonesia. As noted in Section I, her instrument is the product of cohort indicators and the per capita number of new primary schools constructed in each county in Indonesia in the period from 1973–74 through 1978–79. Breierova and Duflo (2004) use the same instrument to estimate the effects of mother’s and father’s schooling on self-reported infant mortality. Osili and Long (2008) adopt this identification strategy to obtain an instrument for mother’s schooling in fertility equations in Nigeria. Clark and Hsieh (2000) apply Duflo’s methodology to the 1968 school reform in Taiwan. They obtain an instrument similar to ours in their study of the impacts of schooling on male earnings in that country. Spohr (2000, 2003) was the first economist to employ the 1968 school reform in Taiwan as an instrument for schooling in his study of the impacts of schooling on labor force participation and earnings of men and women.

Given the five studies just mentioned, our paper obviously is not the first to use school reform in Taiwan and an identification strategy based on cohort-program intensity interactions. Our study does, however, have unique aspects. Unlike Spohr (2003), we exploit both reform and program intensity. Clark and Hsieh (2000) are forced to predict schooling based on county of current residence of males between the ages of 30 and 50 in the years from 1990 through 1997, while we have information on county of birth. Based on our computations from the Taiwan Panel Survey of Family Dynamics, less than 10 percent of the population attended junior high school in a county that differed from their county of birth in the period after 1968. In contrast to Osili and Long (2008), we consider infant health rather than fertility. Unlike Breierova and Duflo (2004), we employ objective measures of infant health from birth certificates and from merging these certificates with infant death certificates. This is in contrast to Breierova and Duflo who rely on women’s reports of deaths of their infants. These reports are likely to contain errors.

III. Empirical Implementation

A. Data

Our data collection consists of all birth certificates and infant death certificates for the years 1978 through 1999. There were more than 300,000 births a year in Taiwan during this period. Birth and death certificates are linked through national identification numbers received by each person born in Taiwan. We consider the following outcomes from these data: the probability of a low-weight (less than 2,500 grams) birth; the probability of a neonatal death, the probability of a postneonatal death, and the probability of an infant death.

Low birthweight has extremely strong positive associations with infant morbidity and mortality. Neonatal deaths pertain to deaths within the 27 days of life, while postneonatal deaths pertain to deaths between the ages of 28 and 364 days. Infant deaths are the sum of those occurring in the neonatal and postneonatal periods. We distinguish between neonatal and postneonatal mortality because their causes are very different. Most neonatal deaths are caused by congenital anomalies, prematurity, and complications of delivery, while most postneonatal deaths are caused by infectious diseases and accidents. Infants who die within the first 27 days of life are excluded when the probability of postneonatal death is the outcome.

In addition to birthweight, birth certificates contain the following information that is relevant for our research: infant’s date of birth, mother’s date of birth, mother’s city or county of birth, father’s date of birth, father’s city or county of birth, mother’s schooling, and father’s schooling. Observations with missing values are deleted. Birthweights under 400 grams or over 6,500 grams are treated as missing. These cases are excluded when the probability of low birthweight is the outcome but are included with the three other outcomes.⁶

When we estimate the effects of mother’s schooling on infant health, we consider births to women who were between the ages of less than 1 and 20 in 1968 and between the ages of 22 and 45 when they gave birth in the period from 1978 through 1999. We do not include births to women under the age of 22 because we do not have birth certificates prior to 1978. The youngest women in the control group were 13 in 1968 and 23 in 1978. When we estimate the effects of father’s schooling on infant health, we consider births to the wives of husbands who were between the ages of less than 1 and 25 in 1968 and between the ages of 22 and 50 when their wives gave birth in the years 1978–1999.⁷ Recall that age in 1968 pertains to age as of September 1. We select a wider age range for fathers than for mothers because husbands typically are older than their wives. Father’s schooling and mother’s schooling are too highly correlated to include both variables in the same regression, especially since the data are aggregated for reasons explained below.

We aggregate the data into mother’s or father’s county of birth, mother’s or father’s cohort in 1968, and child’s year of birth cells. For mothers, there are 21 counties of birth, 21 cohorts (ages less than 1 through 20 in 1968), and 22 child’s years of birth (1978–1999). This gives 9,702 potential cells, but 1,849 have no births. Hence, there are 7,853 observations in the regressions with mother’s schooling. For fathers, there are 26 cohorts (ages less than 1 through 25 in 1968), resulting in 12,012 potential cells. Of these, 1,770 have no births, and there are 10,242 observations in the regressions with father’s schooling.

We aggregate the data for several reasons. First, aside from parents’ schooling, no individual-level variables are employed as regressors. Second and more importantly, ordinary least squares estimates of the effects of schooling on the infant health outcomes that we consider are much bigger in absolute value in the aggregate data than they are in the individual data. In our view the most compelling explanation of this result is that there is random measurement error in the schooling variables, which are obtained from parents. These errors are greatly reduced or eliminated in the aggregate data.

In the infant health outcome equations, variations in predicted schooling are based on an instrument that varies only at the county and cohort levels. Hence, a comparison of the IV estimate of the effect of mother’s or father’s schooling on infant health to the corresponding OLS estimate obtained from the aggregate data reflects inconsistencies due to omitted third variable or reverse causality. On the other hand, the corresponding comparison of the IV estimate to the OLS estimate obtained from individual data reflects inconsistencies due to measurement error in addition to those associated with the two factors just mentioned.⁸ Since our focus is on inconsistencies due to these two factors, we focus on the aggregate data. We want to emphasize that this point pertains to a comparison of individual and aggregate coefficients and not to a comparison of individual and aggregate standard errors of regression coefficients. The two types of standard errors can be made comparable by correcting both types for clustering by county. That is exactly what we did.

To be sure, the finding just described (larger OLS schooling effects in the grouped data than in the individual data) may be due to omitted variables that are reflected by county-cohort interactions. If that were the case, our identification strategy would be compromised since the instrument for schooling varies only by county and cohort. To examine, this issue, we included a full set of county-cohort interactions in the individual and aggregate regression. The inclusion of these variables could not account for the discrepancy between the individual-level and the aggregate-level schooling coefficients. These results are available on request.

B. Construction of Instrument and Its Impacts on Schooling

We begin by defining the program intensity measure in a manner that is analogous to Duflo’s (2001) measure. Consider the model for female schooling. We have 21 female cohorts who were between the ages of less than 1 and 20 in 1968. Those between the ages of less than 1 and 12 were subject to the 1968 school reform and comprise the treatment group. Those between the ages of 13 and 20 were not subject to the increase in compulsory schooling mandated by the law and form the control group. The idea is to interact a program intensity measure that has the same value for each cohort in a given county with a dichotomous indicator for each cohort except 20 year olds. These 20 cohort-intensity variables serve as instruments for years of formal schooling completed in a model that includes dichotomous indicators for each cohort except one and for each county except one. Program intensity is given by the cumulative number of new junior high schools that opened as of 1973 (the total number that opened between 1968 and 1973) per thousand children ages 12–14 in 1968. We interpret this measure as the intended number of new junior high school openings. Following Duflo, we assume that the coefficients of the interaction terms should be negatively correlated with age (should be largest for the youngest cohorts) and should fall to zero for the control cohorts. The cohort dummies capture trends in schooling not associated with reform or program intensity. The county dummies control for cohort-invariant unmeasured factors that vary among counties and may be correlated with schooling and program intensity.

The dependent variable in the regression model is years of formal schooling completed because Shin-Yi Chou et al. (2007) present evidence that the reform had effects on the probabilities of completing schooling levels beyond junior high school. With the intercept and the disturbance term suppressed, the full model that we estimate for mean years of formal schooling completed by women in cohort a (a = 0, 1…, 19, with 20 year olds in 1968 the omitted cohort), born in county j (j = 1, 2,…, 20) and giving birth to a child in a year (t) from 1978 through 1999 (t = 1, 2,…21, with 1999 the omitted year) is

$${\mathrm{S}}_{\text{ajt}}=\sum _{\mathrm{a}=\mathit{0}}^{\mathit{19}}{\alpha }_{\mathrm{a}}{\mathrm{C}}_{\mathrm{a}}+\sum _{\mathrm{j}=\mathit{1}}^{\mathit{20}}{\varphi }_{\mathrm{j}}{\mathrm{X}}_{\mathrm{j}}+\sum _{\mathrm{a}=\mathit{0}}^{\mathit{19}}{\beta }_{\mathrm{a}}{\mathrm{C}}_{\mathrm{a}}{\mathrm{P}}_{\mathrm{j}}+\sum _{\mathrm{t}=\mathit{1}}^{\mathit{21}}{\theta }_{\mathrm{t}}{\mathrm{Z}}_{\mathrm{t}}+\sum _{\mathrm{j}=\mathit{1}}^{\mathit{20}}\sum _{\mathrm{t}=\mathit{1}}^{\mathit{21}}{\lambda }_{\text{jt}}{\mathrm{X}}_{\mathrm{j}}{\mathrm{Z}}_{\mathrm{t}}+\sum _{\mathrm{a}=\mathit{0}}^{\mathit{19}}{\delta }_{\mathrm{a}}{\mathrm{C}}_{\mathrm{a}}{\mathrm{J}}_{\mathrm{j}}+\sum _{\mathrm{a}=\mathit{0}}^{\mathit{19}}{\eta }_{\mathrm{a}}{\mathrm{C}}_{\mathrm{a}}{\mathrm{A}}_{\mathrm{j}}.$$ (5)

Here C_a is a dummy variable for cohort a, X_j is a dummy variable for county j, P_j is program intensity in county j, Z_t is a dummy variable for year of birth of child t, J_j is the fraction of 12–14 year olds enrolled in junior high school in 1966 in county j (hereafter termed the junior high school enrollment rate), and A_j is the fraction of workers in agriculture in 1966 in county j. Clearly, we want to take account of year of birth effects when one of the four infant health measures is the outcome. In part, these effects reflect advances in medical technology, changes in the nature of health insurance coverage for prenatal and neonatal care due to the introduction of National Health Insurance in 1995, the legalization of abortion in 1985, and increases in its availability. The interactions allow these developments to have differential impacts over time in different counties.⁹ Given the two-stage least squares methodology, year and county-year interactions must be included in the first stage equation that predicts schooling if they appear in the second stage. In addition, they control for changes in the composition of births over time.

Taiwanese authorities planned to allocate more new junior high schools to counties where initial enrollment in junior high schools was low. There is some evidence that this allocation was achieved. The simple correlation coefficient between the cumulative per capita number of new junior high schools in 1973 and the junior high school enrollment rate in 1966 across the 21 counties in Table 1 is −0.27, and the corresponding correlation coefficient between the program intensity variable and the fraction of workers in agriculture (an alternative measure of education needs) in 1967 is 0.37.¹⁰ While these correlation coefficients are not significant at conventional levels, they are based on a small number of observations. Moreover, different magnitudes might emerge in the birth certificate data that we utilize and in the specifications that we employ. For these reasons, we include interactions between the cohort indicators and the fraction of workers in agriculture in 1967 and between the cohort indicators and the junior high school enrollment rate in 1966 in equation (5).¹¹

The 1968 legislation was preceded by the introduction of a nationwide family planning program beginning in 1964. The main aspect of the program consisted of the employment of two types of fieldworkers (village health education nurses and pre-pregnancy health workers) to disseminate information concerning family planning (Ronald Freedman and John Y. Takeshita 1969; T. Paul Schultz 1973). The number of person-months of these personnel per thousand women ages 15–49 varied among counties and was higher in rural agricultural areas than in urban areas. Schultz (1973) reports that increases in the measure just described had negative effects on total fertility rates and age-specific birth rates. It is possible that this family planning variable is positively correlated with junior high school program intensity. To examine this possibility, we included interactions between the cohort indicators and the county-specific number of person-months of each type of family planning worker per thousand women ages 15–49 in 1968 in preliminary regressions. These variables had small and statistically insignificant effects in the regressions and almost no impacts on the coefficients of interest. Therefore, they were excluded from our final specifications.¹²

Panel A of Figure 2 plots the coefficients of the interactions between age in 1968 and program intensity in county of birth in the mother’s schooling equation, and panel B plots the corresponding coefficients in the father’s schooling equation. The 95th percent confidence interval also is shown. For each gender, the coefficients are largest for the youngest cohorts and decline with age in 1968. For females, the coefficients fall from 1.30 at age less than 1 to 0.58 at age 19. The mean coefficient in the treatment group is 1.17, while the mean coefficient in the control group is 0.54. There is a sharp break from a coefficient of 1.05 at age 12 to a coefficient of 0.70 at age 13. The 95th percent confidence interval contains a coefficient of zero for each cohort in the control group.

Figure 2.

Coefficients of the Interactions between Age in 1968 and Program Intensity in County of Birth in Schooling Equation with 95th Percent Confidence Interval Bands

For males the oldest members of the control cohort are 25 (the omitted category in the regression), as indicated in Section III.A. Hence, 25 coefficients are plotted in panel A compared to 20 in panel B. Nevertheless, the patterns in panel B mirror those in panel A. The coefficients decline from 1.50 at age less than 1 to 0.11 at age 20 and to 0.02 at age 24. The mean coefficient in the treatment group is 1.17, and the corresponding mean in the control group is 0.32 (0.41 if the control group is limited to 13–20 year olds). The coefficient at age 12 is 1.16, while that at age 13 is 0.79. The 95th percent confidence interval contains a coefficient of 0.11 at age 13 and a coefficient of zero at all older ages.

The results just discussed suggest gains to a specification in which program intensity effects are restricted to the treatment group. In theory the cohorts in the control group should not have been affected by the 1968 legislation, and the findings in Figure 2 justify this proposition. By assuming that the coefficients of the interactions between control group cohort dummies and program intensity are zero (which is equivalent to setting program intensity equal to zero for each cohort in the control group), we reduce the large number of program intensity coefficients that must be estimated. This has the advantage of reducing the degree of multicollinearity among the regressors and improving the efficiency of the estimates.

The precision of the program intensity effects also can be improved by accounting for within county variation in the intensity variable among treatment cohorts (see Table 1). For cohorts ages 12 and under in 1968, our specific procedure is to interact a dichotomous indicator for each of these 13 cohorts with the county-specific cumulative number of new junior high schools per thousand children ages 12–14 in the year in which the cohort entered junior high school (hereafter termed program intensity, P_aj). To be specific, 12 year olds are assigned the program intensity measure in 1968, 11 year olds are assigned the intensity measure in 1969, 10 year olds are assigned the measure in 1970, 9 year olds are assigned the measure in 1971, 8 year olds are assigned the measure in 1972, and those 7 years old and younger are assigned the measure in 1973.

The intensity variable employed to obtain the coefficients in Figure 2 has 22 unique values: one for each of the 21 counties and a value of zero for the oldest cohort regardless of county. On the other hand, the variable just defined has 127 unique values: 126 defined by the product of 21 counties and 6 years from 1968 through 1973 and a value of 0 for each cohort in the control group regardless of county and year. Obviously, there is more variation in the latter measure than in the former.

While the 1968 legislation called for compulsory education through the ninth grade, the percentage of primary school graduates who entered junior high school was only 84 percent in 1973 and did not reach 95 percent until 1978 (see Figure 1). The factors responsible for this lagged response to the legislation are unclear, but candidates include lack of enforcement and capacity constraints. Moreover, while enrollment in junior high school was mandatory as of September 1, 1968, attendance was not compulsory until May 12, 1982 (Tsai 2007a). These factors highlight an identification strategy that takes account of program intensity in the year in which each treatment cohort enters junior high school as well as treatment status. By including the junior high school enrollment rate in 1966 and the percentage of workers in agriculture in 1967, each interacted with the 13 treatment cohort dummies, we control for obvious factors that may be correlated with intensity and schooling.

Table 2 contains coefficients of the interactions between cohort dummies in the treatment group and program intensity from estimates of regressions just specified for mother’s schooling and father’s schooling. The regressions are estimated across 7,853 county-cohort-year of birth cells for mother’s schooling and across 10,242 cells for father’s schooling and are weighted by the square root of the number of births in each cells. The standard errors of regression coefficients are clustered at the county level.¹³

Table 2.

Effects of Educational Reform on Parents’ Years of Formal Schooling Completed ^a

Program intensity* cohort	Mother’s schooling (mean=9.53)	Father’s schooling (mean=10.12)
Age < 1 in 1968	0.707 (0.608)	1.013 (0.481)**
Age = 1 in 1968	0.789 (0.551)	0.731 (0.413)*
Age = 2 in 1968	0.685 (0.505)	0.696 (0.458)
Age = 3 in 1968	0.703 (0.464)	0.606 (0.397)
Age = 4 in 1968	0.557 (0.361)	0.666 (0.393)
Age = 5 in 1968	0.636 (0.386)	0.597 (0.421)
Age = 6 in 1968	0.526 (0.311)	0.682 (0.394)*
Age = 7 in 1968	0.615 (0.282)*	0.699 (0.401)*
Age = 8 in 1968	0.478 (0.309)	0.871 (0.403)**
Age = 9 in 1968	0.489 (0.254)*	0.572 (0.381)
Age =10 in 1968	0.611 (0.240)**	0.726 (0.301)**
Age =11 in 1968	0.486 (0.222)**	0.710 (0.281)**
Age =12 in 1968	0.511 (0.259)*	0.825 (0.331)**
F-test 0,…,12=0	28.58	16.62
Observations	7853	10242
R-squared	0.96	0.92

^aStandard errors, reported in parentheses, are adjusted for clustering at the county level. All regressions include 20 cohort dummies, 20 county dummies, 21 year of birth of child dummies, interactions between each of the treatment cohort dummies and the county-specific junior high school enrollment rate in 1966 and between each of the treatment cohort dummies and the fraction of workers in agriculture in 1967, and interactions between the county and year of birth of child dummies.

^***Significant at the 1 percent level (two-tailed test).

^**Significant at the 5 percent level (two-tailed test).

^*Significant at the 10 percent level (two-tailed test).

Recall that 13 and 14 year olds who had previously ended their education after primary school were allowed to return to school as part of the 1968 reform. To examine whether it is appropriate to include them in the control or treatment groups, we estimated a regression (not shown) for each gender in which program intensity as of 1968 was interacted with indicators for each of these two cohorts, and an F-test was performed of the significance of these two coefficients as a set.¹⁴ The F values were 0.14 for females and 1.14 for male. Hence, we accept the hypothesis that 13 and 14 year olds should be included in the control group.

The results in Table 2 indicate that for females, 5 of the 13 program intensity coefficients are significant at the 10 percent level on a two-tailed test, and 2 are significant at the 5 percent level.¹⁵ More importantly, the F-ratio associated with the test that the 13 coefficients are significant as a set equals 28.58. This is much larger than the critical F-ratio of 10 used to assess whether instruments are weak (for example, Douglas Staiger and James A. Stock 1997; A. Colin Cameron and Pravin K. Trivedi 2005). The Stata Corporation (2005) and William Scribney (1997) recommend an adjustment to the F-ratio when the number of clusters is less than 100.¹⁶ Their adjustment results in an F of 11.43, which still exceeds 10. For males, 8 of the 13 program coefficients are significant at the 10 percent level, and 5 at the 5 percent level. Unadjusted and adjusted F-ratios associated with the test that the 13 coefficients are significant as a set are 16.62 and 6.65, respectively. Both reject the hypothesis that intensity coefficients are not significant as a set. The latter is somewhat smaller than 10 but does exceed the value of 5, which Cameron and Trivedi (2005) propose as a less strict rule of thumb.

For each gender, there is not much variation in the program intensity coefficients. For females, they range from 0.48 to 0.79 with a mean of 0.61. For males, the corresponding range is from 0.57 to 1.01 with a mean of 0.92. Multiplication of the program intensity coefficient for a given cohort by the mean value of program intensity for that cohort yields an estimate of the increase in schooling due to the 1968 compulsory school reform and its aftermath. For females these increases range from 0.17 years for those 1 year old in 1968 to 0.07 years for those 12 years old in 1968. The mean gain is 0.11 years. For males, the increases range from 0.22 for those less than 1 year old in 1968 to 0.11 for those 12 years old in that year. The mean gain is 0.16 years. Given mean levels of female and male schooling of 9.53 years and 10.12 years, respectively, these estimates imply that the program raised female schooling by approximately 1.2 percent and raised male schooling by approximately 1.6 percent.

Since the 13 program coefficients are very similar for each gender, additional gains in precision and efficiency can be obtained by restricting these coefficients to be the same. This can be accomplished by fitting a regression of the form

$${\mathrm{S}}_{\text{ajt}}=\sum _{\mathrm{a}=0}^{19}{\mathrm{\alpha }}_{\mathrm{a}}{\mathrm{C}}_{\mathrm{a}}+\sum _{\mathrm{j}=1}^{20}{\mathrm{\phi }}_{\mathrm{j}}{\mathrm{X}}_{\mathrm{j}}+\mathrm{\beta }{\mathrm{T}}_{\mathrm{a}}{\mathrm{P}}_{\text{aj}}+\sum _{\mathrm{t}=1}^{21}{\mathrm{\theta }}_{\mathrm{t}}{\mathrm{Z}}_{\mathrm{t}}+\sum _{\mathrm{j}=1}^{20}\sum _{\mathrm{t}=1}^{21}{\mathrm{\lambda }}_{\text{jt}}{\mathrm{X}}_{\mathrm{j}}{\mathrm{Z}}_{\mathrm{t}}+\mathrm{\delta }{\mathrm{T}}_{\mathrm{a}}{\mathrm{J}}_{\mathrm{j}}+\mathrm{\eta }{\mathrm{T}}_{\mathrm{a}}{\mathrm{A}}_{\mathrm{j}}.$$ (6)

Here T_a is a dummy variable that equals one for those between the ages of less than 1 and 12 in 1968 and equals zero otherwise. In addition to precision and efficiency criteria, equation (6) is appealing because it recognizes that in a fundamental sense there is one instrument for schooling rather than 13. At the same time, it allows for variations in the effect of the program (βP_aj) on different treatment cohorts. A final advantage of equation (6) is that it avoids discrepancies between t-tests of single coefficients and F-tests of sets of related coefficients that can arise when the number of variables in the set and the number of clusters are similar. We adopt this specification in obtaining estimates of the reduced form schooling and health equations and the structural health equation in the next section.¹⁷ One of the four health outcomes replaces schooling as the dependent variable in the health reduced form equation, and the actual or predicted value of schooling replaces program intensity in the structural health structural equation.

C. Cox’s Modified Logistic Specification

The last issue we address before presenting the full set of results is that of functional form. The infant health outcomes that we investigate are rare events. For example, in the data set for mothers, the percentage of light births is 4.30 percent. The neonatal and infant mortality rates expressed as deaths per thousand live births are 2.32 and 5.89, respectively. The postneonatal mortality rate expressed as deaths per thousand infants who survive the neonatal period is 3.57.¹⁸ These figures, which are very similar in the data set for fathers, translate into probabilities of a light birth, a neonatal death, a postneonatal death, and an infant death of 0.04303, 0.00232, 0.00357, and 0.00589, respectively. Since the outcomes range between 0 and 1 and are uncommon, we apply a logistic transformation to our grouped data. One problem is that a number of cells have no low-weight births or no deaths. Again with reference to the data set for mothers, 8 percent of the 7,853 cells have no low-weight births, 44 percent have no neonatal deaths, 38 percent have no postneonatal deaths, and 28 percent have no infant deaths.¹⁹

Given the nature of the data, we employ David R. Cox’s (1970) modified logistic transformation to the dependent variables in the health outcome equations. Let Y_i ≡ N_i/D_i be one of the four health outcomes in the ith cell. For example, in the case of low birthweight, N_i is the number of light births and D_i is the total number of births. Then the dependent variable is

$$ln{\mathrm{Z}}_{\mathrm{i}}=ln\frac{{\mathrm{Y}}_{\mathrm{i}}+\frac{1}{2{\mathrm{D}}_{\mathrm{i}}}}{1-{\mathrm{Y}}_{\mathrm{i}}+\frac{1}{2{\mathrm{D}}_{\mathrm{i}}}}=ln\frac{{\mathrm{N}}_{\mathrm{i}}+0.5}{{\mathrm{D}}_{\mathrm{i}}-{\mathrm{N}}_{\mathrm{i}}+0.5}.$$ (7)

The regression employs a set of weights given by

$${\mathrm{W}}_{\mathrm{i}}={\left[\frac{{\mathrm{D}}_{\mathrm{i}}({\mathrm{N}}_{\mathrm{i}}+1)({\mathrm{D}}_{\mathrm{i}}-{\mathrm{N}}_{\mathrm{i}}+1)}{({\mathrm{D}}_{\mathrm{i}}+1)({\mathrm{D}}_{\mathrm{i}}+2)}\right]}^{1/2}.$$ (8)

We want to make several comments on the procedure just described. First, we have compared the results to those obtained when the cells with the zeros are deleted and a grouped logit with weights given by [D_iY_i(1 − Y_i)]^1/2 is fit. These results, which are available on request, are very similar. Second, the latter estimates are not sensitive to weighting by predicted as opposed to actual values of Y_i. In the Cox procedure weights must be based on actual values. Third, our procedure is not subject to Cameron and Trivedi’s (2005) criticism that grouped logits should not be obtained when variation in some of the regressors is eliminated by aggregation into cells. In our case schooling is the only right-hand side variable whose variation is reduced by grouping. As we have previously indicated, this is desirable because it reduces measurement error. Finally, there are four sets of weights, one each for low birthweight, neonatal mortality, postneonatal mortality, and infant mortality. Therefore, four reduced form equations for schooling are obtained since the same set of weights is employed in the first and second stages of two-stage least squares estimation.

IV. Results

Table 3 contains means and standard deviations of key variables in the mother’s sample and in the father’s sample. Table 4 contains estimates of the effects of educational reform on mother’s and father’s years of formal schooling completed from the specification given by equation (6). This specification obtains a single program coefficient from the interaction between program intensity and the dichotomous indicator for treatment status. As explained in the previous section, four regressions are estimated for each gender because the weights employed in each of the four health outcome equations differ. Standard errors of regression coefficients are clustered at the county level.

Table 3.

Means and Standard Deviations of Variables ^a

	Mothers	Fathers
Years of formal schooling completed by mother or father	9.53 (1.46)	10.18 (1.15)
Fraction of births in treatment group	0.75 (0.43)	0.62 (0.48)
Program intensityb,c	0.20 (0.11)	0.20 (0.11)
Percentage of low-birthweight births	4.30 (1.24)	4.45 (1.25)
Neonatal mortality (deaths per thousand births)	2.32 (2.38)	2.34 (2.38)
Postneonatal mortality (deaths per thousand neonatal survivors)	3.57 (2.56)	3.63 (2.71)
Infant mortality (deaths per thousand births)	5.89 (3.58)	5.97 (3.67)
Junior high school enrollment rate, 1966b	0.31 (0.13)	0.31 (0.13)
Fraction of workers in agriculture, 1967b	0.47 (0.23)	0.47 (0.23)

^aStandard deviations in parentheses. All means and standard deviations except for the postneonatal mortality rate are weighted by the cell-specific number of births. The mean and standard deviation of the postneonatal mortality rate are weighted by the cell-specific number of infants who survive the neonatal period. The mean and standard deviation of the fraction of births in the treatment group are not weighted.

^bMean and standard deviation pertain to the treatment group.

^cCounty-specific cumulative number of new junior high schools per thousand children ages 12–14 in the year in which each cohort in the treatment group entered junior high school. See text for more details.

Table 4.

Effects of Educational Reform on Parents’ Years of Formal Schooling Completed, Single Program Intensity Measure^a

	Mother’s schooling				Father’s schooling
	Model 1	Model 2	Model 3	Model 4	Model 1	Model 2	Model 3	Model 4
Treatment* program intensity	1.288*** (0.361)	1.045*** (0.328)	1.302*** (0.351)	1.240*** (0.334)	1.143*** (0.390)	0.805* (0.485)	1.087** (0.478)	1.094** (0.462)
R-squared	0.926	0.844	0.856	0.882	0.889	0.800	0.812	0.838
Observations	7853	7853	7853	7853	10242	10242	10242	10242

^aEach of the four models employs a different set of weights. Model 1 uses the weights in the Cox modified logistic equation for low birth weight. Model 2 uses the weights in the equation for neonatal mortality, model 3 uses the weights in the equation for post-neonatal mortality, and model 4 uses the weights in the equation for infant mortality. See equation (8) for more details. Standard errors, reported in parentheses, adjust for clustering at the county level. All regressions include 20 cohort dummies, 20 county dummies, 21 year of birth of child dummies, interactions between the treatment dummy and the county-specific junior high school enrollment rate in 1966 and between the treatment dummy and the fraction of workers in agriculture in 1967, and interactions between the county and year of birth of child dummies.

^***Significant at the 1 percent level (two-tailed test).

^**Significant at the 5 percent level (two-tailed test).

^*Significant at the 10 percent level (two-tailed test).

For females, all four program coefficients are positive and significant at the 1 percent level. More importantly, the F-ratios associated with the test for weak instruments all exceed the critical value of 10 used to assess whether instruments are weak (for example, Staiger and Stock 1997; Cameron and Trivedi 2005). Since the structural health equation is exactly identified, these F-ratios simply are given by the square of the corresponding t-ratios. They are 12.74 with the weights for low birthweight, 10.18 with the weights for neonatal mortality, and 13.76 with the weights for postneonatal or infant mortality.

For males, the program coefficients are somewhat smaller than for females. Three of the four coefficients are significant at the 5 percent level, but only one is significant at the 1 percent level. Moreover, the coefficient with the weights for neonatal mortality is not significant at the 10 percent level. The F-ratios associated with the test for weak instruments are 8.58 with the weights for low birthweight, 2.76 with the weights for neonatal mortality, 5.15 with the weights for postneonatal mortality, and 5.62 with the weights for infant mortality. All of these fall short of the critical value of 10, but three of them exceed the value of 5, which Cameron and Trivedi (2005) propose as a less strict rule of thumb.

For both females and males in the treatment group, the cumulative number of new junior high school openings per thousand children ages 12–14 has a mean of 0.20 (see Table 3). Hence for females, the effect of the 1968 school reform legislation on years of completed schooling is 0.26 years in models 1 and 3, 0.21 years in model 2, and 0.25 years in model 4. For males, the increases are 0.23 years in model 1, 0.16 years in model 2, and 0.22 years in models 3 and 4. An average of these effects gives an increase of approximately one-fourth of a year for females and approximately one-fifth of a year for males. Put differently, the legislation induced 25 percent of women in the treatment group to attend school for an additional year, while it induced 20 percent of men in the treatment group to gain an additional year of schooling.

The smaller F-ratios for males than for females in the weak instruments test suggest that program intensity is a better instrument for mother’s schooling than for father’s schooling. Given these results and the somewhat larger impacts on completed schooling for females, we put more weight on the reduced form and structural infant health equations that contain either mother’s program intensity or mother’s schooling and discuss them first. These estimates are presented in Table 5.

Table 5.

Effects of Program Intensity and Mother’s Schooling on Infant Health^a

	Low birthweight	Neonatal mortality	Postneonatal mortality	Infant mortality
Panel A - Reduced Form Infant Health Cox Modified Logit Regressions, Weighted Least Squares
Treatment* program intensity	−0.249** (0.089)	−0.333*** (0.099)	−0.835*** (0.152)	−0.626*** (0.111)
R-squared	0.445	0.499	0.333	0.365
Mean*100 (or 1000)	4.30	2.32	3.57	5.89
Panel B - Structural Infant Health Cox Modified Logit Regressions, Weighted Least Squares
Mother’s schooling	−0.226*** (0.030)	−0.426*** (0.019)	−0.463*** (0.017)	−0.386*** (0.034)
R-squared	0.534	0.571	0.453	0.463
Panel C - Structural Infant Health Cox Modified Logit Regressions, Weighted Two-Stage Least Squares
Mother’s schooling	−0.194** (0.082)	−0.318* (0.158)	−0.641** (0.258)	−0.505** (0.206)
R-squared	0.532	0.566	0.435	0.454
Wu-Hausman F-ratio	0.23	0.32	0.69	0.46

^aSample size is 7,853 in all regressions. Weights are given by equation (8). Standard errors, reported in parentheses errors adjust for clustering at the county level. All regressions include 20 cohort dummies, 20 county dummies, 21 year of birth of child dummies, interactions between the treatment dummy and the county-specific junior high school enrollment rate in 1966 and between the treatment dummy and the fraction of workers in agriculture in 1967, and interactions between the county and year of birth of child dummies. All means except for the postneonatal mortality rate are weighted by the cell-specific number of births. The mean of the latter variable is weighted by the cell-specific number of infants who survive the neonatal period. For low birthweight, the mean is the percentage of light births. For neonatal and infant mortality, the means are deaths per thousand live births. For postneonatal mortality, the mean is deaths per thousand survivors of the neonatal period.

^***Significant at the 1 percent level (two-tailed test).

^**Significant at the 5 percent level (two-tailed test).

^*Significant at the 10 percent level (two-tailed test).

In each of the four infant health outcome equations, the logit coefficient of mother’s program intensity is negative and significant at the 5 percent level (see panel A). All three mortality coefficients are significant at the 1 percent level. All four mother’s schooling coefficients are significant at the 1 percent level in the structural infant health equations estimated by weighted least squares (WLS, see panel B). These estimates treat mother’s schooling as exogenous and thus ignore the possibility that it is correlated with the disturbance term in the equation.

Perhaps the most interesting set of results in the table pertains to the structural infant health equations estimated by weighted two-stage least squares (WTSLS, see panel C). These estimates treat schooling as endogenous and employ the interaction between treatment status and program intensity as an instrument. Although the schooling coefficients have much larger standard errors in the WTSLS regressions, all are negative and all are significant at the 10 percent level. Only the neonatal mortality coefficient loses its significance at the 5 percent level. Moreover, the WTSLS and WLS coefficients are similar in magnitude. The ratio of the former coefficient to the latter is 0.86 for low birthweight, 0.75 for neonatal mortality, 1.38 for postneonatal mortality, and 1.31 for infant mortality. Finally, the F-ratio resulting from the De-Min Wu (1973)-Jerry A. Hausman (1978) test suggests the estimates that treat schooling as exogenous are consistent. We want to emphasize that this finding cannot be traced to the use of a weak instrument for schooling.

The corresponding estimates of infant health equations that contain either father’s program intensity or father’s schooling are given in Table 6. All four logit coefficients of father’s program intensity are negative, but the neonatal mortality coefficient is not significant at the 10 percent level. The three other coefficients are significant at the 1 percent level (see panel A). This differs from the results for mother’s program intensity in which all four coefficients are significant at 5 percent. Moreover, the father’s coefficients are smaller in absolute value than the corresponding mother’s coefficients. The ratio of the former to the latter ranges from 0.59 in the case of neonatal mortality to 0.87 in the case of low birthweight.

Table 6.

Effects of Program Intensity and Father’s Schooling on Infant Health^a

	Low birthweight	Neonatal mortality	Postneonatal mortality	Infant mortality
Panel A - Reduced Form Infant Health Cox Modified Logit Regressions, Weighted Least Squares
Treatment* program intensity	−0.216*** (0.060)	−0.196 (0.137)	−0.634*** (0.117)	−0.469*** (0.095)
R-squared	0.374	0.461	0.353	0.371
Mean*100 (or 1000)	4.45	2.34	3.63	5.97
Panel B - Structural Infant Health Cox Modified Logit Regressions, Weighted Least Squares
Father’s schooling	−0.253*** (0.027)	−0.434*** (0.020)	−0.442*** (0.019)	−0.369*** (0.018)
R-squared	0.483	0.526	0.443	0.450
Panel C - Structural Infant Health Cox Modified Logit Regressions, Weighted Two-Stage Least Squares
Father’s schooling	−0.189** (0.077)	−0.243 (0.025)	−0.584* (0.357)	−0.429* (0.251)
R-squared	0.476	0.514	0.434	0.448
Wu-Hausman F-ratio	0.53	0.25	0.23	0.07

^aSample size is 10242 in all regressions. Weights are given by equation (8). Standard errors, reported in parentheses, adjust for clustering at the county level. All regressions include 20 cohort dummies, 20 county dummies, 21 year of birth of child dummies, interactions between the treatment dummy and the county-specific junior high school enrollment rate in 1966 and between the treatment dummy and the fraction of workers in agriculture in 1967, and interactions between the county and year of birth of child dummies. All means except for the postneonatal mortality rate are weighted by the cell-specific number of births. The mean of the latter variable is weighted by the cell-specific number of infants who survive the neonatal period. For low birthweight, the mean is the percentage of light births. For neonatal and infant mortality, the means are deaths per thousand live births. For postneonatal mortality, the mean is deaths per thousand survivors of the neonatal period.

^***Significant at the 1 percent level (two-tailed test).

^**Significant at the 5 percent level (two-tailed test).

^*Significant at the 10 percent level (two-tailed test).

When father’s schooling is treated as exogenous, all four coefficients are negative, significant at the 1 percent level, and similar in magnitude to the corresponding mother’s coefficients (see panel B). These coefficients retain their negative signs in WTSLS, but only the low- birthweight coefficient is significant at 10 percent, and none of the coefficients is significant at 5 percent (see panel C). There is more variability in the ratio of WTSLS to WLS coefficients for fathers than for mothers. The former ratio ranges from 0.56 for neonatal mortality to 1.32 for postneonatal mortality. The mother WTSLS coefficients are larger in absolute value than the father WTSLS coefficients The Wu-Hausman test supports the consistency of estimates that treat schooling as exogenous. Some caution is required here because the instrument for father’s schooling does not have an F-ratio in excess of 10.

To gauge the magnitudes of the effects of mother’s or father’s schooling on each of the infant health outcomes, we compute the reduction in each adverse outcome associated with the increase in schooling caused by the 1968 school reform legislation. Refer to equation (7), let K_i ≡ 1/2D_i, let a bar over a variable denote a mean, and let γ be the logit coefficient of schooling in one of the four health outcome equations. Then we compute

$${\mathrm{Y}}_1=\frac{{\mathrm{e}}^{\gamma \mathrm{\Delta }\mathrm{S}}(\overline{\mathrm{Y}}+\overline{\mathrm{K}}\overline{\mathrm{Y}}+\overline{\mathrm{K}}+{\overline{\mathrm{K}}}^2)-\overline{\mathrm{K}}+\overline{\mathrm{K}}\overline{\mathrm{Y}}-{\overline{\mathrm{K}}}^2}{{\mathrm{e}}^{\gamma \mathrm{\Delta }\mathrm{S}}(\overline{\mathrm{Y}}+\overline{\mathrm{K}})+1-\overline{\mathrm{Y}}+\overline{\mathrm{K}}}.$$ (9)

In this equation ΔS =βP̄, where β is the regression coefficient of program intensity in the schooling equation [equation (6)] and P̄ is the mean of program intensity in the treatment group. The absolute difference between Y₁ and Ȳ shows the reduction in one of the four adverse infant health outcomes associated with an increase in schooling of ΔS years.

Table 7 contains the results of the computations just described. For a given parent and a given health outcome, two estimates are shown. The first employs the WLS value of γ, while the second employs the WTSLS value of that coefficient. Our results imply that the WLS value is consistent. Nevertheless, we show both estimates because the Wu-Hausman test may have relatively low power given the loss in efficiency associated with two-stage least squares.

Table 7.

Reductions in Low Birthweight and Mortality Due to Increases in Schooling^a

	Mother’s schooling		Father’s schooling
	Weighted least squares	Weighted two-stage least squares	Weighted least squares	Weighted two-stage least squares
Outcome
Low birthweight
Percentage point reduction	0.237	0.204	0.246	0.185
Percentage reduction in number of light births	5.512	4.744	5.528	4.157
Neonatal mortality
Reduction in number of deaths per thousand live births	0.258	0.195	0.211	0.120
Percentage reduction in number of deaths	11.121	8.405	9.017	5.128
Postneonatal mortality
Reduction in number of deaths per thousand neonatal survivors	0.492	0.665	0.404	0.526
Percentage reduction in number of deaths	13.782	18.627	11.129	14.490
Infant mortality
Reduction in number of deaths per thousand live births	0.600	0.774	0.521	0.602
Percentage reduction in number of deaths	10.187	13.141	8.727	10.084

^aReduction in outcome due to increase in schooling computed by multiplying the coefficient of program intensity in the schooling regression by the mean value of intensity in the treatment group. Percentage reduction assumes no change in the denominator of the relevant outcome.

Focusing on the results for mother’s schooling, one sees that the percentage of low- birthweight-births falls by 0.24 percentage points when the WLS coefficient is employed in the computation. This translates into a percentage reduction in the number of light births in a fixed population of births of 5.5 percent. The WTSLS figures are slightly smaller. The percentage of light births falls by 0.20 percentage points or by 4.74 percent. Reductions in mortality range from a decline of 0.20 neonatal deaths per thousand live births to a decline of 0.77 infant deaths per thousand live births. In percentage terms, the smallest decline is an 8.41 percent fall in the number of neonatal deaths. The largest decline is an 18.63 percent reduction in the number of postneonatal deaths. These absolute and percentage reductions in mortality emerge from WTLS.

With one exception, the reductions associated with increases in father’s schooling are smaller than those associated with mother’s schooling. The exception is the percentage point reduction in the percentage of light births in WLS. Here the reduction for father’s schooling exceeds that for mother’s schooling by only 0.01 percentage points.

Can one conclude from these results that mother’s schooling is a more important determinant of infant health outcomes than father’s schooling? For several reasons, the answer is no. First, the mother’s schooling effects are larger than the corresponding father’s schooling effects in part because the coefficient of program intensity in the reduced form for mother’s schooling is larger than the corresponding coefficient in the reduced form for father’s schooling. Second and more importantly, we exclude father’s schooling from the infant health outcome equations when mother’s schooling is included and exclude mother’s schooling when father’s schooling is included. Given the strong positive correlation between these two schooling variables in our data and in data for practically every developing and developed country, the estimate of the effect of either one on infant health is biased by the omission of the other. As pointed out in Section III, the two schooling variables are too highly correlated to include both in the same regression.

V. Discussion

Our results suggest that parents’ schooling causes favorable infant health outcomes. In particular, an increase in schooling lowers the probability that an infant will be born light or will die in the neonatal or postneonatal periods. Our results also suggest that schooling can be treated as exogenous in estimating these effects.

The last result may seem puzzling because schooling clearly is an endogenous variable. If one recognizes this a priori, then a literal interpretation of our findings is that the schooling-health system is recursive rather than simultaneous and that the disturbance terms in the two equations are not correlated. Lack of simultaneity means that parents ignore the impacts of their schooling on the health of their offspring when they make optimal schooling decisions. Uncorrelated disturbance terms mean that unobserved factors that govern schooling outcomes are not related to unobserved factors that govern infant health outcomes.

This literal interpretation may be too narrow and naive. Parents play an important role in the schooling outcomes of their children and may take account of all potential benefits in allocating resources to their own schooling. But the infant health benefits associated with investments in schooling may be small relative to other benefits in these investments. In this case, a recursive specification may approximate reality.

Even if the recursive specification is correct, the disturbance terms in the two equations may share a common element. Time preference is an obvious candidate, as suggested by Fuchs (1982). In the schooling equation, however, variations in time preference may be small relative to variations in observed determinants of this outcome such as its price. If a minor part of the variation in schooling is due to time preference, the bias introduced by treating it as exogenous will be small.

The endogenous time preference hypothesis proposed by Becker and Mulligan (1997) complicate the situation. If causality runs solely from schooling to time preference, one does not want to control for the latter in estimating the effect of the former on health. Now suppose there is two-way causality between schooling and time preference and that time preference is replaced by its determinants in the health equation. Then the correlation that determines biases is that between schooling and the disturbance term that results from this substitution rather than the correlation between schooling and time preference itself. The former correlation is likely to be smaller than the latter.

An alternative approach to our results is possible. Two-stage least squares estimation results in a loss of efficiency. For example in the infant mortality logit, the standard error of mother’s schooling rises by a factor of 12 when it is treated as endogenous. Hence, one may want to interpret Wu-Hausman consistency tests with some caution. If that approach is taken, our two-stage least squares estimates should be stressed. These estimates allow us to conclude that mother’s schooling causes favorable infant health outcomes without having to dismiss any of the factors that generate inconsistencies when schooling is treated as exogenous. The two-stage least squares estimates do not allow us to conclude that father’s schooling causes favorable infant health outcomes. The conclusions with regard to the TSLS estimates are, however tentative because we do not control for father’s schooling in the equations that include mother’s schooling and vice versa.

Our findings should be placed in the context of the Taiwan experience. One factor that may make them different from results for the U.S. is that postneonatal deaths accounted for 60 percent of all infant deaths in Taiwan during our sample period. By contrast, they accounted for only 36 percent of all infant deaths in the U.S. Parents may play an important role in preventing or dealing with the infectious diseases and accidents that are the major causes of postneonatal mortality.

A second and related factor is that a large percentage of Taiwanese women and children lacked health insurance prior to the enactment of National Health Insurance in March 1995 (see Tung-Liang Chiang 1997 for details). Parents’ education may be an especially important factor in postneonatal infant health outcomes in this setting. The larger absolute and percentage impacts schooling on postneonatal mortality than on neonatal mortality (see Table 7) provide evidence in support of this proposition.

A third factor is that our estimating equation allows the effects of school reform to be larger in counties with more new school construction. These counties had lower junior high school enrollment rates and larger fractions of workers in agriculture. Income is positively correlated with the former variable and negatively correlated with the latter. Hence, the impacts of the school reform that we have studied are larger in poorer area and in rural areas, which by definition have more workers in agriculture. Our results may not generalize to legislation that has a different focus.

In summary, we have used a natural experiment in Taiwan to answer the question: Do increases in parents’ schooling cause better infant health? Our answer to this question is yes. Beyond that we have not investigated the mechanisms via which schooling operates because we lack data on infant health inputs. Studies that examine this issue and that try to sort out the partial effects of mother’s and father’s schooling deserve high priority on an agenda for future research.