It’s that time again

Abstract

How do we estimate duration in a familiar context? A new study shows that it is appropriate to tolerate a small bias in our estimate in order to reduce the overall temporal uncertainty.

Your feet are in the starting blocks, the race official raises the starter pistol and calls “Ready”, “Set”, “Go!” To win the race, you must push off on time. If you start too late, you may not be able to make up the lost time and catch up with your competitors. If you start too early, you may be disqualified for a false start. You cannot wait for the starting pistol to plan your start, as that will certainly lead to a slow start. Rather, you must listen for “Ready” and “Set” and predict the correct starting time based on that time interval and prior knowledge of the rhythms typical of race calls. This is the task studied in a laboratory model by Jazayeri and Shadlen (1) to understand how humans combine uncertain sensory information and prior knowledge in the estimation of duration.

We speak of the perception of time and temporal duration even though, unlike primary sensations (e.g., loudness, pitch, luminance, pressure), there is no specific sensory organ that codes duration per se and, in fact, one can estimate durations both within and across sensory modalities. Yet, the perception of duration shares several traits with other sensory capabilities. Estimation of temporal duration follows Weber’s Law (also called the ‘scalar variability property’ in the time-perception literature (2)): uncertainty scales with duration. Perceived duration is often biased (3). For example, when humans are asked to reproduce various temporal intervals, longer durations are perceived as shorter than the reference and the opposite is true for short durations. This phenomenon of regression to the mean, known as Vierordt’s law (4), is one of the most robust effects in time perception but has eluded a convincing explanation. In this issue, Jazayeri and Shadlen (1) demonstrate that the bias to underestimate long intervals and to overestimate short ones is a consequence of becoming familiar with the range of event durations in a particular context. Moreover, this context-based bias improves performance in the sense of optimizing the tradeoff between bias and variability.

In Jazayeri and Shadlen’s experiment, human participants saw two flashes of light in succession (“Ready” and “Set”), and were required to press a key (“Go”) so that the temporal interval between the first and second flash was equal to the interval from the second flash to the keypress (5). In each block of experimental trials, the displayed durations were chosen randomly and uniformly across a fixed range (e.g., this ‘temporal context’ might range from approx. 500 to 850 msec). They found that participants produced durations that were biased toward the mean of the temporal context, and that this bias increased with increases in the mean of the context.

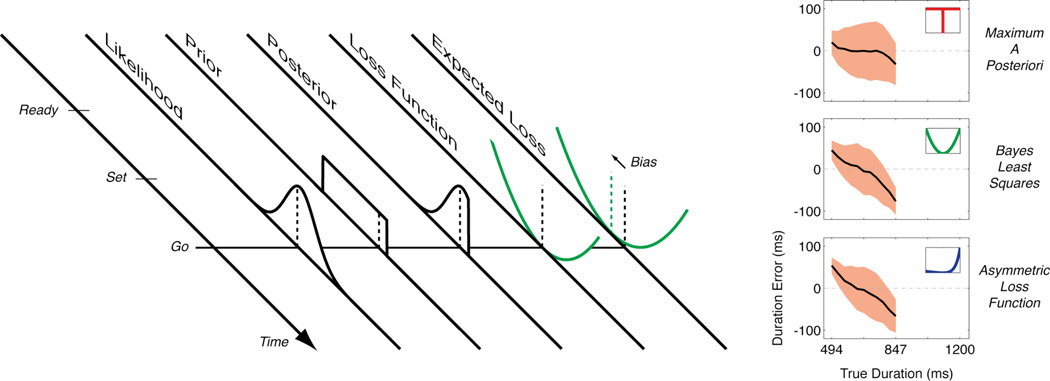
Bayesian models, which have become prevalent in models of perceptual-motor behavior in recent years (e.g. ref. 6), offer a natural setting to explain this temporal bias. Bayesian models are based on three elements: the likelihood function, the prior probability distribution (usually called simply “the prior”), and a loss function (Fig. 1). We concentrate here only on the perceptual side of the problem. The likelihood function represents the observer’s knowledge of measurement uncertainty, e.g., the probability of obtaining the current duration measurement given possible durations that might have actually occurred. The prior is the observer’s knowledge of the statistics of the world; for the Jazayeri and Shadlen experiment, the prior represents knowledge of the temporal context. Finally, the loss function represents the cost to the observer for making a particular estimate, in this case the cost of reproducing an estimated duration that differs slightly from the true duration.

Figure 1.

Left: The participant has to anticipate the “Go” signal after seeing the “Ready” and “Set” preparation signals. Knowing that the variable interval between “Ready” and “Set” is identical to the interval between “Set” and “Go”, what is the best strategy to predict the occurrence of the “Go” signal? A Bayesian decision maker answers this question by combining several pieces of information. The first piece of information is the likelihood function that represents the probability of making the measurement the participant has just made on the present duration from “Ready” to “Set” given various possible true durations The likelihood can be seen as the uncertainty of the measurement. The second piece of information is the prior probability distribution that represents the accumulated knowledge of interval durations over past races run with this race official. The product of the likelihood function and the prior distribution determines the posterior distribution and represents the probability of various possible estimates of the interval duration given the current measurement. The final piece of information is the loss function that represents the costs associated with correct and incorrect estimates. Combining the posterior distribution with the loss function gives the expected loss that represents the anticipated cost associated with different duration estimations. The minimum of the expected loss corresponds to the optimal decision for a Bayesian decision maker, indicated by the dashed green line. This optimal time is negatively biased relative to the veridical duration as a result of the prior (most previous races had a shorter duration). Right: Three Bayesian models of duration estimation for true durations chosen from the lowest range of durations used in the Jazayeri and Shadlen study (ref. 1). Each plot shows the mean ( one standard deviation) estimates over 1000 simulated races. For maximum a posteriori MAP) estimation, the loss function penalizes all errors equally (see top-right inset). This model is accurate (weakly biased) but not very precise (large variability of the estimates). For Bayes least squares (BLS) estimation, the loss function is quadratic. This model has smaller variability but larger bias, especially for long durations. The large bias for long durations is the result of the increased uncertainty of the likelihood function for longer durations (the scalar variability property). The last model is based on an asymmetric loss function that penalizes late starts more than early starts. This model shows similar accuracy and precision to the BLS model. Note in particular the larger biases for longer durations that are now the result of the high cost for overestimates, even if the participant’s internal model of likelihood is incorrect (no scalar variability). Different combinations of likelihood, prior and loss function can lead to similar predictions.

The loss function for perceptual estimation can be thought of as the compromise between accuracy (the amount of bias) and precision (the variability of the estimate). Consider two extreme strategies. First, participants could ignore the current stimulus and, instead, estimate the duration to be the mean of recently experienced durations. This first strategy would result in excellent precision (no variability), but clearly this is achieved at the expense of increased bias. Alternatively, participants could ignore the prior and simply reproduce the current duration measurement; this corresponds approximately to maximum-likelihood estimation. This second strategy would result in maximal accuracy but lower precision, because sensory measurements are uncertain and the participant is ignoring a potential source of information (the prior). The best trade-off between accuracy and precision will depend on the magnitude of the uncertainty. In a Bayesian model, the greater the uncertainty, the more the estimate regresses to the mean of the prior. The amount of bias will depend on the choice of the loss function. Small biases are obtained when the loss function rewards only correct estimates—maximum a posteriori estimation (Fig. 1). In contrast, larger biases but smaller variability are obtained when a quadratic loss function is used—Bayes least squares estimation. This latter loss function may penalize large errors more than human participants do (7). One should also consider asymmetric loss functions (8). Asymmetric loss functions are particularly critical in the time domain (5, 9): consider the different costs in under- and over-estimation of the time to arrive at an appointment or the time until you should have your car brakes checked!

To what extent do participants in Jazayeri & Shadlen’s experiment have access to the appropriate prior, their temporal uncertainty, and a rational loss function? The authors show that participants have knowledge of the prior because timing bias differs across the three temporal contexts. In particular, the same cued duration is reproduced differently in different contexts, always biased toward the mean of the current context. The authors also confirm that participants have some knowledge of their temporal uncertainty (5, 9) (at least implicitly). In particular, they argue that participants know about the scalar variability that rules their temporal uncertainty: variability is larger for larger mean durations, so that a greater bias is obtained. Unfortunately, temporal uncertainty was not measured independently so it is not clear whether participants have perfect knowledge of their own uncertainty. Finally, Jazayeri & Shadlen show that participants’ behavior is consistent with a quadratic loss function so that the optimal estimate is the mean of the posterior distribution. However, other combinations of assumed priors, temporal uncertainty and loss functions might have been consistent with their results (Fig. 1).

For the Bayesian modeler, there are three unknown functions: the likelihood, prior, and loss function. This multiplicity of unknowns is particularly vexing, because the data only tell us the participant’s average response to any given stimulus. This stimulus-response function might well result from multiple Bayesian models. For example, larger bias for long durations results from a likelihood implementing scalar variability combined with a quadratic loss function, but similar results are obtained if the participant assumes variability is constant and uses an asymmetrical loss function with high cost for overestimation (Fig. 1). Previous studies have used a variety of approaches to reduce the number of unknowns. For sensory experiments, the likelihood function can be measured by determining the observer’s ability to discriminate similar stimuli (e.g., ref. 10). The prior distribution can be imposed, as it is here, with training sessions so that participants have an opportunity to learn the prior. It can be measured from the environment and one can ask whether perceptual biases are consistent with the participant computing a Bayesian estimate using this natural prior (e.g. ref. 11). Or, experiments can be designed to estimate the shape of the prior used by the observer (12). The loss function can be imposed by the experimenter (13). Finally, sensory information can be removed, so that performance can only be based on the prior and loss function.

How can the experimenter be assured the participant is truly carrying out the Bayesian computation, rather than a simpler heuristic that has the same net effect? In Jazayeri and Shadlen’s experiment, participants received feedback for responses that were sufficiently close to the correct duration. Thus, it is reasonable to ask whether the resulting biases were learned by effectively computing a linear regression of produced intervals that led to positive feedback as a function of the corresponding measured intervals. A true Bayesian computation would imply the participant has knowledge of the likelihood, prior, and loss function, and can use those elements when one of them, e.g. the context (prior), is changed (14). One strength of the Jazayeri and Shadlen study is that observers were naturally exposed, in different sessions, to three different temporal contexts (ranges of displayed durations), and these priors were learned effortlessly. Other priors can be updated given sufficiently convincing feedback, such as the default prior knowledge that light comes from above our head (15). It is also surprisingly easy for participants to form nearly optimal strategies in pointing tasks to a visual target with arbitrary, experiment-imposed payoffs and penalties (13). The ability of human participants to readily adapt to changes in context or loss function constitutes strong evidence for Bayesian decision theories of perceptual-motor performance (14).