Enumeration of Ring–Chain Tautomers Based on SMIRKS Rules

Abstract

A compound exhibits (prototropic) tautomerism if it can be represented by two or more structures that are related by a formal intramolecular movement of a hydrogen atom from one heavy atom position to another. When the movement of the proton is accompanied by the opening or closing of a ring it is called ring–chain tautomerism. This type of tautomerism is well observed in carbohydrates, but it also occurs in other molecules such as warfarin. In this work, we present an approach that allows for the generation of all ring–chain tautomers of a given chemical structure. Based on Baldwin’s Rules estimating the likelihood of ring closure reactions to occur, we have defined a set of transform rules covering the majority of ring–chain tautomerism cases. The rules automatically detect substructures in a given compound that can undergo a ring–chain tautomeric transformation. Each transformation is encoded in SMIRKS line notation. All work was implemented in the chemoinformatics toolkit CACTVS. We report on the application of our ring–chain tautomerism rules to a large database of commercially available screening samples in order to identify ring–chain tautomers.

Introduction

Tautomers are isomers that can transform into each other through chemical equilibrium reactions.¹ There are two basic, distinct, types of tautomerism: one involving the relocation of a proton with accompanying change of the molecule’s bonding situation (prototropic tautomerism), the other manifesting itself as rapid reorganization of the molecule’s bonding electrons (but not of any atoms including H) accompanied by a geometric change (valence tautomerism). Both these fundamental types of tautomerism may or may not be associated with an intramolecular ring opening or closing. In this work, we will limit ourselves to forms of tautomerism involving proton movement. While both tautomeric variants that either change or preserve the ring structure of the molecule involve proton migration, the typical usage in the field is to call only the latter interconversion “prototropic tautomerism” (proper). The most well-known example for this type of tautomerism is the switch between keto and enol forms. In contrast hereto, “ring–chain tautomerism” requires that the movement of the proton be accompanied by ring opening or closing. Ring–chain tautomerism occurs frequently in sugars such as fructose, the classical example of a molecule that can be present in the cyclic or acyclic form. We will adhere to this terminology in the following.

Tautomers behave like chameleons which have the ability to adapt their appearance to their environment. Depending on conditions including solvent, pH, temperature, and pressure, the equilibrium between tautomers may shift dramatically.^2,3 While generally the capability of a molecule to form tautomers is seen as an “innate” property of the compound, which occurs without intervention by a chemist, it has to be clear that this distinction is mostly in the eye of the beholder. After all, from a physical point of view, it does not matter if, e.g., a sample is heated intentionally by a chemist or by accident during transport or storage. In a similar vein, terms frequently found in the definition of tautomerism such as “rapid interconversion of structures” or “facile proton migration” are rather ill-defined without specifying the units of “rapid” and “facile” in this context as well as under which types and ranges of conditions one is considering these intramolecular reactions.

Most ring–chain tautomers originate from the reversible intramolecular addition of nucleophilic centers to electrophilic ones, to form a cyclic structure as shown in Figure 1.⁴ The nucleophilic center represented by XH usually consists of OH, SH, or NRH functional groups, while the electrophilic center represented by YZ commonly is a C=O, C=S, or C=N group, or, more rarely, a C≡N group. Depending on the location of the nucleophilic attack on the electrophilic center, this can create two possible ring closures. The top of Figure 1 shows the exocyclic process when the bond of the electrophilic group remains outside the ring after the ring closure process has taken place. The bottom of Figure 1 shows the endocyclic process when the electrophilic group becomes part of the ring during ring closure; the electrophilic group in this case may be N=C, represented by ZY.

Figure 1.

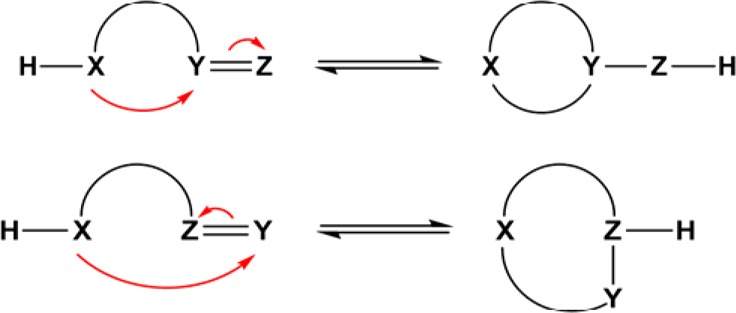
General isomerization scheme for ring–chain tautomers. (Top) Exocyclic ring closure. (Bottom) Endocyclic ring closure.

Why is the existence of multiple possible tautomeric forms of the same molecule of importance in chemoinformatics? One reason is that a careless choice of the prevalent form may negatively impact the outcome of the (in-silico) drug discovery process.^2,5,6 The calculation of physicochemical properties (pK_a, lipophilicity, solubility, etc.) can vary by several orders of magnitude by just calculating their respective values for different tautomers of the same chemical compound.⁶ Likewise, registration and retrieval of small molecules in chemical databases should ideally involve careful consideration of tautomerism. One may otherwise miss relevant information upon searching in the database, or the database contents themselves become error-prone if different tautomeric forms are registered separately while no connection to each other is established.^7,8 This has led to the interesting effect that different tautomeric forms of a compound can be available at different prices from the same vendor.⁹ Also, different tautomers can show different hydrogen-bonding patterns and H-donor or H-acceptor patterns, which may impact virtual screening approaches.¹⁰ Tanimoto similarity between tautomers can be very low,⁸ and tautomerism may affect the results of structure clustering and similarity searching negatively. Finally, tautomerism plays a significant though probably underappreciated role in X-ray crystallography: Crystal structures are generally fraught with uncertainty in this regard, since in macromolecular crystal structures—unless solved at ultrahigh resolution where hydrogen atoms may be resolved—it can be near impossible to know which tautomeric form is present in ligand–protein complexes.¹¹

Several approaches and software tools exist that can handle prototropic tautomerism.^3,7 Commonly, they allow for enumerating all possible prototropic tautomers, identifying a canonical tautomer form of a compound, or both. To our knowledge, current chemoinformatics tools however do not handle ring–chain tautomerism well if at all. Therefore, in this work, we will present a practical approach to enumerate and predict ring–chain tautomers.

In the 1970s, Baldwin published a set of rules to predict the relative facility of ring forming reactions¹² (Table 1, top). Baldwin’s rules consider three main features: (a) the size of the ring being formed indicated through a numerical prefix, from three to seven, (b) the position of the nucleophilic attack during the ring closure: exocyclic (“exo”) or endocyclic (“endo”), and (c) the nature of the electrophilic carbon: tetrahedral/sp3 (“tet”), trigonal/sp2 (“trig”), or digonal/sp (“dig”). These empirical rules were formulated from observations and stereoelectronic reasoning, estimating the kinetic feasibility of a ring closure. According to Baldwin’s rules, a ring closure is favored if the length and nature of the linking chain enables terminal atoms to achieve the necessary geometry to form the ring bond. A ring closure becomes unfavorable if severe distortion of bond angles and distances are required to achieve such geometries, consequently making alternative reaction pathways, if available, the dominant route and the desired ring closure unlikely.¹²

Table 1. (Top) Baldwin’s Rules for Ring Closure and (Bottom) Adaptation to our Ring–Chain Tautomer Rules^a.

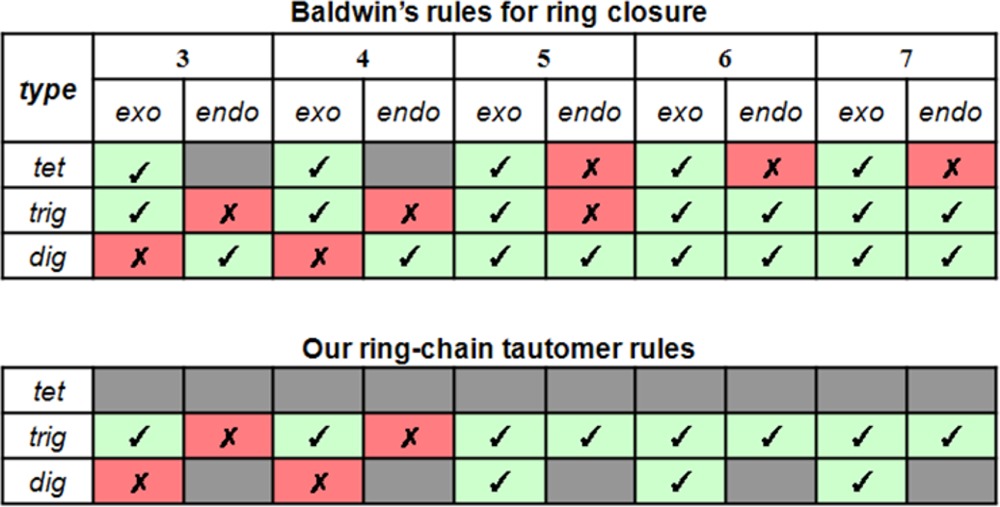
^aColumns represent the size of the ring formed (3–7) and the type of closure process (exocyclic and endocyclic). Rows specify the nature of the electrophilic carbon: tet (tetrahedral/sp3), trig (trigonal/sp2), and dig (digonal/sp). Green (with check mark) indicates favorable cyclizations, red (with cross-out) indicates unfavorable cyclizations, and gray indicates that no prediction was made.

We have defined a set of ring–chain tautomerism rules using Baldwin’s rules as the starting point, as well as a means to classify them. Our rules are encoded in SMIRKS line notation,¹³ allowing for the automatic detection of appropriate substructures in a given compound that can undergo a ring–chain tautomeric transformation. We have validated our rules with several ring–chain tautomerism cases described in the literature. We then applied our ring–chain tautomerism definition to the Aldrich Market Select (AMS) database¹⁴ to obtain a first quantification of the prevalence of ring–chain tautomer tuples in a “real-life” small-molecule database.

Methods

Encoding of Transformations

The transforms used in these tautomer rules were encoded in SMIRKS line notation developed by Daylight Chemical Information Systems, Inc.,¹³ for the description of reaction substructures and the transformation of atoms and bonds during reactions. A reaction encoded as a Reaction SMIRKS expression is a sequence of ASCII characters following a general pattern: a reactant part on the left is separated from the product side on the right by the symbol “≫”. We encoded each transformation in our rule set as one SMIRKS string.

Adaptation of Baldwin’s Rules to Ring–Chain Tautomerism Rules

One of the structural requirements for ring–chain tautomerism with regard to the chain tautomer is that it must possess at least two functional groups, one containing a multiple bond and the other capable of effecting an additive reaction at the multiple bond.

We adapted Baldwin’s rules in three ways in the design of our rules (see Table 1). First, we did not consider ring closure and opening reactions when a tetrahedral electrophilic carbon (i.e., tet) is involved because in this case the breakage of a single bond would cause a loss of atoms to the molecule (or, a separation into two molecules, respectively). Since one stipulation of our tautomer rules is that the interconversion may not produce a compound with different molecular weight, the tet type is rejected for both the exocyclization and endocyclization process. The second departure from Baldwin’s rules concerns the 5-endo-trig rule which predicts this type of ring closure as being unfavorable. However, a rapid equilibrium reaction has been reported in several cases to occur in solution in several different compounds.^15,16 Thus, this type of ring closure reaction has been included as a favorable one in our rule set. Third, the only electrophilic group we accept for the endocyclic process is the N=C group; i.e. the endocyclic bond breaking process for the dig type is disregarded, and a nitrogen atom is the only heteroatom type admitted as the electrophilic group for this type of reaction. By this choice, we want to avoid having to deal with cases where a change of the formal charge between the open and close form of the molecule is required.

Implementation of the Tautomer Generation Process

The code for the evaluation of the ring–chain rules was implemented using the CACTVS chemoinformatics toolkit.¹⁷ The set of ring–chain tautomer transformation rules is applied to every input molecule. CACTVS provides an extended set of attributes for the definition of SMIRKS which have no counterpart in the original SMIRKS syntax; e.g. the attribute “zn” indicates the number n of heteroatoms substituted to the corresponding carbon atom.

We used the following specific CACTVS transformation command for our tautomer enumeration: ens transform $ehandle $SMIRKSlist bidirectional multistep all {checkaro preservecharges setname} maxstructures. The command applies a list of SMIRKS transforms (given as SMIRKSlist) to a molecule (an “ensemble” in CACTVS parlance, identified by its handle ehandle) and returns a list of ensemble handles of transformation products. The transformation products obtained in this way are filtered for duplicates by the HASHISY structure hash function available in CACTVS.¹⁸ The original structure is not included in the list of returned tautomer ensembles. If a transform set does not match any of the SMIRKS, an empty list is returned. If a rule necessitates multiple SMIRKS patterns to fully cover it, the patterns are applied exhaustively. Essentially, the patterns are cycled until a pass has not generated any new structure.

The specific command parameters we applied to the “ens transform” command in CACTVS used for the tautomer generation were direction (we use parameter value bidirectional), reactionmode (value: multistep), selectionmode (value: all), and maxstructures. The direction parameter describes how the SMIRKS transform has to be read. When the bidirectional mode is set, both sides of the transform scheme will be matched to the input molecule, i.e., the corresponding reaction encoded as SMIRKS is considered both in forward and backward directions. The next parameter, reactionmode, will determine how the possibility of multiple occurrences of transform substructures in the original molecule is handled. In the multistep mode, all transform products will be generated by systematically applying the transforms to all structures and constantly resubmitting the results to the transforms, until no new compounds are generated. When the all mode is selected for the selectionmode parameter, all transformations are applied to all result ensembles. This process is repeated until no additional, structurally distinguishable result ensembles determined by the structure hash HASHISY¹⁸ are generated. For some structures, the enumeration of tautomers can run into a combinatorial explosion of structures. In order to mitigate the effects of this problem, we set an upper limit of 1000 transformations (maxtransforms) per input structure.

Besides the parameters described so far, which globally affect the behavior of all SMIRKS transforms, local command flags can be added as part of a specific SMIRKS transform. The checkaro flag invokes aromaticity checking. Atoms specified as aromatic in the transform pattern (represented by lowercase element symbols in SMILES notation) will only match aromatic atoms in the target ensemble, while all other query atoms will only match nonaromatic atoms (represented by uppercase element symbols). Using the preservecharges flag indicates that charges should not be changed. By default, the charge of a matched atom is set to the charge of the matching atom in the transform template, as long as the atom has sufficient free electrons to allow the charge change. This behavior can be overwritten with the preservercharges flag. The setname flag appends string to the compound name property by adding the name of each transform rule with which the corresponding tautomer had been processed. We used this expanded name for keeping track of how a particular tautomer was generated.

Results

Set of Ring–Chain Tautomerism Rules

We compiled a set of 11 rules that encode a wide range of typical ring–chain transformations described in the literature. We named these rules along the lines of the same three major structural features figuring prominently in Baldwin’s rules. Whereas Baldwin’s rules describe eight disfavored ring closures and 20 favored ring closures, our rules describe four possible disfavored and 11 possible favored ring closures and openings (Table 1). The group of favored ring closures/openings constitutes the set of our 11 ring–chain tautomerism rules shown in Table 2. Some of these rules required the definition of more than one variant, yielding a total of 38 SMIRKS rules. This requirement arose from the fact that in some cases a more detailed structural description is needed which could not be covered by a single SMIRKS transformation rule. Our complete list of ring–chain transformations expressed in SMIRKS is included in the Supporting Information.

Table 2. SMIRKS Transforms for Our 11 Ring–Chain Tautomer Rules.

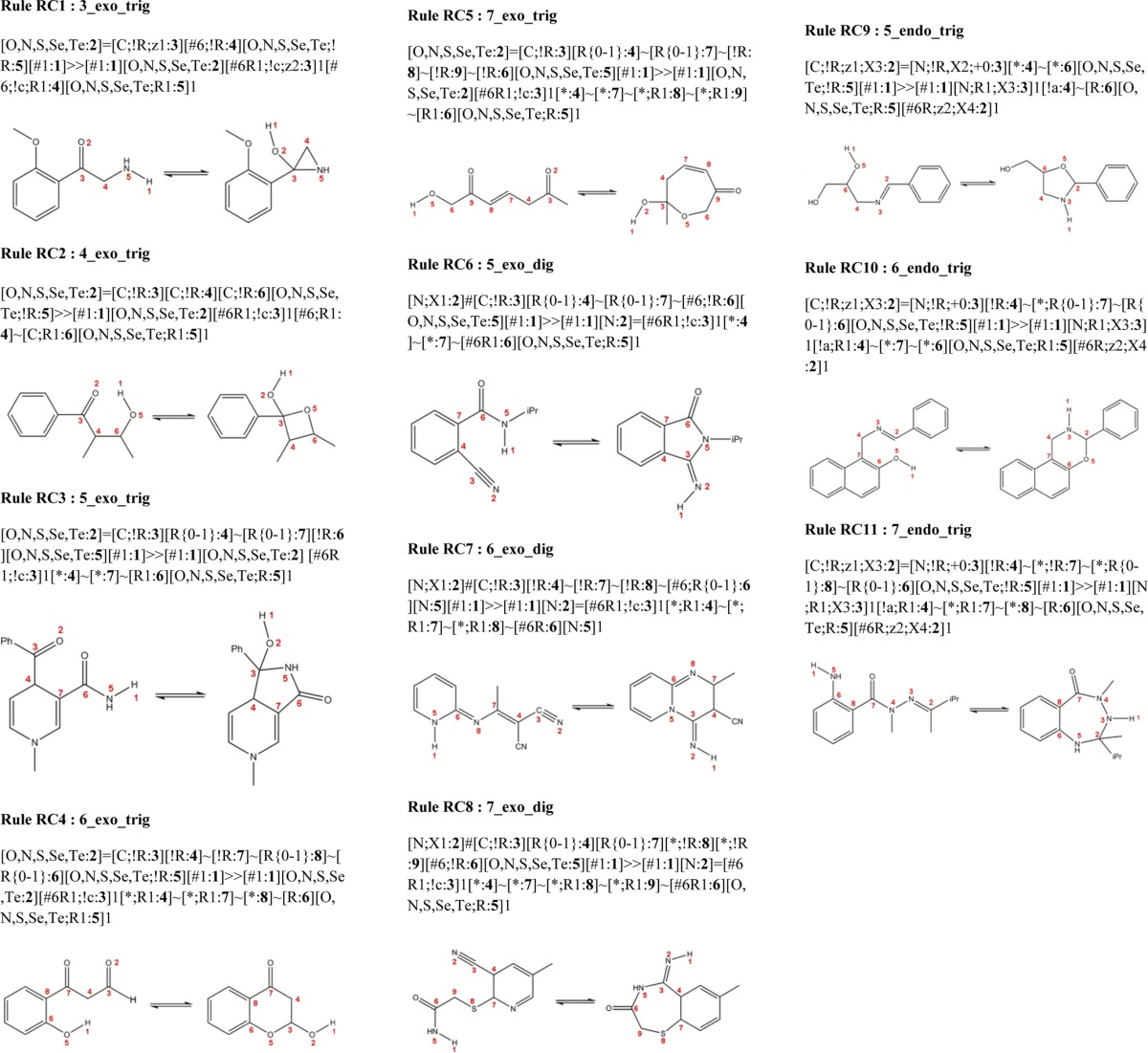
Aside from Baldwin’s rules, we took into account the following additional aspects of tautomer interconversion reactions in the definition of the SMIRKS. (1) Importantly, our SMIRKS strings match molecular patterns in which all atoms are completely connected whichever way the transformation occurs, i.e. from the open to the closed form or vice versa. It is also important to note that our rules do not encompass any disconnection, since this makes sure that the opening or closing of the ring is feasible from a 3D point of view. (2) Aromaticity is preserved in all cases. Our ring–chain rules neither open nor modify any aromatic ring, which is a type of transformation, which based on energetic grounds does not usually occur in tautomeric equilibria. (3) We allow ring sizes from three to seven for the transformations. However, as three- and four-membered rings formed are generally less stable, we defined their respective rules in a more restrictive way.

Stereocenters defined in the input molecules are always retained in the transformed products, as long as they are not part of the reaction center. Stereocenters generated by any ring–chain rule have no defined stereochemistry. Although we are aware of the importance of stereochemistry for molecular recognition and bioactivity, we do not define the configuration of newly generated stereocenters in our rules. We prefer to leave it to a postprocessing step to evaluate which enantiomer or diastereomer is favored. Ring–chain tautomerism, just like prototropic tautomerism,⁸ can change stereochemistry of a compound by either changing E/Z geometry of a stereogenic bond or changing chirality of a stereogenic atom.

Baldwin’s rules only describe the ring closure process; our rules are bidirectional, so they are as valid for closing as well as for opening rings. In general, the opening process has positive free energy; i.e. it is not the spontaneous process. We therefore can expect the closed forms to be favored in tautomeric equilibria. However, this depends both on the substituents and the conditions, thus under the right circumstances the equilibrium can be shifted to the ring-open form. Since our primary goal is to generate all possible tautomers, both directions are considered. It will be left to future work to obtain energetic guidelines for each transformation.

Validation by Experimental Data Extracted from Literature

Some results on ring–chain tautomerism have been published,¹⁵ including the effect of substituents on the tautomeric equilibria,¹⁶ the effect of the solvent,¹⁹ and synthetic applications. Also, computational studies on ring–chain tautomerism have been performed by using quantum chemical calculations to investigate the key structural factors involved in the ring–chain tautomerism equilibrium.²⁰⁻²² Many studied examples represent the well-known case of ring–chain tautomerism in N-unsubstituted 1,3-X,N-heterocyclic compounds (X = O, S, NR).²³ Most of the documented cases of experimentally confirmed ring–chain tautomerism have been obtained by the application of endocyclic transformations.

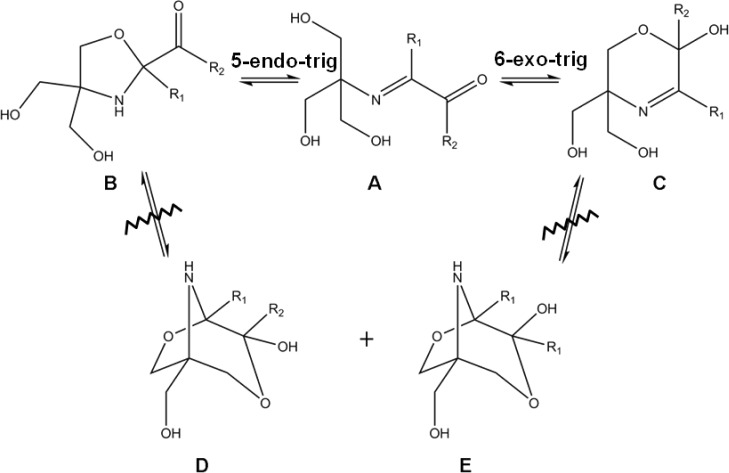
Our rules handle the vast majority of ring–chain tautomerism cases found in the literature,²³⁻²⁹ as we ascertained by a literature survey in the Web of Knowledge. We queried for all English language publications from the year 2000 to date, using the search pattern “ring chain tautomer*” in the Title field. A list of 71 compounds and corresponding tautomer information were extracted from those papers (see Supporting Information) in order to validate our ring–chain rules. For each article, we selected only one representative compound for each chemistry series since typically all of them follow the same transformation rule. A few structures were excluded from our analysis due to their type of ring–chain tautomerism. Specifically, nine compounds were classified as not applicable because their transformation involved halogen anions,^30,31 alkaline solution,³² intermediate reaction forms,³³⁻³⁶ or the molecule did not have the nucleophilic center required for a ring–chain transformation process,³⁷ i.e., were not tautomeric transformations in the strict sense relative to our definition. We were able to predict the documented ring–chain tautomers for 57 out of the remaining 62 compounds. The other five chemistry systems from the literature survey set were not covered by our rules, essentially all those that involve bridged ring systems.^{22,23,38−40} Figure 2 shows an example of those noncovered cases in which the first cyclization of the open form (A) occurs either through 5-endo-trig or 6-exo-trig ring closures to yield regioisomeric oxazolidine (B) and dihydro-1,4-oxazine tautomeric forms (C). However, the second cyclization, which affords methyl-substituted regioisomers of 3,6-dioxa-8-azabicyclo[3.2.1]octanes (D, E), is not covered by our rules. Evidently, those cases could have been handled by a more generic rule; however, we intentionally limited the scope of our rules to avoid artifacts and a high number of unrealistic tautomers. Nonetheless, spiro bicyclic compounds and fused bicyclic compounds are not generally excluded from our rules. In fact, the reason why some of the ring–chain rules appear in several variations is due to the fact that specific fused bicyclic and nonbridged ring systems are handled by specific subrules. The difference between the subrules of the same major rule results from the need to describe the position where the new fused bicycle (i.e., the closed tautomeric form) can be created relative to the original molecule (i.e., the open tautomeric form). For example, rule 5-exo-trig appears as three variations: RC3, RC3′, and RC3″. RC3 allows the fused bicycle between atoms 4 and 7. RC3′ allows the fused bicycle between atoms 7 and 6, and RC3″ allows the fused bicycle between atoms 5 and 6 (see Supporting Information). Concerning the noncovered bridged ring cases, Bredt’s rule⁴¹ restricts the possible stable bridge ring–chain tautomerism cases when it involves a double bond at the bridgehead position, thus not covering such cases in our rules is not a loss of breadth of coverage.

Figure 2.

A case of ring–chain tautomerism not covered by our rules. It involves bridged ring systems (molecules D and E) in the second cyclization reaction of molecule A.

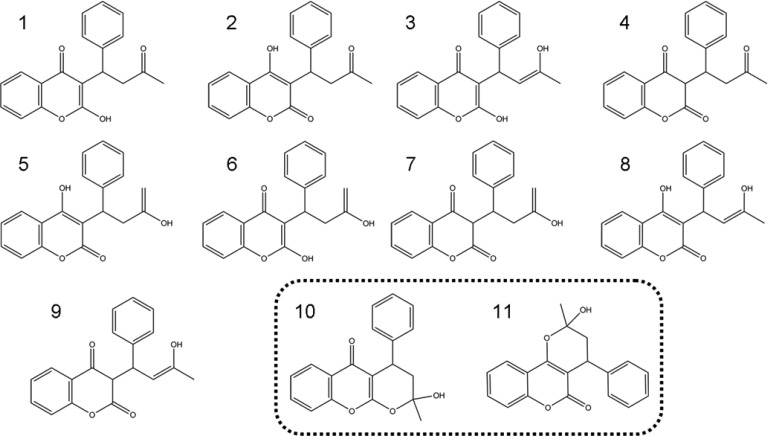
One interesting example of ring–chain tautomerism frequently described in the literature is the molecule warfarin.⁴²⁻⁴⁴ Warfarin has been titled an environment-dependent molecular switch,⁴⁵ for which 11 tautomers have been identified experimentally (Figure 3). Each warfarin tautomer is recognized by a different enzyme, and for all of them pK_a values have been calculated: they vary by 10 orders of magnitude, and log D values vary by 3.4 log units.⁴² The often overlooked ring–chain tautomerism alone produces eight different ring stereoisomers. Applying both ring–chain and prototropic rules, we were able to predict the 11 experimentally confirmed tautomers of warfarin.

Figure 3.

All experimentally found tautomers of warfarin. The cyclic tautomers are in the dashed-line box.

Ring–Chain Tautomeric Analysis of a Large Chemical Sample Database

In a previous study,⁸ we found that tautomerism is not a rare phenomenon in databases. Tautomerism was found to be possible for more than 2/3 of the Chemical Structure DataBase (CSDB) of the NCI/CADD Group, an aggregated collection of over 150 small-molecule databases comprising a total of 103.5 million structures. This analysis was essentially based on the default CACTVS’s tautomerism definition, which at that time was a set of 21 transform rules covering only prototropic tautomerism.

To both test our ring–chain tautomerism definition and to evaluate the impact of ring–chain tautomerism in a “real-life” database, we applied our ring–chain tautomerism rules to the Aldrich Market Select (AMS) database from ChemNavigator/Sigma-Aldrich.¹⁴ The AMS currently comprises over eight million unique chemicals available from more than 60 suppliers worldwide. Our rules indicated that up to 8% (457 710 out of 5 755 574) of the molecules in the AMS can transform into other ring–chain tautomers. Table 3 shows the distribution of tautomers generated. Application of our transforms created a total of 4 065 224 tautomer structures excluding the original input structures, with 22% of the molecules generating one extra tautomer, 47% generating two additional tautomers, and the remainder generating three or more tautomers. The maximum number of tautomers generated for one structure was 925, though this was certainly an exception as the majority of structures (88%) had between one and 10 ring–chain tautomers. Comparing with prototropic rules, ring–chain rules thus turned out to be less frequently applicable and more specific. In contrast hereto, more than 75% of the molecules in the AMS database can generate prototropic tautomers according to CACTVS’s tautomerism definition (see second block of columns in Table 3). Also, we observed that 84% of molecules that can generate prototropic tautomers do not create more than 10 of them. Despite the size ratio of the AMS vs CSDB of only about 8%, the same tautomer set size distribution is observed for prototropic tautomerism for our AMS analysis vs our previous CSDB results;⁸ i.e. about 62% of molecules can generate between one and 10 prototropic tautomers (see second and third block of columns in Table 3). It thus appears that this type of tautomerism analysis is consistent and robust vis-à-vis very different databases and thus provides confidence for our ring–chain analysis of the AMS database. Both prototropic and ring–chain rules were then applied to AMS in order to generate all possible tautomers for each molecule. The results (last column in Table 3) showed that the distribution remains essentially the same as when using only the prototropic tautomerism rules, while somewhat increasing the number of tautomers per molecule. This was expected because we know that the proportion of prototropic tautomers is on average much higher than that of ring–chain tautomers, which gives the prototropic distribution a much greater weight.

Table 3. Distribution of the Number of Tautomers Predicted Per Molecule by Our Ring–Chain Rules, CACTVS Prototropic Rules, and Combined Application of Both Sets of Rules to the AMS (Aldrich Market Select) and CSDB (Chemical Structure DataBase) Databases (See Text)^a.

	ring–chain tautomerism, 11 rules, AMS		prototropic tautomerism, 21 rules, AMS		prototropic tautomerism, 21 rules, CSDB		both types of tautomerism, 32 rules, AMS
	count	%	count	%	count	%	count	%
no tautomers (single molecule)	5 297 864	92.05	1 393 612	24.21	9 756 186	14.06	1 364 937	23.72
one tautomer	101 890	22.26	1 235 979	28.34	10 721 845	17.99	1 093 477	24.90
2–10 tautomers	304 245	66.47	2 428 781	55.68	33 532 284	56.25	2 271 956	51.75
11–50 tautomers	37 267	8.14	584 842	13.41	13 492 899	22.63	722 423	16.45
51–100 tautomers	3905	0.85	72 832	1.67	1 136 066	1.91	136 558	3.11
101–200 tautomers	7078	1.55	35 901	0.82	565 199	0.95	151 384	3.45
201–500 tautomers	3017	0.66	3486	0.08	157 260	0.26	14 734	0.34
501–1000 tautomers	308	0.07	141	0.00	6088	0.01	105	0.00

^aThe reduction of the number of AMS molecules with 501–1000 tautomers when going from 21 to 32 rules stems from the fact that we cut off tautomer generation at 1000 generated tautomers (see text), and more rules pushed more molecules beyond this limit.

The application of the ring–chain rules in the systematic generation of all AMS ring–chain tautomers created a set of 4 065 224 chemical structures excluding the original structures via 21 327 587 transformations. Table 4 shows how often each ring–chain rule from Table 2 was used in the creation of this ring–chain tautomer set. This may provide useful statistics about the prevalence of the various ring–chain transforms encountered in a real database. The distribution varied widely along the three features of ring–chain rules: 5- to 7-exo-trig type rules had the highest frequency by far, almost covering 80% of the transformations applied. The endo type as well as the transformation involving 3- and 4-membered rings was an infrequently found transformation. Results differing from those obtained from the experimental papers were most often observed for endocyclic transformations.

Table 4. Frequency of Application of Ring–Chain Rules in the Systematic Generation of Ring–Chain Tautomers in AMS Database.

SMIRKS rule	count	%
3-exo-trig	65 435	0.31
4-exo-trig	10 560	0.05
5-exo-trig	7 506 722	35.09
6-exo-trig	5 289 114	24.72
7-exo-trig	4 185 292	19.56
5-exo-dig	179 567	0.84
6-exo-dig	472 074	2.21
7-exo-dig	3 293 445	15.40
5-endo-trig	169 007	0.79
6-endo-trig	156 371	0.73
7-endo-trig	65 239	0.30

Comparison with Natural Product and Drug Databases

One question widely discussed in drug design is whether making potential drug molecules more natural product-like would increase the hit rates of active molecules. While many molecular properties have been analyzed in the context of the question, “what is ‘natural product-like’,” we believe that the occurrence rate of possible ring–chain tautomerism is not among them.

We therefore compared three natural product databases and one drug database with the AMS for the occurrence rates of the possibility of both ring–chain and prototropic tautomerism. The natural product databases are CHMIS-C,⁴⁶ an in-house database of natural products (“NCI-NP”), and a Traditional Chinese Medicines (TCM) database. (Somewhat older versions of the CHMIS-C [2004] and TCM [2003] were used, which may not reflect the size of current collections, though we doubt that the overall coverage of chemical space and thus conclusion for our analysis would have much changed.) As an example of a drug database, we downloaded and analyzed the freely available KEGG-MEDICUS database.⁴⁷ Since many existing drugs are derived from, if not outright are, natural product, it is a reasonable assumption that the percentage of natural product-like compounds in a drug database would be higher than in a screening sample database.

Table 5 shows that the natural products and drug databases analyzed here do indeed show a significantly higher occurrence rate of the possibility of ring–chain tautomerism: an average of quite exactly twice the value for the four natural products/drug databases (16%) vs the AMS (8%). In contrast hereto, the occurrence rates for prototropic tautomerism are somewhat lower than for the AMS, though with a significantly smaller relative difference (average of 56% vs 76% for AMS) than the approximately 2:1 ratio we found for ring–chain tautomerism.

Table 5. Comparison of Natural Product and Drug Databases for the Occurrence Rates of the Possibility of Ring–Chain and Prototropic Tautomerism.

		total number of molecules	number of molecules capable of ring–chain tautomerism		number of molecules capable of prototropic tautomerism
databases	database type	count	count	%	count	%
CHMIS-C	natural products (herbal medicines)	8572	1141	13.3	4319	50.4
NCI-NP	natural products (various types)	124 701	22 875	18.3	73 005	58.5
TCM	natural products (traditional chinese medicines)	9127	1381	15.1	4875	53.4
KEGG MEDICUS	drugs	12 041	2180	18.1	7313	60.7
AMS	screening samples and building blocks	5 755 574	457 710	8.0	4 369 069	75.9

Whether this means that a compound’s capability of undergoing ring–chain tautomeric interconversion is an asset or a liability in drug design can be a topic for discussion. It would however seem that ring–chain tautomerism does certainly not need to be avoided to obtain bioactive molecules.

Ring–Chain-Ring Tautomer Interconversion

When the ring–chain tautomerism involves more than two reaction centers (more than one nucleophilic and/or more than one electrophilic center), the outcome can be described as a ring–chain-ring tautomeric interconversion involving at least two ring–chain equilibria.⁴⁸ Taking into account that each rule is a transformation, sometimes it is necessary to apply several transformations to obtain a particular tautomer. This is the reason why we used the multistep mode in the tautomer generation (see above). At the end of this process, a network is created in which each node represents a tautomer and each connection (edge) is a transformation rule, and the way to move around in each network is by applying transformation steps. The situation is growing more complicated as the number of reaction centers increases and, as a consequence, the number of combinations. Such networks can become very large, with several steps required to reach another experimentally found tautomer. However, in the literature examples we studied, we did not find any case where moving from one experimental tautomer to another required application of more than two transformations. With this in mind, one could decide on a maximum number of transformations that are allowed for generating tautomers. However, from a chemoinformatics point of view, it is important to make all possible ring–chain tautomers for a particular compound accessible by the predictive rules.

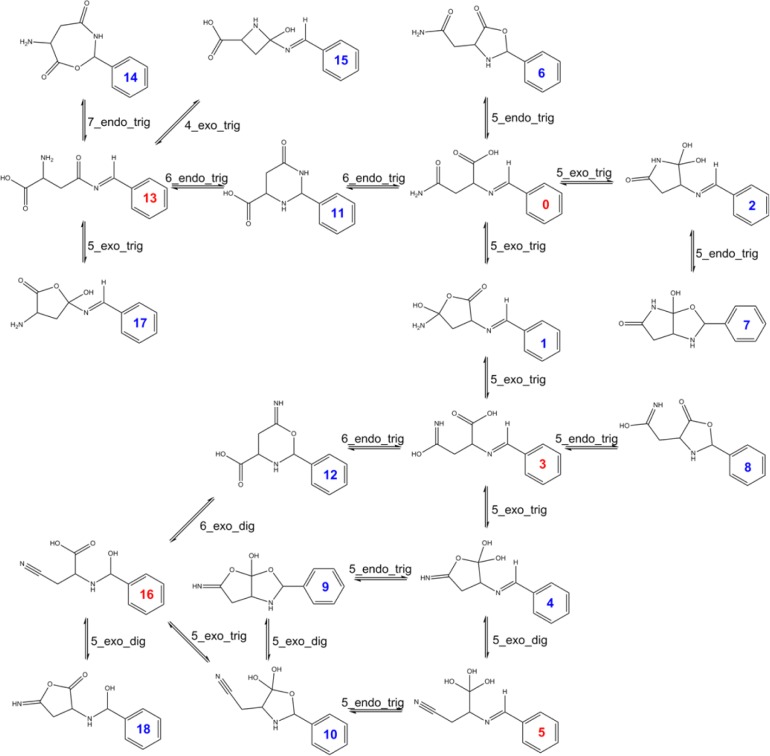
Figure 4 shows an example of the enumeration of all predicted ring–chain tautomers 4-amino-2-(benzylideneamino)-4-oxobutanoic acid. This structure was (molecule 0) extracted from one of our bibliographic examples (see SI2).⁴⁹ We predicted 18 ring–chain tautomers for this molecule. The open form 0 has several ways to close in one step according to our ring–chain rules, forming tautomers 1, 2, 6, and 11, respectively. Tautomer 11 has been experimentally identified by ¹H and ¹³C NMR spectroscopy.⁴⁹ In this example, we only show the ring–chain tautomers predicted by our rules without including prototropic tautomers. It has to be noted that usually fewer ring–chain tautomers than prototropic tautomers are enumerated per molecule; however we wanted to illustrate in this example how complex the generation of just all possible ring–chain tautomers can become.

Figure 4.

Enumeration of all predicted ring–chain tautomers of 4-amino-2-(benzylideneamino)-4-oxobutanoic acid (molecule 0). Blue numbers indicate ring closed tautomers, and red numbers indicate ring opened tautomers.

Recent studies have shown that ring–chain–ring tautomerism is a key pathway for the synthesis of various important compounds. The ring–chain–ring interconversion,^50,51 with the chain form being less stable than the ring form, may explain enantiomeric interconversion of the same cyclic derivative in which a chiral center is formed after the interaction of a single nucleophile–electrophile pair, a process that has been observed in the conversion of systems such as oxazolidine derivates.¹⁹

In the current iteration of our approach, all ring–chain tautomers are simply enumerated by the application of a set of transformations. However, they are not ranked; i.e., we cannot predict the preferred tautomer, or set of tautomers, that have the highest chance to be actually observable or to be the one(s) exerting biological activity, especially when taking into account all the possible condition parameters such as solvent, temperature, pH, binding site, etc. One could consider for this task some known relationships such as the Thorpe–Ingold effect stating that an increasing number of alkyl substituents make the cyclic form more probable.⁵² Likewise, the Hammet relationship predicts that there is a higher tendency for the open form in case of an NO₂ substitution in the ortho position, whereas the cyclic form will be more likely for NH₂ and OH substitutions.⁵³ Fulop et al. published a simple equation to describe ring–chain equilibrium but only applied it to 1,3-oxazines compounds.⁵⁴ In short, much room exists for future expansion of this work in various directions to make it a hopefully yet more useful tool.

Conclusions

We have defined a set of transform rules in computer-interpretable format to predict ring–chain tautomers. We have validated these rules via several ring–chain tautomers found in the literature. Also, we applied our ring–chain tautomerism definition to a large “real-life” database, the Aldrich Market Select (AMS) database, to evaluate the algorithm. As expected, ring–chain tautomerism was found to be less frequent and more specific than prototropic tautomerism.

In this analysis, the 5- to 7-exo-trig rules were the most frequently applicable transformations. Our algorithm is fast and convenient for predicting all possible tautomers. In its current version, it does not confine the enumeration process to energetically reasonable tautomer forms because we do not apply any explicit energetic analysis. Nevertheless, we tried to embody in the presented rules constraints for ring closure that avoid “nonsensical” 3D structures, i.e. very high-energy tautomers. Still, in terms of future development of the approach, it would be of high interest to be able to predict the preferable tautomer(s), which is however not a trivial task since this is a complicated function of a number of micro- and macroenvironmental factors.

We hope that these rules will be found to be useful for predicting ring–chain tautomerism, a task heretofore not widely handled by chemoinformatics toolkits. The set of ring–chain tautomer rules encoded in SMIRKS format can be downloaded for free use as a text file from the Supporting Information.

Glossary

Abbreviations

AMS

Aldrich Market Select

CSDB

Chemical Structure Database

Supporting Information Available

Complete list of ring–chain transformations (Table SI1). Bibliographic examples of ring–chain tautomerism together with predicted tautomers (Table SI2). This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^† Markus Sitzmann: FIZ Karlsruhe – Leibniz-Institut für Informationsinfrastruktur, Hermann von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany.

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States