Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 Sep 4;5(18):3274–3278. doi: 10.1021/jz501655v

Probing Nonadiabaticity in the Proton-Coupled Electron Transfer Reaction Catalyzed by Soybean Lipoxygenase

Alexander V Soudackov 1, Sharon Hammes-Schiffer 1,*
PMCID: PMC4170820  PMID: 25258676

Abstract

graphic file with name jz-2014-01655v_0004.jpg

Proton-coupled electron transfer (PCET) plays a vital role in many biological and chemical processes. PCET rate constant expressions are available for various well-defined regimes, and determining which expression is appropriate for a given system is essential for reliable modeling. Quantitative diagnostics have been devised to characterize the vibronic nonadiabaticity between the electron–proton quantum subsystem and the classical nuclei, as well as the electron–proton nonadiabaticity between the electrons and proton(s) within the quantum subsystem. Herein these diagnostics are applied to a model of the active site of the enzyme soybean lipoxygenase, which catalyzes a PCET reaction that exhibits unusually high deuterium kinetic isotope effects at room temperature. Both semiclassical and electronic charge density diagnostics illustrate vibronic and electron–proton nonadiabaticity for this PCET reaction, supporting the use of the Golden rule nonadiabatic rate constant expression with a specific form of the vibronic coupling. This type of characterization will be useful for theoretical modeling of a broad range of PCET processes.

Proton-coupled electron transfer (PCET) plays a vital role in a wide range of biological processes, including photosynthesis, respiration, and a variety of enzyme reactions.1−3 Often such PCET reactions occur by a concerted mechanism, in which the electron and proton are transferred simultaneously to avoid high-energy intermediates. A well-studied example of concerted PCET is the reaction catalyzed by the enzyme soybean lipoxygenase (SLO), which has been studied extensively with both experimental and theoretical methods.4−10 This enzyme reaction has been shown to have a hydrogen/deuterium kinetic isotope effect (KIE) of ∼80 at room temperature.5 Recently a double mutant of SLO has been shown to have an even larger KIE of ∼700 at room temperature.11 These unusually high KIEs are indicative of hydrogen tunneling and nonadiabatic processes. Rate constant expressions for concerted PCET reactions have been derived in various well-defined regimes,3,12 and determining which rate constant expression is appropriate for a given system is essential for modeling these types of reactions.

In this Letter, we utilize several different diagnostics to characterize the PCET reaction catalyzed by SLO and to identify the appropriate rate constant expression for this system.13−15 In this framework, we divide the system into three components: the electrons, the transferring proton, and all other nuclei. The electrons and the transferring proton are treated quantum mechanically, and the other nuclei are treated classically. We define two types of nonadiabaticity: (1) the vibronic nonadiabaticity, defined as the nonadiabaticity between the electron–proton quantum subsystem and the classical subsystem comprised of the other nuclei, and (2) the electron–proton nonadiabaticity, defined as the nonadiabaticity between the electrons and proton within the quantum subsystem. We utilize a semiclassical formalism16 to determine effective time scales for the proton tunneling and the electronic transition and to calculate an adiabaticity parameter, defined as the ratio of these two time scales.13 We also utilize the constrained density functional theory-configuration interaction (CDFT-CI) formalism17−19 to calculate the energies of and coupling between the two diabatic electronic states along the proton coordinate. Moreover, we use ground state DFT to examine the change in the electronic charge distribution along the proton coordinate. These analyses provide insight into the fundamental nature of the SLO reaction.

According to nonadiabatic PCET theory,3,12 these reactions can be described in terms of nonadiabatic transitions between reactant and product electron–proton vibronic states. Within this theory, the simplest rate constant expression for PCET is3,12

graphic file with name jz-2014-01655v_m001.jpg 1

where the summations are over reactant and product electron–proton vibronic states, Pμ is the Boltzmann probability for the reactant state μ, Vμν is the vibronic coupling between the reactant and product vibronic states μ and ν, λ is the reorganization energy, and ΔGμν0 is the reaction free energy for states μ and ν. This expression has been extended to include the effects of the proton donor–acceptor motion in various limits.20 The derivation of this expression is based on the Golden rule formalism, which requires the vibronic coupling to be much less than the thermal energy, as well as other assumptions that have been discussed throughout the literature.21 Here we define vibronic nonadiabaticity to be associated with the property Vμν ≪ kBT. Furthermore, the form of the vibronic coupling is determined by the degree of electron–proton nonadiabaticity. In the limit of significant electron–proton nonadiabaticity, also denoted electronically nonadiabatic proton transfer, the vibronic coupling has the following form:12,13

graphic file with name jz-2014-01655v_m002.jpg 2

where Vel is the electronic coupling between the two diabatic electronic states22 and Sμν is the overlap integral between the proton vibrational wavefunctions calculated for the reactant and product diabatic potentials. In the opposite, electronically adiabatic regime, the vibronic coupling is half of the tunneling splitting associated with the ground electronic state13 and can be approximated by semiclassical expressions given elsewhere.23

Previously we devised several diagnostics for determining the degree of electron–proton nonadiabaticity.13−15 The first diagnostic relies on the semiclassical formulation of Georgievskii and Stuchebrukhov.16 In this formulation, an adiabaticity parameter is defined as

graphic file with name jz-2014-01655v_m003.jpg 3

where τp = Vel/|ΔF|νt is interpreted as the effective proton tunneling time and τe = ℏ/Vel is interpreted as the effective electronic transition time. In these expressions, |ΔF| is the difference between the slopes of the diabatic proton potential energy curves at the crossing point, and νt = [2(Vc – E)/mp]1/2, where mp is the proton mass, Vc is the energy at which the potential energy curves cross, and E is the tunneling energy (i.e., the energy of the degenerate proton vibrational levels in the reactant and product potential wells). In the electronically adiabatic limit, p ≫ 1, and the vibronic coupling is half of the tunneling splitting associated with the ground electronic state. In the electronically nonadiabatic limit, p ≪ 1, and the vibronic coupling is given by eq 2. Note that this nonadiabaticity parameter is identical to that defined in the Landau–Zener model.24 From a physical perspective, the electronically adiabatic and nonadiabatic limits can be understood in terms of the two effective time scales. In the electronically adiabatic limit, τe ≪ τp, and the electrons move fast enough to respond instantaneously to the proton motion; therefore, the proton remains on the ground electronic state. In the electronically nonadiabatic limit, τe ≫ τp, and the electrons are unable to rearrange quickly enough for the proton to remain on the ground electronic state.

The second diagnostic for determining the degree of electron–proton nonadiabaticity relies on the calculation of the nonadiabatic coupling between the lowest two adiabatic electronic states along the proton coordinate.14,15 This nonadiabatic coupling is given by

graphic file with name jz-2014-01655v_m004.jpg 4

where Ψ1el(re;rp) and Ψ2(re;rp) are the ground and first excited adiabatic electronic state wavefunctions, respectively, along the proton coordinate rp. Note that this coupling is scalar because it is calculated with respect to a one-dimensional proton coordinate, which is typically chosen to be along the proton donor–acceptor axis. The magnitude of this coupling can be compared to that for other systems known to be in the electronically adiabatic or nonadiabatic limit.14,15 From a physical perspective, the nonadiabatic coupling is greater for systems in which the electronic wavefunction changes significantly along the proton coordinate. Thus, this parameter can also be probed by analyzing the changes in the electronic charge distribution along the proton coordinate, as reflected by the dipole moment, partial charges, and electrostatic potentials along the proton coordinate. The degree of electron–proton nonadiabaticity is greater for systems that exhibit a significant and abrupt change in the electronic charge distribution along the proton coordinate.

This interpretation has led to the association of the electronically adiabatic and nonadiabatic limits of proton transfer with the hydrogen atom transfer (HAT) and electron–proton transfer (EPT) mechanisms, respectively.13−15 In the literature, typically HAT denotes reactions in which the electron and proton transfer between the same donor and acceptor, while EPT denotes reactions in which the electron and proton transfer between different donors and acceptors.2,25 Thus, HAT is associated with a virtually neutral hydrogen atom moving a relatively short distance and does not involve much electronic charge redistribution. In contrast, EPT is associated with a significant amount of electronic charge redistribution because the electron and proton travel different distances over distinct paths and, in some cases, move in different directions. Although this terminology is not rigorous, it is useful to differentiate between HAT and EPT processes in order to understand the fundamental nature of the reaction and to identify the appropriate rate constant expression. According to this interpretation,13−15 HAT reactions are electronically adiabatic, while EPT reactions are electronically nonadiabatic, thereby requiring different forms of the vibronic coupling in the rate constant expressions.

Previously we applied these diagnostics13−15 to the self-exchange reactions in the phenoxyl/phenol and benzyl/toluene systems.25,26 We used the complete active space self-consistent-field (CASSCF) method to calculate the ground and first excited electronic states along the proton coordinate and implemented a diabatization procedure14,15 to calculate the reactant and product diabatic electronic states. Within the semiclassical formalism, we determined that τp ≈ 4τe for the benzyl/toluene system and τp ≈ τe/80 for the phenoxyl/phenol system. Within the wavefunction-based formalism, we determined that the nonadiabatic coupling given in eq 4 is substantial for the phenoxyl/phenol system but is negligible for the benzyl/toluene system as the proton moves along the donor–acceptor axis. Similarly, the electronic charge distribution changes significantly along the proton coordinate for the phenoxyl/phenol system but not for the benzyl/toluene system. All of these diagnostics support the characterization of the phenoxyl/phenol system as electronically nonadiabatic and the benzyl/toluene system as electronically adiabatic proton transfer. Further support for this characterization was obtained by calculating the vibronic couplings with the expressions valid in the adiabatic and nonadiabatic limits, as well as with the full quantum mechanical and semiclassical expressions, and comparing the expressions for the specific limits to the general expressions. This comparison confirmed that only the phenoxyl/phenol system exhibits significant electron–proton nonadiabaticity. On the basis of these vibronic couplings, however, both systems were found to be vibronically nonadiabatic because Vμν ≪ kBT at room temperature.

In the application of these diagnostics to SLO, we utilized the CDFT-CI approach17−19 implemented in Q-Chem27 to obtain the diabatic electronic states. To select an appropriate functional for this purpose, we applied the CDFT-CI method to the phenoxyl/phenol system and compared the diabatic and adiabatic states, as well as the electronic couplings and semiclassical parameters, to the CASSCF results for a range of density functionals. These benchmarking calculations are provided in the Supporting Information. To summarize, we found that a long-range corrected functional is required to obtain reasonable agreement with the CASSCF results, and the ωB97X functional28 led to the best agreement. We also found that the adiabatic ground state obtained with the CDFT-CI method agrees well with that obtained from a ground state DFT/ωB97X calculation everywhere except in the crossing region.

On the basis of these benchmarking calculations, we applied the CDFT-CI/ωB97X method to the SLO model system depicted in Figure 1. This small model system is sufficient for characterizing this reaction in terms of the electron–proton and vibronic nonadiabaticity but is not expected to provide quantitatively accurate couplings. Future studies will utilize mixed quantum mechanical/molecular mechanical methods to include the protein environment. We performed calculations on this model system for a number of different geometries and found that the qualitative characterization does not depend strongly on the geometry. Here we present the results for the transition state (TS) geometry obtained with DFT/B3LYP/6-31G**. The C–O distance is 2.61 Å at this geometry. Given that the restraints imposed by the protein are unlikely to allow this distance to become so short, we also present results for geometries in which the C–O distance was increased to 2.7 and 2.8 Å by translating the linoleic acid substrate and Fe-cofactor fragments as rigid molecules along the donor–acceptor axis. The results for the TS geometry obtained with DFT/ωB97X/6-31G**, which has an even shorter C–O distance, are qualitatively similar and are given in Table S2 of the Supporting Information.

Figure 1.

Figure 1

Open in a new tab

SLO model system used in this study. The topology with the substrate and cofactor indicated in green and magenta, respectively, is shown on the left. The TS geometry obtained at the DFT/B3LYP/6-31G** level, with the transferring hydrogen indicated in yellow, is shown on the right.

For each geometry, the energy profiles along the transferring proton coordinate were calculated for a series of structures by placing the hydrogen at grid points along the C–O axis while keeping all other atoms fixed. The calculations were performed for ∼21 equally spaced grid points along the proton coordinate spanning the range from −0.5 to +0.5 Å relative to the midpoint on the proton donor–acceptor axis. The reactant and product diabatic states in the CDFT-CI calculations were defined by constraining the spin densities via Becke populations on the linoleic acid substrate and Fe-cofactor fragments. In the reactant state, the spin density on the substrate was constrained to zero (S = 0), and the spin density on the Fe(III)-cofactor was constrained to five (S = 5/2). In the product state, the spin density on the linoleic acid radical was constrained to one (S = 1/2), and the spin density on the reduced Fe(II)-cofactor was constrained to four (S = 2). The electronic coupling between the diabatic reactant and product states was calculated according to the prescription given in ref (18).

Figure 2 depicts the diabatic electronic states for this model system. We utilized these diabatic electronic states to calculate the effective time scales and the adiabaticity parameter within the semiclassical formalism described above. The results are given in Table 1 for three different C–O distances. In PCET theory,3,12 the vibronic coupling is calculated at the intersection of the reactant and product electron–proton vibronic states along a collective protein/solvent coordinate. This intersection corresponds to the degeneracy of the electron–proton vibronic states in our model calculations. Thus, for the calculation of the semiclassical parameters, the diabatic potentials were shifted so that the ground reactant and product proton vibrational states were degenerate (Figure 2).

Figure 2.

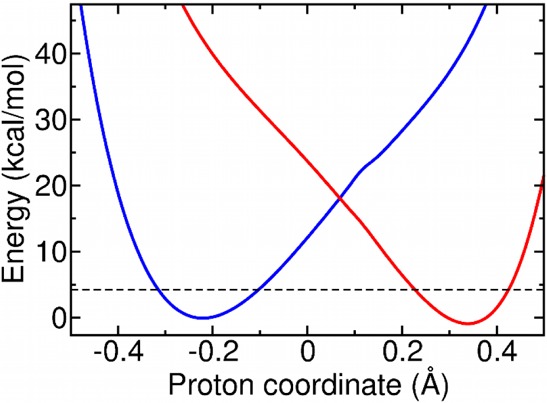
Figure 2

Open in a new tab

Diabatic electronic states obtained with CDFT-CI/ωB97X/6-31G** at the TS geometry for the SLO model system depicted in Figure 1. The diabatic states have been shifted so that the ground proton vibrational energy levels (indicated by the dashed black line) are degenerate. The original diabatic electronic states prior to this shifting, as well as the adiabatic electronic states, are provided in Figure S4 of the Supporting Information.

Table 1. Nonadiabaticity Parameters for the SLO Model Systema.

geometry Vel, cm–1 τp, fs τe, fs p = τp/τe V00, cm–1
TS, R = 2.61 Åb 1637 0.25 3.24 7.8 × 10–2 13.5
R = 2.7 Åc 1607 0.22 3.30 6.6 × 10–2 1.8
R = 2.8 Åc 1575 0.20 3.37 5.9 × 10–2 0.2
Open in a new tab
a

Vel is the electronic coupling at the crossing point calculated with CDFT-CI/ωB97X/6-31G**; τp and τe are the effective proton tunneling and electronic transition times; p is the adiabaticity parameter defined in eq 3; V00 is the vibronic coupling between the ground reactant and product vibronic states defined in eq 2.

b

Transition state (TS) geometry obtained at the DFT/B3LYP/6-31G** level.

c

Geometries obtained from the TS geometry by rigid translation of the substrate and Fe-cofactor along the C–O axis to the C–O distance R.

The electronic and vibronic couplings, as well as the semiclassical parameters, are given in Table 1. For all geometries studied, the semiclassical parameters indicate significant electron–proton nonadiabaticity in the PCET reaction catalyzed by SLO because τe ≫ τp and p ≪ 1. Moreover, the vibronic couplings calculated with eq 2 indicate that the SLO reaction is also vibronically nonadiabatic at room temperature because Vμν ≪ kBT. Although the electronic coupling is greater than the thermal energy (Vel ≫ kBT), this relation is not relevant to the degree of electron–proton nonadiabaticity, which depends on the adiabaticity parameter given in eq 3, nor is it relevant to the degree of vibronic nonadiabaticity, which depends on the overall vibronic coupling rather than the electronic coupling. Similar results were found for a different geometry and with the ωB97X-D functional, as shown in Table S2 of the Supporting Information. Overall, SLO exhibits significant vibronic nonadiabaticity and electron–proton nonadiabaticity, supporting the use of eq 1 with the form of the vibronic coupling given in eq 2.

We also confirmed the results from this semiclassical analysis with an analysis of the electronic charge density distribution. Although we were unable to calculate the nonadiabatic coupling given in eq 4 directly with CDFT-CI due to the lack of well-defined wavefunctions, we analyzed the electronic charge distribution for the adiabatic ground state along the proton coordinate. Figure 3 depicts the spin populations and the dipole moment along the proton coordinate obtained from ground state DFT/ωB97X/6-31G** calculations. The change in dipole moment illustrated in Figure 3 is qualitatively similar to that observed previously for the phenoxyl/phenol system,14 which was determined to be electronically nonadiabatic with an EPT mechanism. For the SLO model, the charge distribution changes because the electron effectively transfers between the π backbone of the linoleic acid substrate and the Fe center of the cofactor, and the proton transfers between the carbon of the linoleic acid and the OH ligand of the cofactor.6 Figure S5 (Supporting Information) illustrates that unpaired spin density is delocalized along the π backbone for the product diabatic state and is localized near the iron atom for both diabatic states. Because the electron and proton transfer between different donors and acceptors along distinct pathways, they travel different distances (i.e., the electron travels further than the proton), leading to a change in the electronic charge distribution. Thus, according to the definitions given above, the SLO reaction corresponds to an EPT mechanism rather than a HAT mechanism.

Figure 3.

Figure 3

Open in a new tab

Spin populations and dipole moment for the ground adiabatic electronic state along the proton coordinate obtained with ground state DFT/ωB97X/6-31G** at the TS geometry for the SLO model system depicted in Figure 1. (a) The spin populations are shown in green and magenta for the substrate and cofactor indicated with these colors in Figure 1, and the dashed black line indicates the spin population on the transferring hydrogen nucleus. (b) The dipole moment was calculated with the origin at the midpoint of the C–O axis, where the solid line indicates the magnitude of the total dipole moment vector and the dotted line indicates its projection onto the axis connecting the donor carbon and the Fe.

To summarize, we used both semiclassical and electronic charge density diagnostics to illustrate electron–proton nonadiabaticity and vibronic nonadiabaticity in the PCET reaction catalyzed by SLO. The vibronic nonadiabaticity supports the use of the Golden rule rate constant expression, and the electron–proton nonadiabaticity supports the form of the vibronic coupling as the product of the electronic coupling and the overlap of the reactant and product proton vibrational wavefunctions. The nonadiabatic rate constant expression in this regime has been used to model the magnitudes and temperature dependences of the rate constants and KIEs for wild-type and mutant SLO.7,9−11,29 These previous calculations provided explanations for the experimentally observed impact of mutating a distal residue I553 to a series of less bulky residues10,29 and, more recently, for the experimentally observed elevated KIE of ∼700 for the L546A/L754A double mutant of SLO.11 The approaches presented in this Letter are applicable to a wide range of systems and can be used to identify the PCET rate constant expression that will enable reliable and physically meaningful modeling of experimental results.

Acknowledgments

This work was funded by NIH Grant GM056207.

Supporting Information Available

Results of the benchmarking CDFT-CI calculations for the phenoxyl/phenol system; results of additional CDFT-CI calculations for the SLO model system; spin densities for diabatic states; Cartesian coordinates for the TS geometries used in calculations. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States

Supplementary Material

jz501655v_si_001.pdf (457.3KB, pdf)

References

  1. Cukier R. I.; Nocera D. G. Proton-Coupled Electron Transfer. Annu. Rev. Phys. Chem. 1998, 49, 337–369. [DOI] [PubMed] [Google Scholar]
  2. Huynh M. H. V.; Meyer T. J. Proton-Coupled Electron Transfer. Chem. Rev. 2007, 107, 5004–5064. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Hammes-Schiffer S.; Stuchebrukhov A. A. Theory of Coupled Electron and Proton Transfer Reactions. Chem. Rev. 2010, 110, 6939–6960. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Kuznetsov A. M.; Ulstrup J. Proton and Hydrogen Atom Tunnelling in Hydrolytic and Redox Enzyme Catalysis. Can. J. Chem. 1999, 77, 1085–1096. [Google Scholar]
  5. Knapp M. J.; Rickert K. W.; Klinman J. P. Temperature Dependent Isotope Effects in Soybean Lipoxygenase-1: Correlating Hydrogen Tunneling with Protein Dynamics. J. Am. Chem. Soc. 2002, 124, 3865–3874. [DOI] [PubMed] [Google Scholar]
  6. Lehnert N.; Solomon E. I. Density-Functional Investigation on the Mechanism of H-Atom Abstraction by Lipoxygenase. J. Biol. Inorg. Chem. 2003, 8, 294–305. [DOI] [PubMed] [Google Scholar]
  7. Hatcher E.; Soudackov A. V.; Hammes-Schiffer S. Proton-Coupled Electron Transfer in Soybean Lipoxygenase. J. Am. Chem. Soc. 2004, 126, 5763–5775. [DOI] [PubMed] [Google Scholar]
  8. Olsson M. H. M.; Siegbahn P. E. M.; Warshel A. Simulations of the Large Kinetic Isotope Effect and the Temperature Dependence of the Hydrogen Atom Transfer in Lipoxygenase. J. Am. Chem. Soc. 2004, 126, 2820–2828. [DOI] [PubMed] [Google Scholar]
  9. Hatcher E.; Soudackov A. V.; Hammes-Schiffer S. Proton-Coupled Electron Transfer in Soybean Lipoxygenase: Dynamical Behavior and Temperature Dependence of Kinetic Isotope Effects. J. Am. Chem. Soc. 2007, 129, 187–196. [DOI] [PubMed] [Google Scholar]
  10. Meyer M. P.; Tomchick D. R.; Klinman J. P. Enzyme Structure and Dynamics Affect Hydrogen Tunneling: The Impact of a Remote Side Chain (I553) in Soybean Lipoxygenase-1. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 1146–1151. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hu S.; Sharma S. C.; Scouras A. D.; Soudackov A. V.; Carr C. A. M.; Hammes-Schiffer S.; Alber T.; Klinman J. P. Extremely Elevated Room-Temperature Kinetic Isotope Effects Quantify the Critical Role of Barrier Width in Enzymatic C–H Activation. J. Am. Chem. Soc. 2014, 136, 8157–8160. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hammes-Schiffer S.; Soudackov A. V. Proton-Coupled Electron Transfer in Solution, Proteins, and Electrochemistry. J. Phys. Chem. B 2008, 112, 14108–14123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Skone J. H.; Soudackov A. V.; Hammes-Schiffer S. Calculation of Vibronic Couplings for Phenoxyl/Phenol and Benzyl/Toluene Self-Exchange Reactions: Implications for Proton-Coupled Electron Transfer Mechanisms. J. Am. Chem. Soc. 2006, 128, 16655–16663. [DOI] [PubMed] [Google Scholar]
  14. Sirjoosingh A.; Hammes-Schiffer S. Proton-Coupled Electron Transfer versus Hydrogen Atom Transfer: Generation of Charge-Localized Diabatic States. J. Phys. Chem. A 2011, 115, 2367–2377. [DOI] [PubMed] [Google Scholar]
  15. Sirjoosingh A.; Hammes-Schiffer S. Diabatization Schemes for Generating Charge-Localized Electron-Proton Vibronic States in Proton-Coupled Electron Transfer Systems. J. Chem. Theory Comput. 2011, 7, 2831–2841. [DOI] [PubMed] [Google Scholar]
  16. Georgievskii Y.; Stuchebrukhov A. A. Concerted Electron and Proton Transfer: Transition from Nonadiabatic to Adiabatic Proton Tunneling. J. Chem. Phys. 2000, 113, 10438–10450. [Google Scholar]
  17. Wu Q.; Van Voorhis T. Constrained Density Functional Theory and Its Application in Long-Range Electron Transfer. J. Chem. Theory Comput. 2006, 2, 765–774. [DOI] [PubMed] [Google Scholar]
  18. Wu Q.; Van Voorhis T. Direct Calculation of Electron Transfer Parameters through Constrained Density Functional Theory. J. Phys. Chem. A 2006, 110, 9212–9218. [DOI] [PubMed] [Google Scholar]
  19. Wu Q.; Cheng C.-L.; Van Voorhis T. Configuration Interaction Based on Constrained Density Functional Theory: A Multireference Method. J. Chem. Phys. 2007, 127, 164119. [DOI] [PubMed] [Google Scholar]
  20. Soudackov A.; Hatcher E.; Hammes-Schiffer S. Quantum and Dynamical Effects of Proton Donor–Acceptor Vibrational Motion in Nonadiabatic Proton-Coupled Electron Transfer Reactions. J. Chem. Phys. 2005, 122, 014505. [DOI] [PubMed] [Google Scholar]
  21. Barzykin A. V.; Frantsuzov P. A.; Seki K.; Tachiya M. Solvent Effects in Nonadiabatic Electron-Transfer Reactions: Theoretical Aspects. Adv. Chem. Phys. 2002, 123, 511–616. [Google Scholar]
  22. Cave R. J.; Newton M. D. Generalization of the Mulliken–Hush Treatment for the Calculation of Electron Transfer Matrix Elements. Chem. Phys. Lett. 1996, 249, 15–19. [Google Scholar]
  23. Kiefer P. M.; Hynes J. T. Kinetic Isotope Effects for Nonadiabatic Proton Transfer Reactions in a Polar Environment. 1. Interpretation of Tunneling Kinetic Isotope Effects. J. Phys. Chem. A 2004, 108, 11793–11808. [Google Scholar]
  24. Zener C. Non-Adiabatic Crossing of Energy Levels. Proc. R. Soc. London, Ser. A 1932, 137, 696–702. [Google Scholar]
  25. Mayer J. M.; Hrovat D. A.; Thomas J. L.; Borden W. T. Proton-Coupled Electron Transfer versus Hydrogen Atom Transfer in Benzyl/Toluene, Methoxyl/Methanol, and Phenoxyl/Phenol Self-Exchange Reactions. J. Am. Chem. Soc. 2002, 124, 11142–11147. [DOI] [PubMed] [Google Scholar]
  26. DiLabio G. A.; Johnson E. R. Lone Pair−π and π–π Interactions Play an Important Role in Proton-Coupled Electron Transfer Reactions. J. Am. Chem. Soc. 2007, 129, 6199–6203. [DOI] [PubMed] [Google Scholar]
  27. Shao Y.; Molnar L. F.; Jung Y.; Kussmann J.; Ochsenfeld C.; Brown S. T.; Gilbert A. T. B.; Slipchenko L. V.; Levchenko S. V.; O’Neill D. P.; et al. Advances in Methods and Algorithms in a Modern Quantum Chemistry Program Package. Phys. Chem. Chem. Phys. 2006, 8, 3172–3191. [DOI] [PubMed] [Google Scholar]
  28. Chai J. D.; Head-Gordon M. Systematic Optimization of Long-Range Corrected Hybrid Density Functionals. J. Chem. Phys. 2008, 128, 084106. [DOI] [PubMed] [Google Scholar]
  29. Edwards S. J.; Soudackov A. V.; Hammes-Schiffer S. Impact of Distal Mutation on Hydrogen Transfer Interface and Substrate Conformation in Soybean Lipoxygenase. J. Phys. Chem. B 2010, 114, 6653–6660. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz501655v_si_001.pdf (457.3KB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES