Incorporating spatial variability within epidemiological studies of environmental exposures

Abstract

Recently there has been great interest in modelling the association between aggregate disease counts and environmental exposures measured at point locations, for example via air pollution monitors. In such cases, the standard approach is to average the observed measurements from the individual monitors and use this in a log-linear health model. Hence such studies are ecological in nature being based on spatially aggregated health and exposure data. Here we investigate the potential for biases in the estimates of the effects on health in such settings. Such ecological bias may occur if a simple summary measure, such as a daily mean, is not a suitable summary of a spatially variable pollution surface. We assess the performance of commonly used models when confronted with such issues using simulation studies and compare their performance with a model specifically designed to acknowledge the effects of exposure aggregation. In addition to simulation studies, we apply the models to a case study of the short–term effects of particulate matter on respiratory mortality using data from Greater London for the period 2002–2005.

1. Introduction

The relationship between air pollution exposure and ill health came to public prominence in the mid 1900’s, as a result of high air pollution episodes in both Europe (Firket, 1936) and America (Ciocco and Thompson, 1961). Since then a large number of epidemiological studies have consistently reported associations between a variety of pollutants at comparatively low levels and health effects, including particulate matter (Laden et al., 2000), sulphur dioxide (Schwartz, 1991), nitrogen dioxide (Zmirou et al., 1998), carbon monoxide (Conceicao et al., 2001) and ozone (Verhoeff et al., 1996). Associations have also been shown within different sub-groups of the population, such as the elderly (Dominici et al., 2000) and children (Lin et al., 2002) for a range of health outcomes, such as asthma (Yu et al., 2000) and respiratory and circulatory illnesses (Gwynn et al., 2000). Recently, large scale studies have investigated health effects in a large number of cities following to a common protocol, such as the NMMAPS studies in the U.S. (Dominici et al., 2002) and the APHEA and APHEA II studies in Europe (Katsouyanni et al., 1997, 2001).

Whilst a number of studies have examined the longer–term effects of air pollution, the vast majority have investigated associations between short-term changes in air pollution and health. These studies relate changes in exposure with subsequent changes in a specified health outcome using daily health counts and measurements of exposure, the latter often coming from a number of monitoring sites located within an urban area. The majority of studies have estimated pollution exposure on a particular day by averaging the spatial observations, either because of lack of access to the raw data or due to the simplicity of the approach. A few studies have incorporated spatial modelling within health studies, see for example Zidek et al. (1998), Zhu et al. (2003), Fuentes et al. (2006) and Lee and Shaddick (2010), primarily because the health and exposure data were recorded at different geographical locations or scales, an issue termed the ‘change of support problem’ by Gelfand et al. (2001). In addition, routinely available covariate information, such as temperature and humidity, is used. Less easily obtainable information on variables that might be expected to have a relationship with pollution (and health), such as traffic density, are often represented by surrogate variables. For example, ‘day of the week’ effects are often used in place of traffic density based on the logical assumptions that there will be less traffic at weekends in urban areas.

These studies are ecological in nature, being based on spatially aggregated health and exposure data modelled at the same resolution. As such, there is the potential for ecological bias; assuming that associations observed at the level of the area hold for the individuals within the areas can lead to the so-called ecological fallacy. Ecological bias can manifest itself in a variety of ways. For a review of the problems of ecological bias and possible approaches for corrections, see Wakefield (2008).

In this paper we investigate the possibility of ecological bias being induced by aggregation within short-term epidemiological studies. Results of using the standard ecological model are compared with those from models which acknowledge such bias. The remainder of this paper is organised as follows. Section 2 describes the ‘standard’ modelling approach used in time–series air pollution and health studies. Section 3 describes the true underlying model at the individual level but for which data are unlikely to be available and compares its aggregated form with the ‘standard’ Poisson or quasi-likelihood model. This section also describes alternative modelling approaches that may alleviate such problems. Section 4 presents a simulation study that assesses the biases that may arise from using the different modelling approaches. Section 5 provides a case study comprising of an epidemiological case study investigating the association between respiratory mortality and particulate matter concentrations in Greater London for the period 2002–2005. Finally, section 6 provides a concluding discussion.

2. Time series studies of air pollution and health

The majority of short-term air pollution and mortality studies are based on an ecological time series design, that use mortality, pollution and meteorological data that relate to a geographical region 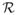(such as a city or extended urban area) for n consecutive days. Only daily counts of mortality or morbidity events from the population living within the study region are available, and are denoted here by y = (y₁, …, y_n). These data are regressed against ambient (background) air pollution concentrations and a vector of q covariates, the latter of which are denoted by the n × q matrix $Z={({\mathbf{z}}_1^{\mathrm{T}},\dots ,{\mathbf{z}}_n^{\mathrm{T}})}^{\mathrm{T}}$ where ${\mathbf{z}}_t^{\mathrm{T}}=(z_{t1},\dots ,z_{tq})$ representing the realisations for day t. The covariates remove the influence of unmeasured risk factors that induce long-term trends, seasonal variation, over-dispersion and temporal correlation into the daily health counts. The influence of such factors are typically modelled by smooth functions of time (i.e. day of the study) and meteorological covariates, as well as indicator variables for ‘day of the week’ effects and influenza epidemics.

The pollution data are obtained from k fixed site monitors located across 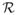and measure ambient pollution concentrations continuously throughout the day. A daily average is typically calculated at each monitoring location, which for day t and spatial location s_l is denoted by w_t(s_l). The set of pollution locations are collectively denoted by 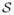= {s₁, …, s_k} (where s_l = (a_l, b_l) ∈ 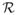), and for day t the pollution levels are summarised by the k × 1 vector w_t( 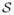) = (w_t(s₁), …, w_t(s_k))^T. The pollution data for all n days are collected into an n × k matrix W( 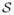) = (w₁( 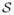)^T, …, w_n( 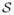)^T)^T, which is likely to contain a small proportion (typically less than 10%) of missing values. From these data the vector of daily pollution exposures are almost exclusively estimated by w = (w₁, …, w_n), where

$$w_t\frac{1}{k}\sum _{l=1}^k{w}_t({\mathbf{s}}_l)\text{for}t=1,\dots ,n,$$ (1)

the average value across the k monitors on day t (missing values are typically ignored).

The relationship between (y, w, Z) is estimated using quasi-Poisson log–linear or additive models, in which only the mean and variance of y_t are specified using a quasi-likelihood approach. The moments resemble those from a Poisson distribution, except that the variance is allowed to be a multiple of the mean. The quasi-Poisson model has expectaton 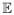[y_t|w̃_t, z_t] = μ_t and variance Var[y_t|w̃_t, z_t] = κμ_t, where κ is the over-dispersion parameter. In addition the vector y₁, …, y_n are assumed to be independent, which may not be true as the number of events on successive days are likely to be correlated. Pollution concentrations at a single or multiple lags can be included into the model, with the specification above incorporating exposures w̃_t = (w_t, w_t−1, …, w_t−l) from the same day up to a maximum lag of l days, where l will typically range from between zero and five (Dominici et al., 2000). The mean log–linear function is given by

$${\mu }_t=exp\left({\alpha }_0+\sum _{j=1}^p{z}_{tj}{\alpha }_j^E+\sum _{j=p+1}^{q}f(z_{tj}\mid {\alpha }_j^E)\right)exp\left({\stackrel{\sim }{\mathbf{w}}}_t^{\mathrm{T}}{\mathit{\beta }}^E\right).$$ (2)

allowing the covariates to have have log–linear (e.g. z_tjα_j) or log non-linear (e.g. f(z_tj|α_j)) relationships with the health data.

A commonly used outcome measure in epidemiology is the Relative risk (RR), which is the rate of risks of an event (or of developing a disease) with the denominator typically a baseline level of exposure. From the above model, the estimate of β^E gives us the relationship between pollution and health and the relative risk is RR = exp(β^E) with interest lying primarily in whether this is significantly greater than one.

3. Statistical modelling

The ‘standard’ ecological model described by (1) and (2) may be defficient in a number of ways, and here we focus on two, (i) the form of the mean function; and (ii) the exposure measure. To illustrate these defficiencies we begin by describing the desired individual level model, and then aggregate it to the ecological level.

3.1. Individual level model

The desired individual level model is based on data (y_it, x_it, z_it) for the entire population of i = 1, …, N individuals living in the study region 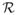over all t = 1, … n days of the study. Here y_it is the Bernoulli indicator variable equalling one if individual i has a mortality or morbidity event on day t and zero otherwise, while x_it is the ambient pollution concentration individual i is exposed to on day t. Finally z_it = (z_it1, …, z_itq) are a vector of q individual level covariates, that would include confounding factors such as age, sex, previous illness, etc. If these data were available they could be modelled by

$$\begin{array}{l}{y}_{it}\mid x_{it},{\mathbf{z}}_{it}~\text{Bernoulli}(p_{it})\text{for}i=1,\dots ,Nt=1,\dots ,n,\\ p_{it}=exp\left({\alpha }_0+\sum _{j=1}^p{z}_{\mathit{itj}}{\alpha }_j+\sum _{j=p+1}^{q}f(z_{\mathit{itj}}\mid {\alpha }_j)\right)exp\left({\stackrel{\sim }{\mathbf{x}}}_{it}^{\mathrm{T}}{\beta }^I\right),\end{array}$$ (3)

The log-linear model is appropriate for a rare outcome and could be replaced by a logistic model for a non-rare outcome. The vector of lagged individual exposures is given by x̃_it = (x_it, x_it−1, …, x_it−l), while ${\mathit{\beta }}^I=({\beta }_1^I,\dots ,{\beta }_k^I)$ are the associated individual level effects. Note that β^I is different from the corresponding ecological parameters β^E, which represent the ecological association with health rather than individual level effect.

However, the data to fit model (3) are very unlikely to be available, and instead routinely collected daily totals of health events $y_t={\sum }_{i=1}^N{y}_{it}$ and summary measures of pollution concentrations on each day x_t are used. Similarly, individual covariate risk factors such as age, sex, etc are unlikely to be available, however their influence might be expected to be limited as the distribution of these characteristics over the population are unlikely to change from day to day. Instead ecological covariates as described in Section 2, that apply to the overall population rather than to individuals, are used. Therefore the desired ecological analysis is obtained by aggregating (3) to a level at which data is available, giving a model for y_t|x̃_t, z_t.

In general, the distribution of y_t|x̃_t, z_t has no closed form expression, because the individual level risk p_it is non-constant over all N individuals, but in the case of a rare events, as is likely in the majority of the type of studies considered in this setting, each of the Bernoulli random variables may be approximated by a Poisson random variable, with a log-linear risk model as given in (3). In practice, the Poisson assumption of equality of mean and variance is often relaxed using quasi-likelihood as described in Section 2.

3.2. Mean function 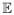[y_t|x̃_t, z_t]

The correct mean function for y_t|x̃_t, z_t is obtained by aggregating the individual level model (3), which leads to

$$\mathbb{E}[y_t\mid {\stackrel{\sim }{\mathbf{x}}}_t,{\mathbf{z}}_t]=exp\left({\alpha }_0+\sum _{j=1}^p{z}_{tj}{\alpha }_j+\sum _{j=p+1}^{q}f(z_{tj}\mid {\alpha }_j)\right){\mathbb{E}}_{{\stackrel{\sim }{\mathbf{X}}}_t\mid {\stackrel{\sim }{\mathbf{x}}}_t}\left[exp\left({\stackrel{\sim }{\mathbf{X}}}_t^{\mathrm{T}}{\mathit{\beta }}^I\right)\right],$$ (4)

where X̃_t = (X_t, X_t−1, …, X_t−l) is a vector of random variables representing the exposure distribution for days t to t − l. Here, for simplicity we have assumed that z_tj and X_tj are independent. Wakefield (2008) considers the more general case. This differs from the ‘standard’ specification (2) in the way that the exposure is incorporated, specifically the mean functions differ in that

$$exp\left({\stackrel{\sim }{\mathbf{w}}}_t^{\mathrm{T}}{\mathit{\beta }}^E\right)\ne {\mathbb{E}}_{{\stackrel{\sim }{\mathbf{X}}}_t\mid {\stackrel{\sim }{\mathbf{x}}}_t}\left[exp\left({\stackrel{\sim }{\mathbf{X}}}_t^{\mathrm{T}}{\mathit{\beta }}^I\right)\right],$$

Hence the correct approach is to calculate the average risk, rather than evaluating the risk at the average exposure. This difference, between β^E and β^I is known as pure specification bias, and occurs because a non-linear risk model changes its form under aggregation. Equality between (β^E, β^I) occurs if (i) the variance of X_t equals zero; (ii) the mean of X_t is independent of the higher moments, or (iii) the exponential risk function above is replaced by a linear alternative, none of which are likely in the type of studies under consideration here.

Two general approaches have been proposed to estimate ${\mathbb{E}}_{{\stackrel{\sim }{\mathbf{X}}}_t\mid {\stackrel{\sim }{\mathbf{x}}}_t}\left[exp\left({\stackrel{\sim }{\mathbf{X}}}_t^{\mathrm{T}}{\mathit{\beta }}^I\right)\right]$. The ‘aggregate’ approach was proposed by (Prentice and Sheppard, 1995) and requires that the available summary measure x̃_t is a sample of m exposures x̃_kt = (x_kt, x_kt−1, …, x_kt−l) for k = 1, …, m. The mean function is given by

$$\mathbb{E}[y_t\mid {\stackrel{\sim }{\mathbf{x}}}_t,{\mathbf{z}}_t]=exp\left({\alpha }_0+\sum _{j=1}^p{z}_{tj}{\alpha }_j+\sum _{j=p+1}^{q}f(z_{tj}\mid {\alpha }_j)\right)\frac{1}{m}\sum _{k=1}^{m}exp\left({\stackrel{\sim }{\mathbf{x}}}_{kt}^{\mathrm{T}}{\mathit{\beta }}^I\right),$$ (5)

which replaces ${\mathbb{E}}_{{\stackrel{\sim }{\mathbf{X}}}_t\mid {\stackrel{\sim }{\mathbf{x}}}_t}\left[exp\left({\stackrel{\sim }{\mathbf{X}}}_t^{\mathrm{T}}{\mathit{\beta }}^I\right)\right]$ with its sample analogue. The same mean function was used by Wakefield and Shaddick (2006) in assessing the possibility of ecological bias in geographical studies of air pollution. They refer to this implementation as a ‘convolution’ model, and that is the term we use here.

Richardson et al. (1987) and Wakefield and Salway (2001) model ecological bias parametrically by incorporating higher order moments (for example the variance) of the exposure distribution. This approach assumes the exposure distribution follows a parametric form. In this case, ${\mathbb{E}}_{{\stackrel{\sim }{\mathbf{X}}}_t\mid {\stackrel{\sim }{\mathbf{x}}}_t}\left[exp\left({\stackrel{\sim }{\mathbf{X}}}_t^{\mathrm{T}}{\mathit{\beta }}^I\right)\right]$ is the moment generating function of the multivariate exposure distribution of X̃_t|x̃_t. For example if X̃_t|x̃_t ~ N(x̄_t, Σ_t), where the summary measure x̃_t comprises the mean and variance of the distribution, then the mean function from (4) becomes

$$\mathbb{E}[y_t\mid {\stackrel{\sim }{\mathbf{x}}}_t,{\mathbf{z}}_t]=exp\left({\alpha }_0+\sum _{j=1}^p{z}_{tj}{\alpha }_j+\sum _{j=p+1}^{q}f(z_{tj}\mid {\alpha }_j)\right)exp\left({\stackrel{\sim }{\mathbf{x}}}^{\mathrm{T}}{\mathit{\beta }}^I+\frac{1}{2}{\mathit{\beta }}^{I^{\mathrm{T}}}{\mathrm{\sum }}_t{\mathit{\beta }}^I\right).$$ (6)

If the daily exposures do not follow a normal distribution equation (6) will be a second order approximation to the true model, which is likely to be adequate provided the distribution of X_t is not heavily skewed. Ott (1990) has shown that a log-normal distribution is appropriate for modelling exposures to pollution, because in addition to the desirable properties of right-skew and non-negativity, there is justification in terms of the physical explanation of atmospheric chemistry. However, under the log-normal assumption ecological bias cannot be modelled in this way because the moment-generating function does not exist. Salway and Wakefield (2008) suggest that if β^I is small (which is likely the case in studies of this type) a Taylor series expansion may be used.

3.3. Pollution exposure estimation

In previous sections, it has been assumed that the summary measure of pollution concentrations x̃_t is known, with the aggregate approach requiring m unbiased sample exposures, while the parametric normal alternative is based on the mean and variance of the exposure distribution (x̄_t, Σ_t). For example, the mean exposure on day t is given by

$$\mathbb{E}[X_t]={\overline{x}}_t={\int }_{\mathcal{R}}N(\mathbf{s})x_t(\mathbf{s})\mathbf{ds}$$ (7)

where x_t(s) is the ambient pollution concentration at location s on day t and N (s) is the population density such that ∫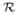 N(s)ds = 1.

However the required information to perform the integral will be unknown, and two general approaches have been adopted in the literature to estimating the required exposures. The simplest approach is to estimate the summary measure x̃_t directly from the ambient monitoring data, which is the approach used by the majority of studies. The most common approach being to estimate the mean exposure by the sample analogue (1).

The second approach is to represent the ambient pollution surface with a spatial or spatiotemporal model, and then to estmate the quantities of interest such as (7) using prediction methods. For example, Carlin et al. (1999) estimate average zip code ozone concentrations based on a Kriging procedure, while Gelfand et al. (2001) and Zhu et al. (2003) adopt a Bayesian approach for the same data set, sampling from a posterior predictive distribution. However in both cases the mean exposure (7) is estimated with the simplifying assumption that the population distribution is spatially constant, that is N(s) = 1/| 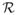|, and the ecological mean function (2) is adopted.

4. Simulation study

In this section we present a series of simulation studies in which we investigate the possible impacts of ecological bias in short-term air pollution and health studies. We compare results from the individual model with those from with ecological alternatives, including the ‘standard’ model (2) and the convolution model (5) which attempts to correct for the effects of ecological bias. Where possible, the parameters used in generating the simulated data are informed by the data used in the case study (Section 5).

4.1. Study region

The study region, 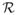, is a unit square 9 × 9 lattice comprising 81 spatial cells C_i, (i = 1, …, 81, each of which contains N_i individuals. Data are generated for this study region over t = 1, …, 730 consecutive days, and the spatial population distribution N₁, … N₈₁ are assumed to be constant over time and for simplicity we assume the population distribution is spatially uniform, that is N_i is constant for all spatial cells i. Each cell in the study region has a single pollution concentration on a given day, and in the first instance we assume there are 81 monitors, one located in each of the cells and that the entire population within a cell is located at the centre. Later, we consider the case where exposures are only available at a subset of the cells and exposures need to be estimated at the other locations.

4.2. Data generation

Logged values of the daily exposures, x_t, are generated from the following model;

$$log(x_{it})={\beta }_{0x}+m_i+w_t$$ (8)

where i = 1, …, 81 and t = 1, …, 730, giving two years of daily exposures at each of the 81 locations.

This comprises of three main components: (i) an intercept term reffecting the overall level of pollution; (ii) a temporal term and (iii) spatial term, m_i

The value used for the overall mean, β_0x = 3.4, is based on the (logged) pollution data. For the temporal component, w_t, the daily average of the measurements from the monitoring sites in Greater London (2002–2003) are used. For the spatial part of the model, m_i were generated from a Gaussian Random Field (GRF) with an exponential covariance structure, where the elements of the covariance matrix, Σ, are equal to ${\sigma }_s^{2}exp(-\phi d_{ij})$, σ² is the overall spatial variance, φ gives the strength of the distance–correlation relationship and d_ij is the distance between locations s_i and s_j. Different combinations of the two parameters are considered, using values of φ = 0.1, 1, 10 and ${\sigma }_s^2=0.001$, 0.019, 0.1 and 0.2, with the second of these reffecting the magnitude of the spatial variation observed in the Greater London data.

After generating exposures on the log scale, the exponentials, z_it = exp(x_it), of these values are used to generate daily health counts at each of the locations;

$$\begin{array}{l}{Y}_{it}~\text{Poisson}({\mu }_{it})\\ log({\mu }_t)={\beta }_{0y}=f(t,df)+f({\mathit{temp}}_t,df)+{\beta }_1{Z}_{it}\end{array}$$ (9)

where β_0y is the overall mean of the health counts, taking the value log(21/81) (again based on the real data) and f(t, df) is a function reffecting the underlying temporal pattern in the health data which here is modelled using basis functions resulting in natural splines based on patterns in the real pollution data. Similarly, the effect of temperature, g(temp_t, df), is based on that seen in the real data. The choice of degrees of freedom for the splines was made according to that which minimised the Bayesian Information Criteria (BIC) (see Section 5.2 for further details) which resulted in a choice of 8 df for time and 3 df for temperature.

Two different values for the relative risk, exp(β₁), were used; 1.02 and 2. The first of these reffects the magnitude of the risks commonly observed in studies of this type for a change of 10 units of pollution and the latter, whilst less realistic, is chosen in order to make possible biases easier to identify.

4.3. Analysis

Each of the simulated datasets were analysed using three models: (i) individual; (ii) ecological and (iii) convolution for both known and unknown exposures. In the case of the latter, exposures at each area i are predicted using spatial models based on exposures measured at a subset of the locations.

To summarise, the following mean functions were used for the three models under consideration;

1. I (individual) model:

   $$log({\mu }_{it})=exp({\beta }_{0y}+\sum _{j=1}^p{z}_j{\alpha }_j)exp({\beta }_1{x}_{it})$$

   where x_it is the true exposures for area i at time t and ${\sum }_{j=1}^p{z}_j{\alpha }_j$ represents the natural splines for underlying temporal patterns and the effect if temperature.

2. E (ecological) model:

   $$log({\mu }_t)=exp({\beta }_{0y}+\sum _{j=1}^p{z}_j{\alpha }_j)exp({\beta }_1{\overline{x}}_t)$$

   where x̄ is the daily average (calculated over all locations) of the true exposures from each of the sub-areas $\overline{x}=\frac{1}{N}{\sum }_{i=1}^N{x}_{it}$.

3. C (convolution) model:

   $$log({\mu }_t)=exp({\beta }_{0y}+\sum _{j=1}^p{z}_j{\alpha }_j)exp(\sum _{i=1}^N{\beta }_1{x}_{it})$$

   where x_it is the true exposures for area i at time t (as in the individual model)

   For the individual and ecological models, inference can be carried out via quasi-likelihood. The convolution model is not a GLM since we do not have a linear predictor, but estimation of the parameters may be carried out using non-linear optimisation, such as the Nelder and Mead method.

For unknown exposures

Three different sets of locations were used, comprising 9, 25 and 81 sites (out of the 81 locations). In each case the set of associated measurements at those locations was used to estimate the exposures at each of the locations by fitting an exponential covariance model, with the parameters being estimated from the data. Predictions at each of the 81 locations were then obtained using kriging. The resulting predictions, x̄_it, are then used in the above three models in place of the known exposures, x_it.

4.4. Results

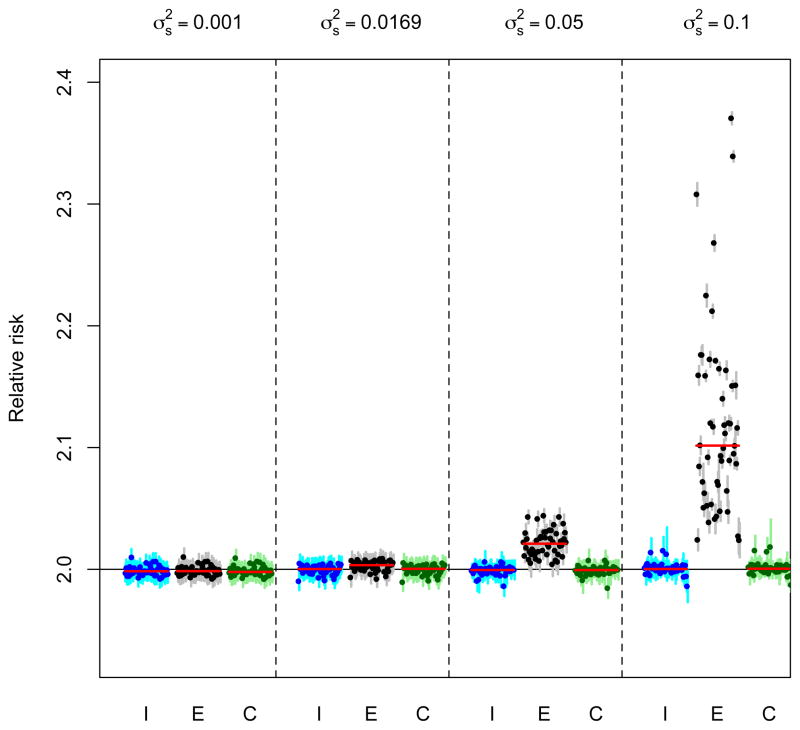
We first consider the case of known exposures for which the results of fitting different levels of spatial variation and distance–correlation relationships with different relative risks can be seen in Figure 1 for the case of φ = 1 and σ² = 0.2 with a true RR of 2. The median relative risk from the 50 simulations is indicated by the horizontal red lines with the dots showing the estimates from the individual simulations together with associated 95% confidence intervals (vertical lines). It can be seen that for the lower levels of spatial variability, all three models accurately estimate the true relative risk, but when spatial variability is increased substantial bias can be seen using the ecological model in comparison to the individual model. The convolution model appears to be able to accurately estimate the risk despite also being based on a single health outcome for each day. Similar patterns are seen with different values of the distance–correlation parameter, φ, with for example the RR from the ecological model being 2.340 and 2.761 for φ = 0.1 and 10 respectively at the highest level of spatial variation (0.2). When the true RR=1.02, negligible biases are observed with the corresponding results (at σ² = 0.2) being 1.020 (φ = 0.1), 1.021 (φ = 1) and 1.021 (φ = 10).

Figure 1.

Results from fitting three models; I: Individual, E: Ecological and C: Convolution to fifty sets of simulated data for two years of daily data using varying degrees of spatial variation. In this case, the exposures used in each model are assumed to be known. Dots show the estimated relative risk from each of the simulations with vertical lines indicating the width of the corresponding 95% confidence intervals. Horizontal red lines indicate the median relative risk from each of the fifty simulation with the horizontal black line showing the ‘true’ relative risk of two.

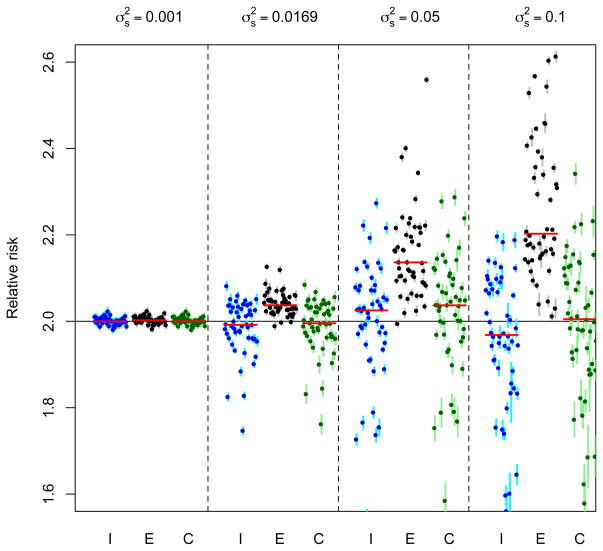
When exposures are not available at each of the sub–areas, as will be the case in analyses using real data, exposures may be estimated at the missing locations. Figure 2 shows the corresponding results to those seen in Figure 1 but where exposures were only available at a random sample of 9 of the locations with predictions for the remaining 72 areas being obtained using a spatial model as described in Section 4.3. The patterns in the medians of the RRs from the individual simulations are similar to those using known exposures, but there is a marked increase in the variability of the estimates around the medians and a reduction in the precision of the individual estimates, resulting in wider confidence intervals, suggesting that within a number of the simulations the spatial model is not able to accurately predict the exposures at the unmeasured locations. Using a larger sample of 25 sites (with predictions at the remaining 56 locations) resulted in the same patterns, although with less variability.

Figure 2.

Results from fitting three models; I: Individual, E: Ecological and C: Convolution to fifty sets of simulated data for two years of daily data using varying degrees of spatial variation. In this case, the exposures are predictions from a spatial model. Dots show the estimated relative risk from each of the simulations with vertical lines indicating the width of the corresponding 95% confidence intervals. Horizontal red lines indicate the median relative risk from each of the fifty simulation with the horizontal black line showing the ‘true’ relative risk of two.

5. Case study

5.1. Data description

We now apply the models previously described to a study of the short–term effects of particulate matter on respiratory mortality within Greater London between 1^st January 2002 and 31^st December 2005. The health data comprise daily counts of respiratory mortality in seniors (over 65 years old) which are only available in aggregate form for the entire region.

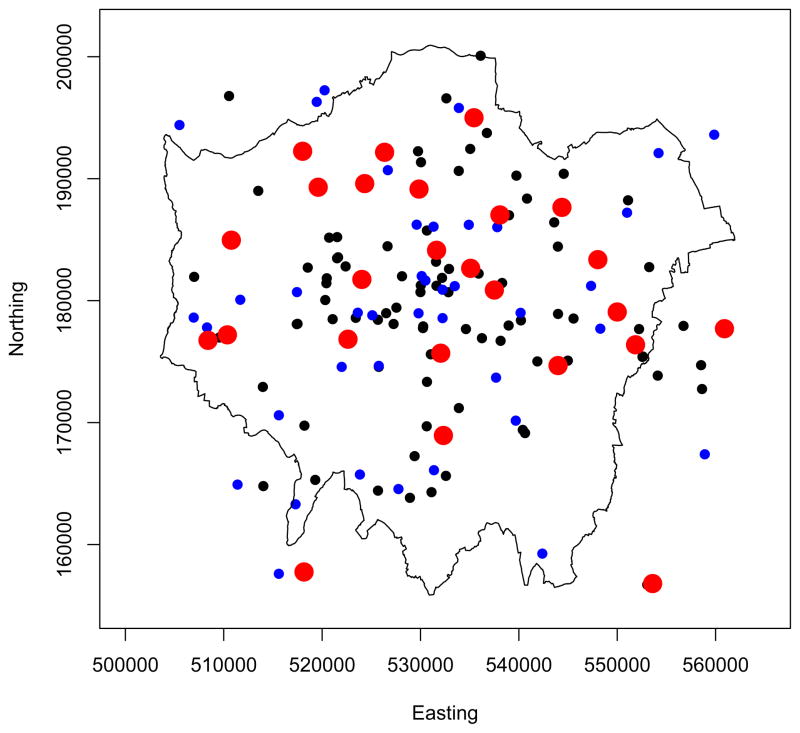
The particulate pollution data in this study are PM₁₀ (particles smaller in size than 10μgm⁻³) concentrations measured at 158 sites in the Greater London area, which include both the London Air Quality Network (LAQN) and the National Network (AURN). However these sites contain a proportion of missing observations, so we only consider the 43 of these that have over 75% of the data present over the study period. The locations of the sites and their classification according to site type can be seen in Figure 3.

Figure 3.

Locations of the pollution monitors within Greater London for the period 2002–2005. Black circles show the location of roadside sites and blue that of background sites. The larger red circles indicate the selection of background sites (with greater than 75% daily measurements) that were used in the analysis (see text for details).

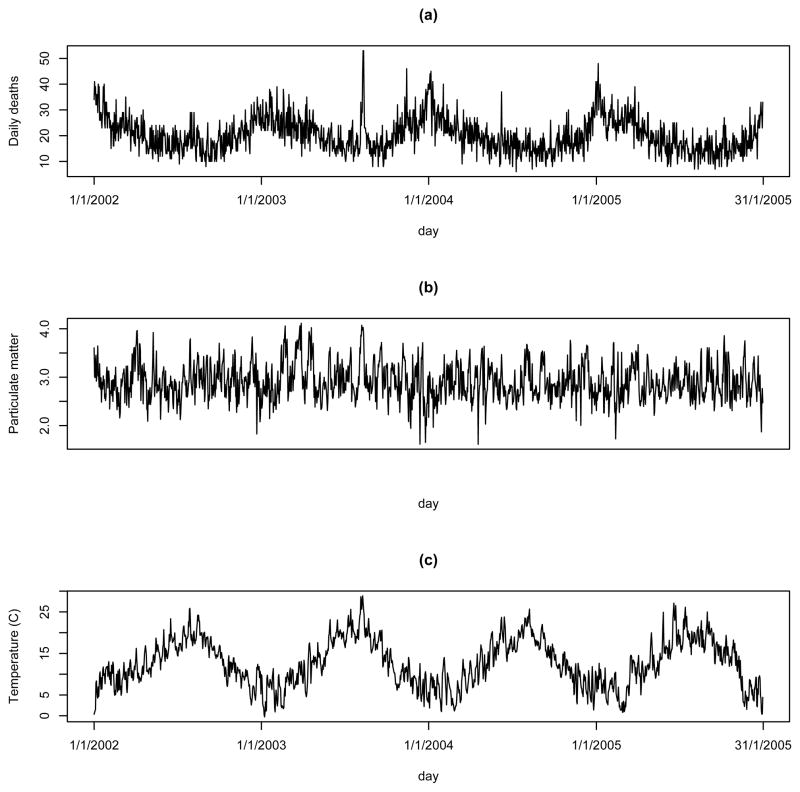
The number of daily respiratory deaths, mean daily temperature and mean, calculated via (1), PM₁₀ exposures are shown in Figure 4, and summarised in Table 2. The mortality counts show little overall trend but a pronounced yearly cycle, exhibiting more deaths in the winter than the summer, as would be expected. Daily mean temperature measurements at 49 sites across London are also available, of which 28 have more than 75% of daily data being available and are used in order to calculate a daily average temperature.

Figure 4.

Summary of data from Greater London for 2002–2005. Panel (a) depicts respiratory mortality counts, (b) shows daily average PM₁₀ concentrations, while (c) displays average temperature levels.

Table 2.

Summary of daily respiratory mortality counts, concentrations of PM₁₀ (in μgm⁻³) and temperature levels in Greater London, 2002–2005.

		Quantiles of distribution
		0%	25%	50%	75%	100%
Respiratory mortality		6	15	19	24	53
PM10	All	6.4	17.9	21.6	28.6	69.6
	Roadside	7.2	20.1	24.3	31.3	74.8
	Background	5.7	15.2	18.7	25.3	64.9
Temperature		−0.9	7.8	12.0	17.2	28.9

Of the 43 monitoring sites that are considered here 16 are roadside sites (roadside or kerbside) which are likely to have higher concentrations as they are closer to the major pollution source (traffic). This can be seen from Table 2 which shows that the average concentrations are 24.3 for roadside sites compared with 18.7 for background sites. They are also less likely to be an accurate reffection of the exposures experienced by members of the study population. Therefore, we use data from the 27 of these sites which are classified as background sites (urban background or suburban).

5.2. Results

5.2.1. Ecological model

The basic model commonly used to analyse data of this sort is the ecological model with a single health count and exposure measure for each day, together with daily covariate information such as temperature. The basic premise of such models is to allow for long–term patterns in mortality and covariate effects before assigning any remaining (temporal) variation in mortality to short–term changes in pollution. The underlying trend and seasonal pattern in the mortality data were modelled by a natural cubic spline of time (i.e., day of the study), where the choice of smoothing parameter was informed by the BIC and plots of the autocorrelation and partial autocorrelation functions of the residuals. The smoother this pattern, the more of the variation is left to be explained by pollution whereas if the underlying temporal pattern is allowed to follow the data too closely, i.e. overfitting, then any effect of pollution is likely to be masked. This resulted in a choice of 32 df in total (8 per year). Temperature has been shown to be an important confounder in these studies (see, Dominici et al. (2002); Carder et al. (2008)), and the shape of its relationship with respiratory mortality, as well as whether it should be lagged, was investigated. Based on the BIC a lag of zero days was chosen, with the relationship being represented by a natural cubic spline with three degrees of freedom. This final set of covariates produced residuals with little temporal correlation or structure, suggesting the model is an adequate fit to the data.

There is likely to be a lag in the effect of pollution, i.e. an increase in pollution may be associated with an increase in mortality after a few days or it may be that it is the combined effect of high pollution over a short period that results in increased mortality. Table 1 shows the results of fitting a series of ecological models with 0, 1, 2 and 3 day lags and with the average of lags 1–3. Significant increases in risk are observed for lags of 0, 1 and 3 days with the largest risk being associated with the average of the previous 1–3 days.

Table 1.

Relative risks (RR) per 10 μgm⁻³ with associated 95% confidence intervals (CI) from fitting models with different lags of exposure and the average of the previous three days. Data from Greater London, 2002–2005

Lag	Exposure	RR	95% CI
0	Xt	1.017	1.001 – 1.034
1	Xt−1	1.021	1.005 – 1.038
2	Xt−2	1.020	1.004 – 1.036
3	Xt−3	1.013	0.997 – 1.029
avg. 1–3	${\sum }_{i=l}^3{X}_{t-l}/3$	1.030	1.010 – 1.050

5.2.2. Convolution model

It is not possible to fit the individual model for this real data example as health and exposure data are not available at a suitable level of disaggregation. However, it may be possible to use the convolution model if exposures can be estimated for sub-areas within which risks can be calculated and then aggregated to the level of the overall study region. As in the simulation examples, we assume that London is made up of 9 × 9 grid and we use the available monitoring information to obtain predictions at the centre of each of the cells assuming an underlying GRF with an exponential correlation–distance model. The parameters of the model were estimated to be σ̂² = 0.03 and φ̂= 0.09, the latter corresponding to a drop in correlation over 10km to approximately 0.4.

Using the average of the pollution levels over lags 1–3 resulted in a significant RR of 1.025 (95% CI 1.000 – 1.050). The RR is slightly smaller with a wider CI than using the ecological model which, although using exposure information at a lower resolution, is based on oserved data. The RR in this case may also be affected by possible misspecification of the spatial model or the number of sub-areas which are used in the aggregation of the risks. Table 3 shows the results from running the same analysis with different numbers of cells at which predictions are made and also the effects of misspecifying the spatial model. Results are given for models using 3 × 3, 5 × 5, 9 × 9 and 20 × 20 cells and for different values of the correlation–distance parameter; φ = 0.09, 1, 10). The results appear robust to the choice of the distance–correlation parameter which is a reffection on the fact that the pollution surface (from background sites) in London is relatively spatially homogeneous. Wider confidence intervals are observed with the smaller number of cells as there are smaller numbers on which to base the estimation. When using 400 cells, the risk is very close to that observed when using 81 when φ = 0.09 (based on the data), but for larger values of φ, which result in a more rapid decrease in correlation over distance and thus allow greater contrast in the exposures an increase in risk can be seen.

Table 3.

Sensitivity to number of cells used in exposure modelling and misspecification of the distance–correlation parameter, φ. Relative risks (RR) per 10 μgm⁻³ PM₁₀ are shown together with associated 95% confidence intervals (CI).

Number of cells	φ = 0.09		φ = 1		φ = 10
	RR	95% CI	RR	95% CI	RR	95% CI
9	1.017	(0.990–1.046)	1.017	(0.990–1.046)	1.017	(0.990–1.046)
25	1.012	(0.987–1.039)	1.012	(0.987–1.039)	1.012	(0.987–1.039)
81	1.025	(1.000–1.050)	1.024	(1.000–1.049)	1.026	(1.001–1.051)
400	1.027	(1.003–1.052)	1.040	(1.014–1.065)	1.039	(1.014–1.064)

6. Discussion

In this paper we have considered the potential for bias in epidemiological analyses that may arise as a result of using aggregate level health data to assess the relationship with exposures which arise from point locations. In the case of studies of the short–term effects of air pollution this may arise by taking a simple daily average of measurements made at a number of monitoring sites throughout an urban area. If there is substantial variability in the underlying spatial process of pollution then taking a simple summary measure may induce bias in the resulting estimated effects on health. Using simulation studies, we have shown that where substantial spatial variation is present, the naïve ecological model is subject to pure specification bias, but that if accurate measures of exposure can be obtained at a higher geographical resolution then a convolution model may be used which is not subject to such bias.

Wakefield and Shaddick (2006) illustrated the potential for ecological bias in area based studies where the relative risk is based on the difference in health between areas of high and low pollution. However, in comparison with such geographical analyses in short–term studies it is temporal changes in exposure that drive the relative risk and the effects of temporal variation are likely to outweigh any spatial variation. The cases of serious bias observed in the simulation studies here arose when using a very high relative risk (=2) with levels of spatial variation which may be far higher than might be expected in real data, whereas negligible bias was seen using a more realistic relative risk of 1.02. It may therefore require possibly unrealistic levels of spatial variability to produce serious levels of bias in practice.

In addition to the issues of spatial variability, there are a number of other factors that may lead to bias in estimates of the effects on health. There might be issues associated with the underlying monitoring network in that both the number and locations of the pollution monitors that will affect the accuracy of any estimates. If monitoring sites are located in areas that are expected to have high (or low) concentrations, as may be the case to assess whether guidelines and policies are being adhered to, then there may be preferential sampling and in such cases, the entire spatial surface may be over- (or under-) estimated. This will arise when the process that determines the locations of the monitoring sites and the process being modelled (concentrations) are in some ways dependent (Diggle et al., 2010).

In the case study of the effects of particulate matter on respiratory mortality in London, significant increases in risks were observed for a number of lags using the common ecological model with a relative risk of 1.030 (95% CI 1.010 – 1.050) being associated with the average of the previous three days. This used a daily mean of pollution ignoring any spatial variability in exposures. It is possible to obtain exposures at a higher resolution by using a spatial prediction model allowing the convolution model to be used. The convolution model produced very similar risks estimates to the ecological model using a variety of levels of aggregation and prediction models. The lack of sensitivity in this case arises largely from the fact that the London pollution field is relatively homogeneous and so any aggregation is unlikely to be that different from taking a daily mean. However, this may not be the case in other urban areas which may have different topology, for example areas of differing elevation or large areas of water. In such cases it will be necessary to have a dense network of monitoring sites that gives sufficient coverage of the area in order to specify a suitable spatial model. If this is not the case then estimated exposures should be used with caution.

In the examples presented here, when predictions of exposure from spatial models were used in the health model, there was no account of the inherent uncertainty in the predictions which may result in confidence intervals for the risk estimates being narrow. The focus of future research will be to combine the exposure and health modelling within a Bayesian hierarchical framework in which the such uncertainties can be correctly acknowledged within a coherent framework.